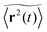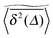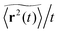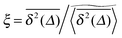Geometry controlled anomalous diffusion in random fractal geometries: looking beyond the infinite cluster
Received
19th June 2015
, Accepted 2nd October 2015
First published on 7th October 2015
Abstract
We investigate the ergodic properties of a random walker performing (anomalous) diffusion on a random fractal geometry. Extensive Monte Carlo simulations of the motion of tracer particles on an ensemble of realisations of percolation clusters are performed for a wide range of percolation densities. Single trajectories of the tracer motion are analysed to quantify the time averaged mean squared displacement (MSD) and to compare this with the ensemble averaged MSD of the particle motion. Other complementary physical observables associated with ergodicity are studied, as well. It turns out that the time averaged MSD of individual realisations exhibits non-vanishing fluctuations even in the limit of very long observation times as the percolation density approaches the critical value. This apparent non-ergodic behaviour concurs with the ergodic behaviour on the ensemble averaged level. We demonstrate how the non-vanishing fluctuations in single particle trajectories are analytically expressed in terms of the fractal dimension and the cluster size distribution of the random geometry, thus being of purely geometrical origin. Moreover, we reveal that the convergence scaling law to ergodicity, which is known to be inversely proportional to the observation time T for ergodic diffusion processes, follows a power-law ∼T−h with h < 1 due to the fractal structure of the accessible space. These results provide useful measures for differentiating the subdiffusion on random fractals from an otherwise closely related process, namely, fractional Brownian motion. Implications of our results on the analysis of single particle tracking experiments are provided.
1 Introduction
Roughly a century after Jean Perrin's groundbreaking experiments on Brownian motion using an elaborate single particle tracking method in 1908,1 nowadays sophisticated single particle tracking of submicron tracer particles and even single molecules have become a routine tool in the study of passive and active transport dynamics in living biological cells as well as in various crowded fluids in vitro.2 Distinguished from traditional ensemble averaging experiments single particle tracking enables one to directly access the diffusive properties of the tracer particles without any loss of information due to ensemble averaging. Based on the single particle tracking technique it was revealed that the tracer motion in ‘superdense’3 biological or complex environments often exhibits anomalous diffusion such that its ensemble averaged mean squared displacement (MSD) grows non-linearly with time in the formwith the anomalous diffusion exponent α. We distinguish subdiffusion for 0 < α < 1 and superdiffusion with α > 1. Examples for subdiffusion include the diffusion of messenger RNA molecules3 and lipid granules in living cells,4–7 and the motion of phospholipid molecules and proteins in the membranes of living cells or in silico membranes.8–12 As examples from in vitro systems we mention the anomalous diffusion of microbeads in polymer networks or gels13–16 and in artificially crowded media17,18 as well as colloidal suspensions.19,20 Examples for superdiffusion due to active motion in living cells were provided in ref. 21–25. Effective superdiffusion on surfaces is also observed due to bulk mediation effects.26,27
Theoretically an anomalous diffusion process characterised by the law (1) may be governed by different stochastic models, each of them underlying a unique physical process.28–30 Despite the common scaling (1) of the ensemble averaged MSD some of these processes are ergodic in the Boltzmann–Khinchin sense that the long time average of physical observables such as the MSD converges to the corresponding ensemble average while in other, weakly non-ergodic processes both kinds of averages remain disparate.28–32 One process, that was identified as stochastic mechanism behind the motion of tracers in living biological cells and structured environments is the continuous time random walk.33 Continuous time random walks give rise to weakly non-ergodic subdiffusion due to multiple binding or caging events characterised by a long-tailed distribution of waiting times between successive motion events which features a diverging mean waiting time.28,29,31 Fractional Brownian motion and the associated fractional Langevin equation describe Gaussian processes in which the power-law correlated displacements give rise to anomalous diffusion.34–40 Such self-affine Gaussian processes have a fractal path and are ergodic, and they were shown to occur in viscoelastic environments.40,41 Another popular ergodic model, which in many ways appears similar to fractional Brownian motion, are random walks on fractal structures.28–30,42,43 Fractals with their scale-free geometry were popularised by Mandelbrot in the 1980's to more closely resemble natural objects such as mountains or coastlines than do classical geometrical bodies.44 De Gennes coined the concept of ant in the labyrinth:45 random fractals such as the statistically self-similar continuum or discrete percolation models effect the subdiffusion of a random walker due to the existence of bottlenecks and cul-de-sacs on all scales.42,43,46–49 Among a variety of applications, this model was used to describe the obstructed diffusion in highly crowded random environments, for instance, the cytoplasm of cells, cell nuclei, and biological membranes.15,50–55 Recently models of mixed origins of anomalous diffusion processes were also suggested.29
Following the advances in single particle tracking techniques it has become possible to garner sufficient evidence to diagnose the statistical characteristics of a stochastic process on the single trajectory level. To identify a specific anomalous diffusion process behind observed data allows one to learn more about the physical nature of the system and predict secondary quantities such as the first passage behaviour responsible for (bio)chemical reactions.29,31,56–59 Weakly non-ergodic processes in Bouchaud's sense exhibit the above-mentioned disparity between the ensemble averaged MSD (1) and the time averaged MSD defined below, even in the limit of long measurement times. Moreover, these processes exhibit ageing, the dependence of observables on the time span between initiation of the process and start of the measurement, and the amplitude of individual time averages fluctuates significantly. This behaviour is shared by continuous time random walks31,60–64 and its variants65–67 as well as heterogeneous diffusion processes with space dependent diffusivity.68–70 In contrast, stochastic motion driven by power-law correlated Gaussian noise and the random motion on fractals are the key ergodic anomalous diffusion processes.29,71 Another class of weakly non-ergodic processes corresponds to scaled Brownian motion with a power-law time dependent noise strength.72–75 It is known that the discrimination between them based on data analysis is challenging, as both models share the same asymptotic scaling behaviour of the velocity autocorrelation functions.76 Theoretical tests differentiating the two were recently proposed on the ground that the fractal dimension—or the number of visited sites—is smaller than the dimensionality of the embedding Euclidean space—or the total number of sites in space.56,77 We here explore in more detail the exact ergodic properties of de Gennes' random ant-in-the-labyrinth motion. Specifically, we analyse the single particle diffusion on two-dimensional percolation clusters at varying densities. Special emphasis is put on the ergodic properties of the motion revealed by the time averaged MSD. Remarkably, our simulations reveal that the fluctuations in the time averaged MSD have a unique statistical feature of geometrical origin which is significantly different from that of fractional Brownian motion.
This paper is organised as follows. In Section 2 we gather the information on the simulation procedure, the definitions of the averaging procedures used in our analysis, and the well known diffusion dynamics on percolation clusters in the framework of ensemble averages. In Section 3 we present our simulation results on the single trajectory level including the time averaged MSD, the amplitude scatter distribution of the time averaged MSD, and the ergodicity breaking parameter. In particular, we analyse the rôle of clusters other than the infinite cluster. In Section 4 we discuss our results and conclude.
2 Methods
2.1 Simulation scheme
Our study is based on a two-dimensional square lattice with periodic boundary conditions, as commonly used in other studies.50,77,78 On this underlying structure we generate our random percolation environments. The system size varies depending on the load of the simulations. For instance, to simulate individual trajectories for analysis in terms of the time averaged MSD a lattice of 4096 × 4096 is considered whereas in more computationally expensive simulations such as labelling clusters with different sizes, the lattice size is set to 1024 × 1024. Each site is either filled with probability p or vacant with probability 1 − p. Here we follow the convention that p refers to the obstacle density in space.50
Percolation theory states that as the percolation density p approaches the critical value pc from above—that is for decreasing obstacle size—separated finite clusters merge and the correlation length ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) of clusters diverges as
of clusters diverges as ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ∼ |p − pc|−ν with ν = 5/36.48 At the percolation threshold pc and for lower obstacle densities p < pc there exists an infinite cluster of empty sites spanning the entire volume.42,48 The probability that a given site belongs to the infinite cluster at criticality scales as P∞ ∼ (p − pc)β where β = 43/18.42,48 Concurrently as p → pc the crossover length rc from anomalous to normal diffusion used below diverges as rc ∼ |p − pc|−ν+β/2. Thus at p = pc anomalous diffusion of the form (1) prevails at all times.42,48,50 Simultaneously the percolation geometry forms scale-free fractal objects over all length scales larger than the lattice constant.42,48,50,79
∼ |p − pc|−ν with ν = 5/36.48 At the percolation threshold pc and for lower obstacle densities p < pc there exists an infinite cluster of empty sites spanning the entire volume.42,48 The probability that a given site belongs to the infinite cluster at criticality scales as P∞ ∼ (p − pc)β where β = 43/18.42,48 Concurrently as p → pc the crossover length rc from anomalous to normal diffusion used below diverges as rc ∼ |p − pc|−ν+β/2. Thus at p = pc anomalous diffusion of the form (1) prevails at all times.42,48,50 Simultaneously the percolation geometry forms scale-free fractal objects over all length scales larger than the lattice constant.42,48,50,79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡ For obstacle percolation considered here the critical percolation threshold is pc = 0.407256.48
‡ For obstacle percolation considered here the critical percolation threshold is pc = 0.407256.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) § This critical case is depicted in Fig. 1.
§ This critical case is depicted in Fig. 1.
 |
| | Fig. 1 Sample realisation of a random percolation geometry at the percolation threshold p = pc on a square lattice of size 1024 × 1024. The copper coloured structure representing the vacant sites of an infinite cluster accessible to the random walker constitutes a statistically scale-free, fractal object. | |
In our simulations, after a random geometry with label ζ of given density p is generated a tracer particle starts to diffuse at its centre if it is vacant. Otherwise a randomly chosen vacant site close to the centre is chosen. In our Monte Carlo simulation, at every unit time step δt = 1 the tracer particle jumps to the nearest vacant site with probability 1/4 on our two-dimensional lattice. Uniform random numbers were generated by the  function taken from Numerical Recipes.81 On an isolated unit cluster no move is allowed and the random walker becomes completely localised. In the limit of p → 0 the diffusivity of the tracer particle is that of a free two-dimensional lattice,
function taken from Numerical Recipes.81 On an isolated unit cluster no move is allowed and the random walker becomes completely localised. In the limit of p → 0 the diffusivity of the tracer particle is that of a free two-dimensional lattice, 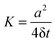 where a is the lattice constant. Our typical simulation time was 106 time steps, unless indicated otherwise. For the evaluation of physical observables Nζ random percolation geometries were generated at a given percolation density p, and N tracer trajectories for each percolation geometry were recorded. For the efficiency of the simulation study, the number Nζ was varied from 50 to 10
where a is the lattice constant. Our typical simulation time was 106 time steps, unless indicated otherwise. For the evaluation of physical observables Nζ random percolation geometries were generated at a given percolation density p, and N tracer trajectories for each percolation geometry were recorded. For the efficiency of the simulation study, the number Nζ was varied from 50 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and N from 3 to 1000 depending on the observables. In each case sufficiently large samples were chosen to ensure a proper statistical convergence. Information on Nζ and N used in the evaluation of each observable are provided in the text and in the figure captions.
000 and N from 3 to 1000 depending on the observables. In each case sufficiently large samples were chosen to ensure a proper statistical convergence. Information on Nζ and N used in the evaluation of each observable are provided in the text and in the figure captions.
2.2 Ensemble averaged mean square displacement
Let us first address the potential ambiguity in defining ensemble averages in percolation systems.42 For a given fractal geometry ζ the MSD of an ensemble of particles starting at the origin at time t = 0 is given by| | 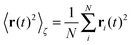 | (2) |
where we choose the coordinate systems such that ri(0) = 0. The MSD 〈r(t)2〉ζ will in general assume different values for different realisations ζ.¶ To avoid the dependence on the specific realisation, an additional (disorder) average of the form| | 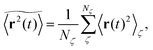 | (3) |
is defined, where Nζ counts the different realisation ζ over which the average is taken. In what follows we refer to this quantity as the ensemble averaged MSD. We note that we did not average over initial positions for a given realisation ζ, however, we expect this averaging to be equivalent to the disorder averaging over different ζ. We also note that similar questions on the averaging arise in the analysis of diffusion in quenched energy landscapes.82
Prior to our study of single trajectories below we here briefly summarise the ensemble averaged MSD for particles diffusing in percolation geometries, and we compare these results with our current Monte Carlo simulation. The ensemble averaged MSD has two distinct scaling regimes over time for percolation densities below the percolation threshold pc, namely42,43,47,48,50
| | 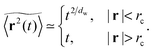 | (4) |
Thus, the diffusion is transiently anomalous below the crossover length
rc(
p), corresponding to times shorter than the crossover time
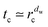
. Here the classical notation involves the walk dimension
dw of the diffusing particle. Generally
dw > 2 implying subdiffusion with 0 <
α = 2/
dw < 1. In the simplest case when we have no obstacles (
p = 0) all sites are accessible to the random walker and we have normal diffusion at all times. In this case the crossover length
rc vanishes. This case is shown in
Fig. 2(a). At finite percolation densities below the percolation threshold, 0 <
p <
pc, the crossover length roughly corresponds to the average cluster size of locally fractal structures: local bottlenecks and cul-de-sacs generate anomalous diffusion, which eventually crosses over to normal diffusion when the typical distance travelled by the random walker exceeds
rc. This case is shown in
Fig. 2(b). We note that compared to the obstacle-free case
p = 0, the effective diffusion coefficient in the case 0 <
p <
pc has a reduced value. At the percolation threshold
p =
pc ≈ 0.407256 the percolation geometry is fractal on all available scales, and the crossover length
rc diverges. Concurrently, the anomalous diffusion regime ranges over all time scales.
|| For the square lattice the anomalous diffusion exponent is 2/
dw ≈ 0.7,
50 which is again confirmed by our simulations, see
Fig. 2. Indeed,
Fig. 2(c) documents the anomalous diffusion at criticality. Anomalous diffusion in effectively two dimensional geometries was indeed verified by NMR measurements in computer generated percolation clusters milled into stacked plastic sheets.
83,84 Above the percolation threshold the diffusion is more and more reduced. In particular, only finite, disjunct clusters remain such that the MSD eventually saturates to a plateau, see
Fig. 2(d).
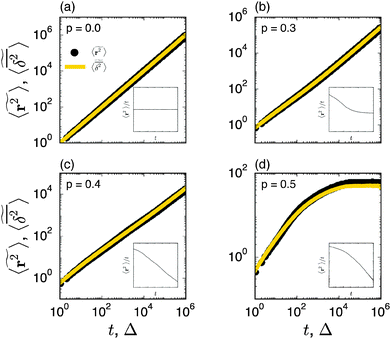 |
| | Fig. 2 Ensemble averaged MSD  (black circles) and mean time averaged MSD (black circles) and mean time averaged MSD 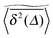 (yellow solid line) for four different percolation densities: (a) p = 0, (b) p < pc, (c) p ≈ pc, and (d) p > pc. In each panel the inset depicts (yellow solid line) for four different percolation densities: (a) p = 0, (b) p < pc, (c) p ≈ pc, and (d) p > pc. In each panel the inset depicts 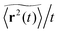 versus t on a double logarithmic scale, the slope is α − 1. Note the terminal Brownian scaling for p < pc with a reduced diffusivity for the finite percolation density (b). The numbers of the random geometries and trajectories used for the plot are Nζ = 50 and N = 1000. versus t on a double logarithmic scale, the slope is α − 1. Note the terminal Brownian scaling for p < pc with a reduced diffusivity for the finite percolation density (b). The numbers of the random geometries and trajectories used for the plot are Nζ = 50 and N = 1000. | |
3 Probing the ergodic behaviour of diffusion on percolation geometries
3.1 Time averaged mean squared displacement
To explore the ergodic properties of the diffusion process on percolation clusters in addition to the ensemble averaged MSD we now consider the time averaged MSD defined in terms of the moving average| | 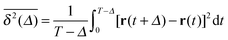 | (5) |
of a single trajectory r(t).28,29,31 Here Δ is the lag time corresponding to the width of the window slid along the time series, and T is the total observation (measurement) time. The time averaged MSD (5) provides information on the diffusive properties of a single particle and is routinely applied to evaluate experimental single particle tracking data. Typically diffusive processes, that are ergodic in the Boltzmann–Khinchin sense, have the property that for sufficiently long observation times T (formally, T → ∞), the time and ensemble averaged MSDs converge to each other,| | 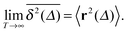 | (6) |
In agreement with previous numerical studies,77 our simulations indeed demonstrate that this ergodicity relation is satisfied for our random walker on the percolation geometry for any percolation density if we average the time averaged MSD over both N individual simulated trajectories (index i) and over an ensemble of Nζ percolation geometries ζ,| | 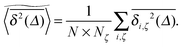 | (7) |
As seen in Fig. 2, this mean time averaged MSD—represented by the yellow solid line—coincides with the ensemble averaged MSD (black circles) for all cases. The equivalence between the two quantities for Nζ = 50 is not significantly improved when the sample size is increased tenfold to Nζ = 500 (not shown).
However, the equality between the ensemble averaged MSD (7) and individual long time averaged MSDs is not always fulfilled. To demonstrate this fact we show in Fig. 3 individual time averaged MSD traces 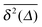 along with the ensemble average
along with the ensemble average 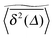 (black solid line) from Fig. 2. As long as p < pc the individual
(black solid line) from Fig. 2. As long as p < pc the individual 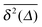 follow nicely the mean
follow nicely the mean 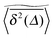 except for long lag times Δ ≈ T when the statistic for the time averaging becomes insufficient (Fig. 3(a) and (b)). In this case the cluster turns from a fully accessible two-dimensional lattice at p = 0 to a geometry with growing but localised clusters of obstacles at 0 < p < pc. The connectivity remains high such that, independent of the initial position, eventually the random walker explores the entire structure, apart from inaccessible areas of sufficiently small measure. Right at the percolation threshold p = pc shown in Fig. 3(c) we already observe significant deviations from the mean
except for long lag times Δ ≈ T when the statistic for the time averaging becomes insufficient (Fig. 3(a) and (b)). In this case the cluster turns from a fully accessible two-dimensional lattice at p = 0 to a geometry with growing but localised clusters of obstacles at 0 < p < pc. The connectivity remains high such that, independent of the initial position, eventually the random walker explores the entire structure, apart from inaccessible areas of sufficiently small measure. Right at the percolation threshold p = pc shown in Fig. 3(c) we already observe significant deviations from the mean 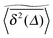 : a smaller number of traces
: a smaller number of traces 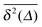 show confinement leading
show confinement leading 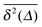 to enter a plateau much earlier than the crossover time of
to enter a plateau much earlier than the crossover time of 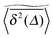 . This is due to the fact that at criticality, when the percolation geometry is fractal, the size of the accessible regions is scale-free and finite accessible clusters of all sizes are created in addition to the incipient infinite cluster. When seeded on such a finite cluster the time averaged MSD of the emanating trajectory will show a plateau depending on the very size of the visited cluster. We thus encounter a non-ergodic scenario in which the irreproducibility of trajectories stems from the quenched geometry. This non-ergodic behaviour is strengthened above the percolation threshold, p > pc, as shown in Fig. 3(d). Individual traces
. This is due to the fact that at criticality, when the percolation geometry is fractal, the size of the accessible regions is scale-free and finite accessible clusters of all sizes are created in addition to the incipient infinite cluster. When seeded on such a finite cluster the time averaged MSD of the emanating trajectory will show a plateau depending on the very size of the visited cluster. We thus encounter a non-ergodic scenario in which the irreproducibility of trajectories stems from the quenched geometry. This non-ergodic behaviour is strengthened above the percolation threshold, p > pc, as shown in Fig. 3(d). Individual traces 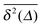 exhibit a pronounced scatter around the average
exhibit a pronounced scatter around the average 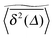 . In the sense of Bouchaud's definition32 the fact that once seeded on a specific cluster the random walker cannot pass to an unconnected cluster is referred to as strong ergodicity breaking. It denotes the case when the phase space of a system consists of disjoint subvolumes and access to each subvolume is determined by the initial position of the particle. It is intrinsic for the percolation system in that it is reproducible when simulations are performed with the same number of runs for given trajectory length T. Moreover, a typical scatter of amplitudes of the plateaus always occurs at any trajectory length T. It is in fact noteworthy that albeit these features of individual tracer motion the ensemble average remains ergodic within the error of our simulations.
. In the sense of Bouchaud's definition32 the fact that once seeded on a specific cluster the random walker cannot pass to an unconnected cluster is referred to as strong ergodicity breaking. It denotes the case when the phase space of a system consists of disjoint subvolumes and access to each subvolume is determined by the initial position of the particle. It is intrinsic for the percolation system in that it is reproducible when simulations are performed with the same number of runs for given trajectory length T. Moreover, a typical scatter of amplitudes of the plateaus always occurs at any trajectory length T. It is in fact noteworthy that albeit these features of individual tracer motion the ensemble average remains ergodic within the error of our simulations.
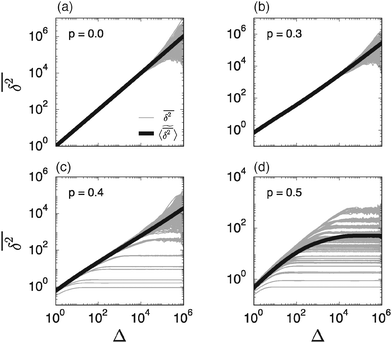 |
| | Fig. 3 Individual time averaged MSD curves 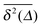 and their mean and their mean 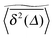 (thick black curve, as already shown in Fig. 2). In each panel the variation of the individual time averaged MSD curves represents 10 different trajectories on each of the overall 50 different simulated percolation geometries. (thick black curve, as already shown in Fig. 2). In each panel the variation of the individual time averaged MSD curves represents 10 different trajectories on each of the overall 50 different simulated percolation geometries. | |
Subdiffusive continuous time random walks31,60,65,67,85,86 show ageing in the sense that the particle encounters longer and longer waiting times on its motion due to the scale free nature of the distribution of waiting times. The amplitude of the time averaged MSD given by the effective diffusivity therefore becomes a decaying function of the observation time T. Analogous ageing effects occur for scaled Brownian motion,87 heterogeneous diffusion processes,68 and their combination. Apart from transient ageing88 the Gaussian processes with correlated increments of the fractional Brownian motion and fractional Langevin equation motion types do not exhibit such effects.9 In Fig. 4 we analyse the dependence of the time averaged MSD on the observation time T using the data from Fig. 3 for fixed lag time Δ = 100. As can be seen no significant ageing can be detected, the traces settle towards a constant function of T. The figure also illustrates the relatively small amplitude scatter below and at the percolation threshold, p ≤ pc, as compared to the behaviour at the higher percolation density, p > pc.
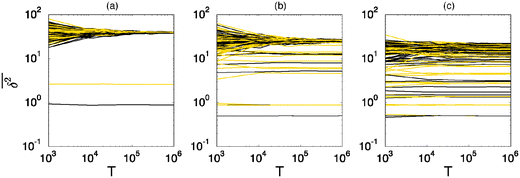 |
| | Fig. 4 Time averaged MSD curves 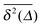 at fixed lag time Δ as a function of the observation time T for Nζ = 2000 and N = 3. We here plot the same data as in Fig. 3, for (a) p = 0.3, (b) 0.4, and (c) 0.5. For all cases Δ = 100 was chosen. No significant dependence on T is visible for any sufficiently small value of Δ/T. The distinct, much lower lines in (a) corresponds to a very rare case of confinement. These cases become increasingly likely in (b) and (c). at fixed lag time Δ as a function of the observation time T for Nζ = 2000 and N = 3. We here plot the same data as in Fig. 3, for (a) p = 0.3, (b) 0.4, and (c) 0.5. For all cases Δ = 100 was chosen. No significant dependence on T is visible for any sufficiently small value of Δ/T. The distinct, much lower lines in (a) corresponds to a very rare case of confinement. These cases become increasingly likely in (b) and (c). | |
3.2 Time averaged occupation probability
To gather more quantitative clues on the above observations of the time averaged MSD we determine the profile of individual time averaged MSDs and explore how it is related to the particles' random paths on a given percolation geometry ζ. To this end we introduce the time averaged occupation probability 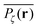 at the lattice point r for a given fractal geometry ζ in the form
at the lattice point r for a given fractal geometry ζ in the form| | 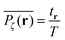 | (8) |
where tr is the accumulated residence time of the particle at the lattice site r averaged over the observation time T.
Fig. 5 presents typical patterns of the time average 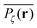 obtained from simulations with N = 104. For the fully accessible two-dimensional lattice (p = 0) the time averaged occupation probability is smoothly spread out from the origin with a uniform radial distribution of bell shape. This is a typically expected result for Brownian motion as well as for other ergodic processes in which the ensemble averaged occupation probability 〈Pζ(r)〉 is identical with its time averaged counterpart. This case is shown in Fig. 5(a). For growing percolation densities below the percolation threshold we therefore observe similar patterns, albeit local fine structure will appear due to the existence of a finite correlation range of obstacles measured by the radius rc introduced above. In particular, growing p will increasingly limit the accessible range for the random walker, that is, the occupation probability at finite T will decay faster from the initial position. At the percolation threshold p = pc the pattern of the time averaged occupation probability
obtained from simulations with N = 104. For the fully accessible two-dimensional lattice (p = 0) the time averaged occupation probability is smoothly spread out from the origin with a uniform radial distribution of bell shape. This is a typically expected result for Brownian motion as well as for other ergodic processes in which the ensemble averaged occupation probability 〈Pζ(r)〉 is identical with its time averaged counterpart. This case is shown in Fig. 5(a). For growing percolation densities below the percolation threshold we therefore observe similar patterns, albeit local fine structure will appear due to the existence of a finite correlation range of obstacles measured by the radius rc introduced above. In particular, growing p will increasingly limit the accessible range for the random walker, that is, the occupation probability at finite T will decay faster from the initial position. At the percolation threshold p = pc the pattern of the time averaged occupation probability 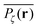 exhibits a structural fingerprint of the specific underlying fractal geometry. Interestingly, we find that
exhibits a structural fingerprint of the specific underlying fractal geometry. Interestingly, we find that 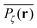 may assume two distinct patterns at the percolation threshold. Thus, while Fig. 5(b) reveals an emerging fractal spreading pattern, Fig. 5(c) shows a uniform distribution within a localised region—note the different scales of the panels. How can this come about? This phenomenon is again related to the fractal nature of the percolation geometry at criticality. In the former case, the tracer particle diffuses on the infinite incipient fractal cluster of vacant sites whose linear size is only limited by the size of the simulated lattice. Thus the corresponding time averaged MSD exhibits the anomalous scaling law (1) and the ergodic property
may assume two distinct patterns at the percolation threshold. Thus, while Fig. 5(b) reveals an emerging fractal spreading pattern, Fig. 5(c) shows a uniform distribution within a localised region—note the different scales of the panels. How can this come about? This phenomenon is again related to the fractal nature of the percolation geometry at criticality. In the former case, the tracer particle diffuses on the infinite incipient fractal cluster of vacant sites whose linear size is only limited by the size of the simulated lattice. Thus the corresponding time averaged MSD exhibits the anomalous scaling law (1) and the ergodic property 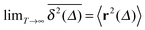 is satisfied.77 The quantity
is satisfied.77 The quantity 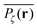 also provides information on how the tracer particle diffuses away from its starting site. It is noteworthy that the spatial gradient of
also provides information on how the tracer particle diffuses away from its starting site. It is noteworthy that the spatial gradient of 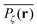 has no obvious discontinuous shape. This means that there are no sites at which the particle is significantly trapped for much longer times than at other neighbouring sites. In contrast to this, the latter case corresponding to Fig. 5(c) represents the case in which over the observation time T the particle visits repeatedly a small range of sites. These are either extremely poorly connected to the infinite cluster or completely separated. Accordingly the corresponding time averaged MSD saturates (outset). As seen in our previous analysis above the percentage of such complete confinement is relatively low compared to the situation above the percolation threshold. In the latter case p > pc confinement will always occur, as no infinite cluster of vacant sites remains. Patterns such as those shown in Fig. 5(c) will then emerge for clusters of varying size. On average clusters of decreasing size emerge when p is increased (not shown).
has no obvious discontinuous shape. This means that there are no sites at which the particle is significantly trapped for much longer times than at other neighbouring sites. In contrast to this, the latter case corresponding to Fig. 5(c) represents the case in which over the observation time T the particle visits repeatedly a small range of sites. These are either extremely poorly connected to the infinite cluster or completely separated. Accordingly the corresponding time averaged MSD saturates (outset). As seen in our previous analysis above the percentage of such complete confinement is relatively low compared to the situation above the percolation threshold. In the latter case p > pc confinement will always occur, as no infinite cluster of vacant sites remains. Patterns such as those shown in Fig. 5(c) will then emerge for clusters of varying size. On average clusters of decreasing size emerge when p is increased (not shown).
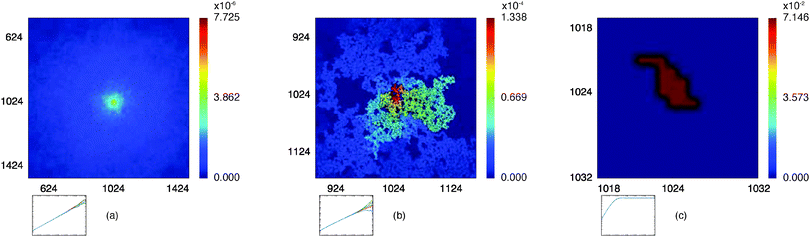 |
| | Fig. 5 Time averaged occupation probability 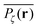 , eqn (8), distributed over three given percolation geometries. This quantity is sampled from an ensemble of 104 particle traces on the same percolation geometry ζ starting from the same initial site. We show results for a two-dimensional lattice corresponding to (a) p = 0.1, (b) at the percolation threshold with p = pc with an emerging fractal pattern, and (c) at the percolation threshold with a localised pattern. The outsets show examples of the corresponding time averaged MSD curves for those particles. , eqn (8), distributed over three given percolation geometries. This quantity is sampled from an ensemble of 104 particle traces on the same percolation geometry ζ starting from the same initial site. We show results for a two-dimensional lattice corresponding to (a) p = 0.1, (b) at the percolation threshold with p = pc with an emerging fractal pattern, and (c) at the percolation threshold with a localised pattern. The outsets show examples of the corresponding time averaged MSD curves for those particles. | |
3.3 Amplitude scatter distribution
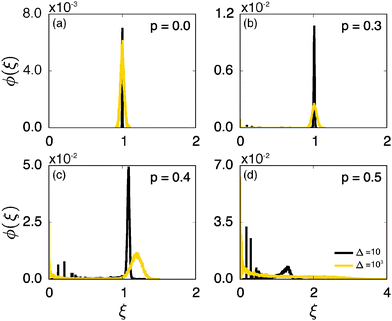
We now quantify the amplitude fluctuations of individual time averaged MSDs seen in Fig. 3 by measuring the normalised distribution ϕ(ξ) as functions of the lag time Δ and the observation time T in terms of the dimensionless variable28,29,60,89| | 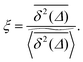 | (9) |
Fig. 6 shows the variation of the scatter distribution ϕ(ξ) at two different values of Δ and for fixed T = 106. As anticipated from the time averaged MSD traces in Fig. 3 the distribution for p < pc represented by Fig. 3(a) and (b), has a narrow, bell-shaped form. Its centre is located at the ergodic value ξ = 1, and the width becomes broader at larger lag times. This is a typical behaviour for ergodic diffusion.89 At and above the percolation threshold p ≥ pc this behaviour changes drastically, and the scatter distribution reveals unique features that are not expected from an ergodic diffusion process, nor are these features known from other weakly non-ergodic processes. Consider first the longer lag time Δ = 103 at p = pc. We first observe an additional peak showing up at around ξ = 0 (Fig. 6(c)). This means that there is a finite contribution from traces in which the particles undergo severely confined diffusion on finite clusters of vacant sites. This peak corresponds to the localised and uniformly distributed time averaged occupation probabilities 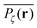 shown in Fig. 5(c). Note that this peak at ξ = 0 is not a statistical error due to an insufficient number of simulation runs. Our further investigation demonstrates that this peak is still observed in larger simulation sets. Second, the position of the main peak is shifted to a larger value above ξ = 1 while the bell-shaped profile is preserved. For the shorter lag time Δ = 10 the shift is less severe, however, one can distinguish a fine structure of different peaks for ξ values closer to zero. These correspond to clusters of different size, which can be resolved here when the overall values of the MSD are smaller.
shown in Fig. 5(c). Note that this peak at ξ = 0 is not a statistical error due to an insufficient number of simulation runs. Our further investigation demonstrates that this peak is still observed in larger simulation sets. Second, the position of the main peak is shifted to a larger value above ξ = 1 while the bell-shaped profile is preserved. For the shorter lag time Δ = 10 the shift is less severe, however, one can distinguish a fine structure of different peaks for ξ values closer to zero. These correspond to clusters of different size, which can be resolved here when the overall values of the MSD are smaller.
 |
| | Fig. 6 Normalised scatter distribution ϕ(ξ) as function of the dimensionless variable 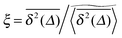 for four different percolation densities. In each panel the curves represent ϕ(ξ) for the lag times Δ = 10 (black) and 103 (yellow), each obtained from 30 for four different percolation densities. In each panel the curves represent ϕ(ξ) for the lag times Δ = 10 (black) and 103 (yellow), each obtained from 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation runs corresponding to Nζ = 10 000 simulation runs corresponding to Nζ = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random geometries and N = 3 different trajectories performed on each geometry. Each single run is of length T = 106. 000 random geometries and N = 3 different trajectories performed on each geometry. Each single run is of length T = 106. | |
Remarkably, when the percolation density exceeds the critical value pc the profile of ϕ(ξ) changes again significantly. In this overcrowded situation vacant sites exist in the form of finite clusters, forcing the tracer particles to undergo confined diffusion. At the shorter lag time, over which the tracer's motion is not seriously hampered by confinement corresponding to Fig. 6(d) at Δ = 10, the distribution ϕ has a dominant contribution at ξ ≈ 1. Concurrently, several peaks close to ξ = 0 reveal again a distribution of cluster sizes. However, at longer lag times the main peak disappears, and the distribution is monotonically decreasing with ξ: localised motion becomes dominant for the statistic.
In Fig. 7 we investigate the variation of the scatter distribution at the percolation threshold, p = pc with changing observation times T for fixed lag time. It shows that the position of the main peak remains largely unchanged while the peak gets increasingly sharper as T is increased. In contrast the height and width of the peak at ξ ≈ 0 is quite insensitive to T. Naively speaking this population splitting of different trajectories into a distribution around ergodic motion ξ = 1 and an almost immobile fraction again results from the coexistence of the two distinct diffusion modes induced by the geometry: unrestricted motion on large (infinite) clusters and confined diffusion on small, finite clusters. The propensities of occurrence depend on the lag time Δ as well as the percolation density p. At criticality both modes are significant. We note that this behaviour is a geometry controlled analogue of the dynamic population splitting into mobile and immobile particles in subdiffusive continuous time random walks85,86 and heterogeneous diffusion processes.90
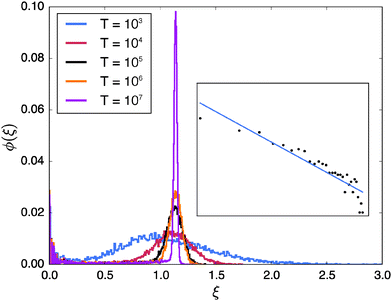 |
| | Fig. 7 Dependence of the scatter distribution ϕ(ξ) on the observation time T at the percolation threshold p = pc and for the lag time Δ = 102. Each distribution was obtained from 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sample trajectories. The inset shows the double-logarithmic plot of the part of the scatter distribution at small ξ for T = 106. The straight line is a fit with the power-law function x−b, see text. 000 sample trajectories. The inset shows the double-logarithmic plot of the part of the scatter distribution at small ξ for T = 106. The straight line is a fit with the power-law function x−b, see text. | |
Let us spin this idea forward with some analytical considerations based on the cluster size (area) distribution (s). Imagine the situation in which a random walker moves on a finite cluster of size s and radius of gyration 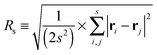 .48 In the limit of sufficiently long trajectories (T → ∞) and for lag times Δ ≥ Δs, where Δs is implicitly defined by the equivalence
.48 In the limit of sufficiently long trajectories (T → ∞) and for lag times Δ ≥ Δs, where Δs is implicitly defined by the equivalence 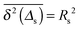 of the time averaged MSD and the squared gyration radius, the time averaged MSD is saturated to the value
of the time averaged MSD and the squared gyration radius, the time averaged MSD is saturated to the value 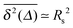 . As the cluster appears fractal on length scales smaller than Rs, it can be reasonably assumed that the size of the cluster is
. As the cluster appears fractal on length scales smaller than Rs, it can be reasonably assumed that the size of the cluster is 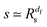 close to the percolation threshold, where df is the fractal dimension. We then relate the distribution of the saturation value of the time averaged MSD to the cluster size distribution
close to the percolation threshold, where df is the fractal dimension. We then relate the distribution of the saturation value of the time averaged MSD to the cluster size distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) in terms of
(s) in terms of
| | 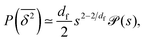 | (10) |
where we used that
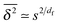
omitting a proportionality constant. Given this latter scaling relation between the saturation value of the time averaged MSD and the size of a cluster, we can use both quantities interchangeably.
Now assume that there are N long (T → ∞) trajectories of tracer particles that performed a random walk on a randomly generated fractal cluster and have a value 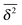 governed by the distribution P. At a given finite lag time Δ, a tracer particle will perform anomalous diffusion of the form
governed by the distribution P. At a given finite lag time Δ, a tracer particle will perform anomalous diffusion of the form 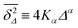 as long as the walker has not yet fully sampled the cluster of size s or, equivalently, the time averaged MSD
as long as the walker has not yet fully sampled the cluster of size s or, equivalently, the time averaged MSD 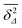 has not reached the saturation value
has not reached the saturation value 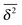 . Among N sample trajectories the fraction showing unrestricted anomalous diffusion will be
. Among N sample trajectories the fraction showing unrestricted anomalous diffusion will be
| | 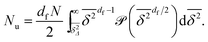 | (11) |
The remainder
N −
Nu then corresponds to saturated diffusion. As demonstrated in
Fig. 7 the scatter distribution for the free diffusion part will be a
δ peak as
T is increased to infinity. Thus in the long time limit this part corresponds to the contribution
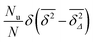
. For the complementary, confined fraction the scatter distribution will be proportional to
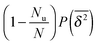
. Therefore the normalised scatter distribution in the long time limit can be written as
| | 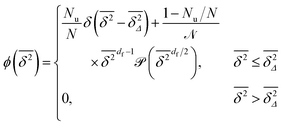 | (12) |
in terms of the variable
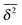
. Here
| | 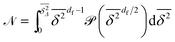 | (13) |
is a normalisation constant. From
eqn (12) the averaged value of the time averaged MSD is calculated to be
| | 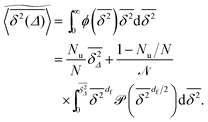 | (14) |
Although the exact form of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is unknown, the fact that
is unknown, the fact that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) is a monotonically decaying distribution leads to the relation
(s) is a monotonically decaying distribution leads to the relation 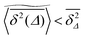 found in Fig. 6 and 7. Eqn (12) tells us that the fluctuations of the time averaged MSD given by ϕ is fully determined by the cluster size
found in Fig. 6 and 7. Eqn (12) tells us that the fluctuations of the time averaged MSD given by ϕ is fully determined by the cluster size ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) distribution as well as the lag time Δ. In percolation theory the form
distribution as well as the lag time Δ. In percolation theory the form
| | ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) ∝ s−τf[(p − pc)sσ] (s) ∝ s−τf[(p − pc)sσ] | (15) |
based on the scaling function
f(
x) is invoked where
τ and
σ are two scaling exponents.
48,91 At the percolation threshold
p =
pc the cluster size distribution asymptotically has the power-law form
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
s) ≃
s−τ with 2 <
τ < 3.
48 Using this information we find that
| | 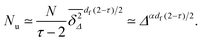 | (16) |
Thus
Nu slowly decreases with increasing
Δ as
τ = 187/91 ≈ 2.05 at
p =
pc on the square lattice. The sharp peak in
ϕ(
ξ) is observed even for long lag times, as evidenced in the plot for
p =
pc in
Fig. 6. For the distribution of finite size clusters, with the above we find the following simplified expression of
eqn (10),
| | 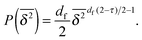 | (17) |
The theoretical value of the scaling exponent of
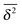
in this relation can be evaluated from the numerical estimation of
df and
τ in our simulations. From approximately 25
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 clusters of various size
s extracted from 9480 percolation geometries
ζ, the fractal dimension
df is estimated via the scaling law
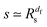
of the gyration radius as
df ≈ 1.865 with the confidence interval (1.824, 1.905) and
τ ≈ 2.03 from
eqn (15).
** This measurement leads to the prediction that the exponent is given by −1.028 with the confidence interval (−1.027, −1.029). In the inset of
Fig. 7 the decaying part of the distribution
ϕ(
ξ) at
Δ = 10
3 is plotted in on a logarithmic scale (black circles). The slope of the linear fit (blue line) is −1.063 with the confidence interval (−1.226, −0.899), agreeing well with the theoretically predicted value.
Above the obstacle percolation threshold, p > pc, when only finite, disjunct cluster remain, the cluster size distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) has the asymptotic form
(s) has the asymptotic form
| | ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) ≃ s−τe−cs (s) ≃ s−τe−cs | (18) |
where 1/
c is the characteristic cluster size.
48 From this result we obtain that
| | 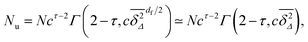 | (19) |
in terms of the incomplete Gamma function
Γ(·,·). The last transformation follows from the fact that for
p >
pc the fractal dimension
df = 2 equals the embedding Euclidean dimension, that is
d = 2 here, corresponding to the locally fully connected, finite clusters. Consequently in this situation we face the scaling
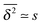
. At large lag times
Δ satisfying the criterion
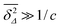
,
Nu is approximated as
| | 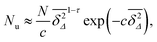 | (20) |
and thus we obtain
Nu ≪
N. Therefore in
eqn (12) the second term involving the cluster size distribution
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
will dominate the scatter distribution
ϕ. This argument supports the monotonically decaying profiles of
ϕ at
Δ = 10
3 and 10
5 in the plot for
p = 0.5 displayed in
Fig. 7 which is accordingly the very profile of
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
. This also underlines the fact that at time scales for which
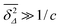
almost all tracer particles undergo confined diffusion. In the opposite case, at short lag times satisfying
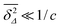
, we see that
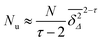
, which is the same as
Nu at
p =
pc with the replacement
df → 2. This means that there are particles performing free diffusion over short lag times
Δ. Thus
ϕ should have a peak around the ergodic value, as shown in the case of
Δ = 10 for
p = 0.5 in
Fig. 6.
3.4 Ergodicity breaking parameter
We now study the functional behaviour of the fluctuations of the time averaged MSD as the observation time T is increased. For this purpose, we use the ergodicity breaking (EB) parameter28,29,31,60| | 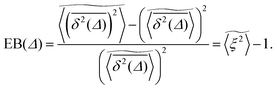 | (21) |
Here the ensemble average 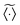 again means the ensemble average over the set of trajectories as well as over the fractal geometries ζ at given lag time Δ and the observation time T, similar to our definition of the ensemble averaged MSD
again means the ensemble average over the set of trajectories as well as over the fractal geometries ζ at given lag time Δ and the observation time T, similar to our definition of the ensemble averaged MSD 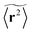 above.
above.
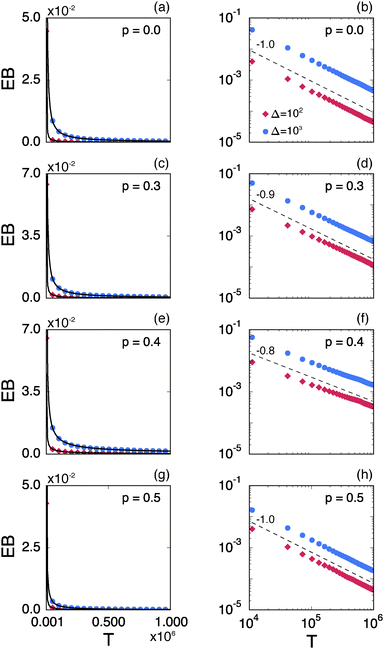
Fig. 8 shows the EB parameter as function of the observation time T for four distinct cases. In each panel two EB curves are plotted at lag times Δ = 10 and 102. At given percolation density p the EB curves are shown on linear (left column) and double logarithmic (right column) scales. At p = 0 when the accessible space is the full two-dimensional square lattice the EB parameter displays the theoretically expected scaling behaviour 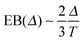 for two-dimensional Brownian motion shown by the dashed slope in the double logarithmic panel for p = 0, see Fig. 8(b).29,92 In this case the fluctuation of the time averaged MSD tend to zero as T → ∞: for this ergodic process the time averaged MSD becomes identical to the ensemble averaged MSD. This conventional convergence continues if the space is filled with obstacles with a concentration p well below the percolation threshold pc, as evidenced for the case p = 0.3 in Fig. 8(d).
for two-dimensional Brownian motion shown by the dashed slope in the double logarithmic panel for p = 0, see Fig. 8(b).29,92 In this case the fluctuation of the time averaged MSD tend to zero as T → ∞: for this ergodic process the time averaged MSD becomes identical to the ensemble averaged MSD. This conventional convergence continues if the space is filled with obstacles with a concentration p well below the percolation threshold pc, as evidenced for the case p = 0.3 in Fig. 8(d).
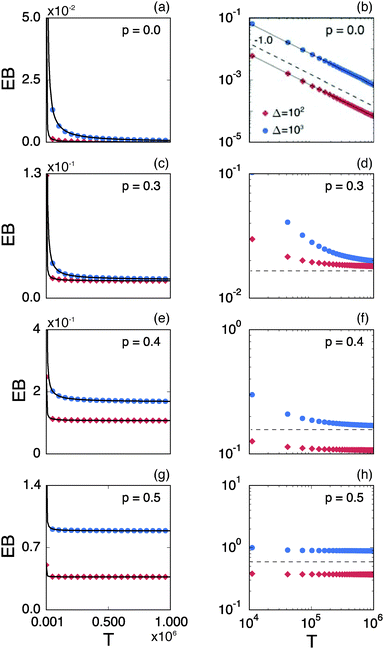 |
| | Fig. 8 Ergodicity breaking parameter EB on linear scales (left column) and on double logarithmic scales (right column) as function of the observation time T. The red curves correspond to Δ = 102 and the blue curves represent Δ = 103. The black solid lines depict the best fits with eqn (23). The grey lines in the double logarithmic plot for p = 0 (b), correspond to the EB parameter for normal Brownian motion with Δ = 102 and 103. The dashed lines in the double logarithmic plots show the asymptotic behaviour of EB. The results are from Nζ = 3000 percolation geometries and N = 3 trajectories. | |
However, the convergence of the EB parameter behaves quite differently when we approach the percolation threshold at p = pc. In this case EB does not converge to zero when T goes to infinity but, as demonstrated in Fig. 8(d), EB converges to the finite residual value
| | 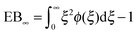 | (22) |
shown by the dotted horizontal line. This value was numerically estimated from the scatter distribution in
Fig. 6. The geometrically induced fluctuations in the time averaged MSD due to the existence of finite clusters do not vanish even in the limit of infinite observation time.
The EB curves shown in Fig. 8 converge towards EB∞ in good agreement with the algebraic form
| | 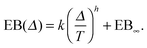 | (23) |
Here
h and EB
∞ ≥ 0 are, respectively, the associated scaling exponent and the limiting value of EB at
T → ∞, and
k is a proportionality constant. In
Fig. 10 we show the functional relations of the exponent
h and of EB
∞versus the percolation density
p as estimated from the EB curves. In
Fig. 8 (left) the solid lines depict the best fit to
eqn (23). We mention the following noteworthy aspects of the results: (i) for percolation densities
p sufficiently below the percolation threshold
pc the EB parameter follows that of normal Brownian diffusion, that is,
h = 1 and EB
∞ = 0, as mentioned above. (ii) For the opposite regime of high obstacle densities,
p >
pc, we find
h = 1 and a non-zero value EB
∞ of the residual EB parameter that tends to increase with the percolation density
p. In this regime the Brownian convergence speed EB ∼
T−1 is derived from the long time confined Brownian motion of tracer particles. The value EB
∞ ≠ 0 is attributed to the heterogeneity of the saturation values of the time averaged MSD and is thus geometry controlled. This statement is also consistent with the fact that EB
∞ depends on the lag time
Δ in
Fig. 8(g) and (h), due to the different resolution set by the value
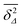
. (iii) Close to the percolation threshold
pc the behaviour of the EB parameter is distinguished from these two regimes. As
p is increased towards the critical point
pc,
h consistently decreases from unity. Thus when the space becomes fractal on all length scales we find that
h ≈ 0.80 and EB
∞ ≠ 0.
We emphasise that the estimated value h < 1 at pc is a genuine convergence property due to the fractal structure of the explored space. To rule out the possibility that the value h ≈ 0.8 < 1 is due to the small finite clusters responsible for EB∞ ≠ 0, we plot in Fig. 9 the EB curves after excluding the contribution of the smallest clusters of size s = 1. The unit sized clusters are the most dominant contribution among the finite clusters, see the form of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s), and results in the vanishing time averaged MSD,
(s), and results in the vanishing time averaged MSD, 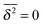 . Fig. 9 shows that after removing these unit size clusters the EB parameter always converges to EB∞ = 0 for all p values. However, the convergence exponent h remains at h ≈ 0.8, compare also Fig. 10. We note that the convergence law of the EB parameter is not the same as that of fractional Brownian motion, although both models share the same anomalous diffusion scaling (1) and are ergodic (for the present case in the sense of the disorder average). For fractional Brownian motion EB was found to have the convergence form
. Fig. 9 shows that after removing these unit size clusters the EB parameter always converges to EB∞ = 0 for all p values. However, the convergence exponent h remains at h ≈ 0.8, compare also Fig. 10. We note that the convergence law of the EB parameter is not the same as that of fractional Brownian motion, although both models share the same anomalous diffusion scaling (1) and are ergodic (for the present case in the sense of the disorder average). For fractional Brownian motion EB was found to have the convergence form 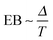 for
for 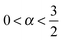 ,
, 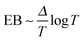 for
for 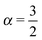 , and
, and 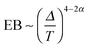 for
for 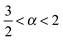 .92–94 Thus, compared to fractional Brownian motion the fractal geometry-induced subdiffusion has a slower convergence to ergodicity. The observed characters of the EB parameter also differ from those of other diffusion models such as scaled Brownian motion, heterogeneous diffusion processes, and continuous time random walk.60,68,95 Therefore, the EB convergence law provides useful information for unveiling the physical origins of anomalous diffusion processes found in complex random media.
.92–94 Thus, compared to fractional Brownian motion the fractal geometry-induced subdiffusion has a slower convergence to ergodicity. The observed characters of the EB parameter also differ from those of other diffusion models such as scaled Brownian motion, heterogeneous diffusion processes, and continuous time random walk.60,68,95 Therefore, the EB convergence law provides useful information for unveiling the physical origins of anomalous diffusion processes found in complex random media.
 |
| | Fig. 9 Ergodicity breaking parameter as a function of the observation time T when clusters with s = 1 are removed. The double logarithmic plot shows a linear behaviour of EB versus the observation time T, independent of the percolation density p. The red curve corresponds to Δ = 102 and the blue curve represents Δ = 103. The black solid lines for the linear scales plots are the best fits to eqn (23), the dashed black lines in the double logarithmic plots show the slope of the EB curves. Same numbers for Nζ and N as in Fig. 8. | |
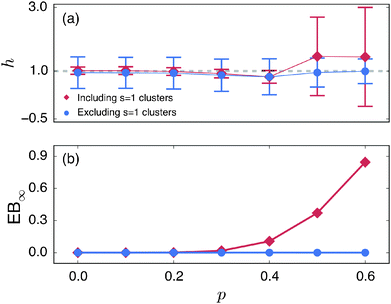 |
| | Fig. 10 (a) Variation of the scaling exponent h and (b) the residual ergodicity breaking parameter EB∞ as function of the percolation density p. Values from fit of the scaling function (23) to the EB curves in Fig. 8 and 9. The results are reported for Δ = 10. Red diamonds: fit from Fig. 8 including the smallest clusters of size s = 1. Blue circles: fit from Fig. 9 neglecting the smallest clusters. | |
4 Conclusion
Based on extensive Monte Carlo simulations we studied the ergodic properties of single particles diffusing in random two-dimensional fractal geometries modelled by a percolation geometry at varying percolation density of obstacles. While the asymptotic equality between the ensemble averaged MSD 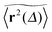 and the time averaged MSD
and the time averaged MSD 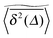 averaged over all individual trajectories and many percolation geometries is observed at any percolation density, individual time averaged MSDs do not always behave like this average and are thus non-ergodic. As we showed here this non-ergodic behaviour is geometry controlled and thus corresponds to strong ergodicity breaking due to a topologically disconnected phase space. Thus, at low obstacle densities p ≪ pc the single particle diffusion exhibits typical ergodic behaviour as seen in the scaling law of the time averaged MSDs, their scatter distribution, and the ergodicity breaking parameter. In this case, the ensemble averaged MSD shows no disparity with individual time averaged MSDs as long as the observation time is sufficiently long. Close to the percolation threshold p ≈ pc, however, such a typical ergodic character is no longer observed. There exists a fraction of time averaged MSDs which significantly deviate from the averaged curve
averaged over all individual trajectories and many percolation geometries is observed at any percolation density, individual time averaged MSDs do not always behave like this average and are thus non-ergodic. As we showed here this non-ergodic behaviour is geometry controlled and thus corresponds to strong ergodicity breaking due to a topologically disconnected phase space. Thus, at low obstacle densities p ≪ pc the single particle diffusion exhibits typical ergodic behaviour as seen in the scaling law of the time averaged MSDs, their scatter distribution, and the ergodicity breaking parameter. In this case, the ensemble averaged MSD shows no disparity with individual time averaged MSDs as long as the observation time is sufficiently long. Close to the percolation threshold p ≈ pc, however, such a typical ergodic character is no longer observed. There exists a fraction of time averaged MSDs which significantly deviate from the averaged curve 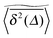 . Using the time averaged occupation probability
. Using the time averaged occupation probability 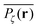 we demonstrated that these outliers correspond to trajectories when the particles motion is restricted on finite clusters of gyration radius Rs significantly smaller than the system size. Other particles moving on the infinite cluster at criticality, however, do show the convergence to the ensemble averaged MSD
we demonstrated that these outliers correspond to trajectories when the particles motion is restricted on finite clusters of gyration radius Rs significantly smaller than the system size. Other particles moving on the infinite cluster at criticality, however, do show the convergence to the ensemble averaged MSD 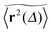 on the single trajectory level. We thus observe ergodic motion for a fraction of particles conditioned to move on the infinite incipient cluster, as reported earlier.77 Due to the mix of confined and freely diffusing trajectories, the scatter distribution of the amplitudes of individual time averaged MSDs shown in Fig. 6 and 7 acquires an asymmetric bell shaped form around the main peak at
on the single trajectory level. We thus observe ergodic motion for a fraction of particles conditioned to move on the infinite incipient cluster, as reported earlier.77 Due to the mix of confined and freely diffusing trajectories, the scatter distribution of the amplitudes of individual time averaged MSDs shown in Fig. 6 and 7 acquires an asymmetric bell shaped form around the main peak at 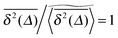 and a second peak at
and a second peak at 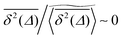 . As shown in Fig. 7, upon increase of the observation time T the latter part is preserved while the main peak around the ergodic value
. As shown in Fig. 7, upon increase of the observation time T the latter part is preserved while the main peak around the ergodic value 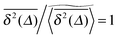 becomes a sharp, almost δ function like peak. Relating the cluster size distribution to the distribution of the time averaged MSDs by eqn (12) we qualitatively explained the observed behaviour of the scatter distribution ϕ. An interesting behaviour is also observed for the ergodicity breaking parameter defined in eqn (21). From numerical analysis we found that EB generally follows an algebraic decay [EB(Δ) − EB∞] ∼ T−h(p) towards the finite residual EB parameter EB∞ reached at T → ∞, and h is a scaling exponent. The exact value of EB∞ depends on the percolation density p. As p is increased to pc the decay of the EB parameter thus deviates from that for typical ergodic diffusion, for which h = 1 and EB∞ = 0. Importantly, on approximating the percolation threshold, p ≈ pc, the EB parameter has a slower convergence with scaling exponent h ≈ 0.8 < 1 as well as a nonzero value EB∞ > 0 due to the contribution of confined particles.
becomes a sharp, almost δ function like peak. Relating the cluster size distribution to the distribution of the time averaged MSDs by eqn (12) we qualitatively explained the observed behaviour of the scatter distribution ϕ. An interesting behaviour is also observed for the ergodicity breaking parameter defined in eqn (21). From numerical analysis we found that EB generally follows an algebraic decay [EB(Δ) − EB∞] ∼ T−h(p) towards the finite residual EB parameter EB∞ reached at T → ∞, and h is a scaling exponent. The exact value of EB∞ depends on the percolation density p. As p is increased to pc the decay of the EB parameter thus deviates from that for typical ergodic diffusion, for which h = 1 and EB∞ = 0. Importantly, on approximating the percolation threshold, p ≈ pc, the EB parameter has a slower convergence with scaling exponent h ≈ 0.8 < 1 as well as a nonzero value EB∞ > 0 due to the contribution of confined particles.
Above pc the particle diffusion always takes place on confined clusters. Large fluctuations from the average 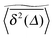 are present in individual time averaged MSDs. The profile of the scatter distribution ϕ(ξ) is quite different from those for critical and lower than critical percolation densities, see Fig. 6. At sufficiently long lag times Δ the distribution decays almost monotonically with the variable ξ, due to the exclusive presence of finite clusters with an exponentially decaying distribution of cluster sizes. This is a purely geometrical effect, as revealed in the distribution of the time averaged MSD which turns out to be independent of the observation time T. In both Fig. 8 and 9 the EB parameter was shown to decay as T−1, corresponding to the convergence to zero of a Brownian particle. This is due to the fact that in this overcrowded obstacle regime the particle explores small clusters with local Euclidean geometries. We note that while the specific values for the scaling exponents and percolation thresholds vary for different lattice types and dimensionality of the embedding dimension the generic features revealed here remain unchanged. This claim is supported by preliminary studies on cubic and hexagonal lattices (not shown).
are present in individual time averaged MSDs. The profile of the scatter distribution ϕ(ξ) is quite different from those for critical and lower than critical percolation densities, see Fig. 6. At sufficiently long lag times Δ the distribution decays almost monotonically with the variable ξ, due to the exclusive presence of finite clusters with an exponentially decaying distribution of cluster sizes. This is a purely geometrical effect, as revealed in the distribution of the time averaged MSD which turns out to be independent of the observation time T. In both Fig. 8 and 9 the EB parameter was shown to decay as T−1, corresponding to the convergence to zero of a Brownian particle. This is due to the fact that in this overcrowded obstacle regime the particle explores small clusters with local Euclidean geometries. We note that while the specific values for the scaling exponents and percolation thresholds vary for different lattice types and dimensionality of the embedding dimension the generic features revealed here remain unchanged. This claim is supported by preliminary studies on cubic and hexagonal lattices (not shown).
Anomalous diffusion in a fractal geometry is a non-Gaussian process42,43,48 and therefore different from the Gaussian fractional Brownian motion on a fundamental level. However, except for the Gaussianity the difference between these two processes has not been studied in detail. In particular, it has been said that both models share the same ergodic behaviour. However, as revealed in our study the ergodic properties of diffusion on fractals displays distinctly different behaviour due to the quenched nature of the underlying geometry. Only in certain cases (low obstacle concentration or conditional seeding of the particle exclusively on the infinite cluster close to criticality) we observe ergodic behaviour. While the statistical fluctuations in the time averaged MSD are homogeneous for fractional Brownian motion, the fractal geometry-induced anomalous diffusion is heterogeneous, and the strength and character of the heterogeneity depend on the obstacle density. Therefore the detailed analysis of the ergodic properties is indeed a useful measure to differentiate the type of ant-in-the-labyrinth motion from other models, along with recently developed theoretical tools estimating the fractal dimension df.56,77 An advantage of the method developed herein studying ergodic properties is more feasible than estimating the fractal dimension df.
As experimental single particle tracking studies become increasingly popular our results are expected to be helpful in analysing and interpreting experimental results for various problems of anomalous diffusion in complex environments. In the case of lateral diffusion in phospholipid membranes some recent simulation studies reported that lipid diffusion is a two dimensional fractional Brownian motion9,37 while conventionally it was understood as diffusion on fractal lattices.43,50,96 In addition for more complex membranes the lateral diffusion exhibits non-ergodic continuous time random walk type motion97 or was identified as the combination of motion on a fractal and continuous time random walks.8 Also fairly complex non-Gaussian ergodic motion types were reported.98 Such a stochastic variety in the lateral diffusion dynamics seems to be natural given the fact that biological membranes have a composition dependent, wide range of structural complexities. From the trajectory analyses presented in this work one can have additional insight about the lateral dynamics and static structural complexity of a membrane system under investigation. For instance, if the plot of EB versus T gives the scaling exponent h < 1 it gives a signature that the lateral anomalous diffusion is not of fractional Brownian motion type. Then the ageing test for the time averaged MSDs along with the moment ratio evaluation further differentiates the fractal induced subdiffusion from non-ergodic continuous time random walk process. The distribution of saturated TA MSDs and a non-vanishing EB∞ may be used to obtain information on the size distribution of confining domains in a membrane, if any. Our analysis can also be applied to nano-particle transport in porous media.52,99 From the profile of the distribution of the time averaged MSD one may obtain information on the pore size distribution as well as the porosity of a medium. Additionally the ageing test for the time averaged MSD shown in Fig. 4 appears to be informative to examining the nano-particle-pore interactions: if the motion exhibits features of ageing it is likely that there are nonspecific interactions between the particles and a porous medium which give rise to the temporal heterogeneity in the time averaged MSD.
Acknowledgements
JHJ and RM acknowledge financial support from the Academy of Finland (Suomen Akatemia) within the Finland Distinguished Professor (FiDiPro) programme awarded to RM.
References
- J. Perrin, Acad. Sci., Paris, C. R., 1908, 146, 967 CAS.
-
Single particle tracking and single molecule energy transfer, ed. C. Bräuchle, D. C. Lamb and J. Michaelis, Wiley-VCH, Weinheim, 1908 Search PubMed.
- I. Golding and E. C. Cox, Physical nature of bacterial cytoplasm, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed.
- I. M. Tolić-Nørrelykke, E.-L. Munteanu, G. Thon, L. Oddershede and K. Berg-Sørensen, Anomalous diffusion in living yeast cells, Phys. Rev. Lett., 2004, 93, 078102 CrossRef PubMed.
- J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed.
- M. A. Taylor, J. Janousek, V. Daria, J. Knittel, B. Hage, H.-A. Bachor and W. P. Bowen, Biological measurement beyond the quantum limit, Nat. Photonics, 2013, 7, 229 CrossRef CAS.
- S. M. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Intracellular transport of insulin granules is a subordinated random walk, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911 CrossRef PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438 CrossRef CAS PubMed.
- J.-H. Jeon, H. M.-S. Monne, M. Javanainen and R. Metzler, Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed.
- G. R. Kneller, K. Baczynski and M. Pasenkiewicz-Gierula, Consistent picture of lateral subdiffusion in lipid bilayers: Molecular dynamics simulation and exact results, J. Chem. Phys., 2011, 135, 141105 CrossRef PubMed.
- M. Javanainen, H. Hammaren, L. Monticelli, J.-H. Jeon, M. S. Miettinen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes, Faraday Discuss., 2013, 161, 397 RSC.
- S. J. Sahl, M. Leutenegger, M. Hilbert, S. W. Hell and C. Eggeling, Fast molecular tracking maps nanoscale dynamics of plasma membrane lipids, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6829 CrossRef CAS PubMed.
- I. Y. Wong, M. L. Gardel, D. R. Reichman, E. R. Weeks, M. T. Valentine, A. R. Bausch and D. A. Weitz, Anomalous diffusion probes microstructure dynamics of entangled F-actin networks, Phys. Rev. Lett., 2004, 92, 178101 CrossRef CAS PubMed.
- J.-H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions, New J. Phys., 2013, 15, 045011 CrossRef.
- N. Fatin-Rouge, K. Starchev and J. Buffle, Size effects on diffusion processes within agarose gels, Biophys. J., 2004, 86, 2710 CrossRef CAS PubMed.
- A. Godec, M. Bauer and R. Metzler, Collective dynamics effect transient subdiffusion of inert tracers in gel networks, New J. Phys., 2014, 16, 092002 CrossRef.
- D. S. Banks and C. Fradin, Anomalous diffusion of proteins due to molecular crowding, Biophys. J., 2005, 89, 2960 CrossRef CAS PubMed.
- J. Szymanski and M. Weiss, Elucidating the origin of anomalous diffusion in crowded fluids, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed.
- S. Burov, S. M. Ali Tabei, T. Huynh, M. P. Murrell, L. H. Philipson, S. A. Rice, M. L. Gardel, N. F. Scherer and A. R. Dinner, Distribution of directional change as a signature of complex dynamics, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19689 CrossRef CAS PubMed.
- T. Turiv, I. Lazo, A. Brodin, B. I. Lev, V. Reiffenrath, V. G. Nazarenko and O. D. Lavrentovich, Effect of collective molecular reorientations on Brownian motion of colloids in nematic liquid crystal, Science, 2013, 342, 1351 CrossRef CAS PubMed.
- J. F. Reverey, J.-H. Jeon, M. Leippe, R. Metzler and C. Selhuber-Unkel, Superdiffusion dominates intracellular particle motion in the supercrowded space of pathogenic Acanthamoeba castellanii, Sci. Rep., 2015, 5, 11690 CrossRef PubMed.
- A. Caspi, R. Granek and M. Elbaum, Enhanced Diffusion in Active Intracellular Transport, Phys. Rev. Lett., 2000, 85, 5655 CrossRef CAS PubMed.
- N. Gal and D. Weihs, Experimental evidence of strong anomalous diffusion in living cells, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 020903(R) CrossRef PubMed.
- D. Robert, Th. H. Nguyen, F. Gallet and C. Wilhelm,
In vivo determination of fluctuating forces during endosome trafficking using a combination of active and passive microrheology, PLoS One, 2010, 4, e10046 Search PubMed.
- I. Goychuk, V. O. Kharchenko and R. Metzler, Molecular motors pulling cargos in the viscoelastic cytosol: power strokes beat subdiffusion, Phys. Chem. Chem. Phys., 2014, 16, 16524 RSC.
-
G. Campagnola, K. Nepal, B. W. Schroder, O. B. Peersen and D. Krapf, Superdiffusion in supported lipid bilayers, E-print arXiv:1506.03795.
- A. V. Chechkin, I. M. Zaid, M. A. Lomholt, I. M. Sokolov and R. Metzler, Bulk-mediated diffusion on a planar surface: full solution, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041101 CrossRef PubMed.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Single particle tracking in systems showing anomalous diffusion: the role of weak ergodicity breaking, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128 RSC.
- I. M. Sokolov, Models of anomalous diffusion in crowded environments, Soft Matter, 2012, 8, 9043 RSC.
- E. Barkai, Y. Garini and R. Metzler, Strange kinetics of single molecules in living cells, Phys. Today, 2012, 65(8), 29 CrossRef CAS.
- C. Monthus and J.-P. Bouchaud, Models of traps and glass phenomenology, J. Phys. A: Math. Gen., 1996, 29, 3847 CrossRef CAS.
- H. Scher and E. W. Montroll, Anomalous transit-time dispersion in amorphous solids, Phys. Rev. B: Solid State, 1975, 12, 2455 CrossRef CAS.
- P. Hänggi, Correlation functions and masterequations of generalized (non-Markovian) Langevin equations, Z. Phys. B: Condens. Matter, 1978, 31, 407 Search PubMed.
- P. Hänggi and F. Mojtabai, Thermally activated escape rate in presence of long-time memory, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 1168 CrossRef.
- R. Kubo, The fluctuation-dissipation theorem, Rep. Prog. Phys., 1966, 29, 255 CAS.
- G. Kneller, A scaling approach to anomalous diffusion, J. Chem. Phys., 2014, 141, 041105 CrossRef PubMed.
- B. B. Mandelbrot and J. W. van Ness, Fractional Brownian motions, fractional noises and applications, SIAM Rev., 1968, 10, 422 CrossRef.
-
A. M. Yaglom, Correlation theory of stationary and related random functions, Springer, Heidelberg, 1987 Search PubMed.
- I. Goychuk, Viscoelastic subdiffusion: from anomalous to normal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046125 CrossRef PubMed.
- J.-H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, New J. Phys., 2013, 15, 045011 CrossRef.
- S. Havlin and D. Ben-Avraham, Diffusion in disordered media, Adv. Phys., 1987, 36, 695 CrossRef CAS.
- F. Höfling and T. Franosch, Anomalous transport in the crowded world of biological cells, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
-
B. B. Mandelbrot, The fractal geometry of nature, W. H. Freeman, New York, NY, 1982 Search PubMed.
- P. G. de Gennes, La Recherche, 1976, 7, 919 Search PubMed.
- J. C. Angles d'Auriac, A. Benoit and R. Rammal, Random walk on fractals: numerical studies in two dimensions, J. Phys. A: Math. Gen., 1983, 16, 4039 CrossRef.
- J.-P. Bouchaud and A. Georges, Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications, Phys. Rep., 1990, 195, 127 CrossRef.
-
D. Stauffer and A. Aharony, Introduction to percolation theory, Taylor and Francis, London, 2nd edn, 1992 Search PubMed.
- F. Höfling, T. Franosch and E. Frey, Localization transition of the three-dimensional Lorentz model and continuum percolation, Phys. Rev. Lett., 2006, 96, 167901 CrossRef PubMed.
- M. J. Saxton, Anomalous diffusion due to obstacles: a Monte Carlo study, Biophys. J., 1994, 66, 394 CrossRef CAS PubMed.
- L. E. Sereshki, M. A. Lomholt and R. Metzler, A solution to the subdiffusion-efficiency paradox: inactive states enhances reaction efficiency at subdiffusion conditions in living cells, Europhys. Lett., 2012, 97, 20008 CrossRef.
- H. Sanabria, Y. Kubota and M. N. Waxham, Multiple diffusion mechanisms due to nanostructuring in crowded environments, Biophys. J., 2007, 92, 313 CrossRef CAS PubMed.
- M. Hellmann, D. W. Heermann and M. Weiss, Enhancing phosphorylation cascades by anomalous diffusion, EPL, 2012, 97, 58004 CrossRef.
- C. C. Fritsch and J. Langowski, J. Chem. Phys., 2010, 133, 025101 CrossRef PubMed.
- C. Loverdo, O. Bénichou, R. Voituriez, A. Biebricher, I. Bonnet and P. Desbiolles, Quantifying Hopping and Jumping in Facilitated Diffusion of DNA-Binding Proteins, Phys. Rev. Lett., 2009, 102, 188101 CrossRef CAS PubMed.
- V. Tejedor, O. Bénichou, R. Voituriez, R. Jungmann, F. Simmel, C. Selhuber-Unkel, L. Oddershede and R. Metzler, Quantitative analysis of single particle trajectories: mean maximal excursion method, Biophys. J., 2010, 98, 1364 CrossRef CAS PubMed.
- K. Burnecki, E. Kepten, Y. Garini, G. Sikora and A. Weron, Estimating the anomalous diffusion exponent for single particle tracking data with measurement errors – an alternative approach, Sci. Rep., 2015, 5, 11306 CrossRef CAS PubMed.
- E. Kepten, A. Weron, G. Sikora, K. Burnecki and Y. Garini, Guidelines for the Fitting of Anomalous Diffusion Mean Square Displacement Graphs from Single Particle Tracking Experiments, PLoS One, 2015, 10, e0117722 Search PubMed.
- A. Robson, K. Burrage and M. C. Leake, Inferring diffusion in single live cells at the single-molecule level, Philos. Trans. R. Soc., B, 2012, 368, 20120029 CrossRef PubMed.
- Y. He, S. Burov, R. Metzler and E. Barkai, Random Time-Scale Invariant Diffusion and Transport Coefficients, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS PubMed.
- A. Lubelski, I. M. Sokolov and J. Klafter, Nonergodicity Mimics Inhomogeneity in Single Particle Tracking, Phys. Rev. Lett., 2008, 100, 250602 CrossRef PubMed.
- I. M. Sokolov, E. Heinsalu, P. Hänggi and I. Goychuk, Universal fluctuations in subdiffusive transport, EPL, 2009, 86, 30009 CrossRef.
- M. J. Skaug, A. M. Lacasta, L. Ramirez-Piscina, J. M. Sancho, K. Lindenberg and D. K. Schwartz, Single molecule diffusion in a periodic potential at a solid-liquid interface, Soft Matter, 2014, 10, 753 RSC.
- M. Khoury, A. M. Lacasta, J. M. Sancho and K. Lindenberg, Weak disorder: anomalous transport and diffusion are normal yet again, Phys. Rev. Lett., 2011, 106, 090602 CrossRef CAS PubMed.
- J.-H. Jeon, E. Barkai and R. Metzler, Noisy continuous time random walks, J. Chem. Phys., 2013, 139, 121916 CrossRef PubMed.
- V. Tejedor and R. Metzler, Anomalous diffusion in correlated continuous time random walks, J. Phys. A: Math. Gen., 2010, 43, 082002 CrossRef.
- M. Magdziarz, R. Metzler, W. Szczotka and P. Zebrowski, Correlated Continuous Time Random Walks in External Force Fields, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051103 CrossRef PubMed.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, Anomalous diffusion and ergodicity breaking in heterogeneous diffusion processes, New J. Phys., 2013, 15, 083039 CrossRef.
- A. V. Cherstvy, A. V. Chechkin and R. Metzler, Particle invasion, survival, and non-ergodicity in 2D diffusion processes with space-dependent diffusivity, Soft Matter, 2014, 10, 1591 RSC.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, Ageing and confinement in non-ergodic heterogeneous diffusion processes, J. Phys. A: Math. Gen., 2014, 47, 485002 CrossRef.
- Y. Meroz and I. M. Sokolov, A toolbox for determining subdiffusive mechanisms, Phys. Rep., 2015, 573, 1 CrossRef.
- S. C. Lim and S. V. Muniandi, Phys. Rev. E, 2002, 66, 021114 CrossRef CAS PubMed.
- F. Thiel and I. M. Sokolov, Phys. Rev. E, 2014, 89, 012115 CrossRef PubMed.
- J.-H. Jeon, A. V. Chechkin and R. Metzler, Scaled Brownian motion: a paradoxical process with a time dependent diffusivity for the description of anomalous diffusion, Phys. Chem. Chem. Phys., 2014, 16, 15811 RSC.
- A. Bodrova, A. V. Chechkin, A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2015, 17, 21791 RSC.
- D. Jacobs and H. Nakanishi, Autocorrelation functions for discrete random walks on disordered lattice, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 706 CrossRef CAS.
- Y. Meroz, I. M. Sokolov and J. Klafter, Test for determining a subdiffusive model in ergodic systems from single trajectories, Phys. Rev. Lett., 2013, 110, 090601 CrossRef PubMed.
- Y. Meroz, I. M. Sokolov and J. Klafter, Subdiffusion of mixed origins: When ergodicity and nonergodicity coexist, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 010101(R) CrossRef PubMed.
-
K. Falconer, Fractal geometry, John Wiley & Sons, Chichester, UK, 1990 Search PubMed.
- J. W. Dollinger, R. Metzler and T. F. Nonnenmacher, Bi-asymptotic fractals: fractals between lower and upper bounds, J. Phys. A: Math. Gen., 1998, 31, 3839 CrossRef.
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical recipes in C: the art of scientific computing, Cambridge University Press, 2nd edn, 1992 Search PubMed.
- A. Godec, A. V. Chechkin, E. Barkai, H. Kantz and R. Metzler, Localization and universal fluctuations in ultraslow diffusion processes, J. Phys. A: Math. Gen., 2014, 47, 492002 CrossRef.
- A. Klemm, H.-P. Müller and R. Kimmich, NMR microscopy of pore-space backbones in rock, sponge, and sand in comparison with random percolation model objects, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4413 CrossRef CAS.
- A. Klemm, R. Metzler and R. Kimmich, Diffusion on random-site percolation clusters: theory and NMR microscopy experiments with model objects, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 021112 CrossRef PubMed.
- J. Schulz, E. Barkai and R. Metzler, Ageing effects in single particle trajectory averages, Phys. Rev. Lett., 2013, 110, 020602 CrossRef PubMed.
- J. H. P. Schulz, E. Barkai and R. Metzler, Aging renewal theory and application to random walks, Phys. Rev. X, 2014, 4, 011028 Search PubMed.
- H. Safdari, A. V. Chechkin, G. Jafari and R. Metzler, Aging Scaled Brownian Motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042107 CrossRef PubMed.
- J. Kursawe, J. H. P. Schulz and R. Metzler, Transient ageing in fractional Brownian and Langevin equation motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062124 CrossRef PubMed.
- J.-H. Jeon and R. Metzler, Analysis of short subdiffusive time series: scatter of the time averaged mean squared displacement, J. Phys. A: Math. Gen., 2010, 43, 252001 CrossRef.
- A. G. Cherstvy and R. Metzler, Population splitting, trapping, and non-ergodicity in heterogeneous diffusion processes, Phys. Chem. Chem. Phys., 2013, 15, 20220 RSC.
- J. Hoshen, D. Stauffer, G. H. Bishop, R. J. Harrison and G. D. Quinn, Monte Carlo experiments on cluster size distribution in percolation, J. Phys. A: Math. Gen., 1979, 12, 1285 CrossRef CAS.
- W. Deng and E. Barkai, Ergodic properties of fractional Brownian-Langevin motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011112 CrossRef PubMed.
- J.-H. Jeon and R. Metzler, Fractional Brownian motion and motion governed by the fractional Langevin equation in confined geometries, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021103 CrossRef PubMed.
- J.-H. Jeon and R. Metzler, Inequivalence of time and ensemble averages in ergodic systems: exponential versus power-law relaxation in confinement, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021147 CrossRef PubMed.
- J.-H. Jeon, A. V. Chechkin and R. Metzler, Scaled Brownian motion: a paradoxical process with a time dependent diffusivity for the description of anomalous diffusion, Phys. Chem. Chem. Phys., 2014, 16, 15811 RSC.
- M. J. Saxton, Lateral diffusion in an archipelago: the effect of mobile obstacles, Biophys. J., 1987, 52, 989 CrossRef CAS PubMed.
- T. Akimoto, E. Yamamoto, K. Yasuoka, Y. Hirano and M. Yasui, Non-Gaussian fluctuations resulting from power-law trapping in a lipid bilayer, Phys. Rev. Lett., 2011, 107, 178103 CrossRef PubMed.
-
J.-H. Jeon, M. Javanainen, H. Martinez-Seara, I. Vattulainen and R. Metzler, manuscript in preparation.
- M. J. Skaug and D. K. Schwartz, Tracking nanoparticle diffusion in porous filtration media, Ind. Eng. Chem. Res., 2015, 54, 4414 CrossRef CAS.
Footnotes |
| † YM and JHJ contributed equally to this work. |
| ‡ Note that for finite sized fractals with lower and upper bound the power-law behaviour levels off at both ends in sigmoidal fashion.80 |
| § Often one considers the percolation of accessible sites, in that case the percolation threshold is 1 − pc ≈ 0.59. |
| ¶ Only for random walker exclusively seeded on the infinite cluster, that is, for obstacle percolation densities p ≤ pc, the MSD 〈r(t)2〉ζ for different realisations ζ of the geometry will converge to approximately the same value. |
| || More accurately, anomalous diffusion is observed when the random walker samples distances above several lattice constants a and will be eventually terminated in our periodic boundary conditions when the percolation structure is fully sampled. |
** The box counting method gives the estimation df ≡ 1.9191 ± 0.0095 from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 infinite clusters in our simulation while the accepted values in literatures are df = 91/48 and τ = 187/91 ≈ 2.05495, respectively. 000 infinite clusters in our simulation while the accepted values in literatures are df = 91/48 and τ = 187/91 ≈ 2.05495, respectively. |
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) of clusters diverges as
of clusters diverges as ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ∼ |p − pc|−ν with ν = 5/36.48 At the percolation threshold pc and for lower obstacle densities p < pc there exists an infinite cluster of empty sites spanning the entire volume.42,48 The probability that a given site belongs to the infinite cluster at criticality scales as P∞ ∼ (p − pc)β where β = 43/18.42,48 Concurrently as p → pc the crossover length rc from anomalous to normal diffusion used below diverges as rc ∼ |p − pc|−ν+β/2. Thus at p = pc anomalous diffusion of the form (1) prevails at all times.42,48,50 Simultaneously the percolation geometry forms scale-free fractal objects over all length scales larger than the lattice constant.42,48,50,79
∼ |p − pc|−ν with ν = 5/36.48 At the percolation threshold pc and for lower obstacle densities p < pc there exists an infinite cluster of empty sites spanning the entire volume.42,48 The probability that a given site belongs to the infinite cluster at criticality scales as P∞ ∼ (p − pc)β where β = 43/18.42,48 Concurrently as p → pc the crossover length rc from anomalous to normal diffusion used below diverges as rc ∼ |p − pc|−ν+β/2. Thus at p = pc anomalous diffusion of the form (1) prevails at all times.42,48,50 Simultaneously the percolation geometry forms scale-free fractal objects over all length scales larger than the lattice constant.42,48,50,79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡ For obstacle percolation considered here the critical percolation threshold is pc = 0.407256.48
‡ For obstacle percolation considered here the critical percolation threshold is pc = 0.407256.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) § This critical case is depicted in Fig. 1.
§ This critical case is depicted in Fig. 1. function taken from Numerical Recipes.81 On an isolated unit cluster no move is allowed and the random walker becomes completely localised. In the limit of p → 0 the diffusivity of the tracer particle is that of a free two-dimensional lattice,
function taken from Numerical Recipes.81 On an isolated unit cluster no move is allowed and the random walker becomes completely localised. In the limit of p → 0 the diffusivity of the tracer particle is that of a free two-dimensional lattice, 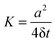 where a is the lattice constant. Our typical simulation time was 106 time steps, unless indicated otherwise. For the evaluation of physical observables Nζ random percolation geometries were generated at a given percolation density p, and N tracer trajectories for each percolation geometry were recorded. For the efficiency of the simulation study, the number Nζ was varied from 50 to 10
where a is the lattice constant. Our typical simulation time was 106 time steps, unless indicated otherwise. For the evaluation of physical observables Nζ random percolation geometries were generated at a given percolation density p, and N tracer trajectories for each percolation geometry were recorded. For the efficiency of the simulation study, the number Nζ was varied from 50 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and N from 3 to 1000 depending on the observables. In each case sufficiently large samples were chosen to ensure a proper statistical convergence. Information on Nζ and N used in the evaluation of each observable are provided in the text and in the figure captions.
000 and N from 3 to 1000 depending on the observables. In each case sufficiently large samples were chosen to ensure a proper statistical convergence. Information on Nζ and N used in the evaluation of each observable are provided in the text and in the figure captions.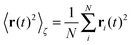
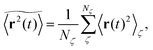
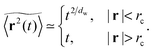
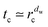 . Here the classical notation involves the walk dimension dw of the diffusing particle. Generally dw > 2 implying subdiffusion with 0 < α = 2/dw < 1. In the simplest case when we have no obstacles (p = 0) all sites are accessible to the random walker and we have normal diffusion at all times. In this case the crossover length rc vanishes. This case is shown in Fig. 2(a). At finite percolation densities below the percolation threshold, 0 < p < pc, the crossover length roughly corresponds to the average cluster size of locally fractal structures: local bottlenecks and cul-de-sacs generate anomalous diffusion, which eventually crosses over to normal diffusion when the typical distance travelled by the random walker exceeds rc. This case is shown in Fig. 2(b). We note that compared to the obstacle-free case p = 0, the effective diffusion coefficient in the case 0 < p < pc has a reduced value. At the percolation threshold p = pc ≈ 0.407256 the percolation geometry is fractal on all available scales, and the crossover length rc diverges. Concurrently, the anomalous diffusion regime ranges over all time scales.|| For the square lattice the anomalous diffusion exponent is 2/dw ≈ 0.7,50 which is again confirmed by our simulations, see Fig. 2. Indeed, Fig. 2(c) documents the anomalous diffusion at criticality. Anomalous diffusion in effectively two dimensional geometries was indeed verified by NMR measurements in computer generated percolation clusters milled into stacked plastic sheets.83,84 Above the percolation threshold the diffusion is more and more reduced. In particular, only finite, disjunct clusters remain such that the MSD eventually saturates to a plateau, see Fig. 2(d).
. Here the classical notation involves the walk dimension dw of the diffusing particle. Generally dw > 2 implying subdiffusion with 0 < α = 2/dw < 1. In the simplest case when we have no obstacles (p = 0) all sites are accessible to the random walker and we have normal diffusion at all times. In this case the crossover length rc vanishes. This case is shown in Fig. 2(a). At finite percolation densities below the percolation threshold, 0 < p < pc, the crossover length roughly corresponds to the average cluster size of locally fractal structures: local bottlenecks and cul-de-sacs generate anomalous diffusion, which eventually crosses over to normal diffusion when the typical distance travelled by the random walker exceeds rc. This case is shown in Fig. 2(b). We note that compared to the obstacle-free case p = 0, the effective diffusion coefficient in the case 0 < p < pc has a reduced value. At the percolation threshold p = pc ≈ 0.407256 the percolation geometry is fractal on all available scales, and the crossover length rc diverges. Concurrently, the anomalous diffusion regime ranges over all time scales.|| For the square lattice the anomalous diffusion exponent is 2/dw ≈ 0.7,50 which is again confirmed by our simulations, see Fig. 2. Indeed, Fig. 2(c) documents the anomalous diffusion at criticality. Anomalous diffusion in effectively two dimensional geometries was indeed verified by NMR measurements in computer generated percolation clusters milled into stacked plastic sheets.83,84 Above the percolation threshold the diffusion is more and more reduced. In particular, only finite, disjunct clusters remain such that the MSD eventually saturates to a plateau, see Fig. 2(d).
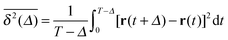
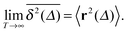
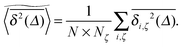
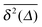 along with the ensemble average
along with the ensemble average 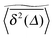 (black solid line) from Fig. 2. As long as p < pc the individual
(black solid line) from Fig. 2. As long as p < pc the individual 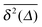 follow nicely the mean
follow nicely the mean 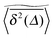 except for long lag times Δ ≈ T when the statistic for the time averaging becomes insufficient (Fig. 3(a) and (b)). In this case the cluster turns from a fully accessible two-dimensional lattice at p = 0 to a geometry with growing but localised clusters of obstacles at 0 < p < pc. The connectivity remains high such that, independent of the initial position, eventually the random walker explores the entire structure, apart from inaccessible areas of sufficiently small measure. Right at the percolation threshold p = pc shown in Fig. 3(c) we already observe significant deviations from the mean
except for long lag times Δ ≈ T when the statistic for the time averaging becomes insufficient (Fig. 3(a) and (b)). In this case the cluster turns from a fully accessible two-dimensional lattice at p = 0 to a geometry with growing but localised clusters of obstacles at 0 < p < pc. The connectivity remains high such that, independent of the initial position, eventually the random walker explores the entire structure, apart from inaccessible areas of sufficiently small measure. Right at the percolation threshold p = pc shown in Fig. 3(c) we already observe significant deviations from the mean 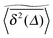 : a smaller number of traces
: a smaller number of traces 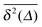 show confinement leading
show confinement leading 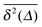 to enter a plateau much earlier than the crossover time of
to enter a plateau much earlier than the crossover time of 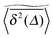 . This is due to the fact that at criticality, when the percolation geometry is fractal, the size of the accessible regions is scale-free and finite accessible clusters of all sizes are created in addition to the incipient infinite cluster. When seeded on such a finite cluster the time averaged MSD of the emanating trajectory will show a plateau depending on the very size of the visited cluster. We thus encounter a non-ergodic scenario in which the irreproducibility of trajectories stems from the quenched geometry. This non-ergodic behaviour is strengthened above the percolation threshold, p > pc, as shown in Fig. 3(d). Individual traces
. This is due to the fact that at criticality, when the percolation geometry is fractal, the size of the accessible regions is scale-free and finite accessible clusters of all sizes are created in addition to the incipient infinite cluster. When seeded on such a finite cluster the time averaged MSD of the emanating trajectory will show a plateau depending on the very size of the visited cluster. We thus encounter a non-ergodic scenario in which the irreproducibility of trajectories stems from the quenched geometry. This non-ergodic behaviour is strengthened above the percolation threshold, p > pc, as shown in Fig. 3(d). Individual traces  exhibit a pronounced scatter around the average
exhibit a pronounced scatter around the average 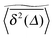 . In the sense of Bouchaud's definition32 the fact that once seeded on a specific cluster the random walker cannot pass to an unconnected cluster is referred to as strong ergodicity breaking. It denotes the case when the phase space of a system consists of disjoint subvolumes and access to each subvolume is determined by the initial position of the particle. It is intrinsic for the percolation system in that it is reproducible when simulations are performed with the same number of runs for given trajectory length T. Moreover, a typical scatter of amplitudes of the plateaus always occurs at any trajectory length T. It is in fact noteworthy that albeit these features of individual tracer motion the ensemble average remains ergodic within the error of our simulations.
. In the sense of Bouchaud's definition32 the fact that once seeded on a specific cluster the random walker cannot pass to an unconnected cluster is referred to as strong ergodicity breaking. It denotes the case when the phase space of a system consists of disjoint subvolumes and access to each subvolume is determined by the initial position of the particle. It is intrinsic for the percolation system in that it is reproducible when simulations are performed with the same number of runs for given trajectory length T. Moreover, a typical scatter of amplitudes of the plateaus always occurs at any trajectory length T. It is in fact noteworthy that albeit these features of individual tracer motion the ensemble average remains ergodic within the error of our simulations.
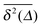 and their mean
and their mean 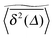 (thick black curve, as already shown in Fig. 2). In each panel the variation of the individual time averaged MSD curves represents 10 different trajectories on each of the overall 50 different simulated percolation geometries.
(thick black curve, as already shown in Fig. 2). In each panel the variation of the individual time averaged MSD curves represents 10 different trajectories on each of the overall 50 different simulated percolation geometries.
 at fixed lag time Δ as a function of the observation time T for Nζ = 2000 and N = 3. We here plot the same data as in Fig. 3, for (a) p = 0.3, (b) 0.4, and (c) 0.5. For all cases Δ = 100 was chosen. No significant dependence on T is visible for any sufficiently small value of Δ/T. The distinct, much lower lines in (a) corresponds to a very rare case of confinement. These cases become increasingly likely in (b) and (c).
at fixed lag time Δ as a function of the observation time T for Nζ = 2000 and N = 3. We here plot the same data as in Fig. 3, for (a) p = 0.3, (b) 0.4, and (c) 0.5. For all cases Δ = 100 was chosen. No significant dependence on T is visible for any sufficiently small value of Δ/T. The distinct, much lower lines in (a) corresponds to a very rare case of confinement. These cases become increasingly likely in (b) and (c).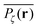 at the lattice point r for a given fractal geometry ζ in the form
at the lattice point r for a given fractal geometry ζ in the form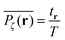
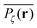 obtained from simulations with N = 104. For the fully accessible two-dimensional lattice (p = 0) the time averaged occupation probability is smoothly spread out from the origin with a uniform radial distribution of bell shape. This is a typically expected result for Brownian motion as well as for other ergodic processes in which the ensemble averaged occupation probability 〈Pζ(r)〉 is identical with its time averaged counterpart. This case is shown in Fig. 5(a). For growing percolation densities below the percolation threshold we therefore observe similar patterns, albeit local fine structure will appear due to the existence of a finite correlation range of obstacles measured by the radius rc introduced above. In particular, growing p will increasingly limit the accessible range for the random walker, that is, the occupation probability at finite T will decay faster from the initial position. At the percolation threshold p = pc the pattern of the time averaged occupation probability
obtained from simulations with N = 104. For the fully accessible two-dimensional lattice (p = 0) the time averaged occupation probability is smoothly spread out from the origin with a uniform radial distribution of bell shape. This is a typically expected result for Brownian motion as well as for other ergodic processes in which the ensemble averaged occupation probability 〈Pζ(r)〉 is identical with its time averaged counterpart. This case is shown in Fig. 5(a). For growing percolation densities below the percolation threshold we therefore observe similar patterns, albeit local fine structure will appear due to the existence of a finite correlation range of obstacles measured by the radius rc introduced above. In particular, growing p will increasingly limit the accessible range for the random walker, that is, the occupation probability at finite T will decay faster from the initial position. At the percolation threshold p = pc the pattern of the time averaged occupation probability 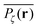 exhibits a structural fingerprint of the specific underlying fractal geometry. Interestingly, we find that
exhibits a structural fingerprint of the specific underlying fractal geometry. Interestingly, we find that 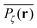 may assume two distinct patterns at the percolation threshold. Thus, while Fig. 5(b) reveals an emerging fractal spreading pattern, Fig. 5(c) shows a uniform distribution within a localised region—note the different scales of the panels. How can this come about? This phenomenon is again related to the fractal nature of the percolation geometry at criticality. In the former case, the tracer particle diffuses on the infinite incipient fractal cluster of vacant sites whose linear size is only limited by the size of the simulated lattice. Thus the corresponding time averaged MSD exhibits the anomalous scaling law (1) and the ergodic property
may assume two distinct patterns at the percolation threshold. Thus, while Fig. 5(b) reveals an emerging fractal spreading pattern, Fig. 5(c) shows a uniform distribution within a localised region—note the different scales of the panels. How can this come about? This phenomenon is again related to the fractal nature of the percolation geometry at criticality. In the former case, the tracer particle diffuses on the infinite incipient fractal cluster of vacant sites whose linear size is only limited by the size of the simulated lattice. Thus the corresponding time averaged MSD exhibits the anomalous scaling law (1) and the ergodic property 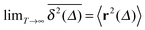 is satisfied.77 The quantity
is satisfied.77 The quantity 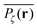 also provides information on how the tracer particle diffuses away from its starting site. It is noteworthy that the spatial gradient of
also provides information on how the tracer particle diffuses away from its starting site. It is noteworthy that the spatial gradient of 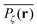 has no obvious discontinuous shape. This means that there are no sites at which the particle is significantly trapped for much longer times than at other neighbouring sites. In contrast to this, the latter case corresponding to Fig. 5(c) represents the case in which over the observation time T the particle visits repeatedly a small range of sites. These are either extremely poorly connected to the infinite cluster or completely separated. Accordingly the corresponding time averaged MSD saturates (outset). As seen in our previous analysis above the percentage of such complete confinement is relatively low compared to the situation above the percolation threshold. In the latter case p > pc confinement will always occur, as no infinite cluster of vacant sites remains. Patterns such as those shown in Fig. 5(c) will then emerge for clusters of varying size. On average clusters of decreasing size emerge when p is increased (not shown).
has no obvious discontinuous shape. This means that there are no sites at which the particle is significantly trapped for much longer times than at other neighbouring sites. In contrast to this, the latter case corresponding to Fig. 5(c) represents the case in which over the observation time T the particle visits repeatedly a small range of sites. These are either extremely poorly connected to the infinite cluster or completely separated. Accordingly the corresponding time averaged MSD saturates (outset). As seen in our previous analysis above the percentage of such complete confinement is relatively low compared to the situation above the percolation threshold. In the latter case p > pc confinement will always occur, as no infinite cluster of vacant sites remains. Patterns such as those shown in Fig. 5(c) will then emerge for clusters of varying size. On average clusters of decreasing size emerge when p is increased (not shown).
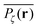 , eqn (8), distributed over three given percolation geometries. This quantity is sampled from an ensemble of 104 particle traces on the same percolation geometry ζ starting from the same initial site. We show results for a two-dimensional lattice corresponding to (a) p = 0.1, (b) at the percolation threshold with p = pc with an emerging fractal pattern, and (c) at the percolation threshold with a localised pattern. The outsets show examples of the corresponding time averaged MSD curves for those particles.
, eqn (8), distributed over three given percolation geometries. This quantity is sampled from an ensemble of 104 particle traces on the same percolation geometry ζ starting from the same initial site. We show results for a two-dimensional lattice corresponding to (a) p = 0.1, (b) at the percolation threshold with p = pc with an emerging fractal pattern, and (c) at the percolation threshold with a localised pattern. The outsets show examples of the corresponding time averaged MSD curves for those particles.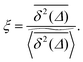
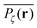 shown in Fig. 5(c). Note that this peak at ξ = 0 is not a statistical error due to an insufficient number of simulation runs. Our further investigation demonstrates that this peak is still observed in larger simulation sets. Second, the position of the main peak is shifted to a larger value above ξ = 1 while the bell-shaped profile is preserved. For the shorter lag time Δ = 10 the shift is less severe, however, one can distinguish a fine structure of different peaks for ξ values closer to zero. These correspond to clusters of different size, which can be resolved here when the overall values of the MSD are smaller.
shown in Fig. 5(c). Note that this peak at ξ = 0 is not a statistical error due to an insufficient number of simulation runs. Our further investigation demonstrates that this peak is still observed in larger simulation sets. Second, the position of the main peak is shifted to a larger value above ξ = 1 while the bell-shaped profile is preserved. For the shorter lag time Δ = 10 the shift is less severe, however, one can distinguish a fine structure of different peaks for ξ values closer to zero. These correspond to clusters of different size, which can be resolved here when the overall values of the MSD are smaller.
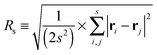 .48 In the limit of sufficiently long trajectories (T → ∞) and for lag times Δ ≥ Δs, where Δs is implicitly defined by the equivalence
.48 In the limit of sufficiently long trajectories (T → ∞) and for lag times Δ ≥ Δs, where Δs is implicitly defined by the equivalence 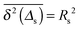 of the time averaged MSD and the squared gyration radius, the time averaged MSD is saturated to the value
of the time averaged MSD and the squared gyration radius, the time averaged MSD is saturated to the value 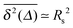 . As the cluster appears fractal on length scales smaller than Rs, it can be reasonably assumed that the size of the cluster is
. As the cluster appears fractal on length scales smaller than Rs, it can be reasonably assumed that the size of the cluster is 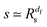 close to the percolation threshold, where df is the fractal dimension. We then relate the distribution of the saturation value of the time averaged MSD to the cluster size distribution
close to the percolation threshold, where df is the fractal dimension. We then relate the distribution of the saturation value of the time averaged MSD to the cluster size distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) in terms of
(s) in terms of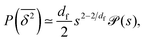
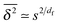 omitting a proportionality constant. Given this latter scaling relation between the saturation value of the time averaged MSD and the size of a cluster, we can use both quantities interchangeably.
omitting a proportionality constant. Given this latter scaling relation between the saturation value of the time averaged MSD and the size of a cluster, we can use both quantities interchangeably.
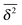 governed by the distribution P. At a given finite lag time Δ, a tracer particle will perform anomalous diffusion of the form
governed by the distribution P. At a given finite lag time Δ, a tracer particle will perform anomalous diffusion of the form 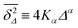 as long as the walker has not yet fully sampled the cluster of size s or, equivalently, the time averaged MSD
as long as the walker has not yet fully sampled the cluster of size s or, equivalently, the time averaged MSD 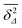 has not reached the saturation value
has not reached the saturation value 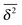 . Among N sample trajectories the fraction showing unrestricted anomalous diffusion will be
. Among N sample trajectories the fraction showing unrestricted anomalous diffusion will be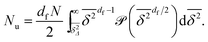
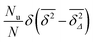 . For the complementary, confined fraction the scatter distribution will be proportional to
. For the complementary, confined fraction the scatter distribution will be proportional to 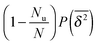 . Therefore the normalised scatter distribution in the long time limit can be written as
. Therefore the normalised scatter distribution in the long time limit can be written as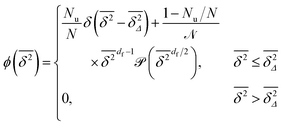
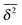 . Here
. Here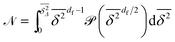
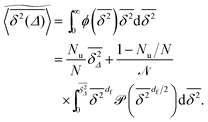
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is unknown, the fact that
is unknown, the fact that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) is a monotonically decaying distribution leads to the relation
(s) is a monotonically decaying distribution leads to the relation 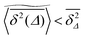 found in Fig. 6 and 7. Eqn (12) tells us that the fluctuations of the time averaged MSD given by ϕ is fully determined by the cluster size
found in Fig. 6 and 7. Eqn (12) tells us that the fluctuations of the time averaged MSD given by ϕ is fully determined by the cluster size ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) distribution as well as the lag time Δ. In percolation theory the form
distribution as well as the lag time Δ. In percolation theory the form![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) ∝ s−τf[(p − pc)sσ]
(s) ∝ s−τf[(p − pc)sσ]![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) ≃ s−τ with 2 < τ < 3.48 Using this information we find that
(s) ≃ s−τ with 2 < τ < 3.48 Using this information we find that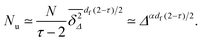
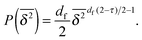
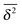 in this relation can be evaluated from the numerical estimation of df and τ in our simulations. From approximately 25
in this relation can be evaluated from the numerical estimation of df and τ in our simulations. From approximately 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 clusters of various size s extracted from 9480 percolation geometries ζ, the fractal dimension df is estimated via the scaling law
000 clusters of various size s extracted from 9480 percolation geometries ζ, the fractal dimension df is estimated via the scaling law 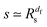 of the gyration radius as df ≈ 1.865 with the confidence interval (1.824, 1.905) and τ ≈ 2.03 from eqn (15).** This measurement leads to the prediction that the exponent is given by −1.028 with the confidence interval (−1.027, −1.029). In the inset of Fig. 7 the decaying part of the distribution ϕ(ξ) at Δ = 103 is plotted in on a logarithmic scale (black circles). The slope of the linear fit (blue line) is −1.063 with the confidence interval (−1.226, −0.899), agreeing well with the theoretically predicted value.
of the gyration radius as df ≈ 1.865 with the confidence interval (1.824, 1.905) and τ ≈ 2.03 from eqn (15).** This measurement leads to the prediction that the exponent is given by −1.028 with the confidence interval (−1.027, −1.029). In the inset of Fig. 7 the decaying part of the distribution ϕ(ξ) at Δ = 103 is plotted in on a logarithmic scale (black circles). The slope of the linear fit (blue line) is −1.063 with the confidence interval (−1.226, −0.899), agreeing well with the theoretically predicted value.
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) has the asymptotic form
(s) has the asymptotic form![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s) ≃ s−τe−cs
(s) ≃ s−τe−cs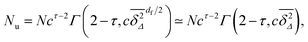
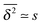 . At large lag times Δ satisfying the criterion
. At large lag times Δ satisfying the criterion 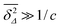 , Nu is approximated as
, Nu is approximated as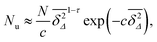
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) will dominate the scatter distribution ϕ. This argument supports the monotonically decaying profiles of ϕ at Δ = 103 and 105 in the plot for p = 0.5 displayed in Fig. 7 which is accordingly the very profile of
will dominate the scatter distribution ϕ. This argument supports the monotonically decaying profiles of ϕ at Δ = 103 and 105 in the plot for p = 0.5 displayed in Fig. 7 which is accordingly the very profile of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) . This also underlines the fact that at time scales for which
. This also underlines the fact that at time scales for which 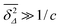 almost all tracer particles undergo confined diffusion. In the opposite case, at short lag times satisfying
almost all tracer particles undergo confined diffusion. In the opposite case, at short lag times satisfying 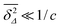 , we see that
, we see that 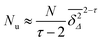 , which is the same as Nu at p = pc with the replacement df → 2. This means that there are particles performing free diffusion over short lag times Δ. Thus ϕ should have a peak around the ergodic value, as shown in the case of Δ = 10 for p = 0.5 in Fig. 6.
, which is the same as Nu at p = pc with the replacement df → 2. This means that there are particles performing free diffusion over short lag times Δ. Thus ϕ should have a peak around the ergodic value, as shown in the case of Δ = 10 for p = 0.5 in Fig. 6.
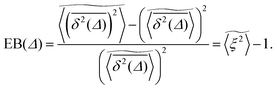
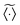 again means the ensemble average over the set of trajectories as well as over the fractal geometries ζ at given lag time Δ and the observation time T, similar to our definition of the ensemble averaged MSD
again means the ensemble average over the set of trajectories as well as over the fractal geometries ζ at given lag time Δ and the observation time T, similar to our definition of the ensemble averaged MSD 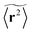 above.
above.
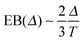 for two-dimensional Brownian motion shown by the dashed slope in the double logarithmic panel for p = 0, see Fig. 8(b).29,92 In this case the fluctuation of the time averaged MSD tend to zero as T → ∞: for this ergodic process the time averaged MSD becomes identical to the ensemble averaged MSD. This conventional convergence continues if the space is filled with obstacles with a concentration p well below the percolation threshold pc, as evidenced for the case p = 0.3 in Fig. 8(d).
for two-dimensional Brownian motion shown by the dashed slope in the double logarithmic panel for p = 0, see Fig. 8(b).29,92 In this case the fluctuation of the time averaged MSD tend to zero as T → ∞: for this ergodic process the time averaged MSD becomes identical to the ensemble averaged MSD. This conventional convergence continues if the space is filled with obstacles with a concentration p well below the percolation threshold pc, as evidenced for the case p = 0.3 in Fig. 8(d).
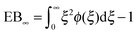
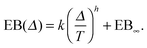
 . (iii) Close to the percolation threshold pc the behaviour of the EB parameter is distinguished from these two regimes. As p is increased towards the critical point pc, h consistently decreases from unity. Thus when the space becomes fractal on all length scales we find that h ≈ 0.80 and EB∞ ≠ 0.
. (iii) Close to the percolation threshold pc the behaviour of the EB parameter is distinguished from these two regimes. As p is increased towards the critical point pc, h consistently decreases from unity. Thus when the space becomes fractal on all length scales we find that h ≈ 0.80 and EB∞ ≠ 0.
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (s), and results in the vanishing time averaged MSD,
(s), and results in the vanishing time averaged MSD,  . Fig. 9 shows that after removing these unit size clusters the EB parameter always converges to EB∞ = 0 for all p values. However, the convergence exponent h remains at h ≈ 0.8, compare also Fig. 10. We note that the convergence law of the EB parameter is not the same as that of fractional Brownian motion, although both models share the same anomalous diffusion scaling (1) and are ergodic (for the present case in the sense of the disorder average). For fractional Brownian motion EB was found to have the convergence form
. Fig. 9 shows that after removing these unit size clusters the EB parameter always converges to EB∞ = 0 for all p values. However, the convergence exponent h remains at h ≈ 0.8, compare also Fig. 10. We note that the convergence law of the EB parameter is not the same as that of fractional Brownian motion, although both models share the same anomalous diffusion scaling (1) and are ergodic (for the present case in the sense of the disorder average). For fractional Brownian motion EB was found to have the convergence form 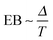 for
for 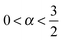 ,
, 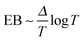 for
for 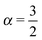 , and
, and 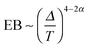 for
for 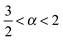 .92–94 Thus, compared to fractional Brownian motion the fractal geometry-induced subdiffusion has a slower convergence to ergodicity. The observed characters of the EB parameter also differ from those of other diffusion models such as scaled Brownian motion, heterogeneous diffusion processes, and continuous time random walk.60,68,95 Therefore, the EB convergence law provides useful information for unveiling the physical origins of anomalous diffusion processes found in complex random media.
.92–94 Thus, compared to fractional Brownian motion the fractal geometry-induced subdiffusion has a slower convergence to ergodicity. The observed characters of the EB parameter also differ from those of other diffusion models such as scaled Brownian motion, heterogeneous diffusion processes, and continuous time random walk.60,68,95 Therefore, the EB convergence law provides useful information for unveiling the physical origins of anomalous diffusion processes found in complex random media.

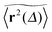 and the time averaged MSD
and the time averaged MSD 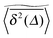 averaged over all individual trajectories and many percolation geometries is observed at any percolation density, individual time averaged MSDs do not always behave like this average and are thus non-ergodic. As we showed here this non-ergodic behaviour is geometry controlled and thus corresponds to strong ergodicity breaking due to a topologically disconnected phase space. Thus, at low obstacle densities p ≪ pc the single particle diffusion exhibits typical ergodic behaviour as seen in the scaling law of the time averaged MSDs, their scatter distribution, and the ergodicity breaking parameter. In this case, the ensemble averaged MSD shows no disparity with individual time averaged MSDs as long as the observation time is sufficiently long. Close to the percolation threshold p ≈ pc, however, such a typical ergodic character is no longer observed. There exists a fraction of time averaged MSDs which significantly deviate from the averaged curve
averaged over all individual trajectories and many percolation geometries is observed at any percolation density, individual time averaged MSDs do not always behave like this average and are thus non-ergodic. As we showed here this non-ergodic behaviour is geometry controlled and thus corresponds to strong ergodicity breaking due to a topologically disconnected phase space. Thus, at low obstacle densities p ≪ pc the single particle diffusion exhibits typical ergodic behaviour as seen in the scaling law of the time averaged MSDs, their scatter distribution, and the ergodicity breaking parameter. In this case, the ensemble averaged MSD shows no disparity with individual time averaged MSDs as long as the observation time is sufficiently long. Close to the percolation threshold p ≈ pc, however, such a typical ergodic character is no longer observed. There exists a fraction of time averaged MSDs which significantly deviate from the averaged curve 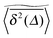 . Using the time averaged occupation probability
. Using the time averaged occupation probability 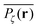 we demonstrated that these outliers correspond to trajectories when the particles motion is restricted on finite clusters of gyration radius Rs significantly smaller than the system size. Other particles moving on the infinite cluster at criticality, however, do show the convergence to the ensemble averaged MSD
we demonstrated that these outliers correspond to trajectories when the particles motion is restricted on finite clusters of gyration radius Rs significantly smaller than the system size. Other particles moving on the infinite cluster at criticality, however, do show the convergence to the ensemble averaged MSD 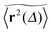 on the single trajectory level. We thus observe ergodic motion for a fraction of particles conditioned to move on the infinite incipient cluster, as reported earlier.77 Due to the mix of confined and freely diffusing trajectories, the scatter distribution of the amplitudes of individual time averaged MSDs shown in Fig. 6 and 7 acquires an asymmetric bell shaped form around the main peak at
on the single trajectory level. We thus observe ergodic motion for a fraction of particles conditioned to move on the infinite incipient cluster, as reported earlier.77 Due to the mix of confined and freely diffusing trajectories, the scatter distribution of the amplitudes of individual time averaged MSDs shown in Fig. 6 and 7 acquires an asymmetric bell shaped form around the main peak at 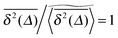 and a second peak at
and a second peak at 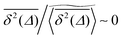 . As shown in Fig. 7, upon increase of the observation time T the latter part is preserved while the main peak around the ergodic value
. As shown in Fig. 7, upon increase of the observation time T the latter part is preserved while the main peak around the ergodic value 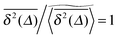 becomes a sharp, almost δ function like peak. Relating the cluster size distribution to the distribution of the time averaged MSDs by eqn (12) we qualitatively explained the observed behaviour of the scatter distribution ϕ. An interesting behaviour is also observed for the ergodicity breaking parameter defined in eqn (21). From numerical analysis we found that EB generally follows an algebraic decay [EB(Δ) − EB∞] ∼ T−h(p) towards the finite residual EB parameter EB∞ reached at T → ∞, and h is a scaling exponent. The exact value of EB∞ depends on the percolation density p. As p is increased to pc the decay of the EB parameter thus deviates from that for typical ergodic diffusion, for which h = 1 and EB∞ = 0. Importantly, on approximating the percolation threshold, p ≈ pc, the EB parameter has a slower convergence with scaling exponent h ≈ 0.8 < 1 as well as a nonzero value EB∞ > 0 due to the contribution of confined particles.
becomes a sharp, almost δ function like peak. Relating the cluster size distribution to the distribution of the time averaged MSDs by eqn (12) we qualitatively explained the observed behaviour of the scatter distribution ϕ. An interesting behaviour is also observed for the ergodicity breaking parameter defined in eqn (21). From numerical analysis we found that EB generally follows an algebraic decay [EB(Δ) − EB∞] ∼ T−h(p) towards the finite residual EB parameter EB∞ reached at T → ∞, and h is a scaling exponent. The exact value of EB∞ depends on the percolation density p. As p is increased to pc the decay of the EB parameter thus deviates from that for typical ergodic diffusion, for which h = 1 and EB∞ = 0. Importantly, on approximating the percolation threshold, p ≈ pc, the EB parameter has a slower convergence with scaling exponent h ≈ 0.8 < 1 as well as a nonzero value EB∞ > 0 due to the contribution of confined particles.
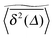 are present in individual time averaged MSDs. The profile of the scatter distribution ϕ(ξ) is quite different from those for critical and lower than critical percolation densities, see Fig. 6. At sufficiently long lag times Δ the distribution decays almost monotonically with the variable ξ, due to the exclusive presence of finite clusters with an exponentially decaying distribution of cluster sizes. This is a purely geometrical effect, as revealed in the distribution of the time averaged MSD which turns out to be independent of the observation time T. In both Fig. 8 and 9 the EB parameter was shown to decay as T−1, corresponding to the convergence to zero of a Brownian particle. This is due to the fact that in this overcrowded obstacle regime the particle explores small clusters with local Euclidean geometries. We note that while the specific values for the scaling exponents and percolation thresholds vary for different lattice types and dimensionality of the embedding dimension the generic features revealed here remain unchanged. This claim is supported by preliminary studies on cubic and hexagonal lattices (not shown).
are present in individual time averaged MSDs. The profile of the scatter distribution ϕ(ξ) is quite different from those for critical and lower than critical percolation densities, see Fig. 6. At sufficiently long lag times Δ the distribution decays almost monotonically with the variable ξ, due to the exclusive presence of finite clusters with an exponentially decaying distribution of cluster sizes. This is a purely geometrical effect, as revealed in the distribution of the time averaged MSD which turns out to be independent of the observation time T. In both Fig. 8 and 9 the EB parameter was shown to decay as T−1, corresponding to the convergence to zero of a Brownian particle. This is due to the fact that in this overcrowded obstacle regime the particle explores small clusters with local Euclidean geometries. We note that while the specific values for the scaling exponents and percolation thresholds vary for different lattice types and dimensionality of the embedding dimension the generic features revealed here remain unchanged. This claim is supported by preliminary studies on cubic and hexagonal lattices (not shown).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 infinite clusters in our simulation while the accepted values in literatures are df = 91/48 and τ = 187/91 ≈ 2.05495, respectively.
000 infinite clusters in our simulation while the accepted values in literatures are df = 91/48 and τ = 187/91 ≈ 2.05495, respectively.