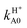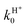Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Born–Oppenheimer and Renner–Teller coupled-channel quantum reaction dynamics of O(3P) + H2+(X2Σg+) collisions
Pablo
Gamallo
*a,
Paolo
Defazio
b,
Miguel
González
*a,
Miguel
Paniagua
c and
Carlo
Petrongolo
d
aDepartament de Química Física i Institut de Química Teòrica i Computacional, Universitat de Barcelona, C/ Martí i Franquès 1, 08028 Barcelona, Spain. E-mail: gamallo@ub.edu; miguel.gonzalez@ub.edu
bDipartimento di Biotecnologie, Chimica, e Farmacia, Università di Siena, Via A. Moro 2, 53100 Siena, Italy
cDepartamento de Química Física Aplicada, Universidad Autónoma de Madrid, C/ Francisco Tomás y Valiente 7, 28049 Cantoblanco, Spain
dIstituto per i Processi Chimico Fisici, Consiglio Nazionale delle Ricerche, Via G. Moruzzi 1, 56124 Pisa, Italy
First published on 10th August 2015
Abstract
We present Born–Oppenheimer (BO) and Renner–Teller (RT) time dependent quantum dynamics studies of the reactions O(3P) + H2+(X2Σg+) → OH+(X3Σ−) + H(2S) and OH(X2Π) + H+. We consider the OH2+ ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ electronic states that correlate with a linear 2Π species. The electronic angular momenta operators
2A′′ and Ã2A′ electronic states that correlate with a linear 2Π species. The electronic angular momenta operators ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) and
and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 are considered in nonadiabatic coupled-channel calculations, where the associated RT effects are due to diagonal VRT potentials that add up to the PESs and to off-diagonal CRT couplings between the potential energy surfaces (PESs). Initial-state-resolved reaction probabilities PI, integral cross sections σI, and rate constants kI are obtained using recent ab initio PESs and couplings and the real wavepacket formalism. Because the PESs are strongly attractive, PI have no threshold energy and are large, σI decrease with collision energy, and kI depend little on the temperature. The
2 are considered in nonadiabatic coupled-channel calculations, where the associated RT effects are due to diagonal VRT potentials that add up to the PESs and to off-diagonal CRT couplings between the potential energy surfaces (PESs). Initial-state-resolved reaction probabilities PI, integral cross sections σI, and rate constants kI are obtained using recent ab initio PESs and couplings and the real wavepacket formalism. Because the PESs are strongly attractive, PI have no threshold energy and are large, σI decrease with collision energy, and kI depend little on the temperature. The ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ PES is up to three times more reactive than the Ã2A′ PES and H2+ rotational effects (j0 = 0, 1) are negligible. The diagonal VRT potentials are strongly repulsive at the collinearity and nearly halve all low-energy observables with respect to the BO ones. The off-diagonal CRT couplings are important at low partial waves, where they mix the
2A′′ PES is up to three times more reactive than the Ã2A′ PES and H2+ rotational effects (j0 = 0, 1) are negligible. The diagonal VRT potentials are strongly repulsive at the collinearity and nearly halve all low-energy observables with respect to the BO ones. The off-diagonal CRT couplings are important at low partial waves, where they mix the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ states up to ∼20%. However, VRT effects predominate over the CRT ones that change at most by ∼19% the BO values of σI and kI. The reaction O(3P) + H2+(X2Σg+) → OH+(X3Σ−) + H(2S) is probably one of the most reactive atom + diatom collisions because its RT rate constant at room temperature is equal to 2.26 × 10−10 cm3 s−1. Within the BO approximation, the present results agree rather well with recent quasiclassical and centrifugal-sudden data using the same PESs.
2A′′ and Ã2A′ states up to ∼20%. However, VRT effects predominate over the CRT ones that change at most by ∼19% the BO values of σI and kI. The reaction O(3P) + H2+(X2Σg+) → OH+(X3Σ−) + H(2S) is probably one of the most reactive atom + diatom collisions because its RT rate constant at room temperature is equal to 2.26 × 10−10 cm3 s−1. Within the BO approximation, the present results agree rather well with recent quasiclassical and centrifugal-sudden data using the same PESs.
I. Introduction
The atom–molecular ion reactions| O(3P) + H2+(X2Σg+) → OH+(X3Σ−) + H(2S), ΔD0 = −2.44 eV proton transfer, H channel, | (1.1) |
| → OH(X2Π) + H+, ΔD0 = −1.74 eV hydrogen transfer, H+ channel, | (1.2) |
The dynamics of the collisions (1.1) and (1.2) was investigated in an old experimental work reported by McClure et al.7 for the deuterated variant D2+, and in some very recent theoretical contributions by Paniagua et al.,8 Martínez et al.,9 and Gannouni et al.10 We plot schematically in Fig. 1 the relevant electronic correlation diagram, simplifying those of ref. 8 and 11 and using the energies given in ref. 8. The two lowest potential energy surfaces (PESs) are barrierless and present strongly bound minima at −8.16 and −7.54 eV with respect to the reactants. The product channels (1.1) and (1.2) are uncoupled within the adiabatic Born–Oppenheimer (BO) approximation and occur, respectively, on the two lowest ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ PESs of OH2+, which transform as 2B1 and 2A1, respectively, in C2v symmetry.
2A′′ and Ã2A′ PESs of OH2+, which transform as 2B1 and 2A1, respectively, in C2v symmetry.
The ground PES (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′) includes the ground electronic state of the water cation, H2O+(
2A′′) includes the ground electronic state of the water cation, H2O+(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1), in the minimum energy path (MEP) connecting reactants and OH+ + H products; while the first excited PES (Ã2A′) includes the first excited electronic state of the water cation, H2O+(Ã2A1), in the MEP involving reactants and OH + H+ products. These two electronic states of H2O+ correspond to the degenerate components of a 2Πu species, when the molecule is in a linear arrangement, and the associated nonadiabatic (NA) Renner–Teller (RT) effects can remarkably influence the dynamics of these collisions, as they also occur for the
2B1), in the minimum energy path (MEP) connecting reactants and OH+ + H products; while the first excited PES (Ã2A′) includes the first excited electronic state of the water cation, H2O+(Ã2A1), in the MEP involving reactants and OH + H+ products. These two electronic states of H2O+ correspond to the degenerate components of a 2Πu species, when the molecule is in a linear arrangement, and the associated nonadiabatic (NA) Renner–Teller (RT) effects can remarkably influence the dynamics of these collisions, as they also occur for the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 − Ã2A1 optical spectrum12 of H2+O.
2B1 − Ã2A1 optical spectrum12 of H2+O.
This is especially important here because the deep potential wells and 2Π configurations are geometrically and energetically close and most collisions proceed via OH2+ intermediate collision-complexes.8,9 When the RT interactions are large, we really have two coupled reactions (1.1) and (1.2) that mainly proceed on both interacting PESs. The contribution of the 2A1 − 2B2 conical-intersection to the dynamics has not been considered in this work, and its influence has been recently studied in the photodissociation of H2O+ of ref. 13.
The ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ PESs are based on ab initio calculations8 at the internally-contracted multi-reference configuration-interaction level, employing the Davidson correction (icMRCI + Q) and the augmented correlation-consistent polarized-valence quadruple-zeta basis set (aug-cc-pvQZ). More than 2000 ab initio points of both PESs were then fitted to a many-body expansion. Paniagua et al.8 also obtained BO quasiclassical trajectories (QCTs), integral cross sections, and thermal rate constants of both reactions and of their deuterated variants (D2+ and HD+) on both PESs. Following that work, Martínez et al.9 employed the quantum-mechanical real wavepacket (RWP) method to obtain BO centrifugal-sudden (CS) initial-state-selected reaction probabilities and cross sections. Large reaction probabilities and decreasing cross sections were obtained for both reaction channels. Channel (1.1) was found to be nearly three times more reactive than (1.2).
2A′′ and Ã2A′ PESs are based on ab initio calculations8 at the internally-contracted multi-reference configuration-interaction level, employing the Davidson correction (icMRCI + Q) and the augmented correlation-consistent polarized-valence quadruple-zeta basis set (aug-cc-pvQZ). More than 2000 ab initio points of both PESs were then fitted to a many-body expansion. Paniagua et al.8 also obtained BO quasiclassical trajectories (QCTs), integral cross sections, and thermal rate constants of both reactions and of their deuterated variants (D2+ and HD+) on both PESs. Following that work, Martínez et al.9 employed the quantum-mechanical real wavepacket (RWP) method to obtain BO centrifugal-sudden (CS) initial-state-selected reaction probabilities and cross sections. Large reaction probabilities and decreasing cross sections were obtained for both reaction channels. Channel (1.1) was found to be nearly three times more reactive than (1.2).
Extending the previous studies,8,9 the present paper reports a RWP study of the dynamics of the (1.1) and (1.2) collisions, at the NA RT coupled-channel (CC) level. We employ the OH2+ ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ PESs of ref. 8 and the NH2 RT matrix elements of Zhou et al.,14 taking into account that these triatoms are isoelectronic and have similar rovibronic structures.12 The RT matrix elements were already employed by Zhou et al.14 and by Lin et al.15 in NH2 and N(2D) + H2(X1Σg+) spectroscopic and collisional studies, respectively. Obviously, the results obtained in this study can be useful for a first estimation of quantum dynamical properties taking into account the presence of nonadiabatic effects in the title reactions. Nevertheless, higher accuracy could be reached once the RT matrix elements for this reaction are explicitly calculated, although small differences between both systems are expected.
2A′′ and Ã2A′ PESs of ref. 8 and the NH2 RT matrix elements of Zhou et al.,14 taking into account that these triatoms are isoelectronic and have similar rovibronic structures.12 The RT matrix elements were already employed by Zhou et al.14 and by Lin et al.15 in NH2 and N(2D) + H2(X1Σg+) spectroscopic and collisional studies, respectively. Obviously, the results obtained in this study can be useful for a first estimation of quantum dynamical properties taking into account the presence of nonadiabatic effects in the title reactions. Nevertheless, higher accuracy could be reached once the RT matrix elements for this reaction are explicitly calculated, although small differences between both systems are expected.
The paper is organized as follows. Section II presents some theoretical and computational details, enlightening the origin, formulae, and physical meanings of the adiabatic (diagonal) and nonadiabatic (off diagonal) RT terms. Section III reports initial-state-resolved reaction probabilities for the lowest rotational states of H2+ in the ground vibrational state, and for the product reaction channels (1.1) and (1.2). We take into account many total angular momentum quantum numbers J, both overall parities p = ±, and the Coriolis couplings among all K ≥ 0 projections of J along the O–(H2+) axis. We report initial-state-resolved integral cross sections and rate constants in Section IV, discussing the influence of the RT effects on both product channels and comparing our BO results with previous QCT8,9 and RWP CS9 calculations and we, finally, present in Section V the main conclusions.
II. Theory and calculation details
Following our previous studies,16–18 the triatomic system ABC is described by the reactant A + BC Jacobi coordinates (R, r, and γ), a body-fixed reference frame with the z axis along R, a spinless rovibronic Hamiltonian Ĥ that contains both the total Ĵ and the electronic![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) angular momentum, and the Cs(M) or C2v(M) permutation-inversion groups that are isomorphic with the Cs or C2v point groups, respectively. As usual, we employ atomic units unless stated otherwise.
angular momentum, and the Cs(M) or C2v(M) permutation-inversion groups that are isomorphic with the Cs or C2v point groups, respectively. As usual, we employ atomic units unless stated otherwise.
The largest RT effects are due to the matrix elements of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2 or
R2 or ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R, which are respectively diagonal or off-diagonal in an adiabatic electronic representation |σΛ〉 with parity σ = ± and orbital angular momentum quantum number Λ ≥ 0 at the linearity. Omitting the
R, which are respectively diagonal or off-diagonal in an adiabatic electronic representation |σΛ〉 with parity σ = ± and orbital angular momentum quantum number Λ ≥ 0 at the linearity. Omitting the ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ± minor contributions, Ĥ contains the
± minor contributions, Ĥ contains the ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2/sin2
R2/sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ, ĴR
γ, ĴR![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R/sin2
R/sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ, and Ĵ±
γ, and Ĵ±![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ operators, and the RT effects are thus responsible for the coupling among three degrees of freedom: the electronic and total rotations around R and the angular motion. The OH2+ electronic states are |−1〉 =
γ operators, and the RT effects are thus responsible for the coupling among three degrees of freedom: the electronic and total rotations around R and the angular motion. The OH2+ electronic states are |−1〉 = ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and |+1〉 = Ã2A′ (or
2A′′ and |+1〉 = Ã2A′ (or ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 and Ã2A1 in C2v, respectively). Eqn (3) of ref. 18 shows that the electronic matrix elements of
2B1 and Ã2A1 in C2v, respectively). Eqn (3) of ref. 18 shows that the electronic matrix elements of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2 and
R2 and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R define two different contributions to the RT effect.
R define two different contributions to the RT effect.
The former RT term is associated with ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2 and is defined by the diagonal potentials
R2 and is defined by the diagonal potentials
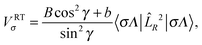 | (2.1) |
The latter RT term is due to ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R and to the real, symmetrical, and (J,K)-dependent off-diagonal couplings
R and to the real, symmetrical, and (J,K)-dependent off-diagonal couplings
 | (2.2) |
Considering H2+ in the ground vibrational state, ν0 = 0, we calculate BO and RT coupled-channel (CC) initial-state-resolved reaction probabilities  , where e0 and (j0,K0) label the initial OH2+ electronic and H2+ rotational state, respectively, and Ecol is the collision energy. We here consider j0 = 0 and 1, Ecol from 0.05 to 0.4 eV, J ≤ 75, and the Coriolis couplings among all K projections. Some checks performed until J = 30 showed that the deep minima involved in this study make necessary the propagation of the full set of K projections. At higher J values a similar behavior is expected according to the general trend observed in insertion reactions occurring through a deep minimum along the MEP.19,20
, where e0 and (j0,K0) label the initial OH2+ electronic and H2+ rotational state, respectively, and Ecol is the collision energy. We here consider j0 = 0 and 1, Ecol from 0.05 to 0.4 eV, J ≤ 75, and the Coriolis couplings among all K projections. Some checks performed until J = 30 showed that the deep minima involved in this study make necessary the propagation of the full set of K projections. At higher J values a similar behavior is expected according to the general trend observed in insertion reactions occurring through a deep minimum along the MEP.19,20
The reaction probabilities are obtained through the real wavepacket (RWP) formalism of Gray and Balint-Kurti,21,22via a scaled and shifted Hamiltonian Ĥs, solving an arccos mapping of the equation of motion. We employ an initial complex Gaussian WP, |ψ0〉 = |a0〉 + i|b0〉, with the R-dependent part given by
 | (2.3) |
| |a1〉 = Ĥs|a0〉 − (1 − Ĥs2)1/2|b0〉, first propagation (complex WP), | (2.4) |
| |an+2〉 = 2Ĥs|an+1〉 − |an〉, other propagations (real WP). | (2.5) |
We propagate CC WPs at J ≤ 10, J = 30, 50, 60, 65, 70, and 75, according to the numerical parameters of Table 1, which correspond to 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042
042![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330 basis states for each electronic species at J = 0, converging the probabilities in the range Ecol = 0.05–0.4 eV within 2% and 40
330 basis states for each electronic species at J = 0, converging the probabilities in the range Ecol = 0.05–0.4 eV within 2% and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations. Owing to the high cost of RT CC calculations and the usual J shifts of the probability thresholds, we employ a J fitting-interpolation technique19 at any (j0,K0) pair for obtaining reaction probabilities
000 iterations. Owing to the high cost of RT CC calculations and the usual J shifts of the probability thresholds, we employ a J fitting-interpolation technique19 at any (j0,K0) pair for obtaining reaction probabilities 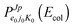 at all non-propagated WP J values. The comparison with some CC data shows that this approach gives good results for probabilities and cross sections, and error bars of ∼2% for room-temperature rates, as Fig. 7 of ref. 20 shows for the conical-intersection collision OH(A2Σ+) + H(2S).
at all non-propagated WP J values. The comparison with some CC data shows that this approach gives good results for probabilities and cross sections, and error bars of ∼2% for room-temperature rates, as Fig. 7 of ref. 20 shows for the conical-intersection collision OH(A2Σ+) + H(2S).
| a Due to the symmetry of the system this corresponds to 70 j values and γ points. | |
|---|---|
| Initial Gaussian g0(R) | |
| Width α, R0 center, and E0 translational energy | 0.3, 30, and 0.4 eV |
| R range and number of grid points | 0–37 and 417 |
| r range and number of grid points | 0.5–18.5 and 207 |
| Associated Legendre functions |jK〉, jmax | 140a |
| R and r absorption start at | 32 and 13.5 |
| Absorption strength | 0.0005 |
| Flux analysis at r | 12.5 |
Cross sections σe0j0(Ecol) and rate constants ke0j0(T), in the temperature range T = 200–900 K, are obtained through the usual expressions
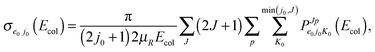 | (2.6) |
 | (2.7) |
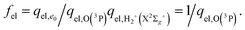 | (2.8) |
(1) 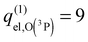 without fine structure, in a fully consistent way with the PES calculation.
without fine structure, in a fully consistent way with the PES calculation.
(2)  , with the SO energy levels26ε2 = 0, ε1 = 158, and ε0 = 227 cm−1 referred to the ground state O(3P2), and with qel,O(3P) increasing with T from 5 to 9. This is the usual procedure which is not, however, strictly consistent with the PES calculation.
, with the SO energy levels26ε2 = 0, ε1 = 158, and ε0 = 227 cm−1 referred to the ground state O(3P2), and with qel,O(3P) increasing with T from 5 to 9. This is the usual procedure which is not, however, strictly consistent with the PES calculation.
(3)  , with ε2′ = −78, ε1′ = 80, and ε0 = 149 cm−1 referred to the O(3P) term.8 This proposal27,28 agrees with the energy zero at the O(3P) + H2+ asymptote without SO and can give a better agreement with the experiment.29 However,
, with ε2′ = −78, ε1′ = 80, and ε0 = 149 cm−1 referred to the O(3P) term.8 This proposal27,28 agrees with the energy zero at the O(3P) + H2+ asymptote without SO and can give a better agreement with the experiment.29 However, 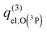 is not fully meaningful, because it evolves from a divergent value at low T up to 9 at high T, and it is not consistent with the PESs.
is not fully meaningful, because it evolves from a divergent value at low T up to 9 at high T, and it is not consistent with the PESs.
In conclusion, the first choice is both fully consistent and physical and we therefore propose using fel = 1/9 through this study, although the other choices are also depicted once for comparison. The H and H+ channels correspond to the cross sections 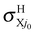 and
and 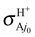 in the BO approximation, respectively, but they are associated with
in the BO approximation, respectively, but they are associated with 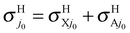 and
and  at the RT level, where the
at the RT level, where the  and
and  cross sections are due to the nonadiabatic couplings CRT of eqn (2.2). Analogous expressions can be considered for the rate constants.
cross sections are due to the nonadiabatic couplings CRT of eqn (2.2). Analogous expressions can be considered for the rate constants.
Note that the parameters of Table 1 produce reliable results just for Ecol ≥ 0.05 eV and that their use at lower energies can give wrong cross sections for the O + H2+ ionic collision. In principle, this drawback can be removed using other initial WPs below 0.05 eV, with larger α, R0, and radial grids, as we did for the H + HeH+ reaction,30 where these modifications described were able to reproduce with high accuracy the close coupling time independent results31 also in the cold energy range. Nevertheless, considering the additional and intensive RT CC calculations that would be necessary, we follow here a simpler strategy. Guided by some time-independent quantum-dynamics calculations through the ABC code32 and by QCT8 results at Ecol < 0.05 eV, in a similar procedure to that employed for the Ne + H2+ reaction,33 we fit here the WP cross sections at Ecol ≥ 0.05 eV using the well known expression34
| σ(Ecol) = CsEscol, | (2.9) |
III. Reaction probabilities
For the reader's convenience, we remember that the product channels H, proton transfer, and H+, hydrogen-atom transfer, eqn (1.1) and (1.2), are separated in the BO approximation, where a given collision always evolves on a single PES (the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ or the Ã2A′ PES). Moreover, the single-state dynamics is affected by the VRT potential (2.1) and the CRT couplings (2.2) vanish identically at J = 0, when the WP remains on the initial surface.
2A′′ or the Ã2A′ PES). Moreover, the single-state dynamics is affected by the VRT potential (2.1) and the CRT couplings (2.2) vanish identically at J = 0, when the WP remains on the initial surface.
Fig. 2 reports BO and RT reaction probabilities PJ−X00 and PJ+A00 for both channels H and H+ and initial electronic states, at J = 0, 10, and 50, p = −(2A′′) or +(2A′), j0 = 0, and K0 = 0. At low J values, the BO probabilities (left panels) do not present any threshold and increase sharply up to high values, with mild oscillations around a value of ∼0.90. The resonance structure found suggests the existence of an indirect insertion mechanism, favored by the deep minima of both PESs. The formation of short-lived collision complexes that break down rather quickly towards the product channels has also been reported in QCT calculations on the same PESs.9 As usual, high J values strongly damp the intensity of the oscillations observed, owing to the averaging effects of the Coriolis couplings among many K values, suggesting an increasing contribution of direct collisions in the process for J ≥ 30, in agreement with QCT results.9
The energy thresholds depend on the BJ(J + 1) centrifugal barriers in the entrance valley and on the J-dependent energy shifts found on the Ã2A′ excited surface, which correlates with the excited OH + H+ products, are much larger than those found on the ground ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ PES. At J = 50, for example, the
2A′′ PES. At J = 50, for example, the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ BO thresholds are equal to ∼0.05 and ∼0.20 eV, respectively. This is consistent with the Ã2A′ D∞h equilibrium geometry, where B ∼ R−2 can achieve large values, with a nearly collinear OHH dynamics on this excited PES, and with the larger values of the
2A′′ and Ã2A′ BO thresholds are equal to ∼0.05 and ∼0.20 eV, respectively. This is consistent with the Ã2A′ D∞h equilibrium geometry, where B ∼ R−2 can achieve large values, with a nearly collinear OHH dynamics on this excited PES, and with the larger values of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ maximum impact parameter, bmax, found in the QCT calculations.8,9 These findings imply that O + H2+ collisions are very reactive and that the H product channel (proton transfer reaction) is favored with respect to the H+ one. We anticipate that cross sections and rate constants confirm these reactivity trends and that including the RT coupling also leads to the same tendency.
2A′′ maximum impact parameter, bmax, found in the QCT calculations.8,9 These findings imply that O + H2+ collisions are very reactive and that the H product channel (proton transfer reaction) is favored with respect to the H+ one. We anticipate that cross sections and rate constants confirm these reactivity trends and that including the RT coupling also leads to the same tendency.
The right panels of Fig. 2 show RT reaction probabilities. The J = 0 RT couplings CRT(2.2) are identically equal to zero, as previously indicated, and they are negligibly small at J ≥ 50. The comparison of the BO and RT reaction probabilities shows that the RT coupling term increases the energy thresholds, reduces significantly the probabilities, and opens both the H and H+ channels at J ∼ 10. The probability lowering occurs even at J = 0, when the two electronic states involved are uncoupled, and it is, therefore, due to the presence of the RT potentials VRTσ(2.1). These are, in fact, quite large in a wide region of the coordinate space, owing to the 1/sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ factor when OH2+ is nearly linear, or due to the large
γ factor when OH2+ is nearly linear, or due to the large ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2 matrix elements when OH2+ bends.14 At low J values, the RT couplings CRT(2.2) between the two electronic states are present but are rather small. Therefore, O + H2+ collisions give preferentially OH+ + H or OH + H+ products when the WP starts on the ground
R2 matrix elements when OH2+ bends.14 At low J values, the RT couplings CRT(2.2) between the two electronic states are present but are rather small. Therefore, O + H2+ collisions give preferentially OH+ + H or OH + H+ products when the WP starts on the ground ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ or excited Ã2A′ surface, respectively. In the latter case, however, the RT effects are larger owing to the linear (2Πu) equilibrium geometry of the minimum. For J > 10, the RT diagonal terms VRTσ are still large but the off diagonal ones CRT decrease and vanish at J ∼ 30.
2A′′ or excited Ã2A′ surface, respectively. In the latter case, however, the RT effects are larger owing to the linear (2Πu) equilibrium geometry of the minimum. For J > 10, the RT diagonal terms VRTσ are still large but the off diagonal ones CRT decrease and vanish at J ∼ 30.
Consequently, the two electronic states involved are, in practice, not RT-coupled at these high partial waves, as the probabilities at J = 50 show. Looking at eqn (2.2), we see that this finding is probably associated with the small 〈![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |
|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R|Ã〉 value at many geometries.14 Dynamic effects can be also operative, with the WP evolution being strongly influenced by the K0 initial value, in agreement with the fast collisions occurring at high-J values. For example, K0 = 0 might be nearly conserved during the high-J dynamics owing to the high number of available K final states opened by RT Coriolis couplings, with CRT ∼ 0. This fact is consistent with a CS approximation that works quite well at the RT level.
R|Ã〉 value at many geometries.14 Dynamic effects can be also operative, with the WP evolution being strongly influenced by the K0 initial value, in agreement with the fast collisions occurring at high-J values. For example, K0 = 0 might be nearly conserved during the high-J dynamics owing to the high number of available K final states opened by RT Coriolis couplings, with CRT ∼ 0. This fact is consistent with a CS approximation that works quite well at the RT level.
We confirm this hypothesis by comparing some CC and CS reaction probabilities in Fig. 3, plotting the BO and RT ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ probabilities P30−X00 at J = 30, p = −, j0 = 0, and K0 = 0. Within the CS approximation, the electronic states are not RT-coupled because only the K = K0 = 0 channel is open and all CRT couplings (eqn (2.2)) are, therefore, identically equal to zero. Other initial conditions give essentially the same scenario. Within the BO approximation, the agreement between CC and CS results is, in general, acceptable, although the CS reaction probability is, as usual, more oscillating and somewhat smaller than the CC one. This is consistent with the CC averaging effects resulting from taking into account 31 K values and the moderate and negative Coriolis couplings that enhance the CC reactivity. On the other hand, the CS approximation works quite well at the RT level because the K-diagonal matrix elements of
2A′′ probabilities P30−X00 at J = 30, p = −, j0 = 0, and K0 = 0. Within the CS approximation, the electronic states are not RT-coupled because only the K = K0 = 0 channel is open and all CRT couplings (eqn (2.2)) are, therefore, identically equal to zero. Other initial conditions give essentially the same scenario. Within the BO approximation, the agreement between CC and CS results is, in general, acceptable, although the CS reaction probability is, as usual, more oscillating and somewhat smaller than the CC one. This is consistent with the CC averaging effects resulting from taking into account 31 K values and the moderate and negative Coriolis couplings that enhance the CC reactivity. On the other hand, the CS approximation works quite well at the RT level because the K-diagonal matrix elements of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2/sin2
R2/sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ, eqn (2.1), predominate over the Coriolis couplings. This fact inhibits more the RT CC probability than the RT CS one that are thus nearly equal, and the initial K0 remains approximately a good quantum number. Note also that RT CC interactions with the excited Ã2A′ electronic state, leading to the OH + H+ products, are fully negligible at J = 30.
γ, eqn (2.1), predominate over the Coriolis couplings. This fact inhibits more the RT CC probability than the RT CS one that are thus nearly equal, and the initial K0 remains approximately a good quantum number. Note also that RT CC interactions with the excited Ã2A′ electronic state, leading to the OH + H+ products, are fully negligible at J = 30.
 | ||
Fig. 3 BO (left) and RT (right) CC (red) and CS (green) reaction probabilities. J = 30, p = −, e0 = ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′, j0 = 0, K0 = 0, Ecol ≥ 0.05 eV. 2A′′, j0 = 0, K0 = 0, Ecol ≥ 0.05 eV. | ||
Fig. 4 shows how the initial K0 value affects the O(3P) + H2+ reaction probabilities, presenting BO and RT probabilities P5−A10 and P5−A11 at e0 = Ã2A′, J = 5, p = −, j0 = 1, and K0 = 0 and 1. The BO results are nearly equal but the RT ones present significant differences depending on the K0 values, because they correspond to the initial Legendre functions |10〉 ∼ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ or |11〉∼sin
γ or |11〉∼sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ for K0 = 0 or 1, respectively. When K0 = 0, the initial WP density is largest at γ = 0 and the RT linear barrier ∼〈Ã|
γ for K0 = 0 or 1, respectively. When K0 = 0, the initial WP density is largest at γ = 0 and the RT linear barrier ∼〈Ã|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R2|Ã〉/sin2
R2|Ã〉/sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ strongly reduces the reactivity. In contrast, the maximum initial density of the latter WP, K0 = 1, occurs at γ = 90°; that is to say, along a more attractive region, where the linear barrier has a minimal contribution. Contrasting the H and H+ reaction channels, we see that ∼15–20% of the WP jumps from the initial excited surface, Ã2A′, to the ground one,
γ strongly reduces the reactivity. In contrast, the maximum initial density of the latter WP, K0 = 1, occurs at γ = 90°; that is to say, along a more attractive region, where the linear barrier has a minimal contribution. Contrasting the H and H+ reaction channels, we see that ∼15–20% of the WP jumps from the initial excited surface, Ã2A′, to the ground one, ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′, at both K0 values.
2A′′, at both K0 values.
 | ||
| Fig. 4 BO (black) and RT (red and blue) CC reaction probabilities. J = 5, p = −, e0 = Ã2A′, j0 = 1, K0 = 0 (left) and 1 (right), Ecol ≥ 0.05 eV. | ||
All these results are typical of barrierless and exothermic RT collisions on bound PESs, because we found similar VRT and K0 effects in the C(1D) + H2(1Σg+) collisions.18
IV. Cross sections and rate constants
Fig. 5 shows the BO and RT reaction cross sections σXj0 and σAj0 for both channels H and H+ and initial electronic states, at j0 = 0 and 1, and Table 2 reports some representative numerical results for j0 = 0. We shall first discuss BO cross sections and then show how RT effects modify the reactivity. The collision energy and rotational effects reflect the barrierless and rather isotropic character of both PESs; that is to say, the cross sections decrease with Ecol without appreciable oscillations and are negligibly affected by the H2+ rotation level j0. The ground-state BO decreases with the collision energy faster than the excited-state BO
decreases with the collision energy faster than the excited-state BO  . For example, Table 2 shows that the BO σHX0 or
. For example, Table 2 shows that the BO σHX0 or 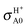 is lowered by a factor of 3.2 or 1.7, respectively, from 0.05 to 0.4 eV, suggesting that for the ground PES it is easier for the system to depart from the MEP as Ecol increases in comparison to the excited PES.
is lowered by a factor of 3.2 or 1.7, respectively, from 0.05 to 0.4 eV, suggesting that for the ground PES it is easier for the system to depart from the MEP as Ecol increases in comparison to the excited PES.
 | ||
Fig. 5 BO (black) and RT (red and blue) CC cross sections. e0 = ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ (above) and Ã2A′ (below), j0 = 0 (left) and 1 (right), Ecol ≥ 0.05 eV. 2A′′ (above) and Ã2A′ (below), j0 = 0 (left) and 1 (right), Ecol ≥ 0.05 eV. | ||
The ground state is also more reactive than the excited one, up to ∼3 times at 0.05 eV, owing to its more attractive character and larger exothermicity shown in Fig. 1, and to the smaller J shifts of the reaction probabilities in Fig. 2. Therefore, more partial waves contribute to the ground-state cross sections in the energy range investigated. As Ecol increases, the reactivity of the electronic states becomes progressively more similar: at j0 = 0, e.g., the H/H+ BO product branching ratio  decreases from 2.9 to 1.5 in the Ecol range 0.05–0.4 eV. On the overall, the proton transfer reaction giving the OH+ + H products is preferred with respect to the hydrogen transfer one leading to OH + H+.
decreases from 2.9 to 1.5 in the Ecol range 0.05–0.4 eV. On the overall, the proton transfer reaction giving the OH+ + H products is preferred with respect to the hydrogen transfer one leading to OH + H+.
The inclusion of the RT effects confirms the behavior of the cross sections with respect to the collision energy, to the initial electronic and rotational states, and to the product channels. The results presented in Fig. 5 and Table 2 clearly point out the differences between BO and RT treatments and the different role of the contributions to RT effects, namely the adiabatic linear barriers VRT(2.1) and the nonadiabatic couplings CRT(2.2) where the former is by far that predominant. In this table, σH0 = σHX0 + σHA0,  , the difference σe00(RT) − σe00(BO) is mainly associated with VRT, whereas σHA0(RT) and
, the difference σe00(RT) − σe00(BO) is mainly associated with VRT, whereas σHA0(RT) and  are essentially due to CRT. In fact, the latter cross sections correspond to NA jumps from the reactant channel on the excited Ã2A′ PES to the product channel on the ground
are essentially due to CRT. In fact, the latter cross sections correspond to NA jumps from the reactant channel on the excited Ã2A′ PES to the product channel on the ground ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ surface (see Fig. 1), and these transitions are induced by the 〈
2A′′ surface (see Fig. 1), and these transitions are induced by the 〈![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |
|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) R|Ã〉 matrix element. RT cross sections are smoother than the BO ones, for example, the RT ratio σH0(0.05)/σH0(0.4) is equal to 2.2 whereas the BO one σHX0(0.05)/σHX0(0.4) is 3.2. In particular, RT effects decrease the reactivity of the system at low-intermediate Ecol values, e.g., it is reduced up to a factor of 1.6 with respect to the BO one at 0.05 eV. This is consistent with the probability results and is due to the diagonal RT barriers VRT. The nonadiabatic couplings CRT are more important when the WP starts on the excited Ã2A′ PES. At Ecol = 0.05 eV, for example, the RT σHA0 and σHA1 contribute by 13.2 and 15.8%, respectively, to the total RT depletion cross sections
R|Ã〉 matrix element. RT cross sections are smoother than the BO ones, for example, the RT ratio σH0(0.05)/σH0(0.4) is equal to 2.2 whereas the BO one σHX0(0.05)/σHX0(0.4) is 3.2. In particular, RT effects decrease the reactivity of the system at low-intermediate Ecol values, e.g., it is reduced up to a factor of 1.6 with respect to the BO one at 0.05 eV. This is consistent with the probability results and is due to the diagonal RT barriers VRT. The nonadiabatic couplings CRT are more important when the WP starts on the excited Ã2A′ PES. At Ecol = 0.05 eV, for example, the RT σHA0 and σHA1 contribute by 13.2 and 15.8%, respectively, to the total RT depletion cross sections  of O + H2+.
of O + H2+.
On the overall, at Ecol ≥ 0.1 eV both VRT and CRT increase a little the observable H/H+ RT branching ratios 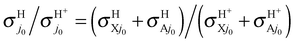 with respect to the BO ones
with respect to the BO ones  . The largest variations occur at 0.1 eV, from the BO ratios of 2.38 and 2.28 at j0 = 0 and 1, respectively, to the RT values equal to 2.71 at both j0; that is a 13.9 or 18.9% of increasing at these rotational levels. This finding is essentially associated with
. The largest variations occur at 0.1 eV, from the BO ratios of 2.38 and 2.28 at j0 = 0 and 1, respectively, to the RT values equal to 2.71 at both j0; that is a 13.9 or 18.9% of increasing at these rotational levels. This finding is essentially associated with 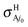 that correspond to Ã2A′ →
that correspond to Ã2A′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ nonadiabatic transitions. For the
2A′′ nonadiabatic transitions. For the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ PES the main result arising from the RT effects is the lowering of the reactivity, as a consequence of the VRT barrier, with a negligible production of the OH + H+ nonadiabatic reaction channel. We close this discussion by plotting in Fig. 6 BO and RT averaged cross sections
2A′′ PES the main result arising from the RT effects is the lowering of the reactivity, as a consequence of the VRT barrier, with a negligible production of the OH + H+ nonadiabatic reaction channel. We close this discussion by plotting in Fig. 6 BO and RT averaged cross sections  and
and 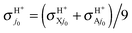 with fel = 1/9, at j0 = 0 and 1. We clearly see the very small role of the H2+ rotational excitation and the H/H+ product branching ratio in the Ecol range investigated.
with fel = 1/9, at j0 = 0 and 1. We clearly see the very small role of the H2+ rotational excitation and the H/H+ product branching ratio in the Ecol range investigated.
 | ||
| Fig. 6 BO (black) and RT (red and blue) CC averaged cross sections, j0 = 0 (full) and 1 (dots), Ecol ≥ 0.05 eV, fel = 1/9. | ||
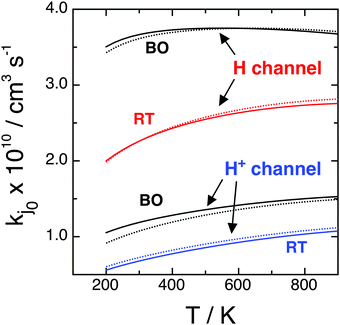
As stated in Section II, rate constants are obtained from RWP cross sections at Ecol ≥ 0.05 eV and from the extrapolated ones down to Ecol = 0.005 eV viaeqn (2.9). Table 3 and Fig. 7 are related to Table 2 and Fig. 6, respectively, and present the H and H+ BO and RT rate constants ke0j0 and kj0 from 200 to 900 K, with 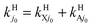 and
and  , with fel = 1/9 and j0 = 0 and 1. These data are consistent with the σ results for the H/H+ branching ratio, for the reactivity of the initial electronic and rotational states, and for the BO or RT findings. All rate constants increase moderately with temperature. Regarding the BO results, kHX0 is almost independent of T and
, with fel = 1/9 and j0 = 0 and 1. These data are consistent with the σ results for the H/H+ branching ratio, for the reactivity of the initial electronic and rotational states, and for the BO or RT findings. All rate constants increase moderately with temperature. Regarding the BO results, kHX0 is almost independent of T and  increases by 46% from 200 to 900 K. On the other hand, RT rate constants increase for both reaction channels by 38 and 91% for kH0 and
increases by 46% from 200 to 900 K. On the other hand, RT rate constants increase for both reaction channels by 38 and 91% for kH0 and  , respectively. As expected, the VRT and CRT effects on the cross sections are confirmed for the rate constants: the former nearly halves the reactivity at room T and the latter is rather small. Table 3 also shows that the RT j0 = 0 branching ratio
, respectively. As expected, the VRT and CRT effects on the cross sections are confirmed for the rate constants: the former nearly halves the reactivity at room T and the latter is rather small. Table 3 also shows that the RT j0 = 0 branching ratio  at 300 K is equal to 3.32 and a value of 3.10 is obtained for j0 = 1. The differences between these values and the BO ones are of only ∼8%, i.e., less than one half of the cross-section values owing to the integration on Ecol. Note that the large kH values for the H channel imply that O(3P) + H2+(2Σg+) → OH+(X3Σ−) + H(2S) is a highly reactive atom + diatom collision. In fact, at room temperature and at the RT level we have kH0(300 K) = kH1(300 K) = 2.26 × 10−10 cm3 s−1 and this value is larger than that of similar RT reactive systems, namely 1.39 × 10−10 cm3 s−1 for C(1D) + H2(1Σg+)18 and 2.20 × 10−12 cm3 s−1 for N(2D) + H2(1Σg+).19 The present H channel reaction (1.1) is so reactive owing to barrierless and strongly attractive character of the ground PES and to the larger exothermicity.
at 300 K is equal to 3.32 and a value of 3.10 is obtained for j0 = 1. The differences between these values and the BO ones are of only ∼8%, i.e., less than one half of the cross-section values owing to the integration on Ecol. Note that the large kH values for the H channel imply that O(3P) + H2+(2Σg+) → OH+(X3Σ−) + H(2S) is a highly reactive atom + diatom collision. In fact, at room temperature and at the RT level we have kH0(300 K) = kH1(300 K) = 2.26 × 10−10 cm3 s−1 and this value is larger than that of similar RT reactive systems, namely 1.39 × 10−10 cm3 s−1 for C(1D) + H2(1Σg+)18 and 2.20 × 10−12 cm3 s−1 for N(2D) + H2(1Σg+).19 The present H channel reaction (1.1) is so reactive owing to barrierless and strongly attractive character of the ground PES and to the larger exothermicity.
In Fig. 8 we compare the present BO CC cross sections and rate constants for j0 = 0 with previous CS and QCT results,9 with fel = 1/9 everywhere. CC and CS data of both channels compare very well, as we have found for probabilities, whereas H-channel QCT results are slightly higher, implying that quantum effects are little important in the investigated reactions.9
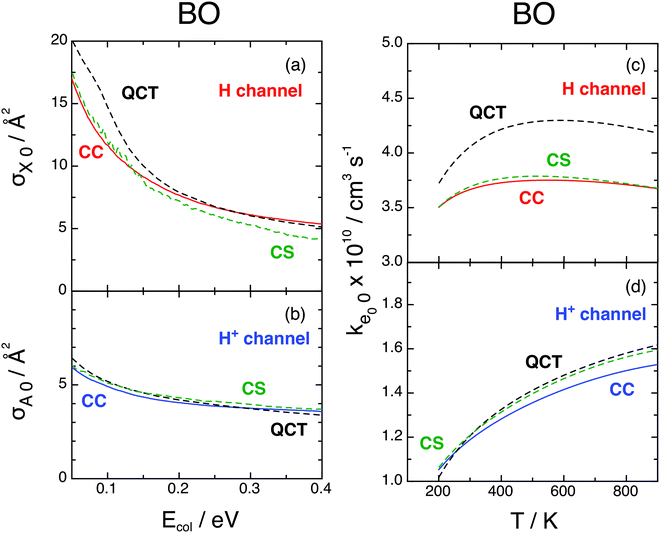 | ||
Fig. 8 BO cross sections (left, Ecol ≥ 0.05 eV) and rate constants (right), e0 = ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ (above) and Ã2A′ (below), j0 = 0, fel = 1/9. CC (red and blue), CS (green), QCT (black). CS and QCT data from ref. 9. 2A′′ (above) and Ã2A′ (below), j0 = 0, fel = 1/9. CC (red and blue), CS (green), QCT (black). CS and QCT data from ref. 9. | ||
Finally, we analyze the influence of the different choices (1), (2), and (3) of the O(3P) partition function presented at the end of Section II, plotting in Fig. 9 the associated RT rate constants k0 = kX0 + kA0 at j0 = 0. We remember that (1) does not consider the O(3P) fine structure, which is taken into account by (2) and (3) with energy zero at the O(3P2) state or at the O(3P) term, respectively. At not too large T values we have f(2)el > f(1)el > f(3)el and, therefore, choices (2) and (3) present opposite effects: the former enhances whereas the latter inhibits k with respect to f(1)el. Moreover, f(2)el decreases whereas f(3)el increases with T. This behavior is confirmed in Fig. 9, where all rate constants increase with T, especially those of the H+ channel, choices (1) and (3) give similar results, and k due to choice (2) is significantly larger. At 300 K kH0 varies within (2.07–3.02) × 10−10 cm3 s−1 and  within (0.55–0.87) × 10−10 cm3 s−1 according to the three choices of fel, and these intervals increase at smaller T. These effects could be validated by further studies that consider the O(3PM) fine structure at low temperatures.
within (0.55–0.87) × 10−10 cm3 s−1 according to the three choices of fel, and these intervals increase at smaller T. These effects could be validated by further studies that consider the O(3PM) fine structure at low temperatures.
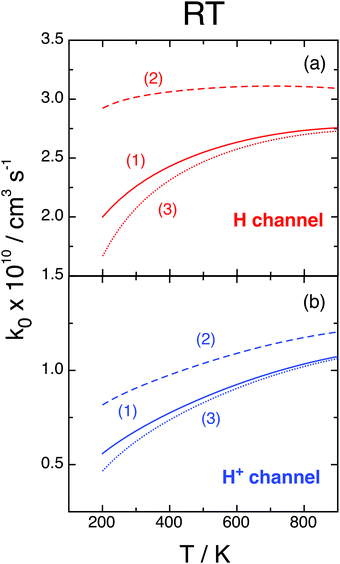 | ||
| Fig. 9 RT rate constants, j0 = 0, fel from eqn (2.8) with qel,O(3P) from choices (1), (2), and (3). | ||
V. Summary and conclusions
We have investigated the reactive collisions O(3P) + H2+(X2Σg+) → OH+(X3Σ−) + H(2S), the H channel, and the → OH(X2Π) + H+, H+ channel, on the OH2+![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ BO uncoupled or RT coupled PESs. Highly accurate MRCI PESs and
2A′′ and Ã2A′ BO uncoupled or RT coupled PESs. Highly accurate MRCI PESs and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) matrix elements, a CC quantum theory of RT atom + diatom collisions up to J = 75, and the time-dependent RWP and flux methods were employed. The electronic states are the degenerate components of a linear 2Π species and are, therefore, strongly perturbed by RT effects due to
matrix elements, a CC quantum theory of RT atom + diatom collisions up to J = 75, and the time-dependent RWP and flux methods were employed. The electronic states are the degenerate components of a linear 2Π species and are, therefore, strongly perturbed by RT effects due to ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) , which modify the BO PESs and couple the electronic states via RT potentials VRT(2.1) and couplings CRT(2.2), respectively. The forms and roles of these RT terms are thoroughly discussed, pointing out that they describe the couplings among total rotation, electronic rotation, and angular motion. In particular, VRT represents a dynamical and linear barrier added to the usual BO PES whereas CRT couples the electronic states when K > 0.
, which modify the BO PESs and couple the electronic states via RT potentials VRT(2.1) and couplings CRT(2.2), respectively. The forms and roles of these RT terms are thoroughly discussed, pointing out that they describe the couplings among total rotation, electronic rotation, and angular motion. In particular, VRT represents a dynamical and linear barrier added to the usual BO PES whereas CRT couples the electronic states when K > 0.
The present RT CC work extends BO QCT and RWP CS studies on the uncoupled PESs reported recently by some of us,8,9 showing that all the theoretical results agree rather well and give a common picture of the reaction dynamics. Thus, reaction probabilities are large and without threshold energy, the cross sections σ decrease with Ecol from large threshold values, and the rate constants k show a small dependence with T, because the PESs are barrierless. The ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ ground electronic state is more reactive up to a factor of ∼3, owing to its larger attractive character and exothermicity, the H product channel is thus favored, and the H2+ rotational excitation does not practically affect the σ and k values.
2A′′ ground electronic state is more reactive up to a factor of ∼3, owing to its larger attractive character and exothermicity, the H product channel is thus favored, and the H2+ rotational excitation does not practically affect the σ and k values.
Owing to the repulsive collinear potentials VRT(2.1), the RT energy thresholds are larger and the reaction probabilities are smaller than the BO ones. This finding is more evident for the Ã2A′ excited state, owing to its 2Πu equilibrium geometry where the rotational constant B is large. The RT couplings CRT(2.2) mix the electronic states up to ∼20% and are more important when the WP starts on the excited PES at low J values and K0 = 0. These couplings, however, decrease quickly at high J values and, on the overall, the reactivity is inhibited when K0 and/or K = 0. These results are explained by considering the expressions of the diagonal and off-diagonal RT terms, the linear values of the initial Legendre functions, and the good agreement between BO CC and CS probabilities at K0 = 0, which implies that the collision dynamics does not appreciably modify the initial K0 value. RT effects smooth the σ(Ecol) curves with respect to the BO ones and the RT diagonal barriers VRT nearly halve the σ and k values at low energy and room temperature. The RT nonadiabatic couplings CRT modify these observables and the H/H+ product branching ratios up to ∼19% with respect to the BO ones. The collision O(3P) + H2+(X2Σg+) → OH+(X3Σ−) + H(2S) is highly reactive, as it comes out from kj0(300) = 2.26 × 10−10 cm3 s−1.
In summary, we note that other nonadiabatic interactions could be important for the collisional dynamics in OH2+ and deuterated variants at low energies. Looking at the correlation diagrams of Fig. 1 and to those more detailed in ref. 8 and 11, we see for example:
(1) A RT-induced charge-transfer quenching (q), OH(X2Π) + D+ → OH+(X3Σ−) + D, and an exchange-quenching (eq), OH(X2Π) + D+ → OD+(X3Σ−) + H, which are in competition with the exchange process (e), OH(X2Π) + D+ → OD(X2Π) + H+, but not with the formation of O(3P) + HD+ that is closed below Ecol = 1.62 eV. Preliminary results suggest a branching ratio [(q) + (eq)]/(e) greater than one, that is significant RT effects larger than those in O(3P) + H2+.
(2) A ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 − Ã2A1 conical intersection (CI) in the O(3P) + H2+(X2Σg+) arrangement, which might decrease the efficiency of the present reactions, mainly for the H+ channel, opening a third product channel, OH+(a1Δ) + H(2S). We plan to investigate this point in a nonadiabatic future work considering
2B2 − Ã2A1 conical intersection (CI) in the O(3P) + H2+(X2Σg+) arrangement, which might decrease the efficiency of the present reactions, mainly for the H+ channel, opening a third product channel, OH+(a1Δ) + H(2S). We plan to investigate this point in a nonadiabatic future work considering ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) − Ã −
− Ã − ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) three-state CI and RT effects.
three-state CI and RT effects.
On the other hand, intersystem-crossing effects among the ã4A′′ quartet, shown in Fig. 1 of ref. 8 and 11, and the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A′′ and Ã2A′ doublets are not expected to be important, taking into account the O(3P,1D) + H2(X1Σg+)35 and O+(4S) + H2(X1Σg+)36 dynamical studies.
2A′′ and Ã2A′ doublets are not expected to be important, taking into account the O(3P,1D) + H2(X1Σg+)35 and O+(4S) + H2(X1Σg+)36 dynamical studies.
Acknowledgements
This work was supported by the Spanish Ministry of Science and Innovation (MICINN projects CTQ2011-27857-C02-01 and CONSOLIDER INGENIO 2010 under grant no. CSD2009-00038 entitled “Molecular Astrophysics: the Herschel and Alma era”). Thanks are also given to the “Generalitat de Catalunya” (Autonomous Government of Catalonia; refs. 2014SGR 25, 2014SGR 1582 and XRQTC) for some help. We gratefully acknowledge H. Guo and D. Xie for the matrix elements of the electronic angular momenta.References
- P. A. Wehinger, S. Wickoff, G. Herzberg and H. Lew, Astrophys. J., 1974, 190, L43 CrossRef CAS PubMed.
- W. T. Huntress Jr., Astrophys. J., Suppl. Ser., 1977, 33, 495 CrossRef.
- G. Herzberg, Ann. Geophys., 1980, 36, 605 CAS.
- E. F. Van Dishoeck, E. Herbst and D. A. Neufeld, Chem. Rev., 2013, 113, 9043 CrossRef CAS PubMed.
- P. Gamallo, F. Huarte-Larrañaga and M. González, J. Phys. Chem. A, 2013, 117, 5393 CrossRef CAS PubMed.
- R. Martínez, J. D. Sierra, S. K. Gray and M. González, J. Chem. Phys., 2006, 125, 164305 CrossRef PubMed.
- D. J. McClure, C. H. Douglas and W. R. Gentry, J. Chem. Phys., 1977, 67, 2362 CrossRef CAS PubMed.
- M. Paniagua, R. Martínez, P. Gamallo and M. González, Phys. Chem. Chem. Phys., 2014, 16, 23594 RSC.
- R. Martínez, M. Paniagua, J. Mayneris-Perxachs, P. Gamallo and M. González, Phys. Chem. Chem. Phys. Search PubMed , under revision.
- M. A. Gannouni, N. E. Jaidane, P. Halvick, T. Stoecklin and M. Hochlaf, J. Chem. Phys., 2014, 140, 184306 CrossRef CAS PubMed.
- K. T. Gillen, B. H. Mahan and J. S. Winn, J. Chem. Phys., 1973, 58, 5373 CrossRef CAS PubMed.
- M. Brommer, B. Weis, B. Follmeg, P. Rosmus, S. Carter, N. C. Handy, H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1993, 98, 5222 CrossRef CAS PubMed.
- J. Suárez, L. Méndez and I. Rabadán, J. Phys. Chem. Lett., 2015, 6, 72 CrossRef PubMed.
- S. Zhou, Z. Li, D. Xie, S. Y. Lin and H. Guo, J. Chem. Phys., 2009, 130, 184307 CrossRef PubMed.
- S. H. Lin, H. Guo, B. Jiang, S. Zhou and D. Xie, J. Phys. Chem. A, 2010, 114, 9655 CrossRef CAS PubMed.
- C. Petrongolo, J. Chem. Phys., 1988, 89, 1297 CrossRef CAS PubMed.
- P. Defazio and C. Petrongolo, J. Chem. Phys., 2006, 125, 064308 CrossRef PubMed.
- P. Defazio, B. Bussery-Honvault, P. Honvault and C. Petrongolo, J. Chem. Phys., 2011, 135, 114308 CrossRef PubMed.
- P. Gamallo, P. Defazio, M. González and C. Petrongolo, J. Chem. Phys., 2008, 129, 244307 CrossRef PubMed.
- P. Gamallo, S. Akpinar, P. Defazio and C. Petrongolo, J. Chem. Phys., 2013, 139, 094303 CrossRef PubMed.
- S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 1998, 108, 950 CrossRef CAS PubMed.
- A. J. H. M. Meijer, E. M. Goldfield, S. K. Gray and G. G. Balint-Kurti, Chem. Phys. Lett., 1998, 293, 270 CrossRef CAS.
- R. Chen and H. Guo, J. Chem. Phys., 1996, 105, 3569 CrossRef CAS PubMed.
- G.-J. Kroes and D. Neuhauser, J. Chem. Phys., 1996, 105, 8690 CrossRef CAS PubMed.
- S. Y. Lin and H. Guo, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 022703 CrossRef.
- NIST Atomic Spectra Database Levels, http://physics.nist.gov/PhysRef Data/ASD/levels_form.html.
- F. Matzkies and U. Manthe, J. Chem. Phys., 1998, 108, 4828 CrossRef CAS PubMed.
- U. Manthe, G. Capecchi and H.-J. Werner, Phys. Chem. Chem. Phys., 2004, 6, 5026 RSC.
- P. Gamallo, R. Francia, R. Martínez, R. Sayós and M. González, J. Phys. Chem. A, 2012, 116, 11783 CrossRef CAS PubMed.
- P. Gamallo, S. Akpinar, P. Defazio and C. Petrongolo, J. Phys. Chem. A, 2014, 118, 6451 CrossRef CAS PubMed.
- D. De Fazio, Phys. Chem. Chem. Phys., 2014, 16, 11662 RSC.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128 CrossRef CAS.
- P. Gamallo, F. Huarte-Larrañaga and M. González, J. Phys. Chem. A, 2013, 117, 5393 CrossRef CAS PubMed.
- R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford University Press, Oxford, 1987, p. 58 Search PubMed.
- T.-H. Chu, X. Zhang and K.-L. Han, J. Chem. Phys., 2005, 122, 214301 CrossRef PubMed and references therein.
- R. Martínez, J. D. Sierra, S. K. Gray and M. González, J. Chem. Phys., 2006, 125, 164305 CrossRef PubMed , and references therein.
| This journal is © the Owner Societies 2015 |