Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluid phase interface properties of acetone, oxygen, nitrogen and their binary mixtures by molecular simulation†
Stefan
Eckelsbach
and
Jadran
Vrabec
*
Thermodynamics and Energy Technology, University of Paderborn, 33098 Paderborn, Germany. E-mail: jadran.vrabec@upb.de; Fax: +49 5251 60 3522; Tel: +49 5251 60 2421
First published on 21st September 2015
Abstract
Vapor–liquid equilibria (VLE) of the pure substances acetone, oxygen and nitrogen as well as their binary mixtures are studied by molecular dynamics (MD) simulation with a direct approach. Thereby, particular attention is paid to the interface behavior on the molecular level, yielding total and partial density profiles as well as surface tension data. The classical approach by van der Waals is used to analyze the total density profiles. It is found that an extended function is needed to describe those profiles for the mixtures containing acetone, due to the strong adsorption of the volatile component at the vapor side of the interface. Based on these representations the interface thickness is studied. The surface tension results are compared to experimental data, correlations thereof and results from other molecular approaches. Due to the scarcity of experiments, the parachor method is employed to obtain predictive surface tension data for the mixtures. Following the same approach, the present surface tension results are correlated for the mixtures containing acetone.
1 Introduction
Interfacial properties are of crucial interest for processes containing two or more phases, which is basically the default case for complex technical and natural systems, including separation processes, chemical reactors, engines and every system containing droplets.1,2 A fundamental understanding of droplet dynamics is thus essential for the optimization of technical processes or the prediction of natural phenomena. Particularly in energy technology, many processes that are associated with droplets occur under extreme conditions of temperature or pressure, e.g. flash boiling in combustion chambers. Such processes are actively being used, although striking gaps remain in the essential understanding of droplet dynamics.2 At the same time, thermodynamic data for most technically interesting fluids are scarce or even unavailable, despite the large experimental effort that was invested over the last century into their measurement.3 This particularly applies to mixtures of two or more components and systems under extreme conditions.In contrast to phenomenological approaches, molecular modeling and simulation is based on a sound physical foundation and is therefore well suited for the prediction of such properties and processes under extreme ambient conditions. In this work a model fuel (consisting of acetone, oxygen and nitrogen) was investigated, using mainly molecular modeling and simulation. MD simulations of VLE interfaces were carried out, focusing on high temperatures in the region that is not too far from the critical line of the binary mixtures containing acetone. Thereby, interface behavior was studied on the molecular level with respect to important thermodynamic properties such as the surface tension. The results are provided as reference values for larger scale models, i.e. computational fluid dynamics, within the collaborative research center SFB-TRR 75 (“Droplet dynamics under extreme ambient conditions”), which investigates this model fuel, particularly the injection of acetone droplets into a gaseous oxygen + nitrogen environment under high pressure.2
2 Simulation
Direct simulations of the VLE were carried out, with particular attention to the interface region, using the highly scalable MD code ls1 mardyn.4 The simulations were performed for the three pure substances acetone, oxygen and nitrogen as well as their binary mixtures. Molecular force field models from previous works of our group were used, i.e. models with two Lennard-Jones sites and one point quadrupole for oxygen and nitrogen5 and a model with four Lennard-Jones sites, one point dipole and one point quadrupole for acetone.6 They were optimized to experimental VLE data (saturated liquid density, vapor pressure and critical temperature) of the pure substances. For each binary mixture, one additional unlike interaction parameter was adjusted to one experimental data point of the vapor pressure or the Henry's law constant,6,7 thus yielding predictive simulation results of interfacial behavior. The parameters of the used force field models were included as ESI.†The present simulation volumes were created as rectangular cuboids, elongated in z direction, with a liquid phase surrounded by the coexisting vapor phase under periodic boundary conditions. The saturated densities of the bulk phases that are needed for this initial setup were taken from earlier simulations, likewise the equilibrium composition of the phases in case of mixtures.6 Due to the inhomogeneity of the systems, a long range correction has to be used, which takes the varying density along the z axis into account. The approach of Janeček8 solves this problem and different implementations based on his method have recently been suggested.9–12 Here, the implementation by Werth et al.13 was used for molecular interactions exceeding the cutoff radius of 2.2 nm. This method was extended for multi-site Lennard-Jones models,13 as they were used in this work, by the conjunction with a centre-of-mass cutoff scheme based on angle averaging.14 It was implemented in the simulation code to correct the potential energy, virial and force. This approach is based on the continuous calculation of the density profiles throughout the simulation, which were also evaluated in this work. However, another formulation of the long range correction, based on Janeček's method, was recently suggested by MacDowell and Blas9 as well as Martínez-Ruiz et al.15 avoiding the continuous evaluation of the density profile. Based on previous work of our group on the regarded systems,6,16 including the binary mixtures, the knowledge of the VLE data was used to straightforwardly conduct simulations in the canonical ensemble. After sufficient equilibration, the molecular systems were sampled with a time step length of 1 fs over 2 ns containing 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and for state points closer to the critical region 48
000 and for state points closer to the critical region 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. Further details of the simulation setup are given as ESI.†
000 molecules. Further details of the simulation setup are given as ESI.†
3 Density profiles across the VLE interface
Among different proposed representations for the ensemble averaged density profile through the VLE interface,17–19 the classical equation following van der Waals20 | (1) |
The density profile across the VLE interface of pure acetone is exemplarily plotted in Fig. 1 for a temperature of 450 K. Note that the critical temperature is about Tc = 508.1 K.23 The simulation data can well be described with function (1) and show only small sinusoidal deviations on the vapor side as seen in prior work for a simple Lennard-Jones model fluid.21 The relative deviations on this side are larger than on the liquid side of the interface mainly because of statistical reasons. First, there are significantly less molecules in the vapor phase, such that the statistical uncertainties are higher, second, the relative deviations are larger due to the lower vapor density. Nonetheless, the relative deviations are small in the entire considered spatial range, i.e. below 1%, and the data in the interfacial region are well represented showing deviations on roughly the same level.
 | ||
Fig. 1 Density profile and deviations from the fitting function in case of acetone at 450 K through the VLE interface. ○ simulation results; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) fit of eqn (1) to the simulation results. The deviations are given as δρ = (ρ − ρfit)/ρfit. fit of eqn (1) to the simulation results. The deviations are given as δρ = (ρ − ρfit)/ρfit. | ||
For the other simulations of acetone as well as pure oxygen and nitrogen, the qualitative behavior of the density profiles was found to be very similar over the whole temperature range and can also be accurately represented by eqn (1). The quantitative results appear as expected. The interfacial thickness D widens and the difference between the saturated bulk densities ρl and ρv declines for higher temperatures closer to the critical point due to the monotonic decrease of the liquid and the monotonic increase of the vapor density. The numerical simulation results are provided as ESI.†
For the binary mixture oxygen + nitrogen at 120 K and an equimolar liquid bulk composition, the total and partial density profiles are depicted in Fig. 2. In the interface region, the partial densities of oxygen and nitrogen show a similar slope in their transition from liquid to vapor density, but with a spatial shift of about 0.28 nm. Thus nitrogen, being the lower boiling component, shows an adsorption layer at the vapor side of the interface, which was also found for different binary mixtures in other work.24–27 This behavior can be explained by the properties of the molecular force field models.24,26,28 The attraction to the liquid phase is larger for both components, due to its higher density. For Lennard-Jones models with similar size parameter, which is the case here (σO = 3.1062 Å and σN = 3.3211 Å), this leads to an easier transition into the liquid phase for the substance with stronger dispersive attraction and an accumulation of the substance with weaker dispersive attraction at the interface. The according parameters of the molecular models are εO/kB = 43.183 K and εN/kB = 34.897 K. The total density profile data were fitted with eqn (1) and show sinusoidal relative deviations as seen for the pure substances. Here, the deviations in the interfacial range are more pronounced, but nonetheless they are only slightly larger than the scatter in the vapor phase. Thus, it was concluded that the total density profile of this mixture can be represented with a sufficient accuracy by function (1).
 | ||
Fig. 2 Total and partial density profiles as well as deviations from the fitting function through the VLE interface of the mixture oxygen + nitrogen at 120 K and an equimolar liquid bulk composition. ○ total density and deviations from the fitting function; ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) partial density of oxygen; – – partial density of nitrogen; — fit of eqn (1) to the simulation results. The deviations are given as δρ = (ρ − ρfit)/ρfit. partial density of oxygen; – – partial density of nitrogen; — fit of eqn (1) to the simulation results. The deviations are given as δρ = (ρ − ρfit)/ρfit. | ||
For a given temperature, the interfacial thickness D of oxygen + nitrogen was found to be between the interface widths of the pure constituent substances. However, regarding the temperature reduced by its critical value of the considered fluid, this binary mixture forms a wider interface than its constituent pure components, which is shown in Fig. 3. This is due to the mixture's more pronounced increase of the interfacial width in relation to its critical temperature, compared to the pure oxygen data, and is caused by the adsorption of nitrogen at the interface (cf.Fig. 2). It can also be seen that the slopes of the simulation results are very similar for oxygen, nitrogen and their mixture. This likewise applies to the acetone data, which are plotted in the ESI,† although their progression towards the critical point is slightly steeper.
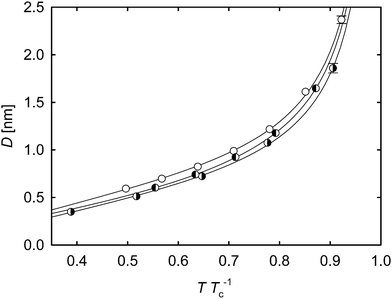 | ||
| Fig. 3 Width of the interface over the reduced temperature TTc−1 of oxygen and nitrogen as well as their binary mixture with equimolar liquid bulk composition. ◑ oxygen; ◐ nitrogen; ○ oxygen + nitrogen with equimolar liquid bulk composition. The lines represent the empirical correlation21D = a(1 − T/Tc)b + c(1 − T/Tc)−0.63 fitted to the data. For the determination of the critical temperatures of the pure substances, the parameters of the corresponding equations of state were applied.29,30 Based on these, the GERG-2004 equation of state31 was used to calculate the critical temperature of the mixture. The statistical uncertainties of the simulation data were considered as the standard error on a 95% confidence interval and are only visible if they exceed the symbol size. | ||
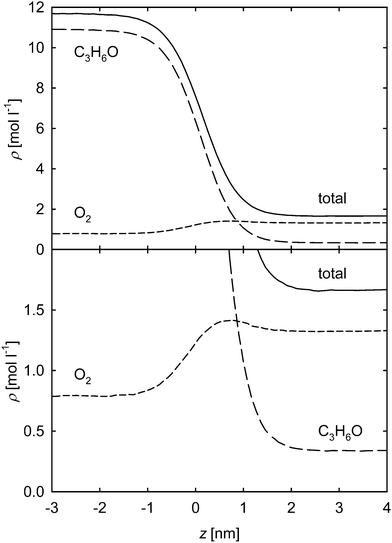
The two mixtures containing acetone show a qualitatively different density and partial density behavior than the mixture oxygen + nitrogen. The attraction between acetone molecules is much more pronounced, not only due to its high Lennard-Jones energy parameters, but also due to its strong dipole moment μ = 3.4 D. Therefore, the adsorption of the volatile component at the interface is more distinct in this case. For simulations not too close to the critical line, this leads to a maximum of the partial density in the interface, which is a known phenomenon.24,26–28,32 This is exemplarily shown in Fig. 4 for oxygen + acetone at 400 K with an oxygen mole fraction in the liquid bulk phase xO2 = 0.05 mol mol−1. In the upper subplot, the density and partial density profiles across the VLE interface are depicted over the whole density range of the liquid and vapor phase. The liquid phase mainly consists of acetone and to a much lesser extent of oxygen, which is represented by the difference in the partial densities. On the contrary, the vapor phase is composed mostly of oxygen. The lower subplot shows the same simulation data scaled up for the interesting region on the level of the vapor density, which clearly exhibits the enrichment of oxygen in the interface, exceeding its partial liquid density. Of course, this accumulation also influences the total density profile.
Due to this behavior, the density profile across the interface is not represented very well by function (1), especially on the vapor side. Hence, the extended equation21
 | (2) |
A comparison of the two functions (1) and (2) is exemplarily shown in Fig. 5 for this mixture (oxygen + acetone at 400 K and xO2 = 0.05 mol mol−1). In the upper panel, the simulation values for the total density and both fitting functions are plotted. It can be seen that eqn (2) provides a significantly better description of the MD data. This is confirmed by the lower subplot, where the deviations of the simulation results from the functions are shown. The largest deviations of 2.6% occur for eqn (1) in the transition region from the interface towards the vapor phase, which are much higher than those in the remaining spatial range, indicating its inability to adequately describe the profile data. On the other hand, the deviations from eqn (2) are on a consistent level over the whole spatial range and do not exceed 0.6%. For the residual sum of squares in the considered region, this means an improvement from 1.9 × 10−2 to 7.1 × 10−4.
 | ||
Fig. 5 Total density profile and deviations from the fitting functions for the mixture oxygen + acetone at 400 K and xO2 = 0.05 mol mol−1 on the vapor side of the VLE interface. ○ simulation results; ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) , ◑ fit of eqn (1) to the simulation results and their deviation; , ◑ fit of eqn (1) to the simulation results and their deviation; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) , ● fit of eqn (2) to the simulation results and their deviation. The deviations are given as δρ = (ρ − ρfit)/ρfit. , ● fit of eqn (2) to the simulation results and their deviation. The deviations are given as δρ = (ρ − ρfit)/ρfit. | ||
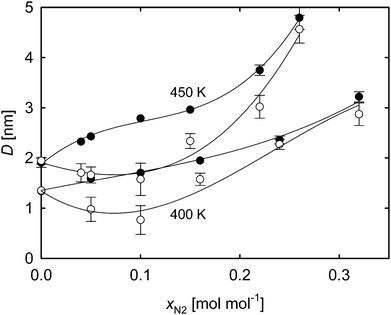
This behavior can be seen over a wide range of composition and for both simulated isotherms of the mixture oxygen + acetone. It can be identified by the difference between the interfacial widths Dl and Dv, which are plotted in Fig. 6. For pure acetone it was discussed above that eqn (1) suffices in describing the density profile (cf.Fig. 1) so that Dl and Dv as well as zl and zv are equal for xO2 = 0 mol mol−1 if eqn (2) is used to represent the simulation data. In the range xO2 = 0.04–0.20 mol mol−1 with pressures reaching from 4.6 to about 20 MPa,6 the simulations show a strong accumulation of oxygen on the vapor side of the interface, thus eqn (2) is needed to describe the total density profiles accurately. Accordingly, the widths show significant differences here. For compositions closer to the critical line, the accumulation of oxygen in the interface vanishes and Dl and Dv converge. This can be understood by considering the convergence of the saturated bulk densities approaching the critical region and finally the disappearance of the phase differences at the critical line.
The widths of the interface of the mixture nitrogen + acetone are shown in Fig. 7. Compared to the results for oxygen + acetone, the slope of the widths is steeper and the lenticular shape is more distinct. Qualitatively, the appearance of the data is similar, also showing increasing differences starting from the pure substance and the agreement of Dl and Dv within their error bars close to criticality.
The convergence of Dl and Dv indicates that eqn (1) can be used to accurately describe the total density profile for high liquid mole fraction values of the more volatile component. In Fig. 8 a state point in the extended critical region is shown for the mixture nitrogen + acetone with a liquid bulk mole fraction of 0.32 mol mol−1 and a corresponding pressure of 43 MPa.6 The proximity to the critical line is obvious considering the small difference between the saturated bulk densities, which is about 3 mol l−1, i.e. only 22% of the liquid density. The plotted total density data show that the accumulation of nitrogen at the vapor side of the interface occurs only slightly and the total density profile is well represented by function (1).
 | ||
Fig. 8 Total and partial density profiles as well as deviations from the fitting function through the VLE interface of the mixture nitrogen + acetone at 400 K and xN2 = 0.32 mol mol−1. ○ total density and deviations from the fitting function; ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) partial density of nitrogen; – – partial density of acetone; partial density of nitrogen; – – partial density of acetone; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) fit of eqn (1) to the simulation results. The deviations are given as δρ = (ρ − ρfit)/ρfit. fit of eqn (1) to the simulation results. The deviations are given as δρ = (ρ − ρfit)/ρfit. | ||
The results from the evaluation of the total density profiles for the mixtures oxygen + nitrogen, oxygen + acetone and nitrogen + acetone were obtained by fitting the discussed functions to the block averaged profiles from present MD simulations with the Levenberg–Marquardt algorithm,33 followed by statistically analyzing the data. For fitting the data with eqn (1), all parameters were adjusted at once. However, due to the increase in the degrees of freedom, the fitting procedure with eqn (2) was found to be less stable. Here, the saturated bulk densities ρl and ρv were determined prior to fitting the other parameters. The numerical results are given in Tables 1–3, respectively.
| T (K) | ρ l (mol l−1) | ρ v (mol l−1) | D (nm) | γ (mN m−1) |
|---|---|---|---|---|
| 70 | 33.801 (4) | 0.020 (2) | 0.592 (6) | 14.7 (3) |
| 80 | 32.239 (5) | 0.123 (2) | 0.697 (6) | 12.2 (3) |
| 90 | 30.601 (5) | 0.346 (5) | 0.823 (6) | 9.7 (2) |
| 100 | 28.854 (6) | 0.721 (9) | 0.988 (8) | 7.3 (3) |
| 110 | 26.891 (9) | 1.35 (1) | 1.22 (1) | 5.1 (3) |
| 120 | 24.63 (2) | 2.39 (2) | 1.61 (2) | 3.2 (2) |
| 130 | 21.73 (3) | 4.19 (3) | 2.37 (4) | 1.3 (2) |
| T (K) | x O2 (mol mol−1) | ρ l (mol l−1) | ρ v (mol l−1) | D l (nm) | D v (nm) | γ (mN m−1) |
|---|---|---|---|---|---|---|
| 400 | 0.00 | 11.211 (5) | 0.284 (4) | 1.34 (1) | 1.35 (5) | 11.0 (4) |
| 400 | 0.05 | 11.682 (5) | 1.659 (5) | 1.45 (2) | 1.22 (3) | 9.8 (3) |
| 400 | 0.10 | 12.139 (4) | 2.989 (7) | 1.62 (2) | 1.1 (2) | 8.8 (3) |
| 400 | 0.15 | 12.605 (5) | 4.443 (5) | 1.70 (2) | 1.41 (6) | 7.2 (3) |
| 400 | 0.20 | 13.026 (4) | 5.717 (6) | 1.80 (3) | 1.53 (7) | 6.0 (3) |
| 400 | 0.24 | 13.378 (7) | 6.821 (6) | 1.88 (5) | 1.78 (6) | 5.1 (4) |
| 400 | 0.26 | 13.519 (7) | 7.218 (9) | 1.98 (5) | 1.84 (6) | 4.4 (4) |
| 450 | 0.00 | 9.656 (9) | 0.839 (9) | 1.90 (9) | 1.94 (7) | 5.0 (3) |
| 450 | 0.04 | 9.88 (1) | 1.613 (6) | 2.19 (4) | 1.78 (9) | 4.4 (2) |
| 450 | 0.05 | 9.952 (8) | 1.785 (9) | 2.24 (3) | 1.6 (2) | 4.3 (3) |
| 450 | 0.10 | 10.21 (1) | 2.716 (8) | 2.4 (1) | 1.9 (1) | 3.7 (2) |
| 450 | 0.15 | 10.49 (1) | 3.602 (9) | 2.66 (5) | 2.1 (3) | 2.9 (3) |
| 450 | 0.20 | 10.69 (3) | 4.300 (6) | 2.79 (5) | 2.4 (2) | 2.4 (3) |
| 450 | 0.24 | 10.87 (5) | 4.96 (2) | 3.5 (2) | 3.5 (3) | 2.3 (2) |
| 450 | 0.26 | 10.74 (8) | 4.91 (3) | 3.6 (2) | 3.4 (5) | 2.1 (2) |
| T (K) | x N2 (mol mol−1) | ρ l (mol l−1) | ρ v (mol l−1) | D l (nm) | D v (nm) | γ (mN m−1) |
|---|---|---|---|---|---|---|
| 400 | 0.00 | 11.211 (5) | 0.284 (4) | 1.34 (1) | 1.35 (5) | 11.0 (4) |
| 400 | 0.05 | 11.518 (2) | 1.983 (4) | 1.58 (1) | 1.0 (2) | 9.1 (3) |
| 400 | 0.10 | 11.857 (4) | 3.801 (4) | 1.70 (2) | 0.8 (3) | 7.3 (4) |
| 400 | 0.16 | 12.231 (6) | 5.72 (1) | 1.95 (3) | 1.6 (1) | 5.2 (4) |
| 400 | 0.24 | 12.824 (7) | 8.309 (6) | 2.36 (8) | 2.3 (1) | 3.1 (4) |
| 400 | 0.32 | 13.342 (8) | 10.37 (1) | 3.2 (1) | 2.9 (2) | 2.1 (4) |
| 450 | 0.00 | 9.656 (9) | 0.839 (9) | 1.90 (9) | 1.94 (7) | 5.0 (3) |
| 450 | 0.04 | 9.783 (9) | 1.743 (9) | 2.32 (4) | 1.7 (2) | 4.1 (2) |
| 450 | 0.05 | 9.80 (1) | 1.92 (1) | 2.43 (4) | 1.7 (2) | 3.9 (3) |
| 450 | 0.10 | 10.01 (1) | 3.151 (6) | 2.79 (4) | 1.6 (3) | 3.0 (3) |
| 450 | 0.15 | 10.18 (1) | 4.296 (9) | 2.96 (6) | 2.3 (1) | 2.0 (3) |
| 450 | 0.22 | 10.37 (1) | 5.759 (6) | 3.7 (1) | 3.0 (2) | 1.1 (3) |
| 450 | 0.26 | 10.42 (4) | 6.60 (3) | 4.8 (2) | 4.6 (3) | 0.7 (3) |
4 Surface tension
The surface tension of planar interfaces can be calculated following the approach by Irving and Kirkwood34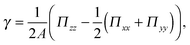 | (3) |
 | (4) |
The surface tension of acetone is given in Fig. 9. Even for this common pure substance, the lack of experimental data is evident. Although there is quite a number of data points in the lower temperature region,37–42 the highest measurements reach up to only 351 K due to the flammability of acetone. The results from density functional theory27,43 of Klink and Gross44 slightly overestimate these laboratory data and a correlation of experimental data over the whole temperature range. For low temperatures, the results of the present work show a similar behavior as those of Klink and Gross, yielding deviations to experimental data of approximately 10%. This coincides with the results by Werth et al.,45 who have shown in their work that an overestimation of the surface tension on this magnitude is typical for molecular simulation data of many pure substances. At higher temperatures, the results are in better agreement with the correlation by Mulero et al.,46 which lies within the statistical uncertainties of the present MD simulation data.
 | ||
Fig. 9 Surface tension over temperature for acetone. ○ molecular dynamics, this work; ● density functional theory, Klink and Gross;44 ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) correlation of experimental data, Mulero et al.;46 + experimental data.37–42 The statistical uncertainties of the simulation data were considered as the standard error on a 95% confidence interval and are only visible if they exceed the symbol size. correlation of experimental data, Mulero et al.;46 + experimental data.37–42 The statistical uncertainties of the simulation data were considered as the standard error on a 95% confidence interval and are only visible if they exceed the symbol size. | ||
Experimental data for the considered mixtures are scarce, especially there are no experimental surface tension data at all. For the mixture oxygen + nitrogen, the surface tension can be determined by correlations46 and binary parameters for the underlying mixing rule.31 However, for the considered mixtures with acetone, there are no correlations available. A simple ansatz to estimate the surface tension is given by the parachor method,47 which can also be used to predict γ for multicomponent mixtures48
 | (5) |
In Fig. 10 the simulated surface tension of oxygen and nitrogen as well as their mixture with an equimolar liquid bulk composition from this work is compared to experimental reference data and to results by Neyt et al.,51 who used direct Monte Carlo simulations. For the pure substances, the data from the simulations show deviations to experimental data and correlations of about 12%, which is similar to the outcome for pure acetone. The present results for oxygen match very well with those by Neyt et al. In fact, the molecular model for oxygen used in their work was adapted from the one used here5 by substituting the point quadrupole of the original model with three electrostatic charges.52 For nitrogen, different force field models were used, yielding some slight differences between the results, however, they still agree within their statistical uncertainties. For the equimolar mixture, the parachor method was used to obtain additional data for comparison. Despite the very good input values for this mixture due to accurate EOS29–31 and γ correlations,46 this approach underestimates the surface tension over the whole temperature range compared to the correlation by Mulero et al.46 by an almost constant value of 0.6 mN m−1. The surface tension results from present MD simulations match with the correlation46 within their statistical uncertainties.
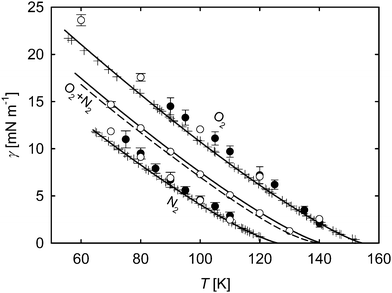 | ||
Fig. 10 Surface tension over temperature for oxygen and nitrogen and their mixture with equimolar liquid bulk phase. ○ molecular dynamics, this work; ● molecular dynamics, Neyt et al.;51 ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) parachor method; parachor method; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) correlation of experimental data, Mulero et al.;46 + experimental data.53–55 The statistical uncertainties of the simulation data were considered as the standard error on a 95% confidence interval and are only visible if they exceed the symbol size. correlation of experimental data, Mulero et al.;46 + experimental data.53–55 The statistical uncertainties of the simulation data were considered as the standard error on a 95% confidence interval and are only visible if they exceed the symbol size. | ||
In Fig. 11 the surface tension of the mixture nitrogen + acetone is plotted over the composition of the saturated liquid bulk phase for the isotherms 400 and 450 K, respectively. The values from present MD simulations as well as their slope nearly coincide with the results from density functional theory by Klink and Gross.44 For small xN2, the surface tension from MD simulation is slightly lower, yielding a good agreement with the correlation of experimental data for pure acetone.46 The prediction with the parachor method starts at exactly this correlation value, because its parameters were adjusted to it. However, with increasing xN2 this method underestimates the surface tension compared to the other results.
 | ||
Fig. 11 Surface tension over the nitrogen mole fraction of the liquid bulk phase xN2 at 400 and 450 K for the mixture nitrogen + acetone. ○ molecular dynamics, this work; ● density functional theory, Klink and Gross;44 × correlation of experimental data, Mulero et al.;46 ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) parachor method; parachor method; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) fit of eqn (6) to the present molecular simulation data. The statistical uncertainties of the simulation data are given as the standard error on a 95% confidence interval. fit of eqn (6) to the present molecular simulation data. The statistical uncertainties of the simulation data are given as the standard error on a 95% confidence interval. | ||
For the mixture oxygen + acetone, the surface tension over the liquid bulk mole fraction xO2 is shown in Fig. 12 for the isotherms 400 and 450 K. The results of the present MD simulations are higher than those of the mixture nitrogen + acetone, but resemble their shape. The surface tension values predicted by the parachor method are again significantly smaller than those from MD simulation.
 | ||
Fig. 12 Surface tension over the oxygen mole fraction of the liquid bulk phase xO2 at 400 and 450 K for the mixture oxygen + acetone. ○ molecular dynamics, this work; × correlation of experimental data, Mulero et al.;46 ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) parachor method; parachor method; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) fit of eqn (6) to the present molecular simulation data. The statistical uncertainties of the simulation data are given as the standard error on a 95% confidence interval. fit of eqn (6) to the present molecular simulation data. The statistical uncertainties of the simulation data are given as the standard error on a 95% confidence interval. | ||
Even though the parachor method is not very reliable for the prediction of the surface tension for the two mixtures containing acetone, it still provides a model for the correlation of the simulation results. For the mixtures oxygen + acetone and nitrogen + acetone, the present MD surface tension data were used to parametrize the parachor-like function
 | (6) |
| Component | T (K) | K 1 ((mN m−1)1/n l mol−1) | K 2 ((mN m−1)1/n l mol−1) | n | |
|---|---|---|---|---|---|
| 1 | 2 | ||||
| O2 | C3H6O | 400 | 0.0015103 | 0.19868 | 3.6662 |
| O2 | C3H6O | 450 | 0.18508 | 0.33430 | 1.7121 |
| N2 | C3H6O | 400 | 0.15825 | 0.32052 | 2.1214 |
| N2 | C3H6O | 450 | 0.084631 | 0.23123 | 2.8564 |
The numerical surface tension results from this work are listed in Tables 1–3 for the three different binary mixtures (oxygen + nitrogen, oxygen + acetone and nitrogen + acetone). For the calculation of the statistical uncertainties in this work, the data of the productive runs with a simulation time of 2 ns were divided into 32 blocks and the errors were estimated from the standard deviation of the mean.
5 Conclusions
Direct VLE simulations of acetone, oxygen and nitrogen as well as their binary mixtures were carried out. In case of the pure substances, it was found that the total density profiles across the interface can be represented very well by the classical van der Waals approach. The binary mixtures exhibit adsorption of the more volatile component at the vapor side of the interface. This accumulation is more distinct for the mixtures containing acetone than for oxygen + nitrogen, leading to a maximum of the volatile component's partial density in the interface, so that an extended function had to be used to accurately describe the total density profile. This allows for a discussion of adsorption via the difference between the interfacial widths Dl and Dv.For the pure substances it was found that the present MD simulations overestimate the surface tension compared to experimental data and correlations by approximately 10 to 12%. However, the results are in line with the data from other simulations and deviations on this order were found to be typical for molecular simulations of many pure substances in earlier work. Due to the scarcity of experiments for the three considered binary mixtures (oxygen + nitrogen, oxygen + acetone and nitrogen + acetone), predictions from the parachor method were considered for comparison. Where available, the correlations of experimental data agree well with the present MD simulation results, however the predictions from the parachor method underestimate the other data consistently. For the mixture nitrogen + acetone, results from density functional theory were available and show a very good agreement with the surface tension data from present MD simulations. For the two mixtures containing acetone, parachor-like correlations were parametrized to describe the surface tension results from this work.
Acknowledgements
The authors thank Christoph Klink and Joachim Groß for the provided data as well as Andreas Köster for helpful discussions. This work was funded by Deutsche Forschungsgemeinschaft, Collaborative Research Center Transregio 75 “Droplet Dynamics Under Extreme Ambient Conditions” and Project Grant VR6/9-1. It was carried out under the auspices of the Boltzmann-Zuse Society of Computational Molecular Engineering (BZS) and the simulations were performed on the Cray XC40 (Hornet) at the High Performance Computing Center Stuttgart (HLRS).References
- J. M. Prausnitz, R. N. Lichtenthaler and E. G. de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice-Hall, Upper Saddle River, NJ, 3rd edn, 1999 Search PubMed.
- B. Weigand and C. Tropea, ICLASS 2012, Heidelberg, 2012 Search PubMed.
- E. Hendriks, G. M. Kontogeorgis, R. Dohrn, J.-C. de Hemptinne, I. G. Economou, L. F. Žilnik and V. Vesovic, Ind. Eng. Chem. Res., 2010, 49, 11131–11141 CrossRef CAS.
- C. Niethammer, S. Becker, M. Bernreuther, M. Buchholz, W. Eckhardt, A. Heinecke, S. Werth, H.-J. Bungartz, C. W. Glass, H. Hasse, J. Vrabec and M. Horsch, J. Chem. Theory Comput., 2014, 10, 4455–4464 CrossRef CAS.
- J. Vrabec, J. Stoll and H. Hasse, J. Phys. Chem. B, 2001, 105, 12126–12133 CrossRef CAS.
- T. Windmann, M. Linnemann and J. Vrabec, J. Chem. Eng. Data, 2014, 59, 28–38 CrossRef CAS.
- J. Stoll, J. Vrabec and H. Hasse, AIChE J., 2003, 49, 2187–2198 CrossRef CAS PubMed.
- J. Janeček, J. Phys. Chem. B, 2006, 110, 6264–6269 CrossRef PubMed.
- L. G. MacDowell and F. J. Blas, J. Chem. Phys., 2009, 131, 074705 CrossRef PubMed.
- F. J. Blas, A. Ignacio Moreno-Ventas Bravo, J. M. Míguez, M. M. Piñeiro and L. G. MacDowell, J. Chem. Phys., 2012, 137, 084706 CrossRef CAS PubMed.
- J. M. Míguez, M. M. Piñeiro and F. J. Blas, J. Chem. Phys., 2013, 138, 034707 CrossRef PubMed.
- F. J. Blas, A. I. Moreno-Ventas Bravo, J. Algaba, F. J. Martínez-Ruiz and L. G. MacDowell, J. Chem. Phys., 2014, 140, 114705 CrossRef CAS PubMed.
- S. Werth, G. Rutkai, J. Vrabec, M. Horsch and H. Hasse, Mol. Phys., 2014, 112, 2227–2234 CrossRef CAS PubMed.
- R. Lustig, Mol. Phys., 1988, 65, 175–179 CrossRef PubMed.
- F. J. Martínez-Ruiz, F. J. Blas, B. Mendiboure and A. I. Moreno-Ventas Bravo, J. Chem. Phys., 2014, 141, 184701 CrossRef PubMed.
- T. Windmann, A. Köster and J. Vrabec, J. Chem. Eng. Data, 2012, 57, 1672–1677 CrossRef CAS.
- F. P. Buff, R. A. Lovett and F. H. Stillinger, Phys. Rev. Lett., 1965, 15, 621–623 CrossRef.
- S. Fisk and B. Widom, J. Chem. Phys., 1969, 50, 3219–3227 CrossRef CAS PubMed.
- J. Lekner and J. R. Henderson, Mol. Phys., 1977, 34, 333–359 CrossRef CAS PubMed.
- J. D. van der Waals, Z. Phys. Chem., 1894, 13, 657–725 Search PubMed.
- J. Vrabec, G. K. Kedia, G. Fuchs and H. Hasse, Mol. Phys., 2006, 104, 1509–1527 CrossRef CAS PubMed.
- J. Lekner and J. R. Henderson, Phys. A, 1978, 94, 545–558 CrossRef.
- E. W. Lemmon and R. Span, J. Chem. Eng. Data, 2006, 51, 785–850 CrossRef CAS.
- I. W. Plesner, O. Platz and S. E. Christiansen, J. Chem. Phys., 1968, 48, 5364–5370 CrossRef CAS PubMed.
- G. A. Chapela, G. Saville, S. M. Thompson and J. S. Rowlinson, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 1133–1144 RSC.
- D. J. Lee, M. M. Telo da Gama and K. E. Gubbins, J. Phys. Chem., 1985, 89, 1514–1519 CrossRef CAS.
- C. Klink and J. Gross, Ind. Eng. Chem. Res., 2014, 53, 6169–6178 CrossRef CAS.
- F. Llovell, A. Galindo, F. J. Blas and G. Jackson, J. Chem. Phys., 2010, 133, 024704 CrossRef PubMed.
- R. Schmidt and W. Wagner, Fluid Phase Equilib., 1985, 19, 175–200 CrossRef CAS.
- R. Span, E. W. Lemmon, R. T. Jacobsen, W. Wagner and A. Yokozeki, J. Phys. Chem. Ref. Data, 2000, 29, 1361–1433 CrossRef CAS PubMed.
- O. Kunz, R. Klimeck, W. Wagner and M. Jaeschke, The GERG-2004 Wide-Range Equation of State for Natural Gases and Other Mixtures, VDI Verlag, Düsseldorf, 2007, vol. 557 Search PubMed.
- J.-C. Neyt, A. Wender, V. Lachet, A. Ghoufi and P. Malfreyt, Phys. Chem. Chem. Phys., 2013, 15, 11679–11690 RSC.
- D. W. Marquardt, J. Soc. Ind. Appl. Math., 1963, 11, 431–441 CrossRef.
- J. H. Irving and J. G. Kirkwood, J. Chem. Phys., 1950, 18, 817–829 CrossRef CAS PubMed.
- M. Horsch, H. Hasse, A. K. Shchekin, A. Agarwal, S. Eckelsbach, J. Vrabec, E. A. Müller and G. Jackson, Phys. Rev. E, 2012, 85, 031605 CrossRef.
- G. V. Lau, I. J. Ford, P. A. Hunt, E. A. Müller and G. Jackson, J. Chem. Phys., 2015, 142, 114701 CrossRef PubMed.
- H. Kahl, T. Wadewitz and J. Winkelmann, J. Chem. Eng. Data, 2003, 48, 580–586 CrossRef CAS.
- W. Ramsay and J. Shields, Z. Phys. Chem., 1893, 12, 433–475 Search PubMed.
- T. Tonomura, Sci. Rep. Tohoku Imp. Univ., Ser. 1, 1933, 22, 104–130 Search PubMed.
- E. Tommila and R. Yrjovuori, Suom. Kemistil., 1969, 42, 90–93 CAS.
- J. Livingston, R. Morgan and F. T. Owen, J. Am. Chem. Soc., 1911, 33, 1713–1727 CrossRef.
- A. I. Rusanov, S. A. Levichev and V. Y. Tyushin, Vestn. Leningr. Univ., Ser. 4: Fiz., Khim., 1966, 21, 121–127 Search PubMed.
- C. Klink, B. Planková and J. Gross, Ind. Eng. Chem. Res., 2015, 54, 4633–4642 CrossRef CAS.
- C. Klink and J. Gross, personal communication.
- S. Werth, K. Stöbener, P. Klein, K. Küfer, M. Horsch and H. Hasse, Chem. Eng. Sci., 2015, 121, 110–117 CrossRef CAS PubMed.
- A. Mulero, I. Cachadiña and M. I. Parra, J. Phys. Chem. Ref. Data, 2012, 41, 043105 CrossRef PubMed.
- S. Sugden, J. Chem. Soc., Trans., 1924, 125, 32–41 RSC.
- Y. Sun and B. Y. Shekunov, J. Supercrit. Fluids, 2003, 27, 73–83 CrossRef CAS.
- T. A. Knotts, W. V. Wilding, J. L. Oscarson and R. L. Rowley, J. Chem. Eng. Data, 2001, 46, 1007–1012 CrossRef CAS.
- R. L. Rowley, W. V. Wilding, T. A. Knotts and N. Giles, DIPPR 801 Database, AIChE, 2014 Search PubMed.
- J.-C. Neyt, A. Wender, V. Lachet and P. Malfreyt, J. Phys. Chem. B, 2011, 115, 9421–9430 CrossRef CAS PubMed.
- Y. Boutard, P. Ungerer, J. M. Teuler, M. G. Ahunbay, S. F. Sabater, J. Pérez-Pellitero, A. D. Mackie and E. Bourasseau, Fluid Phase Equilib., 2005, 236, 25–41 CrossRef CAS PubMed.
- V. G. Baidakov, K. V. Khvostov and G. N. Muratov, Zh. Fiz. Khim., 1982, 56, 814–817 CAS.
- V. B. Ostromoukhov and M. G. Ostronov, Zh. Fiz. Khim., 1994, 68, 39–43 Search PubMed.
- Y. P. Blagoi, V. A. Kireev, M. P. Lobko and V. V. Pashkov, Ukr. Fiz. Zh., 1970, 15, 427–432 CAS.
- D. Broseta, Y. Meleán and C. Miqueu, Fluid Phase Equilib., 2005, 233, 86–95 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp03415a |
| This journal is © the Owner Societies 2015 |