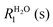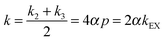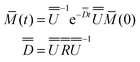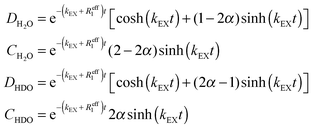Challenges in preparing, preserving and detecting para-water in bulk: overcoming proton exchange and other hurdles

Abstract

Para-water is an analogue of para-hydrogen, where the two proton spins are in a quantum state that is antisymmetric under permutation, also known as singlet state. The populations of the nuclear spin states in para-water are believed to have long lifetimes just like other Long-Lived States (LLSs). This hypothesis can be verified by measuring the relaxation of an excess or a deficiency of para-water, also known as a “Triplet–Singlet Imbalance” (TSI), i.e., a difference between the average population of the three triplet states T (that are symmetric under permutation) and the population of the singlet state S. In analogy with our recent findings on ethanol and fumarate, we propose to adapt the procedure for Dissolution Dynamic Nuclear Polarization (D-DNP) to prepare such a TSI in frozen water at very low temperatures in the vicinity of 1.2 K. After rapid heating and dissolution using an aprotic solvent, the TSI should be largely preserved. To assess this hypothesis, we studied the lifetime of water as a molecular entity when diluted in various solvents. In neat liquid H₂O, proton exchange rates have been characterized by spin-echo experiments on oxygen-17 in natural abundance, with and without proton decoupling. One-dimensional exchange spectroscopy (EXSY) has been used to study proton exchange rates in H₂O, HDO and D₂O mixtures diluted in various aprotic solvents. In the case of 50 mM H₂O in dioxane-d₈, the proton exchange lifetime is about 20 s. After dissolving, one can observe this TSI by monitoring intensities in oxygen-17 spectra of H₂O (if necessary using isotopically enriched samples) where the AX₂ system comprising a “spy” oxygen A and two protons X₂ gives rise to binomial multiplets only if the TSI vanishes. Alternatively, fast chemical addition to a suitable substrate (such as an activated aldehyde or ketone) can provide AX₂ systems where a carbon-13 acts as a spy nucleus. Proton signals that relax to equilibrium with two distinct time constants can be considered as a hallmark of a TSI. We optimized several experimental procedures designed to preserve and reveal dilute para-water in bulk.

---

Introduction

Although water is a fundamental constituent of our biosphere, characterization of some of its most basic properties remains a formidable challenge. Most applications of magnetic resonance imaging (MRI), both in vitro and in vivo, are based on observing the magnetization of the two hydrogen nuclei of water. This is actually limited to the observation of ortho-water. If the populations of the three symmetrical states deviate from Boltzmann equilibrium, they rapidly recover through longitudinal spin–lattice relaxation with a time constant T₁, which is typically on the order of 10 s in neat water. So far, neither NMR nor MRI has been able to exploit the properties of the invisible singlet state S₀, also known as para-water, by analogy to para-hydrogen.^1,2 The following linear combination of populations:

⅓[|T₊₁〉〈T₊₁| + |T₀〉〈T₀| + |T₋₁〉〈T₋₁|] − |S₀〉〈S₀| (1)

where:
is equivalent to a “Triplet–Singlet Imbalance” (henceforth TSI), in analogy to the expression coined by Meier et al.³ for the “A/E imbalance” in ¹³CH₃ groups, which refers to a population imbalance between symmetric and antisymmetric states belonging to the irreducible representations A and E of methyl groups. An A/E imbalance can be induced by cooling down to ca. 1 K molecules such as γ-picoline that contain methyl groups characterized by very low rotational barriers.^3–8 In the high-temperature approximation, i.e., at spin temperatures above a few degree Kelvin, the distribution between para- and ortho-water is given by the ratio 1 : 3. If this ratio is perturbed, as we shall demonstrate in this paper, the resulting TSI in eqn (1) should have a lifetime that might be much longer than the spin–lattice relaxation time (T_TSI > T₁). This is analogous to molecules that contain two magnetically inequivalent protons that can sustain a Long-Lived State (LLS).⁹ Such an LLS can preserve spin order over periods that are much longer than T₁. In ¹²CH₂ groups, for instance, we have shown that one can have lifetimes with ratios T_TSI/T₁ > 36.¹⁰ The LLS can be prepared by several NMR techniques at room temperature^10,11 or by DNP at low temperature.¹² Optimization of nearly-symmetric molecules comprising pairs of ¹³C nuclei has led to very long lifetimes in solution that can exceed one hour at room temperature.¹³ Another intriguing feature of the LLS is that they can be used to improve the sensitivity of drug screening experiments.^14–16 In the past, several studies have focused on the isolation of para-water and the characterization of its long-lived behavior.¹⁷ In crystal water trapped in gypsum (CaSO₄·2H₂O), Pake found evidence of isolated pairs of protons.¹⁸ At T < 100 K, the water molecules trapped in gypsum crystals cannot flip around their two-fold symmetry axis. As a result, the two protons may be at unequal distances from other protons belonging to remote hydration water molecules. Thus the two protons may experience different intermolecular dipolar couplings, and their magnetic equivalence can be lifted. It is therefore possible to populate the antisymmetric state. Eisendrath, Stone and Jeener^19,20 characterized para-water in solid gypsum. More recently, the separation of ortho- and para-water has been achieved in molecular beams travelling through inhomogeneous magnetic fields,²¹ where a beam of ortho-water can be deflected and refocused in the manner of the Stern–Gerlach experiment, or in inhomogeneous electric fields.²² These methods can produce a large TSI but only for very small quantities of water. Isomer enrichment of H₂O in bulk, by means of absorption in column chromatography, has been proposed²³ and later challenged.²⁴ In other studies, the interconversion between para- and ortho-isomers was achieved by isolating water molecules in frozen inert gases^25–27 or by trapping them in C₆₀ cages.²⁸ In the latter case, the conversion has been monitored by a combination of infrared spectroscopy, inelastic neutron scattering and cryo-MAS NMR spectroscopy.²⁹ This allows one to study ortho–para conversion rates³⁰ of isolated water molecules. However, the confinement in C₆₀ cages prevents one from monitoring interactions with surrounding molecules. In this work we shall discuss the possibility of preparing samples of non-confined water characterized by a significant TSI at concentrations on the order of a few mM. Our approach is similar to our strategy for preparing hyperpolarized para-ethanol³¹ and para-fumarate.³²

Methodology

Our approach involves three consecutive steps.

Step 1 – preparing a TSI

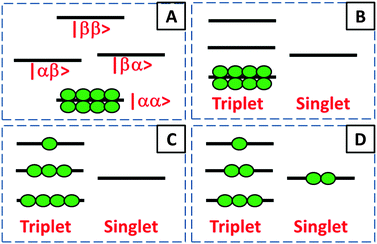
A flow of populations between the triplet and singlet energy levels in water cannot be induced by intramolecular dipole–dipole (DD) interactions between the two protons belonging to the same water molecule, although it may be induced by intermolecular dipole–dipole (DD) interactions^19,20 or by the proton chemical shift anisotropy (CSA) in the condensed phase. In liquid H₂O diluted in D₂O at 300 K, the CSA has been determined to be 28 ppm.³³ In gypsum, the proton CSA of the (hopping) water molecules has been determined to be 10 ppm at 300 K.³⁴ The proton CSA of the hopping water molecules in Ba(ClO₃)₂·H₂O has also been determined to be 10 ppm at 300 K.³⁵ In glassy frozen solutions, the symmetry of the two protons in each H₂O molecule is broken by the anisotropy of the chemical shifts, except for some particular orientations, so that the singlet state |S₀〉 is mixed with the central triplet state |T₊₁〉. Depending on the coupling between the rotational and Zeeman energy levels, two situations can occur. If the energy levels are primarily determined by the rotational quantum numbers, as in the gas phase³⁶ or C₆₀ cages (where the rotational levels typical for the gas phase remain a good approximation), the singlet state S₀ has the lowest energy. On the other hand, if rotational quantization can be neglected, the ground state is |αα〉 = |T₊₁〉 which belongs to the triplet manifold. In our samples, the rotation of water is believed to be hindered by hydrogen bonding with other water and/or solvent molecules. Thus, when H₂O molecules are diluted in a deuterated aprotic solvent, doped with a radical and frozen at low temperatures in a high magnetic field, DNP can be used to achieve a TSI. The ESR transitions of the radical can be saturated by microwave irradiation to populate mostly the |αα〉 = |T₊₁〉 state (Fig. 1A). During dissolution, the magnetic equivalence of the two protons in each H₂O molecule is restored. Hence, our strategy should lead to an excess of the average population of the three triplet states compared to the population of the singlet state (Fig. 1B). This amounts to a TSI. If its life-time is longer than T₁, this may be considered as the hallmark of para-water.

Fig. 1 (A) Schematic representation of the energy levels of the two magnetically inequivalent protons of H₂O in the solid state at 1.2 K. By lowering the spin temperature to a few mK by DNP, only the ground state |αα〉 = |T₊₁〉 is populated. (B) After dissolution with a hot aprotic solvent, the magnetic equivalence is restored. (C) Relaxation in the triplet manifold occurs on a time-scale T₁. (D) Equilibration of the T/S imbalance occurs with a time constant T_TSI that is believed to be much longer than T₁.

Step 2 – protecting the TSI during transfer

After rapid heating of the sample by injection of a hot aprotic solvent, the sample can be transferred³⁷ to an NMR or MRI system. Longitudinal T₁ relaxation in a few seconds leads to the return of the triplet manifold to Boltzmann equilibrium at room temperature (Fig. 1C). However, T₁ relaxation does not affect the TSI, so that the singlet state remains depleted. On a longer time-scale T_TSI, the populations of the triplet and singlet states will return to their Boltzmann equilibrium (Fig. 1D). In the dissolution step, all relaxation mechanisms that could reduce T_TSI must be kept under control. The radicals can be eliminated by chemical reduction with scavengers such as ascorbate.³⁸ Alternatively, porous solids containing covalently bound radicals can be filtered after dissolution.³⁹ Spin rotation (SR) is another mechanism that could cause losses of the TSI. SR is due to the coupling between the nuclear spins and the molecular magnetic dipole induced by the electric dipole moment of the H₂O molecule as it undergoes rotational diffusion. The SR mechanism of ortho–para conversion has been intensively studied.^40,41 Indeed, in the gas phase,^42,43 the longitudinal relaxation times were found to be on the order of T₁ = 20 ms near 0.1 MPa and 373 K at 800 MHz. We believe however that SR is not an efficient mechanism for H₂O in the condensed phase where collisions on the atomic scale should make SR ineffective. This should also be the case when the rotation of a H₂O molecule is hindered because it is trapped in a cage of an aprotic solvent. Finally, one should pay attention to the exchange of protons between different water molecules. In other words, the lifetime τ_EX = 1/k_EX of a water molecule as a molecular entity has to be longer than the lifetime of the TSI. Since the latter lifetime is unknown, the best option is to slow down the proton exchange as much as possible. In pure water the lifetime of proton exchange has been assessed to be τ_EX ≈ 1 ms by studying either linewidths in proton spectra⁴⁴ or intensities of ¹⁷O lines with and without proton decoupling.^45,46 However, it can be shown by EXSY⁴⁷ that dilution in aprotic solvents can effectively slow down the exchange of protons and thus extend τ_EX. This approach should help to preserve the TSI and thus the lifetime of para-water.

Step 3 – detecting TSI relaxation

To detect the relaxation of the TSI, at least four distinct approaches can be used. (i) Direct detection by infrared (IR) spectroscopy relies on the fact that ortho- and para-water give rise to distinct IR absorption bands in the gas phase.^29,36 However, in the condensed phase, in particular, when water is diluted in aprotic solvents, we found that the IR signatures are difficult to identify. (ii) Direct detection by multiplet effects in oxygen-17 NMR. In thermal equilibrium, the oxygen-17 signal of H₂O shows a normal binomial 1 : 2 : 1 triplet. If, however, one is able to populate a TSI, non-binomial multiplets could be observed like in para-ethanol.³¹ (iii) If the proton signals relax back to equilibrium with two different time constants this would be a hallmark of ortho–para conversion. (iv) Long-lived water can be revealed indirectly by chemical addition onto a suitable substrate such as an activated aldehyde or ketone, monitored by ¹H or ¹³C NMR. For this strategy to be successful, the reactivity of water molecules has to fulfill three requirements that are partly contradictory: (a) the water must be sufficiently diluted so that intermolecular ¹H exchange is slowed down; (b) the rate of the chemical addition that is used to reveal the presence of para-water must be faster than the relaxation of the TSI; and (c) the two protons that are added onto the substrate must stem from the same water molecule. Our kinetic measurements show that, under suitable conditions, these requirements may indeed be satisfied.

Results and discussion

Step 1 – preparing a TSI

Unlike Jeener and coworkers^19,20 who postulated that the two protons of a H₂O molecule can have different environments because of intermolecular dipole–dipole interactions in a magnetic field of 0.7 T, we shall assume that the proton chemical shift anisotropy (CSA) makes significant contributions to the breaking of the symmetry at 6.7 T. We diluted water in deuterated dimethylsulfoxide (DMSO-d₆), doped it with ca. 50 mM TEMPOL radicals and froze it to form a glassy state at ca. 1.2 K and 6.7 T. In Fig. 2 we can see proton spectra before (A) and after (B) saturation of the ESR transitions by microwave irradiation at 187.9 GHz with frequency modulation.⁵⁰ Simulations of H₂O powder spectra have been carried out by using the SIMPSON program⁴⁸ on a spin system made up of two protons with shielding anisotropy Δ_CS = −16.19 ppm, asymmetry η_CS = 0.17 and a dipolar coupling d = −30.314 kHz. 4180 crystallite orientations were considered. The relative orientations of the relevant shielding tensors, expressed in a common crystal frame, were given by the Euler angles Ω^H(1) = {−165.11°, 115.33°, 36.75°} and Ω^H(2) = {−14.89°, 115.33°, −36.75°}, with the dipolar coupling tensor between the two protons oriented according to Ω^H(1,2) = {180.00°, 58.83°, 0.00°}. These parameters have been calculated in previous work on water molecules in barium chlorate monohydrate³⁵ by means of DFT and planewave-pseudopotential methods as implemented in the CASTEP code.⁵¹ The shielding ellipsoids have their main components aligned along the OH bonds. A realistic pulse was used, with an rf-field strength ν₁ = 50 kHz and nutation angles β = 90° and 1.8°, in Fig. 2C and D, respectively. The initial density operator was either ρ(0) = I_Z + S_Z to describe the high-temperature approximation (Fig. 2C) or ρ(0) = (1/2)[1/2E + I_Z + S_Z + 2I_ZS_Z] which corresponds to a pure state where only the lowest-lying state is populated at very low spin temperatures (Fig. 2D). The experimental spectra in Fig. 2A and B have larger linewidths than the simulated spectra in Fig. 2C and D: this can be ascribed to the presence of paramagnetic species in solution (TEMPOL) and to intermolecular dipolar couplings that were not considered in the simulations. Finally this evidence suggests that DNP indeed allows one to drive the populations towards the lowest-lying state: since there is some mixing between the central triplet state and the singlet state, a very low spin temperature (on the order of 10 mK in our experiments) is sufficient to generate a TSI.

Fig. 2 Experimental proton spectra of H₂O diluted in DMSO doped with 50 mM TEMPOL and frozen at ca. 1.2 K in a field of 6.7 T, with (A) and without (B) irradiation with a resonant microwave field at 187.9 GHz. Simulations by using SIMPSON⁴⁸ (see text for details) for initial density operators ρ = I_Z + S_Z (C) or ρ = (1/2)[1/2E + I_Z + S_Z + 2I_ZS_Z] (D). The experimental spectra A and B have larger linewidths than the simulated C and D because of intermolecular dipolar couplings and paramagnetic species in the frozen glass.

Step 2 – protecting the TSI during transfer

Proton exchange in water could represent the major source of losses of TSI in our experiment. Hence, we studied the exchange in water in bulk and dilute solutions. The combined effects of proton exchange and proton T₁ relaxation on the transverse T₂ relaxation of ¹⁷O nuclei in H₂¹⁷O can be characterized by using multiple refocusing of transverse ¹⁷O magnetization in the manner of Carr, Purcell, Meiboom and Gill (CPMG). One may compare ¹⁷O echo decays in the presence or absence of proton decoupling, in analogy with a similar work carried out on ¹⁵N.^45,46 Our observations shown in Fig. 3 are in agreement with pioneering studies by Meiboom.⁴⁴ We measured lifetimes τ_EX = 1/k_EX of a few milliseconds in pure water at pH 5.93 and different temperatures. The lifetime of pure water as a molecular entity is clearly too short for our purposes but, as mentioned above, dilution in aprotic solvents can be used to extend this lifetime. In dilute solutions, the proton spectra of mixtures of H₂O and HDO feature two distinct resonances. In order to observe HDO triplets due to ¹J_HD(¹H,¹⁷O) = 80 Hz, the lifetime of HDO has to be τ_EX > 1/¹J_HD(¹H,¹⁷O) = 12.5 ms. Slow exchange rates can be quantified using selective 1D or 2D exchange spectroscopy (EXSY).⁴⁷ The pulse sequence used is shown in Fig. 5. Our samples consisted of a mixture of H₂O, HDO and D₂O diluted in various organic solvents at different concentrations (see Table 1 and Fig. 4). The concentrations [H₂O] and [HDO] have been determined by NMR within ±10%, by scaling their peak intensities to an external reference with a concentration that is known a priori. In nitromethane and dioxane, [H₂O] and [HDO] were increased with respect to other solvents since, at low concentrations, the proton exchange was too slow to be monitored via 1D-EXSY.

Table 1 Proton exchange rates for mixtures of H₂O + HDO diluted in aprotic deuterated organic solvents at 800 MHz and 300 K. The concentrations, protonation fractions α = [H]/([H] + [D]) and chemical shifts ν of H₂O and HDO in the liquid phase are reported. The parameters α, R_eff and k_EX were estimated by global fitting of the four curves in Fig. 5. In order to compare exchange lifetimes, normalized τ_EX have been calculated for [H₂O] + [HDO] = 50 mM, assuming a linear dependence of the exchange rate on the concentration⁴⁹

Solvent	Experiments@800 MHz					Fitting@800 MHz			τ EX (s) normalized to [H2O] + [HDO] = 50 mM
	α	[H2O] (mM)	ν(H2O) (ppm)	[HDO] (mM)	ν(HDO) (ppm)	α	R eff (s)	k EX (s^−1)
Dioxane-d8	0.28	105	∼2.71	169	∼2.67	0.30	0.19	0.14 ± 0.03	20
Nitromethane-d3	0.26	36	∼2.13	50	∼2.10	0.40	0.08	0.30 ± 0.03	3
Acetonitrile-d3	0.19	5	∼2.18	4	∼2.15	0.35	0.15	0.23 ± 0.02	0.4
DMSO-d6	0.06	40	∼3.36	11	∼3.33	0.10	0.55	1.7 ± 0.2	0.06
Acetone-d6	0.22	12	∼2.88	14	∼2.85	0.30	0.17	4.0 ± 0.5	0.04
Dichloromethane-d2	0.73	2	∼1.63	21	∼1.60	0.77	0.15	4.6 ± 0.4	0.001

---

Fig. 3 Measurement of fast proton exchange rates k_EX in pure water. Proton exchange rates as a function of temperature at pH = 5.93 were extracted from ratios of peak heights of oxygen-17 echoes observed without and with proton decoupling.^45,46 The lifetimes τ_EX = 1/k_EX range from 3.6 to 0.9 ms between 275 and 310 K.

Fig. 4 Proton spectrum of 36 mM H₂O (singlet on left-hand side) and 50 mM HDO (triplet due to J(H,D) on the right-hand side) in nitromethane-d₃ at 300 K and 800 MHz.

Fig. 5 [top] Pulse sequence for selective 1D-EXSY experiments. [bottom] Typical build-up and decay curves measured using 1D-EXSY experiments used for the measurement of the lifetime of water as a molecular entity, when diluted in aprotic solvents (acetonitrile-d₃ in this example). Red squares and orange triangles represent intensities of diagonal peaks of H₂O and HDO, respectively; green circles describe magnetization transfer from HDO to H₂O, while blue rhombi describe the reverse reaction. The rates measured for different solvents are reported in Table 1.

The build-up and decay curves shown in Fig. 5 can be fitted to the following functions (see the Appendix for details):

The parameters α, R_eff and k_EX have been determined by global fitting to the curves in Fig. 5 and are shown in Table 1. The rates R₁ = 1/T₁ of H₂O have been determined experimentally by inversion recovery (see Table 2). R_eff is an average of R₁(H₂O) and R₁(HDO) weighted by their concentrations. Hence, a comparison between R_eff in Table 1 and R₁ in Table 2 can only be qualitative because of different experimental conditions. However, in most cases the values are similar. In order to facilitate comparisons, in Table 1 we estimated the lifetimes for a concentration [H₂O] + [HDO] = 50 mM, assuming that the rates vary linearly with concentration.⁴⁹ It is evident that, at concentrations below 50 mM, dioxane allows one to extend the lifetime of water as a molecular entity up to a few minutes. Dioxane, therefore, seems a good solvent for dissolution DNP. However, it has a much higher viscosity and lower heat capacity than water, so that our dissolution apparatus has to be re-designed thoroughly.

Table 2 Longitudinal relaxation rates R₁ of H₂O diluted in aprotic deuterated organic solvents at 600 MHz and 300 K. The rates R₁ were determined by inversion recovery. Their values can be compared to R_eff in Table 1 but only in a qualitative way since R_eff depends on [H₂O], [HDO] and k_EX and for different experimental conditions

Solvent	Experiments@600 MHz
		[H2O] (mM)
Dioxane-d8	0.26	358
Nitromethane-d3	0.08	91
Acetonitrile-d3	0.15	9
DMSO-d6	0.30	42
Acetone-d6	0.17	10
Dichloromethane-d2	0.11	6

---

Step 3 – detecting TSI relaxation

To observe a TSI in H₂O at room temperature after dissolution, we have resorted to a chemical reaction, inspired by the PASADENA¹ and ALTADENA⁵² methods. We have shown recently³² that one can lift the degeneracy of the two protons in fumarate (⁻OOCCH=CHCOO⁻) by addition of D₂O to produce malate (⁻OOCCHDCHODCOO⁻), a reaction that is catalyzed by fumarase. In our work on para-ethanol,³¹ instead, the detection was possible, without any chemical reactions, by monitoring non-binomial multiplets in an AX₂ system. Following a suggestion by Jean-Maurice Mallet we have explored the addition of water (though not yet of para-water) on aldehydes, i.e., RCHO + H₂O → RCH(OH)₂. The C=O double bond of the aldehyde can be activated by substituents such as R = CCl₃, as in chloral (CCl₃CHO, see Fig. 6). When the reaction is carried out in a dilute solution in acetonitrile, the two water protons (highlighted by stars in Fig. 6) may be assumed to end up on the same hydrate molecule. The two OH protons that stem from para-water give rise to degenerate doublets in the vicinity of 6.4 ppm. The lone proton near 5.3 ppm that stems from the aldehyde gives rise to a triplet due to two equal long-range couplings ³J_HH ≈ 6 Hz to the two OH protons. Clearly, as discussed above, deviations from the binomial 1 : 2 : 1 distribution of this triplet can be used for a quantitative determination of the TSI.³¹

Fig. 6 The addition of H₂O to chloral gives chloral hydrate CCl₃CH(OH)₂, where the two protons highlighted by stars can be assumed to stem from one and the same water molecule if the solution is sufficiently dilute.

The relative intensities of the lines in these multiplets can give a measure of the TSI in H₂O, i.e., of the relative populations of ortho- and para-water, much as in the ¹⁷O spectrum of H₂¹⁷O, or in the ¹³C spectrum of the ¹³CH₂ group in partially deuterated ethanol CD₃¹³CH₂OD. We therefore explored the possibility of using reactions like in Fig. 6 to observe the binomial distribution of the triplet of the CH₂ protons. We explored the kinetics of the addition of H₂O onto two different substrates: chloral diluted in acetonitrile and 1,3-dichlorotetrafluoroacetone diluted in dioxane. The main requirement is that the reaction must be faster than the relaxation of the TSI and its decay due to proton exchange. The rate constants found using pseudo-first-order kinetic equations are reported in Table 3, albeit without DNP and thus without TSI. In acetonitrile-d₃, with a 5-fold excess of chloral with respect to H₂O, a pseudo first-order rate constant k_pfo = 0.002 s⁻¹ was observed. This reaction is too slow to be useful for detecting the TSI characteristic of para-water. However, the addition of water onto the more reactive compound (1,3-dichlorotetrafluoroacetone, in dioxane-d₈) was so fast that an accurate determination of the rate was difficult by NMR. A reaction rate k_pfo > 0.1 s⁻¹ makes it a good candidate as a “revealing agent” of TSI in para-water. As an alternative method for detection, one can simply measure the ¹⁷O spectrum in 0.037% natural abundance or with partial isotopic enrichment to improve sensitivity. The ¹⁷O spectrum in Fig. 7 shows a triplet due to ¹J(¹H,¹⁷O) = 80 Hz of 55 mM H₂O in dioxane-d₈ at 298 K and 400 MHz. Using water enriched to 20% ¹⁷O, we were able to acquire an ¹⁷O spectrum in a few seconds, making this method a valid alternative to the use of a chemical reaction. Again, deviations from the binomial distribution of the intensities of the spectral lines should provide the information needed to assess the lifetime of the TSI and hence of para-water.

Table 3 Kinetic pseudo-first-order rate constant k_pfo for hydration of activated C=O bonds observed at 800 MHz and 300 K

Reactant	Solvent	[Reactant] (mM)	[H2O] (mM)	k pfo (s^−1)
Chloral	Acetonitrile-d3	1000	200	0.002
1,3-Dichlorotetra-fluoroacetone	Dioxane-d8	275	55	>0.1

---

Fig. 7 Experimental ¹⁷O spectrum of 20% enriched water, 55 mM in dioxane-d₈, acquired on a 400 MHz NMR spectrometer. The binomial 1 : 2 : 1 distribution of the triplet due to J(¹H,¹⁷O) ∼80 Hz is characteristic of an equilibrium Boltzmann distribution. Deviations from this binomial multiplet are expected if the TSI does not vanish, and could be a hallmark of para-water. Isotopic enrichment of 20% ¹⁷O made it possible to use an acquisition time of a few seconds, making this method suitable for detection of a TSI.

We have optimized the most critical aspects of the experimental scheme suggested in this paper. However, we were not yet able to perform complete experiments since our setup needs to be significantly adapted in order to support dissolution with dioxane.

Conclusions

We have proposed an experimental strategy to produce para-water on a macroscopic scale (i.e. with concentrations in the mM range). Provided that the CSA of the protons is sufficient to lift the degeneracy of the two spins in a frozen sample, we demonstrated that one can use DNP to enhance the population of the ground state of water molecules, thus generating a Triplet–Singlet Imbalance (TSI) that is expected to be a long-lived state analogous to para-water. We proved that the lifetime of water as a molecular entity can be extended up to a few minutes by dilution in aprotic solvents. Several detection strategies can be used either by performing a “revealing” reaction such as the addition of water to an aldehyde or another suitable substrate or by observing the ¹⁷O NMR spectrum of water itself. It is also possible to monitor proton magnetization of water relaxing to equilibrium with two clearly distinct time constants to assess the lifetime of the TSI and hence the amount of para-water in the sample. Similar information can, in principle, be obtained by infrared spectroscopy. The detection of the para-water signal with long lifetimes may open the way to study slow transport phenomena such as flow, diffusion, and electrophoretic mobility.

Appendix

Let us consider a solution of pure H₂O. Let p be the frequency at which a proton is exchanged with another proton belonging to a different water molecule:

p ∝ [H₂O]

Hence, the proton exchange rate k_EX can be defined as:

k_EX = 2p

The factor 2 reflects the fact that a proton belonging to a H₂O molecule can exchange with either of the two protons of another H₂O molecule.

Let us now consider a mixture of H₂O, HDO and D₂O. With the ratio α = [H]/([H] + [D]), their concentrations can be expressed as:

[H₂O] = α²C_TOT

[D₂O] = (1 − α)²C_TOT

[HDO] = 2α(1 − α)C_TOT

where:

C_TOT = [H₂O] + [HDO] + [D₂O]

The equations for the exchange of proton magnetization between two distinct sites can be written in the general form:

where:

Let us consider the following reactions involving the exchange of a proton:

H₂O + D₂O ↔ 2HDO

HDO + D₂O ↔ D₂O + HDO

H₂O + HDO ↔ HDO + H₂O

If we focus attention on the magnetization transfer from H₂O to HDO, there are three possibilities:

(1) H₂O meets another H₂O. The exchange of two protons does not lead to any transfer of magnetization between different environments with distinct chemical shifts.

(2) H₂O meets D₂O. There are four possible exchange processes. Each process leads to the creation of two HDO molecules, and there are two protons that transfer their magnetization between different environments:

k₂ = 8p[D₂O] = 8pα²

(3) H₂O meets HDO. Again, four possible exchange processes can take place, but there is only one proton that transfers its magnetization between different environments:

k₃ = 4p[HDO] = 8pα(1 − α)

If we consider that we should count an exchange process not only for the proton that hops but also for its neighbor, the total exchange rate is:

If we now consider magnetization transfer from HDO to H₂O, there are again three possibilities:

(4) HDO meets H₂O. This is symmetric to case (3) above:

k₁ = 4p[H₂O] = 4p(1 − α)²

(5) HDO meets D₂O. Four possible exchange processes can again occur but none of them leads to any magnetization transfer between different environments.

(6) HDO meets HDO. Again, four possible exchange processes are possible, two of which swap a proton with another proton but do not lead to any magnetization transfer. Two processes swap a proton and a deuteron to create two H₂O molecules, which is accompanied by a transfer of magnetization between different environments:

k₃ = 4p[HDO] = 8pα(1 − α)

In this case we have counted the exchange processes twice: when a molecule i meets a molecule j the effect is of course the same as the case when j meets i. Hence the total rate is:

By including longitudinal relaxation, we find:

This matrix can be diagonalized as:

so that

With the assumption that , we finally find:

In these calculations we have neglected possible kinetic isotope effects on the rates.

Acknowledgements

Geoffrey Bodenhausen is indebted to at least 16 reviewers who wrote constructive critiques of no less than three proposals submitted to the ERC. The authors thank Martial Rey for valuable assistance and André Merbach, Lothar Helm, Malcolm Levitt, Giuseppe Pileio, Jean-Maurice Mallet, and Jean-Nicolas Dumez for many useful discussions.

Notes and references

1. C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648.
2. C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542.
3. B. Meier, J.-N. Dumez, G. Stevanato, J. T. Hill-Cousins, S. S. Roy, P. Hakansson, S. Mamone, R. C. D. Brown, G. Pileio and M. H. Levitt, J. Am. Chem. Soc., 2013, 135, 18746–18749.
4. J. Haupt, Phys. Lett. A, 1972, 38, 389–390.
5. M. Icker, P. Fricke and S. Berger, J. Magn. Reson., 2012, 223, 148–150.
6. M. Tomaselli, C. Degen and B. H. Meier, J. Chem. Phys., 2003, 118, 8559–8562.
7. M. Tomaselli, U. Meier and B. H. Meier, J. Chem. Phys., 2004, 120, 4051–4054.
8. J.-N. Dumez, P. Håkansson, S. Mamone, B. Meier, G. Stevanato, J. T. Hill-Cousins, S. S. Roy, R. C. D. Brown, G. Pileio and M. H. Levitt, J. Chem. Phys., 2015, 142, 044506.
9. M. Carravetta, O. G. Johannessen and M. H. Levitt, Phys. Rev. Lett., 2004, 92, 153003.
10. R. Sarkar, P. R. Vasos and G. Bodenhausen, J. Am. Chem. Soc., 2007, 129, 328–334.
11. M. C. D. Tayler and M. H. Levitt, Phys. Chem. Chem. Phys., 2011, 13, 5556.
12. M. C. D. Tayler, I. Marco-Rius, M. I. Kettunen, K. M. Brindle, M. H. Levitt and G. Pileio, J. Am. Chem. Soc., 2012, 134, 7668–7671.
13. G. Stevanato, J. T. Hill-Cousins, P. Håkansson, S. S. Roy, L. J. Brown, R. C. D. Brown, G. Pileio and M. H. Levitt, Angew. Chem., Int. Ed., 2015, 54, 3740–3743.
14. R. Buratto, D. Mammoli, E. Chiarparin, G. Williams and G. Bodenhausen, Angew. Chem., Int. Ed., 2014, 53, 11376–11380.
15. R. Buratto, A. Bornet, J. Milani, D. Mammoli, B. Vuichoud, N. Salvi, M. Singh, A. Laguerre, S. Passemard, S. Gerber-Lemaire, S. Jannin and G. Bodenhausen, ChemMedChem, 2014, 9, 2509–2515.
16. N. Salvi, R. Buratto, A. Bornet, S. Ulzega, I. Rentero Rebollo, A. Angelini, C. Heinis and G. Bodenhausen, J. Am. Chem. Soc., 2012, 134, 11076–11079.
17. R. F. Curl, J. Chem. Phys., 1967, 46, 3220.
18. G. E. Pake, J. Chem. Phys., 1948, 16, 327.
19. H. Eisendrath and J. Jeener, Phys. Rev. B: Solid State, 1978, 17, 54–60.
20. H. Eisendrath, W. Stone and J. Jeener, Phys. Rev. B: Solid State, 1978, 17, 47–53.
21. T. Kravchuk, M. Reznikov, P. Tichonov, N. Avidor, Y. Meir, A. Bekkerman and G. Alexandrowicz, Science, 2011, 331, 319–321.
22. D. A. Horke, Y.-P. Chang, K. Długołęcki and J. Küpper, Angew. Chem., Int. Ed., 2014, 53, 11965–11968.
23. V. I. Tikhonov, Science, 2002, 296, 2363.
24. S. L. Veber, E. G. Bagryanskaya and P. L. Chapovsky, J. Exp. Theor. Phys., 2006, 102, 76–83.
25. M. E. Fajardo, S. Tam and M. E. DeRose, J. Mol. Struct., 2004, 695–696, 111–127.
26. R. L. Redington and D. E. Milligan, J. Chem. Phys., 1962, 37, 2162.
27. R. Sliter, M. Gish and A. F. Vilesov, J. Phys. Chem. A, 2011, 115, 9682–9688.
28. K. Kurotobi and Y. Murata, Science, 2011, 333, 613–616.
29. C. Beduz, M. Carravetta, J. Y.-C. Chen, M. Concistrè, M. Denning, M. Frunzi, A. J. Horsewill, O. G. Johannessen, R. Lawler, X. Lei, M. H. Levitt, Y. Li, S. Mamone, Y. Murata, U. Nagel, T. Nishida, J. Ollivier, S. Rols, T. Room, R. Sarkar, N. J. Turro and Y. Yang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12894–12898.
30. S. Mamone, M. Concistrè, E. Carignani, B. Meier, A. Krachmalnicoff, O. G. Johannessen, X. Lei, Y. Li, M. Denning, M. Carravetta, K. Goh, A. J. Horsewill, R. J. Whitby and M. H. Levitt, J. Chem. Phys., 2014, 140, 194306.
31. D. Mammoli, B. Vuichoud, A. Bornet, J. Milani, J.-N. Dumez, S. Jannin and G. Bodenhausen, J. Phys. Chem. B, 2015, 119, 4048–4052.
32. A. Bornet, X. Ji, D. Mammoli, B. Vuichoud, J. Milani, G. Bodenhausen and S. Jannin, Chem. – Eur. J., 2014, 20, 17113–17118.
33. K. Modig and B. Halle, J. Am. Chem. Soc., 2002, 124, 12031–12041.
34. P. Tekely, P. Palmas and P. Mutzenhardt, J. Magn. Reson., 1997, 127, 238–240.
35. D. Carnevale, S. E. Ashbrook and G. Bodenhausen, RSC Adv., 2014, 4, 56248–56258.
36. J. Tennyson, J. Phys. Chem. Ref. Data, 2001, 30, 735.
37. J. Milani, B. Vuichoud, A. Bornet, P. Miéville, R. Mottier, S. Jannin and G. Bodenhausen, Rev. Sci. Instrum., 2015, 86, 024101.
38. P. Miéville, P. Ahuja, R. Sarkar, S. Jannin, P. R. Vasos, S. Gerber-Lemaire, M. Mishkovsky, A. Comment, R. Gruetter, O. Ouari, P. Tordo and G. Bodenhausen, Angew. Chem., Int. Ed., 2010, 49, 6182–6185.
39. D. Gajan, A. Bornet, B. Vuichoud, J. Milani, R. Melzi, H. A. van Kalkeren, L. Veyre, C. Thieuleux, M. P. Conley, W. R. Gruning, M. Schwarzwalder, A. Lesage, C. Coperet, G. Bodenhausen, L. Emsley and S. Jannin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14693–14697.
40. P. L. Chapovsky, J. Cosléou, F. Herlemont, M. Khelkhal and J. Legrand, Chem. Phys. Lett., 2000, 322, 424–428.
41. P. L. Chapovsky and L. J. F. Hermans, Annu. Rev. Phys. Chem., 1999, 50, 315–345.
42. P. Cacciani, J. Cosléou and M. Khelkhal, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 012521.
43. N. D. Sergeyeva, V. N. Torocheshnikov and N. M. Sergeyev, Moscow Univ. Chem. Bull., 2010, 65, 98–102.
44. S. Meiboom, J. Chem. Phys., 1961, 34, 375.
45. T. Segawa, F. Kateb, L. Duma, G. Bodenhausen and P. Pelupessy, ChemBioChem, 2008, 9, 537–542.
46. F. Kateb, P. Pelupessy and G. Bodenhausen, J. Magn. Reson., 2007, 184, 108–113.
47. J. Jeener, B. H. Meier, P. Bachmann and R. R. Ernst, J. Chem. Phys., 1979, 71, 4546.
48. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
49. N. M. Sergeyev and N. D. Sergeyeva, Phys. Chem. Chem. Phys., 2002, 4, 2994–2999.
50. A. Bornet, J. Milani, B. Vuichoud, A. J. Perez Linde, G. Bodenhausen and S. Jannin, Chem. Phys. Lett., 2014, 602, 63–67.
51. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
52. M. G. Pravica and D. P. Weitekamp, Chem. Phys. Lett., 1988, 145, 255–258.

---