Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory calculations of the hydrazine decomposition mechanism on the planar and stepped Cu(111) surfaces
Saeedeh S.
Tafreshi
a,
Alberto
Roldan
ab and
Nora H.
de Leeuw
*ab
aDepartment of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK
bSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, UK. E-mail: DeLeeuwN@cardiff.ac.uk; Tel: +44 (0)2920870658
First published on 17th July 2015
Abstract
We have investigated the adsorption of hydrazine (N2H4) and its reactivity on terraces and steps of Cu(111) surfaces by first-principles calculations in order to gain insight into the hydrazine decomposition mechanism. We have investigated different possibilities for the N–N and N–H bond cleavage for any intermediate states by analysing the reaction and barrier energies of each elementary step. We have found that hydrazine dehydrogenation via N–H bond scission is neither energetically nor kinetically favourable on the flat and stepped surfaces, but hydrazine prefers to form NH2via N–N bond decoupling on the Cu(111) with an activation energy below 1 eV. The NH2 molecule reacts fairly easily with co-adsorbed NH2 to form NH3 as well as with N2Hx (x = 1–4) by abstracting hydrogen to produce NH3 and N2 molecules on both the flat and stepped surfaces. We also found that all intermediates except NNH prefer N–N bond breaking as the most likely dissociation pathway, where the amide and imide intermediates produced can be hydrogenated to form NH3 in the presence of hydrogen. NNH is the only intermediate, which prefers to dissociate via a highly exothermic N–H bond breaking process to produce an N2 molecule after overcoming a small barrier energy. We also studied the production of H2 by recombination of hydrogen ad-atoms which, considering the activation energies, is particularly favoured under conditions of moderate temperatures. Our results agree well with experiments suggesting that N2H4 adsorbs dissociatively on copper above ∼300 K leading to N2, NH3 and H2. In general, the lower coordination of the steps is found to lead to higher reactivity than on the flat Cu(111) surface. Furthermore, the calculations show that the influence of step edge atoms is very different for the intra- and intermolecular dehydrogenation mechanisms. They also increase the barrier of N–N decoupling of all the existing species in the reaction.
1. Introduction
Hydrogen has received much attention over the last few decades as an energy resource,1,2 for instance, in the proton exchange membrane (PEM) fuel cells which are some of the new carbon-free technologies for power generators. However, finding materials with a high storage capacity of hydrogen at room temperature is difficult and much effort is spent on developing new materials or employing organic and inorganic compounds for onboard hydrogen generation. Hydrazine (N2H4) with a hydrogen content of 12.5 wt% is a good hydrogen source for PEM fuel cells and since it is liquid at temperatures ranging from 2 °C to 114 °C, it is ideal for portable applications, for example for its current use in space vehicles or satellites.3–5 Although hydrazine is a toxic substance, its decomposition products, N2, H2 and NH3, are non-poisonous and carbon-free.3 Its decomposition over catalysts at room temperature is exothermic without the need for external energy. Hydrazine is also used in a monopropellant thruster to control and adjust the orbits and altitudes of spacecrafts and satellites,4,6 which is based on the production of larger volumes of N2, H2 and NH3 gases from the decomposition of a relatively small volume of liquid hydrazine. The most important catalyst used for this reaction is Ir/Al2O3 with a high loading of iridium (20–40%).4,6–8 However, due to the high price and limited resources of iridium, scientists are seeking to develop new, cheaper, active and readily available alternative catalysts for N2H4 decomposition.We aim to investigate at the molecular level the catalytic activity of Cu towards N2H4 decomposition to understand the thermodynamics and kinetics of the elementary steps, and to evaluate if copper-based catalysts, which are much cheaper than iridium, could be used for hydrazine decomposition. Experimental studies have revealed that adsorption of N2H4 on copper at relatively low temperatures is likely to be reversible and non-dissociative up to ∼300 K, above which hydrazine decomposes and generates the gaseous products NH3, N2 and H2.9,10 There are two typical reactions for hydrazine decomposition;
| N2H4 → N2 + 2H2 | (1) |
| 3N2H4 → 4NH3 + N2 | (2) |
Besides the more stable perfect and planar surfaces, defects and steps are common surface features. Previous experimental and theoretical results have suggested that low-coordinated sites show higher catalytic activity and can influence the overall surface chemistry.14–20 Dahl et al.21 showed that the energy barrier for N2 dissociation is more than 1 eV lower on the Ru(0001) step edge than on the terraces. On the same surface, Zambelli et al.22 have reported that the step edges are the active sites for NO dissociation. Xu and Mavrikakis showed that the tensile strain at steps substantially facilitates the O2 activation on gold surfaces,23 although the effect of steps on O2 dissociation on Cu surfaces is not expected to be as pronounced as in other gas–metal systems.24 The results for CO dissociation on the Ni surface indicate that the energy barriers for CO dissociation strongly favour reactions occurring near surface steps.25 Fu and Somorjai26 were able to provide evidence of the enhanced interaction of CO2 on Cu steps, which results in the sensitivity of the methanol synthesis process to copper surface structures. Some studies have shown that the effect of step edge atoms is very different for the different reaction pathways. For example, Vang et al. in their study on ethylene dissociation on flat and stepped Ni(111) found that on the steps the barrier for C–C bond breaking is lowered significantly more than the barrier for dehydrogenation.
Following our investigation of the adsorption of molecular hydrazine on realistic Cu surfaces,27–29 here we have carried out density functional theory calculations including dispersive interactions,30,31 to characterize the most favourable adsorption sites, geometries and energies of the N2H4 decomposition intermediates. We have suggested and analysed three different decomposition mechanisms, including dehydrogenation via intra- and intermolecular pathways and N–N bond cleavage, on both flat and stepped Cu(111) surfaces.
2. Computational methods
We have carried out electronic structure calculations using DFT as implemented in the Vienna Ab initio Simulation Package (VASP).32–35 The total energy calculations have been performed using the Perdew–Burke–Ernzerhof (PBE)36 form of the generalized gradient approximation (GGA), whereas the projector augmented wave (PAW) method has been used to consider the effect of the inner cores on the valence density.37,38 To improve the description of the long-range interaction, and following our previous work on the Cu–hydrazine system,27 we have employed the DFT-D2 method of Grimme as implemented in VASP,31 which has been shown to improve accuracy on several systems, e.g.ref. 27, 39 and 40. We have used the standard global scaling factor for the PBE functional within a damping function to avoid near singularities at small distances. We have also tested the DFT-D3 method to evaluate its effects on the adsorption energies compared to the DFT-D2 calculations. In line with Almora-Barrios et al.,41 we found that the use of DFT-D3 led to larger binding energies, but also a more pronounced deviation from experimental values of the Cu lattice parameter and cohesive energy compared with those obtained by DFT-D2.42 In this paper, we consider the energy differences between competing reactions to identify the preferred reaction mechanisms and pathways relative to each other, and as such DFT-D2 represents a sufficiently accurate model of the system to identify the reaction trends for hydrazine dissociation on the Cu surface.Plane wave basis sets were used with an energy cut-off of 600 eV, which gave bulk energies converged to within 0.001 eV per atom. A 5 × 5 × 1 and 3 × 5 × 1 Monkhorst–Pack grid43 of k points was used to sample the Brillouin zone for flat and stepped surfaces respectively. Spin polarization has been tested in a few cases but was found to be irrelevant.
The flat and stepped slabs were modelled with a 2 × 2 and 3 × 2 supercell from the full unit cell, p(4 × 4) and p(6 × 4), with 20 Å of vacuum between slabs in the z-direction where Cu–Cu distances were originally taken from the fully optimised bulk geometry. The adsorbate and the top three layers out of four and five layers of the flat and stepped slabs, respectively, were allowed to relax during structural optimisation, in line with previous studies.44,45 Different slab thicknesses were tested until convergence was achieved within 0.01 eV per cell.
We have calculated the adsorption energies of the intermediates from the hydrazine decomposition process relative to the hydrazine molecule in the gas-phase:
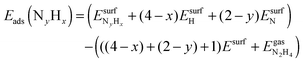 | (3) |
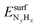 is the total energy of the NyHx species adsorbed on a relaxed surface and
is the total energy of the NyHx species adsorbed on a relaxed surface and 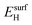 and
and 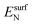 are the energies of an isolated H- and N-atom adsorbed somewhere else on the relaxed surface, at a non-interactive distance. Esurf and
are the energies of an isolated H- and N-atom adsorbed somewhere else on the relaxed surface, at a non-interactive distance. Esurf and 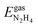 are the energies of the naked surface and isolated gas-phase hydrazine respectively. Within this definition, a negative Eads value means a release of energy during adsorption. A combination of two varieties of the nudged elastic band (NEB) method46,47 and the improved dimer method (IDM)48 was used to identify transition state (TS) structures, which we verified by a single imaginary frequency associated with the reaction coordinate. The reaction energy (Er) was obtained from the difference in energy between final and initial states and a negative Er hence indicates an exothermic process. The forward and reverse activation barriers (Ea) were defined as the energy difference between the TS and the initial state or the final state, respectively.
are the energies of the naked surface and isolated gas-phase hydrazine respectively. Within this definition, a negative Eads value means a release of energy during adsorption. A combination of two varieties of the nudged elastic band (NEB) method46,47 and the improved dimer method (IDM)48 was used to identify transition state (TS) structures, which we verified by a single imaginary frequency associated with the reaction coordinate. The reaction energy (Er) was obtained from the difference in energy between final and initial states and a negative Er hence indicates an exothermic process. The forward and reverse activation barriers (Ea) were defined as the energy difference between the TS and the initial state or the final state, respectively.
3. Results
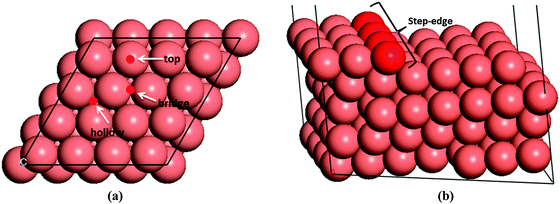
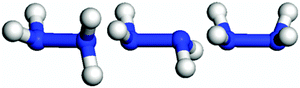
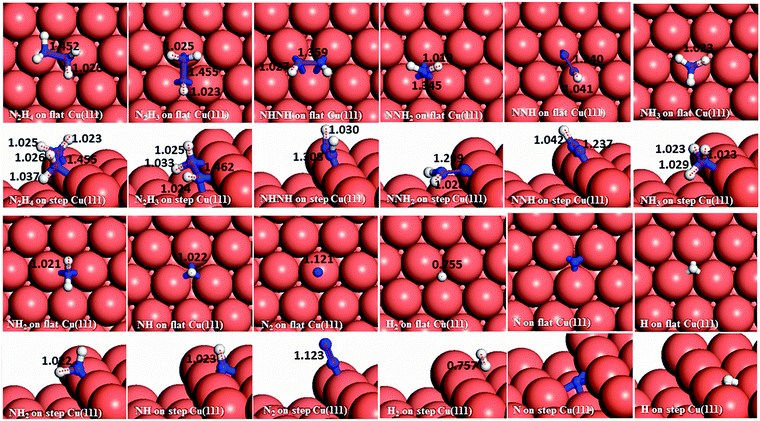
We have first created the perfect Cu(111) surface, which is the close-packed plane of the fcc structure (Fig. 1a) and is the most stable copper surface.49 The surface Cu atoms are arranged in a hexagonal lattice with a separation of 2.52 Å between nearest neighbour atoms. The stepped Cu(111) surface has been studied to investigate the presence of an extended edge of low-coordinated atoms on the N2H4 dissociation behaviour (shown in Fig. 1b). Each unit cell in the stepped slab was offset by one atomic layer with respect to the next cell.50–52The three major conformations of hydrazine in the gas-phase are gauche, trans and eclipsed (Fig. 2), where the gauche conformer is the lowest-energy structure. The trans and eclipsed conformations are 0.13 and 0.36 eV higher in energy, respectively, than the gauche conformation. We have identified the strongest adsorption geometries by placing the different intermediates at a variety of positions on the planar and stepped Cu(111) surfaces. Adsorption energies and structural parameters for various intermediate species in their most stable configurations on the flat and stepped Cu(111) are presented in Table 1 and Fig. 3. We note that because of the lower coordination of the stepped surface atoms, all intermediates are more stable on the step than on the terrace sites.
| Adsorbate | E ads (eV), flat | E ads (eV), step | Cu–N (Å), flat | Cu–N (Å), step | N–N (Å), flat | N–N (Å), step | N–H (Å), flat | N–H (Å), step |
|---|---|---|---|---|---|---|---|---|
| N2H4 | −0.98 | −1.53 | 2.178 | 2.104 | 1.452 | 1.455 | 1.026 | 1.028 |
| N2H3 | −0.85 | −1.21 | 2.023 | 2.033 | 1.455 | 1.462 | 1.024 | 1.027 |
| NHNH | −0.10 | −0.68 | 1.966 | 1.922 | 1.359 | 1.308 | 1.027 | 1.030 |
| NNH2 | −0.18 | −0.66 | 1.946 | 1.904 | 1.345 | 1.299 | 1.019 | 1.028 |
| NNH | 0.37 | −0.39 | 1.971 | 1.938 | 1.240 | 1.237 | 1.041 | 1.042 |
| NH3 | −0.81 | −1.06 | 2.092 | 2.072 | — | — | 1.023 | 1.025 |
| NH2 | −0.13 | −1.42 | 1.982 | 1.942 | — | — | 1.021 | 1.022 |
| NH | 0.38 | −0.58 | 1.898 | 1.566 | — | — | 1.022 | 1.023 |
| N2 | −0.15 | −0.39 | 1.985 | 1.931 | 1.121 | 1.123 | — | — |
| H2 | −0.10 | −0.12 | — | — | — | — | — | — |
| N | 1.32 | 0.87 | 1.838 | 2.002 | — | — | — | — |
| H | −0.28 | −0.36 | — | — | — | — | — | — |
3.1 Adsorption on the planar and stepped Cu(111)
3.2 N2Hx (x = 1–4) decomposition pathways on the planar and stepped Cu(111)
| Reactions | Flat | Step | |||||
|---|---|---|---|---|---|---|---|
| E r (eV) | E a forward (eV) | E a reverse (eV) | E r (eV) | E a forward (eV) | E a reverse (eV) | ||
| Adsorption–desorption | |||||||
| R1 | N2H4 ↔ N2H4* | −0.98 | — | — | −1.53 | — | — |
| R2 | NH3* ↔ NH3 | 0.81 | — | — | 1.06 | — | — |
| R3 | N2* ↔ N2 | 0.15 | — | — | 0.39 | — | — |
| R4 | H2* ↔ H2 | 0.10 | — | — | 0.12 | — | — |
| N2H4 dissociation | |||||||
| R5 | N2H4* ↔ 2NH2* | −0.87 | 0.86 | 1.73 | −1.66 | 0.90 | 2.56 |
| R6 | N2H4* ↔ N2H3* + H* | 0.31 | 1.55 | 1.24 | 0.74 | 1.11 | 0.37 |
| N2H3 dissociation | |||||||
| R7 | N2H3* ↔ NH2* + NH* | −0.30 | 1.06 | 1.36 | −0.76 | 1.27 | 2.03 |
| R8 | N2H3* ↔ NNH2* + H* | 0.74 | 1.53 | 0.79 | 0.75 | 1.77 | 1.02 |
| R9 | N2H3* ↔ NHNH* + H* | 0.84 | 1.61 | 0.77 | 0.69 | 1.56 | 0.87 |
| N2H2 dissociation | |||||||
| R10 | NNH2* ↔ NH2* + N* | 0.13 | 1.42 | 1.29 | 0.18 | 1.52 | 1.34 |
| R11 | NHNH* ↔ 2NH* | −0.34 | 0.85 | 1.19 | −0.76 | 0.93 | 1.69 |
| R12 | NNH2* ↔ NNH* + H* | 0.58 | 1.35 | 0.77 | 0.86 | 0.89 | 0.03 |
| R13 | NHNH* ↔ NNH* + H* | 0.60 | 1.68 | 1.08 | 0.43 | 1.39 | 0.96 |
| NNH dissociation | |||||||
| R14 | NNH* ↔ NH* + N* | 0.16 | 1.47 | 1.31 | −0.41 | 1.89 | 2.30 |
| R15 | NNH* ↔ N2* + H* | −1.50 | 0.37 | 1.87 | −1.11 | 0.62 | 1.73 |
| N2 dissociation | |||||||
| R16 | N2* ↔ 2N* | 3.22 | 4.78 | 1.56 | 1.96 | 6.02 | 4.06 |
| H–H coupling | |||||||
| R17 | 2H* ↔ H2* | 0.43 | 1.08 | 0.65 | 0.81 | 1.28 | 0.47 |
| NHx (x = 1–3) dehydrogenation | |||||||
| R18 | NH3* ↔ NH2* + H* | 0.74 | 1.63 | 0.89 | 0.67 | 1.59 | 0.92 |
| R19 | NH2* ↔ NH* + H* | 0.67 | 1.59 | 0.92 | 1.06 | 1.81 | 0.75 |
| R20 | NH* ↔ N* + H* | 1.46 | 1.97 | 0.51 | 1.36 | 2.07 | 0.71 |
| Interaction of NH2 molecules | |||||||
| R21 | 2NH2* ↔ NH* + NH3* | −0.05 | 0.55 | 0.60 | 0.37 | 2.05 | 1.68 |
| Interaction of NH2 with N2Hx (x = 1–4) | |||||||
| R22 | N2H4* + NH2* ↔ N2H3* + NH3* | −0.35 | 0.59 | 0.94 | −0.22 | 0.03 | 0.25 |
| R23 | N2H3* + NH2* ↔ NHNH* + NH3* | 0.11 | 0.80 | 0.69 | −0.01 | 0.64 | 0.65 |
| R24 | N2H3* + NH2* ↔ NNH2* + NH3* | −0.12 | 0.70 | 0.82 | −0.06 | 0.67 | 0.73 |
| R25 | NNH2* + NH2* ↔ NNH* + NH3* | 0.15 | 0.44 | 0.29 | −0.47 | 0.15 | 0.62 |
| R26 | NHNH* + NH2* ↔ NNH* + NH3* | −0.26 | 0.36 | 0.62 | 0.01 | 1.00 | 0.99 |
| R27 | NNH* + NH2* ↔ N2* + NH3* | −2.13 | 0.14 | 2.29 | −1.60 | 0.57 | 2.17 |
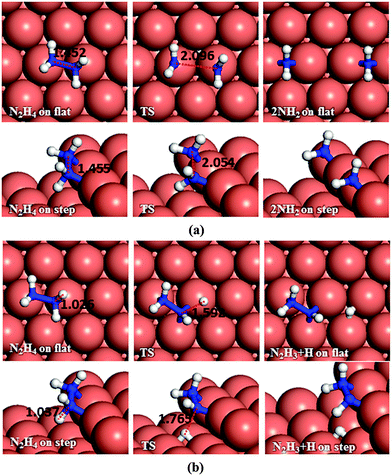
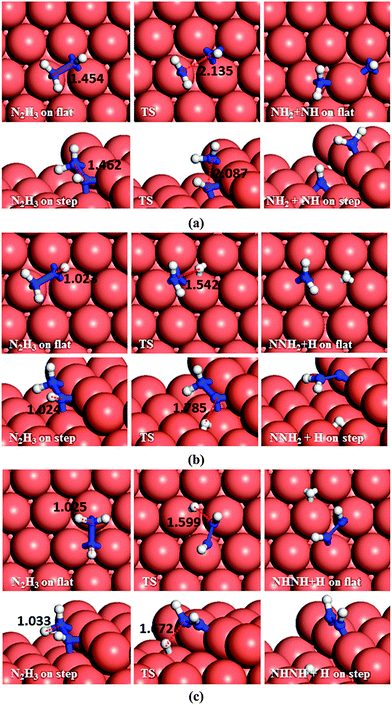
Dehydrogenation of N2H4 was also investigated (Fig. 4b). The energy barrier for this path on the flat surface is 1.55 eV and the process is endothermic by 0.31 eV. The activation energy on the stepped surface decreases to 1.11 eV, but the process becomes less favourable thermodynamically (Er = 0.74 eV).
These results indicate that on Cu(111), with or without surface steps, the N–N bond cleavage of hydrazine is energetically and kinetically preferred over its dehydrogenation, which is in line with a previous experimental study showing that N–H bond breaking requires more energy than N–N breaking.59 From the charge density calculations in our previous work,27 which shows the induced charge density on the Cu(111) surface upon N2H4 adsorption, it can be observed that more charge is accumulated between the N and H atoms of hydrazine than between the two N atoms, which agrees well with these energetic results.
There are two distinct pathways for dehydrogenation of N2H3, respectively, shown in Fig. 5b and c. The one leading to NNH2 and a H atom has a barrier and reaction energy of 1.53 and 0.74 eV, respectively, on the flat surface, and 1.77 and 0.75 eV on the step. The alternative dehydrogenation pathway leads to NHNH and H as products. The barrier for this endothermic process (Er = 0.84 eV) is 1.61 eV on the flat surface, while the step decreases the barrier to 1.56 eV although it is still endothermic (Er = 0.69 eV).
Although NHNH and NNH2 are products of the dehydrogenation of N2H3 on the Cu(111) surface, the N–N bond breaking of N2H3 is energetically more favourable. Our results indicate that low-coordinated atoms make the N–N decoupling of N2H3 more feasible thermodynamically, although they do not affect the kinetics.
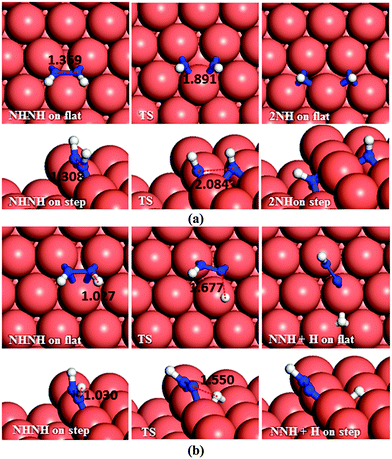
As to N–N bond breaking of NHNH (Fig. 7a), while the reaction barrier is 0.85 eV and the reaction is exothermic by −0.34 eV on the flat surface, these values increase to 0.93 and −0.76 eV, respectively, on the atomic step system. However, the dehydrogenation of NHNH resulting in NNH and an H species has a barrier of 1.68 eV and is endothermic by 0.60 eV on the flat surface (Fig. 7b). The lower coordination of the steps decreases both the barrier and the reaction energy to 1.39 and 0.43 eV respectively. Thus, the production of NH molecules via N–N bond breaking of NHNH is more favourable than other dissociation mechanisms of N2H2 from both thermodynamic and kinetic points of view.
3.3 NHx (x = 1–3) dehydrogenation
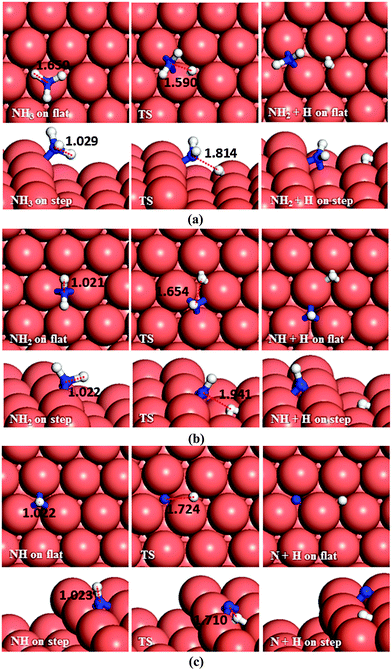
We have also investigated the consecutive dehydrogenation of ammonia, see Fig. 10a. The barrier and the endothermic reaction energy associated with the first N–H bond breaking process are 1.63 eV and 0.74 eV, respectively, on the flat surface, i.e. slightly higher than the barrier of 1.59 eV and a reaction energy of 0.67 eV on the step. The exothermic reverse (hydrogenation) reaction is more likely to happen with energy barriers of 0.89 and 0.92 eV on the terrace and step respectively. The dehydrogenation of NH2 (Fig. 10b) and further dehydrogenation of NH (Fig. 10c) are also unlikely to succeed based on their associated high barrier energies, i.e. 1.59 and 1.97 eV on the flat surface and 1.81 and 2.07 on the stepped surface, respectively. The DFT calculated barrier energies for the dehydrogenation of NH3, NH2 and NH to form HCN on Pt(111) are smaller than our results, i.e. 1.39, 1.30 and 1.40 eV respectively,60 although not significantly.The reverse process, hydrogenation of NH has activation energies of 0.92 and 0.75 eV on the terrace and step, respectively. The hydrogenation of N is energetically favourable (Er = −1.46 and −1.36 eV) leading to NH via energy barriers of only 0.51 and 0.71 eV on the flat and stepped surfaces, respectively. These energies show that the Cu surface could be a good catalyst for ammonia synthesis compared to the Ru(0001) surface, where the calculated barriers for hydrogenation of N, NH and NH2 were found to be more than 1.2 and 1.1 eV on terraces and steps, respectively.61,62
3.4 H–H coupling
We have also considered another secondary process, the pathways for H–H coupling, see Fig. 11. As Table 2 shows, combining two hydrogen atoms on the stepped surface exhibits higher barrier and endothermic reaction energies of 1.28 and 0.81 eV than on the flat surface, Ea = 1.08 and Er = 0.43 eV. The reverse reaction, the exothermic H2 dissociation reaction, has energy barriers of 0.65 and 0.47 eV on the terrace and stepped surfaces, respectively, indicating that H2 should adsorb dissociatively on Cu surfaces and the presence of a step edge makes this process more likely to proceed, due to the stabilisation provided by the low-coordinated atoms, where the electronic structure is different than that for the terrace atoms.27,28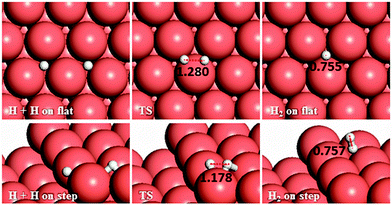 | ||
| Fig. 11 Schematic representation of the initial, transition and final states for H–H coupling pathways on the flat (top-view) and stepped (side-view) Cu(111) surfaces. Bond lengths are given in Å. | ||
3.5 Intermolecular dehydrogenation pathways
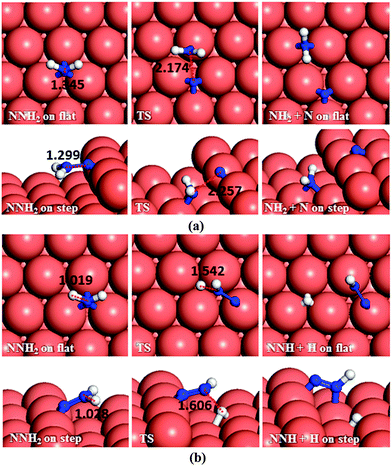
Having investigated the barriers for both N–N and N–H bond scission of the different possible intermediates of N2H4 dissociation, it is evident that breaking the hydrazine N–N bond and producing NH2 fragments is the most likely process to occur on both the flat and stepped Cu(111) surfaces. Furthermore, the dehydrogenation of NH2 is unfavourable to proceed at low temperatures due to the high energy of the transition states. We have therefore investigated other pathways involving the NH2 groups. There are two possibilities: NH2 can either react with another N2Hx (x = 1–4) intermediate and subtract a hydrogen, or react with another NH2 from hydrazine decomposition.In the first suggested process (Fig. 12a), NH2 interacts with N2H4 and abstracts one of its H atoms leading to N2H3 and NH3. The energy barrier for this process is 0.59 eV on the flat surface, but it decreases to only 0.03 eV on the stepped surface, and releases energies of 0.35 and 0.22 eV, respectively. This step therefore could proceed fairly easily on both the flat and stepped Cu(111) surfaces.
In the second process, represented in Fig. 12b and c, the NH2 molecule subtracts a hydrogen from N2H3 leading to NNH2 or NHNH. If NNH2 is formed, the process requires overcoming a barrier of 0.70 eV, but the products are 0.12 eV more favourable than the reactants on the flat surface. The presence of steps on the surface leads to NNH2via a slightly lower barrier (Ea = 0.67 eV), but releasing only 0.06 eV. The alternative pathway, leading to NHNH, has barriers of 0.80 and 0.64 eV on the terrace and step, respectively, while the process is endothermic by 0.11 eV on the terrace and practically in thermodynamic equilibrium (Er = −0.01 eV) on the stepped surface.
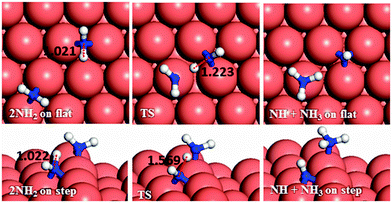
In the next dehydrogenation pathway (Fig. 12d and e), NH2 reacts with either the NNH2 or NHNH structure, leading to the formation of NNH. The dehydrogenation process starting with NNH2 is endothermic by 0.15 eV with an energy barrier of 0.44 eV on the terrace, while on the stepped surface it has a barrier of only 0.15 eV and an exothermic reaction energy of 0.47 eV. However, the interaction between NHNH and NH2 is exothermic by 0.26 with a barrier of only 0.36 eV on the flat surface which increases by 0.64 eV for a thermodynamically equilibrated reaction on the stepped surface (Ea = 1.00 and Er = 0.01 eV). The reaction between NH2 and NHNH is therefore likely to succeed on the flat surface, although the reaction between NNH2 and NH2 is more feasible on the stepped surface.
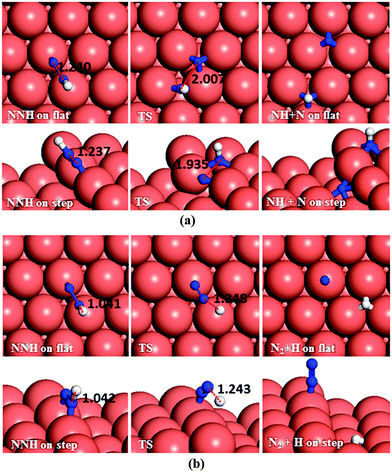
In the last dehydrogenation process, the reaction between NH2 and NNH yields N2 and NH3 (Fig. 12f). This reaction is highly exothermic releasing energies of 2.13 and 1.60 eV on the flat and stepped surfaces, respectively, which may be used for the desorption of N2 and NH3, which requires energies of 0.15 and 0.81 eV on the flat and 0.39 and 1.06 eV on the stepped surfaces, respectively.
4. Discussion
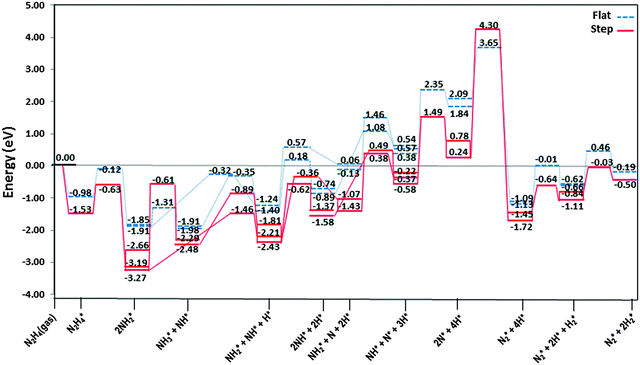
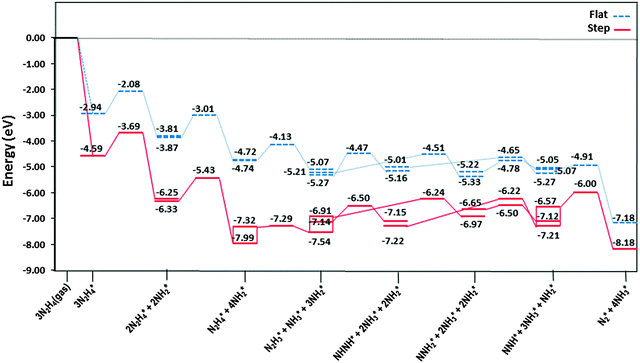
The most stable adsorption structures of the dehydrogenation intermediates showed that their order of stability on the surface with respect to hydrazine is N2H4 > N2H3 > N2H2 > N2H, indicating that more oxidised intermediates are less stable on the Cu surfaces. The same trend is found for the N–N average bond lengths, showing that dehydrogenation results in a shorter and stronger N–N bond and less stable intermediates on the surface.We summarised the energy profiles of the reaction mechanism in Fig. 14–16. The plot in Fig. 14 contains the different pathways for intramolecular dehydrogenation, whereas the N2H4 decomposition via N–N scission and further dehydrogenation reactions are shown in Fig. 15 and Fig. 16 summarises the intermolecular dehydrogenation pathway.
The N2H4 dehydrogenation, N2H4* → N2H3* + H*, and subsequent ones are unlikely to occur under moderate conditions, owing to the high reaction barriers, see Table 2 and Fig. 14. The rate-determining step for the N2H4 intramolecular dehydrogenation mechanism is NHNH* → NNH* + H* on the flat surface with an energy barrier of 1.68 eV, and N2H3* → NNH2* + H* on the stepped surface with an activation barrier of 1.77 eV. It is therefore unlikely that a large amount of N2 is produced via this intramolecular dehydrogenation pathway. Overall, from the investigation of N–H bond scission of all species on the surface, NNH is the only fragment which is easily dehydrogenated to the N2 molecule, with barriers of only 0.37 and 0.62 eV on the flat and stepped surfaces, respectively, and a relatively exothermic reaction (Er ∼ 1.3 eV). These results also suggest that at moderate temperatures the recombination of produced H atoms will lead to the formation of H2; this reaction has activation energies of ∼1.1 eV on the flat and stepped surfaces and the products desorb easily from the surface.
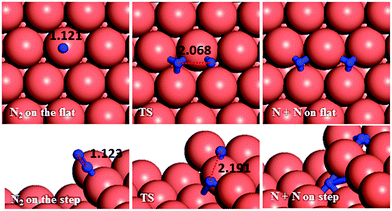
From investigation of N–N bond scission in any intermediate on the surface, we found that the N–N decoupling in N2H4 (N2H4* → 2NH2*), see Table 2 and Fig. 15, is the predominant mechanism, leading to amide intermediate production in agreement with experiment.59 The exothermic decomposition of N2H3 and NHNH fragments via N–N decoupling also has low activation energies compared to the other intermediates on the flat and stepped surfaces.
The production of NH3 takes place from the exothermic reaction of NH2 radicals on the flat surface by an activation energy of only 0.55 eV. Further NH3 production from the interaction of N2Hx (x = 1–4) and NH2 is also possible, resulting in the production of N2; all these steps have barrier energies below 1 eV on either the flat or stepped surfaces, see Table 2 and Fig. 16. The rate-determining step for the intermolecular dehydrogenation via NH2 is the reaction N2H3* + NH2* → NHNH* + NH3* which has an activation energy of 0.80 eV on the flat surface, while on the stepped surfaces NHNH* + NH2* → NNH* + NH3* has a barrier of 1.00 eV where it is the rate-determining step. The N2 molecule produced from one single hydrazine molecule via an intermolecular dehydrogenation mechanism, Fig. 16, is in agreement with experimental reports where N2H4 remains stable during the dissociation process.59,63
Thus we may conclude that the NH2 radical governs the N2H4 dissociation, which agrees well with experimental studies about the role of NH2 in the hydrazine decomposition.64,65 The released energies from the exothermic reactions provide enough energy for the evolution of NH3, N2 and H2 gases from the surface. Experimental studies also revealed that the decomposition of hydrazine on copper films occurs above 300 K with gaseous products of NH3, N2 and some H2,10 which is consistent with the mechanism in Fig. 16.
Furthermore, the calculations showed the influence of low-coordinated atoms on the different N2H4 decomposition pathways, i.e. at the step edges. These surface atoms stabilise some intermediates more than others along the different pathways, although there is no clear trend in the activation energies except to increase the N–N decoupling barriers of the intermediates in the presence of step edge atoms.
5. Conclusions
We have employed DFT level calculations with long-range interaction corrections to carry out a systematic study of the N2H4 decomposition mechanisms on the flat and stepped Cu(111) surfaces. We have identified the most stable adsorption sites for all intermediates along the different mechanisms of N–H and N–N bond scission. We have found that N2H4 dehydrogenation is kinetically an unlikely process on both flat and stepped Cu(111) surfaces due to high barrier energies. However, N–N decoupling is energetically feasible, leading to NH2 intermediates. The intermolecular dehydrogenation reaction is the predominant mechanism between either NH2 fragments on the flat surface, or NH2 and N2Hx (x = 1–4) intermediates on the flat or stepped surfaces, leading to the formation of N2 and NH3, as shown in Fig. 16. This process is highly exothermic, releasing ∼2.50 eV per hydrazine molecule, which agrees well with the use of N2H4 as a rocket fuel. Meanwhile the amide and imide intermediates are hydrogenated to NH3 in the presence of hydrogen, which competes with the recombination of H atoms leading to H2 molecules. We also found that, while the introduction of low-coordinated atoms, as on the step edge on the surface, increases the barrier of N–N decoupling along the reaction, it has different effects on the barriers of intra- and intermolecular dehydrogenation mechanisms.Future work will include microkinetic simulations to develop our understanding of the competing catalytic processes leading to N2H4 dissociation on the planar Cu(111) surfaces.
Acknowledgements
S.S.T acknowledges University College London and the UCL Industrial Doctorate Centre in Molecular Modelling and Materials Science for an Overseas Research Scholarship. N.H.d.L acknowledges the Royal Society for an Industry Fellowship and A.R. is grateful to the Ramsay Memorial Trust and University College London for the award of a Ramsay Fellowship. Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of HECToR and ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme, as well as the UCL Legion High Performance Computing facility (Legion@UCL), and associated support services, in the completion of this work.References
- S. Dutta, J. Ind. Eng. Chem., 2014, 20, 1148–1156 CrossRef CAS.
- L. Schlapbach and A. Zuttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- M. Y. Zheng, R. H. Cheng, X. W. Chen, N. Li, L. Li, X. D. Wang and T. Zhang, Int. J. Hydrogen Energy, 2005, 30, 1081–1089 CrossRef CAS.
- E. W. Schmidt, Hydrazine and Its Deratives: Preparation, Properties, Applications, Wiley, New York, 2001 Search PubMed.
- S. G. Pakdehi, M. Salimi and M. Rasoolzadeh, Researches and Applications in Mechanical Engineering, 2014, 3, 21–25 Search PubMed.
- S. Mary, C. Kappenstein, S. Balcon, S. Rossignol and E. Gengembre, Appl. Catal., A, 1999, 182, 317–325 CrossRef CAS.
- S. Balcon, S. Mary, C. Kappenstein and E. Gengembre, Appl. Catal., A, 2000, 196, 179–190 CrossRef CAS.
- J. P. Contour and G. Pannetie, J. Catal., 1972, 24, 434–445 CrossRef CAS.
- M. H. Matloob and M. W. Roberts, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 1393–1405 RSC.
- Y. K. Alhaydari, J. M. Saleh and M. H. Matloob, J. Phys. Chem., 1985, 89, 3286–3290 CrossRef CAS.
- P. X. Zhang, Y. G. Wang, Y. Q. Huang, T. Zhang, G. S. Wu and J. Li, Catal. Today, 2011, 165, 80–88 CrossRef CAS.
- H. L. McKay, S. J. Jenkins and D. J. Wales, J. Phys. Chem. C, 2011, 115, 17812–17828 CAS.
- T. D. Daff and N. H. de Leeuw, J. Mater. Chem., 2012, 22, 23210–23220 RSC.
- J. K. Norskov, T. Bligaard, A. Logadottir, S. Bahn, L. B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl and C. J. H. Jacobsen, J. Catal., 2002, 209, 275–278 CrossRef CAS.
- Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967 CrossRef CAS PubMed.
- T. Zubkov, G. A. Morgan, J. T. Yates, O. Kuhlert, M. Lisowski, R. Schillinger, D. Fick and H. J. Jansch, Surf. Sci., 2003, 526, 57–71 CrossRef CAS.
- P. Gambardella, Ž. Šljivančanin, B. Hammer, M. Blanc, K. Kuhnke and K. Kern, Phys. Rev. Lett., 2001, 87, 056103 CrossRef CAS PubMed.
- I. M. Ciobica and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 6200–6205 CrossRef CAS.
- N. H. de Leeuw and J. A. Purton, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 195417 CrossRef.
- S. C. Parker, N. H. de Leeuw, D. J. Harris, F. M. Higgins, P. M. Oliver, S. E. Redfern and G. W. Watson, Radiat. Eff. Defects Solids, 1999, 151, 185–195 CrossRef.
- S. Dahl, A. Logadottir, R. C. Egeberg, J. H. Larsen, I. Chorkendorff, E. Tornqvist and J. K. Norskov, Phys. Rev. Lett., 1999, 83, 1814–1817 CrossRef.
- T. Zambelli, J. Wintterlin, J. Trost and G. Ertl, Science, 1996, 273, 1688–1690 CrossRef CAS.
- Y. Xu and M. Mavrikakis, J. Phys. Chem. B, 2003, 107, 9298–9307 CrossRef CAS.
- Y. Xu and M. Mavrikakis, Surf. Sci., 2003, 538, 219–232 CrossRef CAS.
- T. Li, B. Bhatia and D. S. Sholl, J. Chem. Phys., 2004, 121, 10241–10249 CrossRef CAS PubMed.
- S. S. Fu and G. A. Somorjai, Surf. Sci., 1992, 262, 68–76 CrossRef CAS.
- S. S. Tafreshi, A. Roldan, N. Y. Dzade and N. H. de Leeuw, Surf. Sci., 2014, 622, 1–8 CrossRef CAS.
- S. S. Tafreshi, A. Roldan and N. H. de Leeuw, J. Phys. Chem. C, 2014, 118, 26103–26114 CAS.
- S. S. Tafreshi, A. Roldan and N. H. de Leeuw, Surf. Sci., 2015, 637–638, 140–148 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- S. Irrera, A. Roldan, G. Portalone and N. H. De Leeuw, J. Phys. Chem. C, 2013, 117, 3949–3957 CAS.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, J. Chem. Phys., 2013, 139, 124708 CrossRef CAS PubMed.
- N. Almora-Barrios, G. Carchini, P. Blonski and N. Lopez, J. Chem. Theory Comput., 2014, 10, 5002–5009 CrossRef CAS.
- W. Reckien, F. Janetzko, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2012, 33, 2023–2031 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. Koitz, A. P. Seitsonen, M. Iannuzzi and J. Hutter, Nanoscale, 2013, 5, 5589–5595 RSC.
- M. Gajdos and J. Hafner, Surf. Sci., 2005, 590, 117–126 CrossRef CAS.
- G. Mills and H. Jonsson, Phys. Rev. Lett., 1994, 72, 1124–1127 CrossRef CAS PubMed.
- G. Mills, H. Jonsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101 CrossRef PubMed.
- T. D. Daff, D. Costa, I. Lisiecki and N. H. de Leeuw, J. Phys. Chem. C, 2009, 113, 15714–15722 CAS.
- N. H. de Leeuw, S. C. Parker, C. R. A. Catlow and G. D. Price, Am. Mineral., 2000, 85, 1143–1154 CrossRef CAS.
- N. H. de Leeuw and C. J. Nelson, J. Phys. Chem. B, 2003, 107, 3528–3534 CrossRef CAS.
- N. H. de Leeuw, C. J. Nelson, C. R. A. Catlow, P. Sautet and W. Dong, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 045419 CrossRef.
- J. A. Pople and L. A. Curtiss, J. Chem. Phys., 1991, 95, 4385–4388 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules, Van Nostrand Reinhold Company, New York, 1979 Search PubMed.
- G. C. Wang, L. Jiang, X. Y. Pang and J. Nakamura, J. Phys. Chem. B, 2005, 109, 17943–17950 CrossRef CAS PubMed.
- W. Biemolt, P. R. Davies, A. P. J. Jansen and R. A. Vansanten, Catal. Today, 1992, 12, 427–432 CrossRef CAS.
- W. Biemolt, G. J. C. S. Vandekerkhof, P. R. Davies, A. P. J. Jansen and R. A. Vansanten, Chem. Phys. Lett., 1992, 188, 477–486 CrossRef CAS.
- D. R. Lide, CRC Handbook of Cemistry and Physics, CRC Press, New York, 1996 Search PubMed.
- J. Block and G. Schulzek, J. Catal., 1973, 30, 327–329 CrossRef CAS.
- J. Gomez-Diaz and N. Lopez, J. Phys. Chem. C, 2011, 115, 5667–5674 CAS.
- A. Logadottir and J. K. Norskov, J. Catal., 2003, 220, 273–279 CrossRef CAS.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Norskov, Science, 2005, 307, 555–558 CrossRef CAS PubMed.
- R. Maurel and J. C. Menezo, J. Catal., 1978, 51, 293–295 CrossRef CAS.
- K. I. Aika, T. Ohhata and A. Ozaki, J. Catal., 1970, 19, 140 CrossRef CAS.
- A. A. Konnov and J. De Ruyck, Combust. Flame, 2001, 124, 106–126 CrossRef CAS.
| This journal is © the Owner Societies 2015 |


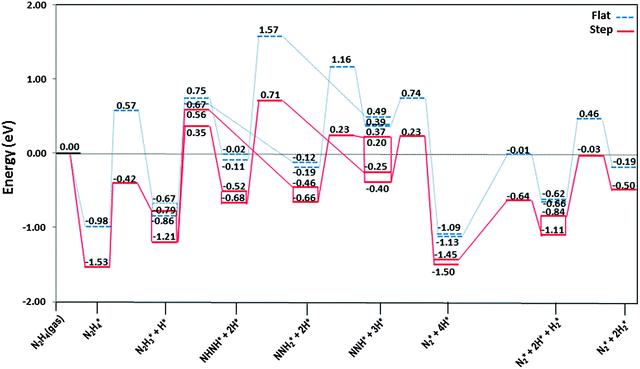
![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) and stepped (—) Cu(111) surfaces. Energies are relative to the energy of the gas-phase hydrazine (in eV). Note that we have considered the diffusion of intermediates to their most stable adsorption sites on the surface as a barrierless pathway.
) and stepped (—) Cu(111) surfaces. Energies are relative to the energy of the gas-phase hydrazine (in eV). Note that we have considered the diffusion of intermediates to their most stable adsorption sites on the surface as a barrierless pathway.