Hole-transfer induced energy transfer in perylene diimide dyads with a donor–spacer–acceptor motif

Abstract

We investigate the photoinduced dynamics of perylene diimide dyads based on a donor–spacer–acceptor motif with polyyne spacers of varying length by pump–probe spectroscopy, time resolved fluorescence, chemical variation and quantum chemistry. While the dyads with pyridine based polyyne spacers undergo energy transfer with near-unity quantum efficiency, in the dyads with phenyl based polyyne spacers the energy transfer efficiency drops below 50%. This suggests the presence of a competing electron transfer process from the spacer to the energy donor as the excitation sink. Transient absorption spectra, however, reveal that the spacer actually mediates the energy transfer dynamics. The ground state bleach features of the polyyne spacers appear due to the electron transfer decay with the same time constant present in the rise of the ground state bleach and stimulated emission of the perylene energy acceptor. Although the electron transfer process initially quenches the fluorescence of the donor it does not inhibit energy transfer to the perylene energy acceptor. The transient signatures reveal that electron and energy transfer processes are sequential and indicate that the donor–spacer electron transfer state itself is responsible for the energy transfer. Through the introduction of a Dexter blocker unit into the spacer we can clearly exclude any through bond Dexter-type energy transfer. Ab initio calculations on the donor–spacer and the donor–spacer–acceptor systems reveal the existence of a bright charge transfer state that is close in energy to the locally excited state of the acceptor. Multipole–multipole interactions between the bright charge transfer state and the acceptor state enable the energy transfer. We term this mechanism coupled hole-transfer FRET. These dyads represent a first example that shows how electron transfer can be connected to energy transfer for use in novel photovoltaic and optoelectronic devices.

---

1 Introduction

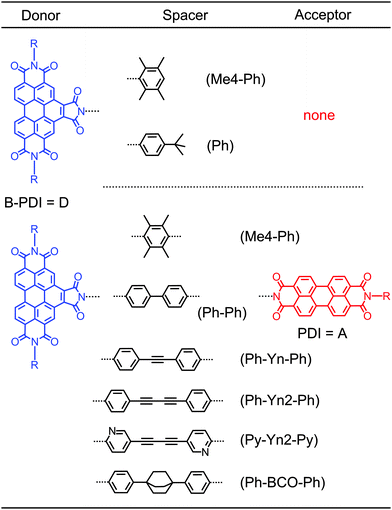
Förster resonant energy transfer (FRET)¹ is a fundamental photophysical process, where electronic energy is transferred from an optically excited donor to a neighbouring acceptor. The process is mediated by multipole–multipole coupling in contrast to Dexter energy transfer, where orbital overlap between the donor and the acceptor is required.^2–6 The probability for Dexter energy transfer decreases exponentially with the distance of the components.^7,8 In contrast, the probability for FRET decreases with the sixth power of the donor–acceptor distance and thus has a much larger range of action. The Förster radii (the donor–acceptor distance at which the rate of energy transfer equals that of fluorescence of the excited donor) lie in the order of 30 Å.

In a recent Feature article Silbey⁹ showed that the habitual formulation of Förster theory for the resonant energy transfer has been successfully applied in many instances. However, due to the approximations done to get to this multipole–multipole description, there are many instances where the theory breaks down and mechanisms that go beyond Förster theory are required to explain the resonant energy transfer.^10–16 Here the light harvesting complex has to be mentioned, where the observation of coherences in the dynamics of the energy transfer cannot be described via the Förster approach.^17,18

Also in simpler systems a breakdown of the standard Förster approach can occur. We have recently shown that in a perylene diimide dyad based on a donor–spacer–acceptor motif (D–(Me4-Ph)–A in Chart 1) rapid FRET from the donor to the acceptor moiety is occurring although the transition dipole moments are orthogonal to each other.¹⁹ According to the point dipole approximation used in Förster theory no energy transfer should occur in an orthogonal arrangement. Experimentally we do, however, observe an ultrafast transfer time of 9.4 ps. The determination of the Coulombic coupling via the transition density cube approach furthermore reveals that in the orthogonal arrangement the higher multipole moments are not responsible for the energy transfer. Pump–probe experiments revealed that the energy transfer rate increases upon increasing the sample temperature.¹⁹ This temperature dependence can only be reproduced within an extended Förster model that includes low wavenumber ground state vibrations and structural and electronic deformations induced by solvent fluctuations.²⁰ These deformations break the orthogonal arrangement of the dipoles and enable the ultrafast and near-unity efficient energy transfer. We termed this energy transfer mechanism noise-induced FRET.

Chart 1 Perylene diimide dyads investigated in this work together with the associated abbreviation used in the paper. B-PDI = benzoperylene diimide; PDI = perylene diimide; Ph = phenyl; Me = methyl; Py = pyridine; Yn = alkyne; BCO = bicyclooctane, R = 1-hexyl-heptyl.

Time-resolved measurements on perylene diimide dyads with orthogonal transition dipole moments and pyridine polyyne spacers of varying length (Chart S1 and Table S1 in the ESI†) show that these dyads also undergo the noise-induced FRET with near-unity quantum efficiency. If the N centres in these spacers are replaced with carbons to form phenyl polyyne spacers the fluorescence quantum yield out of the energy acceptor decreases from the near 100% to below 50%. In ref. 19 it was envisioned that an electron transfer (ET) from the spacer to the energy donor acts as a parasitic process. However, for the corresponding donor–spacer–acceptor system we observe donor fluorescence quantum yields below 1%. The electron transfer times between perylene diimides and electron rich phenyl spacers are in the order of up to 10 ps at most.²¹ With energy transfer times ranging from 10 to 50 ps this would lead to FRET efficiencies below 10%, thus far less than observed.

Here we investigate the photoinduced dynamics of these dyads by pump–probe spectroscopy, time resolved fluorescence and quantum chemical calculations in order to elucidate the steps comprising the full energy transfer mechanism.

2 Experimental determination of energy transfer rates

The theory in ref. 20 predicts that the noise-induced FRET rate has a donor–acceptor distance R dependence that scales with (1/R³). This is in contrast to the standard FRET (1/R⁶) dependence. Time-resolved measurements on perylene diimide dyads with orthogonal transition dipole moments and pyridine polyyne spacers of varying length (Chart S1 and Table S1 in the ESI†) show that the noise-induced FRET indeed deviates from the (1/R⁶) behaviour and points towards a contribution from the predicted (1/R³) distance dependence (Fig. S3 in the ESI†).

We now investigate the difference in behaviour in the related perylene diimide dyads with phenyl polyyne spacers shown in Chart 1. All newly determined transfer rates are collected in Table 1. Selected measurements are discussed in detail to decipher the underlying processes. All other measurements are shown in the ESI.† We start by recording the time resolved fluorescence for the two dyads D–(Py-Yn2-Py)–A and D–(Ph-Yn2-Ph)–A.

Table 1 Global fit results from the transient absorption data in chloroform for all the compounds presented in Chart 1 together with fluorescence quantum yields Φ_Fluo. The global fit results obtained from the time resolved (TR) fluorescence measurements on D–(Ph-Yn2-Ph)–A and D–(Py-Yn2-Py)–A are in italics. The association of the time constants with processes is explained in the footnotes

Compound	τ 1 /ps	τ 2 /ps	τ 3 /ps	τ Fluo /ns	Φ Fluo (%)
a τ 1 corresponds to the vibrational relaxation from the FC point to the π-minimum of the excited B-PDI donor. b For the dyads τ2 = (1/τFRET + 1/τd-CT + 1/τb-CT)^−1. See Fig. 6. c For the dyads τ3 = (1/τHT-FRET + 1/τd-CT→S0)^−1. See Fig. 6. d For the donor–spacer system D–(Ph), this time constant is for the backward electron transfer from the B-PDI donor to the spacer τd-CT→S0. See Fig. 5. e For D–(Me4-Ph)–A and D–(Py-Yn2-Py)–A τ3 = τFRET. f For the donor–spacer systems D–(Me4-Ph) and D–(Ph) τFluo is the lifetime of the bright LE state of the B-PDI donor; for the dyads it is the lifetime of the bright LE state of the PDI acceptor moiety. g The fluorescence quantum yield was determined by excitation at 437 nm with reference to 2,10-bis(1-hexylheptyl)-6-[2-[3,8,9,10-tetrahydro-9-(1-octylnonyl)-1,3,8,10-tetraoxoanthra[2,1,9-d,e,f:6,5,10-d′,e′,f′]diisoquinolin-2(1H)-yl]ethyl]-1H-pyrrolo[3′,4′:4,5]pyreno[2,1,10-d,e,f:7,8,9-d′,e′,f′]diisoquinoline-1,3,5,7,9,11(2H,6H,10H)-hexone RN335458-21-4 with Φ = 1.00.^23 For the donor–spacer systems it is the fluorescence quantum yield of the B-PDI chromophore. For the dyads it is the fluorescence quantum yield of the PDI energy acceptor obtained by excitation of the B-PDI energy donor.
D–(Me4-Ph)	0.2	—	—	1.3	30
D–(Ph)	0.6	5.9	61^d	—	n.d.
D–(Ph-Ph)–A	0.6	4.7	22	2.0	58
D–(Ph-Yn-Ph)–A	0.3	2.6	30	1.5	33
D–(Ph-Yn2-Ph)–A	0.7	4.0	35	2.1	53
In benzonitrile	0.8	8.5	40	2.5	—
TR fluorescence		5.6	35	3.0
D–(Me4-Ph)–A	0.3	—	9.4^e	4.0	100
D–(Py-Yn2-Py)–A	1.5	—	54^e	2.4	100
TR fluorescence		—	53	3.3
D–(Ph-BCO-Ph)–A	0.4	5.0	45	3.3	44

---

2.1 Time resolved fluorescence: two transfer mechanisms

The time resolved fluorescence data of D–(Py-Yn2-Py)–A and D–(Ph-Yn2-Ph)–A were measured using a streak camera setup described in detail in ref. 22 and femtosecond excitation by the frequency doubled output of a CPA-system (CPA-2001; Clark MXR). At the 389 nm wavelength the donor is selectively excited in the S₂ absorption band (Fig. S1 and S2 in the ESI†) as the extinction coefficients of the donor and acceptor are 22 400 L mol⁻¹ cm⁻¹ and 4250 L mol⁻¹ cm⁻¹. For experimental details, see ESI.†

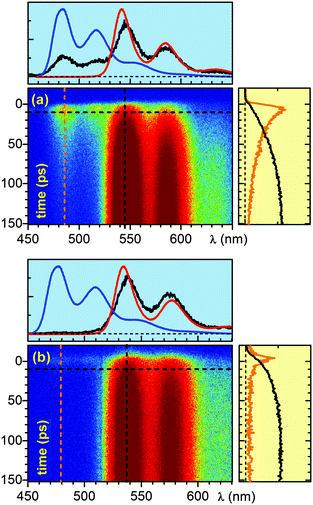
False colour plots of the time-resolved fluorescence data for the 0.5 ns window are shown in Fig. 1a and b. Immediately after excitation of D–(Py-Yn2-Py)–A we observe fluorescence bands which spectrally coincide with the steady state fluorescence bands of the donor and acceptor moieties. With the increasing pump-detection delay we observe a concerted decay of the donor fluorescence and a rise of the acceptor fluorescence which then lasts for several nanoseconds. This behaviour is a clear indication of energy transfer. A global fit analysis as well as single line fits on the five distinct band maxima yields a time constant of 53 ps for the energy transfer from the benzoperylene diimide (B-PDI) to the perylene diimide (PDI) moiety and an acceptor excited state lifetime of 3.3 ns. This compares well with the 3.8 ns time constant reported in ref. 23.

Fig. 1 False colour plots of the time resolved fluorescence of the perylene diimide dyad (a) D–(Py-Yn2-Py)–A and (b) D–(Ph-Yn2-Ph)–A in chloroform. Blue indicates low fluorescence and red indicates high fluorescence. The top profile graphs (blue background) show the fluorescence at a delay of 10 ps (black line) together with the time integrated fluorescence of the free B-PDI donor (blue line) and the free PDI acceptor (red line) for reference. The lineouts on the right side (light yellow background) show the temporal evolution of the fluorescence for the donor (orange line multiplied by 5) at 486 nm and for the acceptor (black line) at 546 nm.

The temporal evolution of the fluorescence for the dyad D–(Ph-Yn2-Ph)–A is substantially different. The shortest time window of 0.2 ns reveals that the donor fluorescence decays within the first 10 ps, while the fluorescence of the acceptor rises on the 30 ps timescale. Global analysis and single line fits yield a time constant of 5.6 ps for the quenching of the donor fluorescence, while the time constant for the acceptor rise is 35 ps. A concerted fluorescence rise and fall characteristic for direct energy transfer is missing.

A change of the spacer from a pyridine to a phenyl unit results in efficient quenching of the fluorescence of the donor. One would expect that this prevents energy transfer from the B-PDI to the PDI moiety. Still a substantial rise of the acceptor fluorescence occurs. This is a clear indication that the mechanisms for energy transfer in D–(Ph-Yn2-Ph)–A and D–(Py-Yn2-Py)–A are different.

2.2 Transient absorption of D–(Ph-Yn2-Ph)–A: the role of the spacer

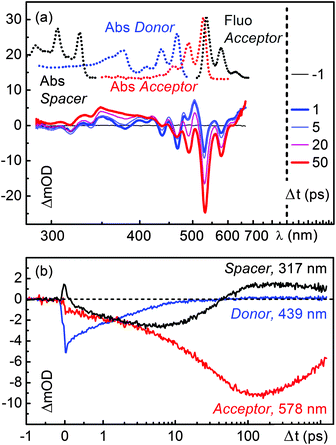
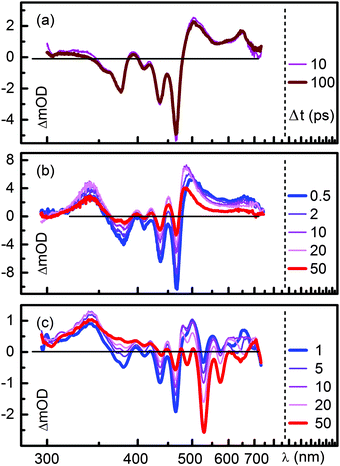
To investigate the dynamics of D–(Ph-Yn2-Ph)–A further, we carried out time-resolved transient absorption measurements using a broadband setup described in detail in ref. 24. The B-PDI donor moiety of D–(Ph-Yn2-Ph)–A was excited at 465 nm with the output of NOPA. The transient absorption spectra in chloroform at various delay times are shown in Fig. 2a and the corresponding transient absorption kinetics at selected wavelengths is shown in Fig. 2b. Immediately after optical excitation we observe the ground state bleach (GSB; between 350 nm to 500 nm). The GSB is partially shifted to positive transient absorption by the overlapping broad excited state absorption (ESA; from 500 to 700 nm) of the blue absorbing B-PDI donor moiety. As the spectra evolve in time, the transient signatures of the donor give way to a GSB signature below 350 nm within the first 10 ps. The usual negative transient absorption of a GSB is shifted into the positive regime by overlapping ESA. However, the GSB spectral structure is matched by the very characteristic triple peaked absorption structure of the isolated diphenyl butadiyne (Ph-Yn2-Ph) spacer with a slightly red shift. Within 50 ps the spacer GSB decays and the GSB, SE and ESA of the green absorbing acceptor rises. These features last for several nanoseconds, the characteristic excited state lifetime of perylene diimides.

Fig. 2 (a) Transient absorption spectra of the perylene bisimide dyad D–(Ph-Yn2-Ph)–A in chloroform. For reference the stationary absorption of the B-PDI donor moiety, the spacer and the PDI acceptor are shown together with the fluorescence spectrum of the PDI in chloroform. (b) Temporal evolution of the ground state bleach (GSB) of the spacer (black line), the GSB of the donor (blue line) and the stimulated emission (SE) of the acceptor (red line).

To quantify the temporal evolution of the absorption changes a maximum entropy analysis²⁵ followed by a global fit analysis²⁶ has been carried out. The results are shown in Fig. S16 (ESI†) and Table 1. The GSB of the B-PDI energy donor moiety decays with two time constants of 4 and 35 ps while the GSB of the spacer rises with the 4 ps time constant and decays with the 35 ps time constant. The GSB, SE and ESA of the PDI energy acceptor rise with the two time constants of 4 and 35 ps. The 4 ps time constant coincides with the fluorescence decay of the donor observed in the time resolved fluorescence measurements suggesting that an electron transfer between the spacer and the energy donor occurs.

Furthermore the presence of this time constant in the initial rise of the spectral signatures of the PDI acceptor indicates that during the quenching process direct energy transfer occurs. The 35 ps time constant associated with the decay of the spacer GSB and the major rise of the spectral signatures of the PDI acceptor coincides with the rise of its fluorescence observed in the time resolved fluorescence measurements. These spectral changes are a clear indication that a substantial part of the excitation energy is transferred from the B-PDI to the PDI moiety with the involvement of the spacer.

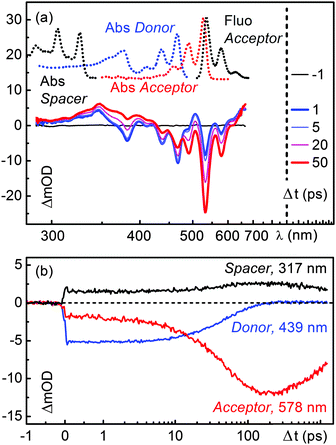
Compared to D–(Ph-Yn2-Ph)–A (Fig. 2), the transient absorption spectra of D–(Py-Yn2-Py)–A in Fig. 3a show a less complex dynamics. The GSB signatures of the initially excited B-PDI donor moiety decay giving directly rise to the GSB, SE and ESA features of the PDI, in analogy to the D–(Me4-Ph)–A dyad published in ref. 19. The time constant for this direct energy transfer is 54 ps.²⁰ The spacer is not electronically involved in the energy transfer process. The transient absorption kinetics in the region of the spacer at 317 nm in fact shows no significant dynamics (Fig. 3b, black line).

Fig. 3 (a) Transient absorption spectra of the perylene bisimide dyad D–(Py-Yn2-Py)–A in chloroform. For reference the stationary absorption of the B-PDI donor moiety, the spacer and the PDI acceptor are shown together with the fluorescence spectrum of the PDI in chloroform. (b) Temporal evolution of the GSB of the spacer (black line), the GSB of the donor (blue line) and the stimulated emission (SE) of the acceptor (red line).

2.3 Transient absorption of a dyad with a Dexter blocker

The two main mechanisms responsible for energy transfer in molecules are FRET¹ and Dexter.⁷ While the former is a through space multipole–multipole interaction, the latter occurs in a through bond fashion via orbital overlap between the donor, spacer and acceptor. To verify which energy transfer mechanism is playing a role in the dyad D–(Ph-Yn2-Ph)–A we carried out transient absorption measurements on D–(Ph-BCO-Ph)–A which contains a chemically engineered Dexter blocker in the spacer moiety. Just like D–(Ph-Yn2-Ph)–A this dyad has electron rich phenyl rings comprising the spacer and thus affords charge transfer from the spacer to the energy donor moiety. Excitation of the donor moiety however leads to fluorescence from the energy acceptor with a quantum yield of 44%.¹⁹ In contrast to D–(Ph-Yn2-Ph)–A the spacer of this dyad also contains the aliphatic, stiff, linear spacer bicyclo[2.2.2]octane. Due to its aliphatic character, this group breaks any π conjugation between the donor, spacer and acceptor and thus acts as a Dexter-type blocker inhibiting any Dexter type energy transfer.

For the time-resolved measurements, D–(Ph-BCO-Ph)–A was selectively excited at 435 nm with the frequency doubled output of NOPA. The 435 nm wavelength ensures the highest contrast between the donor and the residual acceptor excitation at the cost of some vibrational excitation. Supplementary experiments (ESI†) showed, however, that excitation at 465 nm leads to no noticeable differences in the dynamics. As it is technically much less demanding it was used for some of the investigated molecules.

The transient absorption spectra in chloroform of D–(Ph-BCO-Ph)–A at various delay times are shown in Fig. 4c. The optical excitation leads to the GSB between 350 nm to 500 nm and a broad ESA from 500 to 700 nm of the blue absorbing B-PDI moiety. The ESA again shifts the highly structured GSB and SE of the donor and the partially excited acceptor from the expected negative transient optical density into the positive regime. As the spectra evolve in time, the transient signatures of the donor give way to two distinct ESA bands located at 340 nm and 490 nm within the first 10 ps. Within 50 ps these ESA bands decay and the familiar nanosecond long lived GSB, SE and ESA of the green absorbing acceptor rise.

Fig. 4 Transient absorption spectra of (a) the donor–spacer system D–(Me4-Ph) and (b) D–(Ph) together with (c) the perylene diimide dyad D–(Ph-BCO-Ph)–A in chloroform.

To quantify the temporal evolution of the absorption changes again a maximum entropy analysis followed by a global fit analysis has been carried out. The results are shown in the ESI† (Fig. S19). The GSB of the B-PDI donor moiety decays with two time constants of 5 ps and 45 ps. The ESA bands at 340 nm and 490 nm rise with the 5 ps time constant. The decay of the ESA bands and the rise of the GSB, SE and ESA of the PDI energy acceptor occur with a time constant of 45 ps. The observed spectral changes clearly indicate that energy is transferred from the B-PDI to the PDI moiety through an intermediate state which is populated after the excitation of the B-PDI moiety and shows distinct absorption bands at 340 nm and 490 nm. The presence of the bicyclo[2.2.2]octane excludes that a Dexter through bond energy transfer is responsible for the energy transfer in D–(Ph-BCO-Ph)–A and possibly also in D–(Ph-Yn2-Ph)–A.

2.4 Evidence for a charge transfer state

The results obtained from the time resolved fluorescence measurements in Section 2.2 and the transient absorption measurements on D–(Ph-Yn2-Ph)–A in Section 2.3 suggest that after excitation of the B-PDI moiety electron transfer from the spacer to the B-PDI moiety occurs. In order to verify if the intermediate state with the characteristic absorption bands at 340 nm and 490 nm is a charge transfer state we carried out transient absorption measurements on the two systems D–(Me4-Ph) and D–(Ph). These compounds are representative donor–spacer subsystems of the dyads investigated. Furthermore the fluorescence quantum yield of D–(Me4-Ph) is 30%, while for D–(Ph) no noticeable fluorescence could be detected¹⁹ indicating that these are the right candidates for the identification of the charge transfer signatures. The transient absorption spectra of D–(Me4-Ph) and D–(Ph) in chloroform at various delay times Δt are shown in Fig. 4a and b.

The 465 nm optical excitation of D–(Me4-Ph) leads to the GSB features between 350 nm and 500 nm and the broad ESA from 500 to 700 nm of the blue absorbing B-PDI moiety as already observed in D–(Ph-BCO-Ph)–A and D–(Ph-Yn2-Ph)–A. These features show no significant temporal change (Fig. S9 in the ESI†) and the global fit yields a single lifetime of 1.3 ns. In conjunction with the 30% fluorescence quantum yield this compares well to the 6.8 ns fluorescence lifetime in ref. 23. Despite the sizeable fluorescence quantum yield no SE can be observed in the transient spectra. We believe that the spectral signatures of the SE are cancelled out by ESA that matches the spectral features of the SE.

For D–(Ph) the 465 nm optical excitation yields the same GSB and ESA features as for D–(Me4-Ph). However, these features decay within the first 10 ps and give rise to two distinct new ESA bands which coincide spectrally with the intermediate ESA features at 340 nm and 490 nm observed in D–(Ph-BCO-Ph)–A. The whole system returns back to the ground state within 300 ps. The maximum entropy and global fit yield two time constants of 5.9 ps and 61 ps, which we ascribe to electron transfer from the phenyl spacer to the B-PDI chromophore and backward electron transfer to reach the ground state of D–(Ph).

This assignment to a forward and backward electron transfer is further supported by spectroelectrochemical measurements on the unreactive D–(Me4-Ph) in dichloromethane. The results are shown in the ESI† (Fig. S13). With a reducing voltage of 1.4 V two strong absorption bands appear to the red and the blue of the neutral B-PDI absorption bands at 622 nm and below 300 nm. The energy difference between the 622 nm absorption band and the neutral absorption band at 466 nm is 0.7 eV. This compares well to the energy difference between the strongest absorption bands of neutral (518 nm) and monoionic (705 nm) perylene diimides of 0.6 eV reported in ref. 27. We therefore assign the spectral bands to the monoionic B-PDI moiety. This assignment is further supported by ab initio calculations of the D–(Me4-Ph) anion (Table S4 in the ESI†). No signatures that can be ascribed to the anion of the Me4 spacer can be observed.²⁸ The appearance of monoionic absorption bands to the red and the blue of the neutral absorption of D–(Me4-Ph) can be compared to the transient spectra of D–(Ph) that feature distinct ESA signatures on both sides of the GSB signatures (Fig. 4b) albeit the spectral positions do not coincide. We believe that this discrepancy can be ascribed to the absence of the positively charged spacer moiety in the spectroelectrochemical measurements. We therefore assign the ESA signatures at 340 nm and 490 nm observed after excitation of D–(Ph) and D–(Ph-BCO-Ph)–A to the absorption of the B-PDI anion generated by photoinduced charge transfer from the spacer to the donor. The reason why electron transfer occurs in D–(Ph) and not in D–(Me4-Ph) is explained in Section 3, where the results of the ab initio calculations are presented.

The postulated ultrafast electron transfer leads to the population of a charge transfer (CT) state. Due to its high dipole moment it should be strongly influenced by the polarity of the solvent. To test the impact on the energy transfer we performed additional transient absorption measurements of D–(Ph-Yn2-Ph)–A in benzonitrile. The dielectric constant ε is 25.2 for benzonitrile as compared to 4.8 for chloroform. The recording is shown in Fig. S15 of the ESI.† The general appearance is quite similar to the chloroform recording. A closer look reveals that the decay of the donor GSB monitored at 441/439 nm is slowed down in benzonitrile. The spacer GSB at 319/317 nm appears somewhat slower and is weakened in strength as seen from the less negative transient optical density. Finally, the maximum of the GSB of the acceptor at 583/580 nm is decreased roughly by a factor of two as compared to the donor GSB signal at very early times. This suggests a strongly decreased overall energy transfer. The slowing of the processes can also be seen from a comparison of the maximum entropy analyses (Fig. S16 and S17 in the ESI†). The global fit shows that the vibrational relaxation is not much changed between the two solvents (compare τ₁ in Table 1). The first transfer time τ₂ is slowed down from 4.0 to 8.5 ps in benzonitrile. Also the second transfer time τ₃ is increased from 35 to 40 ps.

The results in benzonitrile clearly show that the dynamics are much more severely changed as it would be expected for only locally excited states in basic FRET. The high polarity of benzonitrile might be expected to lower the charge transfer state sufficiently that the energy is trapped there and cannot subsequently be transferred to the acceptor. However, besides the polarity we have to consider the solvation times of the two solvents. The characteristic time 〈τ〉 increases from 2.8 to 5.1 ps from chloroform to benzonitrile.²⁹ As the intrinsic rates of D–(Ph-Yn2-Ph)–A are quite comparable to the solvation times, a full modelling of the increased polarity is well beyond the scope of this work. The intricate interplay between solvent polarity and solvation times on the dynamics of CT states has been documented in detail.³⁰ Furthermore, we find that the weak donor LE dipole moment vector points opposite to the strong CT dipole moment vector. The solvation could well be slowed down even further by this situation and this underscores the importance of the solvation time besides the polarity. Last but not least, the 1/n⁴ scaling of the FRET rate with the refractive index n and possible screening should slow the direct transfer in benzonitrile considerably. The observed behaviour therefore is a highly complex dynamical interplay between the various solvent properties.

Overall we suggest that the observed changes due to the increase in polarity are not compatible with LE state dynamics. Rather they support the suggestion of an intermediate CT state responsible for the complex behaviour in the perylene diimide dyads with phenyl polyyne spacers.

2.5 Towards a detailed model for the complete dynamics

For the dyads D–(Ph-BCO-Ph)–A and D–(Ph-Yn2-Ph)–A the experimental evidence obtained from time resolved fluorescence and time resolved absorption suggests that after excitation of the B-PDI donor, a few ps electron transfer occurs from the spacer to the B-PDI moiety. The tens of ps backward electron transfer from the B-PDI moiety to the spacer excite the green absorbing PDI acceptor. The analysis of the additional systems D–(Ph-Ph)–A and D–(Ph-Yn-Ph)–A fully confirms this interpretation. The presence of the BCO Dexter blocker suggests that this process occurs via a through space interaction. The required multipole–multipole interactions between the charge transfer state of the donor–spacer moiety and the excited state of the acceptor can only exist, if the charge transfer state has some oscillator strength. The existence of partial charge transfer states with oscillator strength has been recently observed in related core-substituted naphthalene diimides^31,32 and postulated to act as energy donors in pyrene-borondipyrromethene dyads³³ albeit in the latter case no spectral or theoretical identification of such a state could be obtained.

3 Ab initio calculations identify a bright charge transfer state

To gain further understanding about the mechanism behind the energy transfer in the dyads D–(Ph-BCO-Ph)–A and D–(Ph-Yn2-Ph)–A, we have carried out an extensive set of quantum chemical calculations. We first investigated the smaller donor spacer systems D–(Me4-Ph) and D–(Ph) at the MP2, CC2 and CASSCF level of theory and then moved onto the larger D–(Ph-BCO-Ph)–A dyad. A detailed description of the calculations can be found in the ESI.†

The excited states involved in the investigation processes of the perylene diimide dyads in this work are all described by π orbitals. Orbitals located on the B-PDI donor are denoted as π_D respectively as π_1D* (LUMO) and π_2D* (LUMO+1, Fig. S20 in the ESI†). The orbitals of the spacer and the acceptor are termed as π_S respectively as π_A and π_A* (Fig. S21 in the ESI†).

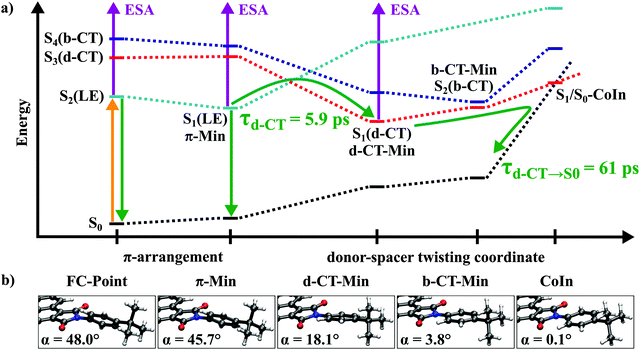
MP2 ground state geometry optimizations for both D–(Me4-Ph) and D–(Ph) result in a planar structure of the B-PDI donor and the spacer rotated about an angle α with respect to the plane of B-PDI. The different spacers lead to a larger torsional angle (α = 67.4°) for D–(Me4-Ph) than for D–(Ph) (α = 48.0°, Fig. 5, FC-point).

Fig. 5 (a) Scheme of the state energies involved in the CT process of the donor–spacer system D–(Ph). Solid arrows indicate optical transitions and dotted lines visualize the different diabatic courses conserving the electronic character (black: ground state; cyan: LE, locally excited state; red: d-CT, dark charge transfer state; and blue: b-CT, bright charge transfer state). The adiabatic states are indicated by the state number with the current electronic character given in parenthesis. (b) Minimum energy geometries for the relevant states (FC, Franck–Condon; CoIn, Conical Intersection). The shown angle α is the torsion angle between the B-PDI donor and the phenyl spacer.

Vertical excitations at the MP2 ground state minima obtained with the CC2 method are shown in Table 2. The first two vertical transitions in both molecules are localized on the B-PDI chromophore. The S₁ state is a dark ππ* transition and is characterized by an excitation from the HOMO (π_D) to an orbital (LUMO+1, π_2D*) with significant contributions on the maleimide ring (Fig. S20 in the ESI†). The S₂ state has a large oscillator strength and corresponds to a transition from the HOMO to the LUMO (π_1D*) which is mainly localized on the perylene diimide framework of the B-PDI moiety (Table 1 and Fig. S20 in the ESI†). The excitation energy of 3.07 eV obtained at the RI-CC2/def2-SV(P) level of theory compares well with the experimental absorption maxima of D–(Me4-Ph) and D–(Ph) at 2.66 eV (465 nm) in CHCl₃ when the 0.2 eV blue-shift intrinsic to the RI-CC2 method and the smaller basis set compared to the benchmark reference are considered.³⁴ We therefore regard this as the locally excited (LE) state that is accessed by the 465 nm excitation in the transient absorption measurements. The S₃ and the S₄ state in both systems are characterized by an excitation from an orbital (HOMO-1, π_S, Fig. S20 in the ESI†) which is mostly localized on the phenyl spacer. The S₃ state has a charge transfer character exhibiting a low oscillator strength and is described by a transition to the LUMO+1 (π_2D*). We denote this state as the dark charge transfer state, d-CT. In contrast the S₄ state has a charge transfer character with sizeable oscillator strength characterized by a transition to the LUMO (π_1D*). This state is denoted as the bright charge transfer state, b-CT.

Table 2 CC2 vertical excitation energies (ΔE) and oscillator strengths (f) of the donor–spacer systems D–(Me4-Ph) and D–(Ph) at the MP2-optimized ground-state equilibrium geometries (LE, locally excited state; d-CT, dark charge transfer state; and b-CT, bright charge transfer state). The calculated energies are compared with the experimental absorption maxima of D–(Me4-Ph) and D–(Ph) in CHCl₃

Transition	Character	D–(Me4-Ph)		D–(Ph)
		ΔE (eV)	f	ΔE (eV)	f
S0 → S1	πD → π2D*	2.99	0.001	2.99	0.004
S0 → S2	πD → π1D* (LE)	3.07	0.545	3.07	0.542
S0 → S3	πS → π2D* (d-CT)	3.56	0.006	3.48	0.024
S0 → S4	πS → π1D* (b-CT)	3.70	0.548	3.64	0.574
Exp.	—	2.66	—	2.66	—

---

Geometry optimizations for the LE, d-CT and b-CT states were carried out using the CC2 method. During the optimizations the electronic character of the adiabatic states changes. Therefore both, the state number and the current electronic character are given e.g. S₁(LE). For both donor spacer systems optimization of the LE state (S₂ state at the FC-point) lowers its energy below the S₁ state and leads to similar local minima with ππ* character (S₁(LE), Fig. 5, denoted as π-Min), exhibiting minor structural changes, mainly bond length rearrangements in the B-PDI chromophore and a small change in the torsional angle α from 67.4° to 66.3°, respectively from 48° to 45.7°. Consequently, the calculated oscillator strengths for the transition to the ground state are almost unchanged from the FC points (f = 0.571/0.570, Table S2 in the ESI†). We ascribe the long lived 1.3 ns fluorescence observed for D–(Me4-Ph) to the emission from this π-Min.

For D–(Me4-Ph) the optimization of the d-CT and b-CT states leads to excited state minima that are much higher in energy than the FC point accessed by the optical excitation. In the case of D–(Ph) optimization of the d-CT state (S₃ state at the FC-point) leads to the global minimum (d-CT-Min) on the S₁ potential energy surface (Fig. 5). This minimum lies 0.4 eV lower than the π-Min and is associated with a large decrease of the angle α to 18.1°. This rotation energetically shifts the spacer orbital π_S above the donor orbital π_D. Thus the global minimum is of CT character with an oscillator strength of 0.003. It results from an electron transfer from the spacer to the maleimide ring of the donor. Therewith it confirms the assumption about the origin of the experimental time constants of D–(Ph) made in Section 2.4.

The large stabilization of the excited d-CT state is accompanied by a considerable destabilization of the ground state. Both states are separated by only 1.56 eV at the d-CT Min. Further rotation of the phenyl ring to a torsional angle α of 0.1° leads to a conical intersection between the d-CT state and the ground state. As the single reference CC2 method breaks down when two electronic states get energetically close to each other, the conical intersection was optimized using the CASSCF method and found to be accessible from the FC point. This explains the fast picosecond backward electron transfer dynamics to the ground state (see Table S3 in the ESI† for details).

CC2 optimization of the b-CT state (S₄ state at the FC-point) in D–(Ph) yields a minimum on the S₂ potential energy surface (b-CT-Min, Fig. 5). The associated structural change is a rotation of the spacer decreasing the angle α to 3.8° (Fig. 5). The electronic structure is characterized by a charge transfer from the spacer to the donor and has a significant oscillator strength of 0.192. At this point the energy difference between the S₂(b-CT) and S₁(d-CT) states is only 0.1 eV. A conical intersection between the two states can be located in the vicinity of the b-CT-Min (Table S3 in the ESI†). Consequently even if the b-CT state in D–(Ph) is populated by relaxation from the π-Min it is quickly depopulated due to this conical intersection.

The theoretical results on the donor spacer systems reveal the existence of a bright charge transfer state which, however, does not seem to play a significant role in their excited state dynamics. This state however may become important for the observed energy transfer in the complete D–(Ph-BCO-Ph)–A dyad. With the focus on this bright charge transfer state we have carried out quantum chemical calculations on the donor–spacer–acceptor dyad D–(Ph-BCO-Ph)–A. Due to the large size of the D–(Ph-BCO-Ph)–A dyad geometry optimizations were carried out using the DFT and TDDFT method with the B3LYP³⁵ and the CAM-B3LYP functional,³⁶ respectively. Excitation energies and oscillator strengths at these geometries were then determined using the more robust and qualitatively correct CC2 method. This strategy of combining TDDFT optimized geometries with CC2 single-point calculations was successfully employed for other large molecules.^37–40

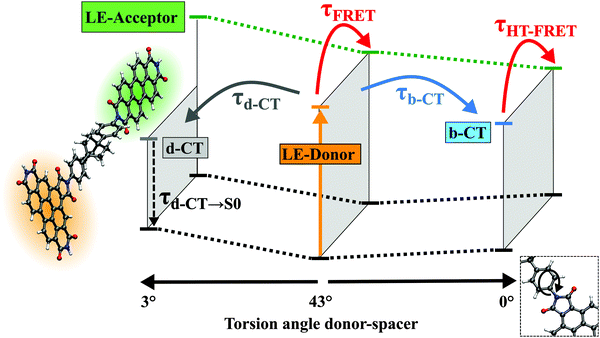
The ground state geometry optimization results in a structure where the spacer (Ph-BCO-Ph) as well as the acceptor is rotated with respect to the B-PDI donor (Fig. 6). The torsional angle α between the phenyl ring of the spacer and the donor is 43.3° and 31.9° between the acceptor and donor. The first excited state is a bright ππ* transition and is localized on the acceptor (Table 3). The CC2 excitation energy of 2.80 eV compares well with the experimental absorption maximum of (Ph)–A at 2.35 eV (527 nm) in CHCl₃ taking the blue-shift corrections into account.³⁴ We therefore regard this as the locally excited (LE_A) state of the acceptor which is populated by the energy transfer. The next four vertical transitions are localized on the donor–spacer moiety and are identical in character and comparable in energy and oscillator strength to those found in the donor–spacer systems D–(Me4-Ph) and D–(Ph). The dark ππ* transition in the dyad is now the S₂ state while the S₃ state is the locally excited (LE_D) donor state with bright ππ* character and accessed by optical excitation. The S₄ and the S₅ states are the d-CT and the b-CT states. The spacer orbital π_S that contributes to the d-CT and b-CT states is mainly located on the phenyl ring attached to the donor (Fig. S21 in the ESI†) and is thus similar to the spacer orbital π_S of the donor–spacer systems D–(Me4-Ph) and D–(Ph).

Fig. 6 Scheme of the coupled hole-transfer FRET mechanism of the donor–spacer–acceptor dyad D–(Ph-BCO-Ph)–A. Arrows indicate the different processes with the corresponding time constants occurring after optical excitation of the B-PDI donor. Horizontal and dotted lines visualize the different electronic states and potential energy surfaces (black: ground state; orange: LE-donor, locally excited donor state; gray: d-CT, dark charge transfer state; blue: b-CT, bright charge transfer state; and green: LE-acceptor, locally excited acceptor state). The d-CT and b-CT excited state minimum geometries are associated with a rotation of the spacer and a decrease of the torsional angle between the B-PDI donor and the first phenyl ring of the spacer to 3° respectively 0°.

Table 3 CC2 vertical excitation energies (ΔE) and oscillator strengths (f) of the donor spacer acceptor dyad D–(Ph-BCO-Ph)–A at the B3LYP-optimized ground-state equilibrium geometry (LE_A, locally excited acceptor state; LE_D, locally excited donor state; d-CT, dark charge transfer state; and b-CT, bright charge transfer state). The calculated energies are compared with the experimental absorption maximum of the donor chromophore (B-PDI) within D–(Ph-BCO-Ph)–A dissolved in CHCl₃

Transition	Character	D–(Ph-BCO-Ph)–A
		ΔE (eV)	f
S0 → S1	πA → πA* (LEA)	2.80	1.024
S0 → S2	πD → π2D*	3.03	0.008
S0 → S3	πD → π1D* (LED)	3.13	0.586
S0 → S4	πS → π2D* (d-CT)	3.46	0.036
S0 → S5	πS → π1D* (b-CT)	3.54	0.715
Exp.	—	2.66	—

---

Geometry optimization of the LE_D state (S₃ state at the FC-point) leads likely for the small subsystems to a local S₁ state minimum with ππ* character requiring minor structural changes (denoted as π-Min). Here the LE_D state is almost isoenergetic to the bright LE_A state of the acceptor (S₂ state). Consequently at this π-Min direct energy transfer from the donor to the acceptor can occur via noise induced FRET. This theoretical result confirms the initial rise of the spectral signatures of the PDI energy acceptor observed in the transient measurements.

Optimization of the d-CT state (S₄ state at the FC-point) leads likely in D–(Ph) to the global minimum on the S₁ potential energy surface associated with a decrease of the torsional angle α to 3.0° (Fig. 6). Optimization of the b-CT state (S₅ state at the FC-point) leads to a third minimum on the S₁ potential energy surface with a torsional angle α of 0.5°. The b-CT state in the dyad is more stabilized than in the donor–spacer system D–(Ph) and becomes the S₁ state. Now the d-CT state is 0.3 eV higher in energy at the b-CT-Min and consequently no fast depopulation from the b-CT to the d-CT state can occur unlike in D–(Ph). Furthermore in the dyad the S₁(b-CT) state at the b-CT-Min is nearly isoenergetic to the S₂(LE_A) acceptor state. Since the transition dipole moments of the b-CT and LE_A states are parallel to each other, an energy transfer from the donor to the acceptor should be possible via multipole–multipole interactions. This energy transfer denoted coupled hole-transfer FRET and enabled by a bright charge transfer state will be discussed in detail in the next section.

4 Discussion and conclusion: the transfer mechanism is a coupled hole-transfer-FRET

The experimental results of Section 2 indicate that for suitable spacers ultrafast electron transfer (ET) is found. The spacer is located between an optically excited B-PDI chromophore that energetically can act as an energy donor and PDI as a potential acceptor. According to established thinking this ET would compete with the through space energy transfer and lower its efficiency dramatically. The quantum chemical calculations of Section 3 and the very good agreement between the experimental and calculated transition energies are now used to derive a detailed picture of the mechanism behind the efficient energy transfer process observed in D–(Ph-BCO-Ph)–A. We will argue that the electron transfer between the spacer and the B-PDI donor does actually not lead to a loss of the energy stored in the bright LE_D donor state as confirmed by the overall energy transfer efficiency. The involvement of the spacer as an intermediate energy storage unit in energy transfer in a donor–spacer–acceptor system has already been postulated.⁴¹

Starting with the donor–spacer subsystems D–(Ph) and D–(Me4-Ph) the following excited state mechanism arises (see Fig. 5): after electronic excitation into the S₂(LE) state both molecules relax into the S₁(LE) state π-Min within a few 100 fs (time constant τ₁ in Table 1). While D–(Me4-Ph) relaxes back into the ground state from the π-Min via fluorescence with τ_fluo = 1.3 ns and moderate internal conversion, D–(Ph) undergoes fluorescence quenching by accessing the d-CT-Min on the S₁ potential energy surface with τ_CT = 5.9 ps. This process is associated with a rotation of the phenyl spacer into the plane of the B-PDI chromophore. A quite similar fluorescence quenching mechanism has already been observed for PDI-based donor–spacer systems.⁴² In D–(Me4-Ph) the rotation is sterically inhibited by the bulky methyl groups on the spacer. This also explains why for the dyad D–(Me4-Ph)–A with the same spacer near-unity fluorescence quantum yield and no fluorescence quenching electron transfer is observed. Furthermore this illustrates the crucial role of the spacer on the energy and electron transfer as also investigated for other donor–spacer–acceptor systems.^{12,15,43–55} From the d-CT-Min, D–(Ph) reaches a S₁/S₀ conical intersection and relaxes back into the ground state with τ_d-CT→S0 = 61 ps.

In the case of D–(Ph-BCO-Ph)–A electronic excitation into the S₃(LE) donor state also leads to a relaxation into the donor S₁(LE_D) state π-Min within a few 100 fs. From this minimum a small part of the molecules undergoes direct noise-induced FRET to the nearly isoenergetic S₂(LE_A) acceptor state with τ_FRET. A second part accesses the d-CT-Min on the S₁ potential energy surface via rotation of the whole spacer–acceptor moiety with τ_d-CT. This motion aligns the planes of the B-PDI chromophore, the phenyl ring attached to the B-PDI chromophore and the PDI acceptor to each other. The remaining third part of the molecules accesses the b-CT-Min with τ_b-CT, which is also located on the S₁ potential energy surface and associated with a rotation of the whole spacer–acceptor moiety into the plane of the B-PDI chromophore. These three processes occur with an overall time constant of τ₂ = (1/τ_FRET + 1/τ_d-CT + 1/τ_b-CT)⁻¹ = 5 ps. In the donor–spacer system D–(Ph) the b-CT-Min is located on the S₂ potential energy surface and isoenergetic to the π-Min of the S₁(LE) state. Thus the population of this state does not lead to any energy stabilization of the system, in contrast to D–(Ph-BCO-Ph)–A, where the b-CT-Min is on the S₁ potential energy surface and lies 0.15 eV below the S₁(LE_D) state π-Min. Furthermore in D–(Ph) the conical intersection in the vicinity of the b-CT-Min leads to a fast population transfer from the b-CT to the d-CT state. For these reasons the b-CT state does not get populated in D–(Ph), while in D–(Ph-BCO-Ph)–A it does. In the D–(Ph-BCO-Ph)–A dyad, the b-CT-Min is nearly isoenergetic to the S₂(LE_A) state of the acceptor. Since the transition dipole moments of the b-CT and LE_A acceptor states are parallel to each other, an efficient energy transfer from the donor to the acceptor occurs via multipole–multipole interactions with τ_HT-FRET. The part of the molecules that have populated the d-CT state undergo backward electron transfer without transferring energy to the acceptor with τ_d-CT→S0, as here the LE_A state of the acceptor is 0.78 eV higher in energy and the d-CT state has negligible oscillator strength. These two processes occur with an overall time constant τ₃ = (1/τ_HT-FRET + 1/τ_d-CT→S0)⁻¹ = 45 ps. The excited PDI acceptor finally relaxes back into the ground state via fluorescence with a time constant τ_Fluo = 3.3 ns.

The ab initio calculations show that the hole-transfer induced FRET mechanism is also present in the molecules D–(Ph-Yn2-Ph)–A, D–(Ph-Yn-Ph)–A and D–(Ph-Ph)–A, even though the spacer is an aromatic π system without an aliphatic Dexter blocker. Geometry optimizations show that in the ground state equilibrium structures the π-planes of the donor, spacer and acceptor have significant torsional angles to each other, which breaks any donor–spacer–acceptor π-conjugation. At the ground state equilibrium structures we find the same states (LE_A, LE_D, d-CT and b-CT) and energetic ordering of them (Tables S5 and S6 in the ESI†) as in D–(Ph-BCO-Ph)–A. Furthermore excited state geometry optimizations locate the same three excited state minima on the S₁ potential energy surface (LE_D donor π-Min, the d-CT and b-CT minima) responsible for the HT-FRET. As the b-CT state has a significant oscillator strength at its minimum, one could expect to observe this state in the time resolved fluorescence measurements on D–(Ph-Yn2-Ph)–A (Fig. 1b). The calculated fluorescence energy at the b-CT minimum is 2.58 eV (Table S6 in the ESI†). Taking into account the blue-shift of ca. 0.4 eV (between theory and experiment, see also Tables 2 and 3) leads to a fluorescence energy of 2.18 eV (569 nm) overlapping with the strong fluorescence of the acceptor (Fig. 1b). Thus it cannot be discriminated in the time-resolved fluorescence measurements. Also one could expect to see the b-CT state in the stationary absorption spectrum. But again, the calculations show that the absorption band of the b-CT state is overlaid by the strong donor absorption bands. For example in D–(Ph-Yn2-Ph)–A the calculated excitation energy into the b-CT (S₅) state including the blue-shift amounts to 3.44 eV, i.e. 360 nm. Comparison with the measured absorption spectrum shown in Fig. S2c (ESI†) reveals the existence of donor absorption bands in this region.

For the through-bond Dexter energy transfer to be active in the dyads with the polyyne spacers significant orbital overlap either directly between the donor and acceptor or indirectly via the spacer would be required.^56,57 No states delocalized over the whole donor–spacer–acceptor π-system, required for the direct donor–acceptor orbital overlap, could be found in the calculations. For the indirect overlap the required donor–spacer and spacer–acceptor charge transfer states are too far apart in energy for an effective coupling. The energetically lowest spacer–acceptor charge transfer states are at least 1 eV above the d-CT or b-CT states in all dyads with the polyyne spacers, i.e. D–(Ph-Yn2-Ph)–A, D–(Ph-Yn-Ph)–A and D–(Ph-Ph)–A.

From the theoretical results we conclude that the experimentally observed τ₂ and τ₃ time constants (see Table 1) are composed of several branching processes. That τ₂ originating from three processes (τ₂ = (1/τ_FRET + 1/τ_d-CT + 1/τ_b-CT)⁻¹) can also be observed experimentally. The existence of the direct noise induced energy transfer pathway τ_FRET is seen in an initial rise of the fluorescence or the GSB, SE and ESA of the PDI energy acceptor. The pathways for τ_d-CT and τ_b-CT are observed in the rise of the GSB of the spacer and the rise of the CT ESA bands characterised by the thus formed B-PDI anion. For the dyads D–(Ph-Yn2-Ph)–A, D–(Ph-Yn-Ph)–A and D–(Ph-Ph)–A we know the direct energy transfer time constants τ_FRET from the analogous systems D–(Py-Yn2-Py)–A, D–(Py-Yn-Py)–A and D–(Py-Ph)–A, where the donor–acceptor distance is the same but no electron transfer from the spacer to the B-PDI energy donor occurs (see Chart S1 and Table S1 in the ESI†). The near-unity fluorescence quantum yield of the PDI energy acceptor obtained by excitation of the energy donor shows that in these dyads no non-radiative process effectively competes with the noise-induced FRET. The quantum yield for the direct noise induced FRET (ϕ_FRET = k_FRET/k₂) is thus 21%, 7% and 9% for D–(Ph-Ph)–A, D–(Ph-Yn-Ph)–A and D–(Ph-Yn2-Ph)–A. Comparing these values with the measured fluorescence quantum yields in Table 1 shows that the direct noise induced FRET has only a minor contribution to the overall energy transfer and that the major part comes from the coupled HT-FRET mechanism. Using ϕ_HT-FRET = ϕ_Fluo − ϕ_FRET we obtain 37% for D–(Ph-Ph)–A, 26% for D–(Ph-Yn2-Ph)–A and 44% for D–(Ph-Yn-Ph)–A. For the dyad D–(Ph-BCO-Ph)–A we do not know the time constant for the direct noise induced FRET as the synthesis of an analogous system where the phenyl rings are replaced by pyridine rings is challenging and still in progress. As the donor–acceptor distance for D–(Ph-BCO-Ph)–A of 26 Å is comparable to that of D–(Py-Yn2-Py)–A, we envision that the coupled HT-FRET contributes to a similar extent to the overall energy transfer and is the major contributor just like in the dyads with the polyyne spacers.

One can determine the quantum yield for the coupled HT-FRET process over a second route. We know that the near-unity quantum yield cannot be achieved using the HT-FRET process as it competes with the relaxation of the d-CT state to the ground state. For D–(Ph-BCO-Ph)–A we can determine the components of τ_HT-FRET = (1/τ₃ − 1/τ_d-CT→S0)⁻¹ as we know τ_d-CT→S0 from D–(Ph), which is chemically most comparable to the donor–spacer moiety of the D–(Ph-BCO-Ph)–A dyad. We obtain that τ_TH-FRET = 172 ps. The quantum yield for the pure coupled HT-FRET process thus would amount to ϕ_HT-FRET = k_HT-FRET/k₃ = 26%.

The coupled HT-FRET process is the major contributor to the energy transfer process that takes place in the perylene diimide dyads investigated in this work. Since this process is mediated by the bright charge transfer state on the donor–spacer moiety, one would expect solvent effects. The measurements on D–(Ph-Yn2-Ph)–A in benzonitrile confirms this expectation. We do find significant changes compared to the chloroform solution. In the ultrafast dynamics investigated solvent effects on the charge transfer dynamics and the resulting energy transfer are highly complex as they depend on the interplay of refractive index, polarity, viscosity and solvation dynamics of the solvent.^21,30,31 A systematic investigation of this issue is thus beyond the scope of this paper taking also into account the complex synthetic routes and the resulting limited availability of the substances.

Energy transfer from states with high charge transfer character has recently been invoked in order to explain the inverse Förster behaviour observed in pyrene-borondipyrromethene dyads³³ or anthracenyl-borondipyrromethene dyads.⁵⁸ The perylene diimide model systems investigated here have shown for the first time by direct experimental observation that a bright charge transfer state can indeed act as an energy donor. We envision that the resulting HT-FRET mechanism mediated by these bright charge transfer states can find applications in artificial photosynthetic systems as well as solar cells. So far in these systems the conversion of light into chemical or electric energy is based on the coupling between energy and electron transfer.^59–61 In these chromophoric systems the energy transfer induces an electron transfer, which then causes the desired charge separation. Chromophoric systems with engineered bright charge transfer states allow one to invert the order of these processes.

Acknowledgements

Financial support of this work by Deutsche Forschungsgemeinschaft through the SFB 749 and the excellence cluster ‘Munich Center for Advanced Photonics’ (MAP) is gratefully acknowledged. We thank F. Graupner for valuable help with the streak camera recordings and A. Walter for the B-PDI-(Null)-PDI synthesis. We also thank P. Schneider for his contribution in the recording of the transient absorption spectra and P. Hummel for his contribution in the analysis of the data.

References

1. T. Förster, Ann. Phys., 1948, 437, 55–75.
2. G.-S. Jiao, L. H. Thoresen and K. Burgess, J. Am. Chem. Soc., 2003, 125, 14668–14669.
3. R. Bandichhor, A. D. Petrescu, A. Vespa, A. B. Kier, F. Schroeder and K. Burgess, J. Am. Chem. Soc., 2006, 128, 10688–10689.
4. W. Lin, L. Yuan, Z. Cao, Y. Feng and J. Song, Angew. Chem., 2010, 122, 385–389.
5. T. G. Kim, J. C. Castro, A. Loudet, J. G.-S. Jiao, R. M. Hochstrasser, K. Burgess and M. R. Topp, J. Phys. Chem. A, 2006, 110, 20–27.
6. Y.-J. Gong, X.-B. Zhang, C.-C. Zhang, A.-L. Luo, T. Fu, W. Tan, G.-L. Shen and R.-Q. Yu, Anal. Chem., 2012, 84, 10777–10784.
7. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
8. A. Osuka, N. Tanabe, S. Kawabata, I. Yamazaki and Y. Nishimura, J. Org. Chem., 1995, 60, 7177–7185.
9. D. Beljonne, C. Curutchet, G. D. Scholes and R. J. Silbey, J. Phys. Chem. B, 2009, 113, 6583–6599.
10. D. Beljonne, G. Pourtois, C. Silva, E. Hennebicq, L. M. Herz, R. H. Friend, G. D. Scholes, S. Setayesh, K. Müllen and J. L. Brédas, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10982–10987.
11. R. Métivier, F. Nolde, K. Müllen and T. Basché, Phys. Rev. Lett., 2007, 98, 047802.
12. B. Fückel, A. Köhn, M. E. Harding, G. Diezemann, G. Hinze, T. Basché and J. Gauss, J. Chem. Phys., 2008, 128, 074505.
13. A. Harriman, L. Mallon and R. Ziessel, Chem. – Eur. J., 2008, 14, 11461–11473.
14. C. Y. Wong, C. Curutchet, S. Tretiak and G. D. Scholes, J. Chem. Phys., 2009, 130, 081104.
15. B. Albinsson and J. Mårtensson, Phys. Chem. Chem. Phys., 2010, 12, 7338–7351.
16. J. Megow, B. Röder, A. Kulesza, V. Bonačić-Koutecký and V. May, ChemPhysChem, 2011, 12, 645–656.
17. J. M. Anna, G. D. Scholes and R. van Grondelle, BioScience, 2014, 64, 14–25.
18. G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Nat. Chem., 2011, 3, 763–774.
19. H. Langhals, A. J. Esterbauer, A. Walter, E. Riedle and I. Pugliesi, J. Am. Chem. Soc., 2010, 132, 16777–16782.
20. P. Nalbach, I. Pugliesi, H. Langhals and M. Thorwart, Phys. Rev. Lett., 2012, 108, 218302.
21. L. Flamigni, B. Ventura, A. Barbieri, H. Langhals, F. Wetzel, K. Fuchs and A. Walter, Chem. – Eur. J., 2010, 16, 13406–13416.
22. G. Ryseck, T. Schmierer, K. Haiser, W. Schreier, W. Zinth and P. Gilch, ChemPhysChem, 2011, 12, 1880–1888.
23. S. Kalinin, M. Speckbacher, H. Langhals and L. B.-Å. Johansson, Phys. Chem. Chem. Phys., 2001, 3, 172–174.
24. U. Megerle, I. Pugliesi, C. Schriever, C. F. Sailer and E. Riedle, Appl. Phys. B: Lasers Opt., 2009, 96, 215–231.
25. R.-J. Kutta, T. Langenbacher, U. Kensy and B. Dick, Appl. Phys. B: Lasers Opt., 2013, 111, 203–217.
26. P. Fita, E. Luzina, T. Dziembowska, Cz. Radzewicz and A. Grabowska, J. Chem. Phys., 2006, 125, 184508.
27. J. Salbeck, H. Kunkely, H. Langhals, R. W. Saalfrank and J. Daub, Chimia, 1989, 43, 6–9.
28. A. Ishitani and S. Nagakura, Mol. Phys., 1967, 12, 1–12.
29. M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337.
30. U. Schmidhammer, U. Megerle, S. Lochbrunner, E. Riedle and J. Karpiuk, J. Phys. Chem. A, 2008, 112, 8487–8496.
31. I. Pugliesi, P. Krok, S. Lochbrunner, A. Błaszczyk, C. von Hänisch, M. Mayor and E. Riedle, J. Phys. Chem. A, 2010, 114, 12555–12560.
32. I. Pugliesi, U. Megerle, S.-L. Suraru, F. Würthner, E. Riedle and S. Lochbrunner, Chem. Phys. Lett., 2011, 504, 24–28.
33. D. Bai, A. C. Benniston, J. Hagon, H. Lemmetyinen, N. V. Tkachenko and R. W. Harrington, Phys. Chem. Chem. Phys., 2013, 15, 9854–9861.
34. N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
36. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
37. K. Sadeghian, M. Bocola and M. Schütz, J. Am. Chem. Soc., 2008, 130, 12501–12513.
38. K. Sadeghian, M. Bocola and M. Schütz, Phys. Chem. Chem. Phys., 2010, 12, 8840–8846.
39. T. Merz, K. Sadeghian and M. Schütz, Phys. Chem. Chem. Phys., 2011, 13, 14775–14783.
40. T. Merz and M. Schütz, in Chemical Photocatalysis, ed. B. König, De Gruyter, Berlin, 2013, vol. 1, ch. 14, p. 263.
41. G. Duvanel, J. Grilj and E. Vauthey, J. Phys. Chem. A, 2013, 117, 918–928.
42. M. W. Holman, P. Yan, K.-C. Ching, R. Liu, F. I. Ishak and D. M. Adams, Chem. Phys. Lett., 2005, 413, 501–505.
43. J.-S. Hsiao, B. P. Krueger, R. W. Wagner, T. E. Johnson, J. K. Delaney, D. C. Mauzerall, G. R. Fleming, J. S. Lindsey, D. F. Bocian and R. J. Donohoe, J. Am. Chem. Soc., 1996, 118, 11181–11193.
44. W. B. Davis, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2001, 123, 7877–7886.
45. W. B. Davis, M. A. Ratner and M. R. Wasielewski, Chem. Phys., 2002, 281, 333–346.
46. T. K. Ahn, Z. S. Yoon, I.-W. Hwang, J. K. Lim, H. Rhee, T. Joo, E. Sim, S. K. Kim, N. Aratani, A. Osuka and D. Kim, J. Phys. Chem. B, 2005, 109, 11223–11230.
47. S. Wallin, L. Hammarström, E. Blart and F. Odobel, Photochem. Photobiol. Sci., 2006, 5, 828–834.
48. A. C. Benniston and A. Harriman, Chem. Soc. Rev., 2006, 35, 169–179.
49. B. Albinsson, M. P. Eng, K. Pettersson and M. U. Winters, Phys. Chem. Chem. Phys., 2007, 9, 5847–5864.
50. O. S. Wenger, Chem. Soc. Rev., 2011, 40, 3538–3550.
51. M. A. H. Alamiry, J. P. Hagon, A. Harriman, T. Bura and R. Ziessel, Chem. Sci., 2012, 3, 1041–1048.
52. C. Schubert, M. Wielopolski, L.-H. Mewes, G. de Miguel Rojas, C. van der Pol, K. C. Moss, M. R. Bryce, J. E. Moser, T. Clark and D. M. Guldi, Chem. – Eur. J., 2013, 19, 7575–7586.
53. M. Natali, S. Campagna and F. Scandola, Chem. Soc. Rev., 2014, 43, 4005–4018.
54. L. G. Heinz, O. Yushchenko, M. Neuburger, E. Vauthey and O. S. Wenger, J. Phys. Chem. A, 2015, 119, 5676–5684.
55. M. Gilbert and B. Albinsson, Chem. Soc. Rev., 2015, 44, 845–862.
56. G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87.
57. J. Otsuki, Y. Kanazawa, A. Kaito, D.-M. S. Islam, Y. Araki and O. Ito, Chem. – Eur. J., 2008, 14, 3776–3784.
58. D. Bai, A. C. Benniston, J. Hagon, H. Lemmetyinen, N. V. Tkachenko, W. Clegg and R. W. Harrington, Phys. Chem. Chem. Phys., 2012, 14, 4447–4456.
59. G. Kodis, P. A. Liddell, L. de la Garza, P. C. Clausen, J. S. Lindsey, A. L. Moore, T. A. Moore and D. Gust, J. Phys. Chem. A, 2002, 106, 2036–2048.
60. M. H. Stewart, A. L. Huston, A. M. Scott, E. Oh, W. Russ Algar, J. R. Deschamps, K. Susumu, V. Jain, D. E. Prasuhn, J. Blanco-Canosa, P. E. Dawson and I. L. Medintz, ACS Nano, 2013, 7, 9489–9505.
61. H.-W. Wang, M.-Y. Yeh, C.-H. Chen, T.-S. Lim, W. Fann and T.-Y. Luh, Macromolecules, 2008, 41, 2762–2770.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental details, Chart S1, Table S1 and Fig. S1–S19. Computational details, Tables S2–S6 and Fig. S20–S24. See DOI: 10.1039/c5cp02981c

‡ These authors contributed equally.

---