A wavelength dependent investigation of the indole photophysics via ionization and fragmentation pump–probe spectroscopies

Abstract

A wavelength dependent study investigating the low-lying ¹L_a and ¹L_b states, both possessing ¹ππ* character, and the ¹πσ* state in the deactivation process of indole is presented here. Relaxation dynamics following excitation at 241, 250, 260, 270, 273, and 282 nm are examined using three gas-phase, pump–probe spectroscopic techniques: (1) hydrogen atom (H-atom) time-resolved kinetic energy release (TR-KER), (2) time-resolved photoelectron spectroscopy (TR-PES), and (3) time-resolved ion yield (TR-IY). Applied in combination, a more complete picture of the indole relaxation dynamics may be gleaned. For instance, TR-PES experiments directly observe all relaxation pathways by probing the evolution of the excited states following photoexcitation; whereas, TR-KER measurements indirectly, yet specifically, probe for ¹πσ*-state activity through the detection of H-atoms eliminated along the indole nitrogen–hydrogen (N–H) stretch coordinate—a possible outcome of ¹πσ*-state relaxation in indole. In addition, mass information obtained via TR-IY monitors fragmentation dynamics that may occur within the neutral electronically excited and/or cationic states. The work herein assesses the onset and importance of the ¹πσ* state at various pump wavelengths by systematically tuning across the ultraviolet absorption spectrum of indole with a particular focus on those pump wavelengths longer than 263 nm, where the involvement of the ¹πσ* state is under current debate. As far as this experimental work is concerned, there does not appear to be any significant involvement by the ¹πσ* state in the indole relaxation processes following excitation at 270, 273, or 282 nm. This investigation also evaluates the primary orbital promotions contributing to the ¹L_a, ¹L_b, and ¹πσ* transitions based on ionization preferences observed in TR-PES spectra. Relaxation time constants associated with dynamics along these states are also reported for excitation at all of the aforementioned pump wavelengths and are used to pinpoint the origin of the discrepancies found in the literature. In this context, advantages and disadvantages of the three experimental techniques are discussed.

---

Introduction

Procuring an exhaustive and, more importantly, consistent understanding of the aromatic heterocyclic molecule indole is immensely important as its presence in nature and application in biological processes is evident. For example, indole serves as a light-absorbing chromophore for the essential amino acid tryptophan and, as a building block of the eumelanin polymer,^1,2 could play a vital role in preventing DNA photodamage linked to harmful ultraviolet (UV) radiation. Several investigations successfully demonstrate that gas-phase experiments may elucidate the photodynamics of certain molecules in the condensed phase;^3–7 hence, a series of gas-phase spectroscopic studies, which complement quantum chemical calculations, is a logical first step toward understanding indole's photodynamic properties in more complex environments and possibly its photoprotective role in eumelanin.

An extensive amount of spectroscopic work exists, and the investigations by Townsend and co-workers,⁸ Stavros and Iqbal,⁹ Ashfold and co-workers,¹⁰ and Ullrich and co-workers¹¹ provide excellent starting points for a more comprehensive review of the existing literature regarding the indole molecule. Here, we will focus primarily on those studies that investigate or aid in the understanding of the low-lying excited states with ππ* and πσ* character that are accessible in our wavelength dependent study. The reported absorption spectra^8,12–14 for the indole molecule are in very strong agreement. A key feature present in these studies is a broad peak spanning from approximately 220 nm to around 280 nm. This signal is predominantly caused by absorption to a ¹ππ* state, which is referred to as the ¹L_a state in accordance with Platt's nomenclature¹⁵ throughout the remainder of this report. Likewise, additional intensity extending to wavelengths longer than 280 nm is mainly due to absorption to the so-called ¹L_b state (also of ¹ππ* character). The indole neutral ground state is denoted as S₀ throughout the present study.

In addition to the ¹L_a and ¹L_b states, other states may participate in the indole relaxation process as well. For example, if an electron from a π (occupied bonding) orbital transitions to the σ* molecular orbital, an electronically excited πσ* state forms. As is the case in certain azoles, phenols, and larger heteroaromatic molecules, this type of excited state can aid in the nonradiative decay processes in indole. However, in contrast to some molecules like pyrrole or imidazole, where the πσ* state may be accessed directly, the πσ* state in indole is predominately populated indirectly via transfer from an optically bright state.¹⁶

The transition to a σ* molecular orbital in indole can create a significant dipole moment of the πσ* state. For instance, Sobolewski and Domcke¹⁷ note in their discussion about indole that the charge distribution of the σ* molecular orbital is located beyond the atomic frame, and as such, the transition from the initial π orbital to the σ* orbital possesses substantial charge-transfer characteristics, the result of which is a dipole moment of the ¹πσ* state. The authors also mention that this charge-transfer character coupled with the antibonding nodal character of the σ* orbital may lead to H-atom dissociation from the nitrogen–hydrogen (N–H) moiety in indole—a process corroborated here and by several other experimental investigations.^9–11,18

Sobolewski and Domcke also report potential energy profiles calculated using multiconfigurational second-order perturbation theory (CASPT2) ab initio techniques¹⁹ and at the CC2/aug-cc-pVDZ level.¹⁷ It should be noted that the results from both works are somewhat different. Their earlier study predicts an excitation energy of 4.30, 4.65, and 5.05 eV for the ¹L_b, ¹L_a, and ¹πσ* states, respectively. In contrast, the latter investigation reports a significant upward shift of the ¹L_b-state and ¹L_a-state minimums and a slight downward shift of the ¹πσ* minimum energy in comparison to their earlier work, creating a near degeneracy between all three states. Theoretical calculations by Townsend and co-workers⁸ are in strong agreement with Sobolewski and Domcke's latter work.¹⁷

An exhaustive amount of information exists regarding the ¹L_b-state region,^20–31 and numerous vibronic bands are identifiable between 4.37, which is very close to the predicted ¹L_b-state onset, and ∼4.58 eV. The experimentally determined ¹L_a onset is located at approximately 4.54 eV,^32,33 which is slightly lower than the predicted excitation energy of 4.65 eV in Sobolewski and Domcke's earlier calculations and even lower than the value predicted by their latter work.

Indole relaxation dynamics may partially be explained by referencing the aforementioned ab initio calculations. According to the potential energy profiles calculated along the N–H stretch coordinate, excitation to the ¹L_a state may indirectly populate the ¹πσ* state via an ¹L_a/¹πσ* conical intersection (CI). Calculations and experiments performed by Schmitt and co-workers^22,34 suggest an ¹L_a/¹L_b CI—accessible through Herzberg–Teller active modes and in very close vicinity to the ¹L_a-state origin—provides an essentially “barrierless” mechanism for an ¹L_a → ¹L_b transition. The minimum-energy-path calculations of Giussani et al.³⁵ substantiate these claims and clearly demonstrate the ¹L_b/S₀ CI that could mediate relaxation from the ¹L_b state back to the ground state. Thus, ¹L_a → ¹L_b → S₀ and ¹L_a → ¹πσ* → S₀ transitions are all possible relaxation mechanisms for the excited indole molecule, and, as mentioned earlier, relaxation along the ¹πσ* state may also lead to H-atom dissociation from the N–H bond.

In regard to the latter process, dissociation along the ¹πσ* relaxation pathway is not the only source of H-atom photoproducts: Several works report H-atom signal arising from statistical unimolecular decay from the vibrationally hot ground state.^9–11,18 Because H-atoms associated with ¹πσ*-state activity are expected to carry higher kinetic energies than H-atoms that emanate from statistical processes, signal associated with the ¹πσ* state may partially be isolated through kinetic energy analysis. This process is aptly demonstrated for indole in a previous work following excitation at 201 nm.¹¹

Several time-resolved experimental studies have been performed on the indole molecule to investigate the dynamics mentioned above, and Table 1 provides a summary of the more recent time constants associated with ¹L_a-state (column 4), ¹L_b-state (column 5), and ¹πσ*-state (column 6) activity at various pump (column 2) and probe (column 3) wavelengths. The differing experimental techniques are also noted (column 1). It should be mentioned that Radloff and co-workers³⁶ report no involvement of the ¹πσ* state in the indole relaxation process. Their photoelectron spectra and photoion results produce only long-lived components (greater than several hundred picoseconds), and the authors ascribe those times to the initially excited ππ* state(s).

Table 1 The time constants presented here for the given pump (λ_pu) and probe (λ_pr) wavelengths are obtained using a variety of experimental techniques: time-resolved ion yield (TR-IY), time-resolved photoelectron spectroscopy (TR-PES), and, specific to H-atom photoproduct detection, time-resolved velocity map imaging (TR-VMI) and time-resolved kinetic energy release (TR-KER). Time constants obtained by our group are shown in bold

Technique	λ pu (nm)	λ pr (nm)	^1La	^1Lb	^1πσ*
a Data from ref. 9. b Data from ref. 11. c Data from ref. 59. d Data from ref. 36, this work does not distinguish between ^1La- and ^1Lb-state relaxation dynamics but instead associates the several hundred picoseconds time constant with relaxation from the initially prepared ππ* state(s)—assuming simultaneous excitation to both states. e Data from ref. 8.
TR-VMI	200^a	243.15	N/A	N/A	100 ± 30 fs
TR-PES	201	294	<100 fs	23 ± 5 ps	405 ± 76 fs
TR-KER	201	243.15	N/A	N/A	367 ± 39 fs
TR-IY	201	294	<100 fs	23 ± 5 ps	385 ± 69 fs
TR-IY	235^c	1305	—	150 ± 20 ps	—
TR-IY	239^d	394	—	>100 ps	—
TR-PES	241	294	<100 fs	371 ± 85 ps	436 ± 157 fs
TR-KER	241	243.15	N/A	N/A	515 ± 63 fs
TR-IY	243^c	1305	22 ± 9 fs	315 ± 50 ps	435 ± 125 fs
TR-IY	248^c	1305	22 ± 9 fs	ps	460 ± 145 fs
TR-PES	249^e	300	<100 fs	350 ps (± 20%)	700 fs (± 20%)
TR-PES	250	294	<100 fs	616 ± 64 ps	413 ± 144 fs
TR-PES	250^d	400	—	>100 ps	—
TR-IY	250^d	400	—	>100 ps	—
TR-KER	250	243.15	N/A	N/A	671 ± 84 fs
TR-IY	255^d	310	—	>100 ps	—
TR-PES	260	294	<100 fs	715 ± 98 ps	505 ± 100 fs
TR-KER	260	243.15	N/A	N/A	932 ± 91 fs
TR-IY	260^c	1305	22 ± 9 fs	7 ± 2 ns	370 ± 110 fs
TR-PES	263^d	395	—	>100 ps	—
TR-IY	269^c	1305	39 ± 12 fs	ns	—
TR-PES	270	294	272 ± 83 fs	ns	—
TR-IY	272.5^c	1305	42 ± 9 fs	ns	—
TR-PES	273	294	276 ± 142 fs	ns	—
TR-PES	273^e	300	<100 fs	∞	1200 fs (± 20%)
TR-IY	278^c	1305	—	ns	—
TR-PES	282	294	—	∞	—

---

Table 1 helps accentuate the widespread disagreement among the reported values. Although disparate experimental techniques and various probing schemes are utilized, it is not unreasonable to believe that closer agreement among the values could be achieved—or at least a more visible trend if one exists. In reference to the aforementioned potential energy profile calculations,^{8,17,19,34,35} the extracted time constants are expected to be somewhat dependent on the pump wavelengths partially due to potential energy barriers that exist within the electronically excited states.

It is the aim of this work to investigate the excited-state relaxation dynamics of the indole molecule via a wavelength dependent study spanning a region above and below the ¹πσ* state onset. This work starts with a series of H-atom time-resolved kinetic energy release (TR-KER) experiments, where H-atoms that photodissociate from the indole molecule are measured. As mentioned earlier, H-atom signal associated with ¹πσ* activity in the electronically excited state is distinguishable from signal resulting from other processes on a kinetic energy basis. Thus an indirect analysis of ¹πσ* dynamics is achieved. More specifically, the point at which ¹πσ*-state relaxation leads to H-atom dissociation is identified. The associated appearance times of this signal at various excitation energies above this onset is also gleaned and the extracted time constants, as is demonstrated by an earlier work following excitation at 201 nm,¹¹ may be viewed as a good estimate for the ¹πσ*-state relaxation time. Our investigation then progresses to a complementary sequence of time-resolved photoelectron spectroscopy (TR-PES) experiments, which afford the unique capability of measuring directly all excited states involved in the indole deactivation process. Finally, a time-resolved ion yield (TR-IY) experiment is also conducted to monitor fragmentation dynamics within the excited state and to confirm that the resulting photoelectron signal is, in fact, originating from indole, not an indole photoproduct. Through a conglomerate analysis involving these three techniques, we aim to clarify the energetic onset of ¹πσ*-state involvement in the indole deactivation process and to decipher the timescales on which indole relaxation dynamics occur at all the aforementioned pump wavelengths. We also elaborate further on the suitability of different probe techniques for monitoring excited-state relaxation dynamics and propose an explanation for the inconsistent time constants found in the literature.

Experimental details

The experimental setup consists of a Ti : Sa oscillator (Coherent Inc. MIRA Model 900-F, which is pumped with a Coherent Inc. Verdi G5), and a regenerative amplifier (Coherent Inc. Legend Elite HE). Details regarding the setup are provided elsewhere,¹¹ and deviations from previous investigations and essential experimental parameters are described as follows. All pump beams utilized in this investigation (241, 250, 260, 270, 273, and 282 nm) are generated using a Coherent Inc. OPerA optical parametric amplifier and span above and below the region where the ¹πσ*-state relaxation pathway becomes an energetically viable avenue for indole deactivation. The probe beams (294 nm for TR-PES and TR-IY; 243.15 nm for TR-KER) are generated with a Coherent Inc. TOPAS-C with UV extension. A probe of 294 nm is applied for TR-IY and TR-PES studies due to its extremely low absorbance in indole^8,12–14—reducing the amount of undesired probe–pump signal. Pump and probe beams are generated with pulse energies around 10 and 30 μJ per pulse, respectively. Before intersecting the molecular beam, the pump pulse energy is reduced to a modest level (<1.7 μJ per pulse) and the probe to approximately 7.0 μJ per pulse for all TR-PES and TR-IY investigations. In regard to the TR-KER investigations, the probe beam pulse energy is set higher and centered around 243.15 nm to promote H-atom detection, which relies on 2 + 1 resonance enhanced multiphoton ionization (REMPI) via the 2s state for neutral H-atoms. Scanning the relative pump–probe delay times is achieved with a motorized delay stage (Newport ILS150PP with ESP300 controller), which is positioned in the TOPAS-C beam path.

A custom-built multipurpose spectrometer is used to record all measurements, and is described in detail elsewhere.^37,38 A magnetic bottle spectrometer, based on the principles delineated by Kruit and Read,³⁹ facilitates the detection of both photoelectrons and H-atoms. A +14 V repelling potential is applied between extraction grids located above and below the ionization region (see ref. 11 for details) to improve H-atom collection performance. The time-of-flight (TOF) mass spectrometer affords measurements of photoions and is based on the Wiley-McLaren configuration.⁴⁰ TR-IY investigations use a +1.5 kV potential difference between the ion repeller and extraction grid and a −1.5 kV potential difference between the extraction and acceleration grids. A field-free region is generated within the flight tube by setting the liner to the acceleration grid potential. The indole sample (≥99%) is purchased directly from Sigma-Aldrich, Inc. and is used without further purification. The sample is heated to 35 °C in a differentially pumped vacuum chamber for all scans, and the resulting indole vapor is co-expanded and transported with a helium carrier gas to the ionization region of the spectrometer. A 50 : 50 mixture of 1,3-butadiene and helium is used to find the Gaussian cross-correlation in each experiment: the results of which are reported below in their respective sections (see Section A for TR-KER results and Section B for TR-PES in Results and Discussion). Photoelectron energy spectra are calibrated with the same butadiene-helium mixture and a 50 : 50 mixture of ammonia and helium using the photoelectron spectra in ref. 41 and 42, respectively.

Results and discussion

A complementary TR-IY scan under otherwise identical experimental conditions was conducted for all of the investigations discussed in detail below. In each case, the resulting mass spectra confirmed the dominating presence of indole in the gas phase. With the chosen pump and probe powers, a negligible amount of fragmentation (i.e., anything other than H-atom dissociation from the N–H moiety) is observed in all cases and does not require consideration in our analyses. As an additional note, the parent ion signal in the TR-IY scans were well described with the same Gaussian convoluted exponential decay functions and time constants (within the given errors) as the TR-PES data presented below.

A. Time-resolved kinetic energy release

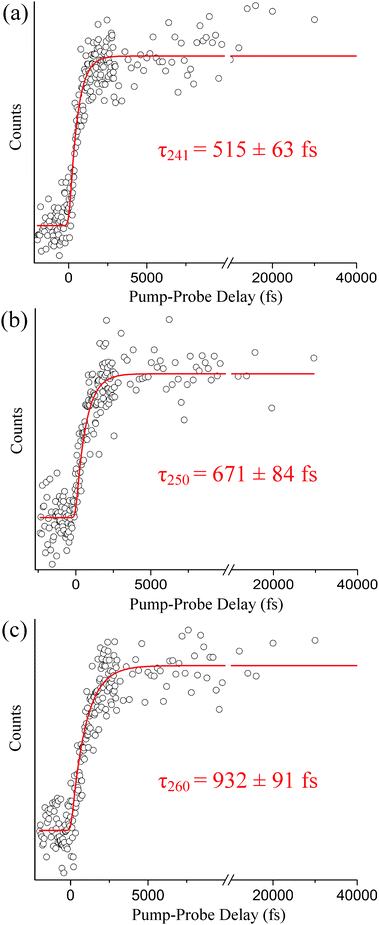
The steady-state H-atom kinetic energy spectra of indole photodissociated at 241, 250, 260, and 273 nm are discussed here. In each case, the probe wavelength is centered at 243.15 nm. The Gaussian cross-correlations, as measured within the spectrometer, are as follows: 248 ± 7, 223 ± 9, 218 ± 9, and 181 ± 8 fs, respectively. As mentioned in the Introduction, H-atoms deriving from direct dissociation along the ¹πσ* state are easily distinguished from H-atoms produced via statistical unimolecular decay on S₀ based on their kinetic energies. To demonstrate this, H-atom kinetic energy spectra recorded at 273 and 250 nm are displayed in Fig. 1(a) and (b), respectively. Contributions from statistical decay are fitted with a Boltzmann distribution (blue) whereas direct dissociation products are described by a Gaussian (red). Clearly, a bimodal distribution is observed at 250 nm but the higher kinetic energy peak is noticeably absent at 273 nm; indications of high-energy H-atom signal become visible in the low- to mid-260 nm range but signal levels are insufficient for further analysis. All of the recorded spectra discussed here resemble low-resolution versions of those attained by Ashfold and co-workers¹⁰ and reproduce their reported onset for direct H-atom elimination. In reference to our discussion in Section B, we briefly note that H-atom detection experiments do not exclude relaxation to S₀via the ¹πσ* state below this onset. In general, our H-atom kinetic energy spectra support earlier high resolution work¹⁰ but do not contribute any additional spectroscopic information. Therefore, the following discussion focuses on the dynamics aspect of direct N–H photodissociation at 241, 250, and 260 nm. Integration over the high-energy H-atom signal in our TR-KER spectra yields the delay traces depicted in Fig. 2, which are then fitted with a Gaussian convoluted single-step function to extract photoproduct appearance times.

Fig. 1 The steady-state H-atom kinetic energy spectra of indole photodissociated at (a) 273 nm and (b) 250 nm are presented here to highlight the presence of a high-energy H-atom distribution at pump wavelengths shorter than ∼263 nm. The low-energy signal in both figures is fitted with a statistical function (shown in blue) while the high-energy H-atom distribution, associated with direct N–H dissociation along the ¹πσ* state, is fitted with a Gaussian function (shown in red).

Fig. 2 Delay traces associated with the high-energy H-atom distributions are shown here for pump wavelengths centered at (a) 241 nm, (b) 250 nm, and (c) 260 nm. A clear increasing trend in photoproduct rise time is visible as the pump wavelength increases.

As shown in Fig. 2(a), a high-energy H-atom rise time of τ₂₄₁ = 515 ± 63 fs is obtained following excitation at 241 nm. When the excitation wavelength increases to 250 nm (see Fig. 2(b)), the rise time associated with the high-energy H-atoms increases to τ₂₅₀ = 671 ± 84 fs. The trend continues when the wavelength is again raised to 260 nm, producing a rise time of τ₂₆₀ = 932 ± 91 fs as presented in Fig. 2(c). While the measured time constants correspond to the appearance of the H-atom photoproduct, it may be regarded as an indirect measurement of relaxation along the ¹πσ* state. As such, the increase in rise time may be suggestive of a barrier existing along the ¹πσ* potential energy profile, as predicted by Townsend and co-workers⁸ and Sobolewski and Domcke,^17,19 which is approached at the longer excitation wavelengths. Although both authors agree a barrier may exist, the height of the barrier is still unsure (ranging from 0.1 eV to approximately 0.5 eV). This picture is revisited in the discussion below (Section B) when TR-KER and TR-PES results are compared and an alternative explanation is offered.

B. Time-resolved photoelectron spectroscopy

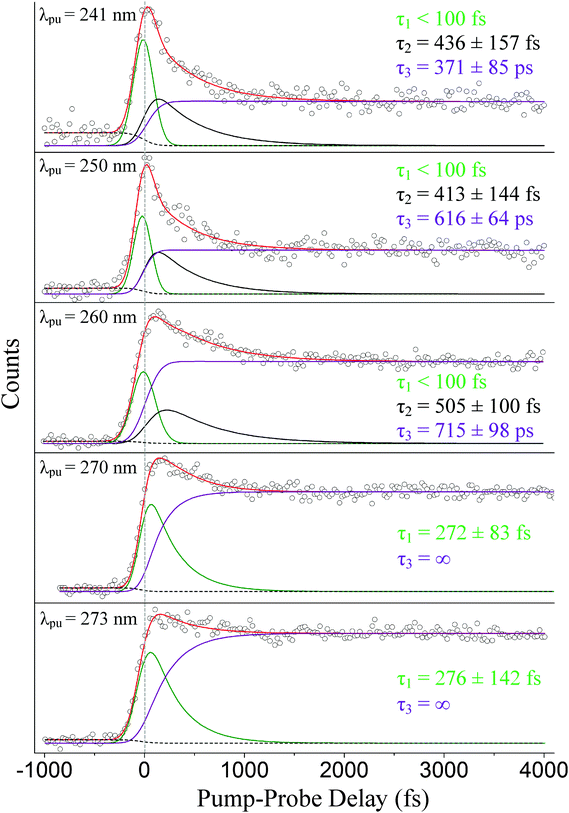
The photoelectron spectra presented here are taken at pump wavelengths of 241, 250, 260, 270, 273, and 282 nm. A 294 nm probe is applied in all cases. A short-range scan with pump–probe delays extending ∼4000 fs beyond time-zero with a step size of 25 fs is reported here at all pump wavelengths. A second set of experiments with pump–probe delays expanding beyond 100 ps with larger, unequal step sizes are also discussed at all pump wavelengths below 282 nm. The Gaussian cross-correlations for the short-range scans are 208 ± 8, 184 ± 5, 237 ± 9, 214 ± 6, 209 ± 9, and 172 ± 8 fs, respectively. Likewise, the Gaussian cross-correlations for the long-range scans are 228 ± 7, 174 ± 6, 237 ± 9, 214 ± 6, and 201 ± 5 fs, respectively. Each short-range scan is deconvoluted into its individual contributions (channels) using a custom LabVIEW program based on a Levenberg–Marquardt optimization algorithm, which simultaneously fits spectra and associated decay dynamics along the energy and pump–probe delay axes. The number of channels assigned in each analysis is based on the necessity to accurately fit the data (i.e., the lowest number of channels where any residual signal is negligible and random noise). The results are then interpreted by considering ionization correlations (discussed in more detail shortly) and comparing our experimental outcomes to the numerous theoretical investigations.^{8,17,19,34,35,43–45} Three excited-state channels are needed to accurately fit the data attained at pump wavelengths centered around 241, 250, and 260 nm. At 270 and 273 nm, only two excited-state channels are required to accurately fit the results and only one at 282 nm. It is assumed in all cases at or shorter than 273 nm that the ¹L_a state is excited almost exclusively, thus a rise time of zero femtoseconds is fixed for the ¹L_a-state contribution throughout our analysis. To account for sequential dynamics from the ¹L_a state, rise times for the ¹L_b-state and ¹πσ*-state contributions, when applicable, remain open during the fitting process and consistently converge to values similar to the ¹L_a-state decay times. Pumping at 282 nm corresponds to direct excitation of the ¹L_b state (i.e., energetically below the ¹L_a onset), hence the rise time associated with the ¹L_b state is fixed at zero femtoseconds in this case.

Similarly, the long-range scans acquired at pump wavelengths of 241, 250, and 260 nm are accurately fitted with a Gaussian convoluted triple exponential decay function, and those at 270 and 273 nm with a Gaussian convoluted double exponential decay function. Again, exponential rises account for the sequential dynamics. The long-range scans are necessary to accurately extract time constants associated with the long-lived ¹L_b channels.

In all cases, an additional channel with a negative decay constant is introduced to account for minor probe–pump signal; however, this channel is unrelated to the excited-state dynamics of interest and not discussed further.

The color maps depicted in Fig. 3 represent the extracted channels at pump wavelengths of 241, 250, 260, 270, and 273 nm as a function of pump–probe delay and electron binding energy. Due to differing dynamics and for clarification, the color maps corresponding to 282 nm excitation are shown separately in Fig. 4. The electron binding energy is readily calculated by subtracting the measured photoelectron kinetic energies from the total pump and probe photon energies. In all cases, it is assumed only one photon from each beam is absorbed by the molecule, which can be justified for the laser powers and focusing conditions applied here. The first vertical ionization potential (labeled IP1) for indole is marked by the yellow-dashed line at 7.90 eV ^46–48 in the second, third, and fourth columns of Fig. 3 and is used to help identify the electronically excited states. The first column in Fig. 3 displays the raw TR-PES signal for comparison to the individual contributions from each excited state. The second column consists of the channels associated with ¹L_a-state deactivation to the ¹L_b state and, at shorter wavelengths, also the ¹πσ* state. As mentioned in an earlier investigation,¹¹ the ¹L_a → ¹L_b and ¹L_a → ¹πσ* competing transitions occur simultaneously and are, in general, not discernable from one another due to spectral overlap in addition to similar ultrafast decay dynamics. Therefore, only a single time constant is assigned to the depopulation of the initially excited ¹L_a state. The third column in Fig. 3 presents a relatively long-lived signal associated with ¹L_b-state relaxation to the S₀ state. Column 4 encompasses the channels associated with deactivation along the ¹πσ* state, which is observed at pump wavelengths of 241, 250, and 260 nm but not at 270 or 273.

Fig. 3 Color maps are presented here for each ¹L_a-state (column 2), ¹L_b-state (column 3), and ¹πσ*-state (column 4) contribution obtained through the global analysis of the raw TR-PES data (column 1) acquired at pump wavelengths of (from top to bottom) 241, 250, 260, 270, and 273 nm. The measured photoelectron kinetic energies are transformed to electron binding energies for comparison to the known indole ionization potentials.^46–48 The yellow-dashed lines mark the first indole vertical ionization potential at 7.90 eV.

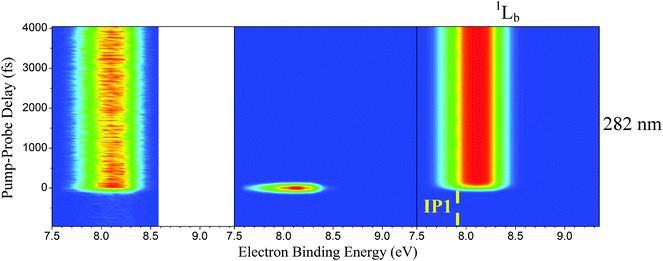Fig. 4 Color maps of the raw TR-PES data set (column 1) and individual channels (columns 2 and 3) are shown for indole photoexcited at 282 nm. Measured photoelectron kinetic energies are transformed to electron binding energies for comparison to the known indole ionization potentials.^46–48 The yellow-dashed line marks the first indole ionization potential at 7.90 eV.

Fig. 4 is structured similarly with the raw TR-PES signal presented in column 1 and contributing channels in columns 2 and 3. IP1 is again marked with a yellow-dashed line in column 3. As mentioned earlier, excitation at 282 nm directly excites the ¹L_b state; however, two channels are needed to accurately fit the data set: one accounting for ¹L_b-state activity (excited-state channel) and another accounting for a Gaussian-shaped contribution. We will elaborate on the assignments by examining the indole ionization correlations in the subsequent paragraphs.

The following discussion commences by examining indole ionization correlations. Because the ¹L_a state is populated from the highest occupied molecular orbital (HOMO)^{8,17,35,43,49} it is supposed that this state preferentially ionizes into the D₀ state, which is associated with IP1 at 7.90 eV. In a very simple picture a Δν = 0 propensity is assumed, where ν is a generalized quantum number and not mode specific, and any vibrational excitation in the ¹L_a state is transitioned to the ionic state. Therefore, shifts relative to the ionization potentials, in this case IP1, on an electron binding energy graph are expected. For example, the indole molecule is at first excited approximately 0.60 eV above the ¹L_a-state origin (located around 273 nm) following absorption of a 241 nm photon. Assuming a Δν = 0 propensity, we predict the maximum signal originating from the ¹L_a state to be positioned near 8.50 eV (i.e., 0.60 eV higher in binding energy than IP1), which is observed in our experimental work (see Fig. 3). Likewise, the ¹L_a-state signal should exhibit shifts from approximately 0.42 to 0 eV when pump wavelengths in the 250 to 273 nm region are employed. This expected and observed trend further ascertains our classification of these signal contributions as originating from the ¹L_a state and confirms an ¹L_a → D₀ (IP1) ionization correlation.

As mentioned by Townsend et al.,⁸ it may be assumed (based on several band decomposition studies^50–54) that, almost exclusively, the ¹L_a state is excited in the pumping process, especially at the excitation wavelengths well above the ¹L_a-state onset of 4.54 eV. As such, population of the ¹L_b state may solely be the result of relaxation from the ¹L_a state. Nevertheless, a similar analysis of the photoelectron spectra is implemented to study signals associated with the ¹L_b state. Based on the orbital calculations of Townsend et al.,⁸ the ¹L_b-state transition is expected to predominantly originate from the HOMO−1 and would therefore preferentially ionize into the D₁ state, which should correspond with indole's second vertical ionization potential (IP2) of 8.35 eV.^46–48 With the ¹L_b-state origin taken to be at 283.8 nm,⁵⁵ vibrational shifts in the approximate range of 0.77 to 0.03 eV above IP2 would be expected as the pump wavelength increases from 241 nm to 282 nm. As shown in Fig. 3 and 4, a general “shifting” trend is observed; however, the maximum signal peaks at all excitation wavelengths are consistently located below these predictions. Most notably for excitation at long wavelengths, the ¹L_b photoelectron signals fall below IP2. Townsend et al. observed a similar discrepancy in their analysis—an outcome they relate to the transmission efficiency of their spectrometer. Instead we challenge the proposed ¹L_b → D₁ (IP2) ionization correlation. According to Platt's notation,¹⁵ the ¹L_b transition originates from LUMO+1 ← HOMO and LUMO ← HOMO−1 excitations. Close inspection of the orbital representations associated with the HOMO and HOMO−1 reveals stark differences throughout the literature and coefficients describing the relative contributions of orbital promotions are also inconsistent.^{8,17,35,43,49,56} Given that theoretical descriptions are presently inconclusive, we propose an ¹L_b → D₀ (IP1) ionization correlation based on our experimental observations. For instance, assuming ionization into the D₀ (IP1) state, vibrational shifts in the approximate range of 0.77 to 0.03 eV above IP1 would be expected as the pump wavelength increases from 241 to 282 nm. This is observed in all cases (see Fig. 3 and 4). Furthermore, the 282 nm TR-PES spectrum in Fig. 4 clearly demonstrates ionization of ¹L_b into D₀ (IP1) and further substantiates our proposal. A similar disparity exists for the ¹πσ*-state ionization correlations and, following the same arguments, we also propose preferential ionization into D₀ (IP1). In any case, assignment of the ¹πσ* channel is unambiguously supported by the above TR-KER measurements.

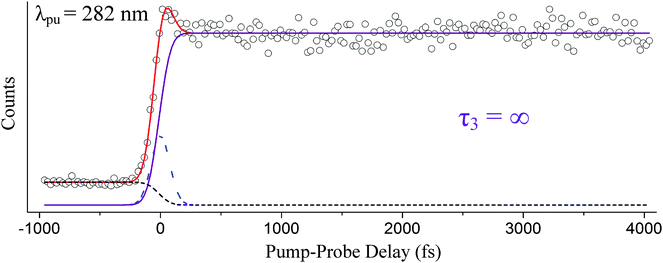
As shown in Fig. 4, two pump–probe channels are needed to accurately fit the raw data set acquired at 282 nm. While the photoelectron spectra of both channels (columns 2 and 3) are very similar (i.e., they fall within the same electron binding energy range), a single exponential decay function would be insufficient to adequately describe the dynamics. With the excitation onset of the ¹L_a state located at 273 nm, it is assumed at 282 nm that we are pumping directly into the ¹L_b state, and we associate the long-lived channel (column 3) with ¹L_b-state activity because this contribution is highly consistent with the ¹L_b-state channels of Fig. 3 and is congruous with our proposed ¹L_b → D₀ (IP1) ionization correlation. Because 282 nm is slightly above the ¹L_b-state onset, it is possible that the signal in column 2 corresponds to motion from the Franck–Condon region toward the ¹L_b minimum. Another likely cause is nonresonant ionization or out-of-resonance adiabatic excitation, which are not related to the excited-state dynamics of interest. A similar effect as these latter contributions has been observed by Longarte et al. in naphthalene and the related tryptophan molecule.^57,58

We now focus our discussion on the associated time traces. The raw data sets, overall fits, and separate channel contributions associated with the short-range experiments administered at 241, 250, 260, 270, and 273 nm are displayed in Fig. 5. Results at 282 nm are shown in Fig. 6. We designate the green delay traces to relaxation originating from the ¹L_a state. All purple and black delay traces are attributed to relaxation along the ¹L_b state and ¹πσ* state, respectively. The black-dashed lines represent the aforementioned probe–pump contributions. In Fig. 6, the blue-dashed line depicts the Gaussian-shaped contribution.

Fig. 5 Short-range TR-PES signal (○), fits (red), and individual contributions (¹L_a – green, ¹πσ* – black, ¹L_b – purple, and probe–pump signal – black-dashed) integrated over all photoelectron kinetic energies are shown at various pump wavelengths: (from top to bottom) 241, 250, 260, 270, and 273 nm. Relaxation times associated with each channel (¹L_a – τ₁, ¹πσ* – τ₂, ¹L_b – τ₃) are also displayed in their respective graphs. The zero position is marked by the gray-dashed vertical line.

Fig. 6 Short-range TR-PES signal (○), fit (red), and individual contributions (¹L_b – purple, nonresonant activity – blue-dashed, and probe–pump signal – black-dashed) integrated over all photoelectron kinetic energies are shown following photoexcitation at 282 nm.

Our discussion will begin with the results obtained following excitation at 241 nm. Three time constants related to excited-state dynamics are needed to properly fit the obtained data set. The green delay trace furnishes the leading contribution to the overall signal and carries a relaxation time on an ultrafast timescale (τ₁ < 100 fs). A second time constant, τ₂ = 436 ± 157 fs, is also extracted from the fitting process and is denoted by the black delay trace. This lifetime, although still extremely fast, is notably longer than the first time constant. The third and final time constant, τ₃ = 371 ± 85 ps, is from the long-lived contribution represented by the purple delay trace. These results are in strong agreement with the TR-IY studies conducted by Longarte et al.⁵⁹ at a pump wavelength of 243 nm. Longarte et al. report time constants of 22 ± 9 fs (similar to our τ₁), 435 ± 125 fs (in agreement with our τ₂), and 315 ± 50 ps (in agreement with our τ₃). It should be noted, however, that Longarte et al. employ a 1305 nm multiphoton probe, which, in principle, could produce contrasting dynamics if intermediate resonances are hit during the ionization process.

Because we associate τ₂ with relaxation along the ¹πσ* state, this time constant can be compared to our independent H-atom TR-KER results discussed in Section A. The time constants are in agreement within the reported error, although the TR-KER value is somewhat longer. While it is certainly possible that this difference corresponds to the additional time required for the formation of the fully separated photoproduct, another possible explanation is discussed below. Likewise, the separate long-range TR-PES scan from which τ₃ derives is described very well with these same time constants (see Fig. 7).

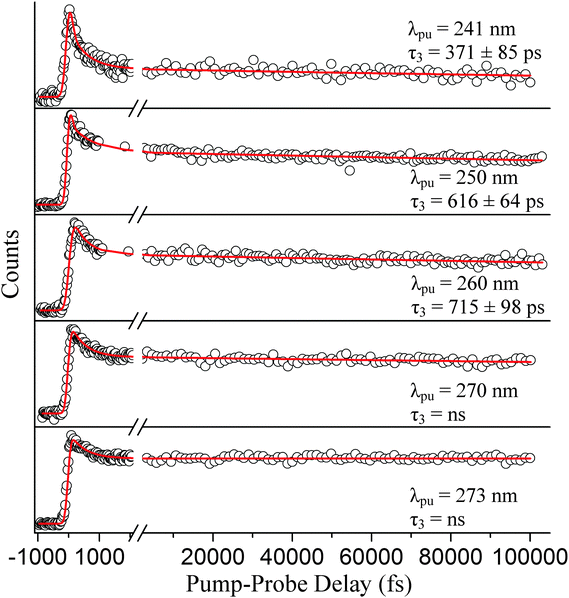Fig. 7 TR-PES signal (○) for the long-range scans and fits (red) integrated over all photoelectron kinetic energies are shown to complement the short-range scans displayed in Fig. 5. The pump wavelengths here (from top to bottom) are 241, 250, 260, 270, and 273 nm. Relaxation times associated with the ¹L_b → S₀ transition (τ₃) are also displayed in their respective graphs.

At a pump wavelength centered around 250 nm, three time constants associated with excited-state relaxation dynamics are gleaned: τ₁ < 100 fs, τ₂ = 413 ± 144 fs, and τ₃ = 616 ± 64 ps. Increasing the pump wavelength from 241 nm to 250 nm did not reveal any pronounced changes in τ₁ or the lifetime associated with ¹πσ*-state activity (τ₂); however, a significant increase in decay time is detected for the ¹L_b-state (τ₃) signal, which is nearly double that at 241 nm. Our result for τ₁ is consistent with that obtained by Townsend et al.,⁸ who report a value of <100 fs at a pump wavelength of 249 nm, and Longarte et al., who report 22 ± 9 fs at a pump wavelength of 248 nm. However, a noticeable difference between our result for τ₂ and Townsend et al. is now made manifest. At essentially the same wavelengths as those applied here, Townsend et al. establish a lifetime of approximately 700 fs for the ¹πσ* state, which is much different than our τ₂ = 413 ± 144 fs. Our results are more comparable to those reported by Longarte et al., who report a ¹πσ*-state lifetime of 460 ± 145 fs. Unlike the case at 241 nm, τ₂ extracted via TR-PES does not corroborate the rise time τ₂₅₀ = 671 ± 84 fs from the previously discussed TR-KER experiments in Section A. We believe the reason for this difference can be linked to the loss of the ionization window between the downward curving ¹πσ*-state potential energy profile^8,17,19 and the upward curving ionic-state potential as the N–H bond length increases,⁶⁰ an issue that has previously been raised in the literature for the case of adenine.⁶¹ Indirect measurements such as TR-KER are unaffected by this issue since the probe process relies on the photoionization of H-atoms. It is therefore our conclusion that the TR-KER results presented in Section A are more representative of the actual relaxation times associated with ¹πσ* decay. Once the ¹πσ*/S₀ CI has been passed, dissociation occurs quickly on the repulsive potential energy curve. Furthermore, the large discrepancy between TR-KER and TR-PES time constants suggests that a significant portion of the dynamics occur at extended N–H distances, most likely in the vicinity of the CI, where they are inaccessible to direct photoionization at the utilized probe wavelength.

It should also be noted that there is a substantial disagreement between our τ₃ and the long-lived component measured by Townsend et al.⁸ These authors report a long-lived component with an associated lifetime of 350 ps, nearly half our value, following excitation at 249 nm. One possible reason for this disparity is the maximum scanning range beyond time-zero. In principle, the extracted time constants should be independent of the selected scanning range, but it is our experience that values can vary significantly due to the presence of noise in real data sets. Townsend et al.'s scan range extends to approximately 50 ps; whereas, this investigation scans slightly over double that range to extract the long-lived contribution to the signal (see Fig. 7). The work of Longarte et al.⁵⁹ reports a value in the picosecond range; however, it is unclear where exactly in the picosecond range their value is located. It should also be noted that none of the studies observe the long-lived signal levels decaying back to a zero baseline. Further insight regarding this disparity may be gleaned by continuing this discussion following the reports at the remaining excitation wavelengths. As such, we will return to this comparison shortly.

Following excitation at 260 nm, time constants of τ₁ < 100 fs, τ₂ = 505 ± 100 fs, and τ₃ = 715 ± 98 ps are acquired. Again, no considerable change in τ₁ or τ₂ is observed in this case, but in comparison to Section A the difference between the TR-KER and TR-PES ¹πσ* time constants increases further. Longarte et al.⁵⁹ report time constants of 22 ± 9 fs and 370 ± 110 fs for activity correlated with ¹L_a-state and ¹πσ*-state deactivation, respectively, following excitation at the same pump wavelength. However, another dissimilarity presents itself between our τ₃ = 715 ± 98 ps and the work of Longarte et al. Scanning nearly 140 ps beyond time-zero, their work reports a lifetime of 7 ± 2 ns associated with ¹L_b-state relaxation. To address this discrepancy, a separate scan (not presented here) extending beyond 200 ps was conducted, and the extracted decay constants verify the values reported here. The reason for this difference is not clear but, as mentioned earlier, could be related to the scanning range or the multiphoton nature of the ionization process employed by Longarte et al. Further picosecond or nanosecond time-resolved studies may aspire to investigate the time constants associated with ¹L_b-state relaxation following excitation at 260 nm to verify these claims.

Following excitation at 270 nm, only two time constants are needed to accurately fit the data set: τ₁ = 272 ± 83 fs and τ₃ = ns. Likewise at 273 nm, two time constants associated with excited-state dynamics are extracted: τ₁ = 276 ± 142 fs and τ₃ = ns. To our knowledge, no prior work associates similar time constants to ¹L_a-state relaxation for excitation close to the origin. However, the aforementioned discussion regarding ionization correlations strongly supports this assignment. Similar to our previous scans, the separate long-range scan is also accurately fitted with these short-range time constants (see Fig. 7). These results challenge the assignment of an ultrafast time constant (i.e., <100 fs) to ¹L_a-state relaxation by Townsend et al. and Longarte et al. We refer to the potential energy profiles calculated along ring deformation coordinates by Giussani et al.³⁵ for further discussion. Their calculation positions the ¹L_a/¹L_b CI in very close vicinity to the ¹L_a-state minimum which, at first sight, seems to strongly support an ultrafast transition. However, Giussani et al. report theoretical ¹L_a- and ¹L_b-state minima that are lower than the experimental onsets according to ref. 32, 33 and 55 by approximately 0.14 and 0.26 eV, respectively. If these same curves are shifted upward to the known experimental values, the separation between the CI and the ¹L_a-state minimum increases and our slightly longer τ₁ constants are certainly not unreasonable.

As far as this experimental work is concerned, there is no apparent contribution originating from the ¹πσ* state at 270 and 273 nm. The fact that a third excited-state relaxation channel is not necessary to accurately fit the short-range scans presented in Fig. 5 or the long-range scans in Fig. 7 supports this claim. As mentioned earlier, the number of channels chosen at each pump wavelength is based on the necessity to obtain an accurate fit. For instance, when the data acquired at 241, 250, and 260 nm is fitted with only two excited-state channels, the residual signal clearly displays unaccounted for contributions to the overall signal, often in the ultrafast region of the spectrum. This is not the case at 270 and 273 nm where both data sets are accurately described using only two excited-state channels. To visualize these effects, Fig. 8 selectively displays the residuals for the 260 and 270 nm TR-PES spectra when fit with only two pump–probe channels. We also note, that forcing an additional, unnecessary channel into the 270 and 273 nm fits leads to a spectral deconvolution into features that are incompatible with our general analysis (i.e., ionization correlations and vibrational shifts are inexplicable).

Fig. 8 When fitted with only two excited-state channels, the residual signal following excitation at 260 nm (left) clearly displays unaccounted for signal, thus requiring the inclusion of a third pump–probe channel. However, the photoelectron signal acquired at 270 nm is adequately described using only two pump–probe channels (right).

The ultrafast electron diffraction results reported by Zewail and co-workers⁶² bolster this interpretation as well. In their experimental work, the authors conclude that the ¹πσ* state does not play a significant role in indole relaxation dynamics following excitation at 267 nm. This is in direct contrast with Townsend et al.,⁸ who compare their results taken at 249 nm, where the ¹πσ* state is actively involved in the relaxation process, and 273 nm to arrive at the conclusion that the ¹πσ* state is participating in the relaxation process at 273 nm. The previously discussed TR-KER results (Section A) provide no evidence for ¹πσ*-state activity at 273 nm either; however, the TR-KER measurements only identify the onset of H-atom dissociation from the N–H moiety along the ¹πσ* state, which may differ from the onset of ¹πσ* → S₀ relaxation. We do acknowledge that, in principle, it is possible for the ¹πσ* state to actively participate in the relaxation process at these longer wavelengths without breaking the N–H bond, but there is no experimental evidence in this current study to suggest such an involvement following excitation at 270 and 273 nm.

Following excitation at 282 nm, the inclusion of a τ₃ = ∞ and an approximately 0 fs component (Gaussian shown as the blue-dashed line) is necessary to accurately fit the data set. The channel associated with τ₃ essentially resembles a step function. τ₃ is highly consistent with the results reported by Longarte et al.⁵⁹ following excitation at 283 nm. However, these authors do not observe the 0 fs relaxation time that we associate with nonresonant signal/motion out of the Franck–Condon region nor do they see signs of such a process when pumping at 278 nm. Instead, Longarte et al.'s TR-IY results at 278 nm contain an exponentially rising signal that they relate to an increase in the overall ionization cross-section.

We now return to the discussion regarding the ¹L_b-state relaxation times. As mentioned earlier, the extracted time constant τ₃ following excitation at 250 nm disagrees with Townsend et al.⁸ by nearly a factor of two. Likewise, τ₃ differs quite significantly with the work of Longarte et al.⁵⁹ following excitation at 260 nm. Yet even with these disagreements, the nanosecond decay times associated with ¹L_b-state activity following excitation at 270 and 273 nm broadly agree with both Townsend et al., who utilize a 273 nm pump, and Longarte et al., who employ pump wavelengths set at 269 and 272.5 nm. However, a strict comparison to our results is not possible because neither Townsend et al. nor Longarte et al. report the ¹L_b-state decay values at these wavelengths, just orders of magnitude or an infinite decay relative to the scanned region. One possible reason, as suggested earlier, for the discrepancies at 250 and 260 nm is the difference in observed pump–probe delay ranges. We simply note the observed trend among our obtained values to bolster these results. According to our study, the ¹L_b state becomes longer lived as the excitation energy decreases—transitioning from a τ₃ = 371 ± 85 ps lifetime at 241 nm to the nanosecond relaxation time observed at 273 nm. This trend is also consistent with our previous work at 201 nm, where an ¹L_b-state lifetime of τ₃ = 23 ± 5 ps is reported.¹¹

Conclusions

Three pump–probe spectroscopic experimental techniques were utilized to study the relaxation dynamics of indole in the gas phase at various excitation wavelengths. The first, TR-IY, revealed negligible excited-state fragmentation other than the N–H dissociation for shorter excitation wavelengths. The second, TR-KER, afforded an analysis of the bimodal, steady-state H-atom kinetic energy spectra. High kinetic energy H-atoms associated with relaxation along the ¹πσ* pathway began emanating from the N–H moiety in the mid- to low-260 nm range, which is in strong agreement with the high resolution work of Ashfold et al.¹⁰ The lack of high kinetic energy H-atoms at longer wavelengths than indicated implies insufficient energy to initiate H-atom dissociation. However, for pump wavelengths centered at 241, 250, and 260 nm, the ¹πσ* relaxation times exhibited a distinct trend of increasing from 515 ± 63 fs to 932 ± 91 fs. This may be indicative of a potential energy barrier existing along the ¹πσ* relaxation pathway as predicted by ab initio calculations,^8,19 but an alternative explanation is proposed below.

These results were complemented with a series of TR-PES studies at 241, 250, 260, 270, 273, and 282 nm. The ¹L_a-state contributions exhibited ultrafast decay times at the shorter wavelengths and time constants of a couple hundred femtoseconds at 270 and 273 nm. No apparent contribution from the ¹L_a state is observed when exciting just above the ¹L_b-state onset at 282 nm. Time constants extracted from the ¹L_b signal contributions exhibited a dependence on pump wavelength: increasing from 371 ± 85 ps to the nanosecond range. In agreement with the results reported by Longarte et al., all ¹πσ*-state relaxation times were ∼450 fs. This result is intriguing in light of the systematic increase in lifetimes observed with TR-KER toward longer excitation wavelengths. We attribute this discrepancy to loss of the ionization window in the TR-PES measurement caused by the downward curving ¹πσ* potential energy curve and the upward trend of the ionic-state potential energy profiles. Moreover, this leads to the notion that motion in the vicinity of the ¹πσ*/S₀ CI, at extended N–H distances, accounts for a significant portion of the relaxation dynamics.

As far as this experimental work is concerned, there is no evidence of ¹πσ*-state involvement in the indole relaxation process following excitation at 270 and 273 nm—in agreement with the ultrafast electron diffraction work of Zewail and co-workers.⁶²

Acknowledgements

This work was supported by the University of Georgia Provosts Faculty Research Grant and the National Science Foundation grant# NSF-CHE-1362237. The authors are also extremely grateful to Mr. D. R. Grimes and Mrs. Patricia Grimes for supporting this work through the Grimes Family Distinguished Graduate Fellowship Award, to the UGA Center for Undergraduate Research Opportunities (CURO) for supporting this work through the CURO Summer Fellowship program, and to Dr. Justin M. Turney for his help regarding theoretical aspects of the indole photophysics.

Notes and references

1. P. Meredith, B. J. Powell, J. Riesz, S. P. Nighswander-Rempel, M. R. Pederson and E. G. Moore, Soft Matter, 2006, 2, 37.
2. P. Meredith and T. Sarna, Pigm. Cell Res., 2006, 19, 572.
3. S. J. Harris, D. Murdock, Y. Zhang, T. A. A. Oliver, M. P. Grubb, A. J. Orr-Ewing, G. M. Greetham, I. P. Clark, M. Towrie, S. E. Bradforth and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2013, 15, 6567.
4. Y. Zhang, T. A. A. Oliver, M. N. R. Ashfold and S. E. Bradforth, Faraday Discuss., 2012, 157, 141.
5. D. Murdock, S. J. Harris, T. N. V. Karsili, G. M. Greetham, I. P. Clark, M. Towrie, A. J. Orr-Ewing and M. N. R. Ashfold, J. Phys. Chem. Lett., 2012, 3, 3715.
6. T. A. A. Oliver, Y. Zhang, M. N. R. Ashfold and S. E. Bradforth, Faraday Discuss., 2011, 150, 439.
7. F. F. Crim, Faraday Discuss., 2012, 157, 9.
8. R. Livingstone, O. Schalk, A. E. Boguslavskiy, G. R. Wu, L. T. Bergendahl, A. Stolow, M. J. Paterson and D. Townsend, J. Chem. Phys., 2011, 135, 194307.
9. A. Iqbal and V. G. Stavros, J. Phys. Chem. A, 2010, 114, 68.
10. M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2006, 8, 2610.
11. T. J. Godfrey, H. Yu and S. Ullrich, J. Chem. Phys., 2014, 141, 044314.
12. H. Lami, J. Chem. Phys., 1977, 67, 3274.
13. H. Lami, Chem. Phys. Lett., 1977, 48, 447.
14. N. A. Borisevich and T. F. Raichuyonok, Dokl. Phys., 2007, 52, 405.
15. J. R. Platt, J. Chem. Phys., 1949, 17, 484.
16. M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218.
17. A. L. Sobolewski and W. G. Domcke, J. Phys. Chem. A, 2007, 111, 11725.
18. M. F. Lin, C. M. Tseng, Y. T. Lee and C. K. Ni, J. Chem. Phys., 2005, 123, 124303.
19. A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 1999, 315, 293.
20. G. A. Bickel, D. R. Demmer, E. A. Outhouse and S. C. Wallace, J. Chem. Phys., 1989, 91, 6013.
21. G. Berden, W. L. Meerts and E. Jalviste, J. Chem. Phys., 1995, 103, 9596.
22. J. Kupper, D. W. Pratt, W. L. Meerts, C. Brand, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4980.
23. T. L. O. Barstis, L. I. Grace, T. M. Dunn and D. M. Lubman, J. Phys. Chem., 1993, 97, 5820.
24. P. R. Callis, J. T. Vivian and L. S. Slater, Chem. Phys. Lett., 1995, 244, 53.
25. J. Hager and S. C. Wallace, J. Phys. Chem., 1983, 87, 2121.
26. D. M. Sammeth, S. X. Yan, L. H. Spangler and P. R. Callis, J. Phys. Chem., 1990, 94, 7340.
27. R. Bersohn, U. Even and J. Jortner, J. Chem. Phys., 1984, 80, 1050.
28. J. R. Cable, J. Chem. Phys., 1990, 92, 1627.
29. J. W. Hager, D. R. Demmer and S. C. Wallace, J. Phys. Chem., 1987, 91, 1375.
30. J. M. Hollas, Spectrochim. Acta, 1963, 19, 753.
31. Y. Nibu, H. Abe, N. Mikami and M. Ito, J. Phys. Chem., 1983, 87, 3898.
32. B. J. Fender, D. M. Sammeth and P. R. Callis, Chem. Phys. Lett., 1995, 239, 31.
33. V. A. Povedailo and D. L. Yakovlev, J. Appl. Spectrosc., 2008, 75, 336.
34. C. Brand, J. Kupper, D. W. Pratt, W. L. Meerts, D. Krugler, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4968.
35. A. Giussani, M. Merchan, D. Roca-Sanjuan and R. Lindh, J. Chem. Theory Comput., 2011, 7, 4088.
36. H. Lippert, H. H. Ritze, I. V. Hertel and W. Radloff, Chem. Phys. Lett., 2004, 398, 526.
37. N. L. Evans, H. Yu, G. M. Roberts, V. G. Stavros and S. Ullrich, Phys. Chem. Chem. Phys., 2012, 14, 10401.
38. N. L. Evans and S. Ullrich, J. Phys. Chem. A, 2010, 114, 11225.
39. P. Kruit and F. H. Read, J. Phys. E: Sci. Instrum., 1983, 16, 313.
40. W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150.
41. D. M. P. Holland, M. A. MacDonald, M. A. Hayes, P. Baltzer, B. Wannberg, M. Lundqvist, L. Karlsson and W. von Niessen, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 3091.
42. R. Locht, K. Hottmann, G. Hagenow, W. Denzer and H. Baumgartel, Chem. Phys. Lett., 1992, 190, 124.
43. L. Serrano-Andrés and B. O. Roos, J. Am. Chem. Soc., 1996, 118, 185.
44. A. C. Borin and L. Serrano-Andrés, Chem. Phys., 2000, 262, 253.
45. J. Catalan, P. Perez and A. U. Acuna, J. Mol. Struct., 1986, 142, 179.
46. L. N. Domelsmith, L. L. Munchausen and K. N. Houk, J. Am. Chem. Soc., 1977, 99, 4311.
47. J. H. D. Eland, Int. J. Mass Spectrom. Ion Phys., 1969, 2, 471.
48. L. J. Dolby, G. Hanson and T. Koenig, J. Org. Chem., 1976, 41, 3537.
49. T. A. A. Oliver, G. A. King and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2011, 13, 14646.
50. B. Valeur and G. Weber, Photochem. Photobiol., 1977, 25, 441.
51. Y. Yamamoto and J. Tanaka, Bull. Chem. Soc. Jpn., 1972, 45, 1362.
52. M. R. Eftink, L. A. Selvidge, P. R. Callis and A. A. Rehms, J. Phys. Chem., 1990, 94, 3469.
53. R. L. Rich, Y. Chen, D. Neven, M. Négrerie, F. Gai and J. W. Petrich, J. Phys. Chem., 1993, 97, 1781.
54. E. Jalviste and N. Ohta, J. Chem. Phys., 2004, 121, 4730.
55. B. C. Dian, A. Longarte and T. S. Zwier, J. Chem. Phys., 2003, 118, 2696.
56. P. R. Callis, J. Chem. Phys., 1991, 95, 4230.
57. R. Montero, A. P. Conde, A. Longarte and F. Castaño, ChemPhysChem, 2010, 11, 3420.
58. V. Ovejas, M. Fernández-Fernández, R. Montero, F. Castaño and A. Longarte, J. Phys. Chem. Lett., 2013, 4, 1928.
59. R. Montero, A. P. Conde, V. Ovejas, F. Castano and A. Longarte, J. Phys. Chem. A, 2012, 116, 2698.
60. J. M. Turney, personal communication.
61. M. Barbatti and S. Ullrich, Phys. Chem. Chem. Phys., 2011, 13, 15492.
62. S. T. Park, A. Gahlmann, Y. He, J. S. Feenstra and A. H. Zewail, Angew. Chem., Int. Ed., 2008, 47, 9496.

---