Donor–anion interactions at the charge localization and charge ordering transitions of (TMTTF)₂AsF₆ probed by NEXAFS

Abstract

High-resolution near-edge X-ray absorption fine structure (NEXAFS) measurements at the As M-edge, F K-edge and S L-edge of the Fabre salt (TMTTF)₂AsF₆ were performed from room temperature (RT) to 90 K, allowing to reach the charge localization regime below T_ρ ≈ 230 K and to cross the charge ordering (CO) transition at T_CO ≈ 102 K. The F K-edge and S L-edge spectra exhibit several transitions which have been indexed on the basis of first-principles DFT calculations. Upon cooling from RT significant energy shifts up to +0.8 eV and −0.4 eV were observed in transitions exhibited by the F 1s and S 2p spectra respectively, while the As 3p doublet does not show a significant shift. Opposite energy shifts found in the F 1s and S 2p spectra reflect substantial thermal changes in the electronic environment of F atoms of the anion and S atoms of TMTTF. The changes found around the charge localization crossover suggest an increase of the participation of the S d orbitals in the empty states of TMTTF as well as an increase of the strength of donor⋯anion interactions. A new F 1s pre-edge signal detected upon entry into the CO phase is a clear fingerprint of the symmetry breaking occurring at T_CO. We propose that this new transition is caused by a substantial mixing between the HOMO of the AsF₆⁻ anion and the unoccupied part of the TMTTF HOMO conduction band. Analysis of the whole spectra also suggests that the loss of the inversion symmetry associated with the CO is due to an anion displacement increasing the strength of S⋯F interactions. Our data show unambiguously that anions are not, as previously assumed, innocent spectators during the electronic modifications experienced by the Fabre salts upon cooling. In particular the interpretation of the spectra pointing out a thermally dependent mixing of anion wave functions with those of the TMTTF chains demonstrates for the first time the importance of anion–donor interactions.

---

I. Introduction

Fabre and Bechgaard salts, (TMTTF)₂X and (TMTSF)₂X respectively, where TMTT(S)F is tetra-methyl-tetra-thia(-selena)-fulvalene and X = PF₆, AsF₆, ClO₄, NO₃, …, are among the most typical examples of novel organic solids whose electronic properties can be tuned by changing the TMTTF/TMTSF nature of the donor, the monovalent anion X or by applying an external parameter such as the pressure.¹ Due to the transfer of one electron from pairs of donors to the anions these salts are quarter filled quasi-one dimensional (1D) metals. While (TMTSF)₂X salts are metallic in a large temperature range above a low temperature metal–insulator transition involving either the spin or the anion orientation degrees of freedom, (TMTTF)₂X salts exhibit a continuous electron localization upon cooling which manifests by the onset of an activated conductivity below T_ρ ∼ 200–250 K.² This effect reveals the presence of sizeable electron–electron repulsions³ which lead to the progressive localization of one hole per TMTTF dimer which is the basic unit of the 1D zig-zag donor stack (Fig. 1(a)). By increasing pressure the charge localization vanishes and the (TMTTF)₂X salts behave as the (TMTSF)₂X ones at ambient pressure.¹ Under higher pressure both series of organic salts become superconductors with T_s ∼ 1 K.

Fig. 1 (a) Centro-symmetric P1̄ structure of TMTTF₂AsF₆ projected along the a stacking direction. Atoms are labelled by different colors (C in black, S in yellow, H of methyl groups in blue and F in orange). The short S⋯F contact distances are indicated. (b) Optical image of one (TMTTF)₂AsF₆ single crystal studied (a and b directions of the platelet are respectively along the long and short directions; the normal to the surface of the platelet is the c* direction).

The charge localization phenomenon of Mott-dimer type³ revealed by the manifestation of an activated electrical conductivity in (TMTTF)₂X below T_ρ does not affect the spin-degrees of freedom. Since the spin susceptibility is not modified at T_ρ² a progressive spin-charge decoupling occurs upon cooling. However the assumed enhancement of localization of the 1D carrier wave function upon cooling has not been really probed at a microscopic level up to now. We shall see below that a convenient tool towards this end is provided by NEXAFS.

During the last decade it has been experimentally observed that electron–electron repulsions induce even more drastic effects well below T_ρ in the (TMTTF)₂X series, consisting in a charge disproportionation between the two TMTTF molecules of each dimer.^4,5 This effect occurs below a well-defined symmetry breaking 2nd order phase transition at T_CO. At this critical temperature a so-called charge ordering (CO) transition breaking all the inversion centers of the high temperature P1̄ structure induces electronic ferroelectricity.⁶ An enhancement of the activation energy of the electrical conductivity, already detected long time ago,⁷ goes together with the CO phenomena. In principle the loss of inversion symmetry should come with a lattice modification which is quite difficult to detect in the Fabre salts because the charge disproportionation between the two TMTTF's forming the dimer of the repeat unit does not change the volume of the unit cell. Only a weak change of intensity of some Bragg reflections has been detected at T_CO in (TMTTF)₂PF₆.⁸ In parallel, high resolution lattice thermal expansion measurements in the PF₆, AsF₆ and SbF₆ salts were able to reveal the presence of a well-defined thermodynamic anomaly at T_CO.^9,10 This anomaly is especially marked for measurements performed in the c* direction which is indeed the direction along which the TMTTF and anion layers alternate (Fig. 1(a)). This feature, together with the observation that T_CO strongly varies with the nature of the anion,¹¹ suggests that anions are certainly involved in the CO process. In this respect the recent detection of a shift to higher binding energy of the F 1s HAXPES core level spectra at the CO transition of (TMTTF)₂SbF₆¹² provides evidence for a cooperative shift of SbF₆ towards the hole rich TMTTF. However, the direction of this shift is unknown. By considering the nature of the cavity where each anion is located (see Fig. 1(a)), the anion shift can occur either toward the S atoms or towards some methyl groups of neighboring TMTTFs.^9,13,14 This shift, which shortens either the F⋯S or F⋯H contacts, should modify the electronic interactions between the anion and the TMTTF donor, and thus the mixing of the corresponding electronic wave functions.

All experimental methods previously used to probe physical properties of the Fabre salts do not provide direct insight into the modification of the electronic structure. Core-level absorption spectroscopy in the soft X-ray range is a useful tool for such studies due to its atomic selectivity and the rather large probing depth of the technique. The depth probed by detecting the sample current (total yield mode) in near edge X-ray absorption fine structure (NEXAFS) spectroscopy in the soft X-ray regime is about 3–5 nm for metals or semiconductors and slightly larger for insulators. This is several times the unit cell length of ∼1 nm in the Fabre salts.

On the other hand, one expects that new spectroscopic information associated with the previously mentioned electronic and structural processes should occur in the Fabre salts upon cooling. Access to specific atoms by the NEXAFS technique allows identifying and evaluating more precisely the charge carrier localization phenomenon below T_ρ as well as charge disproportion occurring in the CO phase. Unfortunately, information concerning the change of electronic structure of organic materials accompanying electronic phase transitions is sparse in the literature. In most cases non-ambiguous spectroscopic signatures are missing. This is partly caused by difficulties in performing photoemission¹⁵ or NEXAFS experiments (very good temperature control, limitation in resolution, etc.) and by the instability of the sample surface under irradiation. A first step in this direction was made by a NEXAFS study of TTF–TCNQ which made possible to relate the deformation of the TCNQ stack, as a result of the Peierls instability, with the change of the electronic structure of the empty molecular states of the acceptor.¹⁶ We have also observed similar changes in earlier work on novel donor–acceptor mixed phases.¹⁷ Here we use NEXAFS spectroscopy to study (TMTTF)₂AsF₆, which exhibits charge localization at T_ρ ≈ 230 K⁷ followed by a CO transition at T_CO ≈ 102 K.^4–7,18 Following our earlier works the purpose of the present study is to clarify the role of both anion and donor molecular orbitals in the charge localization process and to determine how the charge is re-distributed upon entering in the CO phase by probing the NEXAFS spectra of As M-edge, F K-edge and S L-edge of this system.

II. Methods

A. Sample preparation

(TMTTF)₂AsF₆ single crystals, similar to those used in ref. 18, were grown using the standard THF (tetrahydrofuran) procedure. Needle-shaped crystals with typical dimensions of 1.4 × 0.5 × 0.1 mm³ were obtained by this technique. A typical single crystal used for the NEXAFS study is shown in Fig. 1(b).

B. Experimental details

Two (TMTTF)₂AsF₆ single crystals were studied at MAX II (beamline I1011) by means of NEXAFS spectroscopy.¹⁹ The end-station consists of preparation and analytical chambers. All measurements were performed in total electron yield mode. The energy range for such experiments is up to 1200 eV with an energy resolving power of around 5000 at the lowest used photon energies. All measurements were done at grazing incidence with the electric vector being oriented at 20° with respect to the surface normal (c* direction). The measurements were performed for the as-grown crystals, being glued onto copper sample plates using a strain-minimized soft two component glue based on 2-butoxyethyl acetate solution. The surface was inspected by optical microscopy prior to the measurement in order to exclude residues of glue on the surface.

Before starting each experiment at I1011 complete a calibration routine procedure of the beamline itself is done, detailed information about the beamline is included in ref. 19.

The Cu sample holder plate provides a good thermal conductivity between the object studied and the holder. The minimum temperature obtained during the experiment was 70 K, and controlled by a Lake Shore temperature controller. The cooling rate was about 1 K per minute in order to avoid deformation and thermal tension in the object.

Radiation damage was absolutely excluded. Optical microscopy images of the (TMTTF)₂AsF₆ single crystal, taken before and after radiation exposure, show no difference. The final microscopic inspection gave evidence that no visible radiation damage occurred. Our earlier studies revealed that excessive irradiation can lead to transparent spots indicating loss of metallicity. NEXAFS spectra were taken at different sample positions and the results showed identical spectral features. This manipulation was possible due to the small beam size (1 × 0.2 mm²). Samples did not need to be cleaned under ultra-high vacuum conditions since the topmost layer of the as-grown samples was chemically intact.

C. Computational details

The present calculations were carried out using a numerical atomic orbitals density functional theory (DFT) approach^20,21 which was developed for efficient calculations in large systems and implemented in the SIESTA code.^22–24 We have used the generalized gradient approximation (GGA) to DFT and, in particular, the functional of Perdew, Burke and Ernzerhof.²⁵ Only the valence electrons are considered in the calculation, with the core being replaced by norm-conserving scalar relativistic pseudopotentials²⁶ factorized in the Kleinman–Bylander form.²⁷ We have used a split-valence double-ζ basis set including polarization orbitals with an energy shift of 10 meV for all atoms.²⁸ The energy cutoff of the real space integration mesh was 250 Ry. The Brillouin zone was sampled using a grid of (20 × 20 × 10) k-points²⁹ in the irreducible part of the Brillouin zone. Calculations for the “isolated” AsF₆⁻ and TMTTF were carried out exactly as for the TMTTF₂AsF₆ solid using an isolated species within a periodic box of 30 × 30 × 30 ų. In the case of AsF₆⁻ a compensating uniformly distributed background charge amounting to one positive charge per unit cell was included. The experimental 4 K crystal structure of Granier et al.^30a was used for the calculations. Qualitatively similar results are obtained when the room temperature structure^30b is used except for the fact that the unoccupied levels of the anion are higher in energy because of a poor description of the anion in this structure. Since this fact shifts the levels of the anion with respect to those of the donor, the 4 K structure provides a more reasonable description of the electronic structure. Note that this structure is really an average structure. Since the inversion center relating the two TMTTF molecules was kept in the structural determination, the fine structural features due to the CO or Spin-Peierls are absent of this structure. Consequently, this structure is the more convenient one for the purposes of the discussion reported in the present work.

III. Results

The NEXAFS technique does not only provide an access to unoccupied electronic states but is also a sensitive function of the chemical surrounding of each atom probed. In Section A we report the study of the anion by collecting the arsenic M- and fluorine K-edge spectra. In Section B we report the study of the TTF core of the donor by collecting the sulfur L-egde spectra (TMTTF is a TTF molecule with its four terminal H atoms substituted by methyl groups).

A. Arsenic and fluorine M- and K-edge NEXAFS spectra

The results obtained for the arsenic M-edge and fluorine K-edge spectra of the AsF₆⁻ anion are shown in Fig. 2 and 3, respectively. All spectra were normalized to the time-dependent variation of the synchrotron radiation intensity and de-convoluted using a multi-fit peak routine. All fits were performed using the commercial UNIFIT 2013 program.^30c The background for the XAS (X-ray absorption spectroscopy) is quite different from just simple XPS (X-ray photoemission spectroscopy) case. It consists of a 3rd order polynomial with Shirley background included. Both figures show spectra upon cooling from room temperature (RT) down to 90 K.

Fig. 2 As 3p NEXAFS spectra of (TMTTF)₂AsF₆ measured at different temperatures. The peak positions shown by the vertical lines are independent of the temperature.

Fig. 3 (a) F 1s NEXAFS spectra of (TMTTF)₂AsF₆ measured at different temperatures. Each spectrum is de-convoluted using a multi-fit peak routine. In the spectrum taken at 90 K, the additional transition at 681 eV is magnified 20 times. (b) Relative shifts of the peak maxima upon cooling with respect to their RT positions. (c) Thermal dependence of the relative intensities scaled to 1 at 300 K for sake of direct comparison of the trends. Blue, pink, green and red colors correspond to peaks 1, 2, 3 and 4 respectively.

Due to the low intensities and low cross section at the As M-edge, the study of this edge is hampered by an enhanced background contribution. However, the intensity redistribution inside the As 3p_1/2/3p_3/2 fine-structure doublet is clearly visible. Upon crossing T_ρ and the CO transition, respectively, the relative intensity of As 3p_3/2 becomes significantly smaller with respect to the intensity of the As 3p_1/2 transition. However the positions of the As 3p_1/2 and 3p_3/2 peaks remain identical for all temperatures. The change in intensity could reflect a continuous redistribution of charge between the As and the neighboring F atoms upon cooling, while the As atom keeps the same environment. NMR measurements³¹ on the As site show that the central part of the AsF₆⁻ anion feels the CO transition through a sizeable reduction of the electric field gradient fluctuations.¹⁴

Fig. 3(a) presents F K-edge spectra at different temperatures. The signal is clearly composed of four peaks labelled 1 to 4 with increasing photon energy. The de-convolution of the RT spectra into four peaks gives maxima located at 684.6, 687.1, 691.2 and 697.15 eV, respectively.

The number of Gaussian functions included in all fits was chosen according to experimental work in the literature connected with the F 1s and S 2p signals. The position of the first and 4th resonance is clearly fixed and cannot be varied. The positions of the other 2 resonances were automatically calculated (several 1000 iterations) by the program itself until the best overlap of calculated and experimental spectra.

The error bars in the figures show the maximum possible systematic error that can occur during the fitting process by the computer program (UNIFIT 2013), including the effect of the correct choice of the baseline.

These four peaks will be assigned in Section IV.A on the basis of DFT calculations. The plot of the maxima positions vs. temperature in Fig. 3(b) reveals that these four peaks shift to higher photon energy upon cooling. The total shift ranges from +0.2 to +0.85 eV for peaks 1 and 2 respectively. The total shift of peak 1 is five times smaller than the total shift of peak 2. The fact that the shift of peak 1 is smaller, is clearly visible in Fig. 3(a) where the minimum between peaks 1 and 2 becomes more pronounced upon cooling. For all the peaks the shift towards higher photon energies exhibits a steep increase upon cooling between RT and 210 K. In the charge-localization regime and the CO phase the shift of peaks 2 and 4 still sizably increases, while the shift of peaks 1 and 3 slowly decreases.

Relative changes of intensity (with respect to the RT value) of the four de-convoluted signals, which are clearly apparent in Fig. 3(a), are quantified in Fig. 3(c). Because there is no change of the charge transfer between TMTTF and the AsF₆ anion upon cooling, we assume that at each temperature the sum of the four peak intensities of the F K-edge spectra remains equal to 1 (a similar procedure is applied for the S L-edge spectra, see part B). This was done in order to compare the evolution of the relative intensities during cooling on an identical scale. Then the thermal variations of the individual peaks intensity were scaled to the value of 1 at 300 K. The inspection of Fig. 3(a) shows that peak 2 strongly increases by 55% between RT and 210 K, i.e. upon entry in the charge-localization regime, then its intensity drops upon cooling. The intensity variation of the other peaks remains less than 20%. The peak intensities at 90 K are quite uncertain due to the irregular baseline.

The overall inspection of Fig. 3 shows that the charge localization crossover occurring around T_ρ ≈ 230 K significantly manifests in the F K-edge NEXAFS spectra. A more quantitative analysis of the thermal dependence of peak shifts and peak intensities will be the object of Section IV.B.

The appearance of a new peak around 681 eV in the spectrum taken at 90 K (Fig. 3(a)) is very surprising. This new pre-edge peak, located ∼4 eV below peak 1 must be associated to a new spectroscopic transition connected with the symmetry breaking CO phase transition. Its origin will be discussed in Section IV.C.

B. Sulfur L-edge NEXAFS

Fig. 4 shows NEXAFS spectra taken at the sulfur L-egde of TMTTF. The deconvolution of the S 2p NEXAFS spectra gives four prominent resonances observed at 164.3, 165.5, 166.6 and 167.9 eV photon energies at RT. The empty TMTTF molecular orbitals involved in these four transitions, explicitly indicated in part (a) of the figure, are assigned in Section IV.A on the basis of the DFT calculations reported below. The colored curves are the results of a least-squares fit with four Gaussian functions. These de-convoluted signals are labelled 1, 2, 3 and 4 with increasing photon energy. Fig. 4b reports the relative shift of the corresponding maxima of individual signals and Fig. 4c gives their relative intensity as a function of temperature. Note that the error bars are quite important (especially for the intensities) because the four signals strongly overlap. This is especially true for the peak 4 of weaker intensity.

Fig. 4 (a) S 2p NEXAFS spectra of (TMTTF)₂AsF₆ measured at different temperatures. Each spectrum is de-convoluted using a multi-fit peak routine. (b) Relative shifts of the peak maxima upon cooling with respect to their RT positions. (c) Thermal dependence of the relative intensities scaled to 1 at 300 K for sake of direct comparison of the trends. Green, red, blue and pink colors correspond to peaks 1, 2, 3 and 4 respectively. In panel (a) the peaks are also labelled by the empty TMTTF orbitals involved in the transitions.

Fig. 4b shows that all S 2p transitions exhibit a negative shift upon cooling. Upon entering into the CO phase all S 2p transitions still continue to shift to smaller photon energies. The sign of these shifts is of opposite sign as those of the F 1s spectra (Fig. 3b). From these opposite temperature variations and the absence of any peak shift in the As spectra we can exclude artifacts like sample charging effects and other drift effects. Relative changes of intensity (with respect to the RT value) which are visible in the spectra in panel (a) are quantified in panel (c). Upon approaching T_ρ the intensity of signal 2 shows a marked increase of 30% whereas the intensity of signal 1 drops by 20% (peaks 3 and 4 do not change significantly within error bars). Below T_ρ the intensity of peak 2 decreases while the intensity of peak 1 increases. The intensity of peak 3 does not change within experimental errors. Because of its weakness the “erratic” change of the intensity of peak 4 is not significant.

As found for the F K-edge, the charge localization crossover occurring around T_ρ ≈ 230 K also manifests in the S L-edge NEXAFS spectra. A more quantitative analysis of the thermal dependence of peak shifts and peak intensities will be the object of Section IV.B.

C. Energy levels of TMTTF, AsF₆⁻ and (TMTTF)₂AsF₆

The NEXAFS transitions probe the unoccupied orbital structure which spatially overlaps with the initial-state orbital, in our case S 2p in the donor moiety and As 3p and F 1s in the counter-ion. Besides the orbital overlap, the matrix element of the photon operator sorts out the proper angular momenta via the dipole selection rules (Δl = ±1) and the polarization effects due to the orientation of the linearly polarized photon beam. The electric vector is oriented at 20° with respect to the surface normal, i.e. the transition dipole points essentially in the c* direction which is perpendicular to the (a, b) layers of TMTTF molecules (see Fig. 1(a)). Thus, in order to have some guidelines to understand the experimental results we carried out first-principles DFT calculations for metallic (TMTTF)₂AsF₆ compound as well as for the isolated anion AsF₆⁻ anion and the TMTTF donor.

The calculated HOMO (highest occupied molecular orbital), LUMO (lowest unoccupied molecular orbital) and the next six unoccupied molecular orbitals of TMTTF are shown in Fig. 5. The geometry used is the same as in the solid. The labels in parenthesis are those for an ideal TMTTF molecule with D_2h symmetry although in the crystal structure the molecule is slightly distorted. The energy values (in eV) relative to the energy of the HOMO are given in the figure. These orbitals are strongly related to those of TTF used in a previous study of the TTF–TCNQ NEXAFS spectra³² so that we shall not discuss them in detail here. Introduction of the four methyl substituents (to obtain the TMTTF molecule from the TTF one) do not strongly alter the nature and level ordering of these orbitals. The main difference lies in some reduction of the sulfur participation in the LUMO+1 and LUMO+2 orbitals and the order reversal between the LUMO+4 (b_3u) and LUMO+5 (b_2u) levels.

Fig. 5 TMTTF molecular orbitals relevant for the analysis of the NEXAFS spectra of (TMTTF)₂AsF₆. The symmetry labels are those appropriate for D_2h symmetry. Energy values (in eV) are given with respect to the HOMO.

The relevant orbitals of the AsF₆⁻ anion are shown in Fig. 6. Again, these orbitals are obtained using the geometry of the anion in the crystal structure of (TMTTF)₂AsF₆ at 4 K. The energy values (in eV) relative to the energy of the HOMO are given in the figure. In a perfect octahedral environment, the three HOMO, HOMO−1 and HOMO−2 levels would be a degenerate triplet. This is also the case for the three LUMO+1, LUMO+2 and LUMO+3 levels. The LUMO has as the major component, the As 4s orbital which mixes with some F 2p orbitals in an antibonding way. The LUMO+1, LUMO+2 and LUMO+3 levels are strongly antibonding levels composed of the p orbitals of both As and F. In contrast the HOMO orbitals are really nonbonding because there are no As orbitals of appropriate symmetry to mix into.

Fig. 6 AsF₆⁻ molecular orbitals relevant for the analysis of the NEXAFS spectra of (TMTTF)₂AsF₆. Energy values (in eV) are given with respect to the HOMO.

Let us now examine the calculated density of states (DOS) for (TMTTF)₂AsF₆. In Fig. 7a and b we report respectively the DFT DOS and the projections into the local (PDOS) S, C and F contributions. The projection into As orbitals is not shown because it does not add anything to what can be deduced from the F local projection shown in Fig. 7b. In these figures the molecular levels of an isolated TMTTF molecule are also shown. The energy of the LUMO and the corresponding band has been used to align the levels. As indicated in the DOS curve the projection corresponding to F exhibits a single peak practically at the same energy as the bottom part of the second peak of the unoccupied region of the DOS. This is the contribution of the AsF₆⁻ LUMO to the DOS. The next levels of the anion appear at energies higher than those of the figure, at 8.5 eV. However, whereas the contribution of the AsF₆⁻ LUMO is localized in a relatively narrow energy range, the contribution of the triplet LUMO+1/LUMO+2/LUMO+3 although centered and having the maxima at around 8.5 eV, broadens into a large energy range of approximately 8 eV (not shown in Fig. 7). This feature will turn out to be important for the analysis of the spectra and is easily understandable from the orbitals of Fig. 6. The LUMO is heavily based on the inner As s orbital and undergoes relatively weak interactions with the donor orbitals. However, the triplet LUMO+1/LUMO+2/LUMO+3 is more heavily based on the F 2p orbitals and thus experiences much stronger interactions with the neighboring TMTTF molecules and, consequently, the associated bands are very broad.

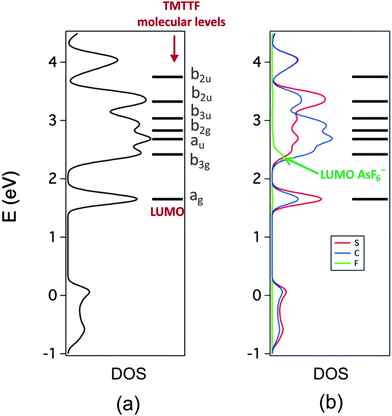Fig. 7 Total DOS (a) and local projections (PDOS) of the contributions of the S, C and F atoms (b) calculated for (TMTTF)₂AsF₆. The molecular energy levels of TMTTF are also included.

The C and S PDOS are further analyzed in Fig. 8a and b respectively where the contributions of the 2p_z and 3p_z orbitals, respectively, are also shown (note that we use a local coordinate system where the inner core of the TMTTF molecule lies in the xy plane). This is useful in separating the contributions of the σ- and π-type orbitals of the TMTTF molecules to the DOS. Note in Fig. 8a that for the region between 2 and 3 eV, when looking at the C contribution (full blue line) practically all the contribution is provided by these 2p_z orbitals (dotted blue line). This means that the three peaks in this region originate from the b_3g, a_u and b_2g π* TMTTF orbitals. The small difference between the two curves is due to the fact that the locally π-type orbitals of the CH₃ substituents were not included in this projection. It is clear from this figure that the HOMO contribution is also purely π. The large difference between the full and dotted blue lines reveals that the first peak associated to the TMTTF's LUMO and the first and two upper peaks of the empty DOS region originate from the σ*-type TMTTF molecular orbitals. Looking at the corresponding S curves of Fig. 8b brings additional and useful information. In the region of the π* orbitals between 2 and 3 eV, the two curves now differ noticeably. The reason is that in addition to the 3p_z orbitals there is a non-negligible participation of the d-type orbitals of S into these π* molecular orbitals. Because of the dipole selection rules, it is through such d-orbital participation that the sulfur contribution becomes so clearly visible in the S 2p spectra.

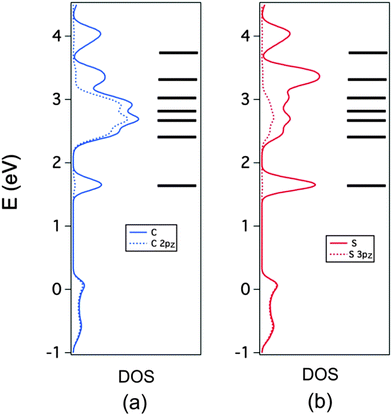Fig. 8 PDOS (full line) and π-type contribution (dotted line) for the C (a) and S (b) atoms in (TMTTF)₂AsF₆. The molecular energy levels of TMTTF are also included.

Consequently, the four different contributions of the S 2p spectra can be attributed (from lower to higher photon energy) to the TMTTF orbitals: σ*(a_g), [π*(b_3g), π*(a_u), π*(b_2g)], [σ*(b_3u), σ*(b_2u)], and σ*(b_2u). This assignment is very similar to that proposed for TMTTF₂ReO₄,³³ the only difference lying in the assignment of the two upper peaks. In the present case, when comparing the band structure and the DOS, it is clear that the upper peak originates from only two bands which are the in-phase and out-of-phase combinations of the upper b_2u TMTTF molecular orbital (there are two bands associated to this orbital because the unit cell contains two TMTTF donors). Thus the upper observed peak originates from this b_2u orbital. This is also consistent with the fact that the area of this peak is about half that of the next lower σ* peak in the DOS which we thus assign to the two σ*(b_3u), σ*(b_2u) orbitals. This assignment is confirmed with a fat-band analysis of the band structure.

The conclusion of our analysis of the unoccupied density of states of (TMTTF)₂AsF₆ is that after the two bands (remind that the repeat unit of (TMTTF)₂AsF₆ contains two TMTTF donors so that each level of TMTTF leads to two bands in the solid) originating from the LUMO of TMTTF (at about 1.7 eV) there is one band originating from the LUMO of AsF₆⁻ (at 2.3 eV), and then a group of six bands originating from the π* TMTTF levels (b_3g, a_u, and b_2g at 2.4–3.0 eV). The highest of these π* levels overlaps with a group of four σ*-type bands originating from the b_3u and b_2u σ* orbitals of TMTTF (at 3.0–3.3 eV). Finally, there are two bands coming from the upper b_2u σ* level of TMTTF (at about 4.0 eV). Considerably higher in energy we find the levels originating from the triplet LUMO+1/LUMO+2/LUMO+3 of AsF₆⁻ which lead to a very broad contribution (∼8 eV) to the DOS which is centered at +8.5 eV (not displayed in Fig. 7 and 8).

IV. Discussion

The assignment of the different peaks of the calculated DOS is clear and can now be compared with the experimental results. Our goal is twofold. First, we need to understand in detail the nature of the peaks of the F 1s and S 2p spectra as well as their energy shift and variation in peak intensity upon cooling. Second, we will try to find if there is some distinctive feature in the spectra related with the occurrence of the CO transition. If this were possible we would like to infer from it the nature of the structural change associated with the CO process. In principle since the inversion symmetry is broken at the CO transition, we can assume that the anion moves either towards the methyl groups or towards the sulfur atoms of TMTTF.^13,14

A. Assignment of the different peaks of the F 1s and S 2p spectra

Let us start with the S 2p spectra. This is a simple task because of the excellent match of the peaks in the DOS with the energies of the discrete TMTTF levels and with the S 2p NEXAFS spectra. Thus, comparison of the results in Fig. 4(a) and 7 immediately leads to the assignment of peak 1 to the TMTTF a_g σ* orbital, peak 2 to the three π* orbitals b_3g, a_u and b_2g, peak 3 to the b_3u and the lower b_2u σ* orbitals, and finally peak 4 to the upper σ* b_2u orbital. This indexation is reported in Fig. 4a. This assignment is consistent with previous studies concerning TTF–TCNQ³² and (TMTTF)₂ReO₄,³³ with the only difference of the assignment of the two upper peaks as previously discussed.

Understanding the nature of the peaks in the F 1s spectra is more challenging. What is clear from the DFT calculations is that there are two possible peaks to be observed: one due to the AsF₆⁻ LUMO (at ∼2.4 eV) and another, around 5.5 eV higher in energy, originating from the group of three nearly degenerate AsF₆⁻ LUMO+1/LUMO+2/LUMO+3 orbitals. In principle, nothing more should be observed because AsF₆⁻ does not possess empty orbitals in between these two groups. This is a strong result coming from very basic chemical bonding arguments which cannot be altered by reasonable distortions of the anion. Thus, it is very surprising to see the presence of four peaks already at room temperature and, even more interestingly, an additional weak contribution around 4 eV below the first strong peak, which appears at temperatures below T_CO. This peak may be an important signature of the CO transition. Because of the energy difference and strong intensities, it is clear that peaks 1 and 3 of Fig. 3(a) must be associated with the AsF₆⁻ LUMO and the group of LUMO+1/LUMO+2/LUMO+3 levels, respectively.

The question which remains to be answered is: what is the origin of the additional peaks 2 and 4? However the fact that the cumulated area of peaks 2, 3 and 4 is approximately three times larger than the area of peak 1 suggests that the set of three orbitals above the AsF₆⁻ LUMO is at the origin of all three peaks. This nicely fits with the observation that the contribution of these three orbitals to the DFT DOS is centered at ∼8.5 eV (i.e. around 6 eV higher in energy than the AsF₆⁻ LUMO peak) and broadens into a large energy range of approximately 4 eV both above and below the more intense peak. This means that because the LUMO+1/LUMO+2/LUMO+3 orbitals are strongly directed outside the F atoms, the F is able to interact and thus mix with some empty TMTTF based molecular orbitals. These last orbitals which then acquire some anion contribution will, consequently, be detected when carrying out the F 1s NEXAFS measurements. Peak 2 occurs approximately halfway between the two genuine AsF₆⁻ peaks, i.e., approximately 3 eV higher than that associated with the LUMO. According to the DFT calculations, this energy difference is too large to be due to primarily empty TMTTF orbitals discussed so far. Consequently, peak 2 in the F 1s spectra should originate from the weak mixing of the triple set of AsF₆⁻ orbitals into either some high-lying antibonding σ* TMTTF orbital or some d-orbitals of the S atoms (see below). The fourth peak lies at very high energies and if this mechanism is correct it should result from the interaction with d orbitals of the S atoms of TMTTF. As a matter of fact, even if the mixing is not strong the large cross section of F should make these additional peaks easily observable. Analysis of the (TMTTF)₂AsF₆ DOS for energies higher than those in Fig. 6 and 7 shows that local maxima of the S and F PDOS match in energy above and below the peak at 8.5 eV. This allows the identification of the TMTTF sulfur d orbitals interacting with the set of three high-lying AsF₆⁻ orbitals: S d_z², d_xz and d_yz for the peak below 8.5 eV and S d_x²–y² and d_xy for the peak above 8.5 eV (remember that the TMTTF molecules are placed in a local axis system such that the long molecular axis runs along the x direction and the molecular plane is perpendicular to the z axis). On the basis of these DFT results we assign peaks 2 and 4 of the F 1s spectra to the interaction of the set of LUMO+1/LUMO+2/LUMO+3 orbitals of AsF₆⁻ with the S d_z², d_xz and d_yz orbitals (peak 2) and S d_x²−y² and d_xy orbitals (peak 4) of TMTTF.

B. Temperature variation of the shift and relative intensity of the main peaks

Before exploring the origin of the additional low energy contribution in the F 1s spectra we should consider if the main trends in the temperature variation of the shifts and relative intensities (Fig. 3b, c, 4b and c) of the different peaks can be reasonably understood on the basis of the above assignments. In general, it can be noticed that peaks in the S 2p spectra exhibit a negative shift when lowering the temperature whereas those of the F 1s spectra are positively shifted. This clearly points to a definite increase in the interaction between the empty levels of the TMTTF and AsF₆⁻ upon cooling. Roughly speaking, the energy shifts measure the mixing between levels of the two partners whereas the intensities probe the relative weight of the S, F or As orbitals. Note however that the relative intensities in Fig. 3c and 4c must be taken with considerable care because of the unavoidable normalization procedure (i.e. the sum of all the peak intensities is taken constant in temperature). In the following we will distinguish between the variations occurring around the charge localization crossover (T_ρ) and the CO transition (T_CO).

After a detailed inspection of Fig. 3b and c and 4b and c several observations can be made:

(i) the peak position associated with the AsF₆⁻ LUMO changes weakly upon cooling: there is a slight shift until T_ρ of peak 1 in the F 1s spectra (Fig. 3b) but there is no shift at all in the As spectra (Fig. 2). There is also a very weak energy shift for all the temperature range of peak 1 of the S 2p spectra corresponding to the TMTTF σ*(a_g) LUMO (Fig. 4b). This clearly shows that the main changes in the wave functions upon lowering the temperature do not affect noticeably the energy of the LUMOs of both partners. In addition, the intensity of peak 1 in the F 1s spectra does not change significantly above T_CO (Fig. 3c) which indicates that the orbital mixing into the AsF₆⁻ LUMO does not really change. This orbital is heavily concentrated on the central As atom so that the interaction between this orbital and the surrounding donor orbitals will not be significant. The σ*(a_g) LUMO of TMTTF has a sizable contribution from the sulfur atoms. The two sets of AsF₆⁻ orbitals HOMO/HOMO−1/HOMO−2 and LUMO+1/LUMO+2/LUMO+3, which have large contributions of the 2p fluorine atoms in the outer part of the anion, are those which will undergo stronger interactions with the σ*(a_g) LUMO of TMTTF. According to the DFT calculations this orbital is around 6 eV higher in energy than the HOMO/HOMO−1/HOMO−2 set of the anion but around 7 eV lower in energy than the LUMO+1/LUMO+2/LUMO+3 set of the TMTTF. Consequently, the two interactions will approximately cancel and the energy evolution of this orbital with temperature should not be very important as assessed by the weak change of position of peak 1 of the S 2p spectra (Fig. 4b). It is worth mentioning that, as it will be discussed in (ii), the σ*(a_g) wave function can be modified without major changes in its energy via an intra-TMTTF polarization mechanism induced by the electron localization which decreases the participation of the sulfur atoms. This mechanism should lead to a decrease of the contribution of σ*(a_g) LUMO of TMTTF in the intensity of peak 1 in the S 2p spectra, as observed in Fig. 4c.

(ii) From room temperature to T_ρ the main changes are the negative shifts of all peaks in the S 2p spectra and a positive shift of all peaks in the F 1s spectra (Fig. 3b and 4b). There is also a sizeable increase of the intensity of peak 2 in the F 1s spectra (Fig. 3c) compensated by smaller decrease of intensity of peaks 1, 3 and 4 (most likely such decrease is overemphasized by the normalization procedure and should be taken with care). Worthy of mention is the intensity increase of 30% of the intensity of peak 2 and 20% decrease of the intensity of peak 1 in the S 2p spectra (Fig. 4c). The variations in the intensity of peaks 3 and 4 cannot be taken as significant.

Let us first consider the S 2p spectra. When charge localization occurs, the delocalized holes of the metallic state become localized within each dimer of the chain. Since these holes belong to the π-type HOMO band, it is expected that the empty π*-type TMTTF levels should feel more strongly the electronic reorganization associated with the charge localization than the σ-type ones. The 30% increase in the intensity of peak 2 in the S 2p spectra (Fig. 4c) indicates an increase in the participation of the S orbitals in the π*-type levels associated with this peak. These orbitals should be d-type orbitals symmetric with respect to the molecular plane (d_z², d_x²−y² and d_xy) because this mixing allows the polarization of these π* TMTTF levels so as to concentrate more electronic density in the intra-dimer region at the expense of the participation in the inter-dimer region. This re-localization of the π* TMTTF levels should not be associated with a considerable change in the binding energy of the peak because increasing/decreasing the localization of the wave function in the intra/inter-dimer regions should have opposite energetic effects. Charge localization also affects the TMTTF σ* levels because of the asymmetry induced above and below the molecular plane. In this case, the d levels mixing into the TMTTF σ* levels are antisymmetric with respect to the molecular plane. However this mixing is smaller because the electronic localization involves the conducting electrons which are related to a π-type orbital. In addition, the increase of participation of sulfur orbitals in the π* molecular orbitals as a result of the hole localization leads, via a polarization-induced charge shift, to the opposite effect in the σ* molecular orbitals. This is why the relative peak intensities of peaks 1, 3 and 4 of the S 2p spectra decrease although we believe that, for the reasons mentioned above, this effect may be exaggerated in Fig. 4c.

The sulfur d orbital participation reinforces the interaction with the F atoms of the anion. Since the anion orbitals which can easily interact with the TMTTF orbitals are those of the LUMO+1/LUMO+2/LUMO+3 set which are higher in energy than the TMTTF orbitals considered so far, the interaction should be stronger as the energy difference decreases, so that the shifts in the S 2p spectra should be larger for peaks 3 and 4 and smaller for peaks 1 and 2 (Fig. 4b). Peaks 2, 3 and 4 of the F 1s spectra sizably shift towards higher energies (Fig. 3b) because these peaks are those originating from the LUMO+1/LUMO+2/LUMO+3 set which are pushed up by such interaction. The effect is weaker for peak 4 of the F 1s spectra because of the large energy difference with the TMTTF orbitals which leads to a weaker interaction (note however that peak 4 in the S 2p spectra is the most strongly affected because it is the highest in energy and may thus interact better). In the case of peak 1 of the F 1s spectra the interaction is quite complex because according to the DFT calculation this peak is almost half-way between the peaks associated with the lower TMTTF LUMO and the higher TMTTF LUMO+4 and LUMO+5 levels and almost at the same energy as the TMTTF π* orbitals. Because of the three competing interactions the final outcome is not easy to predict but apparently the destabilizing interaction of the LUMO and the lower part of the π* orbitals predominates and leads to a moderate shift in energy (Fig. 3b). The increase in the intensity of peak 2 of the F 1s spectra and the decrease of intensity of peaks 1 and 3, even if they may be somewhat overestimated, is easy to understand. Peaks 1 and 3 are associated with AsF₆ orbitals whereas peak 2 is an S d-based orbital of TMTTF which has acquired some fluorine character through donor–anion interaction. Consequently, increasing the interaction between the two partners must increase the weight of the F orbitals in peak 2 but decrease its weight in peaks 1 and 3, as experimentally observed in Fig. 3c.

(iii) Below T_ρ and before the CO transition, peaks 2, 3 and 4 of the S 2p spectra continue to shift down and peak 1 saturates; the intensity of peak 2 decreases while the intensity of peak 1 increases (Fig. 4b and c). Peaks 2 and 4 of the F 1s spectra shift up whereas the position of peaks 1 and 3 slightly decreases (Fig. 3b). The intensity of peak 2 and to a less extent the intensity of peak 4 decreases while those of peaks 1 and 3 does not appreciably change inside experimental errors (Fig. 3c). The enhanced positive shifts of peak 2 and 4 of the F 1s spectra and enhanced negative shift of peaks 2, 3 and 4 of the S 2p spectra clearly indicate an increase in the interaction between the orbitals of the two partners. Because of such increase in the interactions between the two partners, almost all levels interact with levels above and below of the other partner so that there is a noticeable redistribution of the F and S character among the different orbitals. Under such circumstances it is not simple (and probably not very meaningful in view of the experimental uncertainties) to provide a rationalization of the intensity variations. However, it is safe to conclude that in the temperature regime between the charge localization and charge ordering there is an increase of the interactions between the two partners.

(iv) When (TMTTF)₂AsF₆ undergoes the CO transition the peak shift basically follows the same trend as observed above the CO transition (Fig. 3b and 4b). However notable changes affect the peak intensities (Fig. 3c and 4c). The intensity of peaks 2 and 3 of the F 1s spectra and the intensity of peak 2 of the S 2p spectra decrease. In contrast, the intensity of peak 1 of the S 2p spectra and the intensity of peak 1 and 4 of the F 1s spectra increase. A striking observation concerning the F 1s spectra is the very weak variation of the binding energy of peak 1 (less than 0.1 eV) when the charge ordering occurs (note also that the position of the As peak does not change and As is the major constituent of the LUMO of AsF₆⁻). This is in sharp contrast with the situation in the TMTTF₂SbF₆ salt where an important increase of 2.8 eV of the F 1s binding energy was recently observed.¹² Although striking, this feature seems to be consistent with the absence of a noticeable binding energy shift for TMTTF₂PF₆ and the decrease of T_CO from the SbF₆ (154 K) to the AsF₆ (105 K) then to the PF₆ (65 K) salts,⁷ suggesting a progressive decrease of the charge polarization associated with the CO transition.

As shown in Fig. 4b, the four peaks in the S 2p spectra increase their binding energies when the charge ordering occurs and the effect increases from peak 1 to peak 4. If the structural change during the transition mostly affects the anion to methyl groups interactions, this feature should be very difficult to explain because most of the orbitals involved in these interactions have weak contributions on the methyl substituents and practically no change is expected for them. However, if the structural change mostly affects the anion to S interaction, the TMTTF orbitals should interact in a stabilizing way with the higher-lying LUMO+1/LUMO+2/LUMO+3 orbitals of AsF₆⁻ and in a destabilizing way with the lower-lying LUMO. Since the former orbitals are more strongly localized on the F orbitals the stabilizing effect is expected to be dominant and should lead to a decrease in energy shift for all S 2p peaks. Since the energy differences between the LUMO+1/LUMO+2/LUMO+3 orbitals and the TMTTF orbitals should increase from orbitals associated with peak 4 to those of peak 1 in the S 2p spectra, the interaction should decrease which leads to a smaller energy shift from peak 4 to peak 1, as observed in Fig. 4b. The increase of donor⋯anion interactions should lead to a destabilization (i.e. increase of positive shift) of peaks 2, 3 and 4 of the F 1s spectra. This is consistent with the shifts in Fig. 3b if we take into account that, because peak 3 lies in between peaks 2 and 4 which originate from the same anion orbitals, it is most likely that the intended positive shift in peak 3 is hampered by interaction with peak 4. As commented above, peak 1 experiences almost no change because of the weak interactions associated with the AsF₆⁻ LUMO.

We find difficult to give too much significance to the relative intensity peaks in this temperature region. Both the irregular base line in the 90 K F 1s spectra and the seemingly erratic behavior of peak 4 below 210 K in Fig. 4c casts some doubt on the significance of these intensity variations. However, it is striking to see that after the strong change around the charge localization transition, the evolution of the relative intensity peaks of the S 2p spectra looks as if they were trying to recover the situation at RT. Below T_ρ the continuous increase of the donor⋯anion interactions leads to a larger mixing of the orbitals of the two systems and thus to a progressive decrease of the participation of the sulfur orbitals in the TMTTF levels. Consequently, the evolution of the relative intensity peaks should go in the opposite direction before and after T_ρ. When the CO occurs, the donor⋯anion interactions still increase while there is a significant charge disproportion between the two TMTTF donors.^4,5 Thus, at this point an intra-dimer charge shift, which will affect the S atoms, occurs simultaneously. However as our measurements cannot discriminate between the two slightly different TMTTFs it is difficult to push further the analysis of the S 2p spectra in the CO phase. In this respect one can notice that a previous X-ray absorption measurement at the S K-edge of (TMTTF)₂MF₆ (M = P, As and Sb) compound has not evidenced any shift or splitting of the absorption peaks by crossing T_CO.³⁴

To summarize, the temperature evolution of the energy shifts and peak intensities are consistent with a continuous increase of the donor⋯anion interactions, mostly through the F⋯S contacts, as well as with a substantial mixing of the sulfur d-type orbitals on the unoccupied π* and σ* empty molecular orbitals of TMTTF. In the following section we consider a distinctive feature associated with the CO transition in the F 1s spectra.

C. A fingerprint of the charge ordering in the F 1s spectra?

Let us now consider the possible origin of the additional weak contribution in the F 1s spectra appearing around 4 eV below peak 1 in the CO ground state. Since this latter peak is associated to the LUMO which is the lowest empty state of AsF₆⁻, the origin of this new transition is quite mysterious. A possible explanation is the following. At the CO transition there is some shift of the anion towards the hole-rich TMTTF molecule. This means that the interaction between anion and TMTTF, even if small, should increase when the transition occurs. Consequently, there must be some weak mixing of the anion states into the TMTTF ones. At this point we must remind two facts: (i) there are empty levels considerably lower in energy than the anion LUMO: the empty part of the half-filled upper TMTTF conduction band, and (ii) the very large cross section associated with the F 1s measurements. Thus, it is likely that because of the slight displacement of each anion toward the a hole-rich TMTTF donor when the CO occurs, a weak contribution of the occupied anion wave function mixes with the unoccupied TMTTF HOMO conduction band wave function and because of the large cross section of F, this small contribution becomes visible in the F 1s spectra. The orbitals of the anion that mix into the TMTTF HOMO bands are those of the highest occupied set of HOMO/HOMO−1/HOMO−2 levels shown in Fig. 6. These orbitals have a very strong F 2p character which makes them very well suited to interact with the nearest empty TMTTF orbitals, which are those of the partially-filled TMTTF HOMO conduction band. Thus, we conclude that at the CO transition there is a weak mixing of the AsF₆⁻ HOMO orbitals into the empty part of the TMTTF HOMO band leading to the appearance of the low-energy feature in the F 1s spectra. The experimental separation between this additional peak and peak 1 in the F 1s spectra is approximately 1.5 eV larger than found in the calculations, but this is consistent with the well-known underestimation of the energy difference between filled (or partially filled) and empty bands by DFT.

A final question concerning the proposed mechanism is: why a similar feature is not observed in the S 2p spectra? Let us recall that because of the NEXAFS selection rules, the S levels will only be clearly visible if the wave function contains S atomic orbitals of either s or d-type. Because of its antisymmetric character with respect to the molecular plane a π-type TMTTF orbital such as the HOMO has the wrong parity to act as final state in a transition from the S 2p initial state. In contrast with the empty π*-type orbitals, the TMTTF HOMO practically does not contain sulfur d orbital character, as shown in Fig. 8b were the continuous and dotted lines in the region around the Fermi level almost superpose. Thus, the small modification of the electronic structure of the empty part of the TMTTF HOMO bands will be difficult to detect in the S 2p spectra. Only the F 1s spectra can reveal this subtle change when the CO occurs, due to their different parity.

In principle, the extremely weak variation of the binding energy of peak 1 in the F 1s spectra when the charge ordering occurs could have been taken as an indication that the anion movement around T_CO does not involve a displacement towards the S atoms, but towards the methyl groups. However this would not explain the energy shifts and the variations of relative peak intensities of the different peaks in the S 2p spectra. In addition, this would be also at odds with what we believe is one of the more clear fingerprints of the CO transition in (TMTTF)₂AsF₆: the appearance of the new weak contribution below peak 1 in the F 1s spectra, as well as with the proposed origin of peaks 2 and 4 in the F 1s spectra. Our explanation is also consistent with the fact that a small but non-negligible mixing between the HOMOs of the two partners is found in the DFT calculation by analyzing the COOP (crystal orbital overlap population) for the F⋯S interaction whereas nothing similar is found for the F⋯H interactions. Consequently, the present NEXAFS study provides a clear fingerprint of the CO phenomena occurring in (TMTTF)₂AsF₆, which is apparently different from that found for the related (TMTTF)₂SbF₆ Fabre salt.¹² This study also supports the earlier proposal that anion displacement during the CO transition in Fabre salts mostly affects the F⋯S contacts.⁹ This conclusion agrees also with the finding that T_CO of the CO transition of the (TMTTF)₂X series scales with the anion⋯S distance.³⁵ Finally let us note that the increase of hybridization between the anion and the S of TMTTF upon cooling could be enhanced by the lattice contraction, the freezing of the anion reorientation and the modification of the geometry of the anion cavity. However the link with the thermal dependence of the lattice parameters is not straightforward because if the anion methyl group distances decrease upon cooling as expected, a lattice expansion surprisingly occurs for the S⋯F distances.¹⁴ However ¹⁹F NMR indicates that the reorientation movement of octahedral anions freezes upon cooling in two steps, at ∼210 K (≈T_ρ) and ∼135 K in the case of SbF₆ salt.^36,37 If, as expected, the anion dynamics does not vary significantly for octahedral anions, the freezing would help establishing better contacts between TMTTF and AsF₆. In contrast the methyl groups still rotate in the temperature range of our study (their classical rotation movement freezes around ∼55 K in (TMTSF)₂PF₆³⁸) which renders difficult the establishment of hydrogen bonds with the anion.

V. Conclusion

In the present paper we have presented high-resolution near-edge X-ray absorption fine structure measurements on the Fabre salt (TMTTF)₂AsF₆ at different temperatures. The (TMTTF)₂AsF₆ molecular conductor exhibits a charge localization and a CO transition at T_ρ ∼ 230 K and T_CO = 102 K, respectively. Arsenic M-edge, fluorine K-edge and sulfur L-edge spectra were recorded upon cooling (TMTTF)₂AsF₆ down to 90 K. We have clearly established that the charge localization phenomenon and the CO transition of (TMTTF)₂AsF₆ correspond to subtle changes in the electronic structure. The strongest effect was observed for the F and S atomic species exhibiting systematic shifts of the F 1s and S 2p lines up to +0.85 eV and −0.4 eV respectively. Remarkably, these photon energy shifts occur in opposite directions with respect to the RT spectra. In contrast, the As 3p doublet does not show any significant shift. The opposite shifts found in the F 1s and S 2p spectra reflect substantial changes in the electronic environment of the sulfur atoms of TMTTF and the fluorine atoms of the anions. The results are discussed on the basis of first-principles DFT calculations. The changes observed below T_ρ suggest an increase of participation of the S d orbitals in the empty states of TMTTF as well as an increase of the donor⋯anion interactions. We propose that the appearance of a new F 1s pre-edge signal upon entry into the CO phase at 90 K is a clear fingerprint of the charge disproportionation. The data suggest that the loss of the inversion center associated with the CO transition is due to an anionic displacement towards the sulfur atom of the hole-rich TMTTF.

Acknowledgements

We acknowledge Lund University, MAX-lab for the provision of beam time. Special thanks are due to Graduate School of Excellence MAINZ and to Transregio SFB TR49. Work in Spain was supported by MINECO (Spain) through Grants FIS2012-37549-C05-05 and CTQ2011-23862-C02-02, and Generalitat de Catalunya (2014SGR301 and XRQTC). EC thanks Dr Jordi Fraxedas for a very useful discussion.

References

1. C. Bourbonnais and D. Jérome, Science, 1988, 281, 1155.
2. C. Coulon, P. Delhaès, S. Flandrois, R. Lagnier, E. Bonjour and J. M. Fabre, J. Phys., 1982, 43, 1059.
3. V. J. Emery, R. Bruinsma and S. Barisic, Phys. Rev. Lett., 1982, 48, 1039.
4. D. S. Chow, F. Zamborszky, B. Alavi, D. J. Tantillo, A. Baur, C. A. Merlic and S. E. Brown, Phys. Rev. Lett., 2000, 85, 1698.
5. M. Dumm, B. Salameh, M. Abaker, L. K. Montgomery and M. Dressel, J. Phys. IV, 2004, 114, 57.
6. P. Monceau, F. Ya. Nad and S. Brazovskii, Phys. Rev. Lett., 2001, 86, 4080.
7. R. Laversanne, C. Coulon, B. Gallois, J. P. Pouget and R. Moret, J. Phys., Lett., 1984, 45, L-393.
8. P. Foury-Leylekian, S. Petit, G. Andre, A. Moradpour and J.-P. Pouget, Physica B, 2010, 405, S95.
9. M. de Souza, P. Foury-Leylekian, A. Moradpour, J.-P. Pouget and M. Lang, Phys. Rev. Lett., 2008, 101, 216403.
10. M. de Souza, D. Hofmann, P. Foury-Leylekian, A. Moradpour, J.-P. Pouget and M. Lang, Physica B, 2010, 405, S92.
11. J.-P. Pouget, P. Foury-Leylekian, D. Le Bolloc'h, B. Hennion, S. Ravy, C. Coulon, V. Cardoso and A. Moradpour, J. Low Temp. Phys., 2006, 142, 147.
12. K. Medjanik, M. de Souza, D. Kutnyakhov, A. Gloskovskii, J. Müller, M. Lang, J.-P. Pouget, P. Foury-Leylekian, A. Moradpour, H.-J. Elmers and G. Schönhense, Eur. Phys. J. B, 2014, 87, 256.
13. M. de Souza and J.-P. Pouget, J. Phys.: Condens. Matter, 2013, 25, 34320.
14. J.-P. Pouget, Physica B, 2015, 460, 45.
15. M. Grioni, S. Pons and E. Frantzeskakis, J. Phys.: Condens. Matter, 2009, 21, 023201.
16. A. Chernenkaya, K. Medjanik, P. Nagel, M. Merz, S. Schuppler, E. Canadell, J.-P. Pouget and G. Schönhense, Eur. Phys. J. B, 2015, 88, 13.
17. K. Medjanik, D. Chercka, P. Nagel, M. Merz, S. Schupler, M. Baumgarten, K. Müllen, S. A. Nepijko, H.-J. Elmers, G. Schönhense, H. O. Jeschke and R. Valenti, J. Am. Chem. Soc., 2012, 134, 4694.
18. C. Coulon, G. Lalet, J.-P. Pouget, P. Foury-Leylekian, A. Moradpour and J. M. Fabre, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085126.
19. I. A. Kowalik, G. Öhrwall, B. N. Jensen, R. Sankari, E. Wallén, U. Johansson, O. Karis and D. Arvanitis, J. Phys.: Conf. Ser., 2010, 211, 012030.
20. P. Hohenberg and W. Kohn, Phys. Rev., 1965, 136, B864.
21. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
22. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
23. For more information on the SIESTA code visit: http://departments.icmab.es/leem/siesta/.
24. For a review on applications of the SIESTA approach in materials science see: D. Sánchez-Portal, P. Ordejón and E. Canadell, Struct. Bonding, 2004, 113, 103–170.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1966, 77, 3865.
26. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993.
27. L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425.
28. E. Artacho, D. Sánchez-Portal, P. Ordejón, A. García and J. M. Soler, Phys. Status Solidi B, 1999, 215, 809.
29. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
30. (a) T. Granier, B. Gallois, L. Ducasse, A. Fritsch and A. Filhol, Synth. Met., 1988, 24, 343; (b) B. Liautard, S. Peytavin, G. Brun and M. Maurin, Cryst. Struct. Commun., 1982, 11, 1841; (c) http://www.uni-leipzig.de/%E2%88%BCunifit/downloads.htm .
31. F. Zamborszky, W. Yu, W. Raas, S. E. Brown, B. Alavi, C. A. Merlic, A. Baur, S. Lefevre and P. Wzietek, J. Phys. IV, 2002, 12, Pr9-139.
32. J. Fraxedas, Y. J. Lee, I. Jimenez, R. Gago, R. M. Nieminen, P. Ordejon and E. Canadell, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195115.
33. G. Subias, T. Abbaz, J. M. Fabre and J. Fraxedas, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085103.
34. S. Ravy, P. Foury-Leylekian, D. Le Bolloc’h, J.-P. Pouget, J. M. Fabre, R. J. Prado and P. Lagarde, J. Phys. IV, 2004, 114, 81.
35. B. Köhler, E. Rose, M. Dumm, G. Untereiner and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035124.
36. K. Furukawa, T. Hara and T. Nakamura, J. Phys. Soc. Jpn., 2005, 74, 3288.
37. W. Yu, F. Zhang, F. Zamborsky, B. Alavi, A. Baur, C. A. Merlic and S. Brown, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 121101(R).
38. P. Foury-Leylekian, S. Petit, I. Mirebeau, G. André, M. de Souza, M. Lang, E. Ressouche, A. Moradpour and J.-P. Pouget, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 024105.

---