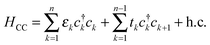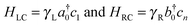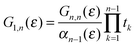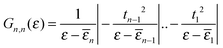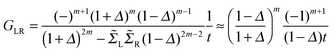Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electron transport in carbon wires in contact with Ag electrodes: a detailed first principles investigation†
Paolo
Bonardi
a,
Simona
Achilli
ab,
Gian Franco
Tantardini
ab and
Rocco
Martinazzo
*ab
aUniversitá degli Studi di Milano, Dipartimento di Chimica, via Golgi 19, 20133 Milano, Italy. E-mail: rocco.martinazzo@unimi.it
bConsiglio Nazionale delle Ricerche, Istituto di Scienze e Tecnologie Molecolari, Milano, Italy
First published on 5th June 2015
Abstract
The structure and electronic properties of carbon atom chains Cn in contact with Ag electrodes are investigated in detail with first principles means. The ideal Ag(100) surface is used as a model for binding, and electron transport through the chains is studied as a function of their length, applied bias voltage, presence of capping atoms (Si, S) and adsorption site. It is found that the metal–molecule bond largely influences electronic coupling to the leads. Without capping atoms the quality of the electric contact improves when increasing the carbon atom coordination number to the metal (1, 2 and 4 for adsorption on a top, bridge and hollow position, respectively) and this finding translates almost unchanged in more realistic tip-like contacts which present one, two or four metal atoms at the contact. Current–voltage characteristics show Ohmic behaviour over a wide range of bias voltages and the resulting conductances change only weakly when increasing the wire length. The effect of a capping species is typically drastic, and either largely reduces (S) or largely increases (Si) the coupling of the wire to the electrodes. Comparison of our findings with recent experimental results highlights the limits of the adopted approach, which can be traced back to the known gap problem of density-functional-theory.
1 Introduction
π-Conjugated carbon systems of several different variants have long been studied for their application as conducting polymers in light emitting diodes, photovoltaic devices and low-frequency logic units in integrated circuits for low-end, high-volume applications. Since the ground-breaking observation that upon doping the conductivity of polyacetilene increases by ∼14 orders of magnitude,1,2 interest in electrically active organic components – as opposed to traditional inorganic semiconductors – has increased enormously, mainly triggered by the reduced cost, high flexibility and functionability of these materials. More recently, the isolation of graphene3 – an all-carbon π-conjugated “crystalline 2D polymer” – and the thorough investigation of its magnetotransport and optical properties4–8 lent support to the idea that performance is not necessarily an issue with organic materials. Such discovery promises to be a big twist in the use of carbon-based materials for traditional as well as novel applications, and suggests that an all-carbon electronics might be possible in the near future. In such hypothetical setting interconnects are made up of 1D-like objects like multi- or single-walled carbon-nanotubes of increasingly reduced diameters, down to the thinnest possible carbon wires, i.e. carbon atom chains of different lengths.Carbon atom chains are particularly attractive, because of the possibility of showing multiple π bonding. Indeed, they are made of sp carbon atoms and present either alternating single–triple bonds (polyynes) or all-double carbon–carbon bonds (cumulenes) depending on the termination and on the number of carbon atoms. In the ideal, infinite case the dimerized form is the most stable, as a consequence of the Peierls distortion which lowers the energy of every occupied energy level. This so-called “carbyne” (the 1D allotropic form of carbon) has been predicted to have extraordinary mechanical properties, and would significantly outperform every known materials (including graphene) in both tensile and bending stiffness, and strength.9 Furthermore, torsional stiffness as induced by the presence of functional groups at the wire ends (namely –CH2 inducing the polyynic to cumulenic transition) has been shown to affect the energy gap and to induce magnetization.9,10 The energy gap is also tunable with an applied strain since stretching of the chain determines an increase of the bond length alternation (BLA) which is a major factor controlling the gap size; actually, when taking into account lattice vibrations, carbyne is predicted to preserve its cumulenic (metallic) character and to transform to the polyynic (insulator) form at around 3% strain.11 All this suggests that carbyne may play a central role in future nanoelectronics as mechanically stable, atomic-thick wire; all the more that at present there exist only three metals which are known to form atomic chains (namely Au, Pt, and Ir).12
Carbyne has not yet been isolated as a macroscopically long carbon chain but several fragments of varying length (so-called “carbynes”) and different ending groups have been obtained by several routes. They are also found to exist in dark interstellar clouds13 and meteorites,14 and in the interior of carbon nanotubes.15,16 Carbynes are thermally and chemically stable (carbyne is predicted to be stable up to ∼3000 K) and spectroscopically well-characterized;17 they are moderately sensitive to light, moisture or oxygen, and can be handled and characterized under normal laboratory conditions.18 In general, fabrication methods range from chemical and electrochemical synthesis, gas phase deposition, epitaxial growth, irradiation or mechanical breaking (“pulling”) of graphene ribbons.19–24 Synthesis of Cn chains up to n = 44 has been reported,18 though bulky end-groups are typically needed to minimize interchain cross-linking. Also the first electrical-transport measurements in monoatomic carbon chains have been reported, for both carbon–graphene24 and carbon–metal contacts.25 Measured conductances have been found to be much lower than theoretically predicted and it has been argued that, in the case of carbon–graphene contacts, this is a consequence of the residual strain in the chain which increases the BLA, hence the band gap.24
A large number of studies addressed theoretically the transport properties of carbon chains. An oscillatory behaviour in the length dependence of their conductance was predicted long ago using model first-principles calculations,26 similarly to the parity oscillations observed in metallic wires.‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 Since then the transport properties of these molecular wires in contact by various means with metallic (and more recently graphenic) electrodes have received increased attention, and several key aspects have been addressed.28–36 However information is very scattered and a well-rounded perspective of the key aspects affecting electron transport in these systems is missing.
27 Since then the transport properties of these molecular wires in contact by various means with metallic (and more recently graphenic) electrodes have received increased attention, and several key aspects have been addressed.28–36 However information is very scattered and a well-rounded perspective of the key aspects affecting electron transport in these systems is missing.
This paper represents one attempt to fill this gap in the case of carbon–metal contacts, using silver as the electrode; a similar study on carbon–graphene contacts will be presented shortly. We assume that coupling to the leads is strong enough that a coherent transport regime is adequate (an assumption which can be justified a posteriori), and apply non-equilibrium Green’s functions (NEGF) techniques in conjunction with density functional theory (DFT) Hamiltonians to study the binding of molecules to metal electrodes, electron transport at zero and finite bias, and the effects that electrode geometry, anchoring species, bond stretching and bending have on the transport properties.
In general, it is well understood that in the considered coherent transport regime the key quantities are the amplitude of the energy gap, its position relative to the Fermi level and the broadening of the molecular orbitals due to the interaction with the substrate, and they in turn depend also on the atomic arrangements of the “extended molecule” forming the junction (the enlarged molecule including parts of the electrodes where screening and geometrical effects are supposed to occur). We use standard first-principles calculations with a semi-local functional to describe these effects; however, since current DFT functionals give only a rough description of the quasi-particle spectra (e.g. they severely underestimate the energy gap) we also critically discuss the reliability of our results using the optical properties of the free molecules to benchmark the adopted functional.
The paper is organized as follows. Section 2 sketches the computational set-up, Section 3 presents the results and Section 4 discusses their reliability; and finally Section 5 concludes.
2 Theory
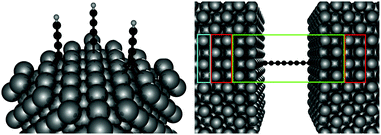
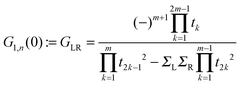
Electronic structure calculations were performed at the density functional theory (DFT) level, using the periodic, pseudopotential, self-consistent method implemented in the SIESTA package37 and the Perdew–Burke–Ernzerhof (PBE) functional in the generalized gradient approximation (GGA)38,39 to handle exchange–correlation effects. Core electrons were described by separable, norm-conserving pseudopotentials40 and a set of atomic orbitals with compact support of the double-ζ plus polarization (DZP) quality was used to expand the wavefunction. Cut-off radii of the atomic orbitals were determined by setting the confinement energy to 0.02 Ry and an energy cutoff of 300 Ry was adopted for the real-space integration of the electron density. A 2 × 2 supercell was chosen along the Ag(100) surface and Brillouin zone sampling was performed following the Monkhorst–Pack scheme using a 5 × 5 k-mesh for the self-consistent steps which was later increased to 10 × 10 for the determination of the transmission probabilities in the transport calculations. Geometry optimizations were performed on a 9-layer Ag(100) slab in which the two topmost surface layers were left free to optimize along with the molecular degrees of freedom. The three highest symmetry sites of the Ag(100) surface – the so called top, hollow and bridge sites – were considered for binding, as shown schematically in the left panel of Fig. 1, and a large vacuum layer (∼15 Å) was introduced along the surface normal between the free-end of the molecule and the repeated image of the slab. Such separation was then reduced to mimic molecular junctions between two metallic electrodes using the previously determined adsorption geometries. In this case, only the electrode layers (two for each electrode) and an additional buffer layer were kept frozen in the optimization step.Transport calculations were performed self-consistently using the TranSIESTA code41 which exploits the non-equilibrium Green’s function approach to the open-system transport problem. These are actually three-step calculations in which one obtains: (i) the “surface” Green’s functions gX(ε) of the uncoupled semi-infinite left (X = L) and right (X = R) electrode from periodic bulk calculations, (ii) the Green’s function G(ε) of the “conductor” (the above mentioned extended molecule) from the scattering-region effective Hamiltonian; the latter includes the self-energies ΣX(ε) = HCXgX(ε)HXC of the electrodes (where HCX and HXC are the Hamiltonian terms coupling the conductor to the X lead) and is made self-consistent (at any applied bias VSD) with the charge density given by G(ε); and (iii) the cumulative transmission function N(ε) of the system
| N(ε) = Tr[G†(ε)ΓR(ε)G(ε)ΓL(ε)] |
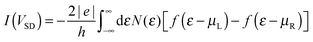 | (1) |
Spatial features of electron transport were analyzed with the help of transmission (left) eigenchannels. They are eigenvectors of the current operator in the scattering-region subspace of the left-incoming states and describe independent transport channels with transmission probabilities (aka eigentransmissions) tk(ε); note that they can in principle be probed by e.g. multiple Andreev reflection between superconducting leads.42 Eigenchannels and eigentransmissions were determined from G and gX with the help of INELASTICA43 as described in ref. 44 and 45.
Furthermore, we made profitable use of analytical results which can be obtained using the well-known n-state “resonant model”.46 In such a model the molecular linker is represented by a tight-binding linear chain
(here ck is an annihilation operator for the k-th site of the linker and a0 and b0 are the corresponding operators for the left and right lead surface states, respectively§). The model is particularly appropriate in our case since conduction properties are solely determined by the π orbitals, two for each atom which form two independent sets of π states. In this case, the transmission function reduces to
| N(ε) = ΓL(ε)ΓR(ε)|G1,n(ε)|2 | (2) |
where Gn,n(ε) is given as a continued fraction
αk(ε) is a polynomial defined by a three-term recursion (α−1(ε) ≡ 0 and α0(ε) = 1)
αk(ε) = (ε − ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) k)αk−1(ε) − tk−12αk−2(ε) k)αk−1(ε) − tk−12αk−2(ε) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) k are re-normalized on-site energies,
k are re-normalized on-site energies, ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) k = εk + δ1kΣL + δnkΣR. Here ΣX = γX2gX are the appropriate self-energies given by the coupling strength γX and the surface Green’s function gX ≡ (gX)00 of the electrode (which, in turn, is entirely determined by ρX, namely through
k = εk + δ1kΣL + δnkΣR. Here ΣX = γX2gX are the appropriate self-energies given by the coupling strength γX and the surface Green’s function gX ≡ (gX)00 of the electrode (which, in turn, is entirely determined by ρX, namely through 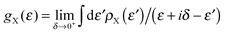 ).
).
Finally, we also performed structural and optical calculations on some free polyynic chains using the Gaussian09 quantum chemistry code,47 adopting the 6-31++G** basis set and some semilocal (PBE) and hybrid (B3LYP) functionals, both in their original formulation and in their long-range-corrected form, namely according to the correction of Hirao and coworkers (LC-PBE)48 and to the Coulomb attenuation method (CAM-B3LYP).49 Optical calculations are of the linear-response TD-DFT type and used the above functionals in the adiabatic approximation, within the Casida’s formulation of the problem of computing the longitudinal dielectric function.
3 Results
In the following we consider the structural, binding and transport properties of several carbon chains Cn in contact with Ag electrodes. We mainly restrict our analysis to the case of an even number of carbon atoms, since they can in principle present either a cumulenic or a polyynic structure. The case of odd n necessarily leads to a cumulenic form (and a resonance at the Fermi level) when employing featureless and symmetric leads, and will only briefly be considered for comparison.3.1 Structure
Binding properties were investigated considering C-side adsorption of –CnH radical species on the ideal Ag(100) surface, and computing the binding energy| Eb = EC + EM − EMC | (3) |
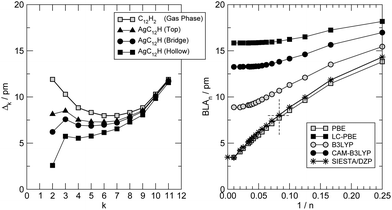
At a closer look though the formation of the metal–carbon bond does influence the structure of the chain, giving it some cumulenic character at its contacted end. This is shown in Fig. 3 (left panel) where the variation of the local bond-length alternation Δk = |dk − dk−1| (dk being the length of the k-th CC bond, counted from the contact) is shown for the –C12H case and compared to the one found in the gas-phase C12H2. As is evident from that figure, in the gas-phase H-terminated molecule, the local BLA decreases (the cumulenic character increases) from the molecule end(s) to the middle whereas the opposite generally holds when a metal–carbon contact is established. The behavior of the BLA signals increasing polyyne–surface coupling in the sequence: top < bridge < hollow. The strength of such coupling is determined by the number of metal atoms coordinating with the polyyne end, since the strength of each C–Ag bond decreases in the order: top > bridge > hollow, according to the bond length (2.01 Å for top, 2.13 Å for bridge and 2.31 Å for hollow). A detailed analysis of the electronic structure by means of crystal orbital overlap and Hamiltonian populations50,51 (COOP and COHP, respectively, see ESI† for details) reveals that binding of the polyyne radicals occurs through hybridization of both the σ and the π orbitals of the molecules with the 4d and 5s orbitals of the Ag surface atoms. In the equilibrium configuration the degree of hybridization of the π orbitals is substantial; in the three different adsorption sites considered above interactions with Ag(4d) orbitals are of similar magnitude and have both bonding and antibonding contributions, whereas interaction with Ag(5s) is bonding in hollow, (very) weakly bonding in bridge and absent in top (see ESI†). As a consequence the broadening of the π resonances increases in the order: top < bridge < hollow, in agreement with the increase of cumulenic character of the chain end shown in Fig. 3 (left panel). In molecular junction configurations, such hybridization controls the coupling of the low energy conducting channels to the electrodes, and manifests itself in the electron transport properties (see below).
Furthermore, since the BLA is a key parameter for the electronic properties; we investigated its dependence on the wire length, using the hydrogen-terminated molecular species HC2mH as test cases. We calculated the BLA on a large set of molecules (n = 2m = 4–100) performing all-electron DFT calculations using the Gaussian quantum chemistry code,47 with different functionals and the standard 6-31++G** Pople’s basis set, as outlined in the previous section. The results of such structural optimizations are shown in Fig. 3 (right panel) where the BLA at the center of the molecule is reported as a function of the inverse number of C atoms in the chain|| 1/n. That figure makes clear that the adopted exchange functional affects such a structural parameter as the BLA (besides having known consequences for the quasi-particle energy gap, see below), and typically increases it when the functional goes beyond the semi-local approximation. It has been argued that the CAM-B3LYP results are the most accurate since they are bracketed (for small n) by coupled-cluster and MP2 results.52 Based on this it is tempting to conclude that the PBE-computed BLA is about three times smaller than the correct value [for the infinite chain (carbyne) we extrapolate ∼4 pm vs. ∼13 pm] and that similar results hold also when the molecule comes into contact with a metal surface. Unfortunately, since hybrid functionals do not generally represent a good solution for metals,53 it is not currently possible to solve this structural issue for the transport problem, but it is important to keep it in mind when discussing the cumulene (metal)–polyyne (insulator) transition using semi-local functionals. Of course, the direct effect of the exchange functional on the quasi-particle gap is much larger (and not easily solvable) that any improvement of the structural predictions at this level would be of minor importance; therefore, in the following we fully rely on the PBE functional and a posteriori critically assess its reliability. Note, on the other hand, that the adopted set-up (pseudopotential approach with a DZP basis-set) does favourably compare with all-electron calculations using Gaussian basis-sets (Fig. 3, star symbols).
3.2 Zero-bias transmission
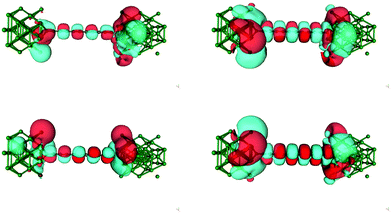
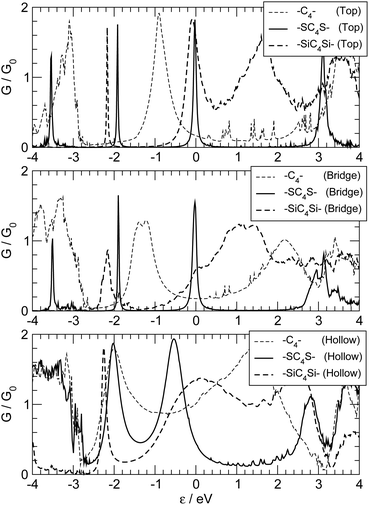
The zero bias transmission function N(ε) is closely related to the equilibrium ground state electronic properties of the system. The electronic states resulting from the metal–chain interaction that are delocalized on the whole junction act indeed as conduction channels for transporting charge from one electrode to the other. Consequently N(ε) closely resembles the density of states (DOS) and in the following we describe the features of N(ε) implicitly assuming their relationship with the electronic states provided by the DOS.The transmission function for C12 adsorbed in the three high-symmetry sites considered above is reported in Fig. 4. As can be seen from that figure N(ε) features a number of resonances describing transmission mediated by molecular orbitals. The latter can be nicely related to the energy levels of the H-terminated polyyne in the gas phase, which broaden and shift downwards in energy as the molecule gets closer to the Ag(100) surface along an adsorption path (see ESI†). Overall, little charge-transfer occurs when establishing the contact: Mulliken population analysis shows that electronic charge is transferred from the leads to the molecule and is of the order 0.2–0.3 |e| for top and bridge geometries and ∼0.5 |e| for adsorption in the hollow position. Such excess charge however does not spread uniformly over the molecule and mainly locates at the contact atoms which become slightly negatively charged (0.1–0.2 |e| each). Importantly, upon separating the π and σ contributions, it is found that 0.3–0.4 |e| are transferred from the metal to the σ orbitals of each contact carbon atom and back-donated by the π orbitals to the metal electrodes (0.25–0.30 |e| per contact, see ESI†). The effects of the bond-forming interaction are evident in the transport properties reported in Fig. 4, which feature a sizable broadening of the molecular levels of increasing magnitude in the order: top < bridge < hollow (from ∼0.2–0.3 eV to ∼1 eV), consistently with the behaviour of the bond strength (Fig. 2). As mentioned above, analysis of the electronic structure reveals that the broadening of the π resonance has two contributions, one almost site-independent due to π–Ag(4d) interactions and one due to π–Ag(5s) hybridization which markedly decreases in the order: hollow > bridge > top, and which is therefore responsible for the different behavior of the adsorption sites. Noteworthy, the value of the transmission reaches at resonance a value close to the maximum allowed by a degenerate π system, indicating that the symmetry around the wire axis is effectively preserved in the metal–molecule system. An exception is the bridge case where the geometry at the contact lifts the degeneracy of the π system and causes the peaks to split and to decrease in magnitude. The calculation of the transmission eigenchannels at the energies of the highest occupied- and lowest unoccupied-resonances confirms that they actually represent the highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals of the free molecule, hybridized with the metal surfaces (see Fig. 5 for adsorption in hollow).
 | ||
| Fig. 4 The zero-bias transmission function for –C12– as a function of energy, referenced to the Fermi level. From bottom to top the case of adsorption on hollow, bridge and top sites, respectively. | ||
Wires of different lengths show similar results. The resonances always resemble the energy levels of the corresponding HCnH in the gas-phase and are differently broadened in the order: top < bridge < hollow. Similarly, the peak transmissions remain close to 2 for adsorption on hollow and top sites, while splitted resonances always appear when adsorption occurs on bridge sites.
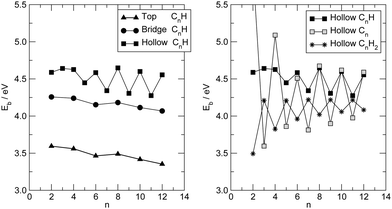
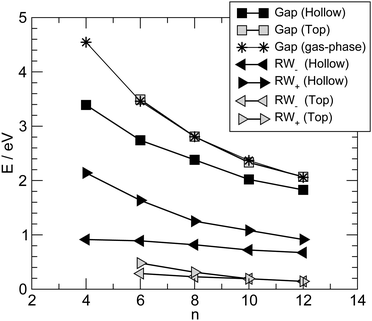
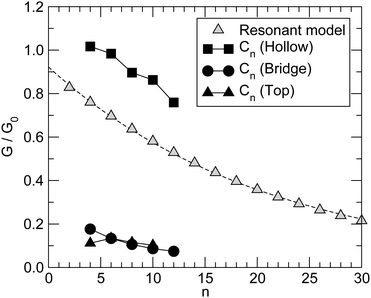
Fig. 6 summarizes the main results for different chain lengths, namely the width of the resonances closest to the Fermi level (computed at the energies where N(ε) = 1) and the gap between them. The results refer only to chains adsorbed in hollow and top sites since, as mentioned above, at bridge sites a small splitting of the resonances occurs which prevents us to perform such a simple analysis. As can be seen from Fig. 6, the width of the resonances decreases when increasing the chain length, particularly for the lowest energy one above the Fermi level. This effect is particularly evident for short chains and is due to the decreasing amplitude that the HOMOs/LUMOs have on the wire ends when increasing the length of the molecular bridge. It only appears in relatively short chains since longer chains present overlapping resonances which resemble the continuos density of states of the infinite chain. Similarly for the energy gap, which decreases as a consequence of the increased delocalization (π conjugation), much like in the gas-phase HCnH molecules. Actually, the gaps for the top case compare quantitatively with the gas-phase values at the same level of theory whereas for the hollow case they are considerably smaller because of the much stronger coupling with the electrodes, hence increased effective delocalization (see Fig. 6).
Similar results are obtained at the tight-binding level, i.e. using the n-state resonant model mentioned in Section 2. We used such a model with parameters appropriate for polyynic chains, without attempting to carefully reproduce the ab initio results since the latter clearly show a broken electron–hole symmetry which would require to go beyond the nearest-neighbor approximation crucial for the model to be analytically solvable. Specifically, we set the hopping energies to t− = 2.65 eV and t+ = 2.80 eV, for the long and the short bonds, respectively. These values are consistent with the hopping energy t ∼ 2.7 eV appropriate to describe CC bonds in graphene that are ∼142 pm long, i.e. intermediate between single and double bonds (in accordance with the resonating valence bond picture). The on-site energies εi were set to zero and the coupling strength to the electrodes γ = 1.75 eV. Furthermore, the chain was in contact with two equal leads described in the wide-band limit (t = 3.0 eV), with on-site energies εi ≡ 0. With these values of the parameters the transmission functions feature a number of broadened yet separated resonances of the kind found in the ab initio calculations, see Fig. 7 (left panel). Fig. 7 (right panel) details the behavior of the lowest energy resonances, namely their full width at half maximum (triangles) – which is the same for the highest resonance below and the lowest resonance above the Fermi level, because of the electron–hole symmetry – and the energy gap between them (squares). Also shown for comparison the ab initio results in Fig. 6, namely the widths of the resonances averaged over the two of lowest energy and the gap between them, for adsorption in the stable hollow position. The figure shows clearly that the model, despite its simplicity, is able to capture the main features of the transmission functions. The parameters were given reasonable (physical) values, and no attempt was made to modify them to reproduce the results for adsorption in top, or to handle the lifting of the degeneracy for the bridge case with the help of two slightly different, yet independent chains.
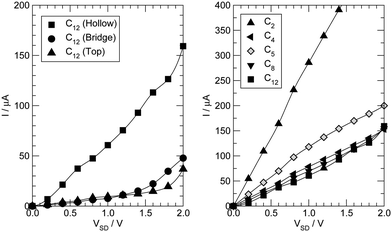
3.3 I–V characteristics
Next we examine the results of the non-equilibrium transport calculations whereby the carbon chain is in contact with two electrodes at different chemical potentials, and a finite current is obtained according to eqn (1). In principle, the I–V characteristic depends on both the voltage-dependent transmission function (the first term in the integral of eqn (1)) and the bias window (second term), but in practice N(ε) depends only weakly on the applied voltage VSD that a linear (Ohmic) behaviour results for reasonably small voltage biases. This is indeed what we found in a rather large voltage window, say up to ∼1.5 V, as shown in Fig. 8 (left panel) for C12 adsorbed at the above hollow, bridge and top sites. Clearly, the results for different adsorption sites parallel those shown in Fig. 4, and the hollow-adsorbed chain provides the largest conductance dI/dVSD. The current linearly increases with VSD and only for a rather large bias (∼2 V) it starts deviating from linearity, without presenting any anomalous behavior. Fig. 8 (right panel) shows the current for chains of different lengths when adsorbed at the stable hollow position. Again, the current linearly increases with VSD in the wide bias window considered and shows a little dependence on the chain length. This is best appreciated in Fig. 9 where we report the zero-bias conductance G = dI/dVSD|VSD=0 as a function of n (n even), for all the cases considered, along with the results for the n-state resonant model used above, multiplied by a factor of two to account for the degeneracy of the π system. The latter qualitatively reproduce the ab initio results for the hollow site and fit well to an exponential decaying function with a characteristic length of ∼20 units, i.e. ∼2.6 nm. In general, an exponential dependence of the conductance on the chain length follows from eqn (2) when |εF − εi| ≫ |ti|, since in that case G1,n is approximately given (at the (n − 1)th order in perturbation theory) by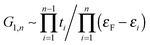 , i.e. for a polyynic chain n = 2m long with on-site energy ε0 and hoppings t±, by G1,n ∼ tm+tm−1−/(εF − ε0)2m. This “off-resonant” limit however does not apply to the case considered in this work since εF ∼ ε0 approximately holds for π-sites in contact with metal electrodes and this invalidates the use of perturbation theory (actually, in the n-state resonant model we set εF = ε0 = 0). Nevertheless, the conductance shows a “resonant” exponential decay which follows from eqn (2) for large n (n even) when setting εi = 0 and computing the transmission at εF = 0. Indeed, for a chain n = 2m long the relevant Green’s function becomes
, i.e. for a polyynic chain n = 2m long with on-site energy ε0 and hoppings t±, by G1,n ∼ tm+tm−1−/(εF − ε0)2m. This “off-resonant” limit however does not apply to the case considered in this work since εF ∼ ε0 approximately holds for π-sites in contact with metal electrodes and this invalidates the use of perturbation theory (actually, in the n-state resonant model we set εF = ε0 = 0). Nevertheless, the conductance shows a “resonant” exponential decay which follows from eqn (2) for large n (n even) when setting εi = 0 and computing the transmission at εF = 0. Indeed, for a chain n = 2m long the relevant Green’s function becomesand, in particular, for a polyynic chain with t± = (1 ± Δ)t, using
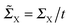 (for X = L, R), we obtain
(for X = L, R), we obtainwhich gives an exponentially decaying transmission probability with a characteristic length β−1 = 1/ln[(1 + Δ)/(1 − Δ)] ≈ 18 units for the values of t± used above. For comparison, note that the characteristic length found here is much larger than that typically found under off-resonant conditions, which is in the range 0.05–0.2 nm for alkanes and sp2 π-conjugated systems.46 This finding agrees well with the experimentally measured conductance of pyridyl-capped oligoynes performed using the STM–molecular break junction technique in a Au–molecule–Au configuration.30 Moreover, the above equation shows that in the absence of dimerization, the dependence of the conductance on the chain length disappears.
Also shown in Fig. 8 (right panel) are the results for the –C5– linker, which are representative of odd-numbered carbon chains. In this case, the transmission function (not shown) features a peak close to the Fermi level due to the approximate electron–hole symmetry of the junction and this results in a conductance sensibly higher than that found for the even-numbered chain. The same holds for any odd-numbered chain and is the origin of the parity oscillations of the conductance.26 Such oscillations are found irrespective of the polyynic–cumulenic character of the chain, even though they are more marked in our first-principles results because the chains turn out to be polyynic for even n and cumulenic for odd n. As mentioned above, they arise because of the (approximate) electron–hole symmetry which, at half-filling (i.e. with one electron per orbital) and for odd n, necessarily leads to an electronic level close to the Fermi level (see, for instance, ref. 54).
Finally, the case n = 2 (triangles (up) in the right panel of Fig. 8) is clearly at odds with the general behavior of even-numbered chains and is discussed at length in the next subsection.
3.4 “Through space” tunneling
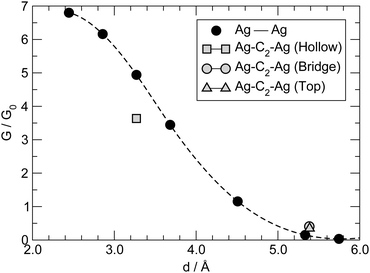
The conductance for the –C2– linker shown in Fig. 8 is one order of magnitude larger than that found for longer linkers, thereby suggesting that a different transport mechanism is at work in this case. C2 is sufficiently small that direct tunneling between the two electrodes can occur. In this “through space” case (as opposed to “through molecule”) the linker mainly acts as a spacer between the leads, controlling the width of the tunneling barrier, hence the conductance. We checked this possibility by performing transport calculations similar to those mentioned above but without any linker, for several values of the distance between the electrodes (defined from the position of the atoms in the top-most layers). The results of such calculations are reported in Fig. 10, along with the results for –C2– adsorbed in hollow, bridge and top positions. As can be seen from that figure, the linker introduces minor modifications in the transport properties of the “empty” junction. The conductance mainly depends on the tunneling width and is larger for C2 adsorbed at hollow sites because of the closer proximity of the leads that this configuration allows. Note that at d ∼ 3.2 Å, as appropriate for hollow-adsorbed C2, G is about 4 for the 2 × 2 electrode configuration considered in the simulation cell, i.e. almost twice the maximum value expected for a degenerate conduction channel due to the linker but consistent with one non-perfectly conducting channel per Ag atom of the leads. The shape of the curve in Fig. 10, though, does not agree with the predictions of common tunneling models,46 and at short distances is determined by the hybridization of the valence orbitals of the leads (the equilibrium Ag–Ag distance in bulk Ag computed with our set-up is 2.92 Å). This is confirmed by COOP/COHP analysis of the electronic structure at equilibrium, which shows non-vanishing hybridization between the 5s orbitals of opposing Ag atoms at the contact. The same analysis suggests that the (small) decrease of the conductance in the presence of the molecular spacer is due to the reduction of the 5s spectral density at the interface for energies close to the Fermi level, which in turn is due to bonding of the metal atoms with the molecule (see ESI† for details).3.5 Bending and stretching
In order to understand the effect that geometrical distortions may have on the transport properties of the chains we considered some (static) displacements of the carbon nuclei from their equilibrium configuration. Specifically, we computed the normal modes of vibrations of the contacted C8 adsorbed in the stable hollow sites and looked at the evolution of the transmission function along a bending and a stretching mode, as representatives of a low- and a high-frequency molecular motion. Since such calculations were only exploratory (and by no means representative of the possible coupling between vibrational and electronic degrees of freedom) we computed the dynamical matrix by shifting only the carbon atoms within the chain and keeping fixed the position of the metal atoms. We found that the two lowest-frequency (and essentially doubly degenerate) modes at 145 cm−1 and 189 cm−1 are orthogonal to the molecular axis, much like transverse phonons, and display either zero or one node along the chain. They are followed by bending modes with an increasing number of nodes up to ∼500 cm−1 where the first “longitudinal” mode appears (541 cm−1). The latter dominates the high frequency region which extends up to 2054 cm−1, the frequency value we found for the –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– stretching.** In general, the computed frequencies compare favorably with those calculated for C8 between Ag(111) electrodes;55 including Ag atoms in the dynamical matrix modifies only the low frequency region of the phonon spectrum (ω ≤ 300 cm−1) and introduces a longitudinal mode for block oscillations of the chain along the surface normal at ∼240 cm−1.
C– stretching.** In general, the computed frequencies compare favorably with those calculated for C8 between Ag(111) electrodes;55 including Ag atoms in the dynamical matrix modifies only the low frequency region of the phonon spectrum (ω ≤ 300 cm−1) and introduces a longitudinal mode for block oscillations of the chain along the surface normal at ∼240 cm−1.
With the normal vibrations and their frequencies at hands we distorted the molecules along a number of modes, according to the average displacement allowed for a (quantum) harmonic oscillator at 500 K. We considered the lowest frequency bending and the highest frequency stretching and found no significative variation in the transport properties (not reported). We thus conclude that the computed properties are rather robust with respect to (small) displacement of the carbon atoms out of their equilibrium position.
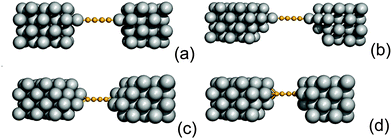
3.6 Tip-like contacts
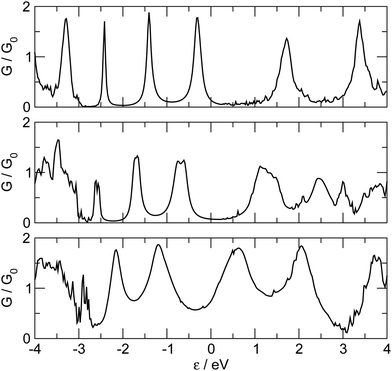
So far we have considered a rather simplified model for the electrodes, namely one in which the metal uses the ideal (100) face for binding the linker and conducting current. This choice allowed us to systematically investigate the transport properties (resonance position and widths) depending on the sites where adsorption may occur. Here we show that such results remain almost unchanged when considering more realistic “tip-like” contacts such as those shown in Fig. 11. Four different cases were considered: two of these feature a top-like contact, whereby the chain binds to a Ag atom placed on a hollow site, either on the ideal (100) surface (Fig. 11(a)) or on four-atom “terrace” (Fig. 11(b)); the remaining two exhibit binding to either a Ag dimer (Fig. 11(c)) or at the center of a four-atom cluster (Fig. 11(d)), both deposited on the flat (100) surface.The –C4– linker was chosen as a representative member of the family under study and transport properties were computed for the four cases above. The results of such calculations are shown in Fig. 12, where the transmission functions are compared with those obtained using model electrodes, namely top-adsorbed chains for cases (a) and (b), bridge for (c) and hollow for (d). As is evident from Fig. 12 the tip geometry has a large influence on transmission which, though, is mostly related to the local binding geometry of the contact only. This is clearly seen when comparing the transmission function obtained using the tips with those computed for the model Ag(100) electrodes. Few differences are worth noticing. First, the width of the resonances is slightly reduced, due to some “incomplete” binding to the leads which occurs with tip-like contacts, compared to the ideal case. This is particularly evident for cases (a) and (b) but also visible for (c) and (d). Second, the tip-like geometry changes the local symmetry of the metal–molecule contact and may enhance the symmetry breaking. This is evident for instance in case (c) where the chain binds to a Ag dimer and splitting of the highest energy peak below the Fermi level is complete.
 | ||
| Fig. 12 Zero-bias transmission functions for the realistic tip-like contacts shown in Fig. 11 (thick lines). Also shown for comparison the results obtained with the model Ag(100) electrodes (thin dashed lines), for adsorption in hollow (bottom panel), bridge (middle panel) and top (top panel). In the top panel, full and dashed thick lines for tip geometries (a) and (b) (Fig. 11). | ||
3.7 Anchoring groups
Finally, we investigated the presence of anchoring groups (atoms) since they are often used in practice to produce stable contacts between the molecular bridge and the electrodes. In general, the effect of an anchoring group can be varied, depending on the coupling strengths of the capping species to the lead and to the molecule, and on the position of its energy level(s). This is nicely seen in the n-state resonant model where an anchoring group modifies the self-energy at the ends of the molecular bridge according to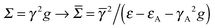 , where
, where ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is the coupling between the molecule and the anchoring group, and εA and γA are the on-site energy and electrode coupling strength of the latter.
is the coupling between the molecule and the anchoring group, and εA and γA are the on-site energy and electrode coupling strength of the latter.
We choose two different kinds of capping atoms: sulphur, because of its well-known affinity towards many transition metal surfaces, and silicon, because of its formal similarity to carbon, and its widespread use in most of the current technologies and its compatibility with carbon chemistry.56 The effect of the anchoring group is in both cases dramatic, as can be seen in Fig. 13 where we report the transmission functions for –SC4S– and –SiC4Si– junctions adsorbed on the top, bridge and hollow positions of the ideal Ag(100) electrode surface.††
The presence of a S atom at the ends of the chain considerably narrows the resonance peaks, especially for adsorption at the top and bridge sites. The sulphur atom reduces the effect of the adsorption site, as can be seen by the close similarity of the transmission functions shown in the three panels of Fig. 13. Remarkably, the resonance peaks shift and get closer to the Fermi level, analogously to what occurs for S-capped polyynes in contact with gold electrodes, where reversed parity oscillations were found for chains of variable length.28 Analysis of the Mulliken population shows that S is only slightly negatively charged (∼0.1 e each) and the carbon chain is essentially neutral. A closer look at the optimized structures reveals that binding is “reversed” when introducing sulfur atoms: –SC4S– adsorbed in a top or in a bridge position has a reduced BLA between C atoms which matches that found for –C4– adsorbed in a hollow position (∼3 pm); on the other hand, such BLA is considerably smaller than that found in –SC4S– adsorbed at the hollow sites and in –C4– adsorbed either in a top or a bridge position (∼10 pm). This suggests that when S binds either in a top or in a bridge site the S–C bond is close to double and that the chain has an increased cumulenic character. The electronic structure analysis (see ESI† for details) reveals that the S(π) orbitals couple strongly with the carbon π orbitals, but only if the chain adsorbs in a hollow position the coupling with the Ag(5s,4d) orbitals of the electrodes is significant, thereby justifying the different widths of the resonance peaks in Fig. 13. Sulphur atoms effectively increase the length of the conjugated chain and may provide up to four π electrons per atom instead of two, which are then necessarily accommodated into antibonding orbitals. The number of contributing π electrons is reduced to about three in top and bridge geometries – the missing electron being arranged in a σ orbital – thereby leaving two electrons free to transmit (i.e. a peak right at the Fermi level). This is likely to occur with different metal surfaces as well, and may explain the above mentioned reversed parity oscillations which were observed when binding –SCnS– chains to a Au(111) surface.28
The effect of Si atoms, on the other hand, is less clear, apart from a general broadening of the resonances, which is mainly due to a sizeable antibonding interaction between the Si(pπ) orbitals and the 4d orbitals of the metal, with an additional, significant bonding contribution from Ag(5s) orbitals when adsorption proceeds in a hollow site (see ESI† for details). The optimized structures point towards an increased cumulenic character in the sequence hollow–bridge–top, with a BLA between C atoms of the order 8–4–1 pm, respectively. Analysis of the Mulliken populations reveals a little overall charge transfer from the leads to the molecule (∼0.1 |e|) which however is unequally shared between the anchoring groups and the molecule: the first gain 0.3–0.4 |e| per atom and the latter is slightly positively charged (∼0.5 |e|).
4 Discussion
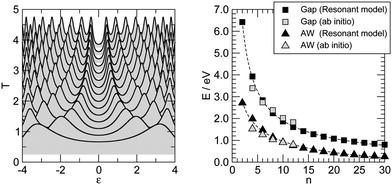
In the previous section we have seen that electron transport in carbon wires is described by well-defined resonances whose features (position and widths) depend on the adsorption site and, more markedly, on the presence of anchoring groups. The widths of such resonances are sufficiently large that we can rule out interaction effects, either with vibrations or with other electrons. The resulting conductances are of the order ∼G0 and give rise to a current of ∼ 10 μA for a voltage bias VSD ∼ 0.1 V, as shown by the I–V characteristics presented in Fig. 8. Recently, La Torre et al.25 formed and characterized several carbon–metal nanocontacts, and found that the monoatomic chains discussed in this work give a current of the order ∼0.2 nA for the same voltage and Fe/graphitic contacts, i.e. 4–5 orders of magnitude smaller than the value we find theoretically. Though the chain length and the exact nature of the contacts remain unknown, such a large discrepancy appears to be a limitation of the DFT-NEGF approach adopted here which relates to the well-known gap problem of current density functionals. Indeed, even though electron transport remains effectively single-particle, the Kohn–Sham potential used here is at most a rough approximation to the non-local, energy-dependent electron self-energy governing the quasi-particle dynamics. As a result, the gap between the resonances closest to the Fermi level is largely underestimated, and the transmission probability at the Fermi level – due to the tails of the broadened resonances – turns out to be much larger than the actual one. DFT represents indeed true improvements over semiempirical approaches for describing binding to the electrodes (and maybe broadening of the resonances) but clearly lacks sufficient accuracy in reproducing the quasi-particle spectrum, something which DFT is not meant to do and is typically left to post-DFT methods (e.g. those that make use of Hedin’s GW approximation to the self-energy57). Here we provide some semi-quantitative assessment of the typical error that we expect for such a band gap with the theory level adopted in this work.To this end, we considered the optical properties of several gas-phase polyynes HCnH, as obtained by linear-response TD-DFT using different density functionals in the adiabatic approximation, as outlined in Section 2. Vertical transitions were computed at the molecular geometries optimized at the same level of theory (see Fig. 3) and are reported in Fig. 14. In such a figure the left panel gives the lowest-energy dipole-allowed transition (C1Σu+ ← X1Σg+) for which experimental data are available (stars), and shows that accurate results can be obtained with long-range corrected functionals over a wide range of molecular sizes, even with modest-sized basis sets, provided diffuse functions are used.‡‡ Particularly impressive is the accuracy of the CAM-B3LYP functional which gives results in very close agreement to the experimental ones, with a maximum deviation of less than 0.1 eV for the molecules considered. When extrapolated to the infinite chain§§ the “optical” gap turns out to be 2.85 eV, in agreement with previous calculations59 and significantly larger than the extrapolated experimental optical gap, 2.3–2.4 eV according to ref. 52; the discrepancy though seems to be related to the model rather than the method, since the calculations refer to the rather idealized situation of isolated linear chains where screening is absent.¶¶ We thus take the CAM-B3LYP results as a reference for computing the gap most relevant for transport, namely the energy of the dipole–forbidden A1Σu− ← X1Σg+ transition. This is reported in the right panel of Fig. 14 for the same functionals used above, along with the HOMO–LUMO gaps obtained in the PBE-based transport calculations at the hollow adsorption geometries (open diamonds). Though the latter refer to a different physical situation (see also Fig. 6 and the related discussion), the same functional (PBE) provides a much smaller gap than the “correct” CAM-B3LYP one, even when corrected at long-range according to the LC-PBE prescription.48 The infinite-chain CAM-B3LYP extrapolated value is found to be 2.19 eV, in reasonable agreement with the non-self-consistent GW result of 2.58 eV obtained at a HSE06 optimized geometry (BLA ∼ 9 pm).9 In order to check the effect that such underestimation of the energy gap has on the transport properties, we modified the hopping energies t± of the n-state resonant model introduced above in such a way that they reasonably describe the computed gaps. We set t+ = 3.2 eV and t− = 2.3 eV to obtain the results shown in the right panel of Fig. 14 using star symbols. When used for computing the transport properties, with the remaining parameters being fixed, we found a two order of magnitude reduction of the conductance for n = 20 and a three order reduction for n = 30. Though not enough to explain the 4–5 order of magnitude discrepancy mentioned above, the results presented here show that the gap-problem of DFT is likely the main source of disagreement with experiments. In particular, we rule out the possibility that the carbon chains are mechanically strained in the transport experiments24 – a possibility which was invoked for carbon wires in contact with graphene electrodes – since carbynes are much stiffer than any metal that any mechanical stress would result in a deformation of the metal only.
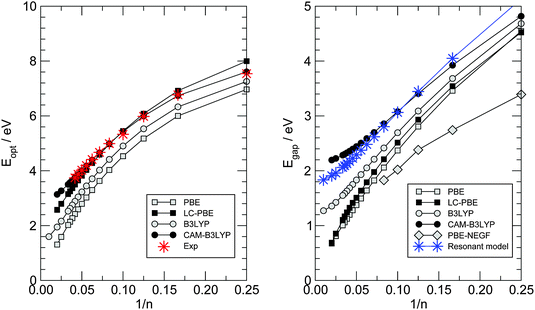 | ||
| Fig. 14 Optical properties of gas-phase HCnH molecules as functions of the number of carbon atoms n. (left) The optical gap defined by the lowest energy dipole-allowed transition. (right) Energy gap between the ground- and the first excited singlet state. Results from linear-response TD-DFT calculations are shown as squares for a semi-local functional (PBE) and as circles for a hybrid functional (B3LYP), with and without long-range correction (filled and open symbols, respectively). In the left panel stars indicate experimental data.17 In the right panel, open diamonds indicate the first-principles HOMO–LUMO gaps of Fig. 7 (right panel) and stars indicate the results of the n-state resonant model with t+ = 3.2 eV and t− = 2.3 eV. | ||
5 Summary and conclusions
We used first-principles methods to investigate in detail electron transport through carbon wires in contact with metal electrodes, and elucidated the influence that the contact geometry, the anchoring species and the chain length have on transport properties. We uncovered the main factors governing the dependence of the transmission function on the chain length, the primary role of the chemical bonds at the contacts in broadening the resonances through the interaction between the π orbitals of the chain and the Ag(5s,4d) orbitals of the substrate, and the dramatic effects that capping species may have on transport, where they generally modify the widths of the molecular resonances but can also introduce novel π states and revert the even–odd alternance. In spite of the success of first-principles methods in elucidating the microscopic details of the molecule–lead interactions, transport results are at odds with recent experimental data by several orders of magnitude. The problem is likely due only to the inadequacy of current density functionals to provide the appropriate quasi-particle spectrum, and can only be solved with higher (much more expensive) levels of theory for the electron transport problem.60,61Acknowledgements
R. M. acknowledges G. Onida, N. Manini and M. I. Trioni for useful discussions. This work has been supported by Regione Lombardia and CINECA HP Center through a LISA Initiative (2014) grant.References
- C. K. Chiang, C. R. Fincher, Y. W. Park, A. J. Heeger, H. Shirakawa, E. J. Louis, S. C. Gau and A. G. MacDiarmid, Phys. Rev. Lett., 1977, 39, 1098 CrossRef CAS.
- A. J. Heeger, Rev. Mod. Phys., 2001, 73, 681 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Gregorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- N. M. R. Peres, Rev. Mod. Phys., 2010, 82, 2673 CrossRef CAS.
- D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Adv. Phys., 2010, 59, 261 CrossRef CAS PubMed.
- S. Das Sarma, S. Adam, E. H. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83, 407 CrossRef CAS.
- M. Katsnelson, Graphene: Carbon in Two Dimensions, Cambridge University Press, 2012 Search PubMed.
- D. N. Basov, M. M. Fogler, A. Lanzara, F. Wang and Y. Zhang, Rev. Mod. Phys., 2014, 86, 959 CrossRef CAS.
- M. Liu, V. I. Artyukhov, H. Lee, F. Xu and B. I. Yakobson, ACS Nano, 2013, 11, 10075 CrossRef PubMed.
- L. Ravagnan, N. Manini, E. Cinquanta, G. Onida, D. Sangalli, C. Motta, M. Devetta, A. Bordoni, P. Piseri and P. Milani, Phys. Rev. Lett., 2009, 102, 245502 CrossRef.
- V. I. Artyukhov, M. Liu and B. I. Yakobson, Nano Lett., 2014, 14, 4224 CrossRef CAS PubMed.
- R. H. M. Smit, C. Untiedt, A. I. Yanson and J. M. van Ruitenbeek, Phys. Rev. Lett., 2001, 87, 266102 CrossRef CAS.
- A. Webster, Mon. Not. R. Astron. Soc., 1980, 192, 7 CrossRef PubMed.
- R. Hayatsu, R. G. Scott, M. H. Studier, R. S. Lewis and E. Anders, Science, 1980, 209, 1515 CAS.
- Z. Wang, X. Ke, Z. Zhu, F. Zhang, M. Ruan and J. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R2472 CrossRef CAS.
- X. Zhao, Y. Ando, Y. Liu, M. Jinno and T. Suzuki, Phys. Rev. Lett., 2003, 90, 187401 CrossRef.
- R. Nagarajan and J. P. Maier, Int. Rev. Phys. Chem., 2010, 29, 521 CrossRef CAS PubMed.
- W. A. Chalifoux and R. R. Tykwinski, Nat. Chem., 2010, 2, 967 CrossRef CAS PubMed.
- F. Cataldo, Polyynes: Synthesis, Properties and Applications, CRC Press, Boca Raton, 2005 Search PubMed.
- C. Jin, H. Lan, L. Peng, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 205501 CrossRef.
- A. Lucotti, M. Tommasini, D. Fazzi, M. Del Zoppo, W. A. Chalifoux, M. J. Ferguson, G. Zerbi and R. R. Tykwinski, J. Am. Chem. Soc., 2009, 131, 4239 CrossRef CAS PubMed.
- F. Cataldo, L. Ravagnan, E. Cinquanta, I. E. Castelli, N. Manini, G. Onida and P. Milani, J. Phys. Chem. B, 2010, 114, 14834 CrossRef CAS PubMed.
- A. Milani, A. Lucotti, V. Russo, M. Tommasini, F. C. Cataldo, A. Li Bassi and C. S. Casari, J. Phys. Chem. C, 2011, 115, 12836 CAS.
- O. Cretu, A. R. Botello-Mendez, I. Janowska, C. Pham-Huu, J.-C. Charlier and F. Banhart, Nano. Lett., 2013, 13, 3487 CrossRef CAS PubMed.
- A. L. Torre, F. B. Romdhane, W. Baaziz, I. Janovska, C. Pham-Huu, S. Begin-Colin, G. Pourroy and F. Banhart, Carbon, 2014, 77, 906 CrossRef PubMed.
- N. D. Lang and P. Avouris, Phys. Rev. Lett., 1998, 81, 3515 CrossRef CAS.
- R. H. M. Smit, C. Untiedt, G. Rubio-Bollinger, R. C. Segers and J. M. van Ruitenbeek, Phys. Rev. Lett., 2003, 91, 076805 CrossRef CAS.
![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) . Crljen and G. Baranović, Phys. Rev. Lett., 2007, 98, 116801 CrossRef CAS.
. Crljen and G. Baranović, Phys. Rev. Lett., 2007, 98, 116801 CrossRef CAS.- V. M. García-Suárez and C. J. Lambert, Nanotechnology, 2008, 19, 455203 CrossRef PubMed.
- C. Wang, A. S. Batsanov, M. R. Bryce, S. Martin, R. J. Nichols, S. J. Higgins, V. M. García-Suárez and C. J. Lambert, J. Am. Chem. Soc., 2009, 131, 15648 Search PubMed.
- B. Song, S. Sanvito and H. Fang, New J. Phys., 2010, 12, 103017 CrossRef.
- M. L. Mayo and Y. N. Gartstein, J. Chem. Phys., 2010a, 132, 064503 Search PubMed.
- M. L. Mayo and Y. N. Gartstein, J. Phys. Chem. A, 2010b, 114, 6444 Search PubMed.
- Z. Zanolli, G. Onida and J. Charlier, ACS Nano, 2010, 4, 5174 CrossRef CAS PubMed.
- C. Fang, B. Cui, Y. Xu, G. Ji, D. Liu and S. Xie, Phys. Lett. A, 2011, 375, 3618 CrossRef CAS PubMed.
- X. Z. Wu, M. Q. Long, L. N. Chen, C. Cao, S. S. Ma and H. Xu, Physica E, 2012, 45, 82 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS.
- M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- E. Scheer, P. Joyez, D. Esteve, C. Urbina and M. H. Devoret, Phys. Rev. Lett., 1997, 78, 3535 CrossRef CAS.
- M. Paulsson and T. Frederiksen, Inelastica, a python package for siesta/transiesta dft codes, http://sourceforge.net/projects/inelastica Search PubMed.
- M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115117 CrossRef.
- T. Frederiksen, M. Paulsson, M. Brandbyge and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205413 CrossRef.
- J. Cuevas and E. Scheer, Molecular electronics: an introduction to theory and experiments, World Scientific, 2010 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr, R. E. Stratmann and J. C. Burant, et al., Gaussian09, Revision A.02, Gaussian Inc., Pittsburgh PA, 2009 Search PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS PubMed.
- R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1987, 26, 846 CrossRef PubMed.
- R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617 CrossRef CAS.
- S. Yang and M. Kertesz, J. Phys. Chem. A, 2006, 110, 9771 CrossRef CAS PubMed.
- J. Paier, M. Marsman and G. Kresse, J. Phys. Chem., 2007, 127, 024103 CrossRef PubMed.
- W. Barford, Electronic and optical properties of conjugated polymers, Oxford science, 2005 Search PubMed.
- L. Nykänen, H. Häkkinen and K. Honkala, Carbon, 2012, 50, 2752 CrossRef PubMed.
- K. M. Baines, Chem. Commun., 2013, 49, 6366 RSC.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- J. Thom H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef PubMed.
- M. J. G. Peach, E. I. Tellgren, P. Salek, T. Helgaker and D. J. Tozer, J. Phys. Chem. A, 2007, 111, 11930 CrossRef CAS PubMed.
- H. H. M. Strange, C. Rostgaard and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115108 CrossRef.
- M. Strange and K. S. Thygesen, Beilstein J. Nanotechnol., 2011, 2, 746 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp02796a |
| ‡ This finding must not be confused with the polyynic-cumulene dichotomy, as it was obtained for cumulenic structures with a variable number of carbon atoms; rather it is related to the electron–hole symmetry of atomic chains with nearest-neighbor interactions only which for odd n, places an electronic level at (close to) the Fermi energy in the free (contacted) molecule. |
| § The structure of leads is irrelevant, in the sense that can be subsumed in their density of states, see below. |
| ¶ Vibrational analysis performed on a few selected cases showed that the hollow, bridge and top structures have zero, one and two imaginary frequencies, as expected. Hence, the adsorption potential energy surface features a stable hollow site and minimum-energy diffusion barriers at the bridge positions. |
| || For comparative purposes note that the computed BLA is much smaller than the difference between the CC bond length in alkanes (∼154 pm) and that in alkynes (∼120 pm). The average bond length is indeed close to that found in double bonds (∼133 pm). |
| ** More precisely, this mode evolves into an optical mode at the Γ point when increasing the chain length. |
| †† In the presence of the above capping species, the hollow position remains the most stable site for adsorption. With a sulphur anchoring atom, adsorption at a hollow site is about 1.9(1.6) eV more stable than at a top (bridge) position, while with Si the corresponding figures are ∼1.7 and ∼3.7 eV, respectively. |
| ‡‡ A basis-set convergence check was performed on TD-DFT calculations against the cc-pVnZ sets reported by Dunning et al.,58 with and without diffuse functions (see ESI,† for details) |
| §§ To this end a Padé functional form which reduces to E∞g − a/n2 (for a large n) was used to fit the computed data. |
| ¶¶ We cannot exclude the possible excitonic effects that cannot be described by TD-DFT in the adiabatic approximation because of the absence of important double excitations needed for exciton binding. |
| This journal is © the Owner Societies 2015 |