Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-innocent adsorption of Co-pyrphyrin on rutile(110)†
Yeliz
Gurdal
*,
Sandra
Luber
,
Jürg
Hutter
and
Marcella
Iannuzzi
Institut für Chemie, Universität Zürich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland. E-mail: yeliz.guerdal@chem.uzh.ch; sandra.luber@chem.uzh.ch; hutter@chem.uzh.ch; marcella.iannuzzi@chem.uzh.ch
First published on 6th August 2015
Abstract
Solar-light driven water splitting is a promising way for the sustainable production of molecular hydrogen, the latter representing an efficient carrier for energy storage and conversion into common liquid fuels. In search of novel catalysts for high-performance water splitting devices, Co-pyrphyrin (CoPy) has been recently synthesized and successfully used as a homogeneous water reduction catalyst. We investigate the adsorption of this molecule on the rutile TiO2(110) surface as a possible first step towards the design of a heterogeneous water reduction system. We find that the adsorption of the molecule is stabilized by the interaction of the cyano groups with the under-coordinated Ti centers present at the surface. This interaction induces the rehybridization of the molecular orbitals localized on the cyano groups and the realignment of the lowest unoccupied molecular states. Moreover, the highest occupied molecular orbital of CoPy@rutile(110) is localized on CoPy and the energy gap turns out to be significantly smaller than the gap of pristine rutile(110). This implies that direct or indirect injection of electrons from CoPy to the rutile(110) surface is in principle possible upon the absorption of light in the visible range. On the other hand, the electronic properties of the Co(II) center are not modified by the adsorption, which suggests that CoPy and its derivatives may be used in water electrolysis for hydrogen production also in the adsorbed state.
I. Introduction
In the quest for renewable energy sources molecular hydrogen is one of the most favoured candidates as an energy carrier. Compared to other means, such as electricity, bio-fuels, or conventional fuels, hydrogen has the highest specific energy content,1 and is also environmentally preferable, because the waste product of its reaction with pure oxygen is simply water.2 However, the large scale production and storage of molecular hydrogen is still an open issue. Several techniques can be employed for its production, such as water electrolysis,3 steam and ethanol reforming,4,5 partial oxidation of hydrocarbons,6 dark fermentation,7 and photo-chemical water reduction. The latter is of particular interest, because it emulates natural processes and needs only solar light as an energy source.8Water reduction in a homogeneous environment has been widely studied.9 Most of the working systems are based on the use of expensive metals as catalytic reduction centers.10 However, it has been shown that also less expensive Co-based catalysts can be employed for H2 production with low over-potentials.11 Peters et al.12 investigated the catalytic activity of several cobalt complexes with BF2 glyoxime or propane bridged tetraimine ligands in acetonitrile. They concluded that with less electron donating ligands the reduction of Co-complexes can be achieved easily, leading to H2 production. Guttentag et al.13 studied the activity of [CoIIIBr2(DO)(DOH)pn] with a photo-sensitizer [Re(CO)3(bipy)(py)]+ in a pure water and an acidic environment, demonstrating that H2 production is possible without organic solvents. Macro-cyclic molecules like metal centered porphyrins are also widely studied alternative catalysts, thanks to their low cost and wide range of light absorption capability.14,15 Solis et al.16 modeled cobalt hangman porphyrins in acetonitrile solution and determined the pathway for proton coupled electron transfer for H2 generation. For recent reviews and studies on homogeneous water reduction we refer to ref. 17–20.
In spite of the established achievements in H2 generation in homogeneous environments, the most important drawback is the rapid recombination of photo-generated products in solution.21 Therefore, it has been proposed that in heterogeneous environments, where the catalyst is combined with a supporting material, the fast back electron transfer can be prevented and the system is stabilized.22 Several studies are already available on the properties of metal centered porphyrins adsorbed on TiO2 surfaces.23–25
Only relatively few studies on the combination of Co-complexes with heterogeneous systems have been published. The Co-based complex [CoIII(dmgH)2(pyridyl-4-hydrophosphonate)Cl] adsorbed on a TiO2 surface via anchoring groups has been considered as a catalyst for proton reduction.26 Yin et al.27 studied the organic dye eosin Y (EY) and several other Co complexes also adsorbed on the TiO2 surface through different anchoring groups. They concluded that TiO2 is able to harvest electrons from the excited EY molecules, thus generating long-lived charge-separated states, which eventually lead to the electron transfer to the Co-catalyst and the reduction process. A similar reductive pathway has also been observed by Lakadamyali et al.,28 who studied the co-adsorption of the CoP catalyst and a ruthenium dye RuP on TiO2. The photo-excitation of RuP induces an electron injection into the conduction band of TiO2. The photo-electrons are then transferred to CoP, where the H2 formation occurs. The photo-excitation of Co(I)-porphyrin on TiO2 in acetonitrile–pyridine solution has also been studied,29 showing that after the rapid electron injection from Co to TiO2 and the coordination of pyridine to Co, the undesired charge recombination is significantly slowed down.
Among the heterocyclic molecules, the porphyrin derived tetra-aza macro-cycle, constituted of four pyridine rings, is named pyrphyrin (Py) but also known as an Ogawa porphyrin like ligand. Pyrphyrin has been introduced first by Ogawa et al.30 in 1984. Later, alkylated pyrphyrin has also been synthesized and its optical properties have been characterized.31 More recently, metal-centered pyrphyrins have been studied both experimentally and theoretically to determine their UV-visible spectra in solution.32–34
The need for new, promising, and feasible photo-catalysts for water reduction and the unexplored potential of pyrphyrin adsorbed on the TiO2 surface are the motivations for the present work. To the best of our knowledge, this is the first time that pyrphyrin on semiconductors is investigated. It is generally accepted that anatase phase of TiO2 exhibits higher photocatalytic activity than rutile TiO2,35 which resulted in theoretical investigation of water–TiO2 interactions mostly with the anatase phase.36 However, in this study only the rutile phase is considered, which is easier to obtain as a high quality single crystal37 and, for this reason, it is going to be employed in upcoming experimental studies of the catalytic activity of supported-CoPy.
We study the structural and electronic properties of the complex, CoPy, adsorbed on the rutile(110) surface, by means of density functional theory (DFT). In the following, we first briefly describe the applied methodology and the models used for the molecule, the surface and the complex. Next, we discuss the possible adsorption configurations of CoPy@rutile(110), and finally we analyze in detail the electronic structure of the most stable configuration.
II. Computational methodology
Electronic structure calculations are performed at the Kohn–Sham DFT level, employing the Gaussian and plane wave (GPW) formalism as implemented in the CP2K/QUICKSTEP package.38 Double-zeta valence plus polarization (DZVP) basis sets, optimized on molecular geometries (Mol-Opt method),39 are employed for all atomic kinds. A cutoff of 600 Ry is used for the auxiliary plane wave basis set. The interaction between the valence electrons and the atomic cores is described through norm-conserving Goedecker–Teter–Hutter (GTH) pseudo potentials.40 The valence shells contain 12, 6, 17, 4, 1, and 5 electrons for Ti, O, Co, C, H, and N, respectively. Periodic boundary conditions are always applied.As exchange–correlation functional, the general gradient approximation (GGA) by Perdew–Burke–Ernzerhof (PBE)41 is used. The dispersion interactions are corrected according to the Grimme-D3 scheme42 for the optimization of the geometries. This level of theory has been proved to be sufficiently accurate to describe the structural properties of the materials involved in this study. Namely, the lattice parameters of bulk rutile turn out to be in agreement with the experimental values within an error of 1%.43 However, PBE is known to underestimate the energy gap of TiO2 as for other oxides.44,45 The most commonly adopted solution to this deficiency is the use of suitable hybrid functionals that can reproduce the experimental value.46,47 For the specific case of TiO2, we find, in agreement with previous studies, that the best accuracy in the energy gap is achieved by applying the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.43,48,49 All hybrid functional calculations are performed with the help of the auxiliary density matrix method (ADMM),50–52 which provides a significant speed up and makes it possible to compute the electronic structure of several hundreds of atoms of condensed matter systems. The required ADMM basis sets have been optimized to reproduce the results of full hybrid functional calculations with very high accuracy. Despite the speed up obtained with ADMM, hybrid functional geometry optimization is still computationally very demanding and does not produce important changes with respect to the PBE optimization. Therefore, our strategy consists in carrying out the refinement of the electronic structure of PBE-optimized geometry using the HSE06 hybrid functional.
III. Structural models
A. Rutile: bulk and (110) surface
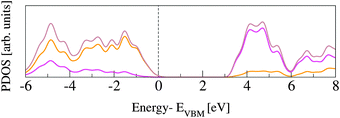
The rutile lattice belongs to the P42/mnm (No. 136) tetragonal space group.53,54 In the bulk, each Ti atom is coordinated by six O atoms, while the O atoms are three-fold coordinated by Ti. In order to assess our PBE computational set up, the lattice parameters are optimized for a 3 × 3 × 3 supercell (162 atoms). This supercell is sufficiently large to converge the bulk structural properties, which turn out to be in very good agreement with previously published data, from both experimental and DFT studies (see Table 1). The corresponding band gap energies, Egap, computed for the PBE and the HSE06 functionals are reported in Table 2 and also compared to previous studies. All GGA and LDA results underestimate Egap by more than 1.2 eV, while PBE0 overestimates it by about the same amount. Only the value obtained with HSE06 approximates the experiment with reasonable accuracy. The slight discrepancies between results obtained with the same functional can be ascribed to different basis sets and pseudopotentials.Fig. 1 shows projected density of states (PDOS) for O and Ti atoms in bulk rutile. The highest occupied states have O-2p character, whereas the lowest unoccupied states are Ti-3d, in agreement with previously published calculations.60,61 The hybridization between O-2p and Ti-3d states results in covalent bonding.62
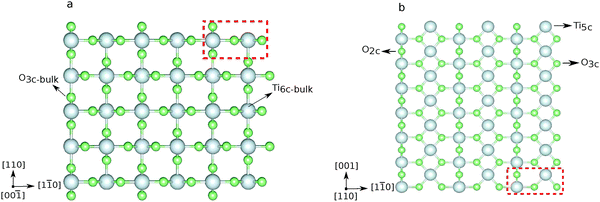
The (110) surface is the most stable surface of rutile, and also the most frequently studied and used one for applications.63 To model such a surface, a symmetric slab consisting of a few atomic layers is cut out from the bulk cleaving along the (110) plane. Above the surface, a sufficiently large amount of vacuum space (20 Å) is added to avoid interactions with the periodic images in the perpendicular direction. The surface unit cell contains two Ti atoms, which lay on the same plane, and four O atoms, two on the same plane as Ti, one above (sticking out O) and one below. One surface Ti atom is still six-fold coordinated, as in the bulk, while the second is five-fold coordinated. Among the O atoms, three are still three-fold coordinated, while the sticking out one is two-fold coordinated. This latter dangling O atom is a particularly active species, which can lead to the formation of vacancies at the surface, or be saturated. Fig. 2 displays the top and side view of a 3 × 7 slab, containing five atomic layers. We label the surface three-fold and two-fold coordinated O atoms with O3c and O2c, while the bulk oxygens are labeled O3c-bulk. We also distinguish between the bulk Ti atoms, labeled Ti6c-bulk, and the under-coordinated Ti atoms at the surface, Ti5c. In order to determine the optimal number of layers for the slab model, we tested the convergence of the surface energy. The surface energy is calculated as
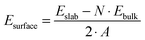 | (1) |
Slabs from 3 to 9 layers have been considered (see ESI†). We conclude that a 5 layer slab is sufficient to model the rutile(110) surface. The surface energy of the 3 × 3 × 5 slab is 0.72 J m−2, in quite good agreement with the values found in the literature.63
The band gap calculated by HSE06 for the rutile slab of five layers, where both exposed surfaces are fully relaxed, is 3.18 eV, in agreement with the experiment.64 The reduction of the energy gap at the surface is due to the presence of energy states in the gap, which are generated by electrostatic shifting of Ti5c states towards O2c and O3c-bulk bands, also discussed in ref. 65. We also computed the electronic properties for slabs of different sizes, concluding that the slab of five layers is a good compromise between accuracy and efficiency, see ESI.†
B. Pyrphyrin
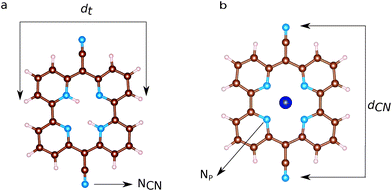
Ball and stick sketches of Py and CoPy are shown in Fig. 3. Py is characterized by CN groups binding to the pyridine rings via sp2 hybridized bridging carbons. We label the nitrogen atoms of the cyano groups NCN to distinguish them from the pyridine nitrogens at the center of the molecule (Np). Two Np are protonated in Py at anti positions,66 while the protons are replaced by the Co(II) cation in CoPy. In the gas phase, both molecules are planar with a vanishing dipole, as discussed in ref. 34. In the center of the molecule, the four Np are symmetrically coordinating Co in CoPy, while the protonated nitrogens in Py are displaced outwards. Along the axis of the cyano groups, dCN, the molecule is slightly shorter for CoPy with respect to Py, due to the interaction between Co(II) and the electronegative nitrogens. Some structural parameters are reported in Table 3.| Molecule | Distances | Length [Å] |
|---|---|---|
| Py | d CN | 11.96 |
| Np–Np (prot.) | 3.98 | |
| Np–Np (not prot.) | 3.80 | |
| d t | 9.45 | |
| CoPy | d CN | 11.78 |
| Np–Np | 3.77 | |
| d t | 9.57 | |
Table 4 shows the energy gaps between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) as computed for Py and CoPy with the PBE and HSE06 functionals. The presence of Co(II) slightly reduces the energy gap; the effect is more pronounced with HSE06, for more discussion see ESI.† Calculations with CoPy are always performed with spin polarization. The lowest energy spin state turns out to be a doublet and the spin density is localized exclusively at the Co center. The HOMO of CoPy in the gas phase has major contributions from the cyano groups, the pyridine carbons, and the Np, but it is also present at Co(II) centers. The LUMO, instead, is uniformly distributed over the pyridine CH groups, the central C atoms, and the Np, but it does not have significant contributions from the cyano groups and the Co(II). The two frontier orbitals of the gas phase molecule are displayed in Fig. 4.
| Molecule | Functional | E gap [eV] |
|---|---|---|
| Py | PBE | 1.52 |
| Py | HSE06 | 2.23 |
| CoPy | PBE | 1.46 |
| CoPy | HSE06 | 2.03 |
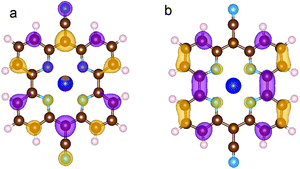 | ||
| Fig. 4 HOMO (a) and LUMO (b) of CoPy in the gas phase. The displayed isosurfaces are obtained at the value of ±0.236 e Å−3. | ||
C. CoPy adsorption on rutile(110)
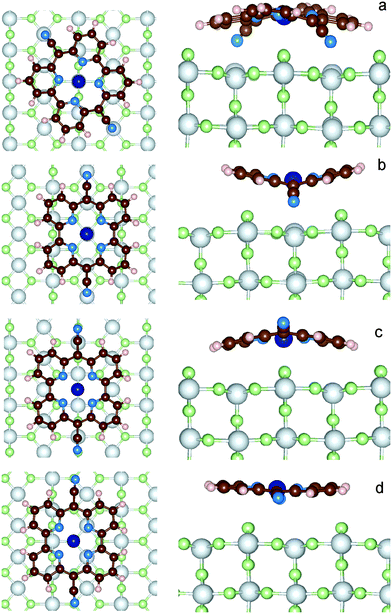
In order to find possible adsorption sites of CoPy on rutile, it is necessary to explore the potential energy surface of the CoPy@rutile complex. We started eleven independent optimizations, changing the initial coordinates of the gas-phase optimized CoPy on rutile. The molecule has always been positioned parallel to the surface at a distance a few Å apart from the topmost atoms moving it rigidly by changing the position of Co(II) and the two NCN with respect to the surface O2c and Ti5c atoms and rotating the molecular axis parallel to the surface (more details in the ESI†). The optimization is carried out by relaxing the molecular geometry and the two top-most layers of the rutile slab. The other three slab layers are kept fixed at bulk coordinates. From these eleven starting positions, only four distinct stable configurations have been obtained. These four structures are displayed in Fig. 5 and are named model-a, b, c, and d. The adsorption energy (Eads) is calculated as| Eads = Ecomplex − (Eslab + Emol) | (2) |
| Edispads = Edispcomplex − (Edispslab + Edispmol) | (3) |
The dispersion contribution is always attractive. The distortion energy of CoPy (Edist) is, instead, the increase in molecular energy due to the geometrical changes induced by the interaction with the surface,
| Edist = Emold − Emol | (4) |
IV. Results and discussion
The resulting four adsorption configurations of CoPy@rutile are characterized by different energies and structural parameters. In Table 5, the above defined Eads, Edispads, Edist values are reported together with the average height of the molecule on the Ti5c layer (hav), the difference in height between the lowest and the highest atoms in the molecule (Δh), which is a measure of the deviation from planarity, the distance between the two NCN atoms (dCN), and the minimum distance between an atom of the molecule and an atom of the surface (dmin).| Model | E ads [eV] | E dispads [eV] | E dist [eV] | h av [Å] | Δh [Å] | d CN [Å] | d min [Å] | Pair |
|---|---|---|---|---|---|---|---|---|
| a | −4.18 | −2.62 | 0.57 | 3.67 | 2.16 | 10.86 | 2.13 | NCN–Ti5c |
| b | −3.56 | −2.34 | 0.40 | 3.89 | 2.34 | 11.14 | 2.22 | NCN–Ti5c |
| c | −3.35 | −2.89 | 0.24 | 3.52 | 1.66 | 11.51 | 2.25 | Co(II)–O2c |
| d | −2.49 | −2.42 | 0.09 | 3.94 | 0.95 | 11.65 | 2.77 | H–O2c |
As a general observation, the interaction to the surface is relatively weak and the major contribution is due to the dispersion term, which varies from 60% to almost 100% of the adsorption energy. The strongest adsorption is obtained for model-a, where the molecule is bent along the dCN axes such that both the NCN atoms can sit exactly on top of Ti5c centers, while Co(II) coordinates two O2c. The interaction is further favored by the upward displacement of the involved Ti atoms by 0.26 Å, thus reducing the N–Ti distance to only 2.13 Å. CoPy is bent along both axes, even if the curvature is more pronounced along dCN, reducing the dCN distance by about 1 Å with respect to the gas phase structure. The geometrical changes correspond to a distortion energy of 0.57 eV. Subtracting from the total adsorption energy the distortion energy, we obtain an interaction energy of −4.75 eV, of which −2.62 eV are attributed to dispersion. The remaining −2.13 eV are mainly due to the chemical bonding between NCN and Ti (≈−1 eV per NCN), which, as it will be discussed in the following, is responsible for the rehybridization of the molecular HOMO with the surface states.
In model-b, both NCN and Co(II) are sitting on top of Ti5c centers, and the dCN axis is oriented along the [001] lattice direction, i.e. rotated by about 30 degrees with respect to model-a. Also in this case, the closest contact between the molecule and the surface is the N–Ti interaction, and the involved Ti atoms are displaced upwards by 0.15 Å. However, in this position, some O2c atoms happen to be in proximity of the pyridine rings, which consequently bend outwards. Overall, the distance between the molecule and the surface (hav = 3.89 Å) is larger than in model-a, and, even though the molecular distortion energy is smaller, the adsorption interaction is weaker. This can be explained in terms of the repulsive electrostatic interaction between Co(II) and Ti and the reduced dispersion contribution due to the larger average distance.
Like in model-a, in model-c Co coordinates the two closest dangling O. The NCN are on top of the surface oxygen giving rise to a repulsive interaction, which causes the upwards bending along the dCN axis. Since only the cyano groups are displaced, the molecule is less distorted than in the two previous configurations, as also indicated by its dCN length and the computed distortion energy. In average, CoPy is closer to the surface and, as a consequence, the dispersion energy term is larger. By subtracting the distortion energy and the dispersion energy from the total adsorption energy, the remaining interaction energy amounts to 0.70 eV.
Finally, in model-d, the most active molecular centers, Co(II) and NCN, are too far from the under-coordinated atoms at the surface. The molecular structure is only slightly modified upon adsorption, since the only attractive interaction is attributed to the dispersion forces. This is a classical example of physisorption, as also confirmed by the almost equal values of Eads and Edispads. Rather weak physisorption has been already reported for the case of a single pyridine ring adsorbed on TiO2.67
The standing adsorption of CoPy on the rutile(110) surface has also been examined. CoPy is positioned perpendicular to the (110) surface, with one NCN on top of one Ti5c, since between these two species the binding is expected to be strongest. After the optimization of the structure, the distance between NCN and Ti5c is 2.09 Å. The resulting adsorption energy Eads is −1.61 eV, i.e. 2.5 eV lower than for the molecule adsorbed flat. The obvious reasons for the weaker binding are that only one direct NCN–Ti5c interaction is available and the significantly smaller contribution of dispersion (−0.65 eV), given the standing geometry.
Pratik et al.68 modeled several different porphyrin-derived molecules adsorbed both horizontally and vertically on anatase nanoparticles. Their calculations show that while horizontal orientation of porphyrin on anatase has Eads of −2.6 eV, porphyrin-4-NO2 has −9.30 eV, and porphyrin-4-NH2 has −4.33 eV, vertical attachment of 1-NMe2–porphyrin-1-COOH results in Eads of −2.80 eV.
In summary, the most effective interactions for the adsorption of CoPy on rutile are those between NCN and the Ti5c surface atoms, followed by the Co(II)–O2c coordination. These are maximized in model-a, which turns out to be the most stable adsorption site. Therefore, the following analysis of the electronic properties of the CoPy@rutile is based on this model.
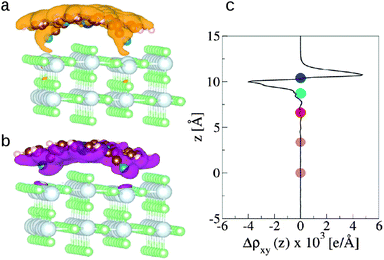
The redistribution of the electronic charge induced by the adsorption is shown in the electron density difference maps. The electron density difference is calculated by subtracting from the total density of the complex ρcomplex(r) the individual electron densities of CoPy and the slab, at the same coordinates as in the complex
| Δρ(r) = ρcomplex(r) − (ρslab(r) + ρmol(r)). | (5) |
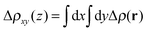 | (6) |
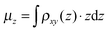 , amounts to 0.5 D.
, amounts to 0.5 D.
The total and projected densities of states, TDOS and PDOS, provide further information on the redistribution of the molecular orbitals upon adsorption and on the nature of the interaction. Spin polarization has been used for all calculations; however, not negligible spin density difference is observed only on Co(II) (see ESI†). Therefore, we plot the distinct alpha and beta spin DOS solely for Co(II). We compare the density of states calculated for the CoPy@rutile complex with those calculated for the optimized molecule in the gas phase and for the pristine rutile surface. All PDOS plots related to the complex are aligned with respect to the corresponding VBM and normalized by the number of atoms considered in the projection.
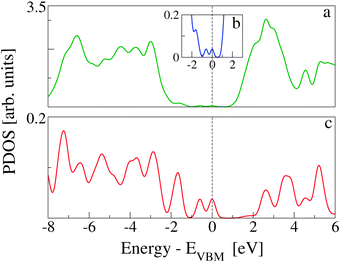
In Fig. 7, the TDOS of CoPy@rutile (top panel) is compared to the contribution obtained from its projection on the CoPy molecule only (bottom panel). The different normalization factor makes the low intensity features of the molecular states appear with more evidence in the bottom panel. The HOMO of the complex is clearly a molecular state of CoPy. The LUMO, on the other hand, is mainly located on the rutile slab. The calculated energy gap turns out to be 1.06 eV, which is 1.22 eV smaller than the gap of rutile(110). The lowest unoccupied states with major contributions on CoPy are about 2.5 eV above the VBM.
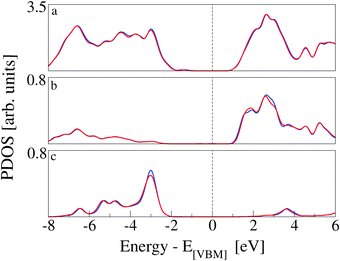
The effects of CoPy adsorption on the DOS of the slab are evaluated by projecting only on the slab's atoms and comparing to the PDOS computed for the pristine slab. In Fig. 8, we distinguish between contributions from surface titanium atoms (b), and surface oxygen atoms (c). The signature of the surface Ti5c atoms is the growth in intensity of the left shoulder of the lowest band of unoccupied states, as compared to PDOS of bulk Ti atoms (see Fig. 1). The center of this band is at about 1.5 eV. Of the 21 Ti5c atoms at the surface in our model slab, only two strongly interact with the molecule via the NCN linkers and are responsible for the small difference between the red (CoPy@rutile) and the blue (clean) curves in panel b. The band of the highest occupied states in rutile is mainly constituted of O-2p orbitals. The differences between the bulk (see Fig. 1) and the surface are more evident in this case since the surface oxygen PDOS present one relatively narrow band at about −3 eV and lower intensity features at lower energies. This pronounced feature is formed by the highest occupied surface states. The effects of CoPy adsorption in the O2c PDOS are ascribed to the two surface oxygens interacting with Co(II).
The electronic structure rearrangements occurring upon adsorption have their major effects on the CoPy molecular orbitals. The PDOS on CoPy adsorbed and in the gas phase are compared in Fig. 9. All the plots are aligned with the HOMO at zero eV. The PDOS of CoPy@rutile (red curves) shows a general broadening of the bands. The occupied states on Co (a), Np (b), and C (d) present the same main features as in the gas phase. The lowest unoccupied states are shifted to higher energies by about 0.5 eV. The projected energy gap becomes 0.48 eV larger than the HOMO–LUMO gap in the gas phase, if one considers the lowest unoccupied state with major contributions on the adsorbed molecule, which actually is at 2.5 eV above the HOMO. The sharp bands characterizing the PDOS on the NCN in the gas phase are most strongly affected by the interaction with the surface. The two localized molecular states at −3.7 eV and −5.5 eV are replaced by a broad distribution due to the re-hybridization with the Ti states. Moreover, the interaction has a clear effect on the charge distribution corresponding to the HOMO of CoPy. As shown in Fig. 10, the orbital extends in the region between the molecule and the surface, thus strengthening the chemical bonding. This electronic rearrangement explains the bending along dCN and the upward displacement of the Ti atoms.
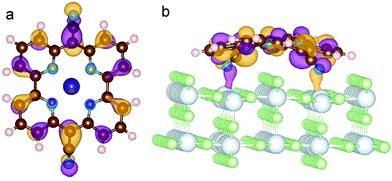 | ||
| Fig. 10 Representation of the HOMO of CoPy adsorbed on rutile(110). Top (a) and side (b) view. The displayed isosurfaces are obtained at ±0.236 e Å−3. | ||
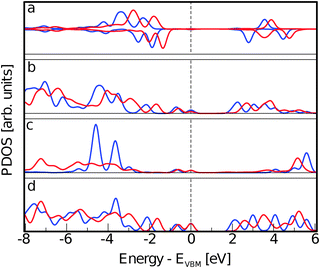
Finally, we separate the contributions to the DOS ascribed to the two Ti5c and the two O2c atoms more directly involved in the interaction. The resulting PDOS are plotted in Fig. 11 and compared with the PDOS obtained from all the Ti5c and O2c present at the slab surface. While no significant difference is observed among the occupied states, a clear effect of the interaction is present for the lowest unoccupied states localized at Ti5c. In particular, we observe the increase in intensity of the first peak and the consequent depletion at higher energies. This result implies the presence of available empty states on the Ti atoms that are also involved in the extension of the molecular HOMO state. On the other hand, the occupied states localized on the surface O atoms are more than 2 eV lower in energy than the CoPy HOMO and are not significantly perturbed by the adsorbate.
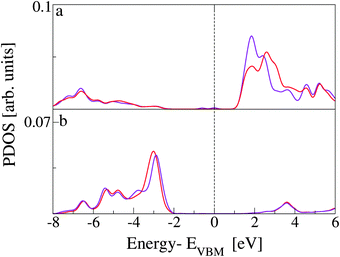 | ||
| Fig. 11 (a) PDOS on Ti5c atoms. The red line is the same PDOS shown in panel b of Fig. 8, related to the complex. The purple line is related to the only two surface Ti atoms interacting directly with NCN. (b) PDOS on O2c atoms. Red line is the same PDOS presented in panel c of Fig. 8. The purple line is obtained by the projection on the two oxygen atoms coordinating the Co(II) in CoPy@rutile(110). | ||
V. Conclusions
We have investigated the adsorption of a porphyrin derived heterocyclic molecule, CoPy, on the rutile(110) surface. This new type of heterocyclic molecule has been experimentally proved to be an active catalyst for hydrogen evolution reactions. However, there are no extensive studies on its properties and, to our knowledge, this is the first time that the adsorption of one of these has been considered. We observe electronic structure rearrangements occurring upon adsorption, mainly due to the interaction of the cyano groups of CoPy with the five-coordinated Ti atoms of rutile(110). The projected densities of states on the different involved species reveal that the molecular orbitals on the NCN atoms undergo a rehybridization, the HOMO is located at the molecule, and the lowest unoccupied states of CoPy are shifted to higher energies. Effects of the electronic redistribution are also recognized from the Ti5c PDOS and the polarization of the electronic density across the molecular plane. The first band of unoccupied states is mainly on rutile and extends from 1.1 to 2.0 eV, with a maximum at 1.5 eV. The lowest unoccupied states localized on CoPy are instead beyond 2.5 eV, i.e., at higher energy with respect to the LUMO of the gas phase molecule. Hence, the adsorption produces a significant reduction of the energy gap with respect to both pristine rutile TiO2 and the isolated molecule, which should facilitate absorption of light in the visible range. This opens up the possibility of achieving electron injection from CoPy to rutile, with a consequent efficient electron–hole separation.On the other hand, but for a rigid shift with respect to the HOMO, we do not observe strong modifications of the electronic structure at the Co(II) center. From these results we expect that the catalytic properties of CoPy are preserved upon adsorption. We plan to extend the study on this system also considering the co-adsorption of water and hydrogen and possible reaction mechanisms leading to the production of molecular hydrogen. We expect that by functionalizing pyrphyrin with different linkers and replacing Co with other transition metals, a further tuning of the coupling with the oxide is possible and improved water splitting performance can be achieved.
Acknowledgements
We gratefully acknowledge the financial support from the University of Zurich, the University Research Priority Program “Solar Light to Chemical Energy Conversion” (LightChEC), National Centres of Competence in Research–Materials Revolution: Computational Design and Discovery of Novel Materials (NCCR–MARVEL), and computing resources from the Swiss National Supercomputer Centre (CSCS) under the project ID s425.References
- W. T. Eckenhoff and R. Eisenberg, Dalton Trans., 2012, 41, 13004 RSC
.
- N. Armaroli and V. Balzani, Angew. Chem., Int. Ed., 2007, 46, 52 CrossRef CAS PubMed
.
- M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901 CrossRef CAS PubMed
.
- T. L. LeValley, A. R. Richard and M. Fan, Int. J. Hydrogen Energy, 2014, 39, 16983 CrossRef CAS PubMed
.
- E. Seker, Int. J. Hydrogen Energy, 2008, 33, 2044 CrossRef CAS PubMed
.
- A. T. Ashcroft, A. K. Cheetham, J. S. Foord, M. L. H. Green, C. P. Grey, A. J. Murrell and P. D. F. Vernon, Nature, 1990, 344, 319 CrossRef CAS PubMed
.
- S. G. Avcioglu, E. Ozgur, I. Eroglu, M. Yucel and U. Gunduz, Int. J. Hydrogen Energy, 2011, 36, 11360 CrossRef CAS PubMed
.
- M. Grätzel, Nature, 2001, 414, 338 CrossRef PubMed
.
- M. Wang, Y. Na, M. Gorlov and L. Sun, Dalton Trans., 2009, 6458 RSC
.
- A. J. Esswein and D. G. Nocera, Chem. Rev., 2007, 107, 4022 CrossRef CAS PubMed
.
- S. Losse, J. G. Vos and S. Rau, Coord. Chem. Rev., 2010, 254, 2492 CrossRef CAS PubMed
.
- X. Hu, B. S. Brunschwig and J. C. Peters, J. Am. Chem. Soc., 2007, 129, 8988 CrossRef CAS PubMed
.
- M. Guttentag, A. Rodenberg, R. Kopelent, B. Probst, C. Buchwalder, M. Brandstätter, P. Hamm and R. Alberto, Eur. J. Inorg. Chem., 2012, 59 CrossRef CAS PubMed
.
- H. Imahori and S. Fukuzumi, Adv. Funct. Mater., 2004, 14, 525 CrossRef CAS PubMed
.
- L. Si and H. He, J. Phys. Chem. A, 2014, 118, 3410 CrossRef CAS PubMed
.
- B. H. Solis, A. G. Maher, T. Honda, D. C. Powers, D. G. Nocera and S. Hammes-Schiffer, ACS Catal., 2014, 4, 4516 CrossRef CAS
.
- S. Soman, Comments Inorg. Chem., 2015, 35, 82 CrossRef CAS PubMed
.
- Z. Han and R. Eisenberg, Acc. Chem. Res., 2014, 47, 2537 CrossRef CAS PubMed
.
- S. Berardi, S. Drouet, L. Francas, C. Gimbert-Surinach, M. Guttentag, C. Richmond, T. Stoll and A. Llobet, Chem. Soc. Rev., 2014, 43, 7501 RSC
.
- A. Rodenberg, M. Orazietti, B. Probst, C. Bachmann, R. Alberto, K. K. Baldridge and P. Hamm, Inorg. Chem., 2015, 54, 646 CrossRef CAS PubMed
.
- C. Kutal, J. Chem. Educ., 1983, 60, 882 CrossRef CAS
.
- C. G. Garcia, J. F. de Lima and N. Y. M. Iha, Coord. Chem. Rev., 2000, 196, 219 CrossRef CAS
.
- R. L. Milot, G. F. Moore, R. H. Crabtree, G. W. Brudvig and C. A. Schmuttenmaer, J. Phys. Chem. C, 2013, 117, 21662 CAS
.
- H. Imahori, S. Kang, H. Hayashi, M. Haruta, H. Kurata, S. Isoda, S. E. Canton, Y. Infahsaeng, A. Kathiravan, T. Pascher, P. Chábera, A. P. Yartsev and V. Sundström, J. Phys. Chem. A, 2011, 115, 3679 CrossRef CAS PubMed
.
- L.-L. Li and E. W.-G. Diau, Chem. Soc.
Rev., 2013, 42, 291 RSC
.
- F. Lakadamyali and E. Reisner, Chem. Commun., 2011, 47, 1695 RSC
.
- M. Yin, S. Ma, C. Wu and Y. Fan, RSC Adv., 2015, 5, 1852 RSC
.
- F. Lakadamyali, A. Reynal, M. Kato, J. R. Durrant and E. Reisner, Chem. – Eur. J., 2012, 18, 15464 CrossRef CAS PubMed
.
- D. Achey, S. Ardo and G. J. Meyer, Inorg. Chem., 2012, 51, 9865 CrossRef CAS PubMed
.
- S. Ogawa, R. Narushima and Y. Arai, J. Am. Chem. Soc., 1984, 106, 5760 CrossRef CAS
.
- S. Ogawa, T. Uchida, T. Uchiya, T. Hirano, M. Saburi and Y. Uchidac, J. Chem. Soc., Perkin Trans. 1, 1990, 1649 RSC
.
- C. Pierre, J.-M. Vincent, J.-B. Verlhac, C. Courseille, A. Dautant and C. Mathoniere, New J. Chem., 2001, 25, 522 RSC
.
- Z. Zhu, K. Takano, A. Furuhama, S. Ogawa and S. Tsuchiya, Bull. Chem. Soc. Jpn., 2007, 80, 686 CrossRef CAS
.
- R. Ibrahim, S. Tsuchiya and S. Ogawa, J. Am. Chem. Soc., 2000, 122, 12174 CrossRef CAS
.
- L. Tim, H. Sandamali, T. Junguang, K. Alan, S. Eli and B. Matthias, Sci. Rep., 2014, 4, 4043 Search PubMed
.
- J. Chen, Y.-F. Li, P. Sit and A. Selloni, J. Am. Chem. Soc., 2013, 135, 18774 CrossRef CAS PubMed
.
- A. G. Thomas and K. L. Syres, Chem. Soc. Rev., 2012, 41, 4207 RSC
.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103 CrossRef CAS PubMed
.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed
.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- T. L. Bahers, M. Rérat and P. Sautet, J. Phys. Chem. C, 2014, 118, 5997 CAS
.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792 CrossRef CAS PubMed
.
- J. Muscat, V. Swamy and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 224112 CrossRef
.
- F. Labat, P. Baranek and C. Adamo, J. Chem. Theory Comput., 2008, 4, 341 CrossRef CAS
.
- H. Xiao, J. Tahir-Kheli and W. A. Goddard, J. Phys. Chem. Lett., 2011, 2, 212 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS PubMed
.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed
.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348 CrossRef CAS
.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2009, 5, 3010 CrossRef CAS
.
- M. Guidon, F. Schiffmann, J. Hutter and J. VandeVondele, J. Chem. Phys., 2008, 128, 214104 CrossRef PubMed
.
- C. J. Howard, T. M. Sabine and F. Dickson, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 462 CrossRef
.
- J. K. Burdett, T. Hughbanks, G. J. Miller, J. W. Richardson and J. V. Smith, J. Am. Chem. Soc., 1987, 109, 3639 CrossRef CAS
.
- H. Perron, J. Vandenborre, C. Domain, R. Drot, J. Roques, E. Simoni, J. J. Ehrhardt and H. Catalette, Surf. Sci., 2007, 601, 518 CrossRef CAS PubMed
.
- Z. Y. Zhao, J. Phys. Chem. C, 2014, 118, 4287 CAS
.
- H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Theor. Chem. Acc., 2007, 117, 565 CrossRef CAS
.
- L. Kavan, M. Grätzel, S. E. Gilbert, C. Klemenz and H. J. Scheel, J. Am. Chem. Soc., 1996, 118, 6716 CrossRef CAS
.
- R. Evarestov and Y. Zhukovskii, Surf. Sci., 2013, 608, 226 CrossRef CAS PubMed
.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53 CrossRef CAS
.
- C. Lun Pang, R. Lindsay and G. Thornton, Chem. Soc. Rev., 2008, 37, 2328 RSC
.
- S.-C. Li and U. Diebold, J. Am. Chem. Soc., 2010, 132, 64 CrossRef CAS PubMed
.
- T. R. Esch, I. Gadaczek and T. Bredow, Appl. Surf. Sci., 2014, 288, 275 CrossRef CAS PubMed
.
- S. Fujiyoshi, T.-A. Ishibashi and H. Onishi, J. Phys. Chem. B, 2005, 109, 8557 CrossRef CAS PubMed
.
- A. T. Paxton and L. Thiên-Nga, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1579 CrossRef CAS
.
- We also optimized the structure of the second isomer of metal-free pyrphyrin finding that when the two protons reside on the same side the molecule is by 0.23 eV less stable.
- S. Suzuki, Y. Yamaguchi, H. Onishi, T. Sasaki, K. Fukui and Y. Iwasawa, J. Chem. Soc., Faraday Trans., 1998, 94, 161 RSC
.
- S. M. Pratik and A. Datta, Phys. Chem. Chem. Phys., 2013, 15, 18471 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp02767e |
| This journal is © the Owner Societies 2015 |