Reactive force fields made simple

Abstract

Generating a reactive force field for a given chemical reaction is turned from a many-months project for experts into a task of a few hours for a non-specialist, by joining the newly developed quantum-mechanically derived force field (QMDFF) and Warshel's time-tested empirical valence bond (EVB) idea. Three first example applications demonstrate that this works not just for simple atom exchange but also for more complicated reactions.

---

In the past decade, reactive force fields¹ have evolved into a general commodity for simulating reactive events with millions or even billions of explicitly treated atoms. Frequently used reactive force fields like COMB and ReaxFF² aim at universal applicability across the whole periodic table of elements. They achieve this in a restricted sense: truly general parameters have not been established yet. Instead, different parameter sets exist, tuned to specific chemical systems and reactions. To construct such parameter sets requires either expert knowledge,² or global optimization tools^3–9 and considerable effort in setting up the reference data. Hence, there is strong need to find alternative ways of constructing reactive force fields.

One important ingredient for this was established recently, with the quantum-mechanically derived force field (QMDFF)¹⁰ by one of the present authors. It eliminates the task of assembling reference data and replaces it with a fixed list of a few items: vibrational frequency information (Hessian matrix), Hirshfeld charges and bond orders at the desired minimum energy configuration. This suffices to generate the QMDFF, covering the whole potential well of the reference structure. Thus, in contrast to most traditional force fields (reactive or non-reactive), there is no need to assemble large sets of reference data, a process for which no good recipes exist and which hence has to be done in lengthy trial-and-error iterations. Nevertheless, the agreement between QMDFF values and reference data is excellent, as documented by a broad array of tests.¹⁰ Also in contrast to many standard force fields, QMDFF is fully anharmonic and allows for smooth dissociation of covalent bonds into atoms, achieving reasonably accurate atomization energies. The price to pay for this combination of simplicity, generality and accuracy is strict specificity for just one potential well of just one chemical system. Hence, apart from dissociation into atoms, no chemical reactions can be described, which typically proceed from one (reactant) minimum over a barrier into another (product) minimum.

However, to fix this latter shortcoming, several well-known recipes exist to couple two non-reactive force fields. The adiabatic reactive molecular dynamics (ARMD) method by Meuwly^11,12 and the reactive molecular dynamics (RMDff) method by Westmoreland¹³ employ switching functions, depending on time or on the spatial reaction coordinate, respectively. The empirical valence bond (EVB) method by Warshel^14,15 employs a different idea: the two force fields are put on the diagonal of the (symmetric) EVB matrix, a suitable off-diagonal coupling element is set up and the EVB matrix is diagonalized. The lower eigenvalue is the desired EVB potential. Besides a simple constant coupling element, several more sophisticated EVB coupling recipes have been proposed: Chang and Miller¹⁶ have used a generalized Gaussian function, without any fitting but with an additional frequency calculation at the transition state. Truhlar and coworkers¹⁷ generate the coupling term via a Shepard interpolation between additional reference data points. In a series of papers, Sonnenberg and Schlegel^18–20 have extended the Chang–Miller approach towards modeling the coupling term with a distributed Gaussian basis.

The core idea communicated here is to apply the EVB force-field coupling method to join two or more QMDFFs, forming a truly reactive force field as result. Clearly, however, ARMD and RMDff and other coupling recipes would also be applicable. Of course, frequently and for a long time, EVB, ARMD and RMDff have been used to couple traditional force fields (see e.g.ref. 21, 22 and literature cited therein). Frequently, as in those works just cited, there also is a need to supplement or improve the traditional force fields themselves. One of they key points here is that this should not be necessary for QMDFF, reducing the task of generating a reactive force field to the far simpler requirement of establishing the force-field coupling.

As first demonstration example, we have selected the textbook S_N2 reaction Cl⁻ + H₃CBr → ClCH₃ + Br⁻, as a simple atom-exchange reaction. To document that EVB-QMDFF works not only for this simple type of reaction, we also present data for two more difficult reactions. In all three cases, these were the very first reactions we tried, so no attempt was made to find particularly suitable cases.

QMDFFs were generated for both reactant and product minima, as described in ref. 10 (readers are advised to consult this paper for all further technical details on QMDFF itself). As quantum-chemical reference level, density-functional theory (DFT) was chosen, with the D3 dispersion correction.²³ In the first two cases, DFT calculations were performed with the ORCA program package.²⁴ For the S_N2 example, the hybrid PBE0 exchange–correlation functional²⁵ was used, with a rather good basis set and integration grid (def2-aug-TZVPP, “grid5”),^26–29 as well as “tight” thresholds for the SCF iterations and geometry optimizations. To demonstrate independence from the level of reference theory, we have chosen the BP86 exchange–correlation functional³⁰ for the Diels–Alder example, with standard thresholds and grids and with the modest SVP basis. The results for the olefin metathesis reaction are based on standard PBE-D3/def2-TZVP calculations.

Using standard ORCA protocols, the minima were locally optimized, followed by frequency calculation and determination of Hirshfeld charges. The information thus obtained at the converged minimum geometries suffices to set up the QMDFFs.

To generate a series of structures between these minima that also contains the transition state (TS) that interconverts between these two minima, the following procedure was employed for the S_N2 reaction: the TS was located by standard local geometry optimization. For simplicity, the remaining 37 structures shown in the plots below were generated by linear extra- and interpolation of the cartesian coordinates of all atoms, between either minimum and the TS. For this reaction, this corresponds fairly closely to most definitions of a reaction path. Additionally, this slightly non-standard prescription emphasizes that there is no need to locate a true reaction path of any kind. For the Diels–Alder example, a similar series of structures was generated with a relaxed scan of the two characteristic C–C distances, starting from the optimized transition state structure for this reaction.

As shown in eqn (1), at each of the 40 structures on this piecewise linear scan (characterized by the C–Cl distance R), the two QMDFFs F₁ and F₂ obtained before are combined via the EVB matrix:

The EVB-QMDFF potential energy is the lower-energy eigenvalue of this matrix, which can be generated directly by the well-known analytic prescription of the textbook “2-level system” (cf. eq. (2) in ref. 15).

As off-diagonal coupling element C(R), two approaches were tried: (1) a simple constant (no R-dependence, one parameter to fit), and (2) the simplest possible Gaussian with two parameters, given in eqn (2):

C(R) = a exp(−b{F₁(R) − F₂(R)}²) (2)

The latter choice is suggested by the finding that for a constant coupling the effect of the coupling is not sufficiently limited to the TS region. Note that the Gaussian off-diagonal element introduced by Chang and Miller already is more sophisticated than the very simple version shown here.

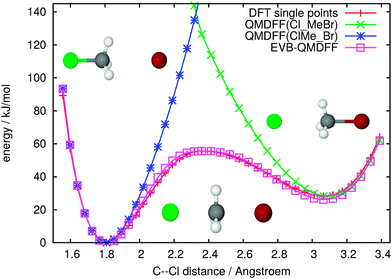
Fig. 1 shows several energy profiles for the chosen S_N2 example reaction. Single-point data at the chosen DFT level are displayed in direct comparison with QMDFF energies for both minima and with EVB-QMDFF data. For the latter, to illustrate the simplicity of the procedure, the two parameters for the off-diagonal Gaussian were fit “by hand” in less than 10 iterations, starting from guessed values, and attempting to minimize the overall deviation between DFT and EVB-QMDFF data in a plot just as the one shown here. Both of the QMDFF potential energy curves are excellent close to their respective reference minima but cannot capture anything of the other minimum. The simple EVB-QMDFF construction described above lowers the QMDFF intersection region and provides agreement between DFT and EVB-QMDFF to well within 2 kJ mol⁻¹ everywhere (residual errors are invisible on this plot).

Fig. 1 Energy profiles along the S_N2 reaction coordinate. Red: DFT single points, green: QMDFF data for the (Cl⁻ MeBr) minimum, blue: QMDFF data for the (ClMe Br⁻) minimum, violet: EVB-QMDFF joining both QMDFFs. The zero of energy was chosen for clarity as the reactant minimum. The three insets show molecular structures at the two minima and at the transition state.

In fact, it is even possible to use the zero-order EVB model with a constant off-diagonal term. Results for this simpler model are shown in the ESI.† They are somewhat less convincing quantitatively but may still be useful. In the ESI† we furthermore demonstrate that the EVB-QMDFF data exhibit good agreement with the DFT reference data also perpendicular to the reaction path and far away from it.

One may object that the good results for this simple S_N2 example cannot be generalized since it is a fairly simple atom-exchange reaction with reactant and product minima being of very similar character. Indeed, there are indications that EVB-coupled force fields can handle more difficult topologies, including bifurcating reaction paths.³¹ Hence, we have included two further, rather different reactions as additional examples.

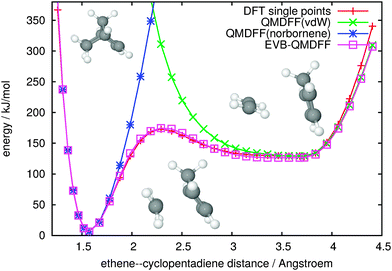
The first one is the Diels–Alder reaction between ethene and cyclopentadiene, yielding norbornene. The product is a single, covalently bound species, whereas the reactants form a complex loosely bound mostly by van-der-Waals (vdW) forces. As additional complication, in the first stage of their approach, ethene and cyclopentadiene change their relative orientation from a tilted T-shaped to a parallel configuration. Nevertheless, as shown in Fig. 2, QMDFF models both minima appropriately. As expected, the accuracy of QMDFF deteriorates upon approach of the reactants from 3.68 Å (the actual minimum) to 3.0 Å. In this region, the rotation into the parallel configuration takes place, and the potential gradients are very small throughout. Note that at larger distances than 3.68 Å and at smaller distances than 1.57 Å (the norbornene minimum), geometries resulting from a linear extrapolation between the TS and the two minima were attached, to probe the QMDFFs and the EVB-QMDFF for very different structures also. The strong gradient differences between the vdW-minimum region and elsewhere apparently lead to some deviations between QMDFF and the DFT single points in this extrapolated part beyond 4.0 Å. However, these high-energy regions are not important for reaction dynamics. As before, it is no problem to find suitable Gaussian parameters in a dozen per-hand iterations, such that the EVB-QMDFF description nicely matches the DFT single-point values from one minimum across the barrier into the other minimum.

Fig. 2 Energy profiles along the Diels–Alder reaction of ethene with cyclopentadiene, forming norbornene. Red: DFT single points, green: QMDFF data for the van-der-Waals reactant complex, blue: QMDFF data for the norbornene minimum, violet: EVB-QMDFF joining both QMDFFs. The zero of energy was chosen for clarity as the reactant minimum. The three insets show molecular structures at the two minima and at the transition state.

As a final and very challenging example for the proposed approach, the ruthenium-catalyzed olefin metathesis of ethylene and RuCl₂(PH₃)₂CH₂ as a model system is investigated. We consider a two-step associative reaction mechanism (for alternatives see ref. 32) in which the ethylene reactant is bound initially by van der Waals forces to the catalyst (E), then coordinates directly to the ruthenium atom as a intermediate (I), and finally undergoes a rotational movement to form a four-membered metalla-cycle with the metal bonded CH₂ group (P). The DFT reaction path was obtained using the WOELFLING tool³³ in the TURBOMOLE package.³⁴ The QMDFFs for the minima E, I, and P were computed as usual at the same level from the analytical Hessian as described above. No special adjustments to the here considered complex reaction mechanism was made except that torsion potentials involving the metal atom were included in the Hessian fit which were omitted in the original QMDFF work.¹⁰ Before judging the results shown below in Fig. 3 one should keep in mind that force fields for such transition metal catalysts are currently (if ever) constructed in laborious “hand-made” fashion and that reactive versions are practically non-existent.

Fig. 3 Energy profiles along the ruthenium-catalyzed olefin metathesis reaction. Red: DFT single points, green/blue/violet: QMDFF data for the reactant, intermediate and product complexes, respectively (see text), turquois: 3 × 3-EVB-QMDFF joining all three QMDFFs. The three insets show molecular structures at the three minima E, I, and P.

As this last example also shows, the plug-in nature of the procedure presented here (and of EVB itself) makes it possible to attach further reaction channels, by successively coupling additional reactant or product minima to a first-stage EVB-QMDFF. In this case, we have employed a 3 × 3-EVB. This alleviates the restriction of EVB-QMDFF to a prescribed reaction path from one reactant minimum to one product minimum and transports the idea to more complicated potential energy surface shapes. As can be seen the entire procedure performs only slightly worse compared to the electronically much simpler S_N2 and Diels–Alder examples which is very encouraging.

The present communication only serves as presentation of the central idea. It remains to be tested in more detail how well EVB-QMDFF potentials perform in regions off the reaction path. We have explored this question to some extent already (as shown in the ESI†) and with good results. More extensive and systematic tests are underway and will be published in a subsequent paper. However, at least for low-energy thermal conversions between just a few minima, we expect reasonable behavior, since QMDFF covers the low-energy region of the minima by construction, and the region around the reaction path is taken care of by EVB. Most of the remaining molecular configuration space is of little relevance since it is too high in energy for normal chemical applications.

Several improvements are possible: of course, the fitting by hand (employed here for demonstration purposes) can easily be replaced by standard least-squares fits or local optimizations, employing a small number of structures along the reaction path, which could still be selected automatically. For higher accuracy requirements, refined models for the EVB coupling matrix element (cf. introduction above) can be employed, in connection with all the experience with these treatments collected in the previous literature for EVB-coupling of more traditional non-reactive force fields.

In this contribution, we have presented a straightforward procedure to obtain a reactive force field for a given reaction, using QMDFF and EVB. The strength of this combination is in its ease of use: for the reactant and product (and possible intermediate) minima, QMDFFs have to be set up, which essentially only requires one frequency calculation each, at these minimum geometries. These QMDFFs are then coupled via EVB, which only requires a small number of reference energy values on the reaction path and fitting of (at least) one or two parameters. Thus, generating EVB-QMDFFs requires no prior experience with non-reactive or reactive force fields, it can be done from scratch (no subsets of parameters have to be taken from previously established force fields), and neither an arduous trial-and-error development of a suitable reference data set is required, nor a global search in a huge and complicated parameter space. Instead, the necessary steps are simple, and can be automatized easily in a black-box fashion.

References

1. K. Farah, F. Müller-Plathe and M. C. Böhm, ChemPhysChem, 2012, 13, 1127.
2. T. Liang, Y. K. Shin, Y.-T. Cheng, D. E. Yilmaz, K. G. Vishnu, O. Verners, C. Y. Zou, S. R. Phillpot, S. B. Sinnott and A. C. T. van Duin, Annu. Rev. Mater. Sci., 2013, 43, 409.
3. P. Pahari and S. Chaturvedi, J. Mol. Model., 2012, 19, 1049.
4. H. R. Larsson, A. C. T. van Duin and B. Hartke, J. Comput. Chem., 2013, 34, 2178.
5. Y. Li and B. Hartke, J. Chem. Phys., 2013, 139, 224303.
6. A. Jaramillo-Botero, S. Naserifar and W. A. Goddard III, J. Chem. Theory Comput., 2014, 10, 1426.
7. J. P. Larentzos, B. M. Rice, E. F. C. Byrd, N. S. Weingarten and J. V. Lill, J. Chem. Theory Comput., 2015, 11, 381,  DOI:10.1021/ct500788c.
8. B. M. Rice, J. P. Larentzos, E. F. C. Byrd and N. S. Weingarten, J. Chem. Theory Comput., 2015, 11, 392,  DOI:10.1021/ct5007899.
9. M. Dittner, J. Müller, H. M. Aktulga and B. Hartke, J. Comput. Chem., 2015 DOI:10.1002/jcc.23966.
10. S. Grimme, J. Chem. Theory Comput., 2014, 10, 4497.
11. J. Danielsson and M. Meuwly, J. Chem. Theory Comput., 2008, 4, 1083.
12. T. Nagy, J. Y. Reyes and M. Meuwly, J. Chem. Theory Comput., 2014, 10, 1366.
13. K. D. Smith, S. I. Stoliarov, M. R. Nyden and P. R. Westmoreland, Mol. Simul., 2007, 33, 361.
14. A. Warshel, J. Am. Chem. Soc., 1980, 102, 6218.
15. F. Jensen and P.-O. Norrby, Theor. Chem. Acc., 2003, 109, 1.
16. Y.-T. Chang and W. H. Miller, J. Phys. Chem., 1990, 94, 5884.
17. Y. Kim, J. C. Corchado, J. Villá, J. Xing and D. G. Truhlar, J. Chem. Phys., 2000, 112, 2718.
18. H. B. Schlegel and J. L. Sonnenberg, J. Chem. Theory Comput., 2006, 2, 905.
19. J. L. Sonnenberg and H. B. Schlegel, Mol. Phys., 2007, 105, 2719.
20. J. L. Sonnenberg, K. F. Wong, G. A. Voth and H. B. Schlegel, J. Chem. Theory Comput., 2009, 5, 949.
21. S. J. Greaves, R. A. Rose, T. A. A. Oliver, D. R. Glowacki, M. N. R. Ashfold, J. N. Harvey, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, Science, 2011, 331, 1423.
22. G. T. Dunning, D. R. Glowacki, T. J. Preston, S. J. Greaves, G. M. Greetham, I. P. Clark, M. Towrie, J. N. Harvey and A. J. Orr-Ewing, Science, 2015, 347, 530.
23. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
24. F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73.
25. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
26. A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
27. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
28. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007.
29. D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358.
30. (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098; (b) J. P. Perdew, Phys. Rev. B, 1986, 34, 7406.
31. B. K. Carpenter, J. N. Harvey and D. R. Glowacki, Phys. Chem. Chem. Phys., 2015, 17, 8372,  10.1039/C4CP05078A.
32. M. Piacenza, I. Hyla-Kryspin and S. Grimme, J. Comput. Chem., 2007, 28, 2275.
33. P. Plessow, J. Chem. Theory Comput., 2013, 9, 1305.
34. TURBOMOLE version 6.7, University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 2014, Karlsruhe, Germany, http://www.turbomole.com.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp02580j

---