Open Access Article
Open Access ArticleMolecular dynamics simulations and NMR spectroscopy studies of trehalose–lipid bilayer systems
Jon
Kapla
a,
Olof
Engström
b,
Baltzar
Stevensson
a,
Jakob
Wohlert
c,
Göran
Widmalm
b and
Arnold
Maliniak
*a
aDepartment of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91 Stockholm, Sweden. E-mail: arnold.maliniak@mmk.su.se
bDepartment of Organic Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91 Stockholm, Sweden
cWallenberg Wood Science Center, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
First published on 22nd July 2015
Abstract
The disaccharide trehalose (TRH) strongly affects the physical properties of lipid bilayers. We investigate interactions between lipid membranes formed by 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and TRH using NMR spectroscopy and molecular dynamics (MD) computer simulations. We compare dipolar couplings derived from DMPC/TRH trajectories with those determined (i) experimentally in TRH using conventional high-resolution NMR in a weakly ordered solvent (bicelles), and (ii) by solid-state NMR in multilamellar vesicles (MLV) formed by DMPC. Analysis of the experimental and MD-derived couplings in DMPC indicated that the force field used in the simulations reasonably well describes the experimental results with the exception for the glycerol fragment that exhibits significant deviations. The signs of dipolar couplings, not available from the experiments on highly ordered systems, were determined from the trajectory analysis. The crucial step in the analysis of residual dipolar couplings (RDCs) in TRH determined in a bicelle-environment was access to the conformational distributions derived from the MD trajectory. Furthermore, the conformational behavior of TRH, investigated by J-couplings, in the ordered and isotropic phases is essentially identical, indicating that the general assumptions in the analyses of RDCs are well founded.
Introduction
The bioprotective properties of saccharides in general and trehalose (TRH) in particular have motivated significant attention in the scientific literature.1–5 These properties have stabilizing effects on biological membranes under extreme thermal and mechanical conditions, which are particularly important during the process of dehydration.6 Although the detailed mechanism of trehalose–membrane stabilization is not yet clarified, the effect of preserving the cell structure and biological function is well known.Several approaches for the molecular description of membrane–sugar interactions have been suggested: (a) a preferential exclusion model, where sugars are excluded from the vicinity of the lipid membrane, thus preserving the natural hydration shell of the bilayer,1,6–9 (b) the water-entrapment hypothesis, resting on the assumption that the sugars interact strongly with both lipids and water, which increases favorable hydration near the membrane,10–15 and the vitrification hypothesis, where a glassy sugar–water matrix that protects the membrane from mechanical stress is formed.16–20 There are, however, clear indications that the explanation may consist of a combination of several hypotheses. Two key concepts relevant for these studies are the hydration process21–24 and the conformational behavior of trehalose.25–27
Many experimental and theoretical approaches have been employed to study membrane–sugar interactions. In particular, computer simulation is a powerful tool for investigations of the detailed picture of complex biological systems, and several studies of lipid bilayer–trehalose interactions have been reported using different degrees of sophistication for the interaction model.22,28–36
Recently,5 we carried out molecular dynamics (MD) computer simulations for analysis of interactions between a 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) bilayer and trehalose (see Fig. 1). Using MD simulations and a simple two-state interaction model we were able to confirm the hypotheses indicated above, suggested for the explanation of the membrane–sugar interactions. We showed, by calculating the net affinity of TRH for the DMPC bilayer, that the concept of attraction (low TRH content) and exclusion (high TRH content) of sugars from the membrane can be used in fully hydrated as well as in dehydrated membranes. Furthermore, the replacement of water by trehalose molecules was observed at the bilayer interface. The compressibility modulus and increased order, manifested by a drastic reduction in the lateral diffusion were attributed to the formation of a glassy state upon increased TRH content.
 | ||
| Fig. 1 Schematic structures of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) lipid and trehalose (TRH) molecules with the relevant coordinate system and dihedral angles. | ||
In the present work we have carried out measurements of NMR spin–spin interactions on trehalose in isotropic and ordered systems. In the isotropic liquid only the J-couplings are observable, whereas the direct dipolar interactions are averaged (by the rapid molecular tumbling) to zero. In the anisotropic systems, on the other hand, direct dipole–dipole interactions can be observed and provide valuable information on the molecular structure and the orientational order. In principle, there are two NMR spectroscopy techniques to study anisotropic dipolar interactions: (a) conventional high-resolution NMR where a weakly ordered solvent37–39 is used, and (b) solid-state NMR.40–43
Weakly ordered anisotropic media, used for measurements of dipolar interactions (frequently referred to as residual dipolar couplings or RDCs), consist of dilute bilayer-like assemblies (bicelles) formed by various lipids, e.g. DMPC and DHPC. For carbohydrates, RDCs provide important information about the complex conformational processes taking place in solution.44–51
We have used trajectories generated in the MD simulations carried out in the previous study5 for interpretation of experimental herein acquired NMR parameters and analyses of the membrane–TRH interactions. A combination of MD computer simulations and NMR spectroscopy is a powerful tool for investigations of the detailed molecular picture of complex chemical systems, since all possible dipolar interactions can readily be calculated from an MD trajectory.
Methods
Molecular dynamics simulations
The trajectories used in the analyses were generated in our previous investigation, focused on the interactions of trehalose and the DMPC bilayer.5The MD computer simulation study was carried out with a lipid bilayer consisting of 128 DMPC molecules with ten different trehalose concentrations: 0–260 TRH molecules (labelled as TRHN, where N is the total number of TRH molecules), corresponding to a maximum trehalose content of wTRH = 0.20 (wt/wt). The water content in all the simulations ranged between 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 14
000 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. Only the most essential details of the methodological aspects are repeated here. The lipid interactions were modeled using the CHARMM-based and AMBER-compatible force field SLIPIDS (Stockholm Lipids).52 The TRH interaction parameters were GLYCAM06-based53 and AMBER-compatible. The water interactions were described using the TIP3P model.54 Both AMBER and SLIPIDS force fields were parameterized employing the TIP3P water model. Whereas the dynamics of TIP3P water is known to be too fast, the equilibrium properties are in good agreement with experimental results.55,56 In particular, the O–O radial distribution function (gO–O) and the heat of vaporization are correctly predicted indicating that hydrogen bonds formed by water are reasonably well described, even though the kinetics is not. The simulations were carried out in the GROMACS v4.5.5 program suite57 in the NPT ensemble at a temperature of 310 K and a pressure of 100 kPa. All electrostatics were treated with the Particle Mesh Ewald (PME) summation method.58 The simulations were subject to 100 ns of equilibration, after which 100–140 ns were used for analysis. The MD simulations of trehalose in the isotropic aqueous solutions were carried out in three different samples with 10, 50 and 100 TRH dissolved in 5000 water molecules, corresponding to 0.1, 0.5 and 1.0 M solutions.
000 molecules. Only the most essential details of the methodological aspects are repeated here. The lipid interactions were modeled using the CHARMM-based and AMBER-compatible force field SLIPIDS (Stockholm Lipids).52 The TRH interaction parameters were GLYCAM06-based53 and AMBER-compatible. The water interactions were described using the TIP3P model.54 Both AMBER and SLIPIDS force fields were parameterized employing the TIP3P water model. Whereas the dynamics of TIP3P water is known to be too fast, the equilibrium properties are in good agreement with experimental results.55,56 In particular, the O–O radial distribution function (gO–O) and the heat of vaporization are correctly predicted indicating that hydrogen bonds formed by water are reasonably well described, even though the kinetics is not. The simulations were carried out in the GROMACS v4.5.5 program suite57 in the NPT ensemble at a temperature of 310 K and a pressure of 100 kPa. All electrostatics were treated with the Particle Mesh Ewald (PME) summation method.58 The simulations were subject to 100 ns of equilibration, after which 100–140 ns were used for analysis. The MD simulations of trehalose in the isotropic aqueous solutions were carried out in three different samples with 10, 50 and 100 TRH dissolved in 5000 water molecules, corresponding to 0.1, 0.5 and 1.0 M solutions.
Experimental
NMR spectroscopy
The disaccharide α,α-trehalose (α-D-Glucopyranosyl α-D-Glucopyranoside) was obtained from Nutritional Biochemicals Corporation (Cleveland, Ohio, USA) and the lipids 1,2-dihexanoyl-sn-glycero-3-phosphocholine (DHPC) and 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) were purchased from Avanti Lipids (Alabaster, Alabama, USA). The lipid bicelle sample was prepared by dissolving DHPC (33 mM) and DMPC (94 mM) in D2O (lipid ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8; lipid concentration 8% w/v). The preparation was vibro-mixed for 5 min, heated to 38 °C for 30 min and then cooled to 5 °C for 30 min. The procedure was repeated three times. The cooled mixture (0.55 mL) was added to an NMR tube containing 9.4 mg of TRH that had been freeze-dried from D2O, resulting in a ∼50 mM solution. Measurements in the isotropic phase were performed on a TRH sample (106 mM) in D2O with trimethylsilyl-2,2,3,3-tetradeuteropropionic acid (TSP, 1 mM) as the chemical shift reference (δH = 0.0). Resonance assignments were facilitated by chemical shift data available from the literature.59 NMR experiments were recorded on a 600 MHz Bruker AVANCE III spectrometer equipped with a 5 mm inverse Z-gradient TXI (1H/13C/31P) probe at 38 °C, calibrated with a methanol-d4 sample.60 The anisotropy of the system was monitored by measurements of the 2H quadrupolar coupling of D2O, ranging between 13.7 Hz and 14.0 Hz as determined prior to and after the experiments had been performed on the sample.
2.8; lipid concentration 8% w/v). The preparation was vibro-mixed for 5 min, heated to 38 °C for 30 min and then cooled to 5 °C for 30 min. The procedure was repeated three times. The cooled mixture (0.55 mL) was added to an NMR tube containing 9.4 mg of TRH that had been freeze-dried from D2O, resulting in a ∼50 mM solution. Measurements in the isotropic phase were performed on a TRH sample (106 mM) in D2O with trimethylsilyl-2,2,3,3-tetradeuteropropionic acid (TSP, 1 mM) as the chemical shift reference (δH = 0.0). Resonance assignments were facilitated by chemical shift data available from the literature.59 NMR experiments were recorded on a 600 MHz Bruker AVANCE III spectrometer equipped with a 5 mm inverse Z-gradient TXI (1H/13C/31P) probe at 38 °C, calibrated with a methanol-d4 sample.60 The anisotropy of the system was monitored by measurements of the 2H quadrupolar coupling of D2O, ranging between 13.7 Hz and 14.0 Hz as determined prior to and after the experiments had been performed on the sample.
The J-HMBC experiments61 were acquired with 32 scans and with scaling factors κ varying between 21 and 27. The number of points in the F2 and F1 dimensions were 8k and 512, respectively; carrier frequencies were set at 3.0 ppm and 55 ppm, respectively, and the spectral widths were set to 6 ppm and 100 ppm, respectively. The free induction decays (FIDs) were zero-filled to 16k in the indirect dimension and linear prediction using 64 coefficients and 512 points were applied to the indirect dimension prior Fourier transformation with magnitude processing in the direct dimension. Two- and three-bond heteronuclear couplings were extracted from projections in the indirect dimension at different 1H chemical shifts. The measured couplings were divided by the corresponding scaling factor and averages from four different experiments were calculated.
The 1H,13C-HSQC-HECADE experiments62,63 were recorded with 16k and 512 data points in the F2 and F1 dimensions, respectively, and the carrier frequencies were set at 3.0 ppm and 60 ppm, respectively, using 16 scans. The duration of the TOCSY mixing time was 80 ms and the scaling factor of the 1JCH splitting in the indirect dimension was set to 0.8. The FIDs were zero-filled once in each dimension and an exponential window function of 0.3 Hz and a cosine window function were applied to the F2 and F1 dimensions, respectively, prior to Fourier transformation. One-, two- and three-bond heteronuclear couplings were extracted from the differences in the peak-position along the F2 dimension of the doublet components (F1 dimension, E.COSY-type cross-peak) and the sign of the couplings was determined from the cross-peak tilt relative to the one-bond couplings that were assumed to be positive.
The 1H,13C-CT-CE-HSQC experiments64 were performed with 64 scans and the number of points in the F2 and F1 dimensions were 1k and 512, respectively; carrier frequencies were set at 3.2 ppm and 77 ppm employing spectral widths of 7 ppm and 165 ppm. The FIDs were zero-filled to 16k in the indirect dimension and linear predictions using 36 coefficients and 512 points were applied to the indirect dimension prior Fourier transformation. One-bond heteronuclear couplings, scaled by a factor of 2.0, were extracted from projections of the indirect dimension at different 1H chemical shifts.
The phase-sensitive 1H,1H-DQF-COSY65 experiments were performed using 8 scans. The carrier was set to 4.65 ppm and the spectral widths were 4 ppm in both dimensions. The number of recorded data points in the F2 and F1 dimensions was 32k and 128, respectively; zero-filling was carried out to 256k and 512 points prior Fourier transformation. Resolution enhancement was achieved in the direct dimension by applying a Lorentzian-to-Gaussian window function (lb = −0.5 Hz and gb = 0.2) to the FIDs. Vicinal 1H,1H couplings were extracted by the analysis of multiplet patterns of cross-peak slices taken in the direct dimension using the J-doubling methodology66 employing an in-house written Matlab script.
Results and discussion
NMR dipole–dipole interactions
 | (1) |
 , where S2 is the orientational order parameter of the vector. Clearly, the order parameters of the C–H vectors in the g2 and g3 groups are too low, which is also reflected in a too small magnitude of the simulated dipolar couplings.
, where S2 is the orientational order parameter of the vector. Clearly, the order parameters of the C–H vectors in the g2 and g3 groups are too low, which is also reflected in a too small magnitude of the simulated dipolar couplings.
 | ||
| Fig. 2 NMR dipolar couplings in DMPC: the negative and positive values of the experimental dipolar couplings correspond to black and blue circles, respectively. The values derived from the trajectory are represented by red crosses with associated error bars (corresponding to 1 SD). In principle, the different fragments of the alkyl chains can correspond to four different dipolar interactions. In the experimental study,42 we were at most able to determine three couplings in one fragment (C2g1 and C2g2). Thus, the individual couplings (A and B) in the methylene group were assigned based on the best agreement between calculated and experimental values. | ||
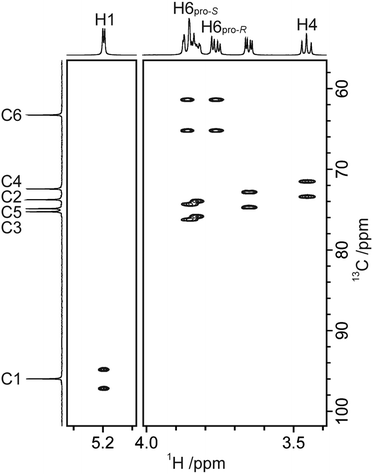
Homonuclear 1H,1H couplings can be measured from the cross-peak patterns in a phase-sensitive DQF-COSY spectrum74 where the active coupling appears as an anti-phase doublet and passive couplings appear in-phase. Small couplings are difficult to extract accurately due to the spectral overlap of the multiplet components; however, these J values can be extracted by utilizing the J-doubling methodology,66 which is based on multiplet deconvolution. One-bond heteronuclear couplings can readily be measured in a 1H,13C-CT-CE-HSQC spectrum,64 as half of the cross-peak splitting in the indirect dimension (Fig. 4). The scaling of the coupling by a factor of two increases the accuracy of the measurement. Two- and three-bond heteronuclear couplings can be accessed from a set of J-HMBC61 experiments. The couplings are measured in the indirect dimension and the problem with spectral overlap can be limited by varying the scaling factor, which also improves the accuracy of the measurements. An advantage of the J-HMBC experiment is that one can determine J couplings across the glycosidic linkage. Single- and multiple-bond heteronuclear couplings can also be accessed by the 1H,13C-HSQC-HECADE62,63 experiment, in which the coupling is measured from a splitting in the direct dimension. The experiment additionally yields information about the relative sign of the coupling.
These NMR experiments were used to generate a data-set of experimentally determined RDCs for trehalose dissolved in the lyotropic liquid crystalline phase consisting of DMPC/DHPC bicelles (Table 1). The different experiments complement each other not only because different types of specific information can be extracted from them (e.g. J couplings of one-, two- and three-bond interactions, relative sign, transglycosidic J couplings) but also due to the fact that the same coupling can be measured in different dimensions thus increasing the reliability of the measurements using two methods. The number of linearly independent dipolar vectors in TRH is reduced, compared to other disaccharides, due to the C2 symmetry of TRH which makes the disaccharide appear as a monosaccharide in the NMR spectrum. The spatial arrangement of atoms in the adopted 4C1 chair conformation of the glucose residues results in several parallel dipolar vectors, which also limits the number of independent RDCs in comparison to other hexose epimers. The magnitude of the experimental RDCs seems to be low relative to similar systems.49,75 In earlier studies of oligosaccharides based on RDC analysis we successfully used DMPC/DHPC lipid concentrations of 8–10% (w/v)76,77 and the study of sucrose49 utilized an even higher concentration, viz., 22%. Herein we used a lipid concentration of 8% and efforts were made to increase the order of the system, thus raising the magnitude of the RDCs, by increasing the lipid concentration (to 12%). These attempts, however, were fruitless as an appearance, in the deuterium NMR spectrum, of an isotropic (central) peak in addition to the quadrupolar coupling of D2O indicated decreased stability of the sample. The physicochemical properties of sucrose and TRH are undeniably different,78,79 even though they are both nonreducing hexose-containing disaccharides, and thus, what appears to be small changes in the molecular structure, are indeed responsible for the experimental difficulties in studying TRH, as compared to sucrose.
| Spin-pairs | Δ | J | d |
|---|---|---|---|
| a Estimated errors are ±0.2 Hz. | |||
| H1–H2 | 2.93 | 3.89 | −0.48 |
| H2–H3 | 10.65 | 9.90 | 0.37 |
| H3–H4 | 8.87 | 9.11 | −0.12 |
| H4–H5 | 8.87 | 9.96 | −0.55 |
| H6pro-R–H5 | 4.78 | 5.25 | −0.24 |
| H6pro-S–H6pro-R | −9.09 | −12.08 | 1.50 |
| C1–H1 | 175.85 | 172.65 | 1.60 |
| C2–H2 | 142.50 | 143.82 | −0.66 |
| C4–H4 | 142.70 | 144.36 | −0.83 |
| C6–H6pro-S | 144.78 | 144.53 | 0.13 |
| C1–H1′ | 3.18 | 3.31 | −0.06 |
| C1–H2 | −1.32 | −0.82 | −0.25 |
| C1–H3 | 1.26 | 0.74 | 0.26 |
| C2–H1 | −1.25 | −1.42 | 0.09 |
| C2–H4 | 1.34 | 1.30 | −0.02 |
| C3–H1 | 5.44 | 5.51 | −0.03 |
| C3–H2 | −4.19 | −4.80 | 0.30 |
| C3–H4 | −4.43 | −4.48 | 0.03 |
| C4–H2 | 1.38 | 1.30 | 0.04 |
| C4–H3 | −4.55 | −4.63 | 0.04 |
| C4–H6pro-R | 1.36 | 1.37 | 0.00 |
| C5–H4 | −4.52 | −3.99 | −0.26 |
| C5–H6pro-R | −1.93 | −1.83 | −0.05 |
| C6–H4 | 3.72 | 3.70 | 0.01 |
In order to derive the information about molecular structure from the experimental and simulated dipolar couplings eqn (1) is transformed into the following relationship80
 | (2) |
The experimental couplings, dexptij, are displayed in Fig. 5A. In the quantitative analysis, we employed a numerical fitting procedure of all the couplings using eqn (2) with the three relevant elements of the order tensor (Szz, Sxx–Syy, Sxy) as the fitting parameters. The fitting was performed using a computer code (Octave, version 3.0, http://www.gnu.org),81 which minimizes the error sum, Q
 | (3) |
In order to include the uncertainties of conformations an error analysis of the back-calculated dipolar couplings, dcalcij, was carried out by calculating normal distributions of dexptij. In practice, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random sets of dipolar couplings were generated by using averaged values of dexptij and the corresponding errors. To ensure the generation of realistic dipolar couplings, the normal distribution was truncated at ±3σ. The five relevant cosines in eqn (2) were determined from the trajectory together with their standard deviations,
000 random sets of dipolar couplings were generated by using averaged values of dexptij and the corresponding errors. To ensure the generation of realistic dipolar couplings, the normal distribution was truncated at ±3σ. The five relevant cosines in eqn (2) were determined from the trajectory together with their standard deviations, 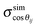
 | (4) |
Again, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 normally distributed cosine-values were generated in the interval
000 normally distributed cosine-values were generated in the interval  . Finally, the data set of dexptij was used together with the cosine-values to fit the order tensors. This procedure resulted in a distribution of back-calculated dipolar couplings that were used to calculate an average and a standard deviation for each coupling, dcalcij, corresponding to dexptij. The agreement between the experimental and back-calculated dipolar couplings (Fig. 5A) is very good. The analysis is however clearly limited by the very small magnitude of experimental dipolar couplings: in fact many couplings are smaller than the experimental errors.
. Finally, the data set of dexptij was used together with the cosine-values to fit the order tensors. This procedure resulted in a distribution of back-calculated dipolar couplings that were used to calculate an average and a standard deviation for each coupling, dcalcij, corresponding to dexptij. The agreement between the experimental and back-calculated dipolar couplings (Fig. 5A) is very good. The analysis is however clearly limited by the very small magnitude of experimental dipolar couplings: in fact many couplings are smaller than the experimental errors.
We have also calculated dipolar couplings using eqn (1) and the TRH20 MD trajectory. These couplings, dcalcij, were analyzed employing the same procedure as for the experimental couplings above, and the results are collected in Fig. 5B. We note that the simulated couplings are three orders of magnitude larger compared with the experimentally determined counterparts. The reason is that in the MD simulations the TRH molecules spend most of the time attached to the surface rather than as free molecules in the bulk water phase. The composition of the experimental sample is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1100 (50
1100 (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127
127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mM) for trehalose, lipids and water, whereas the corresponding ratio in the MD simulation box in the TRH20 system is 1
000 mM) for trehalose, lipids and water, whereas the corresponding ratio in the MD simulation box in the TRH20 system is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.4
6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (20
500 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 given as the number of molecules). Clearly, the real sample contains a larger water bulk and smaller membrane surface per TRH molecule, which may partly explain a weaker association. Other possible sources of the dramatic difference between the experimental and simulated dipolar couplings are associated with a short simulation time (140 ns) that prevents efficient averaging of the couplings, and in addition, a too attractive interaction potential.82
000 given as the number of molecules). Clearly, the real sample contains a larger water bulk and smaller membrane surface per TRH molecule, which may partly explain a weaker association. Other possible sources of the dramatic difference between the experimental and simulated dipolar couplings are associated with a short simulation time (140 ns) that prevents efficient averaging of the couplings, and in addition, a too attractive interaction potential.82
Molecular conformations
In Fig. 6 the conformational distribution functions are displayed for TRH with different lipid concentrations calculated from the MD trajectories for the three relevant torsion angles ϕ, ω and θ in the molecule, corresponding to H1–C1–O1–C1′, O5–C5–C6–O6 and C5–C6–O6–HO6, respectively (cf.Fig. 1). Clearly, there is no significant TRH concentration dependence for any of the torsion angles under the different conditions employed. The distribution functions determined for different concentrations of TRH in the isotropic phase are essentially identical (not shown). The ϕ torsion angle distribution exhibits, as expected, only one state with 〈ϕ〉 = −47.2°. Using a Karplus-type relationship83 an average J coupling for H1–C1′ of 3.54 ± 0.17 Hz was calculated from the TRH20 distribution in Fig. 6A, and 3.62 ± 0.06 Hz in the isotropic phase. The corresponding experimental value was determined to be 3.31 ± 0.25 Hz, in good agreement with literature data of 3.0 ± 0.325 and 3.3 ± 0.5Hz.84 Thus, the heteronuclear J value from the MD simulation agrees well with that of the experiment, for which the error has been estimated by the developers of the NMR experiment.61 Furthermore, the inter-residue conformationally averaged effective proton–proton distances can be compared with experimentally determined 1H,1H-NOE data. Using an 〈r−6〉-relationship the effective distances derived from the MD trajectory of an isotropic solution resulted in and
and 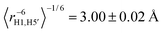 for H1–H1′ and H1–H5′, respectively. The effective distances in the ordered TRH20 sample were essentially identical:
for H1–H1′ and H1–H5′, respectively. The effective distances in the ordered TRH20 sample were essentially identical:  and
and  . In a study of trehalose based on molecular mechanics and NOE data25 the corresponding distances were 2.8 and 2.5 Å. Thus, the effective H1–H1′ inter-residue distance agrees reasonably well with the corresponding one derived from the present MD simulation, whereas for the H1–H5′ distance in experiment and simulations disagree significantly. It can, however, be noted that the estimated error in the experimental H1–H5′ distance is very large (±2.0 Å).25 The ω distributions displayed in Fig. 6B consist of three conformational states: +g (ω = +65°), −g (ω = −65°), and t (ω = 180°), where g and t denote the gauche and trans relationships for O5 and O6. Populations of the three conformational states related to the ω torsion angle were determined by integrating the MD probability distribution functions in Fig. 6B. The populations derived from the different MD trajectories are collected in Table 2, being similar in both the ordered and isotropic phases (distributions not shown here). The populations derived from the experimental spin–spin couplings in the isotropic phase were obtained by fitting 3JH5,H6pro-R = 5.25 Hz and 3JH5,H6pro-S = 2.38 Hz using the +g, −g and t populations as fitting parameters. We have also determined the corresponding J couplings in α-D-Glcp-OMe, 3JH5,H6pro-R = 5.58 Hz and 3JH5,H6pro-S = 2.28 Hz, thus being closely similar and consequently so are the ω torsion angle distributions (Table 2). The relationship between the J coupling and the conformational state (torsion angle) was established employing a Karplus-type equation.85 The corresponding couplings derived from the TRH20 MD trajectory were 3JH5,H6pro-R = 4.9 ± 1.2 Hz and 3JH5,H6pro-S = 2.03 ± 0.41 Hz.
. In a study of trehalose based on molecular mechanics and NOE data25 the corresponding distances were 2.8 and 2.5 Å. Thus, the effective H1–H1′ inter-residue distance agrees reasonably well with the corresponding one derived from the present MD simulation, whereas for the H1–H5′ distance in experiment and simulations disagree significantly. It can, however, be noted that the estimated error in the experimental H1–H5′ distance is very large (±2.0 Å).25 The ω distributions displayed in Fig. 6B consist of three conformational states: +g (ω = +65°), −g (ω = −65°), and t (ω = 180°), where g and t denote the gauche and trans relationships for O5 and O6. Populations of the three conformational states related to the ω torsion angle were determined by integrating the MD probability distribution functions in Fig. 6B. The populations derived from the different MD trajectories are collected in Table 2, being similar in both the ordered and isotropic phases (distributions not shown here). The populations derived from the experimental spin–spin couplings in the isotropic phase were obtained by fitting 3JH5,H6pro-R = 5.25 Hz and 3JH5,H6pro-S = 2.38 Hz using the +g, −g and t populations as fitting parameters. We have also determined the corresponding J couplings in α-D-Glcp-OMe, 3JH5,H6pro-R = 5.58 Hz and 3JH5,H6pro-S = 2.28 Hz, thus being closely similar and consequently so are the ω torsion angle distributions (Table 2). The relationship between the J coupling and the conformational state (torsion angle) was established employing a Karplus-type equation.85 The corresponding couplings derived from the TRH20 MD trajectory were 3JH5,H6pro-R = 4.9 ± 1.2 Hz and 3JH5,H6pro-S = 2.03 ± 0.41 Hz.
 | ||
| Fig. 6 Probability distribution functions, derived from the MD trajectory, for the torsion angles ϕ (A), ω (B) and θ (C) in trehalose, see Fig. 1 for three different samples: TRH50-ISO (green) in the isotropic solution, TRH20 (red), and TRH230 (blue) in the ordered phase. | ||
| Method | g(−60°) | g(60°) | t(180°) | 3 J H5,H6pro-R | 3 J H5,H6pro-S |
|---|---|---|---|---|---|
| a TRH10-ISO: MD simulation of an isotropic phase −10 TRH molecules. b TRH20-128DMPC: MD simulation of a lipid bilayer −20 TRH molecules. | |||||
| NMR | 0.47 | 0.43 | 0.10 | 5.25 | 2.38 |
| TRH10-ISOa | 0.44 | 0.53 | 0.03 | 5.54 ± 0.62 | 1.962 ± 0.052 |
| TRH50-ISO | 0.46 | 0.51 | 0.03 | 5.46 ± 1.62 | 1.98 ± 0.42 |
| TRH100-ISO | 0.44 | 0.52 | 0.04 | 5.36 ± 1.89 | 2.04 ± 0.43 |
| TRH20-128DMPCb | 0.50 | 0.45 | 0.05 | 4.87 ± 1.17 | 2.03 ± 0.41 |
| TRH80-128DMPC | 0.45 | 0.51 | 0.04 | 5.40 ± 1.67 | 2.02 ± 0.50 |
| NMR (α-D-Glcp-OMe) | 0.49 | 0.42 | 0.09 | 5.58 | 2.28 |
We also consider the conformational transitions related to the θ torsion angle. The probability distributions are displayed in Fig. 6C. Here all three conformational states are significantly populated, the trans conformation being the major one and the two gauche conformations are approximately equally populated. Given that the agreement between the experiment and simulation is very good for the ω torsion angle in TRH, we set out to evaluate a relationship, which also includes the θ torsion angle. The 2JH6pro-R,H6pro-S coupling constant is dependent on the conformational distributions at the ω and θ torsion angles and was calculated from the MD trajectories based on two different Karplus-type relationships
2JH6pro-R,H6pro-S = −11.26 + 0.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ω) + 2.02cos(2θ) cos(2ω) + 2.02cos(2θ) | (5) |
2JH6pro-R,H6pro-S = −11.23 + 0.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ω) + 0.74 cos(ω) + 0.74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ω) − 0.82 cos(2ω) − 0.82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) + 2.02 cos(θ) + 2.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θ) cos(2θ) | (6) |
Bilayer–trehalose interactions
In Fig. 8 the orientational probability distributions, P(β), are displayed for the C4–C4′ vector in trehalose relative to the bilayer normal. The TRH20 distribution exhibits one major relatively narrow maximum at β = 35°, which may reflect a single hydrogen bond of the hydroxyl group at the C3 or C4 atoms of TRH to a phosphate oxygen atom. It can be speculated that the high population of large angles, >60°, is related to TRH molecules that form hydrogen bonds with two different lipids, for which the C4–C4′ vector has a perpendicular orientation relative to the bilayer normal, i.e. β ≈ 90°. Upon increased TRH content, the maximum of P(β) shifts to larger angles. At an even higher concentration, in the TRH230 sample, several distinct orientations are present where the TRH molecules interact with both DMPC lipids and associate with each other.
Conclusions
By NMR spectroscopy and molecular dynamics computer simulations the lipid membrane–trehalose interactions and conformations of the TRH molecule have been investigated. Both the previously reported MD simulations5 and the NMR experiments were carried out in the isotropic solution and in the ordered phase. NMR studies in weakly ordered media facilitate the acquisition of both hetero- and homonuclear residual dipolar couplings (RDCs), which provide important information about the molecular conformations and the orientational order. One of the major assumptions in the interpretations of RDC, collected in weakly ordered liquid crystals, is that the molecular conformations in the isotropic liquid and in the ordered phase are similar. Combination of the NMR experiments and MD simulations is a powerful tool to test the validity of this assumption. The RDCs in trehalose calculated from the MD trajectory were three orders of magnitude larger compared with the experimentally determined counterparts. The reason for this dramatic discrepancy has been attributed to: (a) a relatively short simulation time, (b) slow exchange of TRH molecules between the membrane surface and the water bulk, and (c) slightly smaller water bulk and larger membrane surface per TRH molecule in the MD simulation. There was, however, good agreement between the experimental and the MD trajectory calculated scalar J couplings, which indicates a correct description of molecular conformations in the MD simulation. Thus, although the orientational order in the MD simulation was not adequately described, the conformations were, and these were subsequently used in the interpretation of the experimental RDCs. It should, however, be noted that the error of the orientational order is given by , where N is the number of molecules in the MD simulation. Thus, for TRH20 the error is ∼0.2, significantly larger than the experimental order parameter. The molecular conformations in the isotropic and ordered phases were highly similar which, as mentioned above, is the major assumption in all the analyses of RDCs.
, where N is the number of molecules in the MD simulation. Thus, for TRH20 the error is ∼0.2, significantly larger than the experimental order parameter. The molecular conformations in the isotropic and ordered phases were highly similar which, as mentioned above, is the major assumption in all the analyses of RDCs.
Finally, from the MD trajectory we have calculated one-bond C–H NMR dipolar couplings in the DMPC lipids, and compared these with experimental values previously determined42 by solid-state NMR spectroscopy. The agreement between calculated and experimental couplings is very good, except for the glycerol fragment, which depends on the poor description of the torsional potential of this fragment. The dipolar couplings calculated from the MD trajectory also include the sign of the interaction, which is not available from the solid-state NMR experiments.
Acknowledgements
This work was supported by grants from the Swedish Research Council, the Knut and Alice Wallenberg Foundation, the Carl Trygger Foundation and the Swedish National Infrastructure for Computing (SNAC 001-12-102) via PDC (http://www.pdc.kth.se).References
- H. D. Andersen, C. Wang, L. Arleth, G. H. Peters and P. Westh, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1874–1878 CrossRef CAS PubMed.
- C. W. Lee, S. K. Das Gupta, J. Mattai, G. G. Shipley, O. H. Abdel-Mageed, A. Makriyannis and R. G. Griffin, Biochemistry, 1989, 28, 5000–5009 CrossRef CAS PubMed.
- B. A. Brüning, S. Prévost, R. Stehle, R. Steitz, P. Falus, B. Farago and T. Hellweg, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2412–2419 CrossRef PubMed.
- J. Tian, A. Sethi, B. I. Swanson, B. Goldstein and S. Gnanakaran, Biophys. J., 2013, 104, 622–632 CrossRef CAS PubMed.
- J. Kapla, J. Wohlert, B. Stevensson, O. Engström, G. Widmalm and A. Maliniak, J. Phys. Chem. B, 2013, 117, 6667–6673 CrossRef CAS PubMed.
- J. H. Crowe, L. M. Crowe and D. Chapman, Science, 1984, 223, 701–703 CAS.
- L. M. Crowe, R. Mouradian, J. H. Crowe, S. A. Jackson and C. Womersley, Biochim. Biophys. Acta, 1984, 769, 141–150 CrossRef CAS.
- E. A. Golovina, A. V. Golovin, F. A. Hoekstra and R. Faller, Biophys. J., 2009, 97, 490–499 CrossRef CAS PubMed.
- M. Nakagaki, H. Nagase and H. Ueda, J. Membr. Sci., 1992, 73, 173–180 CrossRef CAS.
- G. Cottone, G. Ciccotti and L. Cordone, J. Chem. Phys., 2002, 117, 9862–9866 CrossRef CAS.
- R. D. Lins, C. S. Pereira and P. H. Hünenberger, Proteins, 2004, 55, 177–186 CrossRef CAS PubMed.
- P. S. Belton and A. M. Gil, Biopolymers, 1994, 34, 957–961 CrossRef CAS PubMed.
- C. Lambruschini, A. Relini, A. Ridi, L. Cordone and A. Gliozzi, Langmuir, 2000, 16, 5467–5470 CrossRef CAS.
- L. Cordone, G. Cottone, S. Giuffrida, G. Palazzo, G. Venturoli and C. Viappiani, Biochim. Biophys. Acta, Proteins Proteomics, 2005, 1749, 252–281 CrossRef CAS PubMed.
- A. M. Massari, I. J. Finkelstein, B. L. McClain, A. Goj, X. Wen, K. L. Bren, R. F. Loring and M. D. Fayer, J. Am. Chem. Soc., 2005, 127, 14279–14289 CrossRef CAS PubMed.
- W. Q. Sun and A. C. Leopold, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1997, 117, 327–333 CrossRef.
- K. L. Koster, M. S. Webb, G. Bryant and D. V. Lynch, Biochim. Biophys. Acta, Biomembr., 1994, 1193, 143–150 CrossRef CAS.
- K. L. Koster, Y. P. Lei, M. Anderson, S. Martin and G. Bryant, Biophys. J., 2000, 78, 1932–1946 CrossRef CAS PubMed.
- W. Q. Sun, A. C. Leopold, L. M. Crowe and J. H. Crowe, Biophys. J., 1996, 70, 1769–1776 CrossRef CAS PubMed.
- W. Q. Sun and A. C. Leopold, Ann. Bot., 1994, 74, 601–604 CrossRef.
- L. R. Winther, J. Qvist and B. Halle, J. Phys. Chem. B, 2012, 116, 9196–9207 CrossRef CAS PubMed.
- L. Lupi, L. Comez, M. Paolantoni, S. Perticaroli, P. Sassi, A. Morresi, B. M. Ladanyi and D. Fioretto, J. Phys. Chem. B, 2012, 116, 14760–14767 CrossRef CAS PubMed.
- M. Heyden, G. Schwaab and M. Havenith, J. Phys. Chem. B, 2014, 118, 10802–10805 CrossRef CAS PubMed.
- B. Halle, J. Phys. Chem. B, 2014, 118, 10806–10812 CrossRef CAS PubMed.
- A. Poveda, C. Vicent, S. Penadés and J. Jiménez-Barbero, Carbohydr. Res., 1997, 301, 5–10 CrossRef CAS.
- A. D. French, G. P. Johnson, A. M. Kelterer, M. K. Dowd and C. J. Cramer, J. Phys. Chem. A, 2002, 106, 4988–4997 CrossRef CAS.
- M. M. Kuttel and K. J. Naidoo, Carbohydr. Res., 2005, 340, 875–879 CrossRef CAS PubMed.
- A. Skibinsky, R. M. Venable and R. W. Pastor, Biophys. J., 2005, 89, 4111–4121 CrossRef CAS PubMed.
- C. S. Pereira and P. H. Hünenberger, Biophys. J., 2008, 95, 3525–3534 CrossRef CAS PubMed.
- A. K. Sum, R. Faller and J. J. de Pablo, Biophys. J., 2003, 85, 2830–2844 CrossRef CAS PubMed.
- S. Leekumjorn and A. K. Sum, Mol. Simul., 2006, 32, 219–230 CrossRef CAS.
- M. A. Villarreal, S. B. Díaz, E. A. Disalvo and G. G. Montich, Langmuir, 2004, 20, 7844–7851 CrossRef CAS PubMed.
- C. S. Pereira, R. D. Lins, I. Chandrasekhar, L. C. G. Freitas and P. H. Hünenberger, Biophys. J., 2004, 86, 2273–2285 CrossRef CAS PubMed.
- C. S. Pereira and P. H. Hünenberger, Mol. Simul., 2008, 34, 403–420 CrossRef CAS.
- G. Moiset, C. A. López, R. Bartelds, L. Syga, E. Rijpkema, A. Cukkemane, M. Baldus, B. Poolman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 16167–16175 CrossRef CAS PubMed.
- L. Sapir and D. Harries, J. Phys. Chem. B, 2011, 115, 624–634 CrossRef CAS PubMed.
- A. Bax and N. Tjandra, J. Biomol. NMR, 1997, 10, 289–292 CrossRef CAS PubMed.
- N. Tjandra and A. Bax, Science, 1997, 278, 1111–1114 CrossRef CAS PubMed.
- J. H. Prestegard, H. M. Al-Hashimi and J. R. Tolman, Q. Rev. Biophys., 2000, 33, 371–424 CrossRef CAS PubMed.
- J. D. Gross, D. E. Warschawski and R. G. Griffin, J. Am. Chem. Soc., 1997, 119, 796–802 CrossRef CAS.
- D. McElheny, E. DeVita and L. Frydman, J. Magn. Reson., 2000, 143, 321–328 CrossRef CAS PubMed.
- V. Castro, B. Stevensson, S. V. Dvinskikh, C. J. Högberg, A. P. Lyubartsev, H. Zimmermann, D. Sandström and A. Maliniak, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 2604–2611 CrossRef CAS PubMed.
- S. V. Dvinskikh, D. Sandström, Z. Luz, H. Zimmermann and A. Maliniak, J. Chem. Phys., 2003, 119, 413 CrossRef CAS.
- H. Neubauer, J. Meiler, W. Peti and C. Griesinger, Helv. Chim. Acta, 2001, 84, 243–258 CrossRef CAS.
- C. Landersjö, B. Stevensson, R. Eklund, J. Östervall, P. Söderman, G. Widmalm and A. Maliniak, J. Biomol. NMR, 2006, 35, 89–101 CrossRef PubMed.
- B. Stevensson, C. Landersjö, G. Widmalm and A. Maliniak, J. Am. Chem. Soc., 2002, 124, 5946–5947 CrossRef CAS PubMed.
- M. Staaf, C. Höög, B. Stevensson, A. Maliniak and G. Widmalm, Biochemistry, 2001, 40, 3623–3628 CrossRef CAS PubMed.
- A. Almond, J. Bunkenborg, T. Franch, C. H. Gotfredsen and J. Duus, J. Am. Chem. Soc., 2001, 123, 4792–4802 CrossRef CAS PubMed.
- D. I. Freedberg, J. Am. Chem. Soc., 2002, 124, 2358–2362 CrossRef CAS PubMed.
- X. Yi, A. Venot, J. Glushka and J. H. Prestegard, J. Am. Chem. Soc., 2004, 126, 13636–13638 CrossRef CAS PubMed.
- G. Nodet, L. Poggi, D. Abergel, C. Gourmala, D. Dong, Y. Zhang, J. M. Mallet and G. Bodenhausen, J. Am. Chem. Soc., 2007, 129, 9080–9085 CrossRef CAS PubMed.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Phys. Chem. B, 2012, 116, 3164–3179 CrossRef PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- D. J. Price and C. L. Brooks, J. Chem. Phys., 2004, 121, 10096 CrossRef CAS PubMed.
- S.-T. Lin, P. K. Maiti and W. A. Goddard, J. Phys. Chem. B, 2010, 114, 8191–8198 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- J. Rönnols, R. Pendrill, C. Fontana, C. Hamark, T. Angles d'Ortoli, O. Engström, J. Ståhle, M. V. Zaccheus, E. Säwén, L. E. Hahn, S. Iqbal and G. Widmalm, Carbohydr. Res., 2013, 380, 156–166 CrossRef PubMed.
- M. Findeisen, T. Brand and S. Berger, Magn. Reson. Chem., 2007, 45, 175–178 CrossRef CAS PubMed.
- A. Meissner and O. W. Sørensen, Magn. Reson. Chem., 2001, 39, 49–52 CrossRef CAS.
- W. Koźmiński and D. Nanz, J. Magn. Reson., 1997, 124, 383–392 CrossRef.
- W. Kozmiński and D. Nanz, J. Magn. Reson., 2000, 142, 294–299 CrossRef PubMed.
- F. Tian, H. M. Al-Hashimi, J. L. Craighead and J. H. Prestegard, J. Am. Chem. Soc., 2001, 123, 485–492 CrossRef CAS PubMed.
- A. E. Derome and M. P. Williamson, J. Magn. Reson., 1990, 88, 177–185 Search PubMed.
- F. del Río-Portilla, E. Sánchez-Mendoza, V. U. Constantino-Castillo and J. A. del Río, ARKIVOC, 2003, xi, 213–226 Search PubMed.
- V. Castro, S. V. Dvinskikh, G. Widmalm, D. Sandström and A. Maliniak, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 2432–2437 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS.
- E. R. Henry and A. Szabo, J. Chem. Phys., 1985, 82, 4753–4761 CrossRef CAS.
- O. H. S. Ollila, 2013, arXiv:1309.2131v2 [physics.bio-ph], 7.
- C. Zannoni and M. Guerra, Mol. Phys., 1981, 44, 849–869 CrossRef CAS.
- A. Maliniak and G. Widmalm, in Food Oligosaccharides: Production, Analysis and Bioactivity, ed. F. Javier Moreno and M. Luz Sanz, John Wiley & Sons, Ltd., 2014, pp. 320–349 Search PubMed.
- K. Lycknert, A. Maliniak and G. Widmalm, J. Phys. Chem. A, 2001, 105, 5119–5122 CrossRef CAS.
- N. G. A. Bell, G. Rigg, S. Masters, J. Bella and D. Uhrín, Phys. Chem. Chem. Phys., 2013, 15, 18223–18234 RSC.
- T. Rundlöf, C. Landersjö, K. Lycknert, A. Maliniak and G. Widmalm, Magn. Reson. Chem., 1998, 36, 773–776 CrossRef.
- C. Landersjö, C. Höög, A. Maliniak and G. Widmalm, J. Phys. Chem. B, 2000, 104, 5618–5624 CrossRef.
- M. D. Battistel, R. Pendrill, G. Widmalm and D. I. Freedberg, J. Phys. Chem. B, 2013, 117, 4860–4869 CrossRef CAS PubMed.
- K. Shiraga, T. Suzuki, N. Kondo, J. De Baerdemaeker and Y. Ogawa, Carbohydr. Res., 2015, 406, 46–54 CrossRef CAS PubMed.
- R. Y. Dong, Nuclear Magnetic Resonance of Liquid Crystals, Springer-Verlag, New York, 1994 Search PubMed.
- J. W. Eaton, D. Bateman and S. Hauberg, GNU Octave Manual; Version 3, Network Theory Ltd, 2008 Search PubMed.
- E. Hatcher, E. Säwén, G. Widmalm and A. D. MacKerell Jr., J. Phys. Chem. B, 2011, 115, 597–608 CrossRef CAS PubMed.
- E. Säwén, T. Massad, C. Landersjö, P. Damberg and G. Widmalm, Org. Biomol. Chem., 2010, 8, 3684–3695 Search PubMed.
- G. Batta, K. E. Kövér, J. Gervay, M. Hornyák and G. M. Roberts, J. Am. Chem. Soc., 1997, 119, 1336–1345 CrossRef CAS.
- R. Stenutz, I. Carmichael, G. Widmalm and A. S. Serianni, J. Org. Chem., 2002, 67, 949–958 CrossRef CAS PubMed.
- C. Thibaudeau, R. Stenutz, B. Hertz, T. Klepach, S. Zhao, Q. Wu, I. Carmichael and A. S. Serianni, J. Am. Chem. Soc., 2004, 126, 15668–15685 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |