Self-reactions in the HCl⁺ (DCl⁺) + HCl system: a state-selective investigation of the role of rotation

Abstract

The self-reaction of state-selected HCl⁺ (DCl⁺) ions with HCl has been investigated in a guided ion beam setup. The absolute cross sections for proton transfer and deuteron transfer decrease with increasing center of mass collision energy, E_c.m.. The cross section for charge transfer (DCl⁺ + HCl) exhibits a maximum at E_c.m. = 0.5 eV. The cross section for PT and DT decrease significantly with increasing rotational angular momentum in the molecular ion, for the PT the cross section increases again for the highest angular momentum investigated. The rotational dependence of the cross section is rationalized by a simple model in which both the collision energy and part of the rotational energy are available for the reaction. The contribution of the rotation to the total energy available itself depends on the collision energy.

---

1 Introduction

The role of external rotation in ion-molecule reactions is still not well established. In chemical systems with only high frequency modes of vibration a variation of the ensemble temperature correlates with a variation of the rotational state distribution. Several reactions of the type M⁺ + AB, where M⁺ is either a rare gas cation or a polyatomic ion and AB is a polyatomic neutral molecule have been investigated by the variable temperature selected ion flow drift tube (VT-SIFDT) technique.¹ For most of the reactions reviewed the external rotation has little or no effect on the measured rate constant. Prominent exceptions are the charge transfer reactions of atomic cations with diatomics exhibiting high frequency vibrational mode, e.g. CO, N₂ or HCl. E.g., for the charge transfer reaction Kr⁺ + HCl → Kr + HCl⁺, the cross section decreases with increasing rotational temperature of the neutral HCl.² For related reaction systems such a finding has been rationalized by the inability of the neutral dipole to lock into the preferred orientation when it is rotating with higher angular momentum.^3–5 Interestingly the analogous reaction Ar⁺ + HCl leading to either charge transfer or hydrogen atom abstraction does not exhibit a similar rotational temperature dependence of the rate constant.²

An alternative approach for investigating rotational effects in ion molecule reactions is based on forming molecular ions in selected rotational states and measuring the cross section as a function of the rotational angular momentum of the ion. In pioneering work Gerlich and coworkers have demonstrated that the cross section for the reaction H₂⁺ + H₂ → H₃⁺ + H decreased by about 8% in going from rotational quantum number N = 0 to N = 4.⁶ The dimer formation in the ternary association reaction in the system CO⁺ + CO decreases significantly for increasing rotational angular momentum of the CO⁺.⁷ For H-abstraction by NO⁺ from ethanol⁸ and for charge transfer from N₂⁺ to Ar⁹ no discernible effect of the external rotation on the cross section has been observed. On the other hand a significant increase of the cross section has been reported for increasing rotational energy in H₂O⁺ + D₂ → H₂DO⁺ + D.^10,11

In previous work our group has reported on quantum state effects in the proton transfer (PT) from HBr⁺ to CO₂ leading to HOCO⁺ + Br.^12,13 That particular reaction system offered the rather unique possibility to switch a reaction from an endothermic version to an exothermic version by either addressing the HBr⁺ ions in the spin–orbit ground state, ²Π_3/2, or in the excited spin–orbit state, ²Π_1/2. In the former case the cross section increased with increasing center of mass collision energy, in the latter it decreased. This observation was perfectly in line with many other investigations. For both reactions the cross section decreased significantly with increasing rotational angular momentum in the ion. This proved that the internal degree of rotation and the external degree of translation did not necessarily affect the cross section in the same direction.

In the current contribution we wish to extend our previous investigation to a slightly more complex reaction system, where two specific reaction channels can compete. We have chosen the self-reaction system of HCl⁺ + HCl. In principle two reactions take place, (i) proton transfer (PT) and (ii) charge transfer (CT). PT according to the reaction

HCl⁺ + HCl → H₂Cl⁺ + Cl (ΔH = −0.591 eV) (PT)¹⁴

is easily observed in a mass spectrometer. Charge transfer, on the other hand is not easily observed in a MS. If the reaction leads to a redistribution of internal or external energies it becomes in principle observable, however, we will not pursue this possibility in the current work. Charge transfer does become easily observable upon isotopic substitution of one of the reactants. Along this line we will also investigate the following two reactions.

DCl⁺ + HCl → HDCl⁺ + Cl (ΔH = −0.602 eV) (DT)¹⁵

DCl⁺ + HCl → DCl + HCl⁺ (ΔH = −0.009) (CT)¹⁴

2 Experimental approach

The measurements of the cross sections presented in this work have been conducted in a guided-ion-beam (GIB) machine described in earlier publications.^12,13 The apparatus consists of three zones, (i) the ion source, (ii) the reaction zone and (iii) the analysis zone. In the ion source HCl⁺ (DCl⁺) ions are prepared in controllable rotational angular momentum states by means of resonance enhanced multiphoton ionization (REMPI) via the f³Δ₂(v′ = 0) ← ¹Σ⁺(v′′ = 0) transition.¹⁶ That REMPI spectrum provides rotational resolution. By tuning to a particular pump line molecular ions with specific predominant rotational angular momentum can be formed. In general two rotational angular momentum states dominate the population for each pump line as evidenced by photodissociation spectroscopy.^16–18 Throughout this work experiments have been performed on the pump lines R(1) to R(6) for HCl and R(1) to R(8) for DCl, the corresponding average rotational angular momenta, respectively energies are given in Table 1. The standard deviation on the average rotational angular momentum N⁺ is typically close to 1.

Table 1 Average rotational quantum number and energy of HCl⁺ (DCl⁺) prepared via the pump line indicated

Pump	HCl^+		DCl^+
Line	N^+	E rot/meV	N^+	E rot/meV
R1	0.31	0.85	0.35	0.5
R2	1.12	3.69	0.99	1.7
R3	2.45	11.25	2.44	6.2
R4	3.54	20.73	3.22	9.29
R5	4.59	32.54	4.5	16.14
R6	5.7	47.87	5.46	23.37
R7			6.51	32.20
R8			7.57	42.45

---

The state-selected ions are transferred into an octopole which serves as a radio-frequency ion guide and also defines the reaction zone. Neutral HCl is introduced into this reaction zone under room temperature conditions enforcing single collision conditions. Pressure stages separate the reaction zone from the ion source as well as the analysis zone. All product ions as well as remaining reactant ions are transferred into a quadrupole mass analyzer and detected by a channeltron. All data are processed in a personal computer. The experiment is controlled by means of LabView program suites.

3 Computational approach

Electronic structure calculations have been performed for better understanding the reaction dynamics observed experimentally. All calculations employed the GAUSSIAN 03¹⁹ program suit; for visualization MOLDEN²⁰ was used.

The first set of geometry optimizations started at the published values by Burda²¹ and were performed using the UMP2-level²² of theory and a TZVPP basis set²³ (MP2/tzvpp). A second set of geometry optimization was performed with the CCSD-method²⁴ and the same basis set for comparison (CCSD/tzvpp). Since Coupled Cluster calculations were performed, also optimized basis sets for Coupled Cluster were used, as cc-pVTZ^25,26 (CCSD/ccpvtz) and aug-cc-pVTZ^25,26 (CCSD/augccpvtz). All basis sets not included in GAUSSIAN were downloaded from the EMSL website.²⁷

Due to the different isotopes hydrogen/deuterium it was necessary, that frequency calculations were performed to obtain the zero point vibrational energies. These calculations were performed with MP2/TZVPP and CCSD(T) on aug-cc-pVTZ (CCSDT/augccpvtz) level²⁸ of theory.

4 Results and discussion

Results of cross section measurement

We have measured the cross section for proton transfer (PT) as well as deuteron (DT) and charge transfer (CT) in the deuterated form of the title reaction as a function of the center of mass collision energy as well as of the average angular momentum in the molecular ion.

We start the presentation of results by looking at the cross section for proton transfer as a function of the E_c.m., see Fig. 1.

Fig. 1 Cross sections for proton transfer in the title reaction as a function of the collision energy, E_c.m.. The different traces correspond to different average rotational energies as indicated.

The cross section for PT is largest (ca. 21 Ų) for 〈E_rot〉 = 0.5 meV at the smallest collision energy considered E_c.m. = 0.2 eV. As expected for an exothermic reaction, the cross section decreases with increasing collision energy. The smallest values of the cross section are on the order of 2 Ų at E_c.m. = 2 eV irrespective of the rotational energy. For the smallest collision energy investigated the influence of the external rotation is evident from Fig. 1. The effect is apparently small for the largest collision energy considered.

The cross sections for DT are shown in Fig. 2. Again the largest cross section is observed for the smallest collision energy and the smallest rotational energy. The value of 17 Ų is about 20% smaller than the corresponding cross section for PT. The cross section decreases with increasing collision energy to an extend comparable to PT. The smallest cross section measured here is on the order of 2.5 Ų at E_c.m. = 2 eV, slightly larger than in the PT. The effect of rotation is again largest at the smallest collision energy.

Fig. 2 Cross sections for deuteron transfer in the title reaction as a function of the collision energy, E_c.m.. The different traces correspond to different average rotational energies as indicated.

The cross sections for charge transfer – depicted in Fig. 3 – vary non-monotonically with the collision energy. The cross sections are on the order of 10 Ų at E_c.m. = 0.2 eV. They increase by a few Ų in going to E_c.m. = 0.5 eV before decreasing again for even higher collision energy. The maximum in the cross section observed could possibly indicate an effective barrier for charge transfer. At the smallest center of mass collision energy charge transfer leads to HCl⁺ ions with very low kinetic energy. We cannot categorily rule out the possibility that the low cross section measured for E_c.m. = 0.2 eV are in part the result of instrumental discrimination for the lowest kinetic energies. The smallest cross sections are observed at E_c.m. = 2 eV. Note, that the cross section for CT is smaller than that for DT at 0.2 eV but larger than the latter at 2 eV. Thus, the branching ratio of these two competing molecular processes strongly depends on the collision energy. Interestingly, the largest cross section for CT is observed at a mean rotational energy of 32.2 meV for most of the c.m. collision energies considered, in particular at the lowest E_c.m. and the highest E_c.m..

Fig. 3 Cross sections for charge transfer in the title reaction as a function of the collision energy, E_c.m.. The different traces correspond to different average rotational energies as indicated.

An alternative representation of the data involves plotting the cross section as a function of the rotational energy. Here, we concentrate on the PT and DT, which have analogous characteristics. Fig. 4 and 5 illustrate this alternative representation.

Fig. 4 Cross sections for proton transfer in the title reaction as a function of the average rotational energy, 〈E_rot〉. The different traces correspond to different center of mass energies as indicated. The dashed lines are the result of model calculations. For further details see the text.

Fig. 5 Cross sections for deuteron transfer in the title reaction as a function of the average rotational energy, 〈E_rot〉. The different traces correspond to different center of mass energies as indicated. The dashed lines are the result of model calculations. For further details see the text.

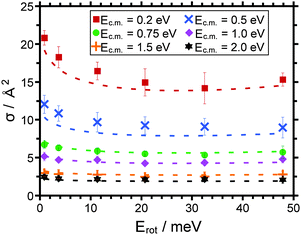
For PT (Fig. 4) the cross sections exhibit a minimum around 〈E_rot〉 = 30 meV, for DT (Fig. 5) the cross sections decrease monotonically with E_rot over the range investigated. The error bars shown reflect statistical standard deviations calculated for repeated measurements of pump line variation. We emphasize that for PT (Fig. 4) the cross section recorded for the highest mean rotational energy of the ion (47.9 meV) has been larger than that for the next lower rotational energy (32.5 meV) for each individual series of pump line variation, in other words, the minimum in the cross section is considered statistically significant. In a later section we will introduce model calculations, the results of which are shown in Fig. 4 and 5 as dashed lines.

Results of quantum chemical calculations

In order to shed additional light on the reaction paths for PT and DT quantum chemical calculations were performed. Similar to our previous work¹² the reacting ions were calculated at zero Kelvin to account for the experimental state-selection. All other species were set to 298 K. The rotational energy and the collision energy have to be considered in addition when discussing the energy balance of the reaction. This approximates the conditions operative in the experiment described above.

The reaction path includes one transition state and two intermediate local minima. The relevant geometries are illustrated in Fig. 6. The two HCl moieties approach with the H–Cl axis pointing in orthogonal directions. In going to the transition state one H atom starts to rotate into the Cl–Cl axis. Beyond the TS one H–Cl bond breaks and another is formed. The reacting system passes through an ion-neutral complex, HClH⁺⋯Cl, before reaching the product state.

Fig. 6 Schematic drawing of the reaction path at the CCSD(T)/aug-cc-pVTZ level, starting point was set to zero. For further details see text.

A similar, however not identical, reaction path has been reported by Burda, Hobza and Zahradník.²¹ The difference appears in the geometry of the transition state, where in our calculations the Cl–Cl distance is slightly larger. We have performed IRC-calculations to ensure, that our proposed transition state is linked to both intermediates shown in the Fig. 6.

The calculated energy values for the proton transfer reaction are listed in Table 2 for the different levels of theory applied. All calculations lead to a self-consistent picture of the reaction path, with only small differences between the methods and basis sets employed. In the following we concentrate on the highest level of computation employed, i.e. the CCSD(T)/aug-cc-pVTZ.

Table 2 Relative energies in eV for the proton transfer reaction, starting point was set to zero

	Method/basis set
Step	MP2/tzvpp	CCSDT/tzvpp	CCSDT/ccpvtz	CCSDT/augccpvtz
start	0	0	0	0
int1	−1.62	−1.58	−1.57	−1.63
ts	−0.87	−0.94	−0.95	−1.00
int2	−1.25	−1.21	−1.22	−1.24
end	−0.93	−0.94	−0.94	−0.93

---

In principle the energetics for PT and DT are not necessarily identical due to the effect of the zero point vibrational energies which may vary differently along the reaction path.

A subtle detail arises from the fact that, in the transition state of DT, we have to specify the position of the deuteron either sitting between the two bridging chlorine atoms (DT2), or terminally (DT1). In total we arrive at three different energetic profiles indicated in Fig. 6, one for the PT and two for the DT. Of course the overall reaction enthalpy does not depend on the position of the deuteron. The exothermicity obtained here is −0.93 eV for the PT versus −0.96 eV for the DT (see Table 4). The absolute value of this difference is slightly larger than the value derived from experiment.¹⁴ The energies of the stationary points for the three energetic profiles mentioned above are given in Table 3. The data reveal that the energies for PT are higher by about 25 meV than DT1. The energies for DT2 always lie between that for PT and DT1. This implies that for DT the deuteron is energetically favored in the terminal position.

Table 3 Relative energies for PT, DT1, DT2 in eV at the CCSD(T)/aug-cc-pVTZ level, starting point was set to zero

Step	PT	DT1	DT2
start	0	0	0
int1	−1.632	−1.659	−1.657
ts	−1.000	−1.024	−1.008
int2	−1.241	−1.267	−1.253
end	−0.931	−0.957	−0.957

---

Table 4 Parameters obtained in the modeling of cross sections for PT and DT according to eqn (3)

	PT	DT
a	25.596	20.704
b	−23.627
c	−17.768
d	−0.098
e	−2.121

---

Experimentally the difference between DT1 and DT2 is not accessible in the current experiment. Only a double isotope labeling (hydrogen and chlorine) would allow measuring the difference.

Modelling of cross section data

In the following section we will attempt to rationalize the experimental findings. We start by comparing the measured cross sections (R5 pump line) with values expected from Langevin and approximate dipole orientation (ADO) theories in Fig. 7. Here, the data measured on the R5 pump line have been chosen since the average rotational energy resembles that of a thermal room temperature sample.

Fig. 7 Comparison of experimental cross sections measured on the R5 pump line (diamonds) to calculations according to the Langevin theory (squares), the original ADO theory (crosses) and parametrized trajectory calculations (TC) (circles).

According to the classical Langevin theory the cross section of an exothermic ion-molecule reaction is given by:²⁹

Evidently our measured cross sections are only about 20% to 30% of the Langevin limit. Furthermore, the cross section does not scale with E^−1/2 but rather with approximately E⁻². Classical Langevin theory only considers the interaction of a point charge with a polarizable molecule.²⁹ Since the HCl molecule has a dipole moment of about 1.1 D³⁰ orientation effects might be expected to play an important role. Such orientation effects have been very successfully described by means of the ADO theory developed by Su and Bowers³¹ and later parametrized against trajectory calculations (TC) by Su.³²

In the framework of the ADO theory the thermal rate constant is given by

where the first term reflects the capture limit and the second term the ion–dipole contribution, c = 0.1724 for the current reaction system.³³ The rate constants are then converted to cross sections via the relation σ = k/v_rel, where v_rel is the relative velocity of the two moieties at the given collision energy.

The ADO theory has been originally setup for the interaction of a point charge with a molecular dipole. It is based on the assumption that the charge–dipole interaction energy contributes to the attractive part of the potential. This intrinsically leads to larger cross sections compared to the Langevin limit, i.e. larger deviation from the experimental data. The parameterized trajectory calculations effectively interpolate between the ADO result at low collision energy and the Langevin result at high collision energy. The average rotational energy of the dipolar molecule enters into both theories as effective temperatures. Evidently our measured cross sections are significantly smaller than the theoretical limits. The title reaction does not conform to the capture limit.

Although the ADO theory has been developed for the interaction of a point charge with a diatomic dipole implying that the rotational energy taken into account is that of the diatomic, the ADO has also been successfully applied to more complex reactions of the type polyatomic–polyatomic, e.g. by Bohme and coworkers.^34,35 This could be the result of rotational effects being averaged over contributions from the ion and from the neutral leading to an effective average angle between the main axes of the two molecules.

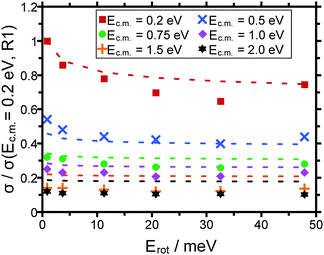
In order to analyze whether the ADO theory can at least in principle account for the rotational energy dependence of the cross sections we have in the following assumed that the rotational energy of the molecular ion can be converted into an effective rotational temperature of the system via E_rot = k_B·T. Since the absolute cross sections predicted by the ADO theory are a factor of 3 to 5 higher than the experimental cross sections, it is not helpful to compare these absolute numbers. Instead we compare the cross sections normalized to the value measured/calculated for the R(1) pump line/rotational energy of 0.5 meV (cf.Fig. 8).

Fig. 8 Cross sections for PT normalized to the value at E_c.m. = 0.2 eV and 〈E_rot〉 = 0.5 meV; symbols experimental data, dashed lines result of parametrized trajectory calculations as outlined in the text.

Intrinsically the ADO theory predicts a monotonic decrease of the cross section with increasing rotational energy/temperature. Thus, the minimum of the experimental cross sections around E = 30 meV, which we consider significant, cannot be rationalized. Still, the relative variation of the cross sections with E_rot is in the correct order for collision energies of 0.2 eV, and 0.5 eV. For all larger collision energies there is a pronounced discrepancy between the experimental and the calculated cross sections. Thus, not only the absolute cross sections predicted are too high (cf.Fig. 7), also the relative variation of σ with E_c.m. does not match the experimental data (cf.Fig. 8).

Evidently theories based on the assumption of a capture limit cannot reflect all details of the experimental observations. Most likely the appropriate theoretical treatment of the data would be performing state-selective molecular dynamics calculations on an ab initio potential energy surface. Such calculations have been reported by Hase and coworkers for the reaction of protonated urea with molecular nitrogen.³⁶ Here, the generation of the appropriate multi-dimensional potential energy surface represents a formidable challenge. In fact very recently Hase and coworkers reported such a PES for the reaction system HBr⁺ + CO₂,³⁷ for which the state-selective cross sections for proton transfer have been reported by Paetow et al.^12,13 Based on this PES MD calculations can now be performed as the next step.³⁸ The ab initio calculations providing the one dimensional reaction path presented in a previous section are a helpful input to more extensive multi-dimensional PES calculations. The latter, however, are beyond the scope of this work.

At this point we have decided to perform some parametric model calculations which we hope provide some guidance to future more elaborate work. In fact there are few reports on a minimum of the cross section for specific rotational angular momentum, N, of one reactant. One possible interpretation is connected to the competition between two processes, the decrease in σ with increasing N due to the decreasing orientation effect and an increase in σ with increasing N due to an energy effect enhancing the reaction probability.^39,40

Clearly the experimental cross sections depend on the center of mass collision energy and the rotational energy of the ion. Consequently we set up a model where the cross section depends on an effective collision energy, E_eff, where E_eff contains contributions from the center of mass collision energy, E_c.m., and from the rotational energy of the two reacting molecules, E_corr., i.e. σ(E_eff) = σ(E_c.m. + E_corr.).

A close inspection of the data suggests that the cross section for PT exhibits a minimum around 30 meV. This corresponds to a situation where the rotational energy of the ion and the neutral and consequently also the rotational velocities are basically equal. In going from the PT to the DT a correspondingly higher rotational energy of the DCl⁺ is required to match the rotational velocity of the neutral HCl. In this case the minimum in σ would be shifted to a rotational energy on the order of 60 meV. This would be just outside the range investigated in our work. The fact that the measured cross section for DT decreases up to the highest rotational energy investigated is at least compatible with this scenario.

Thus, we assume that the correction term, E_corr., scales with (ω_ion − ω_neutral)². Furthermore, the magnitude of the correction term depends on the center of mass collision energy, it is large for small E_c.m. and decreases with increasing E_c.m.. In our model we take that into account by a term c·E^d. Finally as a subtle detail we need a final parameter, e, taking into account the offset of the parabolic term (ω_ion − ω_neutral)². Combining these concepts we arrive at the following expression for the cross section,

where the rotational velocities are entered in GHz, the center of mass energies in eV, the resulting cross sections are in Ų. Ultimately we have determined the parameters a to e by non-linear least square fitting of the model to all experimental data for PT and DT. The optimized parameters are listed in Table 4. The results of the modelling calculations are shown as dashed lines in Fig. 4 and 5. The pivotal point is, that we arrive at a reasonable representation of all data by enforcing that the parameters b to e are identical for PT and DT. The only parameter allowed to be different for PT and DT is the scaling parameter a.

We wish to emphasize that the overall value of the cross section is dominated by the contribution corresponding to a term a·E^e, in principle a scaled Langevin contribution. As already mentioned earlier the exponent is close to e ≈ −2, not untypical for ion-molecule reactions. The parameters b, c and d represent the correction term to the effective energy available to the reacting system, which depends on the relative rotational velocities of the ion and the neutral. This correction term has positive values in the entire range considered, it exhibits a maximum for the PT around 30 meV and decreases with increasing E_c.m..

Evidently the model proposed is capable of describing the experimental data convincingly. Thus, the experimental data are compatible with a model based on the assumption that the relative rotational velocity of ion and neutral determines the rotational energy dependence of the cross section data. Cleary, we cannot exclude the possibility that other models and in particular more sophisticated theories might provide a better description of the cross sections.

It is interesting to compare the rotational angular momenta of the ions to the orbiting angular momenta at specific collision energies. For all collision energies the total angular momentum is dominated by the orbiting angular momentum. At the smallest collision energy of 0.2 eV and the respective highest rotational pump line the ratio of L_orbit : L_ion is about 29 for HCl⁺ + HCl, and about 22 for DCl⁺ + HCl.

Hase and coworkers have reported a number of dynamical studies focussing on anionic reactions aimed at S_N2 reactions. There, statistical theories often don't reproduce the experimentally measured rate constants.⁴¹ An exception appears to be the reaction F⁻ + CH₃Cl → FCH₃ + Cl⁻ where the translational energy dependence observed in the experiment agreed well with numbers derived from statistical theory as well as from trajectory calculations.⁴² The potential energy surface is conceptionally similar to the one operative in the current work in that there are two intermediate local minima separated by an intermediate transition state. In the S_N2 example⁴² the intermediate barrier occurs about 0.5 eV below the entrance channel, yet still affects the dynamics. In the reaction of this work the intermediate barrier is even lower, about 1 eV below the entrance channel. Thus one might expect that its effect on the dynamics is even smaller compared to the CH₃X example. However, we have to note, that the S_N2 reaction mentioned above occurred close to the capture limit, while the title reaction of this work proceeds at only 20% to 30% of the capture limit.

There are few reports on a minimum in the cross section as a function of the angular momentum of one of the reactants. We suggest that such a minimum could originate from the relative rotational velocities of two reacting moieties. In thermal experiments where the average rotational energy of all reactants is changed concomitantly the relative rotational velocity is not changed upon changing the temperature. In fact this is the advantage of the state-selective ion-molecule reaction experiment, where the rotational angular momentum of the ion is systematically changed and the average angular momentum of the neutral is kept constant. Still, to date there are few reports on the rotational energy (or angular momentum) dependence of cross sections for PT in the literature. In most cases the cross section monotonically decreases as a function of E_rot.^3,12,13 We are not aware of another example of the cross section running through a minimum as a function of E_rot. For the reaction H₂O⁺ + H₂ → H₃O⁺ + H the cross section exhibits a maximum around T = 350 K.⁴³ On grounds of dynamical restrictions where the rotational frequency of the molecules involved has to match the orbiting frequency of the collision complex one would expect extrema of the cross section for particular rotational energies of the ion. Such a model has been proposed by Sathyamurthy.⁴⁴

The reaction path for PT and DT involves a hydrogen (deuteron) atom moving in between the two chlorine atoms. This implies that the rotational frequency of the molecules and the orbiting frequency of the colliding system should be different. At this point we speculate that the minimum in the cross section observed correlates with the two relevant angular frequencies matching in an unfavorable manner. Clearly, further theoretical investigations are required to fully understand the dynamics of this PT and DT. However, this is beyond the scope of this work.

Compared to PT and DT there are even less reports on a marked rotational dependence of σ for a charge transfer. The charge transfer from Kr⁺ to HCl was shown to exhibit a minimum as a function of the center of mass collision energy. With increasing rotational temperature of the HCl the rate constant decreased.¹ In a rotationally state-selective experiment Ng have not observed a measurable rotational dependence for the CT N₂⁺ + Ar → N₂ + Ar^+ 9 The cross section for hydride abstraction by NO⁺ from C₂H₅OH did not depend on the rotational angular momentum of the NO⁺ either.⁸ An alternative approach for investigating rotational effects in ion-molecule reactions is based on ion trapping.⁴⁵

5 Summary

The cross sections for proton (deuteron) transfer and charge transfer in the HCl⁺ (DCl⁺) + HCl self-reaction system have been investigated by means of the GIB technique. The cross section for PT and DT decrease with increasing collision energy as expected for an exothermic reaction. The absolute cross sections are about a factor of 3 to 5 smaller than the Langevin limit. The energy dependence of the cross section is considerably steeper than predicted by capture theories. The cross section for CT exhibits a maximum at a collision energy of 0.5 eV, indicating the possible dynamical role of an intermediate barrier.

For small rotational angular momentum of HCl⁺ (DCl⁺) the cross section for PT and DT respectively decrease with increasing rotational angular momentum as observed in several previous investigations of this kind. However, for the largest angular momenta the cross section increases again with N⁺ for PT.

Neither the absolute cross sections nor the energy dependence of the cross sections can be reproduced by simple capture theories based on the approximate dipole orientation theory. Instead, the experimental data have been rationalized by an empirical model accounting for the contributions of the center of mass collision energy as well as relative rotational velocities of the molecular ion and the neutral. A minimum of the cross section for PT transfer occurs if the rotational velocities of the ion and the neutral match. The experimental data for both PT and DT are compatible with this model. The contribution from the rotation of the ion and the neutral to the effective energy available to the reacting system appears to depend on the collision energy. This becomes obvious when plotting normalized cross sections as a function of the rotational energy (provided as ESI†).

Clearly, more sophisticated dynamics calculations, e.g. of the type reported by Hase and coworkers,^36,37 are required for a better understanding of the new results presented here. We hope to stimulate such calculations by this report.

Additional information is available as ESI,† in particular (i) the normalized cross section data, (ii) an alternative model calculation, (iii) geometry and frequency parameters from the ab initio calculations and (iv) a table of relevant orbiting and rotational angular momenta.

Acknowledgements

Financial support of this work by the Deutsche Forschungsgemeinschaft is gratefully acknowledged. We are indebted to Lisa Paetow for her contribution in the early stage of this work. Stimulating discussions with Prof. W. L. Hase are cordially acknowledged.

References

1. A. A. Viggiano and R. A. Morris, J. Phys. Chem., 1996, 100, 19227–19240.
2. A. A. Viggiano, R. A. Morris, F. Dale, J. F. Paulson, K. Giles, D. Smith and T. Su, J. Chem. Phys., 1990, 93, 1149.
3. D. C. Clary, D. Smith and N. G. Adams, Chem. Phys. Lett., 1985, 119, 320–326.
4. C. Rebrion, J. B. Marquette, B. R. Rowe and D. C. Clary, Chem. Phys. Lett., 1988, 143, 130–134.
5. D. C. Clary, Chem. Phys. Lett., 1995, 232, 267–272.
6. T. Glenewinkel-Meyer and D. Gerlich, Isr. J. Chem., 1997, 37, 343–352.
7. D. Gerlich and T. Rox, Z. Phys. D: At., Mol. Clusters, 1989, 13, 259–268.
8. R. J. Green, J. Qian, H. T. Kim and S. L. Anderson, J. Chem. Phys., 2000, 113, 3002–3010.
9. Y. C. Chang, Y. Xu, Z. Lu, H. Xu and C. Y. Ng, J. Chem. Phys., 2012, 137, 104202.
10. Y. Xu, B. Xiong, Y. C. Chang and C. Y. Ng, J. Chem. Phys., 2012, 137, 241101.
11. Y. Xu, B. Xiong, Y. C. Chang and C. Y. Ng, J. Chem. Phys., 2013, 139, 024203.
12. L. Paetow, F. Unger, W. Beichel, G. Frenking and K.-M. Weitzel, J. Chem. Phys., 2010, 132, 174305.
13. L. Paetow, F. Unger, B. Beutel and K.-M. Weitzel, J. Chem. Phys., 2010, 133, 234301.
14. S. G. Lias, Gas-phase ion and neutral thermochemistry, Journal of physical and chemical reference data, Published by the American Chemical Society and the American Institute of Physics for the National Bureau of Standards, Gas-phase ion and neutral thermochemistry, 1988.
15. L. A. Paetow, Untersuchungen zu Energetik und Dynamik von Reaktionen zustandsselektierter HBr+- und HCl+-Ionen, Phd dissertation, Philipps-Universität Marburg, 2011.
16. M. Penno, A. Holzwarth and K.-M. Weitzel, Mol. Phys., 1999, 97, 43–52.
17. M. Penno and K.-M. Weitzel, Z. Phys. Chem., 2004, 218, 311–326.
18. M. Michel, M. V. Korolkov and K.-M. Weitzel, J. Phys. Chem. A, 2004, 108, 9924–9930.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford CT, 2004.
20. G. t. Velde and E. Baerends, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
21. J. V. Burda, P. Hobza and R. Zahradník, J. Phys. Chem. A, 1997, 101, 1134–1139.
22. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
23. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
24. R. J. Bartlett, J. Phys. Chem., 1989, 93, 1697–1708.
25. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
26. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
27. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
28. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
29. G. Gioumousis and D. P. Stevenson, J. Chem. Phys., 1958, 29, 294–299.
30. E. W. Kaiser, J. Chem. Phys., 1970, 53, 1686.
31. T. Su and M. T. Bowers, J. Chem. Phys., 1973, 58, 3027–3037.
32. T. Su, J. Chem. Phys., 1994, 100, 4703.
33. T. Su and M. T. Bowers, Int. J. Mass Spectrom. Ion Phys., 1973, 12, 347–356.
34. R. S. Hemsworth, J. D. Payzant, H. I. Schiff and D. K. Bohme, Chem. Phys. Lett., 1974, 26, 417–421.
35. G. I. Mackay, L. D. Betowski, J. D. Payzant, H. I. Schiff and D. K. Bohme, J. Phys. Chem., 1976, 80, 2919–2922.
36. Y. Jeanvoine, M.-P. Gaigeot, W. L. Hase, K. Song and R. Spezia, Int. J. Mass Spectrom., 2011, 308, 289–298.
37. R. Sun, G. Granucci, A. K. Paul, M. Siebert, H. J. Liang, G. Cheong, W. L. Hase and M. Persico, J. Chem. Phys., 2015, 142, 104302.
38. W. L. Hase, personal communication, 2015.
39. M. Gonzalez, M. Gilibert, A. Aguilar and R. Sayos, Chem. Phys. Lett., 1993, 204, 578–586.
40. L. S. Sunderlin and P. B. Armentrout, Chem. Phys. Lett., 1990, 167, 188–192.
41. H. Wang and W. L. Hase, J. Am. Chem. Soc., 1995, 117, 9347–9356.
42. T. Su, H. Wang and W. L. Hase, J. Phys. Chem. A, 1998, 102, 9819–9828.
43. S. G. Ard, A. Li, O. Martinez, N. S. Shuman, A. A. Viggiano and H. Guo, J. Phys. Chem. A, 2014, 118, 11485–11489.
44. N. Sathyamurthy, Chem. Rev., 1983, 83, 601–618.
45. X. Tong, T. Nagy, J. Y. Reyes, M. Germann, M. Meuwly and S. Willitsch, Chem. Phys. Lett., 2012, 547, 1–8.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp02266e

---