Open Access Article
Open Access ArticleDistortions of ethyne when complexed with a cuprous or argentous halide: the rotational spectrum of C2H2⋯CuF†
Daniel P.
Zaleski
a,
Susanna L.
Stephens
a,
David P.
Tew
b,
Dror M.
Bittner
a,
Nicholas R.
Walker
*a and
Anthony C.
Legon
*b
aSchool of Chemistry, Newcastle University, Bedson Building, Newcastle-upon-Tyne, NE1 7RU, UK. E-mail: nick.walker@newcastle.ac.uk
bSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: a.c.legon@bristol.ac.uk
First published on 18th June 2015
Abstract
A new molecule C2H2⋯CuF has been synthesized in the gas phase by means of the reaction of laser-ablated metallic copper with a pulse of gas consisting of a dilute mixture of ethyne and sulfur hexafluoride in argon. The ground-state rotational spectrum was detected by two types of Fourier-transform microwave spectroscopy, namely that conducted in a microwave Fabry–Perot cavity and the chirped-pulse broadband technique. The spectroscopic constants of the six isotopologues 12C2H2⋯63Cu19F, 12C2H2⋯65Cu19F, 13C2H2⋯63Cu19F, 13C2H2⋯65Cu19F, 12C2D2⋯63Cu19F and 12C2D2⋯65Cu19F were determined and interpreted to show that the molecule has a planar, T-shaped geometry belonging to the molecular point group C2v, with CuF forming the stem of the T. Quantitative interpretation reveals that the ethyne molecule is distorted when subsumed into the complex in such manner that the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond lengthens (by δr) and the two H atoms cease to be collinear with the C
C bond lengthens (by δr) and the two H atoms cease to be collinear with the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C internuclear line. The H atoms move symmetrically away from the approaching Cu atom of CuF, to increase each *
C internuclear line. The H atoms move symmetrically away from the approaching Cu atom of CuF, to increase each *![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H angle by δA = 14.65(2)°, from 180° to 194.65(2)°. Ab initio calculations at the explicitly-correlated level of theory CCSD(T)(F12*)/aug-cc-pVTZ lead to good agreement with the experimental geometry. It is shown that similar distortions δr and δA, similarly determined, for four complexes C2H2⋯MX (M = Cu or Ag; X = F, Cl or CCH) are approximately linearly related to the energies De for the dissociation process C2H2⋯MX = C2H2 + MX.
C–H angle by δA = 14.65(2)°, from 180° to 194.65(2)°. Ab initio calculations at the explicitly-correlated level of theory CCSD(T)(F12*)/aug-cc-pVTZ lead to good agreement with the experimental geometry. It is shown that similar distortions δr and δA, similarly determined, for four complexes C2H2⋯MX (M = Cu or Ag; X = F, Cl or CCH) are approximately linearly related to the energies De for the dissociation process C2H2⋯MX = C2H2 + MX.
1. Introduction
The coordination of transition metal atoms M, cations M+ or polar salts M+X− to alkynes and alkenes has been described in terms of the interaction of the π electrons of the latter compounds with the π* orbitals of the metal atom or ion.1,2 Such interactions achieve importance by virtue of their presence in coordination compounds that feature in hydrogenation and polymerization reactions.3 For that reason, we have recently been investigating systematically a series of simple, gas-phase complexes of the type C2H2⋯MX which contain such interactions, where M is a coinage metal atom and X is a halogen atom.4–6 The advantage of working in the gas phase is that distortions of the alkyne on complex formation are free from lattice or solvent effects and are therefore intrinsic to the interaction of interest. The technique employed in the synthesis of C2H2⋯MX complexes is laser ablation of the metal M in the presence of both ethyne and a source of halogen atom X in a preponderating excess of argon gas. The subsequent, rapid supersonic expansion of the mixture into a vacuum cools and stabilizes the product molecules and allows their rotational spectra to be observed. By these methods it has been possible to determine, with all the precision associated with microwave spectroscopy, the geometries of several species4–6 C2H2⋯MX, where MX is AgCl, AgCCH, or CuCl.In this article, we report the rotational spectra of six isotopologues of C2H2⋯Cu–F. The complexes were produced by the laser ablation of metallic copper in the presence of a pulse of ethyne–SF6–Ar gas mixture and their spectra were detected by two versions of the Fourier-transform microwave technique. Interpretation of the spectroscopic constants thereby determined leads to a precise characterization of the distortion that ethyne undergoes when it is coordinated to CuF. The distortions will be compared with those predicted by an ab initio calculation conducted at the CCSD(T)(F12*)/AVTZ level of theory Such distortions have now been established, both experimentally and ab initio, as accompanying the attachment of C2H2 to MX = CuF, CuCl, AgCl and AgCCH (where M is copper or silver, and X = F, Cl or CCH as appropriate). Variations in these distortions with (1) M and (2) X will be considered.
2. Experimental and theoretical methods
Experimental data for C2H2⋯CuF and C2D2⋯CuF were recorded on a chirped-pulse Fourier transform microwave spectrometer7 operating between 7 and 18.5 GHz. The instrument has been previously described in detail.8,9 A gas sample was prepared containing approximately 1% C2H2 (or C2D2 as appropriate) and 1% SF6 balanced in 6 bar argon. The gas mixture then pulsed over a copper target rod which was ablated with a Nd:YAG laser. The gas pulse was subsequently expanded into a vacuum chamber. For these experiments, the pulsed nozzle was placed perpendicular to the axis of microwave propagation. During each sample injection cycle, 8 free induction decays (FID's) were measured, each 20 μs in duration. For C2H2⋯CuF a total of 480 k FID's were acquired (16 h), for C2D2⋯CuF the total was 780 k (26 h), and 720 k (24 h) for 13C2H2–CuF. In each case, Fourier transformation used a digital Kaiser–Bessel window function.For 12C2H2⋯CuF, data were also recorded on a Balle–Flygare cavity spectrometer,10,11 with an equivalent gas sample. These measurements were acquired with the pulsed nozzle placed coaxial with the direction of microwave propagation. Transitions measured in this arrangement appear as Doppler doublets, each normally with a full-width half maximum (FWHM) of 5 kHz (but see Section 3.1); this is compared to a FWHM of approximately 150 kHz for the perpendicular arrangement found in the broadband instrument. Only samples containing isotopes in natural abundance were employed when using this spectrometer.
Geometry optimizations were performed using CCSD(T)(F12*),12 a coupled-cluster method with single and double excitations, explicit correlation,13 and a perturbative treatment of triple excitations.14 An AVTZ basis set combination was used, by which we mean that the aug-cc-pVTZ basis sets15 were used for the C, F and H atoms and the aug-cc-pVTZ-PP basis for Cu, in combination with the ECP-10-MDF effective core potential on Cu to account for scalar relativistic effects.16,17 The frozen-core approximation was used throughout, and all calculations were performed using the MOLPRO package.18 The equilibrium dissociation energy De for the process C2H2⋯Cu–F = C2H2 + Cu–F was also computed at the CCSD(T)(F12*)/AVTZ level using the counterpoise correction method19 where, for numerical stability, the CABS singles correction was not included in the correction term. The result was De = 170 kJ mol−1.
For the free CuF, the bond length was optimised on a series of potential curves including successive corrections for core correlation, computed at the CCSD(T) level by using the cc-pwCVQZ basis, full triples at the frozen-core level with a cc-pVQZ basis and perturbative quadruples using the cc-pVTZ basis, following a similar procedure to that employed by Gauss et al.20 Post CCSD(T) calculations were performed using the MRCC program21 and yielded the fully corrected bond length re(Cu–F) = 1.7430 Å, with a basis set uncertainty of 0.0006 Å. This result is in good agreement with the experimental value 1.74493 Å calculated from equilibrium rotational constants22 of 63Cu19F and 65Cu19F by using the expression re = {h/8π2μBe}½. At the CCSD(T)(F12*)/aug-cc-pVTZ level of theory, as used for C2H2⋯Cu–F, the equilibrium bond length for the free CuF molecule is predicted to be 1.7422(25) Å, where the error is that estimated (via gaussian error propagation) to arise from basis set incompleteness (0.0007 Å), core valence correlation error (0.0021 Å) and higher-order correlation (0.0011 Å).
3. Results
3.1 Determination of spectroscopic constants
For all six isotopologues investigated, only vibrational ground-state, a-type R-branch transitions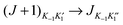 with K−1 = 0 or 1 of the asymmetric-rotor complex C2H2⋯Cu–F were observed under the experimental conditions described in Section 2. Each transition carried a resolvable nuclear quadrupole hyperfine structure resulting from a single quadrupolar nucleus 63Cu or 65Cu (I = 3/2). Transition frequencies of each isotopologue were fitted by means of the program PGOPHER23 with the following choice of Hamiltonian:
with K−1 = 0 or 1 of the asymmetric-rotor complex C2H2⋯Cu–F were observed under the experimental conditions described in Section 2. Each transition carried a resolvable nuclear quadrupole hyperfine structure resulting from a single quadrupolar nucleus 63Cu or 65Cu (I = 3/2). Transition frequencies of each isotopologue were fitted by means of the program PGOPHER23 with the following choice of Hamiltonian:| H = HR − ⅙Q(Cu): ∇E(Cu), | (1) |
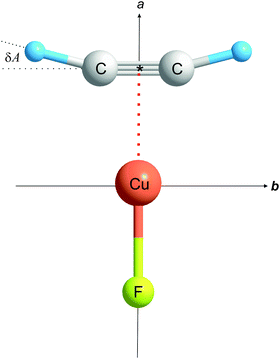
The rotational constants of the most abundant isotopologue 12C2H2⋯63Cu19F are large enough that only one group of J + 1 → J transitions, namely that with J = 1, could be measured in the frequency range available. A set of internally consistent arguments will be presented to show that the geometry of C2H2⋯Cu–F is of the planar, T-shaped type in which the non-covalent interaction of the two component molecules involves primarily the Cu atom of CuF and the π bond of ethyne, as shown in Fig. 1. The experimental consequences of such a geometry are as follows:
(1) The molecule is a nearly prolate, planar asymmetric rotor of molecular point group C2v, with the a axis coincident with the C2 axis. The rotational constant A0 is close in magnitude to the rotational constant B0 of free ethyne. Any difference of the two rotational constants will provide quantitative information about the extent of any geometrical distortion of the ethyne molecule when subsumed into C2H2⋯Cu–F.
(2) The ground-state molecule will have a small positive inertia defect
| Δ0 = I0c − I0b − I0a, | (2) |
(3) A rotation Ca2 exchanges a pair of equivalent protons (I = 1/2) and this endows K−1 = 1 transitions with a nuclear spin statistical weight of 3 relative to that of 1 for K−1 = 0 transitions. This effect is evident in the set of 212 → 111, 202 → 101, 211 → 110 transitions, as can be seen from the recording of these transitions shown in Fig. 2. Similar arguments applied to the 12C2D2⋯Cu19F and 13C2H2⋯Cu19F isotopologues require the corresponding ratios to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 6
2 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, respectively, which were indeed as observed.
10, respectively, which were indeed as observed.
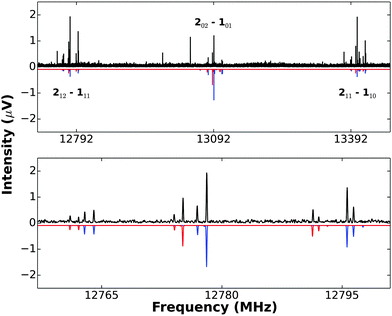 | ||
Fig. 2 A recording (10 × vertical magnification) of the three J = 2 → 1 transitions of 12C2H2⋯63Cu19F and 12C2H2⋯65Cu19F, showing Cu nuclear quadrupole hyperfine structure (upper panel). The downward pointing spectrum is that synthesized by using PGOPHER and the spectroscopic constants given in Table 1 (2 K rotational temperature assumed). This simulation does not include nuclear spin statistics, so the difference between the simulation and observed spectrum shows clearly the presence of nuclear spin statistics in the latter. Even though hyperfine splitting is greater in the two outer transitions 212 → 111 and 211 → 110, their statistical weight advantage (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) over the central 202 → 101 transition is evident. The lower panel gives an expanded version of the 212 → 111 transitions of 12C2H2⋯63Cu19F (blue) and 12C2H2⋯65Cu19F (red). The simulated spectrum (with appropriate scaling of intensities) is again downward pointing. 1) over the central 202 → 101 transition is evident. The lower panel gives an expanded version of the 212 → 111 transitions of 12C2H2⋯63Cu19F (blue) and 12C2H2⋯65Cu19F (red). The simulated spectrum (with appropriate scaling of intensities) is again downward pointing. | ||
(4) Isotopic substitution of 63Cu by 65Cu should leave A0 unchanged.
It is evident that the rotational constant A0 has a central role to play in drawing conclusions about the symmetry and geometry of C2H2⋯Cu–F. Unfortunately, the 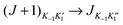 (K−1 = 0 or 1) transition frequencies have a very weak dependence on A0 and it was not possible from the measured transition frequencies to determine A0 independently of the two centrifugal distortion constants ΔJ and ΔJK. (There is insignificant dependence on the remaining centrifugal distortion constants.) This difficulty was circumvented by the following approach.
(K−1 = 0 or 1) transition frequencies have a very weak dependence on A0 and it was not possible from the measured transition frequencies to determine A0 independently of the two centrifugal distortion constants ΔJ and ΔJK. (There is insignificant dependence on the remaining centrifugal distortion constants.) This difficulty was circumvented by the following approach.
It has been shown elsewhere that centrifugal distortion constants of molecules similar to C2H2⋯Cu–F can be calculated ab initio with good accuracy.6 For example, in the closely related species C2H2⋯Cu–Cl calculations at the MP2/cc-pVTZ level of theory reproduced ΔJ and ΔJK to within a few standard deviations of the well-determined experimental values. Here, the five quartic constants (ΔJ, ΔJK, ΔK, δJ and δJK) for C2H2⋯Cu–F were calculated for the optimized geometry at the higher level of theory MP2/aug-cc-pVQZ with the aid of the Gaussian electronic structure package25 for each isotopologue investigated. The calculated constants ΔJ and ΔJK were then fixed in the PGOPHER23 fits of observed frequencies to determine the rotational constants A0, B0 and C0 and the Cu nuclear quadrupole coupling constants χaa(Cu) and χbb(Cu) − χcc(Cu) for the isotopologues 12C2H2⋯63Cu19F and 12C2H2⋯65Cu19F in the first instance. The spectroscopic constants so determined both from measurements made with the Balle–Flygare and the chirped-pulse spectrometers are displayed in Table 1. The residuals of the fit to frequencies collected with the Balle–Flygare spectrometer were poorer than the usual few kHz. This arises because C2H2⋯CuF carries four nuclei (H, H, Cu and F) with magnetic moments of significant magnitude, in addition to the electric quadrupolar moment of the Cu nucleus. Moreover, only the lowest J transitions were available because of the relatively large rotational constants. The magnetic coupling of these nuclei (Cu, F spin–spin coupling, for example) can lead to further complicated but minor, partially resolved splitting or broadening and/or lineshape distortion of each Cu nuclear quadrupole component and is most significant at the lowest J. Therefore assignment of the magnetic sub-structure was not possible in the observed transitions of C2H2⋯CuF, particularly those with K−1 = 1, and hence larger than normal residuals in the fit of the Cu nuclear quadrupole hyperfine structure resulted. When measured with the lower resolution, chirped-pulse instrument, fitted frequencies assigned to Cu quadrupole components gave similar magnitude residuals. Reassuringly, the spectroscopic constants determined independently with the two spectrometers are identical within experimental error.
| Spectroscopic constant | Balle–Flygare | Chirped-pulse | ||
|---|---|---|---|---|
| 12C2H2⋯63CuF | 12C2H2⋯65CuF | 12C2H2⋯63CuF | 12C2H2⋯65CuF | |
| a Values calculated at the MP2/aug-cc-pVQZ level of theory and fixed in the fit. b Number of nuclear quadrupole components included in the fit. c Standard deviation of fit. | ||||
| A 0/MHz | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 749(83) 749(83) |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930(270) 930(270) |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030(230) 030(230) |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020(180) 020(180) |
| B 0/MHz | 3431.4407(48) | 3430.5201(55) | 3431.4404(56) | 3430.5159(42) |
| C 0/MHz | 3116.7391(44) | 3115.9722(55) | 3116.7348(56) | 3115.9752(39) |
| Δ JK /kHza | [38.3] | [38.2] | [38.3] | [38.2] |
| Δ J/kHza | [0.61] | [0.61] | [0.61] | [0.61] |
| χ aa (Cu)/MHz | 69.991(47) | 64.721(53) | 69.979(53) | 64.720(40) |
| {χbb(Cu) − χcc(Cu)}/MHz | −79.17(11) | −73.25(12) | −79.17(13) | −73.224(73) |
| N | 20 | 16 | 18 | 19 |
| σ r.m.s./kHzc | 30 | 33 | 34 | 26 |
Measurements for 13C2H2⋯63,65Cu19F, and 12C2D2⋯63,65Cu19F were made exclusively on the chirped-pulse instrument to conserve the more expensive isotopic materials. The spectroscopic constants for these species were obtained in a similar way and are recorded in Table 2. Detailed fits are available as Supplementary Data26 at http://dx.doi.org/xxxxx. The effect of changes in the assumed values of the centrifugal distortion constants were investigated for the isotopologue 12C2H2⋯63Cu19F. Changes of 10% in the assumed values of the distortion constants ΔJ and ΔJK lead to changes in A that are small compared with the errors shown in Table 1. The standard deviations in A0 values are higher than those identified in other B⋯MX studies because only one J + 1 → J transition is available within the bandwidth of the spectrometer in the present work.
| Spectroscopic constant | 13C2H2⋯63CuF | 13C2H2⋯65CuF | 12C2D2⋯63CuF | 12C2D2⋯65CuF |
|---|---|---|---|---|
| a Values calculated at the MP2/aug-cc-pVQZ level of theory and fixed in the fit. b Number of nuclear quadrupole components included in the fit. c Standard deviation of fit. | ||||
| A 0/MHz | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250(240) 250(240) |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950(290) 950(290) |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208(19) 208(19) |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156(32) 156(32) |
| B 0/MHz | 3302.7667(62) | 3301.4981(98) | 3260.5869(86) | 3259.257(14) |
| C 0/MHz | 2996.4700(43) | 2995.4204(47) | 2881.9524(88) | 2880.939(11) |
| Δ JK /kHza | [34.7] | [34.7] | [30.9] | [30.8] |
| Δ J /kHza | [0.56] | [0.56] | [0.53] | [0.53] |
| χ aa (Cu)/MHz | 70.012(59) | 64.756(71) | 70.051(55) | 64.743(56) |
| {χbb(Cu) − χcc(Cu)}/MHz | −79.23(17) | −73.28(24) | −80.4(38) | −69.8(39) |
| N | 20 | 15 | 17 | 13 |
| σ r.m.s./kHzc | 33.8 | 32.2 | 23.7 | 22.8 |
It is significant that values of the A0 for 12C2H2⋯63Cu19F and 12C2H2⋯65Cu19F (Table 1) are equal within experimental error (as required if Cu lies on the a axis). These values of A0 and their associated uncertainties strongly imply that the average of the two results provides the most reliable value for this quantity, namely 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840(90) MHz (where the quoted error is the range about the mean). This value will be used in geometry determinations set out in Section 3.2, together with the mean value A0 = 33
840(90) MHz (where the quoted error is the range about the mean). This value will be used in geometry determinations set out in Section 3.2, together with the mean value A0 = 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100(150) MHz for the pair (13C2H2⋯63Cu19F, 13C2H2⋯65Cu19F) and A0 = 25
100(150) MHz for the pair (13C2H2⋯63Cu19F, 13C2H2⋯65Cu19F) and A0 = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182(26) MHz for the pair (12C2D2⋯63Cu19F, 12C2D2⋯65Cu19F). We note that A0 = 34
182(26) MHz for the pair (12C2D2⋯63Cu19F, 12C2D2⋯65Cu19F). We note that A0 = 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840(90) MHz is smaller by 435(90) MHz than the B0 value of free 12C2H2 (see Table 3 for various properties of isotopologues of the free molecules ethyne27,28 and cuprous fluoride22). Similar conclusions (see Table 2) apply to the pair (13C2H2⋯63Cu19F, 13C2H2⋯65Cu19F), for which the mean decrease from free 13C2H2 is 464(150) MHz, and the pair (12C2D2⋯63Cu19F, 12C2D2⋯65Cu19F), for which a mean decrease of 236(26) MHz relative to B0 of free 12C2D2 is observed. These decreases, although not well determined, indicate a change in the ethyne geometry when it becomes attached to CuF. Moreover, the very small change in all three rotational constants on substitution of 63Cu by 65Cu establishes that the Cu atom lies close to the centre of mass and therefore that the order along the a axis is *–Cu–F, where * indicates the centre of the C
840(90) MHz is smaller by 435(90) MHz than the B0 value of free 12C2H2 (see Table 3 for various properties of isotopologues of the free molecules ethyne27,28 and cuprous fluoride22). Similar conclusions (see Table 2) apply to the pair (13C2H2⋯63Cu19F, 13C2H2⋯65Cu19F), for which the mean decrease from free 13C2H2 is 464(150) MHz, and the pair (12C2D2⋯63Cu19F, 12C2D2⋯65Cu19F), for which a mean decrease of 236(26) MHz relative to B0 of free 12C2D2 is observed. These decreases, although not well determined, indicate a change in the ethyne geometry when it becomes attached to CuF. Moreover, the very small change in all three rotational constants on substitution of 63Cu by 65Cu establishes that the Cu atom lies close to the centre of mass and therefore that the order along the a axis is *–Cu–F, where * indicates the centre of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond.
C bond.
| Quantity constant | 12C2H2 | 13C2H2 | 12C2D2 | 63Cu19F | 65Cu19F |
|---|---|---|---|---|---|
a
Ref. 27.
b Calculated by fitting the moments of inertia I0b of 12C2H2 and 13C2H2 from ref. 27. See text.
c Calculated by fitting the moment of inertia I0b of 12C2D2 with r(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) fixed at 1.206553 Å.
d
Ref. 28.
e
Ref. 22
.f Calculated from B0 value by using r0 = {h/8π2μB0}½, with B0 estimated from Dunham constants in ref. 22.g Calculated from Be value by using re = {h/8π2μBe}½ with Be from ref. 22.h Calculated at the CCSD(T)(F12*)/aug-cc-pwCVQZ level of theory, with post-CCSD(T) corrections made for basis set incompleteness, core-valence correlation, and higher-order correlations. C) fixed at 1.206553 Å.
d
Ref. 28.
e
Ref. 22
.f Calculated from B0 value by using r0 = {h/8π2μB0}½, with B0 estimated from Dunham constants in ref. 22.g Calculated from Be value by using re = {h/8π2μBe}½ with Be from ref. 22.h Calculated at the CCSD(T)(F12*)/aug-cc-pwCVQZ level of theory, with post-CCSD(T) corrections made for basis set incompleteness, core-valence correlation, and higher-order correlations. |
|||||
| Ethyne | — | — | |||
| B 0/MHz | 35274.9693(54)a | 33564.005a | 25418.6291a | ||
| Geometry | r 0(C2H2)b | r 0(C2D2)c | r e | ||
r(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)/Å C)/Å |
1.206553(6) | (1.206553) | 1.20286(3) | — | — |
| r(C–H)/Å | 1.06238(2) | 1.06011(3) | 1.06166(6) | — | — |
| Cuprous fluoride | — | — | |||
| B 0/MHze | — | — | — | 11325.8910 | 11245.2404 |
| B e/MHze | — | — | — | 11374.2092 | 11293.0426 |
| r 0(Cu–F)/Å | — | — | — | 1.74865f | 1.74863f |
| r e(Cu–F)/Å (experiment) | — | — | — | 1.74493g | 1.74493g |
| r e(Cu–F)/Å (ab initio calc.) | — | — | — | 1.7430(3)h | |
The Cu nuclear quadrupole coupling constants are reasonably well determined. The ratio of the values χaa(63Cu)/χaa(65Cu) = 1.0814(16) lies within experimental error of the known ratio29Q(63Cu)/Q(65Cu) = 1.0806(3) of the nuclear electric quadrupole moments of the copper nuclides. The large difference between χbb(Cu) = −74.58 MHz and χcc(Cu) = 4.59 MHz is evidence of a large anisotropy in the electric field gradient at Cu along the b and c principal inertia axis directions arising from the facts that (1) the Cu atom is close to the ethyne π bond and (2) the electron distribution within the triple bond C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C is different along the two directions. Indeed, the large difference {χbb(63Cu) − χcc(63Cu)} = −79.17(11) MHz provides convincing evidence of the proximity of Cu to the C
C is different along the two directions. Indeed, the large difference {χbb(63Cu) − χcc(63Cu)} = −79.17(11) MHz provides convincing evidence of the proximity of Cu to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond. In the related molecule C2H2⋯Ag–Cl, in which Cl is remote from the ethyne π bond, values of the Cl nuclear quadrupole coupling constants are χaa(35Cl) = −28.9268(78) MHz and {χbb(35Cl) − χcc(35Cl)} = −3.256(7) MHz.
C bond. In the related molecule C2H2⋯Ag–Cl, in which Cl is remote from the ethyne π bond, values of the Cl nuclear quadrupole coupling constants are χaa(35Cl) = −28.9268(78) MHz and {χbb(35Cl) − χcc(35Cl)} = −3.256(7) MHz.
3.2 Molecular geometry
Of the four consequences of a planar geometry of the type shown in Fig. 1, it was indicated in Section 3.1 that three were satisfied by experimental results for C2H2⋯Cu–F. The fourth is that the inertia defect, as defined in eqn (2), should be small and positive. If the Cu atom does lie on the a axis, it is reasonable to use the mean I0a value for a pair of isotopologues mC2nH2⋯63Cu19F and mC2nH2⋯65Cu19F in calculating Δ0 for both members of the pair. The results are Δ0 = 0.365(38) u Å2 and 0.366(38) u Å2 for the 12C2H2⋯63,65Cu19F pair, 0.373(69) u Å2 and 0.373(69) u Å2 for the 13C2H2⋯63,65Cu19F pair, and 0.295(22) u Å2 and 0.293(22) u Å2 for the 12C2D2⋯63,65Cu19F pair. The very similar values, observed across a similar range of isotopologues, for each of the related planar molecules C2H2⋯Cu–Cl6 and C2H2⋯Ag–Cl5 reinforce the conclusion that C2H2⋯Cu–F is also planar.Thus, all the evidence so far presented is consistent with a geometry of C2H2⋯CuF of the planar, T-shaped type of C2v symmetry illustrated in Fig. 1, with the atoms in the indicated order. Quantitative detail of the geometry can be determined experimentally in two ways from the zero-point rotational constants of the six isotopologues of C2H2⋯CuF investigated, namely a partial rs geometry and an almost complete r0 geometry. These results will be compared with the full re geometry obtained from ab initio calculations carried out at the CCSD(T)(F12*/AVTZ) level of theory.
If equilibrium rotational constants (and therefore equilibrium principal moments of inertia) of the various isotopologues of C2H2⋯CuF investigated were available, the equilibrium principal-axis co-ordinates aC, bC, aH, and aCu could be determined by means of eqn (3)–(5). In view of the molecular planarity and the existence of the symmetry operation Ca2, the changes Ib and Ia in the equilibrium principal moments of inertia that accompany the double isotopic substitution of X by X′ (X = 12C or H; X′ = 13C or D, respectively) at symmetrically equivalent atoms are related to the equilibrium coordinates aX and bX by the expressions put forward by Chutjian30
| |aX| = (ΔIb/μD)½, | (3) |
| |bX| = {ΔIa/(2Δm)}½, | (4) |
| |aCu| = {(ΔIb + ΔIc)/2μS}½, | (5) |
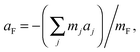 | (6) |
| Atom | r s geometry | r 0 geometry | r e geometrya | |||
|---|---|---|---|---|---|---|
| Coordinateb | Coordinate | Coordinate | ||||
| a/Å | b/Å | a/Å | b/Å | a/Å | b/Å | |
| a The re geometry was optimized at the CCSD(T)(F12*)/aug-cc-pVTZ level of theory. b The errors in rs coordinates aX are those given by δa = (0.0015 Å)/a, as suggested by Costain in ref. 32. The errors in rs coordinates bX are those propagated from the poorly determined rotational constants A0. c Assumed value obtained by adding the difference r0(C–H) − re(C–H) = 0.00072 Å of the quantities for free ethyne to re(C–H) calculated for C2H2⋯Cu–F and given in the final column. See text for discussion. | ||||||
| H | −1.9764(8) | ±1.663(9) | −1.9767(4) | ±1.6587(1) | −1.9762 | ±1.6501 |
| C | −1.7066(9) | ±0.62(4) | −1.7059(4) | ±0.6231(1) | −1.6947 | ±0.6182 |
| Cu | 0.142(10) | 0.0000 | 0.1415(3) | 0.0000 | 0.1412 | 0.0000 |
| F | 1.893(33) | 0.0000 | 1.8961(6) | 0.0000 | 1.8803 | 0.0000 |
| Distance/angle | rs geometry | r 0 geometry or angle | r e geometry |
|---|---|---|---|
r(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)/Å C)/Å |
1.24(4) | 1.2461(1) | 1.2363 |
| r(C–H)/Å | 1.077(4) | [1.07041]c | 1.0697 |
| r(Cu–*)/Å | 1.85(1) | 1.8474(7) | 1.8359 |
| r(Cu–F)/Å | 1.751(10) | 1.7547(9) | 1.7392 |
| Angle A/° | 194.5(6) | 194.65(2) | 195.3 |
The significantly larger magnitude of aH than aC provides experimental evidence that the angular geometry of ethyne is distorted in the manner shown in Fig. 1, that is the H atoms move away from the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C internuclear line when the complex is formed, with the two equivalent angles A = ∠H–C
C internuclear line when the complex is formed, with the two equivalent angles A = ∠H–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) * (see Fig. 1 for definition) exceeding 180°. The value obtained from the rs coordinates in Table 3 is A = 194.5(6)° (see Table 4), where the large error is consequent upon the errors in the A0 values. This distortion is established with greater accuracy in the experimental r0 and ab initio re geometries discussed later (see below). The bond distances implied by the rs coordinates are also included in Table 4.
* (see Fig. 1 for definition) exceeding 180°. The value obtained from the rs coordinates in Table 3 is A = 194.5(6)° (see Table 4), where the large error is consequent upon the errors in the A0 values. This distortion is established with greater accuracy in the experimental r0 and ab initio re geometries discussed later (see below). The bond distances implied by the rs coordinates are also included in Table 4.
When the minimum number of bond lengths and angles required to establish a molecular geometry uniquely is fitted to a sufficient number of zero-point principal moments of inertia by the least-squares method, the result is called a r0 geometry, i.e one obtained when the rovibrational contributions εa = I0a − Iea, etc. to the moments of inertia are ignored. A fit of I0b and I0c (values of I0a were excluded because of their relatively low accuracy) of all six isotopologues of C2H2⋯Cu–F implied by the rotational constants B0 and C0 reported in Tables 1 and 2 to determine r(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) *), r(*–Cu), r(Cu–F), r(C–H), and A = ∠H–C
*), r(*–Cu), r(Cu–F), r(C–H), and A = ∠H–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) * was unsatisfactory, however, because of high correlation between two last-named quantities. To break the correlation, the following approach was used. A good estimate of r0(C–H) is given by adding re(C–H) of C2H2⋯Cu–F from the CCSD(T)(F12*)/AVTZ calculation to the difference r0(C–H) − re(C–H) = 0.00072 Å for free ethyne27,28 (Table 3), with the result r0(C–H) = 1.07041 Å. This value was then fixed in the fit. The geometry and principal axis coordinates were then determined under this assumption with the aid of Kisiel's program STRFIT34 and are included in Table 4. There is excellent agreement with the corresponding rs quantities, given the large error in the bs coordinates propagated through the rotational constants A0.
* was unsatisfactory, however, because of high correlation between two last-named quantities. To break the correlation, the following approach was used. A good estimate of r0(C–H) is given by adding re(C–H) of C2H2⋯Cu–F from the CCSD(T)(F12*)/AVTZ calculation to the difference r0(C–H) − re(C–H) = 0.00072 Å for free ethyne27,28 (Table 3), with the result r0(C–H) = 1.07041 Å. This value was then fixed in the fit. The geometry and principal axis coordinates were then determined under this assumption with the aid of Kisiel's program STRFIT34 and are included in Table 4. There is excellent agreement with the corresponding rs quantities, given the large error in the bs coordinates propagated through the rotational constants A0.
4. Discussion
The new molecule C2H2⋯Cu–F has been synthesized by interaction of the plasma produced by laser ablation of a copper rod with a supersonically-expanded pulse of gas containing SF6 and C2H2 diluted with a large excess of argon. It was detected by means of its ground-state rotational spectrum and was shown to have a planar, T-shaped geometry of C2v symmetry, with the CuF molecule lying along a C2 axis of the C2H2 molecule. Quantitative aspects of the molecular geometry were determined through the investigation of six isotopologues. A significant finding is that the ethyne subunit is considerably distorted by the interaction of its C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond with the Cu atom of CuF. The H atoms move from the C
C bond with the Cu atom of CuF. The H atoms move from the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C internuclear line, in the direction away from the approaching Cu atom, so that the *
C internuclear line, in the direction away from the approaching Cu atom, so that the *![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H angle increases from 180° to 194.65(2)°. The C
C–H angle increases from 180° to 194.65(2)°. The C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond lengthens by ca. 0.04 Å. These distortions are well reproduced in the optimized geometry of C2H2⋯Cu–F obtained from ab initio calculations carried out at the CCSD(T)(F12*)/AVTZ level of theory (see Table 4).
C bond lengthens by ca. 0.04 Å. These distortions are well reproduced in the optimized geometry of C2H2⋯Cu–F obtained from ab initio calculations carried out at the CCSD(T)(F12*)/AVTZ level of theory (see Table 4).
Similar distortions have now been observed in the series of molecules C2H2⋯CuF, C2H2⋯AgCl,4 C2H2⋯AgCCH,5 and C2H2⋯CuCl,6 each of which has the planar T-shaped, C2v geometry with the metal atom adjacent to the ethyne π bond (see Fig. 1). The changes δA in the angle *![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H and δr in the distance r(C
C–H and δr in the distance r(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) are [14.65(2)°, 4.0(1) pm], [7.70(4)°, 2.86(4) pm], [5.9(1)°, 2.61(3) pm] and [12.5(2)°, 2.7(3) pm] respectively, along the series. The corresponding energy changes De accompanying dissociation into C2H2 and MX have been calculated ab initio [at the CCSD(T)(F12*)/AVTZ or AVDZ levels] to be 170, 97.5, 92 and 148 kJ mol−1, respectively. Fig. 3 displays a plot of each of δA and δr versus De for these molecules. The origin has been included as a point in each plot because when the interaction energy De is zero, presumably there is no distortion of the ethyne subunit. Fig. 3 shows that there is an approximate linear relationship between each of the two types of distortion δA and δr and the strength of the interaction De.
C) are [14.65(2)°, 4.0(1) pm], [7.70(4)°, 2.86(4) pm], [5.9(1)°, 2.61(3) pm] and [12.5(2)°, 2.7(3) pm] respectively, along the series. The corresponding energy changes De accompanying dissociation into C2H2 and MX have been calculated ab initio [at the CCSD(T)(F12*)/AVTZ or AVDZ levels] to be 170, 97.5, 92 and 148 kJ mol−1, respectively. Fig. 3 displays a plot of each of δA and δr versus De for these molecules. The origin has been included as a point in each plot because when the interaction energy De is zero, presumably there is no distortion of the ethyne subunit. Fig. 3 shows that there is an approximate linear relationship between each of the two types of distortion δA and δr and the strength of the interaction De.
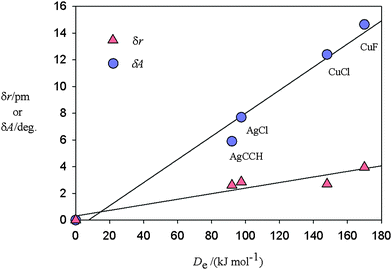 | ||
Fig. 3 Plots of the angular distortion δA (see Fig. 1 for a definition of the angle δA) and the extension δr of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond of ethyne on formation of the complexes C2H2⋯MX against the energy De required for the dissociation reaction C2H2⋯MX = C2H2 + MX. δA and δr are experimentally determined while the De values are calculated ab initio at the CCSD(T)(F12*)/AVTZ or AVDZ level of theory. The origin is included as a point under the assumption that zero interaction energy is associated with δA = 0 and δr = 0. C bond of ethyne on formation of the complexes C2H2⋯MX against the energy De required for the dissociation reaction C2H2⋯MX = C2H2 + MX. δA and δr are experimentally determined while the De values are calculated ab initio at the CCSD(T)(F12*)/AVTZ or AVDZ level of theory. The origin is included as a point under the assumption that zero interaction energy is associated with δA = 0 and δr = 0. | ||
The nature of the ethyne distortions can be understood with the aid of a simple model. The nuclei of each of the C2H2⋯M–X (M = Cu or Ag, X = F or Cl) molecules all lie in the ab principal inertia plane. Let the symmetry plane of one of the ethyne π bonding orbitals lie in this plane, with that of the other π orbital perpendicular to it. When M–X approaches from large separation and takes up its position along a C2 axis of ethyne (which then becomes the a axis of the new molecule), the partial positive charge δ+ that exists on the M atom in the species M–X (the metal halides have large electric dipole moments in the range ∼5 or 6 D)35 polarizes electron density preferentially from the π orbital (πab) in the molecular plane. The larger the polarization, the more the π bonding in the ethyne molecule will resemble that of an ethene molecule in which the symmetry plane of its π bonding orbital is perpendicular to the ab plane and the C–H bonds lie in the ab plane. In the limit of very large polarization of the πab electrons, when both are completely removed from ethyne to yield the ion C2H22+, the distortions would be of the order δA ≈ 60° and δr ≈ 134.5 − 120.6 = 13.9 pm, where 134.5 and 120.6 pm are the CC distances in the ground state 3Σg− of the dication36 C2H22+ and in ethyne,27 respectively. Similar distortions have been observed in C2H4⋯M–X (M = Cu or Ag),6,37 in which M–X lies on the C2 axis of C2H4 that is perpendicular to the plane of the C2H4 nuclei. Similar arguments can be used to rationalize the distortions in these molecules, but with C2H42+ as the limiting dication.
Acknowledgements
We thank the European Research Council for postdoctoral fellowships awarded to D.P.Z. and S.L.S., and for project funding (CPFTMW-307000). ACL thanks the University of Bristol for a Senior Research Fellowship and Newcastle University for a Faculty of SAgE Visiting Professorship. D.P.Z. thanks Newcastle University for the award of a Faculty of SAgE Research Fellowship. D.P.T. gratefully acknowledges the award by the Royal Society of a University Research Fellowship.References
- K. Schroeter, C. A. Schalley, R. Wesendrup, D. Schroder and H. Schwarz, Organometallics, 1997, 16, 986 CrossRef CAS.
- K. Judai, A. S. Worz, S. Abbet, J. M. Antonietti, U. Heiz, A. Del Vitto, L. Giordano and G. Pacchioni, Phys. Chem. Chem. Phys., 2005, 7, 955 RSC.
- A. Molnar, A. Sarkany and M. Varga, J. Mol. Catal. A: Chem., 2001, 173, 185 CrossRef CAS.
- S. L. Stephens, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2012, 137, 174302 CrossRef PubMed.
- S. L. Stephens, D. P. Zaleski, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2014, 140, 124310 CrossRef PubMed.
- S. L. Stephens, D. M. Bittner, V. A. Mikhailov, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, Inorg. Chem., 2014, 53, 10722–10730 CrossRef CAS PubMed.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- S. L. Stephens and N. R. Walker, J. Mol. Spectrosc., 2010, 263, 27–33 CrossRef CAS PubMed.
- D. P. Zaleski, S. L. Stephens and N. R. Walker, Phys. Chem. Chem. Phys., 2014, 16, 25221–25228 RSC.
- T. J. Balle and W. H. Flygare, Rev. Sci. Instrum., 1981, 52, 33–45 CrossRef CAS PubMed.
- R. C. Batten, G. C. Cole and A. C. Legon, J. Chem. Phys., 2013, 119, 7903–7912 CrossRef PubMed.
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2011, 112, 4–74 CrossRef PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS PubMed.
- K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 CrossRef CAS.
- M. Dolg, U. Wedig, H. Stoll and H. J. Preuss, Chem. Phys., 1987, 86, 866–872 CAS.
- H.-J. Werner, P.J. Knowles, R. Lindh, F.R. Manby and M. Schütz, MOLPRO, version 2009.1, a package of ab initio programs; 2009, see http://www.molpro.net.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS PubMed.
- M. Heckert, M. Kállay and J. Gauss, Mol. Phys., 2005, 103, 2109 CrossRef CAS PubMed.
- M. Kállay, MRCC, a generalized CC/CI program, see http://www.mrcc.hu.
- T. Okabayashi, E. Yamazaki, T. Honda and M. Tanimoto, J. Mol. Spectrosc., 2001, 209, 66–70 CrossRef CAS.
- PGOPHER, a program for simulating rotational structure, designed by C.M. Western, University of Bristol, version 6.0.202, 2010, available at http://pgopher.chm.bris.ac.uk.
- J. K. G. Watson, J. Chem. Phys., 1968, 46, 1935 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- See ESI† for assignments of all observed transitions and the fits used to determine the spectroscopic constants of six isotopologues of C2H2⋯Cu–F.
- M. Herman, A. Campargue, M. I. El Idrissi and J. Van der Auwera, J. Phys. Chem. Ref. Data, 2003, 32, 921 CrossRef CAS PubMed.
- J. Lievin, J. Demaison, M. Herman, A. Fayt and C. Puzzarini, J. Chem. Phys., 2011, 134, 064119 CrossRef CAS PubMed.
- W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley, New York, 1984, Appendix E Search PubMed.
- A. Chutjian, J. Mol. Spectrosc., 1964, 14, 361 CrossRef CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17 CrossRef CAS.
- C. C. Costain, J. Chem. Phys., 1958, 29, 864 CrossRef CAS PubMed.
- C. C. Costain, Trans. Am. Crystallogr. Assoc., 1966, 2, 157 CAS.
- Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67 CrossRef CAS.
- NIST Diatomic Spectra Database, http://www.nist.gov/pml/data/msd-di/index.cfm, compiled by F.J. Lovas, E. Tiemann, J.S. Coursey, S.A. Kotochigova, J. Chang, K. Olsen and R.A. Dragoset.
- R. Thissen, J. Delwiche, J. H. Robbe, D. Duflot, J. P. Flament and J. H. D. Eland, J. Chem. Phys., 1993, 99, 6590 CrossRef CAS PubMed.
- S. L. Stephens, D. P. Tew, V. A. Mikhailov, N. R. Walker and A. C. Legon, J. Chem. Phys., 2011, 135, 024315 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp02248g |
| This journal is © the Owner Societies 2015 |