IR spectroscopy of protonated leu-enkephalin and its 18-crown-6 complex embedded in helium droplets

Abstract

Ultracold IR spectra of the protonated five amino acid peptide leu-enkephalin (Tyr-Gly-Gly-Phe-Leu) embedded in superfluid helium droplets have been recorded using a free-electron laser as radiation source. The results show resolved spectra, which are in good agreement with theoretical calculations, as well as with the available gas-phase data indicating that the helium environment does not induce a significant matrix-shift. In addition, the effect of the interaction between the charge and the peptide backbone has been further investigated by complexing protonated leu-enkephalin with one 18-crown-6 molecule. Good agreement between the experimental and theoretical results allow for an assignment of a preferred molecular structure.

---

1 Introduction

Investigating the structure and dynamics of biological molecules in the absence or controlled presence of solvent molecules can yield important information on their intrinsic structural preferences and can serve as calibration points for theoretical methods. Further, for species that are at home in hydrophobic environments with a low relative permittivity, the solvent-free vacuum can even be closer to its natural environment, compared to a polar (aqueous) solution.

To investigate peptides or other biological molecules free of solvation, they can, for example, be studied as neutral molecules in molecular beams using various laser spectroscopic methods.^1–4 While those experiments prove to be highly successful and can yield detailed information, they get quite difficult for larger species.

In a more general approach, charged species can be investigated by combining mass spectrometry with optical spectroscopy. In particular, infrared (IR) spectroscopy on mass-to-charge selected species has become a powerful tool to elucidate the structure of small, as well as large peptide and protein ions.⁵ In a commonly used implementation, the gas-phase ion of interest is irradiated by an intense IR pulse. When the light is resonant with an allowed infrared transition, the absorption of multiple photons can take place, leading to fragmentation. Monitoring the fragmentation as a function of IR wavelength gives an IR spectrum. A drawback of this so called IR multiple photon dissociation (IRMPD) scheme is that peaks in the spectrum get broadened and shifted, and that their relative intensities depend on the mode anharmonicities and on the presence of neighbouring absorptions.⁶ To circumvent those limitations, techniques to investigate biomolecular ions in cooled ion traps have been developed that require only the absorption of one or a few photons. When performing IR/UV double resonance experiments in a cold trap, changes in UV fragmentation yield upon absorption of IR photons are recorded.^7–10 However, the required presence of a UV chromophore limits the applicability of these methods. In another approach, weakly bound adducts of small messenger molecules (e.g. rare gases) are formed, which dissociate from the ion after IR absorption.^11,12 Here again, measuring the dissociation yield as a function of wavelength gives then an IR spectrum.

An alternative method to cool ions is to embed the species of interest in liquid helium nanodroplets.¹³ Those droplets are ultracold, and provide with an equilibrium temperature of ≈0.4 K, an efficient heat bath that is superfluid, only weakly interacting with the dopant and optically transparent from the deep-UV to the far-IR. Because of those properties, liquid helium droplets are considered an ideal matrix for spectroscopic experiments and have been used to investigate a variety of small molecules and molecular ions.¹⁴ In most experiments, dopant molecules are thermally evaporated and picked up by the droplets. However, with the exception of very small species, biological molecules cannot be thermally evaporated and those established methods can not be employed. We devised a scheme in which ions that are brought into the gas phase by electrospray ionization and mass-to-charge selected by a quadrupole mass spectrometer are picked up from an ion trap by helium droplets.¹⁵ It has been shown that this method can be used to pick up species as large as an entire protein.¹⁵ This method can be used to perform spectroscopy and the UV spectrum of mass-to-charge selected [Hemin + H]⁺ has been reported.¹⁶

Here, we apply helium droplet isolation IR spectroscopy to the mass-to-charge selected protonated pentapeptide leu-enkephalin (Tyr-Gly-Gly-Phe-Leu, Leu-Enk) as well as to its complex with one 18-crown-6 ether molecule. Leu-Enk is an endogenous opioid neurotransmitter peptide that can be found in many living organisms. As it is small enough to allow its detailed investigation, yet large enough to be a realistic model peptide, Leu-Enk has been studied using many gas-phase techniques, including mass spectrometry^17,18 and optical spectroscopy.^9,10,19 Using IR/UV double resonance spectroscopy in a cold ion trap, a high resolution IR spectrum has been recorded, allowing for structure assignment¹⁰ and it is found that the structure is dominated by the intramolecular solvation of the charged N-terminus by carbonyl groups. Here, we focus on protonated Leu-Enk as a test case for IR spectroscopy in helium droplets and crown-ether complexed Leu-Enk to investigate the role of internal charge solvation in the molecule.

2 Methods

2.1 Experimental setup

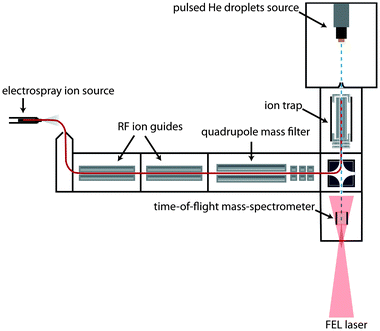
The experimental setup has been described previously¹⁶ and only a brief outline will be given here. A scheme is shown in Fig. 1: ions are generated via electrospray ionization (ESI). After passing through two ion guides, the ions are mass-to-charge selected using a quadrupole mass spectrometer and accumulated inside a 30 cm long linear hexapole ion trap. The radial confinement of the ions is provided by the radio-frequency voltage (1.1 MHz, 200 V_pp) applied to the hexapole rods. Longitudinal trapping is achieved by two endcap electrodes that are kept a few (1–3) volts above the DC potential of the trap. During ion accumulation in the trap, excess kinetic energy of the ions is removed by pulses of helium buffer gas. After a few seconds, the trap loading cycle is stopped and the residual helium buffer gas is pumped away.

Fig. 1 Schematic diagram of the experimental setup. Ions are brought in the gas phase via electrospray ionization. The m/z selected ions are trapped inside a hexapole ion trap, from which they are picked up by a pulsed beam of helium droplets via impact. The doped droplets are interrogated in the detection chamber by the IR light of the FEL.

Helium droplets are produced using a cryogenic Even–Lavie pulsed valve, cooled by a closed cycle cryostat (Sumimoto RDK 408D2). The valve is operated with a repetition rate of 10 Hz and a stagnation pressure of 70 bar. Due to velocity spread, the broadening of each pulse of helium droplets within the laser-interaction region of our instrument is measured to be ≈80 μs. The average size of the generated droplets can be varied by adjusting the nozzle temperature, which is set to 25 K in the current experiment. Under these conditions, helium droplets have a typical size of about 20 000 He atoms. After passing through a skimmer with a diameter of 4 mm placed 13.5 cm away from the nozzle, the beam of helium droplets traverses the ion trap where ion-pickup can take place. Due to their large kinetic energy given by their mass and the beam velocity (≈500 m s⁻¹), the ion-doped helium droplets can overcome the small longitudinal DC trapping potential. Further downstream, the doped droplets can either be detected directly using a Daly type detector or probed using the Fritz Haber Institute IR-free-electron laser (FHI FEL).²⁰ In the latter case, the IR laser overlaps the doped droplet beam counter propagating in the extraction region of a small linear time-of-flight (TOF) mass spectrometer built in-house. The laser beam is mildly focused and converging and has an estimated diameter of 5 to 8 mm during overlap with the droplet beam.

2.2 Laser system

Presently, the FEL is tunable between 3.5 μm and 50 μm. As it is the case for other FELs with a normal conducting accelerator structure, the light comes in macropulses of up to 10 μs in length, each of which contains micropulses of 0.3–5 ps length, spaced by 1 ns.²⁰ The bandwidth is adjustable and transform limited and in present experiments its full width at half maximum is kept near 0.5% of the corresponding wavelength. The total macropulse energy can reach well above 100 mJ. Calibration is performed by measuring the FEL spectrum with a Czerny–Turner grating spectrometer equipped with a pyro array detector for several wavelength points within an experimental spectrum. The spectrometer itself is calibrated against a stabilized HeNe laser. The wavelength calibration and macropulse energy is periodically measured, typically before and after each wavelength scan.

2.3 Materials

Leu-enkephalin (Leu-Enk) was purchased from Sigma Aldrich and used without further purification. It was dissolved at 50 μM in a 1 : 1 H₂O : MeOH solution with 1% formic acid. Deuteration was performed by dissolving Leu-Enk in the respective deuterated solvents. In some experiments, 18-crown-6 ether was added at a concentration of 1 mM.

2.4 Computational methods

2.4.1 Structure of [Leu-Enk + H]⁺. For the calculations, the structure of [Leu-Enk + H]⁺ proposed by Burke et al.¹⁰ was re-optimized at the B3LYP level of theory, using the def2-SVP basis set and adding dispersion corrections using the Grimme D3 method,²¹ as implemented in Gaussian 09.²² The vibrational modes are scaled by a standard scaling factor of 0.965.

2.4.2 Structure of [Leu-Enk + CE + H]⁺. The lowest free energy conformations of [Leu-Enk + CE + H]⁺ were found using a constrained force-field molecular dynamics (MD) approach, followed by a more accurate DFT optimization. In order to obtain a good overview of the conformational space of the molecule, we performed series of MD simulations each of which constrained a single H-bond. [Leu-Enk + CE + H]⁺ is assumed to have five groups that can act as hydrogen bond acceptors and six as hydrogen bond donors. A more detailed discussion on the possible groups will follow later in this work. These hydrogen bond donor and acceptor groups result in a total of 24 single hydrogen bond donor–acceptor permutations. The corresponding hydrogen bond is constrained to be of a fixed length of 2.0 Å in each case. MD calculations are performed using the OPLS2005 force field²³ with no solvation, as implemented in Macromodel.²⁴ From the resulting 24 constrained MD runs, each at 300 K and 10 ns in length, 100 structures are sampled and minimized at the force field level. From each of the sets of 100 structures, the structure with the lowest energy is then minimized at the B3LYP level with the def2-SVP basis set and Grimme D3 dispersion correction, followed by a calculation of their vibrational spectra. The vibrational modes are scaled by a scaling factor of 0.965.

Table S1 (ESI†) lists the (zero point energy corrected) relative B3LYP-D3 energies of those 24 structures, many of which are low in energy. Since they are obtained by straight energy minimization of the MD structures at the B3LYP-D3 level with no further annealing of the orientations of the side-chains or the puckering of the 18-crown-6 molecule, the structures might not be the global minimum structure within their respective hydrogen bond constraint group. The relative energies should therefore just be regarded as a guide.

3 Results and discussion

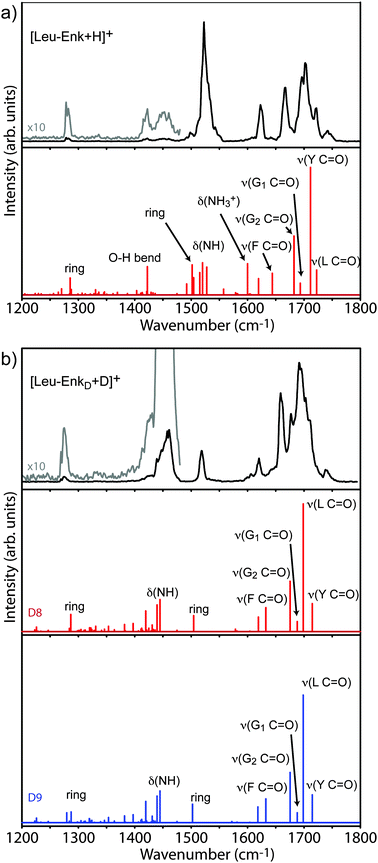
3.1 IR spectroscopy of [Leu-Enk + H]⁺ and [Leu-Enk_D + D]⁺

3.1.1 Ion ejection and laser power dependence. It has been previously observed that when ions embedded in helium droplets absorb light, they can be ejected from the droplets.^14,16,25 While this process is not yet understood, we make use of it by taking the signal of the ejected ion as a marker for photon absorption. IR spectra are then obtained by recording the signal of the ejected ion as a function of IR wavelength.

A typical time-of-flight (TOF) mass spectrum of the ejected ions after resonant IR excitation of droplets doped with protonated leu-enkephalin [Leu-Enk + H]⁺ is depicted in Fig. 2a. The signal at m/z ≈ 556 corresponds to [Leu-Enk + H]⁺, while the peak of small intensity observed at the higher m/z possibly results from a water adduct [Leu-Enk + H₂O + H]⁺. It is observed that fragmentation of [Leu-Enk + H]⁺ can be induced by very high photon densities. On the other hand, when the photon density is reduced, the signal corresponding to [Leu-Enk + H]⁺ and its water adduct diminishes and eventually disappears. However, the remainder of the helium solvation is under no circumstances observed. This is in accordance with the ejection of the ions from the droplet and is difficult to rationalize with a picture in which dopant ions are observed due to the complete evaporation of the helium atoms from the droplet. Furthermore, the total absence of helium adducts in the TOF spectra independent of the photon density suggests a very low interaction between the embedded molecule and the surrounding helium environment.

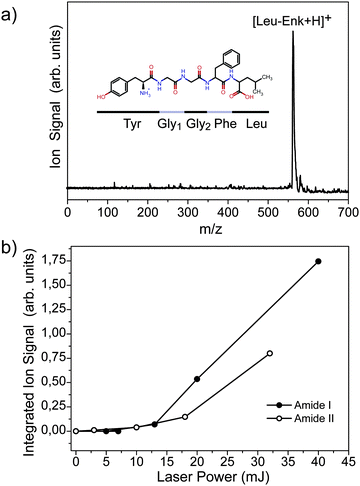Fig. 2 (a) TOF mass spectrum of the ejected ions from the helium droplets upon IR photo excitation. (b) Signal of the ejected ion as a function of laser power.

Fig. 2b shows the signal of the ejected ion as a function of the photon density when excitation occurs at 1530 cm⁻¹ (Amide II) and 1700 cm⁻¹ (Amide I). The laser power dependence is clearly non-linear, implying that the absorption of more than one photon is required in order to eject the ion. A non-linear character of the ejection efficiency of the embedded ion has been previously reported¹⁶ when exciting with UV light. In this experiment, it was shown that the absorption of at least two 378 nm photons is required to efficiently eject [Hemin + H]⁺ from the doped droplet. Fig. 2b further shows that the ejection efficiency depends on the excitation wavelength.

The efficiency of the ion ejection as a function of both, laser power and wavelength, is an important parameter to take into account when recording wavelength spectra of dopant molecules. The output power of the FEL depends strongly on the undulator settings, the precise tuning of the electron beam, the laser cavity, and other parameters. Thus, while scanning over a wide wavelength range, variations in output power will occur which will influence the intensity of the signal. Since the exact laser power dependence of the ejection efficiency is not known, all wavelength spectra shown in the remainder are simply divided by the respective laser power curves that are measured before and after each scan as a first order correction.

3.1.2 Spectroscopy of [Leu-Enk + H]⁺. An average of three individual scans (see Fig. S1, ESI†) provides the IR spectrum of [Leu-Enk + H]⁺, which is shown in Fig. 3a. Five bands occur in the region between 1600 cm⁻¹ and 1800 cm⁻¹ where amide I (C=O stretch) vibrations are expected. One strong and several weaker bands are found in the amide II (N–H bending) region and one weak band appears near 1280 cm⁻¹, in the amide III region, where sidechain vibrations are expected to occur. The IR spectrum of [Leu-Enk + H]⁺ has been investigated before using IRMPD at room temperature¹⁹ as well as by action spectroscopy in a cold ion trap¹⁰ (see Fig. S2, ESI,† for comparison). The spectrum shown here is in good agreement with the latter one, and the two spectra will be compared in more detail later. The lower panel of Fig. 3a shows the predicted vibrational transitions of the lowest energy structure of [Leu-Enk + H]⁺ reported by Burke et al.¹⁰ Although a different computational method has been used to calculate the vibrational spectrum in this work, the obtained results are in very good agreement. A list of the transition frequencies can be found in Table 1. The calculated IR transitions reproduce the majority of the experimentally observed bands in terms of band positions (although their relative intensities differ), and allow for an assignment of the experimental spectrum. Each of the five bands occurring in the amide I region can be assigned to one of the five C=O oscillators contained in [Leu-Enk + H]⁺. The band observed at 1722 cm⁻¹ stems from the C=O stretch of the Leu residue, which is presumably involved in the weakest hydrogen bond. Continuing towards the red, the C=O stretches of the Tyr, the two Gly, and the Phe residues are detected at 1702 cm⁻¹, 1695 cm⁻¹, 1666 cm⁻¹, and 1623 cm⁻¹, respectively. The band of high intensity at 1523 cm⁻¹ can be assigned to the N–H oscillators typical of this region and the weak absorption measured at 1421 cm⁻¹ most likely corresponds to a O–H bend of the Leu residue. The band of low intensity at 1280 cm⁻¹ can be assigned to a mixture of a Tyr ring deformation, C–H, and O–H bending modes. While the calculations fail to predict the absorption band at 1744 cm⁻¹ there are three absorptions (1502 cm⁻¹, 1600 cm⁻¹, and 1619 cm⁻¹) which are predicted by the simulation but not completely reproduced in the experiment. As a result, two bands would be expected between 1490 cm⁻¹ and 1530 cm⁻¹ and three bands between 1600 cm⁻¹ and 1650 cm⁻¹. It is important to note that in the latter region only one band instead of three is present as well in the spectrum obtained using a cold ion trap¹⁰ (see Fig. S2, ESI†), suggesting that this effect may be due to a limitation in the calculation instead of an effect of the helium environment. Indeed, a comparison between the calculated spectra presented in this work and the one performed by Burke et al. show differences in terms of position and intensity of the transitions expected in this spectral region. Therefore, we conclude that the band experimentally observed at 1623 cm⁻¹ most likely corresponds to a mixture of a C=O stretch of the Phe residue together with an antisymmetric NH₃⁺ motion and a deformation of the ring of the Tyr residue.

Fig. 3 (a) IR spectrum of [Leu-Enk + H]⁺ and calculated vibrational transitions. (b) IR spectrum of [Leu-Enk_D + D]⁺, together with the predicted vibrational modes of the fully H/D exchanged molecule (blue, D9), and the molecule in case the Tyr–OH does not H/D exchange (red, D8).

Table 1 Comparison of the vibrational transition frequencies of [Leu-Enk + H⁺] and assignment of the calculated IR bands

He droplets (cm^−1)	Cold trap^10 (cm^−1)	Calc. (cm^−1)	Assignment
1280		1285	Tyr ring deform.
1421		1422	Tyr ring deform.
1451		1467
1498		1502	Tyr ring deform.
	1507		Sym. NH3^+
1523	1529	1520	N–H bend
		1600	Antisym. NH3^+
		1619	Tyr ring deform.
1623	1631	1643	Phe C=O stretch
1666	1675	1682	Gly2 C=O stretch
1695	1689	1693	Gly1 C=O stretch
1702	1710	1711	Tyr C=O stretch
1722	1730	1722	Leu C=O stretch
1744

---

3.1.3 Spectroscopy of [Leu-EnkD + D]⁺. To further investigate the vibrational modes of the molecule, we measured the IR spectrum of the deuterated peptide [Leu-Enk_D + D]⁺. Protonated leu-enkephalin contains a total of nine exchangeable hydrogen atoms from which, on average, eight have been exchanged in our experiment when preparing the sample in deuterated solvents. This is in good agreement with previous experiments²⁶ and presumably results from an inefficient H/D exchange with the H of the OH group of the Tyr residue. Two different calculated spectra are shown in Fig. 3b, corresponding to the spectrum of a fully H/D exchanged molecule (D9, lower panel), and to a molecule in which the H of the Tyr–OH does not exchange (D8, middle panel). Both spectra are highly similar, suggesting that vibrations involving the Tyr–OH do not play a crucial role in this spectroscopic region.

The experimental results displayed in the upper panel of Fig. 3b are in good accord with the calculated transitions. In contrast to the spectrum of the undeuterated molecule, two bands are now observed in the amide II region at 1460 cm⁻¹ and 1518 cm⁻¹, respectively. A complete summary of transition frequencies is reported in Tables S2 and S3 (ESI†). Considering the dominant C=O stretch character of the amide I band, one would expect essentially no changes in the amide I region of the experimental spectrum upon deuteration. However, in addition to a minor redshift of less than 10 cm⁻¹, a more convoluted band at 1694 cm⁻¹ is observed. In order to understand this observation one has to take into account that the C=O stretches typical of this spectral region are not pure amide I transitions, but C=O's which are coupled with other vibrations, such as C–H and N–H bending modes. The effect of deuteration on the IR spectrum is also small for the band observed in the amide III region, which is only slightly shifted towards lower wavenumbers.

The most dramatic changes upon deuteration can be found in the amide II region, where the single band observed at 1523 cm⁻¹ in the spectrum of [Leu-Enk + H]⁺ is now split into two well separated transitions; one of them undergoes a significant redshift (−63 cm⁻¹) while the other remains at a very similar wavenumber position (−5 cm⁻¹). The calculations for the undeuterated molecule show that, in addition to the N–H bending modes, aromatic ring deformation modes are active in this region. The N–D modes will therefore shift and give rise to the band at 1460 cm⁻¹ while ring deformation modes will remain. Those exhibit the largest blue-shifts with respect to the calculations (≈+20 cm⁻¹), which is in line with the results obtained for the undeuterated molecule [Leu-Enk + H]⁺.

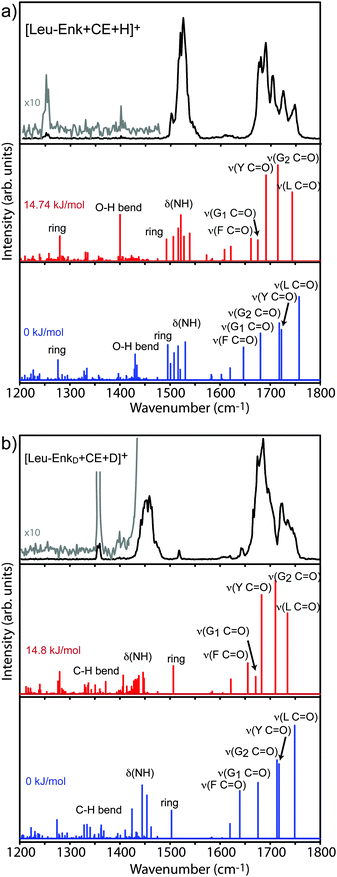
3.2 IR spectroscopy of [Leu-Enk + CE + H]⁺ and [Leu-Enk_D + CE + D]⁺

The low energy structures of [Leu-Enk + H]⁺ are dominated by interactions of the –NH₃⁺ group with surrounding carbonyls.^10,19 This interaction can be significantly reduced by complexing the molecule with a 18-crown-6 molecule (CE), which has a high affinity towards protonated amines²⁷ and is expected to coordinate with the –NH₃⁺ group. Due to steric constraints, the CE solvated –NH₃⁺ group will not be able to interact strongly with other groups.

3.2.1 Conformational search. The lowest free energy conformations of a molecule like [Leu-Enk + CE + H]⁺ can, in principle, be found by performing molecular dynamics (MD) simulations (or accelerated MD simulations such as replica exchange MD) of sufficient duration. A prerequisite for the success of the simulation, however, is that the underlying description of the intra- and intermolecular interactions is sufficiently accurate. While this could be the case when using ab initio MD schemes, their application is computationally very demanding and beyond the scope of this manuscript. On the other hand, resorting to standard force-field MD will likely allow the shortcomings of the employed force fields to yield structures that are not the overall lowest energy conformers. We therefore use a constrained force-field MD approach, which is followed by more accurate DFT optimization to identify low energy structures. For [Leu-Enk + CE + H]⁺, the strongest non-covalent intra- and intermolecular interactions are given by hydrogen bonds. In MD simulations, the length of those bonds can be constrained to that of a typical hydrogen bond. Thus, series of such simulations with constraints applied to different pairs of H-bonding partners should give a good overview of the conformational space of the molecule. However, [Leu-Enk + CE + H]⁺ contains a large number of possible hydrogen bond donor and acceptor groups. This leads to a very large number of possible internal hydrogen bonding patterns. We therefore performed a series of MD simulations, each of which constrained only a single H-bond.

The –NH₃⁺ group in [Leu-Enk + CE + H]⁺ is assumed to only interact with the CE molecule and is therefore not available as a hydrogen bond donor. Likewise, the CE molecule is assumed to exclusively interact with the –NH₃⁺ group. Thus the [Leu-Enk + CE + H]⁺ molecule has six groups that can act as hydrogen bond donors (Fig. 4a): the Tyr–OH group (labeled OHT), four amide N–H groups (labeled NH1–NH4, from the N- to the C-terminus) and the OH from the C-terminal carboxyl group (labeled OHA). Five C=O groups, ranging from the carbonyl group near the N-terminus to the C=O of the C-terminal carboxyl group, can act as hydrogen bond acceptors (labeled O1–O5, see Fig. 4a). While the –OH oxygen can also interact as a hydrogen bond acceptor, those interactions are assumed to be weaker and are not considered. When being in trans conformation, no hydrogen bond between a C=O and N–H group within a peptide bond can be formed. Furthermore, due to steric constraints, an interaction of the OHT with the first carbonyl (O1) is unlikely.

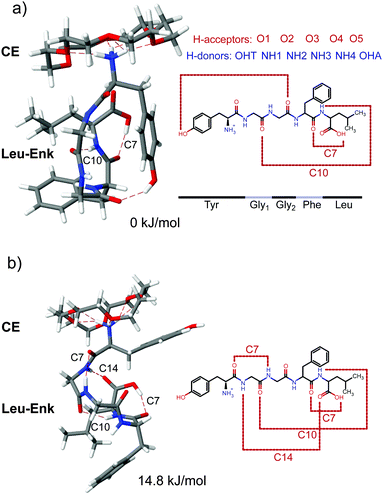Fig. 4 Two most favoured calculated structures of [Leu-Enk + CE + H]⁺ with relative (zero point corrected) energies of 0 kJ mol⁻¹ (a) and 14.8 kJ mol⁻¹ (b).

Considering the hydrogen bond acceptors and donors described above yields 24 hydrogen bond donor–acceptor permutations for which the corresponding hydrogen bond is constrained to be of a fixed length of 2 Å during the simulation. We compared all 24 simulated IR spectra with our experimental results. The spectrum that gives the best match to the experiment resulted from the simulation in which the hydrogen bond length between the first carbonyl group (O1) and the second NH group (NH2) was constrained. Its structure is shown in Fig. 4b, and its corresponding vibrational spectrum in Fig. 5a. This conformer is +14.8 kJ mol⁻¹ higher in energy than the lowest energy structure, due to a constraint between the second carbonyl group (O2) and the Tyr–OH group (OHT), which is shown in Fig. 4a, with its corresponding spectrum in Fig. 5a.

Fig. 5 IR spectrum of [Leu-Enk + CE + H]⁺ (a) and [Leu-Enk_D + CE + D]⁺ (b) and calculated vibrational spectra of the structure with a relative energy of 14.8 kJ mol⁻¹ (red) and 0 kJ mol⁻¹ (blue).

3.2.2 Hydrogen bonding arrangements. The –NH₃⁺ group is solvated by the crown ether molecule in both structures. The structure shown in Fig. 4a (0 kJ mol⁻¹) shows a backbone conformation that is supported by three H-bonds whose donors are the OH groups of the N-terminal Tyr, the C-terminal acidic group, and the Phe-Leu amide bond NH. The hydrogen bond between the OH group of the Leu residue and the amide carbonyl of the Phe residue results in a C7 ring. A C10 H-bonded ring connects the carbonyl of the first Gly residue with the C-terminal amide. The OH group of the Tyr residue forms a hydrogen bond with the carbonyl of the second Gly residue.

The backbone of the structure shown in Fig. 4b (+14.8 kJ mol⁻¹) exhibits four internal H-bonds. Common features of this structure and the one in Fig. 4a, are one of the C7 and the C10 rings. However, the OH group of the Tyr residue is no longer hydrogen bonded to the carbonyl of the second Gly residue. Instead, there is an additional C7 ring that connects the amide NH on the first Gly residue with the Tyr carbonyl, as well as a C14 ring between the amide NH of the Tyr residue and the carbonyl of the Leu residue.

3.2.3 Spectroscopy of [Leu-Enk + CE + H]⁺. The experimental IR spectrum of [Leu-Enk + H]⁺ complexed with 18-crown-6 ([Leu-Enk + CE + H]⁺) is shown in Fig. 5a. Five resolved bands are observed in the amide I region, one high intensity band with a weaker peak on the lower frequency side is present in the amide II region, and only one transition of low intensity is observed in the amide III region. Upon comparing this spectrum with that of the uncomplexed molecule it can be observed that the spectral signature in the amide I region is significantly altered and a general blueshift of the five transitions is observed where the C=O stretches of the five amino acid residues are expected. The spectrum in the amide II region remains essentially unchanged while the low intensity band previously observed in the amide III region is slightly redshifted.

The calculated vibrational transitions for both structures are displayed in Fig. 5a, and a list of the transition frequencies with their corresponding intensities can be found in Table 2 and Table S4 (ESI†). In the wavelength range between 1200 cm⁻¹ and 1400 cm⁻¹, both calculations predict several weak transitions, as well as a stronger transition at 1280 cm⁻¹ and 1276 cm⁻¹ for the +14.8 kJ mol⁻¹ and 0 kJ mol⁻¹ structures, respectively. These transitions originate from a mixture of the Tyr ring deformation, C–H, and O–H bending modes. The stronger mode might correspond to the band experimentally observed at 1253 cm⁻¹, although the shift of ≈−30 cm⁻¹ seems rather large. The calculated vibrational transitions of both structures predict a bending mode of the OH group of the Leu residue at 1400 cm⁻¹ and 1430 cm⁻¹ for the +14.8 kJ mol⁻¹ and 0 kJ mol⁻¹ structure, respectively. The difference of ≈30 cm⁻¹ is the result of the OH hydrogen bond between the Tyr–OH group and the carbonyl oxygen of the Gly₂ residue in the 0 kJ mol⁻¹ structure. Experimentally, a corresponding small peak that is barely above the noise level is observed at 1402 cm⁻¹. The predicted amide II region of both structures contains closely spaced N–H bending modes and a Tyr-ring deformation mode. These modes are similar in intensities and wavenumbers for both structures. In the amide I region between 1650 cm⁻¹ and 1800 cm⁻¹, both calculations predict five transitions corresponding to the five C=O oscillators in the molecule. Their positions and relative intensities differ from each other, reflecting the differences in their hydrogen bonding patterns. Both calculations predict the mode of the Leu C=O group as appearing most to the blue in the spectrum. The H-bond in the +14.8 kJ mol⁻¹ structure causes a red-shift of this mode of −13 cm⁻¹ with respect to the 0 kJ mol⁻¹ structure. Another significant difference between the two calculations stems from the Tyr C=O mode, which for the +14.8 kJ mol⁻¹ structure is shifted towards the red by 30 cm⁻¹, again due to its involvement in a hydrogen bond.

Table 2 Assignment of IR transitions of [Leu-Enk + CE + H]⁺ for the 14.8 kJ mol⁻¹ structure shown in Fig. 4b

Exp. (cm^−1)	Calc. (cm^−1)	Intensity (km mol^−1)	Assignment
1253	1280	134.10	Tyr ring deform.
1402	1400	251.20	Leu O–H bend
1505	1493	117.06	N–H bend
	1507	130.93	Tyr ring deform.
1526	1516	176.59	N–H bend
	1522	248.26	N–H bend
	1528	131.66	Sym. NH3^+ umbrella
	1540	148.97	N–H bend
	1609	60.32	Antisym. NH3^+ umbrella
	1622	76.66	Tyr ring deform.
1678	1662	120.13	Phe C=O stretch
1691	1675	112.14	Gly1 C=O stretch
1705	1692	465.32	Tyr C=O stretch
1725	1715	520.60	Gly2 C=O stretch
1748	1744	373.44	Leu C=O stretch

---

After a comparison of the experimental results with the calculated vibrational transitions, it is evident that the theoretical spectrum of the 14.8 kJ mol⁻¹ structure provides the best agreement with the experimental spectrum of the CE-complexed molecule. The experimentally observed positions and the almost equidistant spacing between the five modes in the amide I range are correctly reproduced by the spectrum of the +14.8 kJ mol⁻¹ structure while the experimental resolution of only four modes would be expected in the spectrum of the 0 kJ mol⁻¹ structure. The amide II region is less informative as both calculations reproduce the experiment. Provided that the weak band at 1402 cm⁻¹ stems from a real transition in the experimental spectrum, the best agreement is given as well by the 14.8 kJ mol⁻¹ structure. The stronger mode calculated in the amide III region is at essentially the same position for both structures and is also ≈30 cm⁻¹ higher in wavenumber than the next corresponding experimental transition.

3.2.4 Spectroscopy of [Leu-Enk_D + CE + D]⁺. Further evidence for the structural assignment comes from deuteration experiments. The experimental results of deuterated [Leu-Enk_D + CE + D]⁺ are displayed in Fig. 5b, along with the calculated vibrational transitions of the +14.8 kJ mol⁻¹ and 0 kJ mol⁻¹ structures. The transition frequencies are summarized in Table S5 (ESI†). As expected, the largest differences between the experimental spectrum of [Leu-Enk + CE + H]⁺ and [Leu-Enk_D + CE + D]⁺ are found in the amide II region. There, the main band is shifted by ≈60 cm⁻¹ and broadened. A similar shift and a slightly broadened peak is predicted by the calculated spectra of both structures. At 1518 cm⁻¹ a small peak remains, which can be assigned on the basis of both calculations as resulting from Tyr sidechain ring deformation modes. The peak observed at 1356 cm⁻¹ could correspond to the various C–H bending modes predicted by the calculation in this range, but an assignment is unclear. The amide I range remains essentially unchanged, but the C=O stretches undergo a small redshift (4–9 cm⁻¹) with respect to the undeuterated molecule, which results in a slightly more congested spectrum. Also in the case of [Leu-Enk_D + CE + D]⁺ the best agreement between theory and experiment is achieved by the 14.8 kJ mol⁻¹ structure.

3.2.5 Effect of charge desolvation. When comparing the spectrum of [Leu-Enk + CE + H]⁺ to that of uncomplexed [Leu-Enk + H]⁺, it is clear that their spectra differ to a large extent. This is especially the case for the amide I range, where the majority of the modes are shifted to the blue after the molecule is complexed with a CE.

A comparison between the H-bonding arrangements of the assigned structures of [Leu-Enk + H]⁺ (available in ref. 10) and [Leu-Enk + CE + H]⁺ (Fig. 4b) shows that the H-bonds involving as donors the –NH₃⁺ group are no longer present when a CE molecule is added. However, the remaining four H-bonds that are not directly coordinated to the protonated amine site are maintained. Burke et al.¹⁰ discussed the importance of charge and charge solvation on the structure and on the C=O oscillator vibrational frequencies. According to their analysis, the solvation of the charge allows a network of H-bonds that, in some cases, cooperatively strengthen one another. This is the case for the C=O groups of the Leu and Gly₂ residues due to their direct coordination to the –NH₃⁺ group. The H-bond of the Phe C=O, which is coordinated to the Leu OH is also strengthened indirectly via the coordination of the –NH₃⁺ group to the Leu C=O.¹⁰ Thus, those three modes are expected to be most affected in the CE-complexed molecule. Indeed, our calculation for the +14.8 kJ mol⁻¹ structure predicts a large blue-shift of the Phe, Gly₂, and Leu C=O stretch frequencies that is further confirmed by the experimental results in which these transitions undergo a blue-shift of +55 cm⁻¹, +59 cm⁻¹, and +26 cm⁻¹ respectively. On the other hand, the C=O stretch modes of Gly₁ and Tyr, whose H-bonds are not strengthened by the solvation of the charge in the uncomplexed molecule and are most likely less affected by its now reduced interaction with the peptide's backbone, undergo a much minor shift of +3 cm⁻¹ and −4 cm⁻¹, respectively. However, the H-bonding pattern of the 0 kJ mol⁻¹ structure would require the breakage of two additional H-bonds, namely C7 and C14 in Fig. 4b, although none of them plays a significant role in the solvation of the charge and therefore should not be affected by the complexation with a CE.

These results further support the conformational assignment of the +14.8 kJ mol⁻¹ structure based on the experimentally obtained infrared spectrum. Further confirmation could be provided, for example, by measurements in the hydride stretch region, where the calculated spectra of both structures present significant differences. This is, however, beyond the scope of this work. It is also important to note that this structure might not be the global minimum structure and, for example, some rotations of the side groups can not be discarded. Nevertheless, the assigned main H-bond pattern shown in Fig. 4b should not be affected.

3.3 Possible effects of the helium environment on the doped ion

An important question is in how far the vibrational spectrum is perturbed by the presence of the helium environment. Out of all possible solvents, superfluid helium is the one that is expected to interact the least with embedded molecules or ions. For neutral species, the interaction is dominated by dispersion and multipole – induced dipole interactions, and it is quite weak. Consequently, only small perturbations in vibrational frequencies in the form of shifts of about 0.6 cm⁻¹ have been observed²⁸. For charged species, there is an additional charge-induced dipole interaction, which decreases proportionally to r⁻⁴. For small ions, this interaction can be reasonably strong, leading to helium localization (snowball formation) with structured solvation shells around the charged center.^29–33 However, as the ion becomes bigger, the distance of the helium atoms to the charge center gets larger and the interaction rapidly becomes weaker. In line with this, in mid-IR studies on small organic cations in helium droplets¹⁴ no deviation of peak positions between gas-phase spectra and spectra recorded in helium droplets could be detected (within the experimental uncertainty of about 1–5 cm⁻¹).

The spectra of [Leu-Enk + H]⁺ shown here can be directly compared to the spectra measured using infrared-ultraviolet (IR-UV) double resonance on [Leu-Enk + H]⁺ in a cold ion trap¹⁰ and to those when performing IRMPD on room temperature [Leu-Enk + H]⁺.¹⁹ In general, there is a very good agreement in peak positions between the helium droplets data and the results obtained using a cold ion trap¹⁰ (see Fig. S2, ESI†). The two spectra have very similar peak positions and peak widths. For most transitions, the differences in wavenumber between the helium droplets and IR-UV gas-phase data are smaller than 11 cm⁻¹ and comparable to the widths of the bands themselves. The fact that the peaks in the spectra shown in this work are mostly shifted uniformly in the same direction (towards the red side of the spectrum) might be due to small errors in the wavelength calibration. Only one transition – the deformation of the Tyr ring – has a considerable shift of ≈20 cm⁻¹ with respect to our calculations and the gas-phase data.

A comparison with IRMPD spectra of room temperature [Leu-Enk + H]^+ 19 shows good agreement between 1200 cm⁻¹ and 1600 cm⁻¹. The same number of bands are shown at similar frequencies. However, between 1600 cm⁻¹ and 1800 cm⁻¹, the disagreement between helium droplets and IRMPD data is more evident. For example, the peak measured at 1623 cm⁻¹ in the helium droplets data is absent in the IRMPD data. This is most likely due to the excitation mechanism intrinsic in the IRMPD process where the absorption of the large number of photons is required, which can lead to shifts and broadenings of the spectral lines due to anharmonicities.⁶ While the absorption of more than one photon is also necessary to eject an ion embedded in a helium droplet, the number of photons required is much smaller than for the IRMPD process. Further, it is likely that after each consecutive absorption in the ≈10 μs long macropulse, the energy is transferred to the helium and the absorption of the next photon will occur from a re-cooled molecule. Therefore, mode anharmonicities are not expected to play a role. The experimental results confirm this, showing well resolved lines that can have a similar bandwidth to that of the laser (≈8 cm⁻¹) for the two investigated molecules. This is also in line with the results reported previously for aniline ions solvated in helium droplets.¹⁴

While peak positions match, comparing the relative intensities of the bands of the spectra shown here to the predictions from theory as well as to the spectrum of the cold trap¹⁰ relatively large deviations can be found. As more than one photon is required to induce signal, the observed peak intensities non-linearly depend on the laser power. The ejection mechanism of the ion and its dependence on laser power is yet not fully understood. As a first approximation, we here perform a linear correction by dividing the signal by the laser power. Likely, the relative intensities depend on laser power in a more complicated manner and are difficult to use as a measure when comparing experiment to theory.

4 Conclusion

In this work, we have recorded the vibrational spectra in helium droplets of [Leu-Enk + H]⁺ and [Leu-Enk + CE + H]⁺ as well as their deuterated counterparts [Leu-Enk_D + D]⁺ and [Leu-Enk_D + CE + D]⁺. The results show highly resolved spectra with sharp transitions for both molecules, some of them with bandwidths similar to the bandwidth of the laser. In addition to the high sensitivity of this method, the non thermal energy dissipation that leads to the ejection of the doped ion from the helium droplet allows for a background free measurement of the vibrational modes of the parent ion. The absence of helium adducts in the signal of the ejected ion further indicates that a possible interaction of the helium atoms surrounding the embedded ion is rather weak. This is indeed confirmed by the good general agreement obtained with both theory and IR-UV data.¹⁰ A comparison between the gas-phase data, and the spectrum recorded using helium droplets show the same number of bands with only small shifts in wavenumber position within the uncertainty of the experiment. Nevertheless, a more detailed understanding of the ion ejection mechanism is necessary to account for the change of the band intensities as a function of photon density.

The high resolution of the IR spectra obtained using helium droplets has been used to further investigate the importance of the charge solvation previously reported by Burke et al.¹⁰ In their analysis, the suggested structure of [Leu-Enk + H]⁺ is supported by seven H-bonds, three of which solvate the –NH₃⁺ group, facilitating a cooperative strengthening of further H-bonds. When a CE molecule is added, its coordination to the –NH₃⁺ group is expected to disrupt those H-bonds. As a result, the H-bonds that were previously strengthened by the charge solvation will become weaker. Indeed, this effect can be observed in the IR spectra of [Leu-Enk + CE + H]⁺. The three C=O oscillators with H-bonds previously strengthened by the solvation of the charge undergo a large blue-shift with respect to the uncomplexed molecule. On the other hand, no essential shift is observed for the two C=O oscillators that were not as strongly influenced by the self-solvation of the charge.

We can conclude that IR excitation of m/z selected peptide ions in helium droplets can be used as a versatile technique to obtain IR spectra of biological molecules. It provides spectra of very cold molecules, does not require the presence of a chromophore, has a rather weak interaction with the helium solvation shell, and can be extended to large species.³⁴

Acknowledgements

The authors are grateful to Nicole L. Burke and Timothy S. Zwier for providing us results prior to publication and to Kevin Pagel for useful discussions.

References

1. M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612.
2. M. Gerhards, C. Unterberg and A. Gerlach, Phys. Chem. Chem. Phys., 2002, 4, 5563–5565.
3. C. Canuel, M. Mons, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Elhanine, J. Chem. Phys., 2005, 122, 07316.
4. T. S. Zwier, J. Phys. Chem. A, 2001, 105, 8827–8839.
5. N. C. Polfer and J. Oomens, Mass Spectrom. Rev., 2009, 28, 468–494.
6. J. Oomens, B. G. Sartakov, G. Meijer and G. von Helden, Int. J. Mass Spectrom., 2006, 254, 1–19.
7. J. A. Stearns, S. Mercier, C. Seaiby, M. Guidi, O. V. Boyarkin and T. R. Rizzo, J. Am. Chem. Soc., 2007, 129, 11814–11820.
8. N. S. Nagornova, T. R. Rizzo and O. V. Boyarkin, Science, 2012, 336, 320–323.
9. T. N. Wassermann, O. V. Boyarkin, B. Paizs and T. R. Rizzo, J. Am. Soc. Mass Spectrom., 2012, 23, 1029–1045.
10. N. L. Burke, J. G. Redwine, J. C. Dean, S. A. McLuckey and T. S. Zwier, Int. J. Mass Spectrom., 2014, 378, 196–205.
11. W. H. Robertson, E. G. Diken, E. A. Price, J. W. Shin and M. A. Johnson, Science, 2003, 299, 1367–1372.
12. N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266–8273.
13. J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648.
14. X. Zhang, N. B. Brauer, G. Berden, A. M. Rijs and M. Drabbels, J. Chem. Phys., 2012, 136, 044305.
15. F. Bierau, P. Kupser, G. Meijer and G. von Helden, Phys. Rev. Lett., 2010, 105, 133402.
16. F. Filsinger, A. G. Meijer and G. von Helden, Phys. Chem. Chem. Phys., 2012, 14, 13370–13377.
17. J. Sztáray, A. Memboeuf, L. Drahos and K. Vékey, Mass Spectrom. Rev., 2011, 30, 298–320.
18. N. C. Polfer, B. C. Bohrer, M. D. Plasencia, B. Paizs and D. E. Clemmer, J. Phys. Chem. A, 2008, 112, 1286–1293.
19. N. C. Polfer, J. Oomens, S. Suhai and B. Paizs, J. Am. Chem. Soc., 2007, 129, 5887–5897.
20. W. Schöllkopf, S. Gewinner, W. Erlebach, H. Junkes, A. Liedke, G. Meijer, A. Paarmann, G. von Helden, H. Bluem, D. Dowell, R. Lange, J. Rathke, A. M. M. Todd, L. M. Young, U. Lehnert, P. Michel, W. Seidel, R. Wünsch and S. C. Gottschalk, Proceedings of FEL, 2014, 2014.
21. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zhend, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, G. Ogliaro, M. Beampark, J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Lyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, E. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. Fox, Gaussian 09, Revision D.01, Wallingford CT, 2013.
23. J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz, J. R. Maple, R. Murphy, D. M. Philipp, M. P. Repasky, L. Y. Zhang, B. J. Berne, R. A. Friesner, E. Gallicchio and R. M. Levy, J. Comput. Chem., 2005, 26, 1752–1780.
24. Schrödinger Release 2014-4: Macromodel, version 10.6, Schrödinger, LLC, New York, NY, 2014.
25. S. Smolarek, N. B. Brauer, W. J. Buma and M. Drabbels, J. Am. Chem. Soc., 2010, 132, 14086–14091.
26. X. Cai and C. Dass, Rapid Commun. Mass Spectrom., 2005, 19, 1–8.
27. R. R. Julian and J. L. Beauchamp, J. Am. Soc. Mass Spectrom., 2002, 13, 493–498.
28. S. Grebenev, B. G. Sartakov, J. P. Toennies and A. F. Vilesov, J. Chem. Phys., 2003, 118, 8656–8670.
29. Y. Kwon, D. M. Ceperley and K. B. Whaley, J. Chem. Phys., 1996, 104, 2341–2348.
30. F. F. da Silva, P. Waldburger, S. Jaksch, A. Mauracher, S. Denifl, O. Echt, T. D. Mark and P. Scheier, Chem. – Eur. J., 2009, 15, 7101–7108.
31. A. Nakayama and K. Yamashita, J. Chem. Phys., 2000, 112, 10966–10975.
32. F. Marinetti, E. Bodo and F. A. Gianturco, ChemPhysChem, 2007, 8, 93–100.
33. C. Di Paola, E. Bodo and F. A. Gianturco, Eur. Phys. J. D, 2006, 40, 377–385.
34. A. I. Gonzalez Florez, D. Ahn, S. Gewinner, W. Schöllkopf, K. Pagel and G. von Helden, in preparation.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated relative energies, additional IR spectra, assignments of vibrational bands. See DOI: 10.1039/c5cp02172c

---