On the tunneling instability of a hypercoordinated carbocation

Abstract

C(CH₃)₅⁺, a pentacoordinate carbocation, was recently described as a “fleeting” molecule, that is, stable only at low temperatures. Herein it is shown using theoretical methods that, owing to carbon tunneling, the molecule is not persistent even at 0 K. One possible way to lengthen its lifespan is by deuterium substitution, in spite of the fact that no bond to hydrogen is broken.

---

A recent communication exploring the limits of carbon bonding by McKee, Schleyer and coworkers¹ described the theoretical existence of C(CH₃)₅⁺ near absolute zero as “fleeting”.² This term was coined by Hoffmann, Schleyer and Schaeffer in their essay: “Predicting Molecules—More Realism, Please!”, indicating a molecule where the sole energetic criterion of its stability is a vibrational analysis (thus being a real minimum in the potential energy surface).

C(CH₃)₅⁺, a C_3h pentacoordinate carbocation, is more a proof of concept for the feasible bonding possibilities of carbon rather than a molecule with real perspectives to be synthesized. Although the “classical” thermal barriers suggest that this carbocation might be detectable at extremely low temperatures, herein it is shown that due to quantum mechanical tunneling (QMT) the existence of C(CH₃)₅⁺ is much more ephemeral than was considered, even at absolute zero.^3,4

The two decomposition pathways for C(CH₃)₅⁺ (described in detail in the original communication¹) are shown in Fig. 1. The first pathway, going through a C₃ symmetry transition state (TS1), involves a CH₃⁺ loss by elongation of an axial methyl C–C bond, followed by a hydrogen abstraction and CH₃ migration, generating a relatively stable tertiary carbocation. This process has a Δ(E + ZPE)^‡ value of 1.65 and a ΔE^‡ value of 4.35 kcal mol⁻¹ (calculated at the CCSD(T)/CBS level, as reported in the original communication¹). The second decomposition pathway, via a transition state of C_s symmetry (TS2), involves a bending mode joining an axial and an equatorial carbon to give ethane and a tert-butyl carbocation, with Δ(E + ZPE)^‡ = 1.37 and ΔE^‡ = 2.32 kcal mol⁻¹. Thus, despite these extremely low degradation barriers, transition state theory in its simplest form predicts that the cation should have a fleeting,² possibly observable existence near absolute zero.

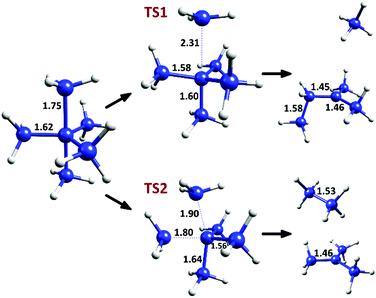Fig. 1 Decomposition pathways for C(CH₃)₅⁺, with selected C–C bond distances at the M06-2X/6-31G(d) level.

However, due to the low and (more critical) narrow^3–6 barriers in the decomposition patterns of C(CH₃)₅⁺, the tunneling effect may be a crucial factor to take into account, even if QMT of “heavy” atoms is involved. Carbon tunneling is an unusual but well documented effect, which has been observed or calculated in reactions such as the automerization of cyclobutadiene and other antiaromatic molecules (starting from the pioneering work of Carpenter),^5,7–13 or in different carbene insertion reactions and other reactive systems.^6,14–17 All these systems have something in common: low and considerably narrow barriers. In the decomposition of C(CH₃)₅⁺ the carbon atoms travel over great distances, but the effective barrier for tunneling is tight (that is, from the reactant stage to the point of the same energy in the product side of the reaction coordinate), and therefore may be prone to reaction by a QMT mechanism.

It must be pointed out that QMT on the related CH₅⁺ carbocation has been thoroughly studied (see for instance ref. 18). However, the differences between both systems are significant. For CH₅⁺, the tunneling concerns only the hydrogens (“light atom” QMT) mostly in its fluxionality;¹⁹ for C(CH₃)₅⁺, tunneling will primarily affect the carbon structure (“heavy atom” QMT) in its chemical degradation.

To study the effect of quantum mechanical tunneling on the degradation of C(CH₃)₅⁺, we used canonical variational theory (CVT) to compute the semi-classical rate constant (without the tunneling component),²⁰ and the small curvature tunneling approximation (SCT)²¹ including the quantized reactant state tunnelling (QRST) approximation²² to compute the rate constant including tunneling. The polyrate²³ program was used for this effect, and Gaussian09²⁴ was employed for the DFT calculations (with Gaussrate²⁵ as the interface between Polyrate and Gaussian). Since high-quality, wave-function-based calculations are not practical for the demanding SCT calculations, all rate constant calculations were carried out using the M06-2X functional²⁶ and the 6-31G(d) basis set. The combination of this functional and basis set has shown good accuracy for tunneling calculations of organic reactions,^12,26 and reasonably agrees with the CCSD(T)/CBS methodology, generating values of 2.27 and 2.16 kcal mol⁻¹ for Δ(E + ZPE)^‡ of TS1 and TS2, respectively.

Table 1 shows the calculated rate constants for both decomposition pathways with (SCT) and without (CVT) tunneling effect included, and the SCT half-life at different temperatures (see the ESI† for the complete tables).

Table 1 Rate constants with and without tunneling correction (SCT and CVT, respectively) in s⁻¹, and half-life in seconds for both decomposition pathways of C(CH₃)₅^+a

T (K)	TS1			TS2
	CVT	SCT	t 1/2	CVT	SCT	t 1/2
a Due to the change in the symmetry number of TS2 (going from a C3h reactant to a Cs transition state), the rate constants for this pathway were tripled and t1/2 were divided by 3.^27
10	1.2 × 10^−39	1.2 × 10^5	6 × 10^−6	6.8 × 10^−36	1.5 × 10^4	4 × 10^−5
20	3.2 × 10^−14	1.2 × 10^5	6 × 10^−6	4.2 × 10^−12	1.6 × 10^4	4 × 10^−5
50	1.0 × 10^2	2.2 × 10^5	3 ×10^−6	1.5 × 10^3	5.6 × 10^5	1 × 10^−6
100	2.8 × 10^7	8.7 × 10^7	8 × 10^−9	2.2 × 10^8	7.0 × 10^8	1 × 10^−9
150	2.5 × 10^9	4.2 × 10^9	2 × 10^−10	1.5 × 10^10	2.2 × 10^10	3 × 10^−11
200	2.6 × 10^10	3.6 × 10^10	2 × 10^−11	1.5 × 10^11	1.6 × 10^11	4 × 10^−12
300	3.1 × 10^11	3.6 × 10^11	2 × 10^−12	1.6 × 10^12	1.6 × 10^12	5 × 10^−13

---

It is clear that the stability of C(CH₃)₅⁺ is strongly influenced by carbon tunneling, with extremely high SCT rate constants, even at cryogenic temperatures. Half-lives (t_1/2 = ln 2/k) of only 6 and 40 μs for the decomposition of C(CH₃)₅⁺ were computed for pathways 1 and 2, respectively, below 20 K. Without the inclusion of QMT, the reaction is predicted to take several millennia to occur even at 20 K, thus confirming the fleeting characteristics of the system based on transition state theory alone (i.e. without considering QMT).

Although the whole QMT picture is more complex than the analysis of the motion of individual particles (since the reduced mass of the whole system in the least action pathway must be considered^28,29), the influence of each atom can still be analyzed by studying the carbon (¹²C/¹³C) and hydrogen (H/D) kinetic isotope effects (KIE) on the SCT rate constant.

Fig. 2 shows the KIE of each inequivalent atom on the TS1 pathway at cryogenic temperatures. The carbon of the departing methyl group is the most crucial carbon atom for the QMT process with a KIE of 1.72, but the central carbon also exerts a significant effect (KIE of 1.20). Surprisingly, the lower axial carbon provides a negative secondary KIE of 0.94. The KIE after substituting all the carbons by ¹³C is 2.03, virtually identical to the product of all the individual substitutions (1.72 × 1.20 × 0.94 × 1.02³ = 2.05). Thus, there is a largely independent contribution of each carbon to the tunneling probability.

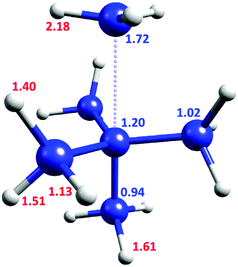Fig. 2 TS1 geometry, with the KIE values for inequivalent atoms in C₃ symmetry. Blue values are for ¹²C/¹³C KIE, red for H/D KIE.

However, the contribution of each H/D substitution is not totally independent. Replacing all of the hydrogen atoms with deuterium results in a KIE of 613. Since no C–H bond is broken, this large value is remarkable. Moreover, it is higher than the product of individual contributions (2.18³ × 1.61³ × 1.51³ × 1.40³ × 1.13³ = 592, see Fig. 2), suggesting a small synergistic hydrogen contribution to the tunneling probability.

The high H/D KIE value goes beyond the effect of the higher mass of the particles on the tunneling probability. As pointed out by a reviewer, more than being exclusively a carbon tunneling process, the process can be considered as a methyl group tunneling, since the hydrogens connected to the dissociating carbon move as well. In that sense, the mass change of one H/D substitution on the departing CH₃ group should be as important for the tunnelling probability as a ¹³C/¹²C substitution on the same group. However, the H/D replacement produces a significantly higher KIE than the carbon replacement (2.18 vs. 1.72). Moreover, all the other hydrogens have a strong influence on the rate, while other carbons do not. This is despite the fact that these hydrogens are not directly “involved” in the C–C breaking process (at least not in the reaction section important to QMT). More than the direct effect of the mass, what is strongly influencing the tunneling rate is a factor that is traditionally connected to a change in the semi-classical KIE, the zero point energy. The ZPE change is also a mass effect, but the extra mass indirectly affects the QMT probability through a higher and broader barrier.

The additive lowering of the ZPE of the reactant by each H/D substitution increases the Δ(E + ZPE)^‡ value and reduces the tunneling probability. One H/D axial methyl group substitution raises the Δ(E + ZPE)^‡ value from 2.27 to 2.39 kcal mol⁻¹, while the replacement of all 15 H's by D's raises the Δ(E + ZPE)^‡ value to 2.99 kcal mol⁻¹ for decomposition viaTS1. Considering that this ZPE difference is a major component relative to the activation energy, the lower ZPE of the reactant in deuterated systems significantly affects the tunneling-based KIE³⁰ of the degradation of C(CH₃)₅⁺ by raising and broadening the barrier, in addition to the increase of the methyl mass. Contrary to this, the ¹²C/¹³C substitution does not change the ZPE appreciably, and therefore its KIE only has a direct mass effect on the tunneling probability.

Notably, this change in the ZPE greatly extends the lifetime of C(CD₃)₅⁺. Its computed half-life of 4 ms is three orders of magnitude longer than that of the C(CH₃)₅⁺ isotopologue. Replacing all the hydrogen atoms with tritium would lead to a Δ(E + ZPE)^‡ value of 3.31 kcal mol⁻¹ and a still brief, but drastically longer, half-life of 0.2 seconds. The Δ(E + ZPE)^‡ values for decomposition through TS2 are less sensitive to an isotopic replacement, with values of 2.16, 2.41 and 2.53 kcal mol⁻¹ for C(CH₃)₅⁺, C(CD₃)₅⁺ and C(CT₃)₅⁺, respectively. Nevertheless, due to the wider barriers, the half-lives of these species considering only decomposition through TS2 are longer than those viaTS1: 40 μs, 60 ms, and 10 s. This technique of prolonging the lifetime and stabilizing a molecule prone to degradation by QMT with H/D substitutions is, to the best of our knowledge, unheard of in reactions not based on hydrogen migration.

Conclusions

Considering the short lifetime of the hypothetical C(CH₃)₅⁺ pentacoordinate carbocation, the definition of a “fleeting system”² as one that can be detected at extremely low temperatures may require revision. Molecules that have a low but definite decomposition barrier (with all positive frequencies in a vibrational analysis) might be expected to be persistent close to 0 K, but QMT calculations may show otherwise. Therefore, is C(CH₃)₅⁺ “fleeting” or not? This semantic problem may be solved by adding a new term, “tunneling stability” (similar to the concept of “tunneling control”³¹) to the already established “kinetic persistence” and “thermodynamic stability” definitions. Indeed, other molecules predicted to be fleeting^32,33 have been computed to be unstable due to tunneling,³⁴ indicating that QMT should be a factor to take into account in stability analyses.

In this sense, the decomposition of C(CH₃)₅⁺ through QMT by no means refutes the hypothetical existence of the five-fold C–C bonding motif of C(CH₃)₅⁺ as predicted by Schleyer et al.¹ However, we now know that it will probably be impossible to detect this cation experimentally due to its exceptionally short life expectancy.

Interestingly, deuterium or tritium substitution is predicted to extend the lifespan of C(CH₃)₅⁺ much more than ¹³C substitution, in spite of the fact that we are breaking C–C and not C–H bonds. The added mass is only one factor for this extra longevity, which is mainly caused by the effect of hydrogen isotopes on the ZPE.

One can only wonder how many other fleeting systems have been theoretically predicted but will not pass the tunneling test. Or, quoting the title of the essay of Hoffmann, Schleyer and Schaeffer,² we may say: “Predicting Molecules—More Realism, Please!”.

Acknowledgements

This research project begun at the University of North Texas, in the Department of Chemistry and Center for Advanced Scientific Computing and Modeling (CASCaM), and finished at Ben-Gurion University. I thank Jay Agarwal for helpful discussions and for aiding in the writing of this manuscript, Professor Weston T. Borden for his chemical insight, and Dr David A. Hrovat for technical and professional help. This communication is dedicated to the memory of Professor Paul von Ragué Schleyer, who actively encouraged this project and the study of chemical stability in all their dimensions.

Notes and references

1. W. C. McKee, J. Agarwal, H. F. Schaefer and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2014, 53, 7875–7878.
2. R. Hoffmann, P. v. R. Schleyer and H. F. Schaefer, Angew. Chem., Int. Ed., 2008, 47, 7164–7167.
3. R. P. Bell, The tunnel effect in chemistry, Chapman and Hall, London, New York, 1980.
4. M. Razavy, Quantum theory of tunneling, World Scientific, River Edge, NJ, 2003.
5. B. K. Carpenter, J. Am. Chem. Soc., 1983, 105, 1700–1701.
6. S. Kozuch, Phys. Chem. Chem. Phys., 2014, 16, 7718–7727.
7. M. J. Huang and M. Wolfsberg, J. Am. Chem. Soc., 1984, 106, 4039–4040.
8. M. J. S. Dewar, K. M. Merz and J. J. P. Stewart, J. Am. Chem. Soc., 1984, 106, 4040–4041.
9. P. Čársky, R. J. Bartlett, G. Fitzgerald, J. Noga and V. Špirko, J. Chem. Phys., 1988, 89, 3008–3015.
10. R. Lefebvre and N. Moiseyev, J. Am. Chem. Soc., 1990, 112, 5052–5054.
11. Kinetics and spectroscopy of carbenes and biradicals, ed. M. Platz, Plenum Press, New York, 1990.
12. S. Kozuch, RSC Adv., 2014, 4, 21650–21656.
13. S. Kozuch, DOI: 10.1021/acs.jctc.5b00321.
14. P. S. Zuev, R. S. Sheridan, T. V. Albu, D. G. Truhlar, D. A. Hrovat and W. T. Borden, Science, 2003, 299, 867–870.
15. R. A. Moss, R. R. Sauers, R. S. Sheridan, J. Tian and P. S. Zuev, J. Am. Chem. Soc., 2004, 126, 10196–10197.
16. S. Kozuch, X. Zhang, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2013, 135, 17274–17277.
17. J. Meisner, J. B. Rommel and J. Kästner, J. Comput. Chem., 2011, 32, 3456–3463.
18. D. Marx and M. Parrinello, Science, 1999, 284, 59–61.
19. P. R. Schreiner, S.-J. Kim, H. F. Schaefer and P. v R. Schleyer, J. Chem. Phys., 1993, 99, 3716–3720.
20. D. G. Truhlar and B. C. Garrett, Annu. Rev. Phys. Chem., 1984, 35, 159–189.
21. A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and T. R. Cundari, John Wiley & Sons, Inc., 2007, vol. 3, pp. 125–232.
22. J. G. Lauderdale and D. G. Truhlar, Surf. Sci., 1985, 164, 558–588.
23. J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE 2010-A: Computer Program for the Calculation of Chemical Reaction Rates for Polyatomics.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.1, Gaussian, Inc., Wallingford CT, 2009.
25. J. Zheng, S. Zhang, J. C. Corchado, Y.-Y. Chuang, B. A. Ellingson, E. L. Coitiño and D. G. Truhlar, GAUSSRATE 2009-A, 2000.
26. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
27. A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. C. Marques and D. G. Truhlar, Theor. Chem. Acc, 2007, 118, 813–826.
28. B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1983, 79, 4931.
29. R. Meana-Pañeda, D. G. Truhlar and A. Fernández-Ramos, J. Chem. Theory Comput., 2010, 6, 6–17.
30. X. Zhang, A. Datta, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2009, 131, 16002–16003.
31. D. Ley, D. Gerbig and P. R. Schreiner, Org. Biomol. Chem., 2012, 10, 3781.
32. G. Martínez-Guajardo, K. J. Donald, B. K. Wittmaack, M. A. Vazquez and G. Merino, Org. Lett., 2010, 12, 4058–4061.
33. G. Markopoulos and J. Grunenberg, Angew. Chem., Int. Ed., 2013, 52, 10648–10651.
34. S. Kozuch, Org. Lett., 2014, 16, 4102–4105.

---

Footnote

† Electronic supplementary information (ESI) available: Complete CVT/SCT rate constant tables, KIE tables, geometries, absolute energies, an example of a Polyrate input, and V_mep and V_a^G for the root reaction of the TS1 pathway. See DOI: 10.1039/c5cp02080h

---