Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interplay of donor–acceptor interactions in stabilizing boron nitride compounds: insights from theory†
Mohammad R.
Momeni
,
Lisa
Shulman
,
Eric
Rivard
* and
Alex
Brown
*
Department of Chemistry, University of Alberta, Edmonton, Alberta, T6G 2G2 Canada. E-mail: erivard@ualberta.ca; alex.brown@ualberta.ca; Fax: +1-780-492-8231; Tel: +1-780-492-4255 Tel: +1-780-492-1854
First published on 27th May 2015
Abstract
The stability of a variety of linear and cyclic (BN)n (n = 1–3) adducts with N-heterocyclic carbene (ImMe2; ImMe2 = [(HCNMe)2C:]), N-heterocyclic olefin (ImMe2CH2) and Wittig (Me3PCH2) donors has been examined using M05-2X/cc-pVTZ computations. The strength and nature of the bonds have been investigated using natural bond orbital (NBO) and atoms-in-molecules (AIM) analyses. Complementary energy decomposition analysis (EDA-NOCV) has been carried out based on BP86/TZ2P computations. In agreement with NBO and AIM analyses, the orbital interaction energy obtained from EDA contributes at least 50% to the total attractive interactions for the carbon–boron bonds indicating their largely covalent nature. The feasibility of isolating monomeric (BN)n units using a donor/acceptor protocol was also investigated in a series of adducts of the general form: LB·(BN)n·BH3 and LB·(BN)n·W(CO)5 (n = 1–3; LB = Lewis bases). Moreover, EDA-NOCV analysis of ImMe2·BN·W(CO)5 and ImMe2·B3N3·W(CO)5 shows that the carbene–boron bonds are stronger in the presence of W(CO)5 as a Lewis acid mainly because of a dramatic decrease in the amount of Pauli repulsion rather than an increase in the electrostatic/orbital attraction terms.
1 Introduction
Boron nitride materials (BN)n are isoelectronic with various carbon allotropes (e.g., diamond, graphene, nanotubes),1–3 however, they possess vastly different properties due to the presence of polarized B–N linkages. Two specific properties, wide electronic band gaps (5.9 eV in hexagonal BN) and chemical inertness,4 make boron nitride of significant interest for the electronics industry, with the construction of devices based on BN/graphene heterostructures being a promising recent development.5,6 One hindrance to the widespread examination and application of BN materials is the harsh conditions required for their syntheses, i.e., heating above 900 °C and/or the use of plasma conditions.1–3 With these challenges in mind, we have embarked on a program wherein complexes of the general form [LB·BN]n (n ≥ 1; LB = Lewis base) might be formed with suitable carbon-based donors. Upon heating in solution, the target [LB·BN]n complexes could afford bulk boron nitride and free Lewis base. To provide a solid fundamental basis for future experimental explorations, we present quantum mechanical computations on the Lewis base-stabilized linear and cyclic boron nitride species (BN)n (n = 1–3) including the donor–acceptor adducts LB·(BN)n·LA (n = 1–3, LA = Lewis acid). Recent examples of stabilizing main group element units (e.g., Si2) with the aid of strong carbon-based donors are numerous in the literature.7–15 Moreover, donor–acceptor stabilization has been used to great success to isolate heavier group 13–15 element species,16–21 while related computational studies have been reported.22,23 More specifically, DFT predicted a significant thermodynamical stabilization of group 13–15 cubane systems (e.g., B4N4) upon addition of NH3 and BH3 as donor and acceptor molecules, respectively.22In this work we present our analyses of the bonding within Lewis base-substituted boron nitride compounds in the presence and/or absence of Lewis acid. Specifically we examined the binding of the carbon-based donors, ImMe2 (ImMe2 = [(HCNMe)2C:]), ImMe2CH2 and Me3PCH2 to (BN)n units, given our use of their sterically hindered analogues to bind/stabilize inorganic methylene and ethylene units (EH2 and H2EE′H2; E and E′ = Si, Ge and/or Sn).14,24–31 We also provide computations on LB·(BN)n·BH3 and LB·(BN)n·W(CO)5 adducts (n = 1–3) featuring coordinated (BN)n units and show that this overall donor–acceptor approach is a viable means of intercepting a complex of molecular boron nitride. Finally, based on detailed EDA-NOCV computations, we will comment on the strength and nature of both the carbene–boron and nitrogen–tungsten donor acceptor bonds in the ImMe2 substituted BN·W(CO)5 and B3N3·W(CO)5 adducts.
2 Computational methods
Geometry optimizations were performed using density functional theory (DFT) with the M05-2X32 functional. The computations employed the following basis sets: cc-pVTZ33,34 for all period 1, 2 and 3 atoms and cc-pVTZ-PP,35,36 combined with the corresponding small core (60 electrons) effective core potential (ECP) for tungsten (W). The basis set and ECP for tungsten were obtained from the basis set exchange.37,38 For convenience, these computations are simply labeled as M05-2X/cc-pVTZ throughout the text. Triplet states for BN, linear BNBN, and cyclic B2N2 were computed using an UHF reference. For geometry optimizations, “Tight” convergence criteria were applied: maximum force = 1.5 × 10−5 a.u., RMS force = 1.0 × 10−5 a.u., maximum displacement = 6.0 × 10−5, and RMS displacement = 4.0 × 10−5. The grid used for numerical integration in DFT was set to “Ultrafine” with a pruned grid of 99 radial shells and 590 angular points per shell. Harmonic vibrational frequencies were computed analytically at the same level of theory in order to characterize the stationary points as minima, representing equilibrium structures on the potential energy surfaces.Energy decomposition analyses (EDA) were performed for all the mono-substituted complexes using the GGA BP86 density functional39,40 and the TZ2P basis set;41 relativistic effects were considered for the tungsten atom using the ZORA approximation. As originally developed by Morokuma,42 Ziegler and Rauk,43 EDA analysis can provide valuable insight into the nature and strength of a bond. It decomposes the bond dissociation energy (De) between two fragments (A and B) into the interaction energy (ΔEint) and the preparation energy (ΔEprep):
| −De = ΔEint + ΔEprep. | (1) |
| ΔEprep = EA − E0A + EB − E0B. | (2) |
The interaction energy (ΔEint) can be decomposed into three terms: (1) the Pauli exchange repulsion term (ΔEPauli), (2) the electrostatic interaction energy (ΔEelstat) between charge densities of the fragments, and (3) the orbital interaction energy (ΔEorb) which results from orbital mixing of the A and B fragments:
| ΔEint = ΔEPauli + ΔEelstat + ΔEorb. | (3) |
The natural orbitals for chemical valence (NOCV) approach can be utilized to obtain both a qualitative and quantitative picture of the chemical bond (eqn (4)).49 In this approach, the deformation density Δρ(r) is decomposed into pairwise ψk and ψ−k complementary eigenfunctions (NOCVs) with eigenvalues of νk and ν−k that have the same magnitude but opposite sign:
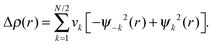 | (4) |
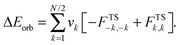 | (5) |
The nature of the bonding in the Lewis base (LB) substituted adducts was also assessed using both natural bonding orbital (NBO)50 and atoms-in-molecules (AIM)51 analyses. NBO population analyses were done at the M05-2X/cc-pVTZ level of theory by using the NBO suite available in Gaussian 09.52 AIM analyses were carried out at the same level of theory using the AIMALL software package.53 Nucleus independent chemical shift (NICS)54 computations were also performed using the gauge-independent atomic orbital (GIAO) method at the center of and 1 Å above the ring at the M05-2X/cc-pVTZ level of theory. All the electronic structure calculations were performed using Gaussian 0952 and ADF 201355 packages.
3 Results and discussion
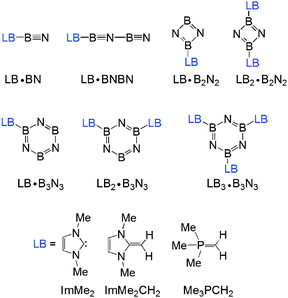
As mentioned in the Introduction, the use of N-heterocyclic carbene (NHC),56–58 N-heterocyclic olefin (NHO)59–66 and Wittig (R3PCR′2)31,67,68 donors is becoming prevalent in main group element chemistry. Accordingly ImMe2, ImMe2CH2 and Me3PCH2 were chosen as donors within the boron nitride adduct series shown in Fig. 1.The isolated (BN)2 and (BN)3 species, as well as higher oligomers, have been the subjects of numerous computational investigations;69–74 monomeric BN has also been studied extensively.75–77 The isolated systems are not the focus of the present study, however, results for the isolated species are reported for the corresponding isomers considered in the complexes for completeness. The isolated (BN)n (n = 1–3) molecules are discussed in the ESI.†
3.1 Geometries of the Lewis base (LB) adducts LB·(BN)n (n = 1–3)
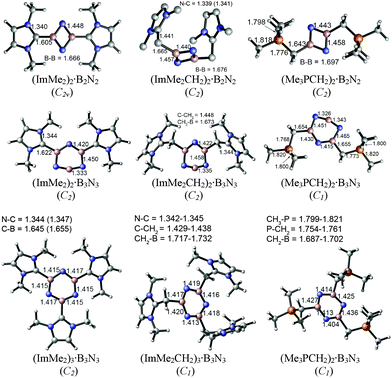
The M05-2X/cc-pVTZ optimized geometries of the mono-ligated boron nitride oligomers, LB·(BN)n (n = 1–3), are depicted in Fig. 2 (LB = ImMe2, ImMe2CH2, and Me3PCH2); see Fig. S1, ESI† for the optimized structures of the isolated species.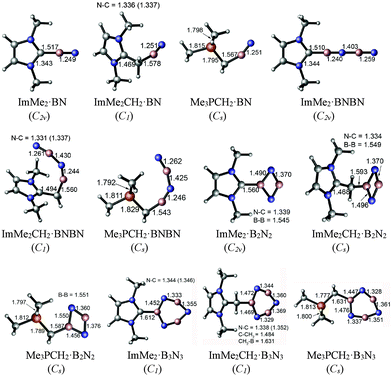 | ||
| Fig. 2 M05-2X/cc-pVTZ optimized geometries including important bond lengths and corresponding symmetries of the mono-substituted adducts in the gas phase. | ||
In each case, the carbon-based donors were bound to electron deficient boron sites, in line with prior adduct formation with amino-boranes (R2N–BH2).78–81 The NHC-bound adducts of the BN chains, ImMe2·BN and ImMe2·BNBN, each adopt linear CImMe2–(BN)n configurations; geometry optimizations initiated with non-linear configurations return to linearity. On the other hand, appreciably bent C–B–N and intrachain N–B–N angles are found within the related ImMe2CH2 and Me3PCH2-capped boron nitride adducts. For example, the C–B–N angles of the ImMe2CH2 substituted BN and BNBN adducts are 162.57° and 152.26°, respectively, and the C–B–N bond angles are 156.50° and 156.32° for the corresponding Me3PCH2 substituted analogues. In general, within the monoadducts, the B2N2 and B3N3 rings adopt planar geometries; the B3N3 rings in ImMe2 and ImMe2CH2 are slightly puckered. The B–N bond lengths involving the donor-bound boron atoms in these B2N2 and B3N3 rings are each ca. 0.12 Å longer than the remaining B–N bonds involving donor-free, two coordinate boron centers. This bond lengthening implies an increase in B–N π-interactions and/or enhanced ionic contribution to the B–N σ-bonds. Within the ImMe2 monoadduct series, the formally dative C–B linkages range from 1.510 Å in the terminal adduct ImMe2·BNBN to elongated values of 1.560 and 1.612 Å in the heterocyclic B2N2 and B3N3 adducts. For comparison, the C–B bond length in the coordinatively saturated amino-borane adduct IPr·BH2–NHDipp (IPr = [(HCNDipp)2C:]; Dipp = 2,6-iPr2C6H3) was determined to be 1.627(4) Å,81 while in the diboryne adduct IPr·B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B·IPr this bond length is 1.491(4) Å (avg.).7 In general the computed C–B bonds in the ImMe2 adducts were shorter by ca. 0.02 to 0.05 Å compared to the corresponding ImMe2CH2 and Me3PCH2 complexes; of note, it has been found that N-heterocyclic carbenes are stronger σ-donors than their N-heterocyclic olefin counterparts (such as IPrCH2).62 The coordination of the Me3PCH2 units to boron leads to a large increase in the ylidic P–C bond length from 1.672 Å in the free ligand to bond length values as long as 1.829 Å in Me3PCH2·BNBN. This observation could be traced to a reduction of H2C → P–C(σ*) hyperconjugative interactions31,82 in Me3PCH2 as the terminal CH2 unit participates in coordination to boron. The same phenomenon can be observed in the case of the ImMe2CH2 adducts: the terminal C–C bond length increases from 1.353 Å in the free ligand to 1.494 Å in the BNBN substituted adduct ImMe2CH2·BNBN. For the isolated ImMe2CH2 and Me3PCH2 ligands, the P–C and C–C bonds have Wiberg bond indices (WBIs) of 1.328 and 1.613, respectively, based on NBO analyses, see section 3.3. These are reduced to 0.906–1.046 and 1.026–1.284, respectively, upon binding of the (BN)x units reflecting the loss of double bond character, and, hence, the corresponding bond elongation.
B·IPr this bond length is 1.491(4) Å (avg.).7 In general the computed C–B bonds in the ImMe2 adducts were shorter by ca. 0.02 to 0.05 Å compared to the corresponding ImMe2CH2 and Me3PCH2 complexes; of note, it has been found that N-heterocyclic carbenes are stronger σ-donors than their N-heterocyclic olefin counterparts (such as IPrCH2).62 The coordination of the Me3PCH2 units to boron leads to a large increase in the ylidic P–C bond length from 1.672 Å in the free ligand to bond length values as long as 1.829 Å in Me3PCH2·BNBN. This observation could be traced to a reduction of H2C → P–C(σ*) hyperconjugative interactions31,82 in Me3PCH2 as the terminal CH2 unit participates in coordination to boron. The same phenomenon can be observed in the case of the ImMe2CH2 adducts: the terminal C–C bond length increases from 1.353 Å in the free ligand to 1.494 Å in the BNBN substituted adduct ImMe2CH2·BNBN. For the isolated ImMe2CH2 and Me3PCH2 ligands, the P–C and C–C bonds have Wiberg bond indices (WBIs) of 1.328 and 1.613, respectively, based on NBO analyses, see section 3.3. These are reduced to 0.906–1.046 and 1.026–1.284, respectively, upon binding of the (BN)x units reflecting the loss of double bond character, and, hence, the corresponding bond elongation.
The M05-2X/cc-pVTZ optimized geometries of the di- and tri-substituted adducts (LB·(BN)n, n = 2 and 3) are depicted in Fig. 3. In general, addition of a second equivalent of Lewis base to the B2N2 and B3N3 units leads to elongation of the average C–B bond length. The C–B bonds increase in length by ca. 0.06–0.09 Å for the B2N2 rings, while a more modest increase of ca. 0.01 to 0.04 Å was noted upon binding two donors to a B3N3 unit. Despite the planar nature of the B2N2 rings, the intraring B–N distances within the bis-adducts (ImMe2)2·B2N2, (ImMe2CH2)2·B2N2, and (Me3PCH2)2·B2N2 all lie within a narrow range of 1.440 to 1.448 Å and suggest the absence of strong B–N π-bonding. To compare, iminoboranes (RB![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) NR′) have B–N triple bond lengths in the range of 1.23 to 1.26 Å,83–86 while the diborylamide anion [Mes2B
NR′) have B–N triple bond lengths in the range of 1.23 to 1.26 Å,83–86 while the diborylamide anion [Mes2B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BMes2]− (Mes = 2,4,6-Me3C6H2), which has significant B
BMes2]− (Mes = 2,4,6-Me3C6H2), which has significant B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond character, has B–N lengths of 1.343(5) and 1.348(5) Å.87 The central B3N3 units in each complex adopt nearly planar arrangements with intraring B–N bond lengths that are typical for short B–N single bonds (1.404 to 1.436 Å). Each of the coordinative C–B distances are slightly longer in (ImMe2)3·B3N3 (1.645 to 1.655 Å) in relation to the values found in the bisadduct (ImMe2)2·B3N3 (1.622 Å). The ylide-bound tris adducts (Me3PCH2)3·B3N3 and (ImMe2CH2)3·B3N3 feature very long C–B bonds of 1.717–1.732 and 1.687–1.702 Å, respectively, suggesting that these species would have reduced stability.
N double bond character, has B–N lengths of 1.343(5) and 1.348(5) Å.87 The central B3N3 units in each complex adopt nearly planar arrangements with intraring B–N bond lengths that are typical for short B–N single bonds (1.404 to 1.436 Å). Each of the coordinative C–B distances are slightly longer in (ImMe2)3·B3N3 (1.645 to 1.655 Å) in relation to the values found in the bisadduct (ImMe2)2·B3N3 (1.622 Å). The ylide-bound tris adducts (Me3PCH2)3·B3N3 and (ImMe2CH2)3·B3N3 feature very long C–B bonds of 1.717–1.732 and 1.687–1.702 Å, respectively, suggesting that these species would have reduced stability.
 | ||
| Fig. 3 M05-2X/cc-pVTZ optimized geometries and symmetries of the di- and tri-substituted adducts in the gas phase (C–H bonds are omitted in the case of (ImMe2CH2)2·B2N2 for clarity). | ||
Very recently, Tai and Nguyen have studied the stability of (ImMe2·B)n (n = 1–6) adducts using quantum mechanical computations with the B3LYP method.88 They attributed the stability of these systems to the degree of π conjugation and aromatic character within the core Bn (n = 3–6) rings. In order to probe the aromaticity in the (BN)x rings, NICS analyses of the free (singlet) B2N2 and B3N3 molecules as well as their adducts were performed using the GIAO method at the M05-2X/cc-pVTZ level of theory. The NICS results were compared to the corresponding values determined at the same level of theory for well known aromatic benzene and anti-aromatic cyclobutadiene molecules (Table S1, ESI†) to examine changes in aromaticity upon binding of Lewis bases. NICS data are sensitive to the position at which they are evaluated and to interference from other parts of the molecule, especially for non-planar compounds.23 The changes in aromaticity/anti-aromaticity are discussed in terms of NICS (1.00)zz values, see Table S1, ESI† for complete NICS data. Interestingly, NICS (1.00)zz values show aromatic character for the free B2N2 and B3N3 molecules (−15.12 and −6.51 ppm, respectively, compared to −31.06 ppm for benzene). However, the free B2N2 loses aromatic character upon binding of one LB ligand (i.e., NICS (1.00)zz values of +2.55, +8.46, and +8.60 ppm for B2N2 complexed with Me3PCH2, ImMe2, and ImMe2CH2, respectively). For the doubly-bound adducts, (LB)2·B2N2, the B2N2 unit becomes significantly anti-aromatic: +12.62, +13.94, and +9.04 ppm for the Me3PCH2, ImMe2, and ImMe2CH2 adducts, respectively (see Table S1, ESI†). On the other hand, B3N3 remains moderately aromatic upon attachment of 1, 2, or 3 equivalents of Lewis base. The NICS (1.00)zz decrease upon attaching two Lewis bases to the B3N3 ring with values of −8.55 and −3.19 ppm for ImMe2 and ImMe2CH2 ligands, respectively, but slightly increases from −6.95 ppm to −6.39 ppm upon attaching the second Me3PCH2 ligand. For the case of the three LB bound adducts, the NICS (1.00)zz values all increase (−2 to −3 ppm) upon attachment of the third ligand (Table S1, ESI†).
3.2 Energies of the Lewis base (LB) bound LB·(BN)n (n = 1–3) adducts
The total stabilization energies and Gibbs free energies of the (BN)n (n = 1–3) molecules upon complexation with the three Lewis bases were computed using the M05-2X/cc-pVTZ level of theory and the results are summarized in Table 1. The sequential stabilization energies, ΔEseq., (ΔE + ZPE)seq., and , which take into account the impact of adding one additional Lewis base to the existing (LB)x·B2N2 and (LB)x·B3N3 (x = 0–2) complexes were also evaluated. Notably, in two separate articles, Jones, Frenking and co-workers have studied the ImMe2- and phosphine-bound Group 13 element complexes along with their possible applications for hydrogen storage.89,90 More specifically, they found that the Gibbs free energies of −29.8 and −45.8 kcal mol−1 for the Me3P and ImMe2 bound BH3 adducts, respectively, at the RI-BP86/def2-TZVPP level of theory; which is very close to the −46.9 kcal mol−1 computed for the latter complex, ImMe2·BH3, at the M06-2X/cc-pVDZ level of theory.91 In another recent study, Sarmah et al. examined complexes of normal and abnormal N-heterocyclic carbenes with Group 13 element based Lewis acids (EX3; E = B, Al, Ga; X = H, F, Cl, OH, NH2, CH3, CF3) and performed corresponding NBO and AIM analyses of the adducts.92 They computed a complexation energy of −49.2 kcal mol−1 at the B3LYP/6-31 + G* level of theory for the ImMe2·BH3 adduct which is close to the values found previously by Frenking, Jones and co-workers89,90 as well as Brown and coworkers.91 The complexation (stabilization) energy associated with the formation of our mono-substituted (BN)n (n = 1–3) adducts was computed to be greater than −100 kcal mol−1 for all species except the B3N3 adducts, where zero-point corrected energies (ΔE + ZPE) are in the range of −57.4 to −69.7 kcal mol−1. The ZPE correction to the electronic energies changes the value of ΔE by ∼4–10 kcal mol−1. The Gibbs free energy differences are also lower than the ZPE corrected values by ∼10–40 kcal mol−1. For the sake of brevity and consistency, the Gibbs free energy differences will be discussed throughout the text. We will comment on the nature of the formed carbene–boron bonds including their degrees of ionic/covalent character based on EDA as well as NBO/AIM analyses. The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) increases for all of the boron nitride species upon binding of the carbon-based ligands; the exceptions to this trend are the B3N3 adducts (Fig. S3, ESI†). For B3N3, the ImMe2 and ImMe2CH2 bound adducts exhibit a modest decrease in the HOMO–LUMO gap upon binding the first ligand (for Me3PCH2 there is a small increase of ≈0.3 eV) and then for all ligands, there is a larger (≈1 eV) decrease upon binding the second and third ligands.
, which take into account the impact of adding one additional Lewis base to the existing (LB)x·B2N2 and (LB)x·B3N3 (x = 0–2) complexes were also evaluated. Notably, in two separate articles, Jones, Frenking and co-workers have studied the ImMe2- and phosphine-bound Group 13 element complexes along with their possible applications for hydrogen storage.89,90 More specifically, they found that the Gibbs free energies of −29.8 and −45.8 kcal mol−1 for the Me3P and ImMe2 bound BH3 adducts, respectively, at the RI-BP86/def2-TZVPP level of theory; which is very close to the −46.9 kcal mol−1 computed for the latter complex, ImMe2·BH3, at the M06-2X/cc-pVDZ level of theory.91 In another recent study, Sarmah et al. examined complexes of normal and abnormal N-heterocyclic carbenes with Group 13 element based Lewis acids (EX3; E = B, Al, Ga; X = H, F, Cl, OH, NH2, CH3, CF3) and performed corresponding NBO and AIM analyses of the adducts.92 They computed a complexation energy of −49.2 kcal mol−1 at the B3LYP/6-31 + G* level of theory for the ImMe2·BH3 adduct which is close to the values found previously by Frenking, Jones and co-workers89,90 as well as Brown and coworkers.91 The complexation (stabilization) energy associated with the formation of our mono-substituted (BN)n (n = 1–3) adducts was computed to be greater than −100 kcal mol−1 for all species except the B3N3 adducts, where zero-point corrected energies (ΔE + ZPE) are in the range of −57.4 to −69.7 kcal mol−1. The ZPE correction to the electronic energies changes the value of ΔE by ∼4–10 kcal mol−1. The Gibbs free energy differences are also lower than the ZPE corrected values by ∼10–40 kcal mol−1. For the sake of brevity and consistency, the Gibbs free energy differences will be discussed throughout the text. We will comment on the nature of the formed carbene–boron bonds including their degrees of ionic/covalent character based on EDA as well as NBO/AIM analyses. The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) increases for all of the boron nitride species upon binding of the carbon-based ligands; the exceptions to this trend are the B3N3 adducts (Fig. S3, ESI†). For B3N3, the ImMe2 and ImMe2CH2 bound adducts exhibit a modest decrease in the HOMO–LUMO gap upon binding the first ligand (for Me3PCH2 there is a small increase of ≈0.3 eV) and then for all ligands, there is a larger (≈1 eV) decrease upon binding the second and third ligands.
| Species | ΔEtota | (ΔE + ZPE)tota | ΔEseq.b | (ΔE + ZPE)seq.b | ||
|---|---|---|---|---|---|---|
| a For the reaction: (BN)n + x·LB → (LB)x·(BN)n (n = 1–3, x = 1–3). b For the reaction: LBx·(BN)n + LB → (LB)x+1·(BN)n (n = 1–3, x = 0–2). | ||||||
| ImMe2·BN | −144.1 | −140.5 | −131.1 | — | — | — |
| ImMe2CH2·BN | −128.6 | −123.8 | −113.5 | — | — | — |
| Me3PCH2·BN | −145.7 | −141.0 | −130.7 | — | — | — |
| ImMe2·BNBN | −129.5 | −124.9 | −114.5 | — | — | — |
| ImMe2CH2·BNBN | −126.6 | −120.6 | −107.7 | — | — | — |
| Me3PCH2·BNBN | −145.3 | −139.7 | −127.0 | — | — | — |
| ImMe2·B2N2 | −118.2 | −114.8 | −103.5 | −118.2 | −114.8 | −103.5 |
| (ImMe2)2·B2N2 | −171.8 | −165.9 | −142.4 | −53.6 | −51.2 | −38.9 |
| ImMe2CH2·B2N2 | −108.6 | −104.0 | −91.9 | −108.6 | −104.0 | −91.9 |
| (ImMe2CH2)2·B2N2 | −143.4 | −136.1 | −109.6 | −34.8 | −32.0 | −17.7 |
| Me3PCH2·B2N2 | −121.8 | −117.7 | −106.6 | −121.8 | −117.7 | −106.6 |
| (Me3PCH2)2·B2N2 | −172.5 | −166.2 | −142.7 | −50.7 | −48.4 | −36.1 |
| ImMe2·B3N3 | −71.5 | −68.7 | −57.6 | −71.5 | −68.7 | −57.6 |
| (ImMe2)2·B3N3 | −122.9 | −117.5 | −92.6 | −51.4 | −48.9 | −35.0 |
| (ImMe2)3·B3N3 | −153.6 | −147.4 | −109.9 | −30.7 | −29.9 | −17.3 |
| ImMe2CH2·B3N3 | −61.0 | −57.4 | −45.4 | −61.0 | −57.4 | −45.4 |
| (ImMe2CH2)2·B3N3 | −97.9 | −91.2 | −65.3 | −36.9 | −33.8 | −19.8 |
| (ImMe2CH2)3·B3N3 | −110.8 | −102.0 | −61.9 | −12.9 | −10.8 | +3.4 |
| Me3PCH2·B3N3 | −72.8 | −69.7 | −58.5 | −72.8 | −69.7 | −58.5 |
| (Me3PCH2)2·B3N3 | −121.1 | −116.3 | −94.1 | −48.4 | −46.6 | −35.6 |
| (Me3PCH2)3·B3N3 | −141.5 | −133.1 | −96.3 | −21.1 | −18.4 | −4.6 |
The free energies associated with the sequential addition of Lewis base equivalents to molecular B2N2 and B3N3 molecules  follow the general trend that it becomes increasingly less favorable to bind multiple donors to these rings (Fig. 4).
follow the general trend that it becomes increasingly less favorable to bind multiple donors to these rings (Fig. 4).
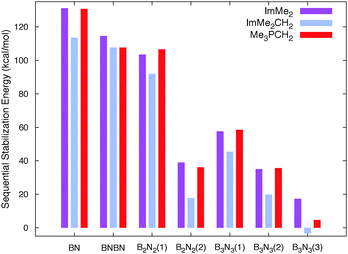 | ||
| Fig. 4 The absolute values of the computed M05-2X/cc-pVTZ sequential Gibbs free stabilization energies (in kcal mol−1) of all the adducts studied in this work. Numbers in parenthesis denote the number of Lewis base molecules attached to the B2N2 and B3N3 molecules. See Table 1 for the values. | ||
This effect can be explained by a decrease in Lewis acidity of the (BN)n rings as electron density is being donated from the carbon-based ligands; this phenomenon can be easily observed from the gradual destabilization of the LUMO energy levels of the B2N2 and B3N3 rings after addition of the Lewis bases (Fig. S3, ESI†). Overall, the binding of subsequent equivalents of Lewis base to the BN rings is exergonic, however, a slightly disfavoured binding event was computed for the formation of the tris adduct (ImMe2CH2)3·B3N3 (+3.4 kcal mol−1), placing this species on the cusp of stability.
3.3 Bonding properties through NBO and AIM analyses
NBO and AIM computations were performed on all (BN)n species including their free and as well as their ligand bound forms at the M05-2X/cc-pVTZ level of theory (see Table 2; for the NBO and AIM analyses of the di- and tri-substituted compounds see Tables S2–S9 and Fig. S2, ESI,† respectively). The computed NBO atomic charges of the boron atoms show a significant decrease (0.5 to 0.6 e−) upon attachment of the Lewis bases. However, the change in charge of the bonding carbon atom upon complexation is much more modest ca. 0.1 to 0.2 (Table 2 and Table S2, ESI†). The charge transfer to the boron center is highest for the ImMe2 and lowest for the Me3PCH2 substituted BN and BNBN adducts. For both B2N2 and B3N3 adducts, the highest charge transfer to the boron atom belongs to the ImMe2 and Me3PCH2 ligands, respectively, but the lowest to the ImMe2CH2 ligand (Table 2). Interestingly, the NBO analysis does not show a significant charge difference for the nitrogen atom attached to the boron center in the LB·BN adducts compared to the isolated species (Tables S2 and S3, ESI†). On the other hand, in LB·BNBN adducts, the terminal nitrogen gains about 0.4–0.8 electrons and the central N atom loses about 0.2–0.4 electrons relative to the free species. For B2N2, the boron loses 0.1–0.2 electrons, while the nitrogen shows a 0.4 electron gain upon complexation; the changes in partial charges of B and N in B3N3 are very modest (0.1–0.2 e−). Therefore, there is stronger electronic communication in the BNBN complexes compared to the other adducts. Also, the Wiberg bond index (WBI) shows the following trend for all the C–B bonds in the mono-substituted adducts: LB·BNBN > LB·BN > LB·B2N2 > LB·B3N3; a rather similar trend can be observed for the AIM electron densities (ρ) of these bonds (Table 2). On the other hand, the trend of the WBI for the B–N bonds is LB·BN > LB·BNBN > LB·B2N2 ≈ LB·B3N3.| Species | q C | q B | q LA | WBIC–B | WBIB–N | ρ(rC–B) | H(rC–B) | ρ(rB–N) | H(rB–N) |
|---|---|---|---|---|---|---|---|---|---|
| ImMe2·BN | +0.203 | +0.230 | −0.524 | 0.944 | 2.622 | 0.179 | −0.175 | 0.300 | −0.324 |
| ImMe2CH2·BN | −0.821 | +0.367 | −0.551 | 0.772 | 2.656 | 0.163 | −0.158 | 0.298 | −0.324 |
| Me3PCH2·BN | −1.046 | +0.382 | −0.565 | 0.872 | 2.604 | 0.166 | −0.162 | 0.299 | −0.325 |
| ImMe2·BNBN | +0.140 | +0.608 | −0.553 | 0.966 | 2.062 | 0.189 | −0.193 | 0.290 | −0.295 |
| ImMe2CH2·BNBN | −0.794 | +0.838 | −0.628 | 0.898 | 2.018 | 0.180 | −0.184 | 0.298 | −0.320 |
| Me3PCH2·BNBN | −1.075 | +0.858 | −0.603 | 0.931 | 1.997 | 0.185 | −0.191 | 0.298 | −0.322 |
| ImMe2·B2N2 | +0.235 | +0.654 | −0.651 | 0.861 | 0.998 | 0.171 | −0.170 | 0.192 | −0.199 |
| ImMe2CH2·B2N2 | −0.738 | +0.783 | −0.622 | 0.801 | 0.969 | 0.166 | −0.168 | 0.189 | −0.194 |
| Me3PCH2·B2N2 | −1.037 | +0.769 | −0.622 | 0.840 | 1.096 (0.846) | 0.167 | −0.168 | 0.204 (0.172) | −0.214 (−0.171) |
| ImMe2·B3N3 | +0.251 | +0.749 | −0.592 | 0.837 | 1.082 | 0.154 | −0.149 | 0.192 (0.192) | −0.192 |
| ImMe2CH2·B3N3 | −0.763 | +0.863 | −0.578 | 0.749 | 1.022 (1.096) | 0.157 | −0.157 | 0.184 (0.185) | −0.183 (−0.182) |
| Me3PCH2·B3N3 | −1.062 | +0.690 | −0.572 | 0.689 | 1.145 (1.143) | 0.154 | −0.152 | 0.194 (0.255) | −0.195 (−0.179) |
Analysis of the energy density (H(r)) at the C–B and B–N bond critical points shows that all of these bonds are predominantly covalent in character (i.e., negative values for H(C–B) and H(B–N)). This data agrees well with the EDA-NOCV results which will be discussed later and points to the existence of covalent bonding between the carbon donors and boron acceptors, which is accompanied by π-backbonding in these systems as previously noted in LB·BX3 (X = H, F, Cl) adducts.93,94 The computed value of the electron density (ρ) for the C–B bonds also shows that its strength decreases in the order of ImMe2 > Me3PCH2 > ImMe2CH2 in the case of the BN, BNBN, and the B2N2 adducts. For the mono-substituted B3N3 adducts, the trend in ρ is ImMe2CH2 > ImMe2 ≈ Me3PCH2 (Table 2) although the differences in ρ are very small (<0.003 e−). The ρ values for the B–N bonds in each of the adducts increase from 0.185 e− to 0.300 e− on going from the B3N3 adducts to the BN adducts, in line with the corresponding increase in WBI values for these species. From the optimized geometries, we found that the C–B bond length increases upon substituting more Lewis bases. AIM data are in agreement with the geometries as, for example, the ρ value for this bond decreases from 0.154 e− in the ImMe2·B3N3 complex to 0.136–0.139 e− in (ImMe2)3·B3N3 while the C–B bond length increases from 1.612 Å to ∼1.650 Å (Fig. S2, ESI,† and Fig. 2 and 3). This trend mirrors the variation in stabilization energies, and indicate that the interaction between the Lewis base and the boron atoms becomes weaker in the presence of added equivalents of donor. The ρ values of the C–B bonds for (ImMe2CH2)n·B3N3 and (Me3PCH2)n·B3N3 also decrease by going from mono- to tri-substituted adducts: from 0.157 e− to 0.120 e− and from 0.154 e− to 0.127 e−, respectively (Fig. S2, ESI†); a trend reflected in the corresponding C–B bond length.
3.4 Energy decomposition analysis (EDA-NOCV)
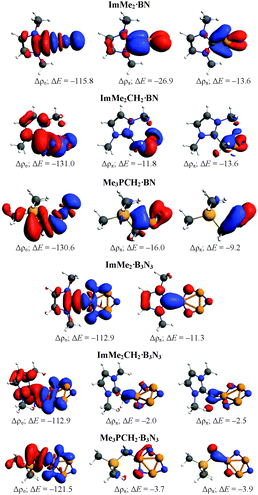
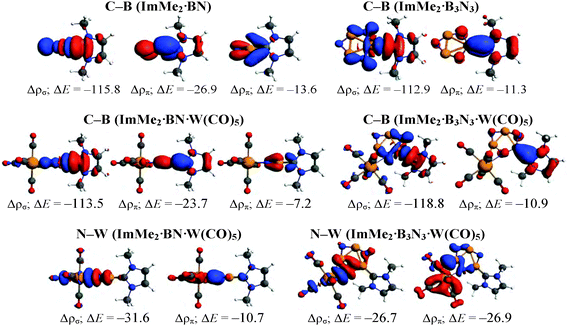
To understand the nature of the bonding between different Lewis bases and the cyclic and acyclic boron nitride oligomers (LB·(BN)n, n = 1–3), EDA-NOCV computations were performed using the GGA BP86 functional and the TZ2P basis set (Table 3). For brevity, we only focus on the most stabilized and least stabilized boron nitride species, i.e., LB·BN and LB·B3N3, respectively. The order of bond dissociation energies (De) for the different Lewis bases follows the series ImMe2 > Me3PCH2 > ImMe2CH2. More specifically, the C–B bonds in the ImMe2 substituted adducts are 4.3–21.7 kcal mol−1 stronger than their Me3PCH2 and ImMe2CH2 analogues. For a given boron nitride adduct, there is a clear correlation between C–B bond length on one hand and bond dissociation energy and Pauli repulsion values on the other hand (Table 3).| ImMe2·BN | ImMe2CH2·BN | Me3PCH2·BN | ImMe2·B3N3 | ImMeCH2·B3N3 | Me3PCH2·B3N3 | |
|---|---|---|---|---|---|---|
| a For deformation densities see Fig. 5. b Percentage contributions to the total attractive interactions (ΔEelstat + ΔEorb) provided in parenthesis. c Percentage contributions to the total orbital interactions ΔEorb provided in parenthesis. | ||||||
| ΔEint | −136.1 | −127.9 | −135.8 | −93.8 | −84.5 | −94.4 |
| ΔEPauli | 211.6 | 187.7 | 215.1 | 203.9 | 173.5 | 191.3 |
| ΔEelstatb | −168.3 | −139.3 | −168.2 | −151.5 | −116.2 | −139.0 |
| (48.4%) | (44.1%) | (47.9%) | (50.9%) | (45.0%) | (48.7%) | |
| ΔEorbb | −179.3 | −176.3 | −182.7 | −146.2 | −141.8 | −146.7 |
| (51.6%) | (55.9%) | (52.1%) | (49.1%) | (55.0%) | (51.3%) | |
| ΔEorb,σc | −115.8 | −131.0 | −130.6 | −112.9 | −118.9 | −121.5 |
| (64.6%) | (74.3%) | (71.5%) | (77.2%) | (83.9%) | (82.8%) | |
| ΔEorb,πc | −40.5 | −33.8 | −25.2 | −16.7 | −4.5 | −7.6 |
| (22.6%) | (19.2%) | (13.8%) | (11.4%) | (3.2%) | (5.2%) | |
| ΔEorb,restc | −19.5 | −11.5 | −26.9 | −16.6 | −18.4 | −17.6 |
| (12.8%) | (6.5%) | (14.7%) | (11.4%) | (12.9%) | (12.0%) | |
| ΔEprep | 1.7 | 15.2 | 8.6 | 26.8 | 31.8 | 31.7 |
| −De | −134.4 | −112.7 | −127.2 | −67.0 | −52.7 | −62.7 |
| R | 1.508 | 1.582 | 1.569 | 1.605 | 1.658 | 1.647 |
The percentage contribution of the electrostatic attraction (ΔEelstat) and orbital interaction (ΔEorb) terms to the total attractive energies are also provided in Table 3. Overall, the orbital interaction makes a significant contribution to the total attractive energy (more than 50%) in all complexes except ImMe2·B3N3 where it is 49.1%. This high contribution indicates that C–B bonds retain substantial covalent character which is in agreement with our NBO/AIM results discussed above. The percentage contributions of the σ and π orbitals to the total orbital interaction are shown in Table 3 while the relevant deformation densities (Δρ) are depicted in Fig. 5. Notably, the ImMe2CH2·B3N3 adduct shows the lowest π-contribution to the C–B orbital interaction (3.2%) amongst the compounds investigated, while in contrast, the ImMe2·BN and ImMe2CH2·BN adducts show the highest degree of π-character with 22.6% and 19.2% contributions, respectively. Thus from both Table 3 and Fig. 5 it is evident that π-backbonding between the boron nitride oligomers and the carbon-based ligands can be quite significant in some cases. The preparation energy (ΔEprep), the difference between the fragment energies in their complexed and free geometries, is the lowest for the ImMe2·BN while it is the highest for the ImMe2CH2·B3N3 adduct (Table 3).
Our −De values for the carbene–boron bonds are significantly more negative than the reported −De values for the H3B·NH3 (−31.9 kcal mol−1) and H3B·NMe3 (−36.2 kcal mol−1) bonds computed at the BP86/TZ2P level of theory.93–95 Tonner and Frenking have shown that replacing ammonia with the ImMe2 ligand to form the ImMe2·BH3 adduct changes the −De to −57.9 kcal mol−1 computed at the same level.96 Also, the amount of π-backbonding in H3B·NH3, Me3N·BH3, and ImMe2·BH3 are 10.1%, 13.0%, and 9.4%, respectively. The values are comparable to each other for all these three systems and are close to the corresponding value for the ImMe2·B3N3 complex (Table 3).
3.5 Stabilization through donor–acceptor interactions
The HOMOs of both the ImMe2·BN and ImMe2·BNBN adducts have π character localized on the (terminal) BN unit as well as on the ImMe2 ring (Fig. 6). On the other hand, the HOMO−4 of both complexes shows a directional lone pair on the terminal nitrogen atom (with some mixing with a B–N σ bond) ready to be captured by a Lewis acid (LA). Herein we consider the previously employed donor–acceptor approach for stabilizing highly reactive heavier Group 14 element dihydrides,14 by using BH3 and W(CO)5 as Lewis acids (LA), and ImMe2 as a Lewis base. The M05-2X optimized Lewis acid/base bound (BN)n complexes as well as their complexation Gibbs free energies are shown in Fig. 7 (for a comparison between their electronic energies and Gibbs free energies see Table S12, ESI†). The C–B bond lengths in the Lewis acid bound adducts ImMe2·BN·LA and ImMe2·BNBN·LA (LA = BH3 and W(CO)5) are in the narrow range of 1.513 to 1.517 Å and are nearly identical to the values found in the Lewis acid free BN and BNBN adducts (1.517 and 1.510 Å, respectively). However, in the donor–acceptor complexes, the B–N bond lengths in BN and BNBN slightly increase by 0.001–0.035 Å showing (modest) π-electron transfer from the B–N bond to the LA molecule. The computed N–B and N–W bond lengths for the BN and BNBN adducts (1.521–1.627 Å and 2.155–2.332 Å, respectively) are shorter than the BP86/TZ2P values for the H3N–BH3 and H3N–W(CO)5 complexes (1.657 and 2.350 Å, respectively) due to a change in hybridization at nitrogen from sp3 to formally sp.95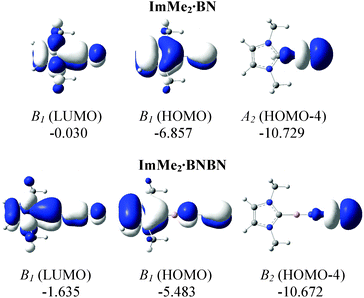 | ||
| Fig. 6 M05-2X/cc-pVTZ computed relevant MOs for the ImMe2·BN and ImMe2·BNBN substituted adducts in the gas phase. Symmetries as well as energies (in eV) are also provided. | ||
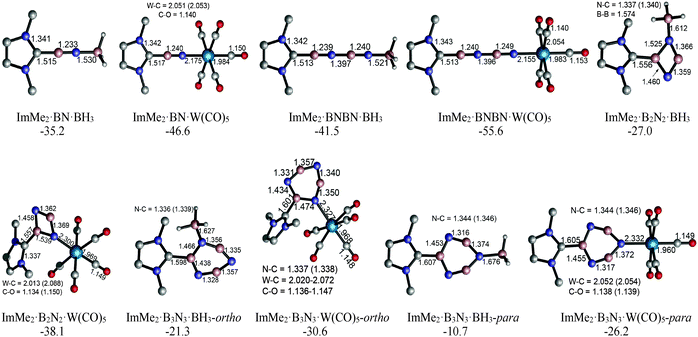 | ||
| Fig. 7 M05-2X/cc-pVTZ optimized geometries and Gibbs free energies of the BH3 and W(CO)5 substituted boron nitride adducts in the gas phase (C–H bonds are omitted for clarity). | ||
Overall, W(CO)5 appears to be a stronger Lewis acid compared to BH3 as the ΔG° values for the former adduct series are more favorable (negative) by 9.3–15.5 kcal mol−1 (Fig. 7); a similar conclusion regarding the relative Lewis acidity of W(CO)5versus BH3 has been made previously.46 These results support our experimental results within the IPr·GeH2·LA complexes (LA = BH3 and W(CO)5) where the W(CO)5 adduct is more stable.25
The impact of complexing ImMe2 and BH3 molecules concurrently to the B2N2 and B3N3 units was studied. More specifically, the Gibbs free energies for the addition of the ImMe2 ligand to the ImMe2·B2N2·(BH3)2 and (ImMe2)2·B3N3·(BH3)3 adducts to form the fully saturated (ImMe2)2·B2N2·(BH3)2 and (ImMe2)3·B3N3·(BH3)3 complexes were found to be −74.2 and −60.9 kcal mol−1, respectively (Table S10, ESI†).
3.6 EDA-NOCV for BN and B3N3 LB/LA substituted adducts
To further study the impact of adding a Lewis acid on stabilizing BN and B3N3 molecules, C–B and N–W bonds in the ImMe2·BN·W(CO)5 and ImMe2·B3N3·W(CO)5 adducts were examined using the EDA-NOCV approach (Fig. 8 and Table 4); their corresponding deformation densities are presented in Fig. 9. | ||
| Fig. 8 Different fragments (shown in green and red colors) utilized for the EDA-NOCV computations of the C–B and N–W bonds in the ImMe2·BN·W(CO)5 and ImMe2·B3N3·W(CO)5 adducts. | ||
| ImMe2·BN·W(CO)5 | ImMe2·B3N3·W(CO)5 | |||
|---|---|---|---|---|
| C–B | N–W | C–B | N–W | |
| ΔEint | −172.6 (−136.1) | −57.6 | −92.0 (−93.8) | −45.1 |
| ΔEPauli | 151.1 (211.6) | 106.5 | 203.9 (220.7) | 113.0 |
| ΔEelstat | −154.4 (−168.3) | −105.7 | −151.5 (−158.1) | −89.8 |
| ΔEorb | −169.4 (−179.3) | −58.4 | −146.2 (−154.6) | −68.3 |
| ΔEorb,σ | −113.5 (−115.8) | −31.6 | −112.9 (−118.8) | −26.7 |
| ΔEorb,π | −30.9 (−40.5) | −10.7 | −16.7 (−10.9) | −26.9 |
| ΔEorb,rest | −25.0 (−19.5) | −16.1 | −16.6 (−24.9) | −14.7 |
Comparing the interaction energies in the BN and the B3N3 adducts reveals that the C–B bond becomes 36.5 kcal mol−1 stronger upon W(CO)5 Lewis acid attachment in the former adduct, but surprisingly it becomes 1.8 kcal mol−1 weaker in the latter (Fig. 7). More specifically, addition of tungsten pentacarbonyl as a Lewis acid significantly decreases the Pauli repulsion portion of the C–B bond; from 211.6 kcal mol−1 in ImMe2·BN to 151.1 kcal mol−1 in ImMe2·BN·W(CO)5 but increases it from 203.9 kcal mol−1 in ImMe2·B3N3 to 220.7 kcal mol−1 in ImMe2·B3N3·W(CO)5 (Fig. 7). Lewis acid attachment also decreases the contribution of electrostatic and orbital interactions by 13.9 and 9.9 kcal mol−1 for ImMe2·BN adduct but it increases them to 6.6 and 8.4 kcal mol−1 for the ImMe2·B3N3 adduct. An inspection of the σ and π orbital interaction components for the C–B bonds in the BN adduct proves that the decrease in ΔEorb upon bonding to the Lewis acid comes mainly from the decrease of π-backbonding rather than σ-donation. Moreover, comparing the percent contribution of the ΔEorb component to the total interaction energy confirms the ionic nature of the N–W bonds (35.6% and 43.2% for the BN and B3N3 adducts, respectively). It is also worthwhile mentioning that no stationary point was found for the BN·W(CO)5 or B3N3·W(CO)5 adducts which points towards the instability of the N–W bond in these species in the absence of the Lewis base.
Given that the free energies of complexation associated with coordinating ImMe2·BN and ImMe2·BNBN units by BH3 and W(CO)5 are quite favorable, Lewis acid coordination can provide even more stability for these highly elusive boron nitride species,83,97,98 and research towards preparing these compounds in the laboratory is ongoing.
4 Conclusions
A variety of acyclic and cyclic (BN)n (n = 1–3) adducts with different Lewis bases including an N-heterocyclic carbene, an N-heterocyclic olefin and a Wittig donor were examined using M05-2X/cc-pVTZ computations. Considering the Gibbs free energies, values greater than −50 kcal mol−1 were found for the complexation energies. From the NBO, AIM and EDA-NOCV approaches, the existence of a polar covalent bond between carbene and boron atom was confirmed in each adduct studied. On the other hand, computed NPA charges illustrated rather significant amounts of charge transfer from the carbene center towards the boron atom upon C–B bond formation. A donor–acceptor strategy, in analogy with our synthesis of heavier group 14 element dihydride adducts,14 show that LB·(BN)nW(CO)5 (n = 1–3) complexes could be experimentally achievable. Finally, both the C–B donor and N–W acceptor bonds were decomposed into their σ and π bonding components in the ImMe2 substituted BN and B3N3 adducts with and without W(CO)5 as a Lewis acid. Analysis of the EDA-NOCV results in these adducts showed that the carbene–boron bonds are stronger in the presence of W(CO)5 as a Lewis acid mainly because of a dramatic decrease in Pauli repulsion rather than an increase in the electrostatic/orbital attraction.Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada (Discovery Grants to A.B. and E.R.), the Canada Foundation of Innovation, and Alberta Innovates-Technology Futures (New Faculty Award to E.R.). L.S. thanks the Undergraduate Research Initiative at the University of Alberta and NSERC (Undergraduate Student Research Award) for financial support. Compute/Calcul Canada is acknowledged for providing computational resources.References
- R. T. Paine and C. K. Narula, Chem. Rev., 1990, 90, 73–91 CrossRef CAS.
- D. Golberg, Y. Bando, C. Tang and C. Zhi, Adv. Mater., 2007, 19, 2413–2432 CrossRef CAS PubMed.
- M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766–3798 CrossRef CAS PubMed.
- K. Watanabe, T. Taniguchi and H. Kanda, Nat. Mater., 2004, 3, 404–409 CrossRef CAS PubMed.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726 CrossRef CAS PubMed.
- H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Science, 2012, 336, 1420–1422 CrossRef CAS PubMed.
- R. Kinjo, B. Donnadieu, M. A. Celik, G. Frenking and G. Bertrand, Science, 2011, 333, 610–613 CrossRef CAS PubMed.
- Y. Wang, Y. Xie, P. Wei, R. B. King, H. F. Schaefer III, P. von R. Schleyer and G. H. Robinson, Science, 2008, 321, 1069–1071 CrossRef CAS PubMed.
- Y. Wang and G. H. Robinson, Dalton Trans., 2012, 41, 337–345 RSC.
- D. J. D. Wilson and J. L. Dutton, Chem. – Eur. J., 2013, 19, 13626–13637 CrossRef CAS PubMed.
- Y. Wang and G. H. Robinson, Inorg. Chem., 2014, 53, 11815–11832 CrossRef CAS PubMed.
- C. Jones, A. Sidiropoulos, N. Holzmann, G. Frenking and A. Stasch, Chem. Commun., 2012, 48, 9855–9857 RSC.
- E. Rivard, Dalton Trans., 2014, 43, 8577–8586 RSC.
- K. C. Mondal, H. W. Roesky, A. C. Stückl, F. Ehret, W. Kaim, B. Dittrich, B. Maity and D. Koley, Angew. Chem., Int. Ed., 2013, 52, 11804–11807 CrossRef CAS PubMed.
- U. Vogel, A. Y. Timoshkin and M. Scheer, Angew. Chem., Int. Ed., 2001, 40, 4409–4412 CrossRef CAS.
- U. Vogel, P. Hoemensch, K.-C. Schwan, A. Y. Timoshkin and M. Scheer, Chem. – Eur. J., 2003, 9, 515–519 CrossRef CAS PubMed.
- K.-C. Schwan, A. Y. Timoskin, M. Zabel and M. Scheer, Chem. – Eur. J., 2006, 12, 4900–4908 CrossRef CAS PubMed.
- C. Marquardt, A. Adolf, A. Stauber, M. Bodensteiner, A. V. Virovets, A. Y. Timoshkin and M. Scheer, Chem. – Eur. J., 2013, 19, 11887–11891 CrossRef CAS PubMed.
- A. Adolf, U. Vogel, M. Zabel, A. Y. Timoshkin and M. Scheer, Eur. J. Inorg. Chem., 2008, 3482–3492 CAS.
- U. Vogel, A. Y. Timoshkin, K.-C. Schwan, M. Bodensteiner and M. Scheer, J. Organomet. Chem., 2006, 691, 4556–4564 CrossRef CAS PubMed.
- A. Y. Timoshkin, Inorg. Chem., 2009, 48, 8145–8153 CrossRef CAS PubMed.
- A. S. Lisovenko and A. Y. Timoshkin, Inorg. Chem., 2010, 49, 10357–10369 CrossRef CAS PubMed.
- K. C. Thimer, S. M. I. Al-Rafia, M. J. Ferguson, R. McDonald and E. Rivard, Chem. Commun., 2009, 7119–7121 RSC.
- S. M. I. Al-Rafia, A. C. Malcolm, S. K. Liew, M. J. Ferguson and E. Rivard, J. Am. Chem. Soc., 2011, 133, 777–779 CrossRef CAS PubMed.
- S. M. I. Al-Rafia, A. C. Malcolm, R. McDonald, M. J. Ferguson and E. Rivard, Angew. Chem., Int. Ed., 2011, 50, 8354–8357 CrossRef CAS PubMed.
- S. M. I. Al-Rafia, A. C. Malcolm, R. McDonald, M. J. Ferguson and E. Rivard, Chem. Commun., 2012, 48, 1308–1310 RSC.
- S. M. I. Al-Rafia, O. Shynkaruk, S. M. McDonald, S. K. Liew, M. J. Ferguson, R. McDonald, R. H. Herber and E. Rivard, Inorg. Chem., 2013, 52, 5581–5589 CrossRef CAS PubMed.
- S. M. I. Al-Rafia, M. R. Momeni, M. J. Ferguson, R. McDonald, A. Brown and E. Rivard, Organometallics, 2013, 32, 6658–6665 CrossRef CAS.
- S. M. I. Al-Rafia, A. C. Malcolm, S. K. Liew, M. J. Ferguson, R. McDonald and E. Rivard, Chem. Commun., 2011, 47, 6987–6989 RSC.
- A. K. Swarnakar, S. M. McDonald, K. C. Deutsch, P. Choi, M. J. Ferguson, R. McDonald and E. Rivard, Inorg. Chem., 2014, 53, 8662–8671 CrossRef CAS PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef.
- T. H. Dunning Jr., J. Chem. Phys., 1990, 90, 1007–1023 CrossRef PubMed.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS PubMed.
- K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 CrossRef CAS.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 CrossRef PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1971, 55, 716–723 CrossRef CAS PubMed.
- K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS PubMed.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1–86 CAS.
- G. TeVelde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Shijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS PubMed.
- G. Frenking, K. Wichmann, N. Fröhlich, C. Loschen, M. Lein, J. Frunzke and V. M. Rayón, Coord. Chem. Rev., 2003, 238, 55–82 CrossRef.
- M. Lein and G. Frenking, Theory and Applications of Computational Chemistry: The First 40 Years, Elsevier, Amsterdam, 2001, pp. 367–414 Search PubMed.
- G. Frenking and F. M. Bickelhaupt, The Chemical Bond. 1. Fundamental Aspects of Chemical Bonding, Wiley-VCH, Weinheim, Amsterdam, 2014, pp. 121–158 Search PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision B.1, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. A. Keith, AIMAll (version 13.01.27), TK Gristmill Software: Overland Park, KS, USA, 2013 Search PubMed.
- P. von R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef.
- ADF2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- C. Jones, Chem. Commun., 2001, 2293–2298 RSC.
- N. Kuhn and A. Al-Sheikh, Coord. Chem. Rev., 2005, 249, 829–857 CrossRef CAS PubMed.
- G. Prabusankar, A. Sathyanarayana, P. Suresh, C. N. Babu, K. Srinivas and B. P. R. Metla, Coord. Chem. Rev., 2014, 269, 96–133 CrossRef CAS PubMed.
- N. Kuhn, H. Bohnen, J. Kreutzberg, D. Bläser and R. Boese, J. Chem. Soc., Chem. Commun., 1993, 1136–1137 RSC.
- A. Fürstner, M. Alcarazo, R. Goddard and C. W. Lehmann, Angew. Chem., Int. Ed., 2008, 47, 3210–3214 CrossRef PubMed.
- A. Dumrath, X.-F. Wu, H. Neumann, A. Spannenberg, R. Jackstell and M. Beller, Angew. Chem., Int. Ed., 2010, 49, 8988–8992 CrossRef CAS PubMed.
- A. C. Malcolm, K. J. Sabourin, R. McDonald, M. J. Ferguson and E. Rivard, Inorg. Chem., 2012, 51, 12905–12916 CrossRef CAS PubMed.
- S. M. I. Al-Rafia, M. R. Momeni, R. McDonald, M. J. Ferguson, A. Brown and E. Rivard, Angew. Chem., Int. Ed., 2013, 52, 6390–6395 CrossRef CAS PubMed.
- Y. Wang, M. Y. Abraham, R. J. Gilliard, Jr., D. R. Sexton, P. Wei and G. H. Robinson, Organometallics, 2013, 32, 6639–6642 CrossRef CAS.
- R. S. Ghadwal, S. O. Reichmann, F. Engelhardt, D. M. Andrada and G. Frenking, Chem. Commun., 2013, 49, 9440–9442 RSC.
- C. J. Berger, G. He, C. Merten, R. McDonald, M. J. Ferguson and E. Rivard, Inorg. Chem., 2014, 53, 1475–1486 CrossRef CAS PubMed.
- H. J. Bestmann, K. Sühs and T. Röder, Angew. Chem., Int. Ed., 1981, 20, 1038–1039 CrossRef PubMed.
- F. Breitsameter, H.-P. Schrödel, A. Schmidpeter, H. Nöth and S. Rojas-Lima, Z. Anorg. Allg. Chem., 1999, 625, 1293–1300 CrossRef CAS.
- H. Xu, C. U. Pittman Jr. and S. Saebø, Struct. Chem., 2013, 24, 1383–1393 CrossRef CAS PubMed.
- W. Cui, C. Wang, J. Shao and X. Zhu, Int. J. Quantum Chem., 2013, 113, 2251–2260 CrossRef CAS PubMed.
- A. Sutjianto, R. Pandey and J. Manuel Recio, Int. J. Quantum Chem., 1994, 52, 199–210 CrossRef CAS PubMed.
- J. M. L. Martin, J. El-Yazal and J.-P. Francois, Chem. Phys. Lett., 1996, 248, 95–101 CrossRef CAS.
- J. M. L. Martin, J. El-Yazal, J.-P. Francois and R. Gijbels, Chem. Phys. Lett., 1995, 232, 289–294 CrossRef CAS.
- J. M. L. Martin, J.-P. François and R. Gijbels, Chem. Phys. Lett., 1992, 193, 243–250 CrossRef CAS.
- J. M. L. Martin, Mol. Phys., 2014, 112, 785–793 CrossRef CAS PubMed.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2006, 125, 144313 CrossRef PubMed.
- J. M. L. Martin, T. J. Lee, G. E. Scuseria and P. R. Taylor, J. Chem. Phys., 1992, 97, 6549–6556 CrossRef CAS PubMed.
- D. P. Curran, A. Solovyev, M. Makhlouf Brahmi, L. Fensterbank, M. Malacria and E. Lacôte, Angew. Chem., Int. Ed., 2011, 50, 10294–10317 CrossRef CAS PubMed.
- K. J. Sabourin, A. C. Malcolm, R. McDonald, M. J. Ferguson and E. Rivard, Dalton Trans., 2013, 42, 4625–4632 RSC.
- N. E. Stubbs, T. Jurca, E. M. Leitao, C. H. Woodall and I. Manners, Chem. Commun., 2013, 49, 9098–9100 RSC.
- S. M. I. Al-Rafia, R. McDonald, M. J. Ferguson and E. Rivard, Chem. – Eur. J., 2012, 18, 13810–13820 CrossRef CAS PubMed.
- A. E. Reed and P. von R. Schleyer, J. Am. Chem. Soc., 1990, 112, 1434–1445 CrossRef CAS.
- P. Paetzold, C. von Plotho, G. Schmid, R. Boese, B. Schrader, D. Bougeard, U. Pfeiffer, R. Gleiter and W. Schäfer, Chem. Ber., 1984, 117, 1089 CrossRef CAS PubMed.
- E. Rivard, W. A. Merrill, J. C. Fettinger, R. Wolf, G. H. Spikes and P. P. Power, Inorg. Chem., 2007, 46, 2971–2978 CrossRef CAS PubMed.
- W. Luthin, G. Elter, A. Heine, D. Stalke, G. M. Sheldrick and A. Meller, Z. Anorg. Allg. Chem., 1992, 608, 147–152 CrossRef CAS PubMed.
- G. Elter, M. Neuhaus, A. Meller and D. Schmidt-Bäse, J. Organomet. Chem., 1990, 381, 299–313 CrossRef CAS.
- R. A. Bartlett, H. Chen, H. V. Rasika Dias, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 1988, 110, 446–449 CrossRef CAS.
- T. B. Tai and M. T. Nguyen, Angew. Chem., Int. Ed., 2013, 52, 4554–4557 CrossRef CAS PubMed.
- N. Holzmann, A. Stasch, C. Jones and G. Frenking, Chem. – Eur. J., 2011, 17, 13517–13525 CrossRef CAS PubMed.
- N. Holzmann, A. Stasch, C. Jones and G. Frenking, Chem. – Eur. J., 2013, 19, 6467–6479 CrossRef CAS PubMed.
- M. R. Momeni, E. Rivard and A. Brown, Organometallics, 2013, 32, 6201–6208 CrossRef CAS.
- S. Sarmah, A. K. Guha and A. K. Phukan, Eur. J. Inorg. Chem., 2013, 3233–3239 CrossRef CAS PubMed.
- C. Loschen, K. Voigt, J. Frunzke, A. Diefenbach, M. Diedenhofen and G. Frenking, Z. Anorg. Allg. Chem., 2002, 628, 1294–1304 CrossRef CAS.
- F. Bessac and G. Frenking, Inorg. Chem., 2003, 42, 7990–7994 CrossRef CAS PubMed.
- F. Bessac and G. Frenking, Inorg. Chem., 2006, 45, 6956–6964 CrossRef CAS PubMed.
- R. Tonner and G. Frenking, Chem. – Eur. J., 2008, 14, 3273–3289 CrossRef CAS PubMed.
- R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877–3923 CrossRef CAS PubMed.
- G. He, O. Shynkaruk, M. W. Lui and E. Rivard, Chem. Rev., 2014, 114, 7815–7880 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: NICS values for all the B2N2 and B3N3 species (Table S1), NBO results for all the species (Tables S2–S9), M05-2X/cc-pVTZ computed gas phase XYZ coordinates for all the structures (Table S10), BP86/TZ2P computed gas phase XYZ coordinates for all the mono-substituted adducts (Table S11), M05-2X/cc-pVTZ computed gas phase complexation energies for the Lewis acid bound adducts (Table S12), M05-2X/cc-pVTZ optimized structures of the isolated species in the gas phase (Fig. S1), AIM results for all the species (Fig. S2), and frontier molecular orbitals of all the studied systems (Fig. S3). See DOI: 10.1039/c5cp01993a |
| This journal is © the Owner Societies 2015 |