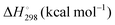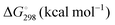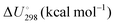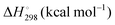Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nanodusty plasma chemistry: a mechanistic and variational transition state theory study of the initial steps of silyl anion–silane and silylene anion–silane polymerization reactions†
Junwei Lucas
Bao
 ,
Prasenjit
Seal
and
Donald G.
Truhlar
*
,
Prasenjit
Seal
and
Donald G.
Truhlar
*
Department of Chemistry, Chemical Theory Center, and Supercomputing Institute, University of Minnesota, Minneapolis, Minnesota 55455-043, USA. E-mail: truhlar@umn.edu
First published on 18th May 2015
Abstract
The growth of nanodusty particles, which is critical in plasma chemistry, physics, and engineering. The aim of the present work is to understand the detailed reaction mechanisms of early steps in this growth. The polymerization of neutral silane with the silylene or silyl anion, which eliminates molecular hydrogen with the formation of their higher homologues, governs the silicon hydride clustering in nanodusty plasma chemistry. The detailed mechanisms of these important polymerization reactions in terms of elementary reactions have not been proposed yet. In the present work, we investigated the initial steps of these polymerization reactions, i.e., the SiH4 + Si2H4−/Si2H5− reactions, and we propose a three-step mechanism, which is also applicable to the following polymerization steps. CM5 charges of all the silicon-containing species were computed in order to analyze the character of the species in the proposed reaction mechanisms. We also calculated thermal rate constant of each step using multi-structural canonical variational transition state theory (MS-CVT) with the small-curvature tunneling (SCT) approximation, based on the minimum energy path computed using M08-HX/MG3S electronic structure method.
1. Introduction
Pioneering research work on plasmas is quite old,1 and research interest continues due to their increasing application in industry, such as fabrication of chips and other microelectronic devices. Dusty plasmas (sometimes called complex plasmas) contain dispersed particulates, which may have various sizes. Methodologies for synthesizing and growing nanosized particles are a major subject of research in material sciences, and plasmas are promising media for such synthesis. Silane-based reactive plasmas2 are widely used in the semiconductor industry, and understanding the mechanisms of growth of dust particles with sizes ranging from a few nanometers to several tens of microns is of great importance in nanodusty plasma chemistry, plasma physics, and engineering, for synthesis of desired nanoparticles, for avoiding the production of undesired ones (contaminants), and for equipment design.In reactive plasmas, beginning with the formation of subnanometer-sized precursor particles nucleated as a result of heterogeneous or homogeneous processes, the generated nanodusty particles will eventually become micron-sized dust by slowly accreting ionic or neutral monomers.3–5 Bhandarkar6–8 and Gallagher9 utilized steady-state homogenous nucleation models to describe the initial stages of the growth of dust particles in pure silane plasma; in these models SiH3− or neutral SiHm10–12 (such as SiH2 radical, SiH4 molecule etc.) triggers the particle growth process, which polymerizes the monomers to silicon hydride clusters with a large number of silicon atoms.
Silicon hydride clustering in plasmas is governed by reactions between cations, anions, and neutrals.7,8 Anion–neutral reactions, involving negative ions trapped by the ambipolar potential in the plasma, are an especially important route for generating nanodusty powder in silane-based chemically active plasmas; these reactions can increase the average residence time of the clusters13 and enable their growth to a critical size. By using time-resolved mass spectrometry, Hollenstein et al. concluded14 that the anionic pathway is the chief route for generating nanosized particles in silane plasmas. Howling and coworkers15 also experimentally observed the existence of anionic species with various sizes ranging from monosilicon anions to nanometer clusters.
Bhandarkar and co-workers8 studied the following two classes of anion–neutral polymerization reactions:
1. Silylene anion–neutral silane reactions:
| Sin+1H2n+2− + SiH4 → Sin+2H2n+4− + H2; |
2. Silyl anion–neutral silane reactions:
| SinH2n+1− + SiH4 → Sin+1H2n+3− + H2. |
| Si2H4− + SiH4 → Si3H6− + H2 | (R1) |
| Si2H5− + SiH4 → Si3H7− + H2 | (R2) |
2. Computational details
Geometry optimizations are carried out with the M08-HX16 exchange–correlation functional and the MG3S17 basis set, and we perform frequency analysis in order to characterize the stationary points as either equilibrium structures (no imaginary frequencies) or transition structures with one imaginary frequency. The MG3S basis set is an all-electron basis set that for silicon and hydrogen atoms is equivalent to Pople's triple-zeta split-valence basis with diffuse functions added on silicon atoms and polarization functions on both silicon and hydrogen atoms, in particular 6-311+G(3d2f,2p).18–20 The global-hybrid meta-GGA density functional M08-HX is chosen based on its superb performances for main-group reaction barrier heights, reaction energies, and thermochemistry.21 The numerical integrations were performed using a grid with 99 radial shells around each atom and 974 Lebedev angular points22 in each shell. All the electronic calculations were carried out with locally modified Gaussian 09 software.23,24In order to help us understand the proposed reaction mechanisms, CM5 charges25 were calculated using the code package CM5PAC.26 The CM5 model involves a parametrized mapping of Hirshfeld charges,27 where the parameters were determined25 to reproduce accurate dipole moments.
Rate constants were calculated by multi-structural canonical variational transition state theory28–31 with small-curvature tunneling32 (MS-CVT/SCT) by using the following equation:
| kMS-CVT/SCT = FMS-TactkCVT/SCT | (1) |
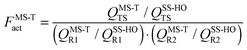 | (2) |
The CVT/SCT thermal rate constants were computed by M08-HX/MG3S with minimum-energy paths (MEPs) calculated for the range from s = −2.0 to +2.0 bohr, where s is the signed distance along the MEP. The generalized normal mode analyses were performed using non-redundant curvilinear coordinates35,36 with a scaling factor of 0.973.37 All the direct dynamics calculations were performed with the Polyrate38 and Gaussrate39 programs.
Energetic results will be reported as relative energies, relative to the reactants of (R1) and (R2): potential energies, V, thermodynamic energies, 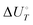 , at temperature T, and standard-state enthalpies,
, at temperature T, and standard-state enthalpies, 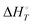 , and standard-state Gibbs free energies,
, and standard-state Gibbs free energies, 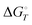 , also at a given temperature. Potential energies contain neither zero point energy (ZPE) nor thermal electronic–vibrational–translational–rotational energies. All partition functions include electronic degeneracies, and vibrational anharmonicity and rotations are included by the MS-T coupled method. Potential energies, enthalpies, and free energies of transition structures relative to reactants are called classical barrier heights, enthalpies of activation, and free energies of activation; the latter two quantities are quasithermodynamic variables since the transition structures exclude the reaction coordinate. As usual, the standard state for gaseous species is taken as an ideal gas at 1 bar partial pressure. Thermodynamic and quasithermodynamic quantities are given for T = 298 K in the paper, and results for T = 0, 400, 500, 600, 700, 800, 900, 1000, and 1500 K are given in the ESI.† At 0 K, the standard-state thermodynamic energy and standard-state enthalpy are equal to the standard-state free energy, and all three reduce to the summation of potential energy and zero-point vibrational energy.
, also at a given temperature. Potential energies contain neither zero point energy (ZPE) nor thermal electronic–vibrational–translational–rotational energies. All partition functions include electronic degeneracies, and vibrational anharmonicity and rotations are included by the MS-T coupled method. Potential energies, enthalpies, and free energies of transition structures relative to reactants are called classical barrier heights, enthalpies of activation, and free energies of activation; the latter two quantities are quasithermodynamic variables since the transition structures exclude the reaction coordinate. As usual, the standard state for gaseous species is taken as an ideal gas at 1 bar partial pressure. Thermodynamic and quasithermodynamic quantities are given for T = 298 K in the paper, and results for T = 0, 400, 500, 600, 700, 800, 900, 1000, and 1500 K are given in the ESI.† At 0 K, the standard-state thermodynamic energy and standard-state enthalpy are equal to the standard-state free energy, and all three reduce to the summation of potential energy and zero-point vibrational energy.
3. Results and discussions
3.1 Proposed mechanisms and potential energetics for silane–silylene/silyl anion polymerization reactions
In order to propose a reasonable reaction pathway, both the thermodynamic and kinetic feasibilities have been taken into consideration. In the present case there is little experimental information to guide the selection of a pathway, so in order to find a chemically reasonable mechanism we mainly relied on exploration of the thermodynamic and kinetic requirements for producing possible intermediates. The mechanism we propose is given in the next two paragraphs. The chemical reasonableness of our proposed reaction mechanism is illustrated by CM5 charge calculations, which will be discussed in Section 3.3.For the silane–silylene anion reaction (R1 with n = 1), the first step is the nucleophilic attack of the disilan-1,1-diyl anion (Si2H4−, doublet state) on SiH4 to produce trisilan-2-yl anion (Si3H7−, singlet state) and hydrogen radical. The second step is the abstraction of H atom from the terminal silyl (–SiH3) group of trisilan-2-yl anion by H radical to produce trisilan-1,2-diyl anion (Si3H6−, doublet state) and molecular H2. The final step is an intramolecular 1,2 hydrogen transfer from one isomer of Si3H6−, i.e., trisilan-1,2-diyl anion, to another one, which is the final product, the trisilan-1,1-diyl anion (singlet state) along with the H2 released in the second step. Total charge is conserved at every step, and all steps are spin-allowed. These reactions are summarized in Table 1, and the potential energy profile for the mechanistic pathway just specified is given in Fig. 1. The classical barrier heights for the first, second and third step are calculated to be 21.1, 1.1, and 23.0 kcal mol−1, respectively.
| Reaction | Step | Chemical equation |
|---|---|---|
| 1 | 1 | Si2H4− + SiH4 → SiH3SiHSiH3− + H |
| 1 | 2 | SiH3SiHSiH3− + H → SiH2SiHSiH3− + H2 |
| 1 | 3 | SiH2SiHSiH3− → SiHSiH2SiH3− |
| 2 | 1 | Si2H5− + SiH4 → Si2H6 + SiH3− |
| 2 | 2 | Si2H6 + SiH3− → SiH2SiH2SiH3− + H2 |
| 2 | 3 | SiH2SiH2SiH3− → SiH3SiHSiH3− |
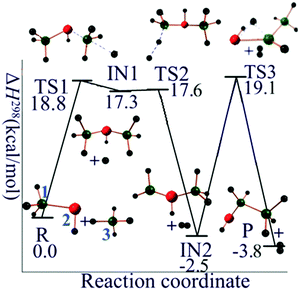 | ||
| Fig. 1 Reaction mechanism profile for SiH4 + Si2H4−. Green balls are silicon atoms, and small black balls are hydrogen atoms. The silicon atoms in red carry one negative formal charge. | ||
For silane–silyl anion reaction (R2 with n = 2), the reaction mechanism starts with the abstraction of Hydrogen atom from SiH4 by disilan-1-yl anion (Si2H5−, singlet state) to form disilane (Si2H6) and silyl anion (SiH3−, singlet state). The second step is the formation of molecular H2 by the reaction of Si2H6 and SiH3− yielding trisilan-1-yl anion (Si3H7−, singlet state). The terminally negatively charged (formal charge) trisilan-1-yl anion could react with another SiH4 molecule and thus generate higher order homologues. In order to get an isomer of Si3H7− with lower energy, an intramolecular 1,2 hydrogen transfer from trisilan-1-yl anion to trisilan-2-yl anion (singlet state) could further occur. The potential energy profile for the mechanistic pathway of reaction R2 is shown in Fig. 2. The classical barrier heights for the first, second, and third step are calculated to be 15.0, 13.0, and 27.4 kcal mol−1, respectively.
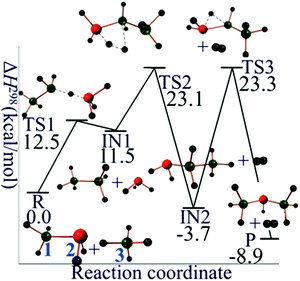 | ||
| Fig. 2 Reaction mechanism profile for SiH4 + Si2H5−. Green balls are silicon atoms, and small black balls are hydrogen atoms. The silicon atoms in red carry one negative formal charge. | ||
3.2 Thermodynamic and quasithermodynamic quantities
The M08-HX/MG3S calculated potential energy change for the overall reaction, Si2H4− + SiH4 → Si3H6− + H2, is −3.1 kcal mol−1, and the reaction enthalpy at 298 K is −3.8 kcal mol−1. The thermodynamic and quasithermodynamic functions are given for T = 298 K in Table 2 and for other temperatures in ESI.†The M08-HX/MG3S calculated potential energy of reaction for the overall reaction, Si2H5− + SiH4 → Si3H7− + H2, is −8.0 kcal mol−1, and the reaction enthalpy at 298 K is −8.9 kcal mol−1. The thermodynamic and quasithermodynamic functions are given for T = 298 K in Table 3 and for other temperatures in ESI.†
3.3 CM5 charge analysis of reaction mechanisms
In order to further understand the proposed reaction mechanism, we computed partial atomic charges on the species in the mechanism. We did this by employing the CM5 charge model to extract partial atomic charges for all silicon-containing species from the Slater determinants employed in the Kohn–Sham density functional calculations. We report the charges in Fig. 3 by taking the charge unit as the charge on a proton; the labels of the silicon atoms in Fig. 3 are consistent with the labels in Fig. 1 and 2 (the numbers 1, 2, 3 marked in blue). Notice that in some cases the labels of the two symmetric silicon atoms are interchangeable (such as Si-1 and Si-3 in intermediate 1 of R1, Si-1 and Si-2 in disilane of R2).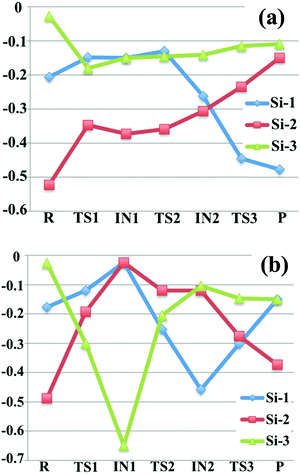 | ||
| Fig. 3 Computed CM5 charges (in the unit of elementary charge) for all the silicon-containing species in reaction (a) SiH4 + Si2H4− (b) SiH4 + Si2H5−. The labels of the silicon atoms are consistent with Fig. 1. | ||
For reaction Si2H4− + SiH4 → Si3H6− + H2, as we can see from Fig. 3(a) that the charges on Si-3 remain almost the same after the first step, while Si-1 and Si-2 have changed considerably. In the starting reactant, SiH3SiH−, Si-2 possesses the most negative charge (−0.52), which is consistent with the formal charge −1 assigned on this silicon in the Lewis structure. In the first step of nucleophilic reaction, a portion of the negative charge of silicon-2 is transferred to the silane silicon (Si-3), which raises the charge carried by Si-2 by 0.18, and lowers the charges on Si-3 by 0.15 in the transition structure TS1. In intermediate 1, SiH3SiHSiH3−, Si-2 still has the most negative charge (−0.37), and the silicon atoms in the two terminal –SiH3 group have the same amount of charge (−0.15) due to the Cs point group symmetry. After the first step, Si-3 remains as part of a –SiH3 group and therefore the CM5 charge on Si-3 is almost unchanged. In the following hydrogen abstraction step, Si-1 loses one bonded hydrogen atom, which lower the charges on Si-1. In the resulting intermediate 2, the amounts of charge carried by Si-1 and Si-2 are very close. After the hydrogen abstraction step, the charges on Si-1 and Si-2 change significantly because of the transfer of the hydrogen from Si-1 to Si-2, which further lower the charge on Si-1 and increases the charges on Si-2. For the overall process, most negative of the charge has been transferred from Si-2 to Si-1, which exchanges the location of the formal charge.
The CM5 charges for Si atoms in the mechanistic pathway of reaction Si2H5− + SiH4 → Si3H7− + H2 are shown in Fig. 3(b). In the first step, SiH3SiH2− abstracts a hydrogen atom from the SiH4 molecule, leading to the formation of SiH3− anion, which significantly lowers the charges on Si-3 (from −0.03 to −0.30 in TS1, and to −0.65 in SiH3− anion) and increases the charges on Si-1 and Si-2. Then SiH3− attacks disilane to become an –SiH3 group, in which the Si-3 partially transferred its negative charge to Si-1 and Si-2 and remains only slightly negatively charged during the remaining steps. In step 2, which eliminates molecular hydrogen, one of the silicon atoms in disilane gains more negative charges than the other one, which introduces a negative formal charge on the terminal silicon atom. The terminal negative charge could be further transferred to the middle silicon, which lower the energy of the molecule and leads to a thermodynamically more stable isomer.
3.4 Multi-structural torsional anharmonicity factors
Multi-structural effects are very important and must be considered in the high temperature range especially for branched silane with long silicon-chain.40 Multi-structural anharmonicity and torsional anharmonicity are included in our calculations by the MS-T coupled method (MS-T(C)). The local periodicities of the –SiH3 groups are assigned as 3. The calculated multi-structural torsional anharmonicity factors for activation of steps 1–3 in reactions R1 and R2 at various temperatures are listed in Table 4. Because of the relatively small sizes of the molecules we considered in the current work, the MS-T factors do not significantly deviate from unity. Nevertheless, we find that ignoring such MS-T corrections can still cause an error ranging from 10–75% in the final predicted thermal rate constants. For instance, at 1500 K, for R1 step 2 of reaction R1, an error of 75% would be introduced by not multiplying the rate constant with a MS-T factor of 4.13; even at room temperature (∼298 K), in the case of step 2 of reaction R2, the multi-structural rate constant differs from the single-structural rate constant by 69%.| T/K | R1 | R2 | ||||
|---|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 1 | Step 2 | Step 3 | |
| 298 | 1.78 | 2.01 | 0.92 | 2.18 | 0.59 | 1.38 |
| 300 | 1.78 | 2.01 | 0.92 | 2.18 | 0.59 | 1.38 |
| 400 | 1.79 | 2.19 | 0.84 | 2.13 | 0.60 | 1.29 |
| 500 | 1.78 | 2.38 | 0.78 | 2.08 | 0.61 | 1.27 |
| 600 | 1.75 | 2.57 | 0.74 | 2.03 | 0.63 | 1.27 |
| 700 | 1.72 | 2.76 | 0.71 | 1.99 | 0.65 | 1.30 |
| 800 | 1.68 | 2.94 | 0.69 | 1.95 | 0.68 | 1.34 |
| 900 | 1.64 | 3.13 | 0.67 | 1.92 | 0.70 | 1.38 |
| 1000 | 1.60 | 3.31 | 0.66 | 1.89 | 0.72 | 1.42 |
| 1500 | 1.44 | 4.13 | 0.61 | 1.78 | 0.84 | 1.65 |
The numbers of distinguishable structures found for Si2H4−, TS1, SiH3SiHSiH3−, TS2, SiH2SiHSiH3−, TS3 and SiHSiH2SiH3− are 1, 2, 1, 2, 2, 2, and 2, respectively for R1; and they are 1, 2, 1, 2, 3, 2 and 1 for Si2H5−, TS1, Si2H6, TS2, SiH2SiH2SiH3−, TS3 and SiH3SiHSiH3−, respectively for R2. For all species with 2 distinguishable structures, the two structures are a pair of energetically equivalent non-superimposable mirror images. For SiH2SiH2SiH3− anion, there is one Cs-symmetry conformer, which is the global minima, and one pair of mirror images, which are 0.76 kcal mol−1 higher in potential energy.
3.5 Thermal rate constants
The computed MS-CVT/SCT rate constants of step 1–3 of net reactions R1 and R2 are listed in Table 5 for various temperatures. Steps 1 and 2 are bimolecular reactions, and step 3 is a unimolecular reaction.| T/K | R1 | R2 | ||||
|---|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 1 | Step 2 | Step 3 | |
| 298 | 6.17 × 10−28 | 1.11 × 10−11 | 7.82 × 10−4 | 6.22 × 10−22 | 5.76 × 10−24 | 1.12 × 10−8 |
| 300 | 7.65 × 10−28 | 1.12 × 10−11 | 1.00 × 10−3 | 7.23 × 10−22 | 6.41 × 10−24 | 1.52 × 10−8 |
| 400 | 2.86 × 10−24 | 1.73 × 10−11 | 1.04 × 101 | 2.37 × 10−19 | 5.11 × 10−22 | 1.48 × 10−3 |
| 500 | 5.03 × 10−22 | 2.79 × 10−11 | 2.30 × 103 | 9.46 × 10−18 | 1.03 × 10−20 | 1.44 |
| 600 | 1.80 × 10−20 | 4.16 × 10−11 | 8.90 × 104 | 1.27 × 10−16 | 9.22 × 10−20 | 1.47 × 102 |
| 700 | 2.57 × 10−19 | 5.90 × 10−11 | 1.22 × 106 | 8.98 × 10−16 | 4.98 × 10−19 | 4.08 × 103 |
| 800 | 2.01 × 10−18 | 7.24 × 10−11 | 8.82 × 106 | 4.16 × 10−15 | 1.93 × 10−18 | 5.02 × 104 |
| 900 | 1.05 × 10−17 | 9.47 × 10−11 | 4.07 × 107 | 1.45 × 10−14 | 5.89 × 10−18 | 3.46 × 105 |
| 1000 | 4.08 × 10−17 | 1.21 × 10−10 | 1.39 × 108 | 4.07 × 10−14 | 1.52 × 10−17 | 1.68 × 106 |
| 1500 | 3.17 × 10−15 | 3.10 × 10−10 | 5.58 × 109 | 1.24 × 10−12 | 3.77 × 10−16 | 2.08 × 108 |
The MS-CVT/SCT rate constants for the forward reactions of steps 1–3 in R1 and R2 are fitted using recently proposed41,42 multi-parameter fitting expressions. In particular, for endothermic reactions (steps 1 of R1 and R2)
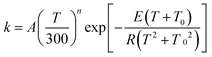 | (3) |
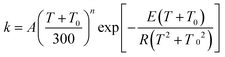 | (4) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
n | T 0 | E | |
|---|---|---|---|---|
| a The units of A for steps 1 and 2 are cm3 molecule−1 s−1 and s−1 for step 3; the parameters T0 and E are in units of K and kcal mol−1 respectively, and n is unitless. | ||||
| R1, step 1 | −36.026 | 4.560 | 113.71 | 13.060 |
| R1, step 2 | −26.272 | 2.530 | 334.20 | 0.532 |
| R1, step 3 | 28.201 | 0.667 | 11.56 | 20.190 |
| R2, step 1 | −31.420 | 4.400 | 112.61 | 8.534 |
| R2, step 2 | −41.694 | 5.100 | 158.70 | 6.924 |
| R2, step 3 | 26.161 | 1.060 | 5.00 | 25.910 |
The computed CVT recrossing transmission coefficients Γ and small-curvature tunneling transmission coefficients κ are shown in Table 7.
| T/K | R1-step 1 | R1-step 2 | R1-step 3 | R2-step 1 | R2-step 2 | R2-step 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Γ | κ | Γ | κ | Γ | κ | Γ | κ | Γ | κ | Γ | κ | |
| 298 | 0.98 | 1.87 | 0.90 | 1.43 | 0.98 | 1.65 | 0.97 | 2.48 | 0.99 | 10.21 | 0.84 | 1.61 |
| 300 | 0.98 | 1.85 | 0.90 | 1.42 | 0.99 | 1.64 | 0.97 | 2.45 | 0.99 | 9.82 | 0.84 | 1.60 |
| 400 | 0.98 | 1.39 | 0.97 | 1.22 | 0.99 | 1.52 | 0.98 | 1.71 | 0.99 | 3.23 | 0.88 | 1.39 |
| 500 | 0.98 | 1.23 | 0.97 | 1.14 | 0.99 | 1.26 | 0.98 | 1.42 | 0.98 | 2.05 | 0.91 | 1.23 |
| 600 | 0.98 | 1.14 | 0.97 | 1.09 | 0.99 | 1.17 | 0.98 | 1.28 | 0.98 | 1.63 | 0.92 | 1.15 |
| 700 | 0.97 | 1.10 | 0.98 | 1.07 | 0.99 | 1.12 | 0.98 | 1.20 | 0.98 | 1.42 | 0.93 | 1.11 |
| 800 | 0.97 | 1.07 | 0.99 | 1.05 | 1.00 | 1.08 | 0.98 | 1.15 | 0.98 | 1.30 | 0.94 | 1.08 |
| 900 | 0.97 | 1.05 | 0.98 | 1.04 | 1.00 | 1.06 | 0.98 | 1.12 | 0.98 | 1.23 | 0.96 | 1.06 |
| 1000 | 0.97 | 1.04 | 0.97 | 1.03 | 1.00 | 1.04 | 0.99 | 1.09 | 0.98 | 1.18 | 0.96 | 1.05 |
| 1500 | 0.96 | 1.01 | 0.95 | 1.01 | 0.99 | 1.01 | 0.98 | 1.04 | 0.97 | 1.08 | 0.96 | 1.02 |
The variational effects for the systems studied in this work are not particularly significant, the largest variational effect occurs at 298 K in the last step of R2, with a recrossing transmission coefficient Γ = 0.84 and a generalized transition state (GT) 0.0579 Å away from the saddle point (s = 0), which is very close to the conventional transition state. The potential energy (VMEP) along the ground-state minimum energy path (MEP) as a function of the reaction coordinate s for step 3 of reaction R2 is shown in Fig. 4(a); the vibrationally adiabatic ground-state potential energy (VGa), which is the sum of VMEP and the zero point energies of all the vibrational modes that are orthogonal to the reaction coordinate, is depicted in Fig. 4(b).
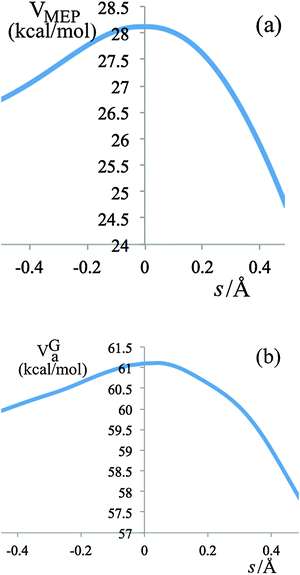 | ||
| Fig. 4 V MEP and VGa for step 3 of reaction R2 as a function of reaction coordinate s, where s is the signed distance along the MEP in isoinertial coordinates scaled to a reduced mass of 1 amu. | ||
Quantum tunneling effect is especially important for light atoms (such as hydrogen) at low temperature range, and the tunneling transmission coefficient gradually converges to unity as the temperature increases. For instance, in the second step of reaction R2, tunneling at 298 K increases the thermal rate constant by an order of magnitude. The SCT tunneling transmission factors at various temperatures for this step are depicted in Fig. 5.
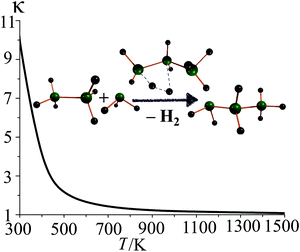 | ||
| Fig. 5 SCT tunneling transmission coefficients (κ) for step 2 of reaction R2 at various temperatures. | ||
3.6 Activation energies
Arrhenius activation energies (kcal mol−1) of steps 1–3 in the reaction pathways of R1 and R2 at various temperatures are listed in Table 8. Temperature-dependence of the activation energy is depicted in Fig. 6. Arrhenius activation energies are calculated as the slopes of the Arrhenius plots (plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k vs. 1/T).43 Based on the fitting formulas we adopted in this paper, Arrhenius activation energies can be derived as follows:
k vs. 1/T).43 Based on the fitting formulas we adopted in this paper, Arrhenius activation energies can be derived as follows: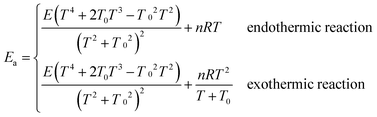 | (5) |
| T/K | R1 | R2 | ||||
|---|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 1 | Step 2 | Step 3 | |
| 298 | 18.8 | 0.9 | 21.7 | 13.1 | 9.5 | 27.4 |
| 300 | 18.8 | 0.9 | 21.7 | 13.2 | 9.5 | 27.4 |
| 400 | 20.3 | 1.5 | 21.8 | 14.4 | 11.4 | 27.4 |
| 500 | 21.1 | 2.0 | 21.8 | 15.2 | 12.6 | 27.5 |
| 600 | 21.8 | 2.5 | 21.8 | 15.9 | 13.6 | 27.6 |
| 700 | 22.4 | 3.0 | 21.8 | 16.6 | 14.6 | 27.7 |
| 800 | 23.1 | 3.5 | 21.8 | 17.3 | 15.5 | 27.9 |
| 900 | 23.8 | 4.0 | 21.9 | 18.1 | 16.4 | 28.1 |
| 1000 | 24.5 | 4.4 | 22.0 | 18.8 | 17.3 | 28.3 |
| 1500 | 28.4 | 6.8 | 22.5 | 22.8 | 21.9 | 29.2 |
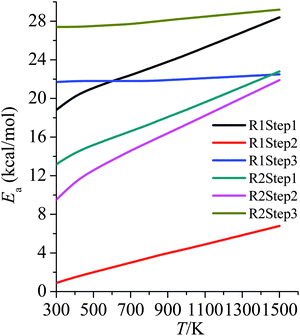 | ||
| Fig. 6 Activation energies (kcal mol−1) at various temperatures (K) for all of the steps in R1 and R2. | ||
Arrhenius activation energies are temperature-dependent due to the deviation of Arrhenius plots from straight lines. The differences between Ea at 298 K and at 1500 K for step 1–3 of R1 and R2 are, respectively, 9.6, 5.9, 0.8, 9.7, 12.4, 1.8 kcal mol−1. Therefore one would make serious errors if one assumed the simple Arrhenius form for the temperature dependences of the rate constants.
3.7 Additional mechanistic steps
The rate constants we report here are in the high-pressure limit. In the high-pressure limit, all of the species are fully thermalized (satisfying the Boltzmann distribution), which means that the rates of the collisional energy transfer steps that maintain the equilibrium of reactants and intermediates are faster than the rates of reaction. To include the deviation from the high-pressure limit would require adding collisional energy transfer steps to the mechanism and considering the rates of reaction as functions of internal energy distributions.44,45Another mechanistic complication is that in real systems there are other species present. Consequently, Si3H7− (intermediate 1 of reaction R1) may collide with SiH4 before it collides with an H atom, and an H atom may collide with SiH2− before it collides with Si3H7−. Similarly, all the other intermediates generated during the reaction mechanisms can possibly collide with other species in real chemically active plasma systems. Thus the present work provides the beginning of a quantitative mechanism by presenting forward and reverse rate constants for six elementary steps in the high-pressure limit, but a full mechanism involves many more reactions.
4. Summary
The present work is dedicated to understanding the reaction mechanisms in the initial steps of the growth of nanoparticles in nanodusty plasmas. We have proposed three-step mechanisms for the initial steps of the SiH4 + Si2H4− and SiH4 + Si2H5− polymerization reactions. CM5 charges were used to interpret the proposed reaction mechanisms, and rate constants for all the reactions were calculated by multi-structural canonical variational transition state theory with the small-curvature tunneling approximation.Acknowledgements
This work is supported by National Science Foundation under award no. CHE11–24752.References
- I. Langmuir, C. G. Found and A. F. Dittmer, Science, 1924, 60, 392–394 CAS
.
- S. E. Beck, S. M. Collins and J. F. O'Hanlon, IEEE Trans. Plasma Sci., 1994, 22, 128–135 CrossRef CAS
.
- L. Boufendi and A. Bouchoule, Plasma Sources Sci. Technol., 1994, 3, 262–267 CrossRef CAS
.
- L. Boufendi and A. Bouchoule, Plasma Sources Sci. Technol., 1993, 2, 204–213 CrossRef
.
- L. Boufendi and A. Bouchoule, Plasma Sources Sci. Technol., 2002, 11, A211–A218 CrossRef CAS
.
- U. R. Kortshagen and U. V. Bhandarkar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 887–898 CrossRef CAS
.
- U. V. Bhandarkar, M. T. Swihart, S. L. Girshick and U. R. Kortshagen, J. Phys. D: Appl. Phys., 2000, 33, 2731–2746 CrossRef CAS
.
- U. V. Bhandarkar, U. R. Kortshagen and S. L. Girshick, J. Phys. D: Appl. Phys., 2003, 36, 1399–1408 CrossRef CAS
.
- A. Gallagher, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2690–2706 CrossRef CAS
.
- Y. Watanabe, M. Shiratani and K. Koga, Phys. Scr., 2001, 89, 29–32 CrossRef
.
- Y. Watanabe, Plasma Phys. Controlled Fusion, 1997, 39, A59–A72 CrossRef CAS
.
- K. Koga, Y. Matsuoka, K. Tanaka, M. Shiratani and Y. Watanabe, Appl. Phys. Lett., 2000, 77, 196–198 CrossRef CAS PubMed
.
- S. J. Choi and M. J. Kushner, J. Appl. Phys., 1993, 74, 853–861 CrossRef CAS PubMed
.
- C. Hollenstein, Plasma Phys. Controlled Fusion, 2000, 42, R93–R104 CrossRef CAS
.
- A. Howling, C. Courteille, J. L. Dorier, L. Sansonnens and C. Hollenstein, Pure Appl. Chem., 1996, 68, 1017–1022 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS
.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384–1388 CrossRef CAS
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS PubMed
.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS PubMed
.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS PubMed
.
- J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 808–821 CrossRef CAS
.
- V. I. Lebedev and L. Skorokhodov, Russian Acad. Sci. Dokl. Math., 1992, 45, 587–592 Search PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D. 01), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed
.
-
Y. Zhao, R. Peverati, K. Yang and D. G. Truhlar, MN-GFM version 5.2 computer program module, University of Minnesota, Minneapolis, 2011 Search PubMed
.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhalr, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS
.
-
A. V. Marenich, C. J. Cramer and D. G. Truhalr, CM5PAC version 2013, University of Minnesota, Minneapolis, 2013 Search PubMed
.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS
.
- T. Yu, J. Zheng and D. G. Truhlar, Chem. Sci., 2011, 2, 2199–2213 RSC
.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS PubMed
.
- B. C. Garrett and D. G. Truhlar, Acc. Chem. Res., 1980, 13, 440–448 CrossRef
.
-
D. G. Truhlar, A. D. Isaacson and B. C. Garrett, in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, 1985, pp. 65–137 Search PubMed
.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D.-H. Lu and D. G. Truhlar, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS
.
- J. Zheng and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 1356–1367 CrossRef CAS
.
-
J. Zheng, S. L. Mielke, K. L. Clarkson and D. G. Truhlar, MSTor computer program, version 2011, University of Minnesota, Minneapolis, MN, 2011 Search PubMed
.
- K. A. Nguyen, C. F. Jackels and D. G. Truhlar, J. Chem. Phys., 1996, 104, 6491–6496 CrossRef CAS PubMed
.
- C. F. Jackels, Z. Gu and D. G. Truhlar, J. Chem. Phys., 1995, 102, 3188–3201 CrossRef CAS PubMed
.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS
.
-
J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Vill_a, I. Rossi, E. L. Coitino, J. Pu, T. V. Albu, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE, version 2010-A, University of Minnesota, Minneapolis, 2010 Search PubMed
.
-
J. Zheng, S. Zhang, J. C. Corchado, Y. Y. Chuang, E. L. Coitiño, B. A. Ellingson and D. G. Truhlar, GAUSSRATE, version 2009-A, University of Minnesota, Minneapolis, 2010 Search PubMed
.
- P. Seal and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 2786–2799 CrossRef CAS PubMed
.
- J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2010, 12, 7782–7793 RSC
.
- J. Zheng, P. Seal and D. G. Truhlar, Chem. Sci., 2013, 4, 200–212 RSC
.
- D. G. Truhlar, J. Chem. Educ., 1978, 55, 309–311 CrossRef CAS
.
- A. Fernández-Ramos, J. A. Miller, S. J. Klippenstein and D. G. Truhlar, Chem. Rev., 2006, 106, 4518–4584 CrossRef PubMed
.
- S. J. Klippenstein, V. Pande and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 528–546 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of M08-HX/MG3S optimized structures of all the species in the proposed reaction mechanisms; thermodynamic and quasithermodynamic quantities at various temperatures. See DOI: 10.1039/c5cp01979f |
| This journal is © the Owner Societies 2015 |