Open Access Article
Open Access ArticleOrbit and spin resolved magnetic properties of size selected [ConRh]+ and [ConAu]+ nanoalloy clusters
Dennis
Dieleman
*a,
Matthias
Tombers
b,
Lars
Peters
a,
Jennifer
Meyer
b,
Sergey
Peredkov
c,
Jeroen
Jalink
a,
Matthias
Neeb
d,
Wolfgang
Eberhardt
e,
Theo
Rasing
a,
Gereon
Niedner-Schatteburg
b and
Andrei
Kirilyuk
*a
aRadboud University Nijmegen, Institute for Molecules and Materials, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands. E-mail: d.dieleman@science.ru.nl; a.kirilyuk@science.ru.nl
bFachbereich Chemie und Forschungszentrum OPTIMAS, TU Kaiserslautern, 67663 Kaiserslautern, Germany
cMax-Planck-Institut für Chemische Energiekonversion, Stiftstr. 34-36, D-45470, Mülheim an der Ruhr, Germany
dHelmholtz-Zentrum Berlin für Materialien und Energie, BESSY II, Albert-Einstein-Strasse 15, 12489 Berlin, Germany
eInst. für Optics and Atomic Physics IOAP, TU-Berlin, Strasse des 17. Juni 135, 10623 Berlin, Germany
First published on 19th June 2015
Abstract
Bi-metallic nanoalloys of mixed 3d–4d or 3d–5d elements are promising candidates for technological applications. The large magnetic moment of the 3d materials in combination with a high spin–orbit coupling of the 4d or 5d materials give rise to a material with a large magnetic moment and a strong magnetic anisotropy, making them ideally suitable in for example magnetic storage devices. Especially for clusters, which already have a higher magnetic moment compared to the bulk, these alloys can profit from the cooperative role of alloying and size reduction in order to obtain magnetically stable materials with a large magnetic moment. Here, the influence of doping of small cobalt clusters on the spin and orbital magnetic moment has been studied for the cations [Co8−14Au]+ and [Co10−14Rh]+. Compared to the undoped pure cobalt [CoN]+ clusters we find a significant increase in the spin moment for specific CoN−1Au+ clusters and a very strong increase in the orbital moment for some CoN−1Rh+ clusters, with more than doubling for Co12Rh+. This result shows that substitutional doping of a 3d metal with even just one atom of a 4d or 5d metal can lead to dramatic changes in both spin and orbital moment, opening up the route to novel applications.
1 Introduction
The study of finite size effects on magnetism has been an active research theme for years. It is widely known that reducing the dimensionality of a system gives rise to a generally much higher magnetic moment than in the bulk system.1,2 This is attributed to a reduced coordination number of the surface atoms for the smaller system, leading to less quenching of the magnetic moment. This increase of the magnetic moment is experimentally observed for the smallest possible systems, namely clusters consisting only out of a few atoms. Initially this was measured using Stern–Gerlach deflection, where only the total magnetic moment is resolved,3 but recently also using X-ray Magnetic Circular Dichroism (XMCD), which is sensitive to the spin and orbital magnetic moments.4,5Not only does this enhancement of the magnetic moment occur for the 3d materials that are ferromagnetic in the bulk (Fe, Co, Ni).3–5 It is even shown that 4d or 5d systems, which are non-magnetic in the bulk, can show a substantial magnetic moment when they are reduced in size. This is true for example in 4d rhodium clusters.6,7 It has also been shown that alloying 3d and 4d metals can induce a magnetic moment on the 4d atoms. For CoRh this is observed experimentally (in the bulk,8 for clusters on a Xe matrix9 and for chemically prepared nanoparticles in a polymer matrix10–12). Also there has been a certain amount of theoretical work for CoRh, some of which included spin–orbit coupling (SOC)10,11,13–15 but most without.16–21 The reason that most work does not fully include SOC is that modern calculations still have difficulties properly accounting for the degree of quenching of orbital moments. However, the inclusion of SOC is important for comparison with the observed effects in this work. Specifically it is necessary in order to obtain values for the orbital magnetic moments in calculations.
We have studied the spin and orbit resolved magnetic moments of small (8 ≤ N ≤ 14) cobalt clusters doped with either one rhodium or one gold atom using XMCD on the L-edge of cobalt. We directly compare with the undoped cobalt clusters measured earlier,4 this enables us to isolate the specific change that alloying introduces on the magnetic properties. We observe in certain cases dramatic changes in both the spin and orbital moments upon doping the cobalt clusters. In the case of going from Co13+ to Co12Rh+ the orbital moment for example increases with more than 150%, indicating that even the substitution of one atom can have enormous consequences.
2 Experimental details
The experimental setup that we used is described in detail by Peredkov et al.4,22 In short we used X-ray Magnetic Circular Dichroism (XMCD) at the L2 and L3 absorption edge of cobalt to probe the magnetization in a spin and orbit resolved fashion.2.1 Setup
Clusters are produced using pulsed laser vaporisation of a rotating thin foil which has a composition of either Co90Rh10 or Co90Au10. The ablation laser is a Nd:YAG-laser which is frequency doubled to emit at 532 nm with a repetition rate of 20 Hz and an energy per pulse of about 10 mJ. A piezo-valve pulses (≈40 μs) a helium carrier gas jet at a backing pressure of ≈15 bar into the source chamber. The Nd:YAG laser ablates atoms from the target foil into this helium pulse, which then condense into clusters of different charges and with a broad mass distribution. This cluster–helium mixture is then guided through a skimmer and through ion-optics in a manner that in our case only selects the positively charged cation clusters. Subsequently the clusters are steered by 90° by an electrostatic quadrupole deflector and guided via ion-optics into a Fourier-Transform Ion Cyclotron Resonance (FT-ICR) ion trap. This FT-ICR serves multiple purposes of ion-trapping, mass selection, X-ray interaction region and mass detection. For these purposes the trapping cell is placed in a superconducting magnet which generates a homogeneous field of 7 T at the interaction region. The direction of the magnetic field is parallel to the initial cluster propagation and anti-parallel to the incoming X-ray beam. The ion trap is filled with around 20 clusters packages generated by 20 shots of the Nd:YAG laser and the unwanted masses are subsequently ejected. Once mass selection is achieved, a cryogenic He pulse is allowed to interact with the clusters. Through collisional cooling the clusters will achieve a thermal equilibrium at about 20 K. All experiments were performed at the GAMBIT setup at the UE52-PGM beamline at the Helmholtz-Zentrum Berlin.2.2 XMCD spectroscopy on clusters
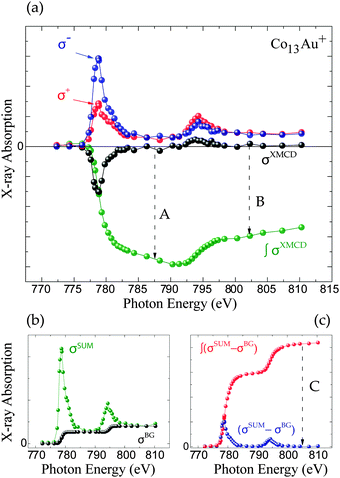
In bulk materials the interaction of X-rays with samples can directly be monitored by looking at the change that the propagating light undergoes by for example being absorbed by a target. For free clusters in the gas phase this is not possible due to the low density of the clusters, which produce thus no observable change in the intensity of the X-rays upon absorption by the clusters. Therefore we need to employ an action-spectroscopy technique. In our case this means we look at the generated product ions after the interaction with the X-ray beam, as detailed in Fig. 1. By counting the obtained fragments as a function of the X-ray energy and polarization we can reconstruct the X-ray absorption spectra (XAS). From these XAS we extract the integral parameters A, B and C as shown in Fig. 2 and calculate the spin and orbital magnetization using the Sum rules:23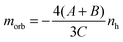 | (1) |
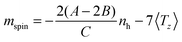 | (2) |
 | ||
| Fig. 1 The action spectroscopy method used to obtain the XMCD signal. (a-I) First a cation is allowed to interact with the X-ray, depending on the XMCD resonance conditions this will excite a 2p electron towards the 3d band, leaving a hole behind in the 2p shell. With Auger decay this hole will be filled up with an intermediate electron, releasing energy in the process. (a-II) This energy can trigger an avalanche of more electrons being excited, subsequently leading to ejections of electrons, leaving the cation more unstable. (a-III) This instability leads to the explosion or fragmentation of the cluster. (b) The fragments can be detected in the mass spectrum and counted as function of X-ray energy to give a X-ray absorption spectrum (XAS), see Fig. 2. | ||
3 Results
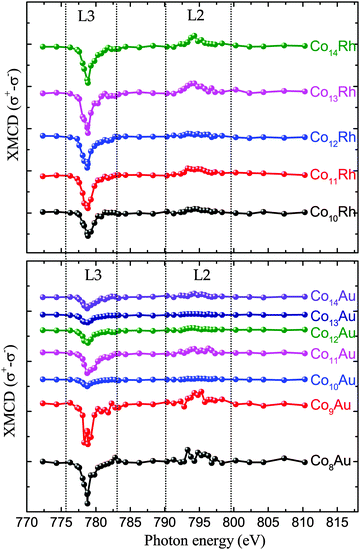
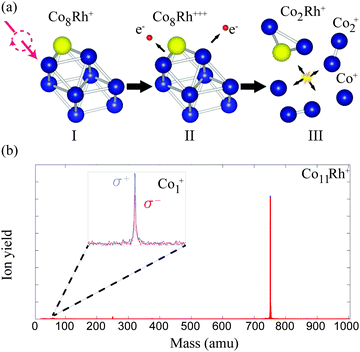
All measured XMCD spectra are plotted in Fig. 3. All of the spectra clearly show the two resonant transitions, on both the L3 and L2 edge. Some features can be pointed out specifically. For ConRh it can clearly be seen that the XMCD signal on the L2 edge around 795 eV is changing strongly with cluster size. Especially for Co12Rh the XMCD signal at the L2 edge almost disappears. Using the sum rules (2) it can be understood that relatively speaking, the lower the L2 dichroism signal is, the lower (more negative) B will be, indicating an increased orbital moment for this cluster.The main results are shown in Fig. 4. Here our obtained results are compared with the magnetic moments of the pure cobalt clusters from Peredkov et al.4 The results are already temperature corrected using the Langevin function. To compare with the results from Peredkov et al., as was done before by Langenberg et al., we have reanalysed their data in a way that does not assume a decoupling of the spin and orbital moments, contrary to their original interpretation. From the figure it becomes clear that not all clusters show a significant deviation from their undoped counterpart. Also, doping with either Rh or Au does not always systematically increase or decrease and μspin. For example, whereas for Co8Au+ the gold atom introduces a decrease of μorb, for Co12Au+ the gold doping slightly increases μorb. The influence of doping is thus strongly dependent on the cluster size. It therefore becomes necessary to consider each individual cluster size.
 | ||
| Fig. 4 The Langevin scaled spin (full symbols) and orbital (empty symbols) magnetic moments of CoNRh+ (red triangles) and CoNAu+ (blue squares), assuming nh = 2.5. Also plotted are the results obtained for pure cobalt clusters obtained by Peredkov et al.4 using the same setup as this work (black circles). | ||
 | ||
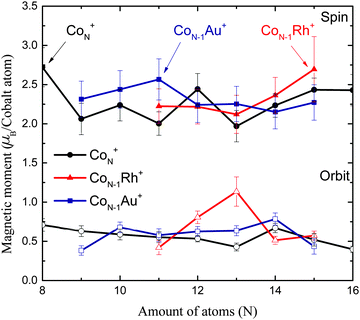
| Fig. 5 Percentile increase of the magnetic moments compared to the pure Co clusters measured by Peredkov et al.4 | ||
For Co11Rh+ the spin moment overlaps with Co11Au+ but the orbital moment is significantly enhanced, with 51% compared to Co12+, starting an increase of orbital moment which will have it’s maximum for Co12Rh+. It is not clear where this strong increase of the orbital moment comes from. We will discuss possible reasons later on, in the context of an even stronger increase for Co12Rh+. Also for this size there have been no calculations with spin–orbit coupling fully included to compare with.
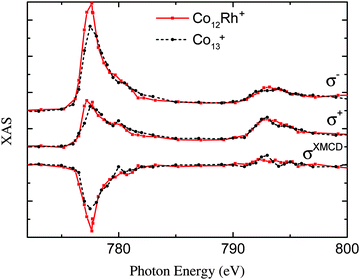
We can see this difference already originate in the XAS spectra as visualized in Fig. 6. This most visible change is that the σ−of the L3 edge is much lower for Co13+ than for Co12Rh+. This gives a larger XMCD signal for this edge as indicated in the graph. For the positive XAS the difference is less pronounced. This in combination with an already low XMCD signal on the L2 edge, as pointed out before, indicates a high orbital moment.
In Fig. 7 some geometries of Co13 and Co12Rh are depicted. The icosahedron geometry for Co13 is found from density function theory (DFT) calculations that we did28 using the RevTPSS functional without spin–orbit coupling fully included. The found geometries are subsequently compared with experimental data using vibrational spectroscopy in order to determine the geometrical ground state. We are aware that theoretical studies exist that find a preference for a hexagonal growth pattern in Co clusters,32 and specifically a slight preference for hexagonal geometry for Co1333 but in those studies there has been no comparison with experimental data. The geometry for Co12Rh is taken with permission from Aguilera-Granja et al.,21 calculated using the PBE form of GGA, without calculating the orbital magnetic moments.
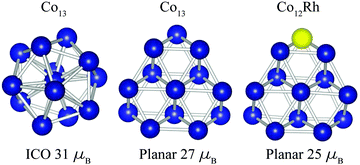 | ||
| Fig. 7 Geometry of the Co13 cluster as calculated in our group by Jalink et al.28 (left and middle) compared with Co12Rh as calculated by Aguilera-Granja et al.21 (right). | ||
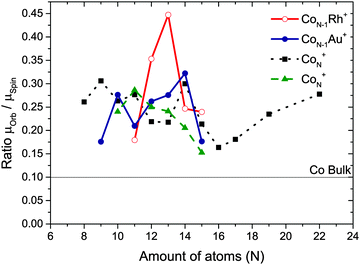 | ||
| Fig. 8 The ratio of the orbital and spin magnetic moment μorb/μspin compared with Peredkov et al.4 (black squares) and Langenberg et al.25 (green triangles). | ||
When we consider the absolute increase of orbital moment per atom, from 0.43 ± 0.05 μB per atom to 1.14 ± 0.19 μB per atom, taking the error bars into account this would give a minimum increase of 0.47 μB per atom. This strong increase in orbital moment can either be attributed to a polarization of the Co atoms surrounding the dopant Rh atom or to a dopant induced geometry change.
3.1 Comparison with previous XMCD experiments
As stated before, we consider the ranges of [Co8−14Au]+ and [Co10–14Rh]+, always attaching one single dopant atom to a cobalt cluster. Recently, Langenberg et al. remeasured XMCD data for pure Co clusters.25 They found that the spin moments they obtain are larger than the spin moments obtained for the same clusters by Peredkov et al. In fact, their range of spin moments is closer to our results for CoNAu+ clusters. However, as also pointed out before,25 the orbit/spin ratio is a more reliable way of comparing data because this will cancel out possible errors in for example the degree of circular polarization and the number of occupied 3d states. In Fig. 8 it is shown that the μorb/μspin ratio obtained by Peredkov et al. and Langenberg et al. are comparable. Is has to be noted that since our results are measured using the same experimental setup as Peredkov et al.4 used, our results can be directly compared to their measurements for pure cobalt clusters even when the results from Langenberg et al. do not match completely.3.2 How can doping influence the magnetic properties?
As briefly discussed later, theory cannot yet give a full explanation of the magnetic properties in small transition metal clusters. We are therefore forced to form models based on more qualitative arguments.In general the magnetic moment of a doped material can change in three ways. First, the dopant atom can have a very high magnetic moment, which it can either intrinsically posses, or it can be polarized by the parent atoms. Second, the dopant may be a source of magnetic polarization on the neighbouring parent atoms. This it can do by hybridization with the parent orbitals, which can either lead to a different orbital moment or to a change in the spin moment. Third, the dopant can energetically favour a different ground state isomer geometry, which can lead to different magnetic properties.
The first option, the magnetic moment on the dopant atoms itself has been studied for example by Harp et al.8 Here they discuss doping a bulk transition metal with a different transition metal. They note that the magnetic polarization on the impurity atoms depends on its d-band occupation number. When the occupation number of the dopant is the same or higher than the parent material, it generally polarizes ferromagnetically and when it’s lower, it will normally polarize anti-ferromagnetically. In our case we study the parent material cobalt, with the same d-band occupation number as the dopant rhodium, hence rhodium is expected to magnetize ferromagnetically in a cobalt environment. For gold the situation is similar.
In particular this ferromagnetic coupling of the dopant is calculated by Aguilera-Granja et al.21 They find for Co12Rh an induced spin moment on the Rh atom of 1.09 μB per atom while for Rh13 a spin moment of 0.69 μB per atom is found. This shows that the magnetic polarization increases when the Rh atom is in a Co environment. In our measurements we cannot say anything about the polarization of the Rh atom since we just probe the L-edge of the cobalt atoms, providing exclusively information about the magnetic properties around these atoms.
Possible origins for the strong increase in the orbital moment for substitutional doping with Rh have thus to be found in an induced magnetic polarization on the Co atoms or in a possible geometry change. For the latter it is known19 that the strong spin–orbit coupling in the 4d and 5d metals can influence the geometry of the system. Since orbital quenching is a purely geometric effect, a drastic change in geometry could in principle lead to a dramatic enhancement of the orbital moment. An induced magnetic polarization of the 3d atoms by a 4d or 5d material has been observed before in both experiment and calculations.14,27 Proposed mechanisms for this can be found in hybridization of the 3d Co bands with the dopant 4d/5d bands as well as in the increased MAE at the interface between the Co and Rh/Co atoms.
4 Theoretical models
So far for Co12Rh, to the best of our knowledge, only Aquilera-Granja et al. have calculated this cluster, see Fig. 7. For Co12Rh Aquilera-Granja et al. find a spin moment of 1.92 μB per atom,21 and for Co13μspin = 2.08 μB per atom, which is thus a small decrease in the spin moment when doped with Rh. These spin magnetic moments are comparable to our measured moments of 2.12 μB per atom for Co12Rh+ and 2.25 μB per atom for Co12Au+. The orbital moments were unfortunately not calculated by Aquilera-Granja et al.In an attempt to reproduce the giant increase in the orbital moment when going from Co13+ to Co12Rh+ we have performed calculations using various approaches. Starting points for these calculations were the non spin–orbital coupled density function theory (DFT)34,35 calculations that we have performed earlier for a range of cobalt clusters28 and which are compared with their experimentally obtained vibrational spectra in order to confirm their ground state geometry. We have calculated the orbital and spin moments using both the generalized gradient approximation (GGA) functional defined by Perdew–Burke–Ernzerhof (PBE)36 and the GGA + U method. DFT in its GGA form is derived in the limit of a nearly uniform electron gas, which usually works well for itinerant electron systems. However, for electrons with a more localized character, i.e. strongly correlated electrons, the electron–electron interaction is not properly described by GGA. We have tried to treat electron correlations on a higher level, i.e. via the GGA + U method. This method treats on-site Coulomb interactions within the static mean field approximation. One would thus expect that the description of the orbital moment improves in GGA + U with respect to plain GGA.
We found however that both GGA and GGA + U approaches cannot produce orbital moments comparable with the experiment. Both methods underestimate the experimental values. See for a full discussion our upcoming publication.37 In short, most likely the reason for this underestimation is related to the way how electron correlation effects are taken into account. Broadly speaking when looking in terms of energy ordering, Hund’s first rule treats the spin moments on a larger energy scale than the second rule, which is related to the orbital moment. The smaller the differences in energy become, the more important it becomes to properly take effects like electron correlation into account as the introduced error will be more important. This also means that if the electron correlation for a certain cluster size increases, the calculations will be less accurate. This can possibly also explain the discrepancies that we observed. In the future it would thus be highly interesting to see whether a more sophisticated method like DFT in combination with the dynamical mean field theory (LDA + DMFT)38 would be able to produce orbital moments in agreement with experiment.
5 Conclusions
In conclusion, we have measured the orbital and spin magnetic moments of cobalt clusters which are substitutionally doped with either a rhodium or a gold atom. Comparing with pure cobalt clusters the spin and orbital moments are either increased or decreased in a way that is very dependent on the specific cluster size, no general trend can be extracted. For some sizes the changes are very extreme, for example in Co12Rh+ the orbital moment more than doubles compared to the pure cobalt clusters. The origins hereof remain to be clarified. In case of the Co12Rh+ cluster we propose that only a change of geometry or electronic structure compared to the pure Co13+ cluster can explain the strong increase. This transition could be brought about by the strong spin–orbit coupling present in the Rh atom. In the future our next step will be to compare these experimental results with the computationally expensive LDA + DMFT method.Acknowledgements
We thank the Helmholtz-Zentrum Berlin for the allocation of synchrotron radiation beamtime and the excellent support from the beamline scientists. This work has been supported by the Deutsche Forschungsgemeinschaft in the framework of the Transregional Collaborative Research Center SFB/TRR 88 “3MET.de”. We also acknowledge support from the Stichting voor Fundamenteel Onderzoek der Materie (FOM) and the EC FP7 contributions under Grant No. 257280 (Femtomagnetism) and NMP-3-LA-2010-246102 (IFOX).References
- Y.-W. Jun, J.-W. Seo and J. Cheon, Acc. Chem. Res., 2008, 41, 179–189 CrossRef CAS PubMed.
- H. Haberland, Clusters of Atoms and Molecules, Springer Berlin Heidelberg, Berlin, Heidelberg, 1994, vol. 52, p. 422 Search PubMed.
- I. M. Billas, A. Châtelain and W. A. de Heer, Science, 1994, 265, 1682–1684 CAS.
- S. Peredkov, M. Neeb, W. Eberhardt, J. Meyer, M. Tombers, H. Kampschulte and G. Niedner-Schatteburg, Phys. Rev. Lett., 2011, 107, 233401 CrossRef CAS.
- M. Niemeyer, K. Hirsch, V. Zamudio-Bayer, A. Langenberg, M. Vogel, M. Kossick, C. Ebrecht, K. Egashira, A. Terasaki, T. Möller, B. v. Issendorff and J. T. Lau, Phys. Rev. Lett., 2012, 108, 057201 CrossRef CAS.
- A. Cox, J. Louderback, S. Apsel and L. Bloomfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 12295–12298 CrossRef CAS.
- A. Cox, J. Louderback and L. Bloomfield, Phys. Rev. Lett., 1993, 71, 923–926 CrossRef CAS.
- G. Harp, S. Parkin, W. O’Brien and B. Tonner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 37–40 Search PubMed.
- V. Sessi, K. Kuhnke, J. Zhang, J. Honolka, K. Kern, C. Tieg, O. Šipr, J. Minár and H. Ebert, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 184413 CrossRef.
- M. Muñoz Navia, J. Dorantes-Dávila, D. Zitoun, C. Amiens, B. Chaudret, M.-J. Casanove, P. Lecante, N. Jaouen, A. Rogalev, M. Respaud and G. M. Pastor, Faraday Discuss., 2008, 138, 181 RSC.
- M. Muñoz-Navia, J. Dorantes-Dávila, D. Zitoun, C. Amiens, N. Jaouen, A. Rogalev, M. Respaud and G. M. Pastor, Appl. Phys. Lett., 2009, 95, 233107 CrossRef PubMed.
- D. Zitoun, M. Respaud, M.-C. Fromen, M. Casanove, P. Lecante, C. Amiens and B. Chaudret, Phys. Rev. Lett., 2002, 89, 037203 CrossRef.
- H. K. Yuan, H. Chen, A. L. Kuang, B. Wu and J. Z. Wang, J. Phys. Chem. A, 2012, 116, 11673–11684 CrossRef CAS PubMed.
- M. Muñoz Navia, J. Dorantes-Dávila and G. M. Pastor, J. Phys.: Condens. Matter, 2004, 16, S2251–S2256 CrossRef.
- M. Muñoz Navia, J. Dorantes-Dávila, M. Respaud and G. M. Pastor, Eur. Phys. J. D, 2009, 52, 171–174 CrossRef PubMed.
- S. Dennler, J. Morillo and G. Pastor, Surf. Sci., 2003, 532–535, 334–340 CrossRef CAS.
- S. Dennler, J. Morillo and G. M. Pastor, J. Phys.: Condens. Matter, 2004, 16, S2263–S2272 CrossRef CAS.
- L. E. Daz-Sánchez, J. Dorantes-Dávila and G. M. Pastor, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 134423 CrossRef.
- E. Berlanga-Ramrez, F. Aguilera-Granja, J. Montejano-Carrizales, A. Daz-Ortiz, K. Michaelian and A. Vega, Phys. B, 2004, 354, 278–281 CrossRef PubMed.
- J. Lv, X. Bai, J.-F. Jia, X.-H. Xu and H.-S. Wu, Phys. B, 2012, 407, 14–21 CrossRef CAS PubMed.
- F. Aguilera-Granja, R. C. Longo, L. J. Gallego and A. Vega, J. Chem. Phys., 2010, 132, 184507 CrossRef PubMed.
- S. Peredkov, A. Savci, S. Peters, M. Neeb, W. Eberhardt, H. Kampschulte, J. Meyer, M. Tombers, B. Hofferberth, F. Menges and G. Niedner-Schatteburg, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 113–118 CrossRef CAS PubMed.
- C. Chen, Y. Idzerda, H. Lin and N. Smith, Phys. Rev. Lett., 1995, 75, 152–155 CrossRef CAS.
- R. Wu and A. Freeman, Phys. Rev. Lett., 1994, 73, 1994–1997 CrossRef CAS.
- A. Langenberg, K. Hirsch, A. Ławicki, V. Zamudio-Bayer, M. Niemeyer, P. Chmiela, B. Langbehn, A. Terasaki, B. v. Issendorff and J. T. Lau, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184420 CrossRef.
- F. Luis, J. Bartolomé, F. Bartolomé, M. J. Martínez, L. M. García, F. Petroff, C. Deranlot, F. Wilhelm and A. Rogalev, J. Appl. Phys., 2006, 99, 08G705 CrossRef PubMed.
- J. Bartolomé, L. Garca, F. Bartolomé, F. Luis, R. López-Ruiz, F. Petroff, C. Deranlot, F. Wilhelm, A. Rogalev, P. Bencok, N. Brookes, L. Ruiz and J. González-Calbet, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184420 CrossRef.
- J. Jalink, J. M. Bakker, D. Dieleman, D. Kiawi, T. Rasing and A. Kirilyuk, Phys. Chem. Chem. Phys., 2015 Search PubMed , submitted.
- J. Montejano-Carrizales, F. Aguilera-Granja, C. Goyhenex, V. Pierron-Bohnes and J. Morán-López, J. Magn. Magn. Mater., 2014, 355, 215–224 CrossRef CAS PubMed.
- B. Reddy, S. Khanna and B. Dunlap, Phys. Rev. Lett., 1993, 70, 3323–3326 CrossRef CAS.
- F. Aguilera-Granja, A. Garca-Fuente and A. Vega, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134425 CrossRef.
- S. Datta, M. Kabir and T. Saha-Dasgupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075429 CrossRef.
- S. Datta, M. Kabir, S. Ganguly, B. Sanyal, T. Saha-Dasgupta and A. Mookerjee, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014429 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- L. Peters, D. Dieleman and A. Kirilyuk, to be submitted.
- S. Chadov, J. Minár, M. I. Katsnelson, H. Ebert, D. Ködderitzsch and A. I. Lichtenstein, EPL, 2008, 22, 62–63 Search PubMed.
| This journal is © the Owner Societies 2015 |