Ultrafast coherent oscillations reveal a reactive mode in the ring-opening reaction of fulgides

Abstract

The ultrafast ring-opening reaction of photochromic fulgides proceeds via conical intersections to the ground state isomers involving activation barriers in the excited state. The coherent oscillations observed in the femtosecond transient absorption signal of a methyl-substituted indolylfulgide were analysed in the framework of vibrational wavepackets to expose a dominant low-frequency mode at ∼80 cm⁻¹. The quantum chemical calculations in the relaxed excited state geometry of this fulgide revealed that the experimentally observed vibrational normal mode has a dominant contribution to the relevant ring-opening reactive coordinate.

---

Introduction

The mounting interest from both industry and science for highly selective and efficient control of different (bio)physical processes and (bio)chemical reactions has placed an enormous demand on the research and development of molecular-based switches.^1,2 The basic principle of operation of molecular switches is the reversible transition of the switching molecule between forms with different physicochemical properties.^3,4 Photochromic switches, in which this transition is triggered by electromagnetic radiation,² represent one of the widely employed groups of molecular switches. The utilization of light as a trigger for the switching process allows easy manipulation with a high degree of spatiotemporal control. This, combined with the nearly instantaneous property change of the molecule, gives photoswitches perhaps the greatest application potential.

The fulgide family is a major group of photochromic compounds, which has attracted considerable attention since their discovery.^5,6 Fulgides are derivatives of dimethylene-succinic anhydrides, substituted with an aromatic ring (Fig. 1) and depending on the aryl substitution they are termed phenyl-, furyl-, thienyl-, pyrryl- or indolylfulgides. The wide range of photochromic reactions observed in fulgides (fulgimides, fulgenates, or fulgenolides) is well described in a comprehensive review by Yokoyama.⁷ Substitution of an aromatic ring at the fulgenic acid leads to the formation of the well-known 1,3,5-hexatriene motif, which allows the 6π-electrocyclization reaction to cyclohexadiene (Fig. 1C). The photochromism of these switches is therefore mainly based on interconversion of the open (colourless hexatriene motif) and the closed (coloured cyclohexadiene motif) forms via ring-closing and ring-opening reactions. The open (cyclisable) isomer of the fulgide investigated here is termed E-form and the closed isomer as C-form. There exist two non-desired pathways, reducing the yield of the closing reaction: (i) the photochemical E/Z isomerization between the cyclisable open E-form and a noncyclisable open Z-form and (ii) the thermal enantiotopomerization along the single bond of the open hexatriene motif, leading to a fast racemization of the chiral molecules in the electronic ground state (GS). Both disturbing processes, E/Z isomerization and enantiotopomerization,^8,9 require an extensive rotational movement and thus can be strongly reduced by bulky substituents.^10,11 In contrast, the ring-opening/closing reaction is space-saving with a limited movement of side groups. In this respect, indolyl-substituted fulgides show a very low contribution (typically <10%) of noncyclisable open form molecules in the photostationary state (PSS) and an increased barrier for GS enantiotopomerization.¹² Therefore we have focused the current study on investigating the ring-opening reactions of an indolylfulgide derivative.

Fig. 1 Absorption spectra of methylfulgide in pure E-form and in PSS generated by 365 nm illumination: (A) in benzene (ε_E,365 = 7026, ε_C,530 = 4886); (B) in acetonitrile (ε_E,365 = 6533, ε_C,530 = 5453). (C) Chemical structure of MIF (closed form (C); cyclisable open form (E); noncyclisable open form (Z)). The extinction coefficients, ε, are given in [l mol⁻¹ × cm⁻¹].

Indolylfulgides were investigated by several groups before.^8,13–15 These molecules feature thermally stable GS isomers, thus structural changes can be initiated exclusively by optical excitation.⁷ The photochemical stability is very high and they can be switched between the open and closed forms several thousand times without significant degradation.¹⁶ Moreover, the extension of the closed and open form absorption spectra into the visible spectral range enables UV-free switching experiments, which is advantageous especially for biological applications.¹⁷ A major problem here is the relatively low stability of indolylfulgides in aqueous solution, which is due to the high reactivity of the succinic anhydride ring towards protic solvents. Nevertheless, there are first studies demonstrating that the stability of these compounds in protic solvents can be improved by replacing the succinic anhydride ring with a succinimide ring.¹⁸

The ring-opening,^19–22 the ring-closing^14,19 as well as the E/Z isomerization^8,9 reactions of fulgides were studied in the last years with femtosecond time resolution. After photoexcitation of the C-form in the Franck–Condon (FC) region of the first singlet ES (S₁) the molecule promptly relaxes to a local minimum on the S₁ potential energy surface (PES). At least two conical intersections to the GS^23,24 are accessible via barriers on the S₁ PES, which leads to ring-opening reaction times of a few picoseconds. It was observed that this reaction depends strongly on the experimental conditions – solvent polarity, temperature (activated process), even excitation wavelength (spectral tuning in the S₁ absorption band).^22,25 Furthermore, a strong increase in the quantum efficiency (QE) and the reaction speed is observed after excitation in the higher electronic states, which clearly shows that different reaction pathways are accessible.²⁶ In contrast, the ring-closing is totally robust against external factors (e.g. solvent (polarity), temperature, or excitation wavelength).²⁷ The studies show that changes in these factors do not influence the observed dynamics and QE; no indication for an activated behaviour is detected. The ring-closing reaction is ultrafast and proceeds typically in the sub-ps time-range. In summary, the dominant photochromic reactions occurring in indolylfulgides (ring-opening and ring-closing) are ultrafast and occur without involvement of long-lived intermediates.

We focus here on the excited state (ES) properties of the C-form of a methyl-substituted indolylfulgide (MIF), monitored by femtosecond transient absorption (TA) spectroscopy as a function of solvent polarity and excitation wavelength. The vibrational wavepacket motion, observed in the TA data is discussed within the frame of quantum chemical calculations. The investigation is supported by a thorough steady-state characterization in dependence of solvent polarity, excitation wavelength and temperature.

Materials and methods

Sample preparation

The synthesis of the investigated methyl substituted indolylfulgide (MIF), has been previously described in detail.²⁸ The so-synthesized MIF in pure crystalline E-isomer form was dissolved for the experiments either in benzene (Sigma-Aldrich) or in acetonitrile (VWR International). The extinction coefficients of interest are given in the caption of Fig. 1. The ratio of the different forms, Z/E : C, in the PSS^UV (405 nm) in benzene was determined using HPLC to be 19 : 81.

Steady-state spectroscopy and QE determination

Absorption spectra were recorded on a Specord S600 (Analytik Jena) absorption spectrometer using a fused silica cuvette with 1 cm optical path length. The temperature dependence (10–50 °C) of the QE was determined using a home-built thermostated holder, which can be installed directly in the absorption spectrometer. The holder is equipped with connectors for attaching optical fibers guiding to the sample illumination light from mounted high-power LEDs (ThorLabs, M365L2, M385L2, M530L2, M565L2, driver DC4100). The light from the optical fibers emerges directly at the surface of the cuvette with the sample, which ensures that the sample is illuminated by the complete output of the fiber. The intensity of the light coming out of the optical fiber was determined using a calibrated light detector (P-9710, Gigahertz-Optik). The PSS^VIS (530 nm or 565 nm illumination) and the PSS^UV (365 nm or 385 nm illumination) were always prepared at 20 °C and the sample was continuously stirred using a magnetic stirrer (Thermo Scientific). The induced absorption changes at 530 nm for both the ring-opening and the ring-closing reaction were monitored for 15–60 min, depending on the conversion rate of the given sample. For the calculation of the QE only the initial change of the absorbance (first few min) was used (cf. ESI,† Fig. S1). During this period, the photons are absorbed only by the reactant as there is negligible amount of product formed and thus the absorbance changes are in linear dependence with the amount of absorbed light. To minimize the effect of the spectrometer measuring light on the QE determination an optical filter was used to cut active spectral contributions.

Quantum efficiency calculation

The photochemical QE is defined as the ratio of the reacted molecules (N_react) and the number of absorbed photons (N_abs). N_react for a photochromic compound with thermally stable isomers can be determined by the associated absorbance changes (ΔOD) in a range specific for the product or the reactant:where N_A – Avogadro’s number, V – the volume of the sample, ε – the extinction coefficient at the wavelength where the absorbance changes are measured; l – the optical path length.

The N_abs can be calculated via:

where N_hν – number of incident photons, A₀ – absorbance at the excitation wavelength (λ_exc), h – Planck’s constant, c – speed of light, P – radiation power, t – time interval.

Thus the QE can be calculated by the following equation:

VIS–pump–probe spectroscopy

The time-resolved TA measurements were performed using a home-built pump–probe setup. Ultrashort laser pulses (150 fs) were provided by an oscillator–amplifier system (Clark, MXR-CPA-iSeries) operating at a repetition rate of 1 kHz (775 nm). The pump pulses between 500 and 570 nm (see text and figures for specific excitation wavelength) were generated in a home-built two stage NOPA (non-collinear optical parametric amplifier)^29,30 and focused to a diameter of ∼200 μm at the sample position. A prism compressor placed between the two NOPA stages was used to compress the pump pulses to about 60–80 fs (determined with a PulseCheck USB 15 ShortPulse Autocorrelator, APE). The pulse energy was adjusted to ensure that <10% of the molecules are excited per pulse. Single filament white light (WL) pulses covering a spectral range between 300 nm and 700 nm were generated by focusing the laser fundamental in a 5 mm thick CaF₂ crystal. The WL pulses were split into two parts – probe and reference. The reference beam was guided directly to a spectrograph, while the probe beam was focused to a diameter of ∼100 μm at the sample position and then collected and guided to a second spectrograph. Both spectrographs (AMKO Multimode) were equipped with 1200 grooves per mm gratings blazed at 500 nm and a photodiode array (PDA) combined with a signal processing chip (Hamamatsu Photonics, S8865-64) and a driver circuit (Hamamatsu Photonics, C9118), which allows single shot detection with kHz rate. The analog PDA signals were digitized at 16 bits by a data acquisition card (National Instruments, NI-PCI-6110). The detection range was set to 420–650 nm with a spectral resolution of 3.6 nm. The experiments were performed under magic angle conditions (54.7° pump–probe polarization angle difference) to eliminate anisotropic contributions. The instrument response function (IRF) was typically in the range of 80 fs. The sample was contained in a fused silica cuvette with 1 mm optical path length. The cuvette was continuously moved in the plane perpendicular to the direction of probe pulse propagation. The cuvette was continuously illuminated with a high-power 385 nm LED (ThorLabs, M385L2) to keep the sample in the PSS^UV.

Data analysis

The time-resolved data were analysed by means of Global Lifetime Analysis (GLA),^31,32 which represents simultaneous analysis of all transients at different detection wavelengths with a single set of exponential functions. Furthermore, the data were subjected to Lifetime Density Analysis (LDA),³² where the pre-exponential amplitudes in a sum of a large number (∼100) of exponential functions with fixed, equally spaced (on a decimal logarithm scale) lifetimes are determined. In contrast to GLA, LDA is a model independent type of data analysis that naturally deals with non-exponential or stretched exponential kinetics.^32,33 The LDA recovers the lifetime distribution at each detection wavelength and thus the results can be presented in the form of a contour map called Lifetime Density Map (LDM). The coherent artifact contribution in the transient signals at time zero position was approximated with a function composed of a Gaussian and/or its first and second derivative^32,34 and fitted within the same routine as the GLA and LDA. The data analysis was performed using OPTIMUS a program recently developed in our group.³²

Quantum chemical calculations

The quantum chemical calculations were performed with the help of TURBOMOLE v6.4³⁵ using the TDDFT BHLYP functional^36–40 and the 6-31G* basis set.^41,42

Results and discussion

Stationary spectroscopy and QE determination

The structures of the different forms of the MIF studied here are illustrated in Fig. 1C. The stationary absorption spectra of the pure open E-form dissolved in benzene and acetonitrile as well as the corresponding PSSs generated after 365 nm illumination are shown in Fig. 1A and B. The PSSs show absorption bands in the visible spectral range characteristic for the closed C-form. The change in solvent polarity from the non-polar benzene to the polar acetonitrile leads to a bathochromic shift of the C-form band from 535 nm to 547 nm. Illumination of the C-form with visible light (530 nm LED) induces the reverse reaction. The stability of the compounds in the two solvents was evaluated by a series of UV-VIS illumination cycles. The illumination was performed until a PSS is achieved and absorbance changes were measured at 530 nm (ESI,† Fig. S2). After 18 cycles the absorbance of the MIF in benzene is changed only slightly (2.5%), while in acetonitrile the absorbance is reduced by 15% in only 9 cycles. The decrease of the photostability of fulgides in aprotic polar solvents was reported previously and attributed to degradation due to hydrogen migration followed by tautomerization.¹⁷

The temperature dependence of the QE of the ring-opening and the ring-closing reactions was evaluated in the range of 10–50 °C. The ring-closing reaction was initiated by illumination at 365 and 385 nm, while the ring-opening reaction was initiated with 530 and 565 nm. The results are summarized in Table 1. The QE of the formation of the closed form in benzene is ∼14–15%, while in acetonitrile it is reduced to ∼5%. Within the error limits of the experiments, the QE of the ring-closing reaction does not show a significant temperature or excitation wavelength dependence (Table 1). However, the results show a clear solvent dependence with a 3-fold decrease of the QE from non-polar (benzene) to polar (acetonitrile) solvents. The QEs of the ring-opening reaction show an even stronger decrease (∼5-fold) with the increase of solvent polarity (Table 1). Furthermore, in contrast to the ring-closing, the ring-opening is characterized by pronounced temperature and excitation wavelength dependence (Table 1). The temperature dependent increase of the QE of the ring-opening reaction in benzene is ∼28% for 530 nm illumination and ∼34% for 565 nm illumination. In acetonitrile the temperature dependence of the QE is even stronger (Table 1) showing a ∼3-fold increase. In benzene the excitation wavelength dependent (565 nm → 530 nm) increase of the QE of the ring-opening reaction is in the range of ∼30%, while in acetonitrile it is less distinct. Similar dependence of the QE of the ring-opening reaction has been observed previously for both indolylfulgides and indolylfulgimides.²⁵ The excitation wavelength dependence of the QE for the ring-opening reaction is due to the presence of an energetic barrier in the S₁ ES. Such a barrier is easier to overcome when more optical excess energy is available after excitation with shorter wavelengths and for ultrafast reactions occurring before the dissipation of this excess energy to the environment. Assuming k_non-reactive ≫ k_reactive, the temperature dependence of the QE should be governed by the reactive rate and show an Arrhenius dependence.⁴³ Hence, we were able to calculate the activation energy, E_a, for the ring-opening photoreaction, which in the case of MIF in benzene is ∼400 cm⁻¹ (∼4.8 kJ mol⁻¹), while in acetonitrile is about four times higher, ∼1700 cm⁻¹ (∼20 kJ mol⁻¹). See Fig. S3 (ESI†) for the Arrhenius plots.

Table 1 Temperature, excitation wavelength and solvent dependence of the QE of the ring-opening and the ring-closing reactions of the MIF. Typical relative error for the determined values ∼2–5%

[°C]	QE of ring-closing, [%] Φ^UVE→C				QE of ring-opening, [%] Φ^VISC→E
	Benzene [nm]		Acetonitrile [nm]		Benzene [nm]		Acetonitrile [nm]
	365	385	365	385	530	565	530	565
10	15.2	14.7	5.1	5.3	6.3	4.9	0.57	0.54
20	14.7	14.1	4.8	5.2	6.8	5.1	1.0	0.83
30	14.5	14.8	5.5	5.1	7.1	5.6	1.2	1.0
40	14.3	13.5	5.0	5.1	7.7	6.1	1.6	1.3
50	13.9	14.7	5.1	5.0	8.1	6.6	1.9	1.5

---

Ultrafast transient absorption

A series of TA experiments with <100 fs resolution was performed to determine the solvent and excitation wavelength dependence of the ultrafast ring-opening C → E reaction of the MIF. In Fig. 2A and C the TA data of the sample in benzene and acetonitrile after excitation at the corresponding absorption maxima (538 and 555 nm) are shown (cf. ESI,† Fig. S4 for a complete overview). The coherent artifact contributions in the transient data at delay times ∼0 ps were fitted and subtracted from the experimental data for clearer representation.³² In addition, the delay time zero dispersion was also corrected.^31,32 The TA data of MIF in benzene and in acetonitrile are characterized by the presence of pronounced excited state absorption (ESA) over the whole detection wavelength range. In acetonitrile, three distinct ESA bands (<440 nm, ∼500 nm and ∼600 nm) can be observed, while in benzene only two (∼460 nm and ∼620 nm) are visible. The lack of a third ESA band in benzene is due to the strong overlap between the ESA and the GS bleach (GSB) signals in the 450–650 nm range, which diminishes the transient signal in this region. The ESA bands in acetonitrile appear to be blue-shifted by about 10–20 nm as compared to benzene. The red-most, strongest band in both solvents (600 nm in acetonitrile and 620 nm in benzene) shows a clear time-dependent blue shift on the time scale of a few ps. The open-form product formation is discernible only in benzene at delay times longer than 10 ps by the remaining GSB signal of the C-form (500–600 nm). In acetonitrile, this GSB contribution is negligible due to the low conversion QE (Table 1). Qualitatively, the results for different excitation wavelengths in the S₀ → S₁ absorption band appear to be very similar (Fig. S4, ESI†).

Fig. 2 (left side) TA data of MIF C-form in (A) benzene and (C) acetonitrile; (right side) DAS obtained from the GLA of the TA data of MIF C-form in (B) benzene and (D) acetonitrile. For a complete overview of the excitation wavelength dependence please see ESI,† Fig. S4 and S5.

Global lifetime analysis (GLA) of the time-resolved data

The TA data were analysed by means of GLA^31,32 to determine the main lifetime components contributing to the observed kinetics. The decay-associated spectra (DAS) obtained from the GLA of the transient data from MIF in benzene and acetonitrile after excitation in their corresponding S₀ → S₁ absorption maximum are shown in Fig. 2B and D and a summary for all excitation wavelengths is shown in Fig. S5 (ESI†) and in Table 2. The fastest lifetime component, τ₁, (Fig. 2B and D and Fig. S5, ESI†) shows a typical positive-negative amplitude feature in the 550–650 nm range where the main ESA band is located. This effect describes the time-dependent blue shift of the ESA band (positive amplitude in the DAS – decay of ESA, negative amplitude – rise of ESA). The DAS of the second lifetime component is positive over the whole detection wavelength range and accounts for the overall decay of the ESA. The infinite spectrum shows the remaining bleach of the initial absorption of the C-form and thus reports on the amount of product (open-form) formation. A clear difference in the infinite spectrum of the MIF in benzene and in acetonitrile is the lack of GSB feature in the acetonitrile spectra reflecting the very low conversion QE.

Table 2 Excitation wavelength and solvent dependence of the lifetimes recovered from GLA of the transient data of the MIF ring-opening reaction

MIF in benzene				MIF in acetonitrile
λ exc [nm]	τ 1 [ps]	τ 2 [ps]	τ 3 [ps]	λ exc [nm]	τ 1 [ps]	τ 2 [ps]	τ 3 [ps]
505	1.74	6.70	Inf	520	0.73	14.32	Inf
538	1.90	7.31	Inf	555	0.67	14.24	Inf
555	2.01	7.58	Inf	570	0.85	14.61	Inf

---

The excitation wavelength dependence of the shape and the spectral position of the DAS is very weak for MIF in both solvents. However, the amplitudes do show a trend of decrease with the shift of the excitation wavelength to the red side of the corresponding absorption spectra. This decrease cannot be assigned solely to a change in the excitation energy, as this energy was roughly the same for all experiments. Furthermore, a subtle excitation wavelength dependence trend, which results in shorter lifetimes for higher excitation photon energies, can also be observed for the lifetimes (Table 2).

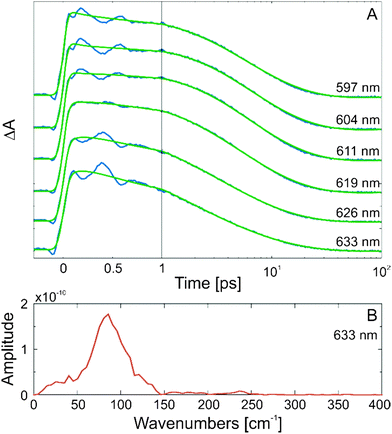
Coherent oscillations

On the sub-ps timescale, the TA data of MIF are characterized by the presence of strong signal modulation in the ESA bands in both solvents (benzene and acetonitrile). These signal oscillations are particularly distinct above 560 nm (Fig. 2 and Fig. S4, ESI†) and persevere until ∼0.8–1 ps. A comparison of the TA data at a wavelength within the ESA (580–640 nm) band containing the time-dependent signal modulation pattern with the fit yielded from the GLA is shown in Fig. 3A. The Fourier transform of the residuals resulting from the subtraction of the fit from the experimental data allowed extraction of the frequency of the signal modulation. An example of the frequency spectra is shown in Fig. 3B. The main oscillation frequency appears to be ∼80 cm⁻¹, although contribution from other frequencies in this range cannot be excluded.

Fig. 3 (A) Comparison of transient absorption data and fit of MIF in benzene for the wavelength range with strongly pronounced transient signal oscillation. (B) Fourier transform of the oscillatory pattern.

Excited state relaxation dynamics

The photochemical ring-opening reaction of MIF occurs with the transition from the electronic ES to the GS (S₁ → S₀) and is reflected by the decay of the ESA signal in the TA data. The GLA of the ultrafast time-resolved data shows that the dominant ESA decay (all-positive DAS, Fig. 2) is characterized by ∼7 ps lifetime in benzene and by ∼14 ps lifetime in acetonitrile. Our theoretical calculations (see Experimental section) yielded a dipole moment of MIF in the GS state of ∼6.7 D, which grows to ∼12.1 D in the S₁ FC point and decreases to ∼11.3 D in the relaxed S₁ state. This change in dipole moment leads to an energetic stabilization of the S₁ state in polar surrounding, which is in agreement with the red shift of the steady-state absorption maximum (Fig. 1) and the corresponding blue shift of the ESA maximum (Fig. 2) in acetonitrile. The S₁ state stabilization has two consequences. On the one hand, it leads to an increase of the ES reaction barrier (400 cm⁻¹ in benzene, and ∼1700 cm⁻¹ in acetonitrile) as confirmed by the quantum efficiency experiments (Table 1). On the other hand, we have shown for a similar compound that the internal conversion pathway is thermally activated²², thus a stabilization of the S₁ state in polar solvents will also increase this energetic barrier. In effect, the polar solvent induced stabilization of the S₁ state leads to an increase of the ES lifetime of the MIF C-form as observed in our ultrafast experiments (∼7 ps in benzene, ∼14 ps in acetonitrile). No picosecond GS cooling dynamics, as the one observed in other fulgide compounds,²¹ has been resolved by the GLA of the MIF TA data. The lack of an additional GS cooling lifetime component is due to the temporal overlap of this process with the dominant ES relaxation signal.

On the earlier timescale, the TA changes are associated with dynamics on the ES PES. The DAS of the shorter lifetime component (∼1.9 ps in benzene and ∼0.7 ps in acetonitrile) shows a positive–negative amplitude feature (Fig. 2, >560 nm), characteristic for relaxation from the FC region. The strong solvent dependence of this FC relaxation lifetime (nearly 3 times shorter in acetonitrile as compared to benzene) hints at significant involvement of ES-induced solvent reorganization dynamics.

The GLA of the TA data of the MIF C-form indicated a potential contribution in the ultrafast dynamics by a <0.5 ps lifetime component. However, since the processes (wavepacket motion, vibrational energy redistribution, and solvation dynamics) occurring at this ultrafast timescale have non-exponential nature, it is hard to unambiguously assign the lifetime components obtained from GLA. Henceforth, to confirm the presence of even faster dynamics in the TA data of the ring-opening reaction of MIF, we have performed a model-independent lifetime density analysis (LDA).³² The results from the LDA are shown in Fig. 4 (cf. Fig. S6 and S7, ESI† for details) in the form of lifetime density maps (LDMs). Indeed, the LDMs show ∼100–200 fs lifetime distribution features, particularly pronounced for the ring-opening reaction of MIF in benzene (Fig. 4A, >570 nm). The same lifetime distributions appear to be shifted to even shorter lifetimes in acetonitrile (Fig. 4B and Fig. S6, ESI†) in line with the previously discussed FC relaxation solvent dependence. The shortest lifetime component, τ₁, in the GLA (Fig. 2B and D) is associated with the lifetime distributions located at ∼1 ps in benzene (Fig. 4A and Fig. S5, ESI†) and at ∼500–600 fs in acetonitrile (Fig. 4B and Fig. S6, ESI†). Interestingly, the wavelength shift between the ∼100 fs lifetime distributions and the ∼0.5–1.5 ps lifetime distributions (Fig. 4, >570 nm) is significant in benzene but not so pronounced in acetonitrile. The difference in the energetics between those two lifetime distributions is indicative of the presence of a quasi-two step relaxation reaction in the S₁ ES. The first step could tentatively be assigned to the relaxation of the MIF from the FC region, while the second step should be linked to changes of the S₁ PES due to solvent reorganization.

Fig. 4 LDM obtained from the transient absorption data of MIF in (A) benzene after 538 nm excitation; and (B) acetonitrile after 555 nm excitation. The reading of the LDMs is as for DAS with positive (red) amplitudes accounting for decay of absorption or rise of GSB and negative (blue) amplitudes accounting for rise of absorption or decay of GSB.

The LDMs are dominated by the broad positive lifetime distributions on the picosecond lifetime scale, which account for the decay of the ESA and thus for the photochemical reaction of ring-opening. The positive picosecond lifetime distributions (>2 ps lifetime in Fig. 4 and Fig. S5 and S6, ESI†) show a strongly elongated shape, which could be associated with the time overlap of the ES relaxation and the GS cooling processes.

Excited state coherent dynamics

The strong coherent oscillations of the TA signal from the ring-opening reaction of MIF appear at the position of the strongest ESA band (in the 560–640 nm range, Fig. 2 and Fig. S3, ESI†). The oscillatory pattern shows a phase shift with a zero position at the maximum of the ESA band (Fig. 3A) and thus the coherent oscillations can be assigned straightforwardly to wavepacket motion on the ES PES of the MIF C-form. Such a wavepacket dynamics has been previously observed for similar compounds^9,25,44 but has not been studied in detail. Here, we have analysed the coherent oscillations of the TA signal and obtained the frequency spectrum (Fig. 3B). The spectrum is centred at about ∼80 cm⁻¹ in benzene and is slightly blue shifted in acetonitrile. Nevertheless, the band covers a relatively broad frequency range from ∼40 to ∼150 cm⁻¹. To determine whether higher frequency coherent oscillations are potentially detectable at the given experimental limits, a damping curve (Fig. 5A) for TA signal oscillations was simulated by convoluting a 80 fs FWHM IRF with cosine functions of different frequencies.⁴⁵ The result of this simulation indicates that in our TA experiment only coherent oscillations with frequencies below ∼200 cm⁻¹ are detectable.

Fig. 5 (A) Parameters defining the observable modes in a TA experiment with a given time-resolution. The damping factor was calculated using 80 fs FWHM IRF. (B) Contribution of the different normal modes to the S₁^FC → S₁^rel relaxation within harmonic oscillator approximation. (C) Normal modes contribution to the planarity distortion of the MIF molecule responsible for the induction of the ring-opening reaction. See text for detail.

In an attempt to assign the experimentally observed coherent oscillation to a specific molecular vibration, quantum chemical calculations using TURBOMOLE³⁵ were performed for the S₀ minimum and the S₁ minimum structures. In addition, the energy of the FC point and the vibrational normal modes for the structure were also calculated. MIF comprises 39 atoms and thus 111 vibrational modes (ν_i) and their respective displacement vectors (x_i). Since the oscillatory wavepacket motion is observed in the ESA TA signal, we calculated which normal modes induce the largest shift, , in the respective transition energies (cf.Fig. 5A and Fig. S8, ESI†).⁴⁶ In the low frequency range, accessible within the time resolution of our experiments, the ∼80 cm⁻¹ mode causes the largest shift in accord with the experimentally observed coherent oscillation (Fig. 3B).

Evidently, significant amount of excitation energy is deposited in the ∼80 cm⁻¹ mode of the molecule, however, some of this energy could also be redistributed into other normal modes during the relaxation from the to the geometry. A measure of the excitation energy distribution over the different normal modes can be obtained by projecting the difference vector of these two geometries onto the basis set of the displacement vectors of the relaxed S₁ vibrational normal modes (x_i) (see Fig. 5B). From this analysis, we find that there are a number of modes that are being populated during the relaxation. However, the highest amount of energy is distributed again into the ∼80 cm⁻¹ mode.

Our results clearly indicate that the experimentally observed ∼80 cm⁻¹ mode plays a dominant role in the ES dynamics of MIF. Thus, the question arises whether this mode also participates in the photochemical ring-opening reaction. Previous theoretical studies^23,47 on the reactive coordinates involved in a ring-opening reaction have demonstrated that the critical coordinates defining the reaction are the dihedral angle, φ, accounting for distortion of the molecule from planarity, and the length of the diagonal (r) as defined in the inset of Fig. 5C for MIF. To verify whether the ∼80 cm⁻¹ mode plays also a role in the ring-opening reaction we calculated the abovementioned dihedral angles and distances for each normal mode of the molecule. Since the coordinates of those modes are given by TURBOMOLE in Cartesian normalized units appropriate normalization is necessary to correctly evaluate the effect of a given mode on the structure of the molecule. Thus we calculated a reduced mass (μ) and frequency (ω) weighted displacement scaling (DS) factor (eqn (4), Fig. 5A).³⁵ We used this factor to scale the relative dihedral angle change (φ) and the distance changes (r₁ and r₂) in Fig. 5C.

The results of the calculation demonstrate that while many of the normal modes have an effect on the diagonal distances r₁ and r₂, the largest effect on the dihedral angle φ and thus the strongest planarity distortion of the ring in the relaxed S₁ electronic state of MIF is caused by the ∼80 cm⁻¹ mode (Fig. 5C).

In our theoretical analysis, we have examined three different factors that contribute to the amplitude of the vibrational wavepacket observed in the TA data: (i) temporal resolution (Fig. 5A) (ii) influence of different normal modes on the ESA transition wavelength (Fig. 5A) (iii) energy distribution into the different vibrational normal modes during the relaxation from the FC region (Fig. 5B). In all three cases the ∼80 cm⁻¹ vibrational mode has a dominant impact on the observed TA signal. Independently, our calculations (Fig. 5C) showed that this mode also possesses the highest contribution to structural changes that relate to the reactive coordinates.

Conclusions

Based on our results we propose the following molecular mechanism for the ring-opening reaction (Fig. 6). After excitation of the C-form of the MIF compound in the FC region the molecule undergoes an ultrafast intramolecular relaxation (∼100 fs, Fig. 4), which is followed by a sub-ps solvent reorganization dynamics (Fig. 3 and 4). After this initial relaxation in the ES, the molecule is stabilized and needs to overcome an energetic barrier to reach the CI leading to the GS isomers. Furthermore, the observed coherent oscillation (wavepacket) of the TA signal, which according to our theoretical analysis can be assigned to an out-of-plane movement of the indolyl and the succinic acid rings, has a pronounced contribution to the reactive coordinates of the ring-opening reaction (Fig. 5C and ref. 23). This coherent motion can drive the molecule over the energetic barrier and to the CI. In this respect, we present an experimental evidence for a previously proposed theoretical reaction mechanism,²³ which opens the road to targeting via chemical modification the active vibrational mode for achieving higher switching efficiency or manipulating the reaction rate as suitable for specific application.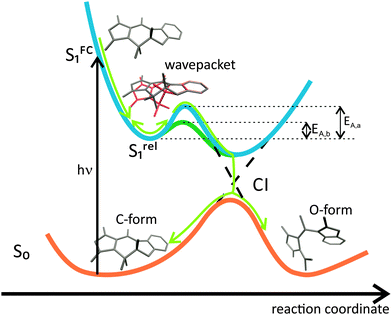

Fig. 6 Reaction scheme for the ring-opening of the MIF C-form. See also Fig. S9 (ESI†).

Acknowledgements

We thank Dr Miquel Huix-Rotllant for insightful discussions. Chavdar Slavov and Josef Wachtveitl acknowledge DFG (Grant WA 1850/4-1).

References

1. B. L. Feringa, W. F. Jager and B. Delange, Tetrahedron, 1993, 49, 8267–8310.
2. H. Bouas-Laurent and H. Dürr, Pure Appl. Chem., 2001, 73, 639–665.
3. G. H. Brown, Photochromism, Wiley, New Yourk, 1971.
4. Photochromism: Molecules and Systems, ed. H. Dürr and H. Bouas-Laurent, Elsevier, Amsterdam, 2003.
5. H. Stobbe, Ber. Dtsch. Chem. Ges., 1905, 38, 3673–3682.
6. H. Stobbe, Ber. Dtsch. Chem. Ges., 1907, 40, 3372–3382.
7. Y. Yokoyama, Chem. Rev., 2000, 100, 1717–1739.
8. F. Renth, M. Foca, A. Petter and F. Temps, Chem. Phys. Lett., 2006, 428, 62–67.
9. R. Siewertsen, F. Renth, F. Temps and F. Sönnichsen, Phys. Chem. Chem. Phys., 2009, 11, 5952–5961.
10. S. Uchida, S. Yamada, Y. Yokoyama and Y. Kurita, Bull. Chem. Soc. Jpn., 1995, 68, 1677–1682.
11. M. A. Wolak, C. J. Thomas, N. B. Gillespie, R. R. Birge and W. J. Lees, J. Org. Chem., 2003, 68, 319–326.
12. Y. Yokoyama, Y. Shimizu and S. Uchida, J. Chem. Soc., Chem. Commun., 1995, 785–786.
13. A. Santiago and R. S. Becker, J. Am. Chem. Soc., 1968, 90, 3654–3658.
14. M. Handschuh, M. Seibold, H. Port and H. C. Wolf, J. Phys. Chem. A, 1997, 101, 502–506.
15. B. Otto and K. Rück-Braun, Eur. J. Org. Chem., 2003, 2409–2417.
16. N. I. Islamova, X. Chen, S. P. Garcia, G. Guez, Y. Silva and W. J. Lees, J. Photochem. Photobiol., A, 2008, 195, 228–234.
17. Y. Yokoyama and K. Takahashi, Chem. Lett., 1996, 1037–1038.
18. N. I. Islamova, X. Chen, J. A. DiGirolamo, Y. Silva and W. J. Lees, J. Photochem. Photobiol., A, 2008, 199, 85–91.
19. H. Port, P. Gärtner, M. Hennrich, I. Ramsteiner and T. Schock, Mol. Cryst. Liq. Cryst., 2005, 430, 15–21.
20. F. O. Koller, W. J. Schreier, T. E. Schrader, A. Sieg, S. Malkmus, C. Schulz, S. Dietrich, K. Rück-Braun, W. Zinth and M. Braun, J. Phys. Chem. A, 2006, 110, 12769–12776.
21. S. Malkmus, F. O. Koller, B. Heinz, W. J. Schreier, T. E. Schrader, W. Zinth, C. Schulz, S. Dietrich, K. Rück-Braun and M. Braun, Chem. Phys. Lett., 2006, 417, 266–271.
22. S. Draxler, T. Brust, S. Malkmus, J. A. DiGirolamo, W. J. Lees, W. Zinth and M. Braun, Phys. Chem. Chem. Phys., 2009, 11, 5019–5027.
23. D. Geppert, L. Seyfarth and R. de Vivie-Riedle, Appl. Phys. B: Lasers Opt., 2004, 79, 987–992.
24. A. Nenov, W. J. Schreier, F. O. Koller, M. Braun, R. de Vivie-Riedle, W. Zinth and I. Pugliesi, J. Phys. Chem. A, 2012, 116, 10518–10528.
25. T. Brust, S. Malkmus, S. Draxler, S. A. Ahmed, K. Rück-Braun, W. Zinth and M. Braun, J. Photochem. Photobiol., A, 2009, 207, 209–216.
26. T. Cordes, S. Malkmus, J. A. DiGirolamo, W. J. Lees, A. Nenov, R. de Vivie-Riedle, M. Braun and W. Zinth, J. Phys. Chem. A, 2008, 112, 13364–13371.
27. T. Cordes, T. T. Herzog, S. Malkmus, S. Draxler, T. Brust, J. A. DiGirolamo, W. J. Lees and M. Braun, Photochem. Photobiol. Sci., 2009, 8, 528–534.
28. K. Rück-Braun, M. Å. Petersen, F. Michalik, A. Hebert, D. Przyrembel, C. Weber, S. A. Ahmed, S. Kowarik and M. Weinelt, Langmuir, 2013, 29, 11758–11769.
29. T. Wilhelm, J. Piel and E. Riedle, Opt. Lett., 1997, 22, 1494–1496.
30. E. Riedle, M. Beutter, S. Lochbrunner, J. Piel, S. Schenkl, S. Spörlein and W. Zinth, Appl. Phys. B, 2000, 71, 457–465.
31. I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104.
32. C. Slavov, H. Hartmann and J. Wachtveitl, Anal. Chem., 2015, 87, 2328–2336.
33. P. Trojanowski, J. Plötner, C. Grünewald, F. F. Graupner, C. Slavov, A. J. Reuss, M. Braun, J. W. Engels and J. Wachtveitl, Phys. Chem. Chem. Phys., 2014, 16, 13875–13888.
34. S. A. Kovalenko, A. L. Dobryakov, J. Ruthmann and N. P. Ernsting, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 2369–2384.
35. TURBOMOLE V6.4 2012, A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, 2007.
36. P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733.
37. J. Slater, Phys. Rev., 1951, 81, 385–390.
38. A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
39. C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
41. J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947.
42. M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803.
43. T. Brust, S. Draxler, S. Malkmus, C. Schulz, M. Zastrow, K. Rück-Braun, W. Zinth and M. Braun, J. Mol. Liq., 2008, 141, 137–139.
44. T. Brust, S. Draxler, A. Popp, X. Chen, W. J. Lees, W. Zinth and M. Braun, Chem. Phys. Lett., 2009, 477, 298–303.
45. S. Malkmus, R. Dürr, C. Sobotta, H. Pulvermacher, W. Zinth and M. Braun, J. Phys. Chem. A, 2005, 109, 10488–10492.
46. F. Schweighöfer, L. Dworak, M. Braun, M. Zastrow, J. Wahl, I. Burghardt, K. Rück-Braun and J. Wachtveitl, Sci. Rep., 2015, 5, 9368.
47. A. Hofmann and R. de Vivie-Riedle, J. Chem. Phys., 2000, 112, 5054–5059.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary figures. See DOI: 10.1039/c5cp01878a

---