Stability and ionic mobility in argyrodite-related lithium-ion solid electrolytes

Abstract

In the search for fast lithium-ion conducting solids for the development of safe rechargeable all-solid-state batteries with high energy density, thiophosphates and related compounds have been demonstrated to be particularly promising both because of their record ionic conductivities and their typically low charge transfer resistances. In this work we explore a wide range of known and predicted thiophosphates with a particular focus on the cubic argyrodite phase with a robust three-dimensional network of ion migration pathways. Structural and hydrolysis stability are calculated employing density functional method in combination with a generally applicable method of predicting the relevant critical reaction. The activation energy for ion migration in these argyrodites is then calculated using the empirical bond valence pathway method developed in our group, while bandgaps of selected argyrodites are calculated as a basis for assessing the electrochemical window. Findings for the lithium compounds are also compared to those of previously known copper argyrodites and hypothetical sodium argyrodites. Therefrom, guidelines for experimental work are derived to yield phases with the optimum balance between chemical stability and ionic conductivity in the search for practical lithium and sodium solid electrolyte materials.

---

Introduction

Developing electrochemical storage devices with high energy densities is vitally important for powering our future society and the increasing demand for high energy and high-power rechargeable batteries has become the major driving force for further advances in battery technology. The available organic liquid electrolytes more and more are recognised as a bottle-neck in the effort to develop safe high-performance systems. Instead, inorganic fast ion-conducting solids^1,2 with high electrochemical stability in contact with the anode (often Li metal) and cathode material, favourable mechanical properties, cost-efficient low temperature synthesis and sufficient kinetic stability for operation over a wide temperature window increasingly appear as key components in most of the promising next generation energy storage systems including both all-solid state batteries as well as (Li–air, Li–sulphur, Li-redox flow) battery concepts wherein electrode liquids or slurries are combined with solid electrolytes to facilitate scalability.

High ionic conductivity is essential to achieve a high capacity, while low electronic conductivity mitigates the electron transport through the solid electrolyte, thus preventing self-discharge of the batteries. On the other hand a certain local concentration of mobile electrons at the electrode:electrolyte interfaces mitigates charge transfer resistances (which may become a challenge for some oxide solid electrolytes). Among the solid-state Li ion conductors developed so far, the most favourable characteristics for application in electrochemical cells in terms of record ionic conductivity and lowest charge transfer resistances have been achieved by lithium thiophosphates and related compounds such as Li₇P₃S₁₁,^3,4 LGPS,^5,6 thio-Lisicon⁷ and a recent report on a “Li₇P₂S₈I” of unknown structure.⁸ Therefore, it is critical to explore more in detail sulphide-based solid electrolytes to identify the most favourable compositions and structures for application as solid electrolytes in batteries. One of the ways to widen the range of known solid electrolytes with technologically interesting performance is to explore compounds containing more than one type of anions. Solid solutions of oxide- or sulphide-based solid electrolytes with alkali halides have in the past proven to be a successful strategy to enhance ionic conductivity in a wide range of Ag⁺, Cu⁺ or alkali based systems.^2,9 This straightforwardly leads to the exploration of the fast-ion conducting halide-containing lithium argyrodites that are in the focus of this work.¹⁰

The argyrodite family of compounds with the general formula A_12−m−x⁺(M^m+Y₄²⁻)Y_2−x²⁻X_x⁻ where A⁺ = Li⁺, Cu⁺, Ag⁺; M^m+ = Si⁴⁺, Ge⁴⁺, Sn⁴⁺, P⁵⁺, As⁵⁺; Y²⁻ = O²⁻, S²⁻, Se²⁻, Te²⁻; X⁻ = Cl⁻, Br⁻, I⁻; 0 ≤ x ≤ 2 are named after the mineral Ag₈GeS₆.¹¹ Only a few argyrodites with trivalent M³⁺ = Fe³⁺, Al³⁺, Ga³⁺ have been reported.¹² A wider range of silver and copper argyrodites had been described 70 years ago¹³ and subsequently studied more in depth by Kuhs et al.¹⁴ and Evain et al.¹⁵ Temperature-dependent order–disorder transitions and cationic disorder in the high-temperature phase yield moderately high ionic conductivity for the high-temperature polymorphs of quaternary Cu and Ag-containing argyrodites,^14,16 while the corresponding halide-free ternary argyrodites are generally found to be semiconductors, for which changes in the fundamental absorption-edge related to the polymorphic transitions were evidenced.¹⁷ Lithium argyrodites first reported by the Deiseroth group¹⁰ are promising candidates for solid electrolytes. The most commonly studied argyrodite-type lithium ion conductor, Li₆PS₅Br, is reported to have a conductivity of 0.7−1 × 10⁻³ S cm⁻¹.^18,19 The wide electrochemical window and applicability of lithium argyrodites in various types of rechargeable all-solid batteries have been demonstrated earlier by our group.^20,21 Still, as for most fast-ion conducting lithium thiophosphates, such as Li₇P₃S₁₁ ³ or LGPS,^5,6 the structures of the known lithium argyrodites such as Li₆PS₅Br are only metastable limiting choices in their synthesis and raising questions about the long-term structural stability. More importantly, the lithium thiophosphates are typically unstable with respect to hydrolysis, so that they can only be handled in dry atmospheres, which is a serious cost factor for their technical application. Therefore this study aims at exploring the effect of possible changes in composition on the structural stability and hydrolysis stability.

Most argyrodites adopt a cation-disordered high-temperature cubic “aristotype” phase in space group F4̄3m (see Fig. 1a) with a characteristic anion arrangement in interpenetrating icosahedral cages, but argyrodites may also crystallize in an intermediate state of disorder in the lower-symmetry cubic space group P2₁3, as well as in cation-ordered low-temperature phases in orthorhombic space group Pmn2₁ (e.g. for Cu₈GeS₆ below 330 K²²), Pna2₁ (e.g. for Ag₈SiS₆ below 507 K¹⁴) and/or a monoclinic structure in space group Cc (e.g. for Cu₆PS₅Br²³).

For the halide-rich range of the possible argyrodite stoichiometries the argyrodite structure type is in competition to a distinct orthorhombic structure in space group Pnma (see Fig. 1b): Ag₆(GeS₄)X₂ (X = Cl, Br)^24,25 as well as Ag₆(SnS₄)Br₂²⁶ have been found experimentally as the first members of this family of “non-metallic filled NaHg₂ phases”, i.e. the partial structure of the non-metal atoms S and X (Cl, Br) corresponds to the arrangement of Na and Hg atoms in NaHg₂ (=X₂S₄) with Ge located in tetrahedral holes exclusively and Ag located in tetrahedral as well as octahedral holes.

Besides the required high ionic and low electronic structural conductivity, a solid electrolyte also needs to exhibit high hydrolysis stability. Structural stability affects how easily a material can be synthesized and how stable it is against degradation during cycling. Hydrolysis stability is especially important for alkali sulphide materials, most of which will rapidly degrade in contact with humid air (or aqueous catholytes). Therefore, a dry atmosphere is critically required throughout their preparation and battery assembly, increasing production costs and decreasing reliability of the batteries. When comparing compounds containing the same type of elements and hence the same potential decomposition products, the hydrolysis stability is obviously related to the structural stability of the compound.

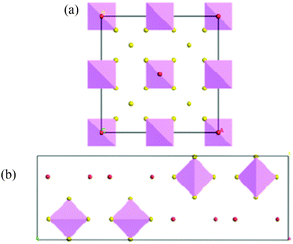Fig. 1 (a) Argyrodite structure and (b) NaHg₂-related structure. Purple tetrahedrons represent MS₄^8−m groups; red spheres represent X⁻ anions; the mobile A⁺ ions are omitted.

While structural stability, hydrolysis stability, ionic conductivity and electronic conductivity can in principle be determined experimentally, synthesis of some materials could be difficult, expensive or hazardous, so that computational approaches become beneficial to estimate these properties of materials, thus providing guidance to experimentalists whether synthesizing a new material appears worthwhile. Structural stability and hydrolysis stability can be assessed from the dissociation energy of the material. While the structural stabilities of various phases in the quaternary system Li–P–S–O are available in the literature,²⁷ in this work we designed a systematic way to examine structural and hydrolysis stability of any phase of known stoichiometry based on the calculated formation energies. Predicting the ionic conductivity requires identifying the ion migration pathways of the mobile ions and their activation energies. We employed the empirical bond valence-based softBV method developed in our group.^28–30 Electronic conductivity can be estimated from the determination of the bandgap by DFT calculations.

In this work, argyrodite-type and orthorhombic NaHg₂-related phases of 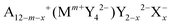with A⁺ = Li⁺, Cu⁺, Ag⁺; M^m+ = Si⁴⁺, Ge⁴⁺, Sn⁴⁺, P⁵⁺, As⁵⁺; Y²⁻ = O²⁻, S²⁻, Se²⁻, Te²⁻; X⁻ = Cl⁻, Br⁻, I⁻ are studied computationally to explore the suitability of this class of materials for practical applications in energy storage systems. Their structural stability and hydrolysis stability are determined by calculating the dissociation energies of the respective relevant critical reactions from ab initio data, and their ionic conductivities are assessed by empirical bond valence methods.

Depending on the halide content x (that may also adopt non-integer values), the cubic argyrodite phase may exhibit various degrees of site-inversion between anions X⁻ and Y²⁻.^10,18,19,21 Moreover, the effect of anion site-inversion on stability and conductivity on the argyrodites and related phases is examined in this study. To limit the computational effort, generally only stoichiometric compositions with integer values of x = 0, 1, 2 are considered.

Computational methodology

Structural stability

Structural stabilities are evaluated by the dissociation energy of the compound, which is the reaction energy of its critical reaction. Taking Li₃PS₄ for instance, its critical reaction is:

Li₃PS₄ ↔ ½S + ½Li₂S + ½Li₄P₂S₆ (1)

Accordingly, the reaction energy is computed as:

ΔE = 0.5 × E(Li₄P₂S₆) + 0.5 × E(Li₂S) + 0.5 × E(S) − E(Li₃PS₄) (2)

Here, E is the formation energy of the compound calculated by DFT methods. In this example, the resulting value ΔE = 0.205 eV is positive, suggesting that Li₃PS₄ is a stable compound and will not decompose.

Formation energy of compounds

The formation energy of a compound from its constituting elements is calculated by DFT methods as implemented in the VASP package³¹ based on a planewave basis set with using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation parametrized general gradient approximation (GGA)³² and projector augmented-wave pseudopotentials (PAW).^33,34 The cutoff threshold is set to 400 eV and convergence is by force < 0.03 eV Å⁻¹. Each compound has a k-mesh with a density of at least 30 k-points × Å³. Although +U techniques help in more precisely evaluating energies of many transition metal oxides³⁵ such as copper oxide, it is not applied here for two reasons: U values for most sulphides are not available in the literature; U values for oxides and sulphides are different, but in calculating hydrolysis stability, a single consistent U value would have to be used.

Critical reaction

With the formation energy of a compound known, the respective critical reaction remains to be determined in order to calculate the dissociation energy. The critical reaction is the reaction with the most negative reaction energy among all conceivable dissociation reactions of the compound. While experimental observation and experience is helpful in identifying such critical reactions, it appears to be more consistent for the screening approach of this work here to follow a generally applicable and exhaustive approach.

Consider a compound with formula A_1b1A_1b2…A_mbm, where A_i are distinct elements, b_i are the stoichiometric ratios, and i = 1, 2,…,m. Suppose there are n compounds in the phase diagram of A₁–A₂–…–A_m, each is denoted by A_1a1jA_2a2j…A_mamj, where j = 1, 2,…,n, and a_ij ≥ 0. Then all possible reaction equations can be summarized in the following form:

A_1b1A_2b2…A_mbm ↔ x₁A_1a11A_2a21…A_mam1 +…+ x_nA_1a1nA_2a2n…A_mamn (3)

with i = 1, 2, …,m, where m is the total number of elements, m ≥ 1 and j = 1, 2,…,n, where n is the total number of compounds, n ≥ m.

Provided that the complete list of compounds in the phase diagram is known, the search for the critical reaction can be converted into a standard linear programming problem:

Minimize E = E·x = E₁ × x₁ + E₂ × x₂ +…+ E_n × x_n, subject to the constraint A·x = b where:

A = {a_ij} are stoichiometric numbers of each element A_i in each of the conceivable decomposition products j;

b = {b_i} are stoichiometric numbers of each element in the reference compound;

E = {E_i} are calculated formation energies of each compound;

x = {x_i} are the coefficients of each compound to which the reference compound dissociates, x is the unknown to be solved and x ≥ 0;

This minimization task has a unique solution and is here solved by a simple program written with GLPK libraries³⁶ that is available from the supplementary material.

Effects of anion site-inversion

In the aristotype argyrodite structures of Li_11−m(M^m+Y₄)YX, each unit cell contains four free Y²⁻ anions that are not part of rigid (MY₄)^(8−m)− groups and four X⁻ anions. To study the effect of anion site-inversion, the stabilities of five configurations are calculated for each composition by swapping zero to four pairs of Y²⁻/X⁻ anions. The degree of site-inversion is defined to be 0% when all four free Y²⁻ anions are located at the regular Y site, i.e. the 4d site‡ (¾, ¾, ¾), (¼, ¼, ¾), (¾, ¼, ¼), (¼, ¾, ¼), and four X⁻ anions located at the 4a site (0, 0, 0), (½, ½, 1), (½, 1, ½), (1, ½, ½), which corresponds to the experimentally observed structure of Li₆PS₅I in space group F4̄3m. By swapping one pair of Y²⁻/X⁻ per unit cell, the degree of site-inversion is increased to 25%. To study the effect of site-inversion more in detail, a four-fold supercell has been constructed for the model compound Li₆PS₅Br, so that the model contains 16 pairs of swappable anions and the degree of site inversion can be modelled in steps of 6.25%.

Hydrolysis stability

Hydrolysis stability of the lithium-containing sulphides is estimated by assuming the formation of the primary products LiOH and H₂S. The calculation method is essentially the same as for evaluating structural stabilities. To identify the critical reaction of hydrolysis, it is assumed that an excess number n of water molecules is available and the resulting hydrolysis products contain oxides. In the system Li–P–S–H–O, the critical reaction is:

Li₃PS₄ + nH₂O ↔ 4H₂S + (n − 4)H₂O + Li₃PO₄ (4a)

Eliminating the excess H₂O on both sides leads to the final critical hydrolysis reaction:

Li₃PS₄ + 4H₂O ↔ 4H₂S + Li₃PO₄ (4b)

For many compounds hydrolysis reactions may consist of more than one reaction step. To simplify the simulation, the final products of hydrolysis are here consistently limited to the most basic products, e.g. LiOH instead of the corresponding hydrated LiOH·xH₂O.

In practice, hydrolysis reactions may be more complex. The products may e.g. be amorphous and non-stoichiometric, and the actual reaction path may depend on a number of factors such as humidity, temperature, and reaction time. Thus, the results presented in this study can only provide a rough guideline for comparing the relative (thermodynamic) hydrolysis stability of different argyrodites.

Electronic conductivity

To compare the electronic conductivities of the argyrodite phases, the bandgaps of the structures are calculated by DFT calculations using VASP. Since the employed GGA functional has the intrinsic tendency to underestimate the bandgap, the resulting values have to be understood as lower bounds to the true bandgaps.

Pathway for and activation energy of ionic conductivity

All cubic phases of argyrodites exhibit a three-dimensional network of pathways connecting partially occupied sites for the migration of the monovalent A⁺ ions and hence show ionic conductivity. In this report the activation energy for ion migration is estimated as the main influencing factor. Our empirical bond-valence based softBV forcefield³⁷ is used to analyse the site energies of Li⁺ ions E_BVSE(Li) throughout the structures of lithium argyrodites. Migration pathways for Li⁺ are then analysed as regions of low E_BVSE(Li) in the resulting grids spanning the structure model with a resolution of typically (0.1 Å)³, which has been demonstrated to be a simple and reliable way of identifying transport pathways in local structure models,^29,30 provided that the local structure model captures the essential structural features. For the purpose of analyzing E_BVSE(Li) landscapes Coulomb repulsions are considered only between mobile and immobile cations (here e.g. Li⁺–P⁵⁺), while Coulomb attraction terms are generally integrated in the Morse attraction term. Starting from an analysis of local minima and saddle points of E_BVSE(Li), the grid analysis utilizes a modified Dewar, Healy and Stewart (DHS)-type path finding algorithm³⁸ to identify low energy paths connecting the local site energy minima.³⁹

Such energy landscapes based on rigid structure models without the possibility for structural relaxation inherently overestimate the energy barriers. In order to factor in the reduction of energy barriers by relaxation effects, the initially observed barriers needs to be scaled down by an empirical factor ≈0.5 that slightly depends on both the mobile ion and on the anion in its first coordination shell. For details on the scaling factor see Table S1 in the ESI.† By means of this scaling, the scaled predicted activation energies should become comparable to each other and to experimental results, while unscaled activation energies can only be compared among compounds with similar compositions.

Results and discussion

Substitution of M^m+ and X⁻ in Li_12−x−m(M^m+S₄)S_2−xX_x

Structural stability. In the lithium argyrodites Li_7−x(PS₄)S_2−xX_x, P⁵⁺ may be substituted by As⁵⁺, Si⁴⁺, Ge⁴⁺, or Sn⁴⁺ with lithium contents adjusted to the halide content x and the charge of the respective high-valent cation M^m+. When comparing the resulting compounds with respect to their structural stability, it turns out that all the Li_12−x−mM^m+S_6−xX_x compounds share the same critical (decomposition) reaction expressed as eqn (5):

Li_12−x−mM^m+S_6−xX_x ↔ Li_8−mM^m+S₄ + (2 − x)Li₂S + xLiX (5)

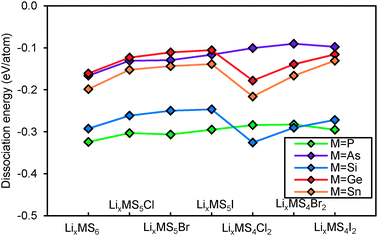
The results summarised in Fig. 2 show that most of the argyrodites are metastable, and thus may only be synthesized with suitable non-equilibrium low-temperature methods, as they might decompose at higher temperatures. With increasing halogen content, the structural stability of the NaHg₂-related orthorhombic phases is enhanced when compared to the argyrodite phases of the same composition. In other words, the calculations show that for Li₆MS₄X₂ phases with M⁴⁺ cations the NaHg₂-related structures are more stable than the argyrodite phases (see Fig. 2a). For the M⁵⁺ cations the overall tendency is the same, but for the halide-richest compositions Li₅MS₄X₂ the dissociation energies of argyrodite and NaHg₂-phases are closely similar (see Fig. 2b).

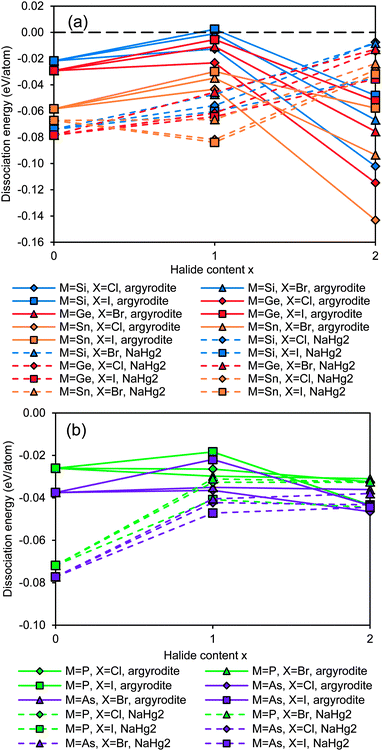Fig. 2 Structural stability of (a) Si,Ge,Sn-argyrodites and (b) P,As-argyrodites. Higher positions in the graph indicate higher stability.

Compounds based on the heavier M^m+ cations As⁵⁺ and Sn⁴⁺ are overall less stable than those with the lighter M^m+ cations and the least stable compounds involve these heavy M⁺ cations in combination with the lightest halide X⁻ = Cl⁻, so that the thermal stability will be further reduced and it may become more difficult to synthesize and stabilize them. In line with this, it was e.g. found that while argyrodites with M = P can be formed for X = Cl, Br or I, for M = As only those with X = Br and I can be synthesized.⁴⁰ In terms of choices of halogen elements, argyrodite phases containing iodide are more stable than those containing bromide and chloride.

When considering the dependence of the structural stability of the Li_12−x−m(M^m+S₄)S_2−xX_x argyrodites on the halide content x, the dissociation energies shown in Fig. 2 as a function of halide content x exhibit a clear maximum at x = 1 for M⁴⁺ compounds (cf. solid lines in Fig. 2a), while among the M⁵⁺ compounds only those with X⁻ = I⁻ show a comparatively pronounced stability maximum. Therefrom it may be concluded that for these two groups of argyrodites a (near) stoichiometric composition with x = 1 will be preferred (as also found experimentally for Li₆M⁵⁺S₅I argyrodites).^10,19,40 For the M⁵⁺ argyrodites with the lighter halide anions Br⁻ and Cl⁻ the dissociation energy decreases slightly as x increases from 0 to 1 (for the case of M = P) or is practically constant (for M = As). In these compounds the entropy influence may preferentially lead to non-stoichiometric compounds with compositions controlled by details of the sample preparation conditions. Such a behaviour is experimentally observed for Li_7−xMS_6−xX_x (with M = P, X = Cl or Br and to some extent for M = As, X = Br, where only a slight deviation from stoichiometry is noted).^10,21,40

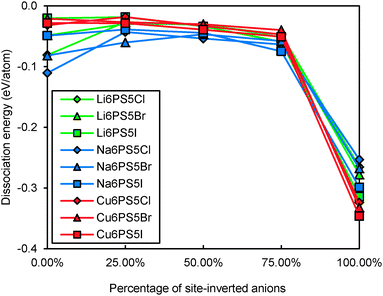
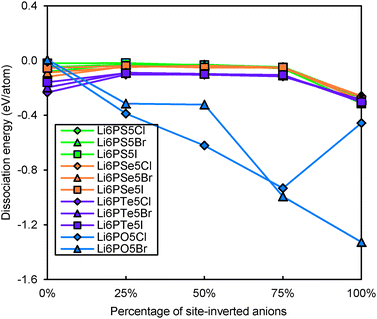
Even for stoichiometric argyrodites Li_11−mMS₅X (which are, as mentioned above, often close to the most preferable composition) the influence of disorder may be relevant for their structural stability. From earlier structural studies, it is known that e.g. in Li_7−xPS_6−xX_x with X = Cl, Br the experimentally observed S²⁻/X⁻ anion distribution is disordered in the sense that there is a partial inversion between the occupancies of the nominal S²⁻ and X⁻ sites. Detailed neutron diffraction studies indicate a temperature dependence of this disorder.²¹ Here we studied whether there is a thermodynamic driving force for the site inversion. Fig. 3 surveys the effect of site-inversion on the dissociation energies of the studied argyrodites with x = 1. Swapping the occupancies of the four pairs of S²⁻/X⁻ anions per unit cell allows varying the site occupancies in steps of 25%. From the results in Fig. 3 the effect of the S²⁻/X⁻ site-inversion on the structural stability seems to depend on the oxidation state m of the M^m+ cation and the type of halogen atom involved. In argyrodites containing M⁵⁺ cations, chlorides and bromides prefer around 25% site-inversion while iodides prefer the fully ordered structure (0% site-inversion). This suggests that the experimentally observed site-inversion for Li₆PS₅Cl and Li₆PS₅Br (and fully ordered nature of the anion distribution in Li₆PS₅I) is caused by an enthalpic driving force and not only a kinetic effect.

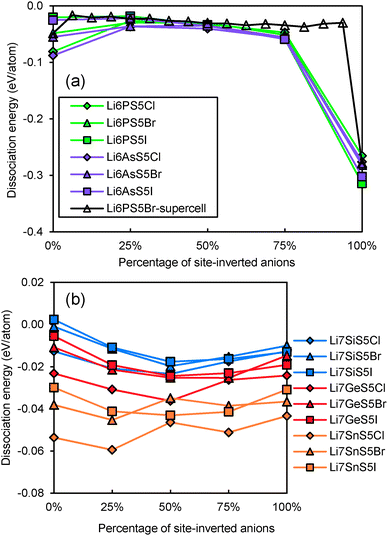Fig. 3 Variation of dissociation energies of (a) P,As-argyrodites and (b) Si,Ge,Sn-argyrodites with the degree of S²⁻/X⁻ anion site-inversion.

To understand more in detail the correlation between anion site-inversion and stability, configurations with random pairs of S²⁻/Br⁻ swapped have also been calculated for a four-fold supercell in the case of Li₆PS₅Br. Results are shown as open triangles in Fig. 3(a). Both fully ordered structures (no inversion or complete inversion) exhibit significantly more negative dissociation energy than the structures with partial S²⁻/Br⁻ swapping. The dissociation energy reaches its least negative value for low degrees of site inversion (6–19%) but show only a minute decrease towards higher degrees of site inversion before suddenly shooting down to the most negative value for the fully-inverted structure. The energies found for the same degrees of site inversion for the single cell and four-fold supercells of Li₆PS₅Br reasonably agree with each other, so that the fundamental variations for the other compounds may be estimated from the computationally less demanding single unit cell calculations in Fig. 3. In argyrodites containing M⁴⁺ cations (see Fig. 3(b)), the influence of site-inversion on structural stability is mostly reversed. Structures with 0% and 100% site-inversion are typically similar in dissociation energy and more stable than structures with 25–75% site-inversion. As mentioned above the compounds with M = Sn show the lowest stability independent of the site inversion and a less regular variation of the dissociation energy with the degree of anion site inversion.

Hydrolysis stability. In contrast to the discussion of structural stability above, the critical reactions for stability against hydrolysis are no longer the same for all argyrodites but depend on the choice of the cation M^m+ according to eqn (6)–(10):

Li_7−xPS_6−xX_x + (8 − 2x)H₂O ↔ xLiX + Li₃PO₄ + (6 − x)H₂S + (4 − 2x)LiOH (6)

Li_7−xAsS_6−xX_x + (7 − 2x)H₂O ↔ xLiX + 0.5As₂S₃ + S + (3.5 − x)H₂S + (7 − 2x)LiOH (7)

Li_8−xSiS_6−xX_x + (9 − 2x)H₂O ↔ xLiX + Li₂SiO₃ + (6 − x)H₂S + (6 − 2x)LiOH (8)

Li_8−xGeS_6−xX_x + (8 − 2x)H₂O ↔ xLiX + GeS₂ + (4 − x)H₂S + (8 − 2x)LiOH (9)

Li_8−xSnS_6−xX_x + (8 − 2x)H₂O ↔ xLiX + SnS₂ + (4−x)H₂S + (8 − 2x)LiOH (10)

When comparing the resulting hydrolysis stability values for Li_12−x−mM^m+S_6−xX_x argyrodites in Fig. 4 it becomes obvious that all these lithium argyrodites will decompose in contact with water, as indicated by the negative dissociation energies. Phosphorus and silicon argyrodites are highly sensitive to moisture (with the commonly studied P-compounds typically being the worst case in terms of hydrolysis stability), while germanium, tin and arsenic argyrodites are significantly less vulnerable to hydrolysis. It should however be kept in mind that the latter two also have a lower structural stability. In terms of the halide content, compounds without any halogen atoms demonstrate lower hydrolysis stability, and the vulnerability to hydrolysis only slightly decreases with the increase of the size of the halogen atom among the Li_11−mM^m+S₅X argyrodites with the same halide content.

Fig. 4 Hydrolysis dissociation energy of argyrodites with different halide contents. Compounds containing the same cation M (M = P, As, Si, Ge, Sn) are connected by lines as a guide to the eye.

Activation energy for Li⁺ migration. Fig. 5 compares the activation energies for Li⁺ migration in the compounds containing various M^m+ cations as derived from our bond-valence based site energy mapping. For the sake of simplicity this comparison is based on the fully anion-ordered argyrodite structure models. It should also be noted that the DFT geometry optimisation will lead to some deviation of the unit cell volume from the experimentally observed room temperature values limiting the accuracy of the activation energy prediction while semiquantitative trends should be preserved. The cubic or pseudocubic argyrodites are obviously 3D conductors so that also for the ab initio geometry-optimised local structure models (formally in space group P1) the percolation thresholds for 1D, 2D and 3D long-range Li⁺ ion migration differ only minutely. In contrast, the NaHg₂-related phases are essentially 2D ionic conductors where the migration perpendicular to the fast-ion-conducting planes requires significantly higher activation energy than within the planes.

Fig. 5 Comparison of activation energies required for Li⁺ motion in 2D percolating pathways in geometry-optimised models of various argyrodites and NaHg₂-related phases: (a) Si,Ge,Sn-compounds and (b) P,As-compounds. Fully ordered argyrodite structure models (0% anion site-inversion) are used consistently in these activation energy calculations.

Li⁺ migration in argyrodites Li_12−mM^m+S₆ and Li_11−mM^m+S₅X requires lower activation energies than in halide-rich argyrodites Li_10−mM^m+S₄X₂. Moreover argyrodites containing I⁻ tend to have higher activation energies than those containing Cl⁻ and Br⁻ in line with a more general rough trend that the more stable (anion ordered) compounds tend to show somewhat higher activation energies also for the Li⁺ mobility. In addition, the lower repulsion of M⁴⁺ and higher concentration of mobile charge carriers seems to favour on average somewhat lower activation energies in Li₇M⁴⁺S₅X than in Li₆M⁵⁺S₅X compounds. Moreover, NaHg₂-related Li₇M⁴⁺S₅X phases are found to have higher (and the Li₆M⁴⁺S₅X₂ compounds lower) activation energies than the argyrodites of the same composition, while for the phases containing M⁵⁺ no such systematic difference between the two structure types can be observed in terms of their activation energy for Li⁺ migration. The influence of the S²⁻/Br⁻ anion site-inversion in local supercell structure models of the Li₆PS₅Br on the predicted activation energy barrier for Li⁺ is demonstrated in Fig. 6. Configurations of 100%, 50% and 0% site-inversion are found to have the smallest activation energies. The specific choice of local structures may affect this finding. Still, the observation that the difference in activation energy between the highest and lowest activation energy configurations for the same composition reaches about 0.20 eV suggests that anion disorder in argyrodites strongly influences the local and overall lithium ion conductivity.

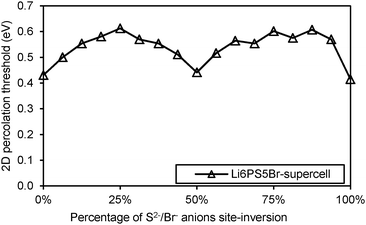Fig. 6 Activation energy required for Li⁺ migration in site-inverted configurations of Li₆PS₅Br supercell.

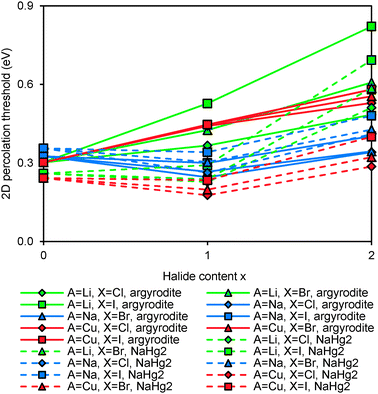
To assess the accuracy of the empirical approach for estimating migration barriers from structure models using the softBV forcefield, experimental activation energy data from the literature conductivity and NMR studies are compared to the calculated migration barriers.^16,41–45 While local structures generated from DFT geometry-optimisation do not readily accommodate fractional occupancy and show some deviation in lattice parameters compared to experimentally determined structures, these comparisons are based on experimental structure data.,^10,40,46 Results are summarised in Fig. 7. It should be noted that among the calculated barrier energies values <0.2 eV refer to barriers for local hopping and the corresponding experimental data are NMR data, while values >0.2 eV correspond to the migration barrier for percolating pathways. As seen from Fig. 7 the limiting factor for the quality of the correlation is less the quality of the computational prediction but the large spread in the experimental activation energies reported in the literature for the same compound.

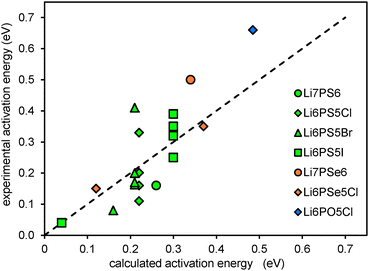Fig. 7 Comparison of experimental activation energies to calculated activation energies based on experimentally determined structures.

Li⁺ ions in argyrodites are generally found to be distributed over three types of sites. Site A (48 h) refers to the equilibrium site that hosts the bulk of Li⁺ ions in all argyrodite structures. Interstitial sites of type B (48 h) are located in-between A sites, so that 3A and 3B sites nearly form a low energy pathway hexagon. In combination with local paths connecting directly two A sites 4 such A–B hexagons form a local pathway cage around each S²⁻ anion in Li₆PS₅I. The A sites in these cages are then connected via type C interstitial sites (16e) to a 3-dimensional migration pathway network. In Li₆PSe₅Cl the local (A–B)₃ pathway hexagons are bridged by A–C–A pathways to local pathway cages around the halide ion that only for higher activation energies merge to a percolating pathway network by direct A–A bridges.

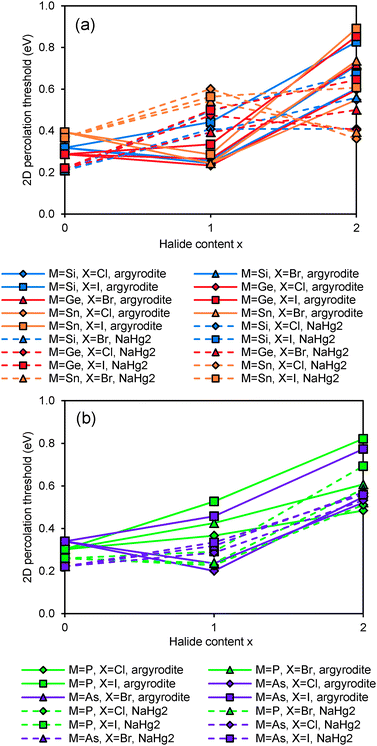
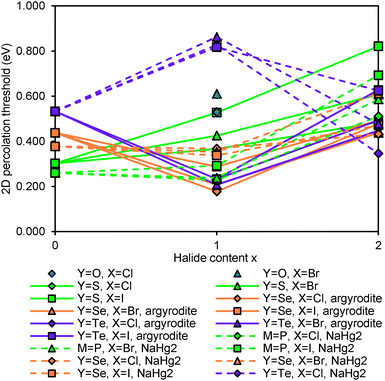
The relative site energies and activation barriers between sites are summarised in Fig. 8, in which the lowest site energy among the three types of sites is set to 0 eV. The percolation threshold (or the long-range activation energy) equals to the maximum of the three relevant migration barriers, i.e. either the barrier between two A sites or between an A site and a C site. It may also be noted that their respective barrier heights are anticorrelated. Li₆PS₅I, for example, shows a very low activation energy between two A sites which may correspond to the experimentally observed short-range activation energy of 0.04 eV, but the much larger activation energy between A and C sites causes the relatively high activation energy of about 0.35 eV for dc conductivity.⁴⁴ When the size of the halide ion is reduced by substituting I⁻ by Br⁻ the A–C barrier shrinks and the A–A barrier increases so that the activation energy for local motions slightly increases, while the activation energy for dc conductivity is considerably reduced.

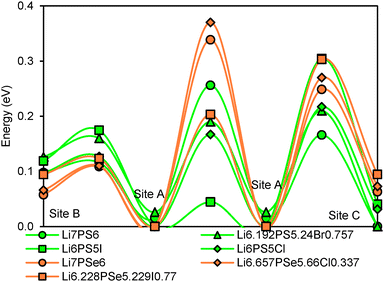Fig. 8 Site energies and activation barriers between neighbouring sites in sulphide and selenide argyrodites.

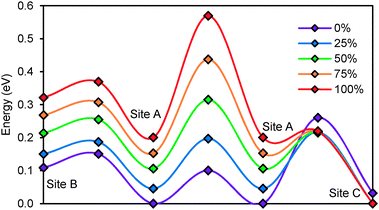
To study the effect of anion disorder on the migration barriers between the different sites, we analysed the barriers in hypothetical structures derived from the experimental structure of Li₆PS₅Br. A fully stoichiometric and anion ordered structure is compared to structures with mixed anion site occupancy, where in steps of 0.25 increasing fractions of Br⁻ are assigned to the 4d sites, while the corresponding amount of S²⁻ is redistributed to the 4a sites. The effect of the different degrees of anion disorder on the migrations barriers in Li₆PS₅Br are summarized in Fig. 9. The increase in anion disorder has little effect on the height of the migration barrier between A and B sites, but consistently increases barrier heights between two A sites and decreases activation energies between A and C sites. For the case of Li₆PS₅Br the lowest activation energy for long-range ion migration (dc conductivity) results for 25% anion disorder, when the barrier heights for A–A and A–C hops are almost equal.

Fig. 9 Site energies and activation barriers between neighbouring sites in Li₆PS₅Br with different degree of anion disordering. 0% refers to the fully ordered structure corresponding to the experimental structure of Li₆PS₅I.

Selection guidelines. To select a structure with suitable properties for application as solid electrolyte, the requirement of low activation energy for lithium ion migration effectively limits the choices to the Li_11−mM^m+S₅X compounds with X = Cl and Br or the halide-free Li_12−mM^m+S₆. Among these compounds, the structural stability of the argyrodite phases is higher than the one of the corresponding NaHg₂-related phases. Further examination on their dissociation energies suggests that the argyrodites with M = P, Ge and Si have higher stability, and structures with halide content (Li_11−mM^m+S₅X) are more stable than those without (Li_12−mM^m+S₆). The halide content also somewhat mitigates the vulnerability to hydrolysis. Especially the germanium compounds show more favourable relative hydrolysis stability. In summary, except for the known Li₆PS₅X and Li₇PS₆ compounds, the most promising candidates in the search for lithium-ion conducting compounds with technically interesting properties would be Li₇GeS₅X, Li₇SiS₅X, Li₈GeS₆ and Li₈SiS₆ where X = Cl or Br.

Substitution of A⁺ and X⁻ in A_7−x(PS₄)S_2−xX_x argyrodites

Structural stability. Lithium ions in lithium argyrodites can be substituted by a number of monovalent cations. Here the lithium compounds are compared to the previously known copper argyrodites and possible analogous sodium argyrodites due to the lower cost and higher earth abundance of sodium compared to lithium.

Critical reactions for structural stability are given in eqn (5), (11) and (12) for A = Li, Na or Cu, respectively:

Na_7−xPS_6−xX_x ↔ xNaX + (2 − x)Na₂S + Na₃PS₄ (11)

Cu_7−xPS_6−xX_x ↔ xCuX + (0.5 − 0.25x)Cu + (0.5 − 0.25x)Cu₇S₄ + Cu₃PS₄ (12)

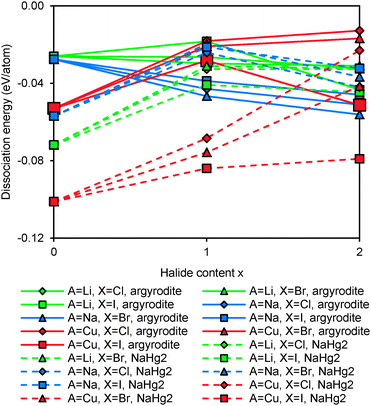
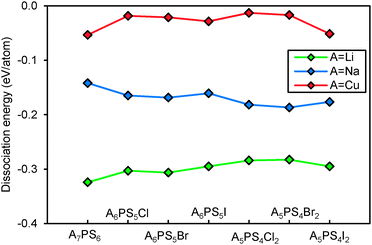
Fig. 10 compares the structural stability of compounds containing different mobile cations A⁺. Sodium argyrodites are found to be less stable than lithium and copper argyrodites, consistent with the fact that most of the discovered argyrodites contain copper, silver and lithium instead of sodium. From Fig. 10, Na₇PS₆ may be the only practically accessible sodium argyrodite phase. Among the studied phases copper argyrodites are found to be the most stable, in line with the existence of natural copper-containing argyrodite Ag_3.48Cu_4.68GeS₆ in minerals.⁴⁷ Copper argyrodites are always more stable than the NaHg₂-related phases of the same composition. Similar to Li₆PS₅I and in line with experimental structure determinations, Cu₆PS₅I is expected to be stoichiometric from the pronounced stability maximum around x = 1.^48,49

Fig. 10 Structural stability of compounds containing A⁺ = Li⁺, Na⁺ and Cu⁺.

Again we explored possible effects of anion site site-inversion on stability of A-argyrodites and the findings are summarized in Fig. 11. The overall shapes of the stability vs. degree of site inversion curves are similar for all three types of compounds: with the increase in size of halogen anions (and thus in the X⁻ sulphide size difference), the most stable degree of site-inversion shifts from 25% towards 0%. Argyrodites containing I⁻ always prefer the fully ordered configuration. This suggests that the nature of the A⁺ ion has only a minor influence on the preferable degree of site inversion.

Fig. 11 Effect of anion site-inversion on the dissociation energy of A-argyrodites.

Hydrolysis stability. Critical reactions for hydrolysis stability are given in eqn (6), (13) and (14) for A = Li, Na or Cu, respectively:

Na_7−xPS_6−xX + (8 − 2x)H₂O ↔ xNaX + Na₃PO₄ + (6 − x)H₂S + (4 − 2x)NaOH (13)

Cu_7−xPS_6−xX_x + 5/32(2 − x)H₂O ↔ xCuX + 1/32(2 − x)P₂O₅ + 1/16(14 + x)Cu₃PS₄ + 5/16(2 − x)Cu₇S₄ + 5/32(2 − x)H₂ (14)

Fig. 12 shows the relative stability against moisture of compounds containing the three types of mobile A⁺ cations. Argyrodites containing copper are much more stable to moisture than the alkali argyrodites. This is because copper sulphide (Cu₇S₄) and copper thiophosphate (Cu₃PS₄) are more stable than their lithium and sodium counterparts in water. The predicted decomposition reaction of copper argyrodites would thus release H₂ rather than H₂S (as released by Li and Na argyrodites) and the released amount is much smaller compared to that of H₂S in the case of the alkali. The higher hydrolysis stability of sodium argyrodites compared to lithium argyrodites is less intuitive. It may be affected by our approach of limiting ourselves to the primary reaction products AOH and hydrogen-free A oxides. Both of them will further react with water and the reaction energy depends largely on element A.

Fig. 12 Comparison of hydrolysis stability of argyrodites containing different A⁺ cations.

Activation energy for A⁺ migration. From the overview of activation energies for A⁺ motion in Fig. 13 it can be seen that sodium compounds overall demonstrate lower activation energy than lithium and copper compounds, but due to the instability of these structures the knowledge of the low activation energy may be of limited usefulness, and only Na₇PS₆ may be practically accessible. Copper argyrodites have similar level of activation energies compared to Li₆PS₅Br, and the type of halide atoms seems to affect the activation energies of copper argyrodites much less than for their alkali counterparts. The activation energies of copper argyrodites show almost linear dependence on halide content x, which is a characteristic shared by lithium argyrodites. Although NaHg₂-related copper compounds seem to be much more conductive than the argyrodite structures of the same composition, stability calculations (see Fig. 10) indicate that they are much harder to form than the argyrodite structures.

Fig. 13 Activation energies required for A⁺ migration where A⁺ = Li⁺, Na⁺ and Cu⁺ as a function of the halide content.

Selection guidelines. Judging from the low activation energy and the high concentration of mobile cations and free sites in the robust 3D network of migration pathways in lithium and copper argyrodites both will show reasonably high conductivity and (meta)stability. The alternative of sodium-ion conducting argyrodites appears less attractive as sodium argyrodites (except for Na₇PS₆) are unstable, and the predicted activation energy for Na₇PS₆ is slightly higher than for Li₇PS₆ (while in general the fast sodium-ion conducting solids can reach considerably lower activation energies than the best known Li⁺-ion conductors).

Substitution of Y²⁻ and X⁻ in Li_7−x(PY₄)Y_2−xX_x argyrodites

Structural stability. Softer anions are expected promote ionic conductivity, which is why the sulphide-based solid electrolytes generally reach higher conductivities than oxide-based ones. This invites the idea that selenium and tellurium argyrodites should show even higher ionic conductivity. However, their stability may be limited and electronic conductivity due to the increase of electron density may prevent their use as solid electrolytes. For comparison, two types of experimentally known oxygen argyrodites (with low ionic conductivity) will also be investigated.⁴⁵

Critical reactions for structural stability are determined as eqn (5) and (15)–(19):

Li₆PO₅X ↔ LiCl + Li₂O + Li₃PO₄ (15)

Li₇PSe₆ ↔ 2Li₂Se + Li₃PSe₄ (16)

Li₆PSe₅X ↔ 0.5Se + 1.5Li₂Se + LiX + 0.5Li₄P₂Se₆ (17)

Li₅PSe₄X₂ ↔ 0.5Se + 0.5Li₂Se + 2LiX + 0.5Li₄P₂Se₆ (18)

Li_7−xPTe_6−xX_x ↔ xLiX + P + 2.5Te + (3.5 − x)Li₂Te (19)

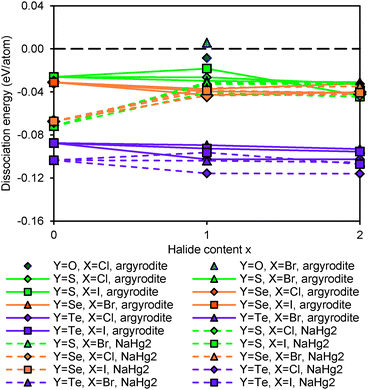
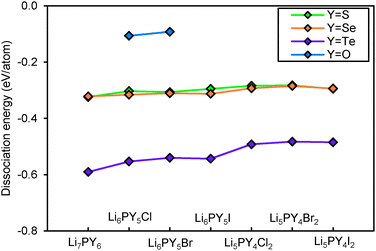
Fig. 14 shows the dissociation energy of compounds containing different Y²⁻ anions. The structural stability of lithium argyrodites containing Y²⁻ increases in the order of Te < Se < S < O. The tellurium compounds show considerably more negative dissociation energies indicating that they may practically not be accessible. Selenium compounds, on the other hand, have similar dissociation energies to those of sulphur compounds. Except for Li₇PSe₆ which has been successfully synthesized in the argyrodite structure,⁴⁶ the likelihood for selenium compounds containing halogen elements to crystallize in argyrodite phase and NaHg₂-related phase are almost equal. It should be stressed that the critical reaction of selenium argyrodites takes only three Li–P–Se ternary compounds into consideration. Two of them are Li₄P₂Se₆⁵⁰ and Li₇PSe₆ as reported in a study by Francisco.⁵¹ Another compound Li₄PSe₃ is constructed by replacing sulphur atoms in Li₃PS₄ with selenium atoms. Li₄P₂Se₆ is found to be the most stable ternary compound calculated so far. With the addition of new compounds into the phase Li–P–Se diagram, the critical reaction may change and the dissociation energy may become more negative. For all the different chalcogenide compounds studied the argyrodite phases are significantly preferred over NaHg₂-related phases in the absence of halide anions, while for the halide-containing compounds the stability differences between the compounds with the two structure types are much smaller.

Fig. 14 Structural stability of compounds containing anions Y²⁻ = O²⁻, S²⁻, Se²⁻ and Te²⁻.

Fig. 15 plots the dissociation energy versus degree of site-inversion in Y-argyrodites. Selenium and tellurium argyrodites share the same trend as sulphur argyrodites that fully ordered configurations are less stable. In contrast the oxygen argyrodites can only exist in the fully ordered configuration. This is consistent with the experimental structure determination of oxygen argyrodites.⁴⁵

Fig. 15 Effect of anion site-inversion on the dissociation energy of Y-argyrodites where Y = O, S, Se, Te as a function of the halide content.

Hydrolysis stability. Critical reactions for determining the hydrolysis stabilities of argyrodites containing different Y²⁻ anions are eqn (6), (20), and (21):

Li₆PO₅X + H₂O ↔ LiX + Li₃PO₄ + 2LiOH (20)

Li₆PSe₅X + (8 − 2x)H₂O ↔ xLiX + Li₃PO₄ + (6 − x)Se + (6 − x)H₂ + (4 − 2x)LiOH (21)

Li₆PTe₅X + (8 − 2x)H₂O ↔ xLiX + Li₃PO₄ + (6 − x)Te + (6 − x)H₂ + (4 − 2x)LiOH (22)

Fig. 16 shows the resulting hydrolysis dissociation energies of argyrodites. Oxygen argyrodites have the highest calculated hydrolysis stability, in line with the general tendency that oxides are more stable to moisture than sulphides, selenides and tellurides. Similar to the findings for structural stability, selenium argyrodites and sulphur argyrodites have nearly the same level of hydrolysis stability. The hydrolysis products are different, with selenium argyrodites releasing H₂ while sulphur argyrodites releasing H₂S. Though H₂Se and H₂Te exist in gaseous form, they are not stable and would decompose into H₂ and Se/Te.

Fig. 16 Hydrolysis stability of Y-argyrodites.

Activation energy for Li⁺ migration. Fig. 17 shows the activation energy for the migration of Li⁺ in the compounds containing different Y²⁻ anions. Consistent with experimental observation, activation energies of Li₆PO₅Cl and Li₆PO₅Br are higher than those of Li₆PS₅Cl and Li₆PS₅Br. The comparison to selenide- and telluride-based compounds is based on an estimated scaling factor of 0.5, as only two experimental activation energies 0.49 eV of Li₇PSe₆⁵² and 0.20 eV of Li₆PSe₅Br⁴³ are available for comparison. Unlike for the case of the sulphur argyrodites, among the argyrodites with Y = Se, Te the Li₆PY₅X compositions with intermediate halide content have lower activation energies than the halide-free Li₇PY₆ and halide-rich Li₅PY₄X₂ argyrodites. In fact the activation energies predicted for Li₆PSe₅X with X = Cl, Br are the lowest of all the studied argyrodite compositions. The Li₆PY₅X argyrodites with Y = Se, Te also have somewhat lower activation energies than the NaHg₂-related phases of the same composition.

Fig. 17 Activation energies for Li⁺ migration in compounds containing different Y²⁻ anions.

Bandgaps and selection guidelines. The DFT-calculated bandgaps of argyrodites Li₆PY₅Br decrease in the order O > S > Se > Te as tabulated in Table 1. In general bandgaps are predicted to decrease as the period of anion Y increases since higher electron density should promote electronic conduction. The high bandgap of the oxide argyrodite clearly qualifies it as an insulator. From the calculations Li₆PS₅Br should be a semiconductor with a bandgap of 2.12 eV. Still it has to be kept in mind that DFT calculations using GGA functionals tend to underestimate the band gap and practically an electrochemical window >4 eV has been concluded from cyclovoltammetry.²⁰ Similarly, prediction of Li₆PTe₅Br to be a metal in practice might suggest that it is a narrow-band semiconductor, but definitely not suitable as a solid electrolyte. For Li₆PSe₅Br the intermediate bandgap may indicate that this may be a mixed conductor with (in view of the low activation energy for Li⁺ migration) mainly ionic conductivity but substantial contributions of electronic conductivity preventing use of pure selenides as a solid electrolyte, but potentially of interest in compounds with e.g. S²⁻/Se²⁻ anion disorder.

Table 1 Bandgaps of argyrodites Li₆PY₅Br containing different Y²⁻ anions

Argyrodite cubic phase	Calculated bandgap (eV)
Li6PO5Br	5.67
Li6PS5Br	2.12
Li6PSe5Br	1.00
Li6PTe5Br	0.00

---

Based on these calculations the stability and electrochemical window of argyrodites should increase in the order of Te ≪ Se < S < O. While selenium argyrodites might be accessible, their limited stability will probably remain an issue for practical applications. Among the four classes of argyrodites, sulphur argyrodites still strike the best balance between stability and conductivity.

Concluding remarks

The search for solid electrolyte materials is often a compromise between chemical stability and ionic conductivity of a compound. Using argyrodite systems as an example, a systematic evaluation of structural stability, hydrolysis stability, ionic conductivity and electronic conductivity is achieved combining various computational techniques. The results show that there is significant room for synthesizing argyrodite compounds with improved stability and conductivity as solid electrolyte materials for ion-conducting rechargeable batteries.

Acknowledgements

This research is supported by the National Research Foundation, Prime Minister's office, Singapore under its Competitive Research Programme (CRP Awards No. NRF-CRP 10-2012-6 and NRF-CRP 8-2011-04).

References

1. M. Tatsumisago, M. Nagao and A. Hayashi, J. Australas. Ceram. Soc., 2013, 1, 17–25.
2. P. Knauth, Solid State Ionics, 2009, 180, 911–916.
3. H. Yamane, M. Shibata, Y. Shimane, T. Junke, Y. Seino, S. Adams, K. Minami, A. Hayashi and M. Tatsumisago, Solid State Ionics, 2007, 178, 1163–1167.
4. Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631.
5. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Matsui, Nat. Mater., 2011, 10, 682–686.
6. S. Adams and R. P. Rao, J. Mater. Chem., 2012, 22, 7687–7691.
7. R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Solid State Ionics, 2000, 130, 97–104.
8. E. Rangasamy, Z. Liu, M. Gobet, K. Pilar, G. Sahu, W. Zhou, H. Wu, S. Greenbaum and C. Liang, J. Am. Chem. Soc., 2015, 137, 1384–1387.
9. S. Adams and J. Swenson, Phys. Chem. Chem. Phys., 2002, 4, 3179–3184.
10. H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755–758.
11. C. Winkler, Ber. Bunsen-Ges., 1886, 19, 210–211.
12. D. Frank, B. Gerke, M. Eul, R. Pöttgen and A. Pfitzner, Chem. Mater., 2013, 25, 2339–2345.
13. C. Palache, H. Berman and C. Frondel, Dana's system of mineralogy, John Wiley & Son's, New York, 7th edn, 1944, vol. 1, pp. 356–358.
14. (a) W. F. Kuhs, R. Nitsche and K. Scheunemann, Mater. Res. Bull., 1979, 14, 241–248; (b) W. F. Kuhs and G. Heger, in Fast ion transport in solids: electrodes, and electrolytes, ed. P. Vashishta, J. N. Mundy and G. K. Shenoyeds, Proceedings of the International Conference on Fast Ion Transport in Solids, Electrodes, and Electrolytes, Lake Geneva, Wisconsin, USA, May 21–25, Elsevier, Amsterdam, 1979, pp. 233–236.
15. (a) M. Evain, E. Gaudin, F. Boucher, V. Petricek and F. Taulelle, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 1998, 54, 376–383; (b) E. Gaudin, F. Boucher, V. Petricek, F. Taulelle and M. Evain, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2000, 56, 402–408; (c) E. Gaudin, V. Petricek, F. Boucher, F. Taulelle and M. Evain, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2000, 56, 972–979.
16. (a) H. Wada, J. Alloys Compd., 1992, 178, 315–323; (b) H. Wada, A. Sato, M. Onoda, S. Adams, M. Tansho and M. Ishii, Solid State Ionics, 2002, 154–155, 723–727.
17. A. S. Kinduris, R. A. Bendoryus and D. B. Senulene, Sov. Phys. Semicond., 1976, 10, 916–917.
18. (a) R. P. Rao and S. Adams, Phys. Status Solidi A, 2011, 208, 1804–1807; (b) S. Adams and R. Prasada Rao, Understanding Ionic Conduction and Energy Storage Materials with Bond-Valence-Based Methods, in Bond Valences, Structure and Bonding, ed. I. D. Brown and K. R. Poeppelmeier, Springer, Berlin, Heidelberg, 2014, vol. 158, pp. 129–159.
19. R. P. Rao, N. Sharma, V. K. Peterson and S. Adams, J. Solid State Electrochem., 2012, 16, 1807–1813.
20. M. Chen, R. P. Rao and S. Adams, Solid State Ionics, 2014, 262, 183–187.
21. R. P. Rao, N. Sharma, V. K. Peterson and S. Adams, Solid State Ionics, 2013, 230, 72–76.
22. M. Ishii, M. Onoda and K. Shibata, Solid State Ionics, 1999, 121, 11–18.
23. A. Haznar, A. Pietraszko and I. P. Studenyak, Solid State Ionics, 1999, 119, 31–36.
24. (a) M. Wagener, H.-J. Deiseroth and C. Reiner, Z. Kristallogr., 2006, 221, 533–538; (b) M. Wagener, PhD thesis, University of Siegen, 2005.
25. M. V. Moroz, P. Y. Demchenko, L. G. Akselrud, O. G. Mykolaychuk and R. E. Gladyshevskii, Chem. Met. Alloys, 2010, 3, 161–168.
26. O. G. Mykolaychuk, N. V. Moroz, P. Yu. Demchenko, L. G. Akselrud and R. E. Gladyshevskii, Inorg. Mater., 2010, 46, 590–597.
27. N. A. W. Holzwarth, N. D. Lepley and Y. A. Du, J. Power Sources, 2011, 196, 6870–6876.
28. S. Adams, Solid State Ionics, 2000, 136, 1351–1361.
29. (a) S. Adams and R. P. Rao, Phys. Status Solidi A, 2011, 208, 1746–1753; (b) S. Adams and R. P. Rao, in Bond Valences, ed. I. D. Brown and K. R. Poeppelmeier, Springer-Verlag, Berlin Heidelberg, 2014, ch. 5, pp. 129–159.
30. S. Adams and R. P. Rao, Solid State Ionics, 2011, 184, 57–61.
31. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
34. G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
35. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
36. GNU Linear Programming Kit, version 4.55, http://www.gnu.org/software/glpk/glpk.html.
37. S. Adams, Practical Considerations in Determining Bond Valence Parameters, in Bond Valences, Structure and Bonding, ed. I. D. Brown and K. R. Poeppelmeier, Springer, Berlin, Heidelberg, 2014, vol. 158, pp. 91–128.
38. L. L. Wong, H. M. Chen and S. Adams, Phys. Chem. Chem. Phys., 2015, 17, 9186–9193.
39. M. J. S. Dewar, E. F. Healy and J. J. P. Stewart, J. Chem. Soc., Faraday Trans. 2, 1984, 280, 227–233.
40. S.-T. Kong, H.-J. Deiseroth, C. Reiner, Ö. Gün, E. Neumann, C. Ritter and D. Zahn, Chem. – Eur. J., 2010, 16, 2198–2206.
41. H.-J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S.-T. Kong and C. Reiner, Z. Anorg. Allg. Chem., 2011, 637, 1287–1294.
42. S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Solid State Ionics, 2012, 221, 1–5.
43. V. Epp, Ö. Gün, H.-J. Deiseroth and M. Wilkening, J. Phys. Chem. Lett., 2013, 4, 2118–2123.
44. O. Pecher, S.-T. Kong, T. Goebel, V. Nickel, K. Weichert, C. Reiner, H.-J. Deiseroth, J. Maier, F. Haarmann and D. Zahn, Chem. – Eur. J., 2010, 16, 8347–8354.
45. S.-T. Kong, H.-J. Deiseroth, J. Maier, V. Nickel, K. Weichert and C. Reiner, Z. Anorg. Allg. Chem., 2010, 636, 1920–1924.
46. S.-T. Kong, O. Gün, B. Koch, H.-J. Deiseroth, H. Eckert and C. Reiner, Chem. – Eur. J., 2010, 16, 5138–5147.
47. W. H. Paar, A. C. Roberts, P. Berlepsch, T. Armbruster, D. Topa and G. Zagler, Can. Mineral., 2004, 42, 1757–1769.
48. A. Ggor, A. Pietraszko and D. Kaynts, J. Solid State Chem., 2005, 178, 3366–3375.
49. T. Nilges and A. Pfitzner, Z. Kristallogr., 2005, 220, 281–294.
50. Q. Shi, Master thesis, Shandong University, 2012.
51. R. H. P. Francisco, J. Solid State Chem., 1993, 107, 452–459.
52. V. Epp, Ö. Gün, H.-J. Deiseroth and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 7123–7132.

---

Footnotes

† Electronic supplementary information (ESI) available: Program to evaluate critical reactions; tabulated values used to plot graphs. See DOI: 10.1039/c5cp01841b

‡ The Wyckoff site names 4d and 4a strictly speaking apply only to the most common case of space group F4̄3m. For the lower symmetry cubic Argyrodites both sites would be of type 4a, but still symmetry-independent.

---