Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An important impact of the molecule–electrode coupling asymmetry on the efficiency of bias-driven redox processes in molecular junctions
Ioan
Bâldea†
Theoretische Chemie, Universität Heidelberg, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany. E-mail: ioan.baldea@pci.uni-heidelberg.de
First published on 6th May 2015
Abstract
Two recent experimental and theoretical studies (Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1282–1287; Phys. Chem. Chem. Phys., 2014, 16, 25942–25949) have addressed the problem of tuning the molecular charge and vibrational properties of single molecules embedded in nanojunctions. These are molecular characteristics escaping so far from an efficient experimental control in broad ranges. Here, we present a general argument demonstrating why, out of various experimental platforms possible, those wherein active molecules are asymmetrically coupled to electrodes are to be preferred to those symmetrically coupled for achieving a(n almost) complete redox process, and why an electrochemical environment has advantages over “dry” setups. This study aims at helping to nanofabricate molecular junctions using the most appropriate platforms allowing the broadest possible bias-driven control over the redox state and vibrational modes of single molecules linked to electrodes.
1 Introduction
In spite of impressive advances in nanoelectronics,1–4 detailed characterization and control of molecular properties under in situ conditions continue to remain important challenges for fabricating and understanding single-molecule junctions. To this aim, more recent studies have emphasized the need to go beyond electronic transport.5–7 Vibrational properties studied via inelastic electron tunneling spectroscopy (IETS)8 and surface enhanced Raman spectroscopy (SERS)5,6,9–12 may represent such a valuable piece of information, ideally if they are acquired concomitantly using transport measurements. This has been demonstrated in a recent joint experimental theoretical study on fullerene-based electromigrated junctions13 and a theoretical study14 on viologen-based junctions in the electrochemical (EC) scanning tunneling microscope (STM) setup. The latter was based on experimental data reported previously.15Ref. 13 and 14 indicated that a significant tuning of vibrational frequencies and Raman scattering intensities can be obtained via bias-driven changes in the charge of the active molecule in a current carrying state; tuning the molecular charge via applied biases allows us to control chemical bond strengths and, thence, vibrational properties.
Obviously, the broadest control that can be achieved pursuing this route corresponds to the complete change in the average redox state of the molecule by adding an entire electron. To be specific, we limit ourselves to n-type (LUMO-mediated) conduction (orbital energy offset ε0 > 0), as this is the case for the molecular junctions reported in ref. 13, 14 and 16. Reaching this ideal limit was impossible in the experiments reported in ref. 13. On the other hand, ref. 14 indicated that an almost perfect reduced (n ≈ 1) state can be reached in electrolytically gated junctions.15
Are the obstacles to obtaining a full reduction in some molecular junctions merely of technical nature? This is the question that initiated the present study. By comparing performances of various nanofabrication platforms and identifying the ones (depicted in Fig. 5a and 6a below) that are most advantageous for achieving an almost complete reduction, the present study aims at helping to design molecular junctions allowing the broadest bias-driven control over the molecular charge and vibrational properties.
2 Model
The framework adopted here is provided by the single-level Newns–Anderson model, which was discussed17,18 and validated for a variety of molecular junctions,19–21 including those used in the existing SERS-transport studies.13,14 We checked that reorganization effects14,17,18,22–24 do not qualitatively change the present conclusions. This is illustrated by the comparison between Fig. 3 and 4, Fig. 1 and 2, and between panels b and c of Fig. 6. To make the presentation as simple and clear as possible, we will give below only formulae wherein reorganization effects are disregarded; details of the ensemble averaging needed to include these effects are not given here but can be found elsewhere.17,18,24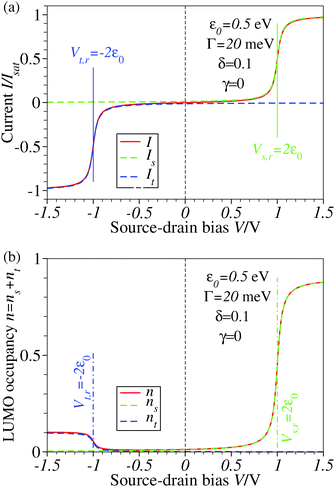 | ||
| Fig. 1 Results for ε0 = 0.5 eV, Γ = 20 meV, δ = 0.1, and γ = 0 showing that the biases V where steps and plateaus in the current I and LUMO occupancy n occur are controlled by the values Vs,r and Vt,r (see eqn (5) and (6) of the main text) where the LUMO becomes resonant with the Fermi levels of electrodes s(ubstrate) and t(ip), respectively. Note that the reduction efficiency (quantified by the LUMO occupancy n) is strongly dependent on the bias polarity in the case of an asymmetric molecule electrode coupling (Γs ≠ Γt), unlike the current plateau value, which is unchanged upon bias polarity reversal. ns and nt represent the separate electrodes' contributions to the LUMO occupancy n expressed by the first and second terms in the RHS of eqn (5) from the main text. For better readability, a vertical dashed line marks the zero bias reference. | ||
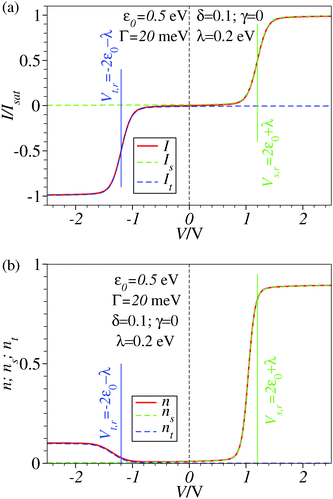 | ||
| Fig. 2 Results similar to those of Fig. 1 including reorganization effects quantified by the reorganization energy λ whose value is given in the legend. For better readability, a vertical dashed line marks the zero bias reference. | ||
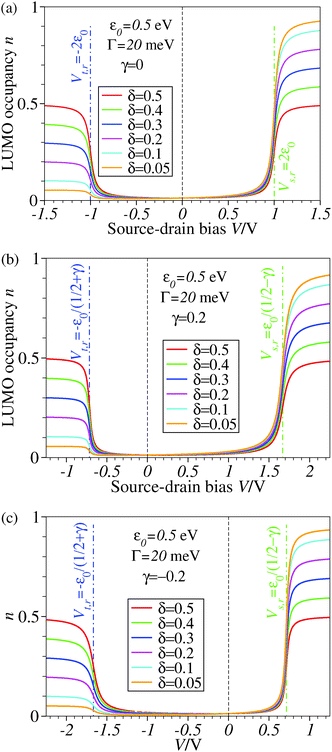 | ||
| Fig. 3 The stronger the asymmetry of molecule–electrode couplings (smaller δ′s), the more efficient is the LUMO reduction. Note that a nonvanishing value of γ (panels b and c) breaks the bias reversal symmetry (n(−V) ≠ n(V)) but does not change the plateau values of n with respect to the case γ = 0 (panel a). The values of ε0 and Γ are comparable to those used in existing concurrent SERS-transport studies.13,14 For better readability, a vertical dashed line marks the zero bias reference. | ||
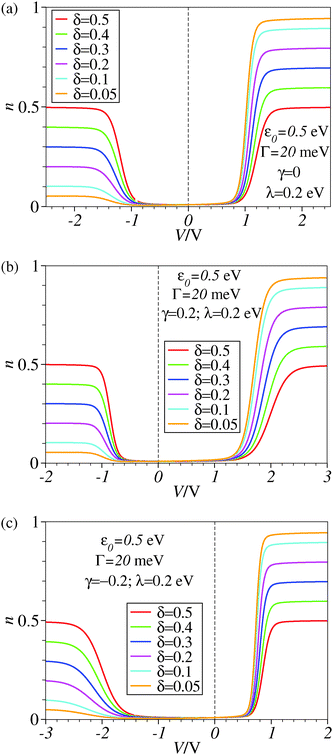 | ||
| Fig. 4 Results similar to those of Fig. 3 including reorganization effects quantified by the reorganization energy λ whose value is given in the legend. For better readability, a vertical dashed line marks the zero bias reference. | ||
Eqn (1), (5), (3) and (4),17,18,24 which allow us to express the current I and the LUMO occupancy n, constitute the framework of the present discussion (e and h are the elementary charge and Planck's constant, respectively).
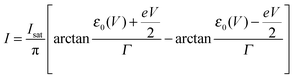 | (1) |
| Isat = 2πeΓsΓt/(hΓ) | (2) |
| ε0(V) = ε0 + γeV | (3) |
| Γs = 2Γ (1 − δ); Γt = 2Γδ | (4) |
| n = ns + nt | (5) |
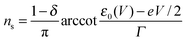 | (6) |
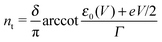 | (7) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) t −
t − ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) s). Using a potential origin located symmetrically between the electrodes' Fermi energies (−e
s). Using a potential origin located symmetrically between the electrodes' Fermi energies (−e![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) s,t = ±eV/2), −1/2 < γ < 1/2. γ is positive (negative) if the bias shifts the LUMO towards the Fermi level of electrode s (t).
s,t = ±eV/2), −1/2 < γ < 1/2. γ is positive (negative) if the bias shifts the LUMO towards the Fermi level of electrode s (t).
Similar to I (Fig. 1 and 2),14 the LUMO occupancy exhibits substantial changes within ranges δV ∼ Γ (which are narrow in typical non-resonant cases Γ ≪ ε0) at the biases (case λ = 0)
| Vr,s = ε0/(1/2 − γ) | (8) |
| Vr,t = −ε0/(1/2 + γ) | (9) |
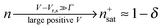 | (10) |
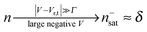 | (11) |
3 Results and discussion
The impact of the source–drain bias on the molecular charge is depicted in Fig. 3 and 4. It is worth noting that the asymmetry in electronic coupling (δ ≠ 1/2, Γs ≠ Γt) is physically distinct from the asymmetry (γ ≠ 0) in the electric potential drop across a molecular junction.14,19,28 Their impact on n is completely different. The comparison between Fig. 3a and b reveals that γ ≠ 0 merely breaks the bias reversal symmetry (n(V) ≠ n(−V)). This is the counterpart of current rectification (I(−V) ≠ −I(V), cf.eqn (1) and (3)). As long as the molecule–electrode coupling is symmetric (δ = 1/2), the plateau values at either bias polarity are equal, n+sat = n−sat = 1/2.From the perspective of achieving a full redox process in biased molecular junctions, this result for symmetric coupling is disappointing: whatever high is the source–drain bias which a molecular junction can withstand (|V| ≫ Vr,s or |Vr,t|), whether the potential profile is symmetric (γ = 0) or asymmetric (γ ≠ 0), the average molecular charge cannot exceed half of an electron (n±sat = 1/2 for δ = 1/2, cf.eqn (5)). This is a surprising result; intuitively, one may expect a full change in the molecular redox state (n = 1) at biases corresponding to resonant transport (ε0(V) ≈ μs(V) or μt(V)).13 In fact, exactly on resonance (V = Vr,s or Vr,t) the average molecular charge is even smaller: n ≈ 1/4, see eqn (12) and (13) for δ = 1/2, Γ ≪ ε0.
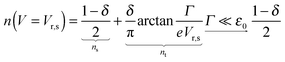 | (12) |
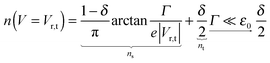 | (13) |
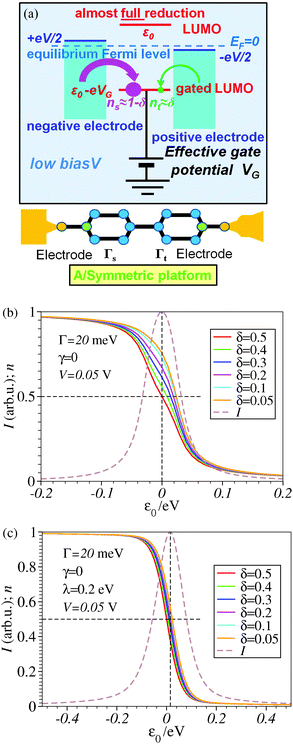
The foregoing analysis demonstrated that an almost complete reduction can be obtained (i) for a molecule highly asymmetrically coupled to electrodes and (ii) for sufficiently high biases. While the first condition (Γt ≪ Γs) can be easily satisfied in asymmetrical EC-STM (see Section 4.2)14,26 setups, the second condition seems problematic. Fig. 1 illustrates that the biases needed for an almost perfect reduction are those where current plateaus occur.
As experiments on molecular junctions did not routinely report currents exhibiting plateaus with increasing bias (we are aware of one exception29), this appears to be an important practical limitation.
A nearly complete reduction would be possible if the LUMO lies below the Fermi level of the strongest coupled electrode (n ≈ 1 − δ for δ ≪ 1 form eqn (5)) or below the Fermi levels of both electrodes (Fig. 6). This results from eqn (5): n ≈ (1 − δ) + δ = 1 for ε0 < 0 (the LUMO below the Fermi level EF(= 0) of unbiased electrodes). In the absence of any bias, ε0 > 0; the Fermi level lies within the HOMO–LUMO gap of a molecule linked to electrodes (charge neutrality). However, ε0 < 0 becomes possible during electrostatic gating.15,30–32 An appropriate gate potential VG (overpotential in the electrochemical language, on which the LUMO energy ε0 linearly depends15,25,26,31) can lower the LUMO energy below EF (Fig. 6a). I–VG (I–ε0) transfer characteristics exhibiting maxima, which occur at resonance (ε0 ≈ 0),15,18,24 can be taken as an indication of a substantial change in the molecular redox state (from n ≈ 0 for ε0 > 0 to n ≈ 1 for ε0 < 0). This is illustrated in Fig. 6b, which emphasizes that it is not the (source–drain) bias V, but rather the overpotential that determines the reduction efficiency in the electrochemical environment.
4 Specific remarks
In this section we will address three specific issues related to the results reported above.4.1 Rectification vs. reduction
To avoid possible misunderstandings, in this subsection we briefly discuss some of the present results in the context of those reported previously.In agreement with previous work (e.g., ref. 33 and 34), eqn (1)–(3) show that asymmetric molecule–electrode couplings alone (i.e., Γs ≠ Γt (or δ ≠ 1/2) and γ = 0) do not yield rectification: the aforementioned equations yield I(−V) = −I(V) for γ = 0 irrespective of the value of δ.
The fact that a potential profile asymmetry (γ ≠ 0) yields current rectification has been amply discussed. A very incomplete list includes ref. 19, 29, 34 and 35; note that the parameters p of ref. 29 and 35 and a of ref. 34 correspond to that denoted by γ in this paper. In particular, the present eqn (1) coincides with eqn (4b) of ref. 34. This is why all conclusions on the current asymmetry (“current rectification”) emerging from our eqn (1) are not new; they coincides with those of the earlier studies based on the same formula for the current I = I(V).
Important new results reported in the present paper are that an applied bias can yield an asymmetric molecular reduction n(−V) ≠ n(V) and that current asymmetry I(−V) ≠−I(V) and reduction asymmetry n(−V) ≠ n(V) are conceptually different. In particular, a symmetric current I(−V) = −I(V) (no rectification) does not rule out an asymmetric LUMO occupancy n(−V) ≠ n(V) (cf.Fig. 1) and current rectification I(−V) ≠ −I(V) does not rule out symmetric plateau values of the reduction degree (n(V ≪ −2ε0) = n(V ≫ 2ε0) = 1/2 for Γs = Γt).
Concerning the current rectification a final comment is in order, however. Similar to ref. 33 and 34, eqn (1)–(3) refer to situations wherein reorganization effects are ignored (i.e., λ ≡ 0). As recent work demonstrated,26 in cases where reorganization effects are non-negligible (λ ≠ 0), the asymmetry Γs ≠ Γt yields current rectification (I(−V) ≠ −I(−V)) even if there is no bias-induced shift of the LUMO energy (γ = 0); see eqn (13), (18) to (23) of ref. 26 and 36 Without intending to be exhaustive (current rectification in not our primary aim here), we mention that, in cases wherein Γs ≠ Γt and γ = 0, current rectification may also appear due to charging effects.37,38
4.2 Symmetric vs. asymmetric contact couplings and experimental platforms
The above analysis demonstrated the key role played by the molecule–electrode couplings (Γx, x = s,t) in determining the reduction efficiency. For electrodes with wide flat band structures around the Fermi energy, Γs,t can be expressed in terms of the electrode density of states at the Fermi level ρs,t and effective transfer integrals ts,t quantifying the charge transfer between electrodes and the dominant molecular orbital (LUMO in the specific case considered here)39| Γx = ρxtx2 | (14) |
In typical STM or CP-AFM experiments, molecules forming regular self-assembled monolayers (SAMs) are (covalently) bound to the substrate. A difference ρs ≠ ρt (yielding Γs ≠ Γtviaeqn (14)) may exist because the substrate surface is typically monocrystalline (e.g., Au(111)) while the tip facet is undefined. Still, it is more probable that not the difference ρs ≠ ρt but rather the charge transfer efficiency (ts ≠ tt) determines the contact coupling asymmetry Γs ≠ Γt.
Quantifying the asymmetry Γs ≠ Γt from transport measurements is not straightforward; we have seen above that (nearly) symmetric curves I(−V) ≈ −I(V), which are measured in numerous junctions based on symmetric (and occasionally also asymmetric) molecules, do not exclude (highly) asymmetric contact couplings.
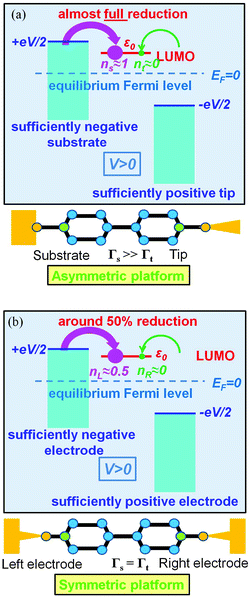
A coupling asymmetry Γs > Γt has been concluded in ref. 41 after a detailed analysis of the transport data in CP-AFM junctions. In CP-AFM setups such an asymmetry appears to be plausible because one can expect that ts > tt, given the fact that a stable molecule–tip chemical bond is hard to imagine; normally, charge transport only occurs by applying a loading force at the CP-AFM tip.42 A similar inequality (ts > tt, Γs > Γt) can also be expected for STM break junctions; the formation of a stable molecule–tip chemical bond is implausible during repeated processes of rapidly crashing the tip into and retracting it away from the substrate.43,44 So, although per se the asymmetric outlook of the STM and CP-AFM setups does not necessarily imply Γs > Γt, this inequality can be expected in view of the different bond strength at the contacts. The fact that the symmetry of the electromigration platform and the asymmetry of the STM platform do not merely refer to the usual schematic illustrations of these setups (like those in Fig. 5 and 6), but also have a physical content has been recently quantified.45,46
Out of the various experimental platforms employed, the EC-STM setup appears to be the most favorable, allowing almost perfect reduction. In the electrochemical environment (EC-STM),15 the tip typically approaches but does not come in contact with the free end of the molecules. The different through-bond vs. through-space charge transfer mechanisms at the (EC-)STM substrate and the tip reflect themselves in significantly different transfer integrals (ts ≫ tt) responsible for the high asymmetry Γs ≫ Γt (cf.eqn (14)); in agreement with this analysis, our recent studies demonstrated very highly asymmetric molecule–electrode couplings: δ ∼ 10−4 (ref. 26) and δ ∼ 10−2 (ref. 14).
4.3 The Newns–Anderson model
As noted in the Introduction section, the present study has been motivated by the findings reported in ref. 13 and 14, which demonstrated that reduction is possible in molecular junctions in current carrying states and concluded that the Newns–Anderson model (single level + Lorentzian transmission) represents an adequate theoretical framework. In favor of the the Newns–Anderson model one can still add its ability to excellently describe the charge transport by tunneling in a variety of molecular junctions.19,20,21,33 The aforementioned findings represent a sufficient justification for adopting the Newns–Anderson model in the present study.Still, for reasons delineated below we believe that our main conclusion on the impact of coupling asymmetry (Γs ≠ Γt) on the reduction efficiency holds beyond the Newns–Anderson framework.
Using the expressions of the partial LUMO occupancies ns and nt given in eqn (6) and (7), respectively, eqn (1) can be rewritten as follows
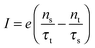 | (15) |
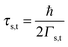 | (16) |
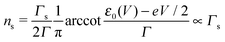 | (17) |
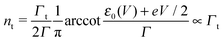 | (18) |
Eqn (17) and (18) yield the following limiting (plateau) values
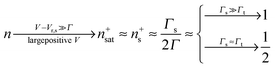 | (19) |
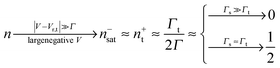 | (20) |
Obviously, the aforementioned findings should not be taken as an attempt to discourage alternative approaches of redox processes in molecular junctions based on other theoretical models utilized in the literature39 or by further refinements of the Newns–Anderson model itself. Concerning the latter possibility, an extension that appears to us as particularly important in studying charge transport through redox units is to consider population dependent contact couplings Γs,t = Γs,t(n) and LUMO energy ε0 = ε0(n).
From numerous studies on redox electrochemical systems,47 it is known that changes in the reduction (or oxidation) degree—with accompanying redistributions of the electronic charge over the whole molecule—have an overall, although selective impact on the chemical bond strengths between various molecular constituents and molecular orbital energies. For molecular junctions, the influence of the reduction (or oxidation) degree on the bond strengths at the contacts is of particular interest; so, the transfer integrals ts,t (and thence Γs,t, cf., eqn (14)) are expected to be affected.
5 Conclusions
We believe that the new theoretical results reported in the present paper offer relevant information for a better theoretical understanding of the microscopic processes occurring in molecular junctions away from equilibrium and useful hints for future experimental investigation.We have identified experimental platforms allowing almost complete bias-controlled redox processes in molecular junctions. Information on the bias (V and VG ∼ ε0) dependent LUMO (in the specific case examined) occupancy n, the quantity on which we have focused our attention, can be obtained from bias dependencies of vibrational frequencies ων(V,ε0) = [1 − n(V,ε0)]ωnν + n(V,ε0)ωaν and Raman scattering intensities Aν(V,ε0) = [1 − n(V,ε0)]Anν + n(V,ε0)Aaν extracted from simultaneous SERS-transport measurements, which take values interpolating between the relevant (neutral n and anionic a) charge species.14 We have demonstrated that the experimental setup asymmetry plays an essential role in achieving an almost perfect reduced state via bias tuning; efficient reduction is possible within some molecular electronic platforms, but definitely impossible within other platforms. We have shown that reduction can at most reach 50% in two-terminal setups wherein a molecule is symmetrically coupled to electrodes (Fig. 5b). In contrast, an almost complete redox process can be obtained in cases of highly asymmetric molecule–electrode couplings (Fig. 5b). On this basis, an improved reduction can be expected in fullerene-based junctions if an STM platform (highly asymmetric coupling) is adopted instead of the electromigration platform (symmetric couplings) utilized in experiments.13
Further, we found that an almost full reduction in two-terminal setups is accompanied by current plateaus. Because such plateau effects have been observed in molecular junctions based on the zwitterionic molecule hexadecylquinolinium tricyanoquinodimethanide (C16H33Q3−CNQ)29 (seemingly the only known example), concurrent SERS-transport measurements13,14 on this system could be of interest to investigate bias-driven changes in molecular vibrational properties.
The fact that, unlike existing orbital gating measurements using “dry”' platforms,32 experiments resorting to electrolyte gating15,30,31 succeeded to reveal such a maximum renders the electrochemical three-terminal (EC-STM) platform a promising route in achieving an efficient reduction in molecular electronic devices,14 also because it does not require high biases hardly accessible experimentally and the coupling asymmetry is not critical (cf.Fig. 6b).
Acknowledgements
Financial support provided by the Deutsche Forschungsgemeinschaft (grant BA 1799/2-1) is gratefully acknowledged.References
- S. J. Van der Molen, N. R. Naaman, E. Scheer, J. B. Neaton, A. Nitzan, D. Natelson, N. J. Tao, H. van der Zant, M. Mayor, M. Ruben, M. Reed and M. Calame, Nat. Nanotechnol., 2013, 8, 385–389 CrossRef PubMed.
- M. A. Ratner, Nat. Nanotechnol., 2013, 8, 378–381 CrossRef CAS PubMed.
- S. H. Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486 CrossRef CAS PubMed.
- E. Lörtscher, Nat. Nanotechnol., 2013, 8, 381–384 CrossRef PubMed.
- J.-H. Tian, B. Liu, X. Li, Z.-L. Yang, B. Ren, S.-T. Wu, N. Tao and Z.-Q. Tian, J. Am. Chem. Soc., 2006, 128, 14748–14749 CrossRef CAS PubMed.
- D. R. Ward, D. A. Corley, J. M. Tour and D. Natelson, Nat. Nanotechnol., 2010, 6, 33–38 CrossRef PubMed.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410 CrossRef CAS PubMed.
- B. C. Stipe, M. A. Rezaei and W. Ho, Science, 1998, 280, 1732–1735 CrossRef CAS PubMed.
- L. L. Zhao, L. Jensen and G. C. Schatz, Nano Lett., 2006, 6, 1229–1234 CrossRef CAS PubMed.
- Z. Liu, S.-Y. Ding, Z.-B. Chen, X. Wang, J.-H. Tian, J. R. Anema, X.-S. Zhou, D.-Y. Wu, B.-W. Mao, X. Xu, B. Ren and Z.-Q. Tian, Nat. Commun., 2011, 2, 305 CrossRef PubMed.
- B. Liu, A. Blaszczyk, M. Mayor and T. Wandlowski, ACS Nano, 2011, 5, 5662–5672 CrossRef CAS PubMed.
- T. Konishi, M. Kiguchi, M. Takase, F. Nagasawa, H. Nabika, K. Ikeda, K. Uosaki, K. Ueno, H. Misawa and K. Murakoshi, J. Am. Chem. Soc., 2013, 135, 1009–1014 CrossRef CAS PubMed.
- Y. Li, P. Doak, L. Kronik, J. B. Neaton and D. Natelson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1282–1287 CrossRef CAS PubMed.
- I. Bâldea, Phys. Chem. Chem. Phys., 2014, 16, 25942–25949 RSC.
- I. V. Pobelov, Z. Li and T. Wandlowski, J. Am. Chem. Soc., 2008, 130, 16045–16054 CrossRef CAS PubMed.
- The discussion in this paper, couched in terms of the LUMO and reduction, refers to molecular junctions exhibiting n-type conduction. For molecular junctions with p-type conduction, the following replacements should be done: LUMO → HOMO, reduction → oxidation, ε0 = εLUMO
![[quadruple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e003.gif) ELUMO − EF → −ε0 = εHOMO
ELUMO − EF → −ε0 = εHOMO ![[quadruple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e003.gif) EF − EHOMO > 0 and γ → −γ.
EF − EHOMO > 0 and γ → −γ. - W. Schmickler, J. Electroanal. Chem., 1986, 204, 31–43 CrossRef CAS.
- I. G. Medvedev, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125312 CrossRef.
- I. Bâldea, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035442 CrossRef.
- I. Bâldea, J. Am. Chem. Soc., 2012, 134, 7958–7962 CrossRef PubMed.
- (a) I. Bâldea, Nanoscale, 2013, 5, 9222–9230 RSC; (b) I. Bâldea, Z. Xie and C. D. Frisbie, Nanoscale, 2015 10.1039/c5nr02225h.
- W. Schmickler and N. Tao, Electrochim. Acta, 1997, 42, 2809–2815 CrossRef CAS.
- A. N. Kuznetsov and W. Schmickler, Chem. Phys., 2002, 282, 371–377 CrossRef CAS.
- I. Bâldea, J. Phys. Chem. C, 2014, 118, 8676–8684 Search PubMed.
- I. G. Medvedev, J. Electroanal. Chem., 2007, 600, 151–170 CrossRef CAS.
- I. Bâldea, J. Phys. Chem. C, 2013, 117, 25798–25804 Search PubMed.
- F. Zahid, M. Paulsson and S. Datta, Electrical Conduction through Molecules, Advanced Semiconductors and Organic Nano-Techniques, Academic Press, 2003, vol. 3 Search PubMed.
- J. Hodgkiss, E. Zysman-Colman, S. Higgins, G. Solomon, I. Bâldea, I. Samuel, L. Venkataraman, F. Wudl, B. Xu, R. Venkatramani, H. Ottosson, D. Perepichka, U. Lemmer, P. Skabara, A. Mount and D. Bradley, Faraday Discuss., 2014, 174, 125–151 RSC.
- R. M. Metzger, T. Xu and I. R. Peterson, J. Phys. Chem. B, 2001, 105, 7280–7290 CrossRef CAS.
- N. J. Tao, Phys. Rev. Lett., 1996, 76, 4066–4069 CrossRef CAS PubMed.
- A. Alessandrini, S. Corni and P. Facci, Phys. Chem. Chem. Phys., 2006, 8, 4383–4397 RSC.
- H. Song, Y. Kim, Y. H. Jang, H. Jeong, M. A. Reed and T. Lee, Nature, 2009, 462, 1039–1043 CrossRef CAS PubMed.
- I. Bâldea, Chem. Phys., 2012, 400, 65–71 CrossRef.
- G. Zhang, M. A. Ratner and M. G. Reuter, J. Phys. Chem. C, 2015, 119, 6254–6260 CAS.
- I. R. Peterson, D. Vuillaume and R. M. Metzger, J. Phys. Chem. A, 2001, 105, 4702–4707 CrossRef CAS.
- For clarity, let us still mention that, although present, current rectification is hardly visible within the drawing accuracy shown in Fig. 2.
- F. Zahid, A. W. Ghosh, M. Paulsson, E. Polizzi and S. Datta, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245317 CrossRef.
- We note that, in fact, the current rectification driven by the charging effects reported in ref. 37 relies just upon the population asymmetry n(−V) ≠ n(V) discussed in the present paper.
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific Publishers, 2010 Search PubMed.
- For the sake of simplification, the present discussion ignores the fact that the C60 molecule has a threefold degenerate LUMO. The bias range sampled in the experiment is far away from the current plateaus (cf. Fig. S1–S3 of ref. 13), and even multiplied by 3; the n-values are less than 10% (cf.Fig. 4b and Fig. S7, ESI of ref. 13).
- X. Lefèvre, F. Moggia, O. Segut, Y.-P. Lin, Y. Ksari, G. Delafosse, K. Smaali, D. Guérin, V. Derycke, D. Vuillaume, S. Lenfant, L. Patrone and B. Jousselme, J. Phys. Chem. C, 2015, 119, 5703–5713 Search PubMed.
- D. J. Wold and C. D. Frisbie, J. Am. Chem. Soc., 2000, 122, 2970–2971 CrossRef CAS.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- S. Guo, J. Hihath, I. Diez-Pérez and N. Tao, J. Am. Chem. Soc., 2011, 133, 19189–19197 CrossRef CAS PubMed.
- I. Bâldea, Nanotechnology, 2014, 25, 455202 CrossRef PubMed.
- As a word of caution, one should mention that the foregoing analysis on the coupling (a)symmetry refers to symmetric molecules (and C60 of ref. 13 is one thereof).
- A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, Wiley, New York, 1980 Search PubMed.
Footnote |
| † National Institute for Lasers, Plasmas, and Radiation Physics, Institute of Space Sciences, Bucharest, Romania. |
| This journal is © the Owner Societies 2015 |