Generating hydrated electrons through photoredox catalysis with 9-anthrolate

Abstract

Hydrated electrons are among the strongest reductants known. Adding the ascorbate dianion as a sacrificial donor turns the photoionization of 9-anthrolate in water into a catalytic cycle for their in situ production with near-UV light (355 nm). The photoionization step is exclusively biphotonic and occurs via the first excited singlet state of the catalyst. Neither triplet formation nor any photochemical side reactions interfere. The ionization by-product, the anthroxy radical, is inert towards the ascorbate monoanion but is rapidly reduced by the dianion, thereby recovering the starting catalyst. A sufficient amount of the sacrificial donor makes that reduction quantitative and leads to a sustainable generation of hydrated electrons, as is evidenced by electron yields greatly surpassing the catalyst concentration. Control experiments established that the superincrease is indeed due to the catalyst regeneration and not to an ionization of other species involved in the reaction.

---

1 Introduction

The interest in photoredox catalysis as a synthetic tool has been growing exponentially during the last few years.^1–11 This method exploits that an excited state is both a better electron acceptor and a better electron donor than the ground state; it thus takes advantage of the photon energy to prepare a stronger oxidant or a reductant as an intermediate that activates a substrate through a (direct or mediated) photoinduced electron transfer; sacrificial donors or acceptors, although less favourable from the point of view of atom economy,^8,9 provide a very flexible way of regenerating the photocatalyst.

It seems to be natural to extend this idea to less reactive substrates by utilizing two photons to afford a “super oxidant” or a “super reductant” in situ. The archetypal example of the latter is the solvated or hydrated electron e_aq˙⁻ (E° = 2.77 V vs. normal hydrogen electrode NHE, comparable to activated alkali metals),¹² which has already been shown to be capable of reductively detoxifying chloro-^13,14 and fluoroorganics¹⁵ as well as directly reducing molecular nitrogen¹⁶ and carbon dioxide.¹⁷ Generating e_aq˙⁻ with a single photon necessitates energy-rich light (UV-C in all the cited examples), which is strongly absorbed by many substrates. However, the two-photon approach to e_aq˙⁻ elegantly circumvents that potential problem by shifting the required wavelengths to the UV-A¹⁸ or even the visible.¹⁹ As a photoreleased “super reductant”, e_aq˙⁻ should have one intrinsic advantage over an excited radical anion, which was successfully employed for that purpose recently,²⁰ namely a much longer natural life, microseconds (compare, Fig. 4 and 5) against nanoseconds or shorter.

Depending on whether the photocatalyst is an electron acceptor or an electron donor, two basic catalytic cycles that produce e_aq˙⁻ by consuming two photons and a sacrificial donor are conceivable. As opposed to the numerous examples we have reported for the former (Scheme 1a),^{18,19,21–25} none are known for the latter. In this work, we present a detailed mechanistic investigation of the first photocatalytic system according to Scheme 1b, where the catalyst is recovered by a thermal reaction with a sacrificial donor after the photoionization.

Scheme 1 Turning the photoionization of (a) an electron acceptor A and (b) an electron donor D into a catalytic cycle by a sacrificial donor D_sac. The colour code for all the species in (b) is used throughout this study. For further explanation, see the text.

The anions of hydroxy-substituted aromatic compounds appear to be particularly well suited for the purpose because they are very good electron donors, their ionic nature increases the solubility in the aqueous medium, and—as the main advantage over their protonated parent compounds—they cannot undergo homolytic cleavage to give hydrogen atoms as a competing reaction to photoionization.²⁶ Increasing the size of the conjugated system brings a twofold benefit, namely, a shift of the absorption towards the red and a reduction of the ionization energy: phenolate can only be ionized in the UV-C owing to its absorption properties,^26,27 whereas 2-naphtholate is already (biphotonically) ionizable at 337 nm,²⁸via its first excited singlet state S₁. For the present work, we have selected the higher homologue 9-anthrolate, which we excite into S₂ with 355 nm; the 1,8-dihydroxy derivative of that anion is thought to be the active form of a popular antipsoriasis agent.²⁹

Our experimental method is two-pulse–two-colour laser flash photolysis. To minimize interpretational uncertainties, we monitor all species occurring in the reaction mechanism, Scheme 1b.

2 Results and discussion

2.1 Relevant ground- and excited-state properties of the photocatalyst

In aqueous medium, the enol 9-anthrol enjoys merely a fleeting existence owing to two fast equlilibria, one for its deprotonation to give the anthrolate AOL⁻ (pK_a ≈ 7.8), the other for its tautomerization to give the ketone 10H-anthr-9-one AON (K ≈ 150).³⁰ As summarized in Scheme 2, this results in an apparent single equilibrium between the last two species with a pK_a′ value of 10, which facilitated choosing conditions such as to allow the photoionization of AOL⁻ to be studied without interference from other forms of that compound, namely, sufficiently high pH (mostly above 12) combined with laser excitation at 355 nm, where the molar absorption coefficient of AOL⁻ dwarfs that of AON by almost two orders of magnitude. Quantum-mechanical calculations indicate (compare, Section S1 of the ESI†) that our photocatalyst AOL⁻ is best described as a carbanion.

Scheme 2 Different forms of the photocatalyst in its ground state. Owing to the displayed fast equilibria³⁰ only the ketone AON and the anthrolate AOL⁻ are relevant. For further information, see the text.

As opposed to AON, AOL⁻ is extremely susceptible to oxidation by molecular oxygen, the end product being 9,10-anthraquinone.³¹ To circumvent this in preparing our solutions, we exploited the above-mentioned fast equilibria by adding the required amount (typically, one percent of the final volume) of a freshly made and deoxygenated millimolar solution of AON in iso-propanol to a deoxygenated aqueous solution at the desired pH using syringe techniques. Even though iso-propanol is a very good hydrogen donor, its presence does not interfere with the reactions of Scheme 1b, as evidenced by control experiments (see below). Spectrophotometry on the final solutions before and after each series of experiments served to determine the actual AOL⁻ concentration and stability, and in particular to ascertain the absence of quinone.

Fig. 1 contains the absorption and luminescence spectra of AOL⁻.

Fig. 1 Calibrated absorption spectra—except for the curve labelled L, which is the uncalibrated luminescence spectrum of the anthrolate S₁—of all species relevant for this work, with the same colour coding as in Scheme 1b; the assignment is given by the labels at the curves. The inset has exactly the same horizontal and vertical scale as the main plot, and merely serves to avoid overcrowding in the region below 450 nm. For further explanation, see the text.

In the pH range (10.5 ≤ pH ≤ 13) and concentration range (5 μM ≤ [AOL⁻] ≤ 40 μM) used in this work, we did not detect any deviations from the Beer–Lambert law nor changes in the spectral shape. The S₁ and S₂ excited states of AOL⁻ correspond to the featureless ¹L_a and to the vibrationally structured ¹L_b band,³² at 433 nm and 359/376 nm in our medium. The higher-energy vibrational feature of the latter transition almost perfectly matches our excitation wavelength (355 nm), and the lower-energy subpeak (ε₃₇₆ = 9900 M⁻¹ cm⁻¹) allows a convenient monitoring of the AOL⁻ ground-state concentration. A contamination by oxidation can be detected with good sensitivity in the region of low absorbance at around 330 nm, where anthraquinone absorbs strongly (spectrum not shown).

The fluorescence spectrum of AOL⁻ (maximum at 525 nm) exhibits a mirror-image relationship with the ¹L_a absorption band. The curve crossing at 487 nm puts the energy of the 0–0 transition at 2.55 eV. Because this is considerably less than the formation energy of e_aq˙⁻, the S₁ state obviously cannot autoionize. Neither S₁ nor S₂ are quenched by iso-propanol, as experiments with different alcohol concentrations showed.

We determined the fluorescence quantum yield φ_lum against fluorescein as the standard, and at low absorbance (A ≤ 0.1) to avoid inner filter effects. These measurements gave a wavelength-independent value of 0.073 ± 5% between 355 and 420 nm, which indicates that the ¹L_b state (S₂) also does not autoionize to a significant degree. As a corollary, e_aq˙⁻ formation should not have a pronounced monophotonic component.

To estimate the excited-state life, we carried out quenching experiments with I⁻. We found no evidence for the formation of ground-state complexes, and we obtained a linear Stern–Volmer plot with a Stern–Volmer constant of 15.8 M⁻¹. Modifying the accepted value for a diffusion controlled reaction between uncharged species in water (6.5 × 10⁹ M⁻¹ s⁻¹)³³ by the Debye formula³⁴ with an encounter distance of 5.6 Å (the sum of the van-der-Waals radius of I⁻ and the geometric mean of the molecular radii of AOL⁻ in the direction of the three principal axes; for the latter, we added the van-der-Waals radii of the terminal atoms to the quantum-mechanically computed distances O–H₁₀ and H₂–H₇, and took the separation of adjacent layers in graphite as the third component),³⁵ we obtained a quenching rate constant of 3.2 × 10⁹ M⁻¹ s⁻¹, so a singlet lifetime τ_S of 4.9 ns. The latter value is practically identical to the duration τ_L of our laser pulses (5.0 ns).

A sensitization experiment served as the test for a potential participation of the triplet state in the photochemistry of AOL⁻ at 355 nm. The sensitizer naphthalene possesses a long-lived (17 μs as measured in our medium) and efficiently formed T₁, which lies even slightly above the S₁ of AOL⁻, so is expected to undergo rapid triplet–triplet energy transfer to the AOL⁻ ground state;³³ its generation is feasible with 308 nm, i.e., a wavelength within the low-absorptivity window of AOL⁻ in the UV. By employing a naphthalene concentration of 400 μM, which necessitated increasing the iso-propanol admixture to 10% to overcome the limited solubility of the arene in water, an AOL⁻ concentration of 10 μM, similar to that in most experiments of this work, and a very low energy of the 308 nm laser pulse we were able to suppress the photoionizations of naphthalene and AOL⁻ such as to be nondetectable while still producing a sufficient amount of the naphthalene T₁ and an observable degree of quenching. This resulted in two new bands centered at 330 and 475 nm, the rise time of which was equal to the decay time (15 μs in the two-component system) of the naphthalene triplet at 390 nm.³⁶ Absent were the absorptions of the anthroxy radical AOL˙ (Fig. 1) and, in particular, those of the naphthalene radical anion around 700 nm,¹⁸ so an electron transfer from the naphthalene triplet is ruled out, and the quenching mechanism can only be energy transfer. On these grounds, we must assign these bands to the T₁ state of AOL⁻ or to a secondary product of that state formed through rapid quenching, e.g., by the iso-propanol; in any case, their occurrence is indicative of an involvement of the AOL⁻ triplet. Because these signals—which fall into spectral regions free from other peaks (compare, Fig. 1) and would thus be difficult to overlook—did not arise in all other experiments of this work, we conclude that the triplet state of AOL⁻ does not play any role in our system.

2.2 Photoionization step

Irradiation of AOL⁻ with a sufficiently intense 355 nm pulse leads to photoionization, as is evidenced by the typical signature of the hydrated electron e_aq˙⁻, a very intense and broad band centered slightly above 700 nm.¹² For the calibrated spectrum of Fig. 1, we prepared e_aq˙⁻ independently, i.e., directly in our reaction medium but without AOL⁻, by two-photon ionization of water with 266 nm,³⁷ and set the molar absorption coefficient at maximum (718 nm under our conditions) to the recently redetermined value of 22 700 M⁻¹ cm⁻¹.³⁸ Our iso-propanol admixture does not react with e_aq˙⁻.¹² The signals of e_aq˙⁻ and the other transients are conveniently separated by exploiting that only e_aq˙⁻ absorbs above 700 nm in our system; hence, we simply weighted an absorption trace in that region with the appropriate ratio of molar absorption coefficients and subtracted it from the trace at a shorter wavelength of interest.

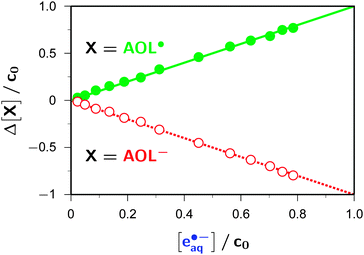
In this way, we obtained the spectrum (Fig. 1) of the anthroxy radical AOL˙, the necessary by-product of the photoionization of AOL⁻. The primary separation result is an uncalibrated difference spectrum of AOL˙ and AOL⁻, which is characterized by a positive maximum at 360 nm and a negative minimum of almost equal magnitude at 375 nm. The former indicates a strong absorption of AOL˙ at our excitation wavelength, so the question arises whether AOL˙ might itself be photoionizable (to give a nonradical cation). This issue—which is crucial not only for a unique spectral decomposition but also for a correct analysis of the intensity dependences—can be resolved by an absorbance-difference diagram,³⁹ with the modification of varying the reaction progress by varying the laser intensity: the absorbance changes at these two key wavelengths and at, e.g., 824 nm (a wavelength that allows a very sensitive monitoring of e_aq˙⁻, for instrumental reasons explained in the Experimental section) are found to be strictly proportional to one another over the accessible turnover range; hence, AOL⁻, AOL˙, and e_aq˙⁻ are connected by a single reaction step, and there is no possibility of a photoreaction consuming AOL˙.

Fig. 2 reproduces this absorbance-difference diagram in a slightly modified form, using concentrations instead of absorptions. This recalculation is based on our observation (see below) that the addition of a sufficiently high amount of the ascorbate dianion completely restores the starting concentration of AOL⁻ in the dark period after the laser flash, which establishes that the photoionization is not accompanied by any other photochemical reaction, so not only affords identical amounts of AOL˙ and e_aq˙⁻ but also consumes the very same amount of AOL⁻. This stoichiometric relationship allows a precise calibration of the molar absorption coefficient of AOL˙ against that of e_aq˙⁻; the obtained value for ε(AOL˙) at the 358 nm maximum is 15 600 M⁻¹ cm⁻¹. Because both the signal to be calibrated and the reference absorption is derived from the same experiment, all uncertainties of the optical path length are eliminated.

Fig. 2 Concentration changes Δ[X] as a function of the electron concentration [e_aq˙⁻], all taken relative to the starting anthrolate concentration c₀ (11.5 μM); red open circles, for AOL⁻; green filled circles, for AOL˙. The broken red and solid green lines have (negative and positive) unit slope and pass through the origin. Experimental pH, 12.3; each triple of concentration changes recorded at constant intensity of a 355 nm laser flash; maximum laser intensity, 315 mJ cm⁻². Wavelengths for the concentration determinations were 824 nm (e_aq˙⁻), 375 nm (bleaching of AOL⁻) and 360 nm (AOL˙). For further explanation, see the text.

As is explained above, our preparation method necessitated an iso-propanol content of the solutions of typically 1%, i.e., 0.13 M. To test whether a reaction of AOL˙ with this good hydrogen donor needs to be taken into account, we increased the iso-propanol concentration by a factor of twenty in a control experiment. This should accelerate a hydrogen abstraction by the same factor, so should shorten the life of AOL˙ if that reaction played a role; instead, we observed a doubling of the AOL˙ life, which can be quantitatively rationalized by the effect of the higher solution viscosity⁴⁰ on the diffusion-controlled dimerization of AOL˙ and recombination with e_aq˙⁻. The same control experiment also ruled out an influence of the iso-propanol admixture on the photoionization: the initial absorbance directly after the laser pulse changed by as little as 5%, which can be traced back to a slight solvatochromic shift.

Fig. 3 displays intensity dependencies not only for the e_aq˙⁻ concentration but also for the luminescence (compare, Fig. 1) originating from the first excited state of AOL⁻; owing to the short life of that state, the total (i.e., integrated) luminescence was used. It is obvious that more reliable and detailed information about a potentially complex photoreaction mechanism can be obtained by observing more than one species.

Fig. 3 Dependence of the e_aq˙⁻ concentration relative to the starting catalyst concentration c₀ (blue filled circles and solid line) and of the integrated luminescence L (yellow open circles and dashed line) on the laser intensity I₃₅₅; experimental parameters, c₀ = 11.5 μM, pH 12.3, L observed at 520 nm. The lines were calculated by a simultaneous fit of eqn (S6) and (S8) of the ESI,† with fixed parameter φ_mono = 0. For further explanation, see the main text and Section S2 of the ESI.†

These intensity dependencies can be fitted perfectly with the kinetic model explained in Section S2 of the ESI.† Simultaneous fits to both data sets require adjusting only two intensity-proportional photokinetic parameters (one for the primary excitation, and one for the ionization of the S₁ excited state by a second photon) and two constants (the quantum yield φ_mono of spontaneous electron ejection from S₁, and a scaling factor for the luminescence because our laser flash photolysis setup is not capable of measuring absolute luminescence).

The already mentioned wavelength-independence of φ_lum up to wavelengths where the energy balance of electron ejection from S₁ becomes thermodynamically unfavourable militates against a significant monophotonic contribution to electron formation. Yet, those features of the electron yield as a function of the laser intensity that are indicative of a biphotonic ionization, namely, an upward curvature in the low-intensity range and a deviation from zero of the intercept when the curve is back-extrapolated linearly,⁴¹ are almost absent with that system (compare, Fig. 3). The origin of such a phenomenon is known to be an unfavourable combination of molar absorption coefficients and quantum yields;⁴¹ as an aggravation, in the relevant intensity region the electron signal is smallest, so the sensitivity is lowest, which further hampers the analysis.

On the following grounds, the simultaneous monitoring of the electron concentration and the luminescence appears to be better suited to the task. Because luminescence emission and monophotonic electron formation originate from the same intermediate through the same type of process (i.e., with light-independent rate each), the amount of e_aq˙⁻ from the monophotonic pathway must be strictly proportional to the total luminescence, with the constant of proportionality being φ_mono/φ_lum (compare, eqn (S6) and (S8) of the ESI†). As a corollary, a high degree of similarity of the intensity dependencies of L and of the electron concentration would thus indicate a predominance of the monophotonic ionization pathway. The method further has the advantage that the observables are analyzed over the whole intensity range, not only within the region of the intrinsically worst signal-to-noise ratio.

Treating the complete parameter set as adjustable gave a best-fit value of only 0.007 for φ_mono and no better representation of the experimental data than a fit with φ_mono set to zero. In accordance with the principle of Occam's razor and the preceding reasoning based on the wavelength-independence of φ_lum, we take this to mean that there is no monophotonic ionization in our system. Despite the need of absorbing a second photon during the short life of the S₁ excited state, near-quantitative ionization of the catalyst is nevertheless attainable with a single laser pulse, as Fig. 3 shows.

2.3 Control experiments on the sacrificial donor

To turn this photoionization into a catalytic cycle according to Scheme 1b by regenerating the electron source AOL⁻ from its radical AOL˙, we need to add a sacrificial donor that must be a strong, water-soluble reductant and should absorb as weakly as possible at the ionization wavelength, 355 nm. All these requirements are met by the well-known antioxidant ascorbic acid (vitamin C). Its fully protonated form (pK_a1 = 4.25)⁴² plays no role at all in our basic medium; only its monoanion HAsc⁻ (pK_a2 = 11.79,⁴²E°(HAsc˙/HAsc⁻) = 0.300 V vs. normal hydrogen electrode NHE⁴³) and—dominating at our typical pH well above 12—its even more strongly reducing dianion Asc²⁻ (E°(Asc˙⁻/Asc²⁻) = 0.015 V vs. NHE)⁴³ are relevant.

At 355 nm, HAsc⁻ is not photoionized, but Asc²⁻ produces a small amount of e_aq˙⁻ despite its minute molar absorption coefficient (see, Fig. 1). We corrected for that effect in all the experiments on mixed AOL⁻–Asc²⁻ systems by subtracting the e_aq˙⁻ and Asc˙⁻ signals obtained in experiments without AOL⁻ but otherwise identical; in the worst case, this correction amounted to less than 10%.

The control experiment displayed in Fig. 4 addresses the question of whether Asc˙⁻ is photoionizable with 355 nm, a wavelength almost coinciding with its absorption maximum in the near UV. To that end, we first prepared Asc˙⁻ by 308 nm photoionization of Asc²⁻, which gave the spectrum of the radical shown in Fig. 1 as an additional benefit; by an absorbance-difference diagram similar to Fig. 2, we ascertained the absence of a 308 nm photoreaction of Asc˙⁻, so established the stoichiometric relationship between [e_aq˙⁻] and [Asc˙⁻] necessary for precisely calibrating the Asc˙⁻ molar absorption coefficient at maximum (ε₃₆₀ = 4500 M⁻¹ cm⁻¹). Having produced Asc˙⁻ and e_aq˙⁻ by a 308 nm pulse, we then applied an intense 355 nm pulse after a short delay. As is evident from Fig. 4, that second pulse has no effect on the slow decay of the Asc˙⁻ concentration and does not produce any new electrons. Hence, Asc˙⁻ is photoionizable neither with 308 nm nor with 355 nm.

Fig. 4 Two-pulse experiment (first pulse at t = 0, 308 nm, 280 mJ cm⁻²; second pulse at t = 5.5 μs, 355 nm, 212 mJ cm⁻²) on a 50 μM solution of Asc²⁻ at pH 12.4 showing the time dependence of the Asc˙⁻ (brown) and e_aq˙⁻ (blue) concentrations. The negative spike of the Asc˙⁻ curve at the moment of the second pulse is an artifact caused by insufficient stray-light suppression because the excitation and observation wavelengths differed by 5 nm only. For further explanation, see the text.

Such experiments also provide clear evidence that Asc˙⁻ is very stable in our medium except for its recombination with e_aq˙⁻: the Asc˙⁻ concentration exhibits a small initial decay, by some 15% in Fig. 4, which comes to a complete standstill after e_aq˙⁻ has vanished. A quantitative comparison of the electron decay in the absence of Asc˙⁻ (i.e., when we generated the same amount of e_aq˙⁻ from water with 266 nm at identical pH) and in its presence merely gave the difference expected from that recombination; hence, scavenging of e_aq˙⁻ by Asc²⁻ plays no role under our conditions. Lastly, at the concentrations used in this work Asc²⁻ does not react with the S₁ excited state of AOL⁻, as follows from the lack of a luminescence quenching.

2.4 Regeneration step

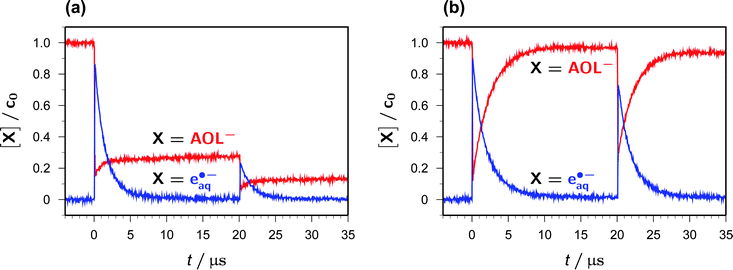
Fig. 5a and b juxtapose the concentration traces for AOL⁻ and e_aq˙⁻ in two-pulse experiments (355 nm/355 nm) that were identical twins except for the addition of Asc²⁻ in the second case. The first pulse produces the same concentration of e_aq˙⁻ in both experiments, about 85% of the starting catalyst concentration, which is accompanied by a decrease of the AOL⁻ concentration to about 15% of its inital value.

In the absence of Asc²⁻, the recombination of e_aq˙⁻ with AOL˙ inefficiently (and, of course, undesirably because it removes the species of interest) regains about the same amount of AOL⁻ during the interpulse delay (Fig. 5a). In contrast, when Asc²⁻ has been added, this sacrificial donor largely suppresses that recombination through competition, thus even slightly lengthening the life of e_aq˙⁻ stemming from the first pulse, and instead regenerates AOL⁻ almost completely (Fig. 5b).

Fig. 5 Two-pulse (both 355 nm) laser flash photolysis on an 11.9 μM solution of AOL⁻ at pH 12.4; interpulse delay, 20 μs; first pulse, 437 mJ cm⁻²; second pulse, 308 mJ cm⁻². Shown are the concentration traces of e_aq˙⁻ (blue) and AOL⁻ (red) scaled to the starting catalyst concentration c₀. Graph (a), without Asc²⁻; graph (b), with 0.6 mM Asc²⁻ added. For further explanation, see the text.

The second pulse finally acts on the AOL⁻ molecules available at that point of time, so—in keeping with their concentration ratio—affords more than three times the amount of e_aq˙⁻ in the solution containing Asc²⁻. In the examples, the total amount of e_aq˙⁻ extracted from the system by two laser flashes is thus found to surpass the starting catalyst concentration only slightly in the absence of Asc²⁻ (and that excess is merely due to the described recombination artifact) but by more than 60% in the presence of the sacrificial donor Asc²⁻. Furthermore, it is clearly seen from the second post-flash period in Fig. 5b that this sequence of ionization and regeneration could be repeated a substantial number of times until the system were exhausted.

Without ascorbate, and after e_aq˙⁻ has died down, the further fate of AOL˙ is dimerization to give one or several products absorbing below 370 nm. While these absorbances have only a negligible influence on the quantitative monitoring of AOL⁻ at 375 nm, as can be seen in Fig. 5a (the minute apparent rise of the AOL⁻ trace in the interval between 10 and 20 μs), they do interfere with the concentration determination of AOL˙ at our usual wavelength, 360 nm. We, therefore, observed the AOL˙ decay at above 500 nm where no other species besides e_aq˙⁻ absorbs (Fig. 1). In N₂O-saturated solution, where e_aq˙⁻ is quantitatively removed within the duration of our laser pulses through a scavenging cascade, ultimately yielding dimethyl ketyl radical anions in our medium,¹² we found a clean second-order decay of AOL˙ over an 80 μs time interval with a rate constant k_d of 2 × 10⁹ M⁻¹ s⁻¹. We obtained the same value when we repeated the experiment in Ar-saturated solution and analyzed only the part of the trace after e_aq˙⁻ had disappeared, so the thermodynamically feasible secondary production of AOL˙ by the attack of the dimethyl ketyl radical anions on residual AOL⁻ must be insignificant.

To determine whether only the dianion Asc²⁻ is capable of regenerating AOL⁻ from AOL˙, or also the monoanion HAsc⁻, we used the pH to vary the concentration ratio between HAsc⁻ and Asc²⁻. Fig. 6 shows the outcome of two such experiments, at pH 10.8 and pH 12.7.

Fig. 6 Laser flash photolysis (355 nm, 179 mJ cm⁻² at time t = 0) on two solutions containing 13 μM AOL⁻ as the actual species concentration plus ascorbate at different pH. The dots represent the measured concentration traces of AOL⁻ normalized to the starting concentration c₀; the solid curves are best fits of r_∞ − (r_∞ − r₀) exp[−k_rt] to each data set after the flash. Black, pH 10.8; weight-in concentration of AON, 15.0 μM; weight-in concentration of ascorbate, 4.26 mM corresponding to 3.86 mM HAsc⁻ and 0.395 mM Asc²⁻; best-fit parameters, r_∞ = 0.98, r₀ = 0.47, k_r = 2.67 × 10⁵ s⁻¹. Gray, pH 12.7; weight-in concentration of AON, 13.0 μM; weight-in concentration of ascorbate, 0.678 mM corresponding to 74.2 μM HAsc⁻ and 0.604 mM Asc²⁻; best-fit parameters, r_∞ = 0.99, r₀ = 0.43, k_r = 4.14 × 10⁵ s⁻¹. For further explanation, see the text.

By adjusting the weight-in concentrations of AON according to the protonation equilibria of anthrol (see the above discussion and explanation of the sample preparation method), we ensured equal concentrations of AOL⁻ in both solutions. At the lower pH, where the AON concentration is about 15% of the AOL⁻ concentration, we searched for additional transients but found none; hence, neither the triplet nor the radical anion is formed under our conditions.

The integrated rate law for the regeneration of AOL⁻ through a first-order reduction of AOL˙ by Asc²⁻ (rate constant k_r) competing with a second-order dimerization of AOL˙ (rate constant k_d) can be derived in closed form. Numerically, however, the resulting expression is virtually indistinguishable from the much simpler form r_∞ − (r_∞ − r₀) exp[−k_rt] under the conditions of Fig. 5b and 6, where the dimerization is only a small perturbation. The simpler form is thus to be preferred, in particular, because the additionally competing regeneration of AOL⁻ by the recombination of AOL˙ with e_aq˙⁻ had to be neglected even in the more complete solution. The parameters r₀ and r_∞ are the relative concentrations of AOL⁻ immediately after and at long times after the laser flash; the limiting value r_∞ can be related to the kinetic parameters and the starting catalyst concentration c₀ through the more compete solution,

but when calculated in this way slightly underestimates the actual value because of the neglect of the recombination of AOL˙ with e_aq˙⁻.

The ratio [HAsc⁻] : [Asc²⁻] changes by a factor of 80 between the pH values of the two experiments, from 9.8 : 1 at pH 10.8 to 0.12 : 1 at pH 12.7. When we chose appropriate weight-in concentrations of ascorbate to keep the dianion concentrations, hence the rates of AOL⁻ regeneration by Asc²⁻, within a narrow corridor of 1 : 1.53, we measured the same ratio of reaction rates (1 : 1.55; the minute deviation is clearly due to experimental uncertainty because otherwise the monoanion reaction would have to have a negative reaction rate).

We, therefore, conclude that within the detection limits of our measurements HAsc⁻ does not reduce AOL˙ whereas Asc²⁻ does; from the best-fit rates given in the caption of Fig. 6, the bimolecular rate constant k of the latter reaction is calculated to be 6.8 × 10⁸ M⁻¹ s⁻¹. Identifying the ability to react with the thermodynamic feasibility, in other words with a more positive potential of the couple AOL˙/AOL⁻ compared to the potential of the pertaining ascorbate-radical/ascorbate couple, E°(AOL˙/AOL⁻) is thus seen to fall into the range from 0.015 V to 0.300 V vs. NHE.

The two issues limiting the maximum turnover numbers of the catalytic cycle displayed in Scheme 1b are chemical processes competing with the photoionization step or with the regeneration step. Complete restoration of the starting catalyst by the sacrificial donor naturally implies the absence of both problems. An effective Asc²⁻ concentration of 0.6 mM already suffices to recover AOL⁻ to within 3% of its initial concentration when the post-flash concentration of AOL˙ is 10⁻⁵ M (Fig. 5b), and to within 1% of c₀ when that radical concentration is about halved (Fig. 6, pH 12.7); when the ratio [Asc²⁻] : [AOL˙] is increased still further, no deviations from a complete recovery can be detected. This trend in the limiting values is perfectly reproduced by eqn (1). These findings rule out a catalyst consumption through photochemical processes other than the photoionization, because the associated catalyst loss could not be undone by Asc²⁻, and identify radical–radical coupling of AOL˙ as the only side reaction competing with the regeneration of of AOL⁻.

The very low molar absorption coefficient of Asc²⁻ at 355 nm allows a substantial concentration increase over 0.6 mM before inner filter effects start to interfere with electron ejection from our photoredox catalyst AOL⁻. This increase would result in a concomitantly larger amount of e_aq˙⁻ formed by photoionization of our sacrificial donor Asc²⁻ itself, an effect entirely unwanted in the mechanistic investigations of this work but entirely welcome in potential applications of our system as an efficient electron source.

3 Conclusions

In this work, we have shown and thoroughly investigated a novel mechanism of generating hydrated electrons e_aq˙⁻ through photoredox catalysis, namely, by combining the near-UV (355 nm) ionization of 9-anthrolate with a subsequent thermal reconversion of the resulting 9-anthroxy radical into the starting form of the catalyst using the ascorbate dianion as a sacrificial donor. The photoionization step proved to be efficient enough to produce near-quantitative turnover of the catalyst with a single pulse from a commercial laser, and is entirely free from chemical side reactions, thus allowing a complete regeneration after the pulse. As an obvious asset of such a catalytic cycle for preparing the “super reductant” e_aq˙⁻, only the cheap sacrificial donor is expended whereas the molecule actually liberating the electron is not, so the latter can be tailor-made for the purpose with little regard to cost. While we have not yet performed a test for applications, an interference of the intermediates, products, or by-products formed during the reductive degradation of, e.g., halogenated organic compounds with this catalytic cycle is very unlikely because its only ingredients, anthrolate and ascorbate, are not even attacked by the “super reductant” e_aq˙⁻ and the sacrificial donor ascorbate is a classical free-radical scavenger. Compared to the already known acceptor-based cycle of Scheme 1a, which invariably consumes two photons per electron, the donor-based cycle investigated in this work (Scheme 1b) can equally accommodate a monophotonic ionization of the catalyst, and thus use the photons more efficiently.

4 Experimental section

Laser flash photolysis was carried out using a setup described elsewhere.¹⁸ For each experiment, two of the following three lasers and wavelengths can be combined as desired with freely chosen delay between the pulses: Lambda Physik LPX-210i, 308 nm with pulse width >50 ns; continuum Surelite-III and Surelite EX, both 266 nm or 355 nm with pulse widths of 5 ns. To provide homogeneous excitation, the beams are individually collimated and sent through the same volume element of a suprasil cell, and the absorptions of the solutions at the laser wavelengths are kept below 0.02. Transient absorption and luminescence are measured at right angle to the excitation. A syringe-driven flow-through system ensures that each trace is recorded on fresh solution.

We monitored e_aq˙⁻ not at its absorbance maximum but much further in the red, at 824 nm, where the xenon lamp serving as our light source displays a very strong emission spike. This superincrease of the light flux considerably improves the sensitivity, and the e_aq˙⁻ absorption at 824 nm is still very high; as a beneficial side effect, there are no residual absorptions of other species at that wavelength (see, the spectra in Fig. 1).

AON (>99%, Merck) was sublimated several times until no anthraquinone content was detectable. All other chemicals were obtained in the highest available purity and used as received (sodium ascorbate, 99%, Alfa Aesar; iso-propanol, >99.7%, Sigma Aldrich; sodium hydroxide for adjusting the pH, 99%, Grüssing; potassium iodide, puriss., VEB Laborchemie Apolda; fluorescein, >99.5%, Fluka; naphthalene, 99.6%, Alfa Aesar). The solvent was ultrapure Millipor MilliQ water (specific resistance, 18.2 MΩ cm); for deoxygenating the solutions, we used argon 5.0 (Linde) or N₂O 5.0 (Air Liquide).

Steady-state absorption and fluorescence spectra were measured using a Shimadzu UV-2102 and a Perkin-Elmer LS 50B spectrometer.

Acknowledgements

Financial support from the Chemical Industry Funds (PhD scholarship) and the SFi Halle (young researchers award) to C.K. are gratefully acknowledged.

References

1. K. Zeitler, Angew. Chem., Int. Ed., 2009, 48, 9785–9789.
2. J. M. R. Narayanam and C. R. J. Stephenson, Chem. Soc. Rev., 2011, 40, 102–113.
3. J. W. Tucker and C. R. J. Stephenson, J. Org. Chem., 2012, 77, 1617–1622.
4. J. Xuan and W.-J. Xiao, Angew. Chem., Int. Ed., 2012, 51, 6828–6838.
5. Chemical Photocatalysis, ed. B. König, DeGruyter, Berlin, 2013.
6. C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363.
7. D. Ravelli, M. Fagnoni and A. Albini, Chem. Soc. Rev., 2013, 42, 97–113.
8. M. Reckenthäler and A. G. Griesbeck, Adv. Synth. Catal., 2013, 355, 2727–2744.
9. Y.-Q. Zou, J.-R. Chen and W.-J. Xiao, Angew. Chem., Int. Ed., 2013, 52, 11701–11703.
10. D. P. Hari and B. König, Chem. Commun., 2014, 50, 6688–6699.
11. D. A. Nicewicz and T. M. Nguyen, ACS Catal., 2014, 4, 355–360.
12. J. W. T. Spinks and R. J. Woods, An Introduction to Radiation Chemistry, Wiley, New York, 2nd edn, 1976.
13. X. Li, J. Ma, G. Liu, J. Fang, S. Yue, Y. Guan, L. Chen and X. Liu, Environ. Sci. Technol., 2012, 46, 7342–7349.
14. X. Liu, S. Yoon, B. Batchelor and A. Abdel-Wahab, Sci. Total Environ., 2013, 454–455, 578–583.
15. Z. Song, H. Tang, N. Wang and L. Zhu, J. Hazard. Mater., 2013, 262, 332–338.
16. D. Zhu, L. H. Zhang, R. E. Ruther and R. J. Hamers, Nat. Mater., 2013, 12, 836–841.
17. L. Zhang, D. Zhu, G. M. Nathanson and R. J. Hamers, Angew. Chem., Int. Ed., 2014, 53, 9746–9750.
18. C. Kerzig and M. Goez, Phys. Chem. Chem. Phys., 2014, 16, 25342–25349.
19. M. Goez, C. Kerzig and R. Naumann, Angew. Chem., Int. Ed., 2014, 53, 9914–9916.
20. I. Ghosh, T. Ghosh, J. I. Bardagi and B. König, Science, 2014, 346, 725–728.
21. V. Zubarev and M. Goez, Angew. Chem., Int. Ed. Engl., 1997, 36, 2664–2666.
22. M. Goez, V. Zubarev and G. Eckert, J. Am. Chem. Soc., 1998, 120, 5347–5348.
23. M. Goez and V. Zubarev, Chem. Phys., 2004, 307, 15–26.
24. M. Goez and B. H. M. Hussein, Phys. Chem. Chem. Phys., 2004, 6, 5490–5497.
25. M. Goez and C. Kerzig, Angew. Chem., Int. Ed., 2012, 51, 12606–12608.
26. R. Hermann, G. R. Mahalaxmi, T. Jochum, S. Naumov and O. Brede, J. Phys. Chem. A, 2002, 106, 2379–2389.
27. X. Chen, D. S. Larsen and S. E. Bradforth, J. Phys. Chem. A, 2011, 115, 3807–3819.
28. U. Lachish, M. Ottolenghi and G. Stein, Chem. Phys. Lett., 1977, 48, 402–406.
29. P. J. Hayden and C. F. Chignell, Chem. Res. Toxicol., 1993, 6, 231–237.
30. B. Freiermuth, B. Hellrung, S. Peterli, M.-F. Schultz, D. Wintgens and J. Wirz, Helv. Chim. Acta, 2001, 84, 3796–3809.
31. Y. Ogata, Y. Kosugi and K. Nate, Tetrahedron, 1971, 27, 2705–2711.
32. G. Torosian, H. McVeigh, P. J. Kovi and S. G. Schulman, Spectrosc. Lett., 1973, 6, 77–85.
33. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, Taylor and Francis, Boca Raton, 3rd edn, 2006.
34. P. Debye, Trans. Electrochem. Soc., 1942, 82, 265–272.
35. M. Goez, Z. Phys.–Chem. Materialforsch., 1990, 169, 133–145.
36. G. Grabner, K. Rechthaler, B. Mayer, G. Köhler and K. Rotkiewicz, J. Phys. Chem. A, 2000, 104, 1365–1376.
37. C. L. Thomsen, D. Madsen, S. R. Keiding, J. Thgersen and O. Christiansen, J. Chem. Phys., 1999, 110, 3453–3462.
38. P. M. Hare, E. A. Price and D. M. Bartels, J. Phys. Chem. A, 2008, 112, 6800–6802.
39. H. Mauser, Z. Naturforsch., 1968, 23B, 1025–1030.
40. F.-M. Pang, C.-E. Seng, T.-T. Teng and M. H. Ibrahim, J. Mol. Liq., 2006, 136, 71–78.
41. U. Lachish, A. Shafferman and G. Stein, J. Chem. Phys., 1976, 64, 4205–4211.
42. M. B. Davies, J. Austin and D. A. Partridge, Vitamin C: Its Chemistry and Biochemistry, The Royal Society of Chemistry, Cambridge, 1st edn, 1991.
43. P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp01711d

---