The rate constant of the reaction NCN + H₂ and its role in NCN and NO modeling in low pressure CH₄/O₂/N₂-flames

Abstract

Bimolecular reactions of the NCN radical play a key role in modeling prompt-NO formation in hydrocarbon flames. The rate constant of the so-far neglected reaction NCN + H₂ has been experimentally determined behind shock waves under pseudo-first order conditions with H₂ as the excess component. NCN₃ thermal decomposition has been used as a quantitative high temperature source of NCN radicals, which have been sensitively detected by difference UV laser absorption spectroscopy at [small nu, Greek, tilde] = 30383.11 cm⁻¹. The experiments were performed at two different total densities of ρ ≈ 4.1 × 10⁻⁶ mol cm⁻³ and ρ ≈ 7.4 × 10⁻⁶ mol cm⁻³ (corresponding to pressures between p = 324 mbar and p = 1665 mbar) and revealed a pressure independent reaction. In the temperature range 1057 K < T < 2475 K, the overall rate constant can be represented by the Arrhenius expression k/(cm³ mol⁻¹ s⁻¹) = 4.1 × 10¹³ exp(−101 kJ mol⁻¹/RT) (Δlog k = ±0.11). The pressure independent reaction as well as the measured activation energy is consistent with a dominating H abstracting reaction channel yielding the products HNCN + H. The reaction NCN + H₂ has been implemented together with a set of reactions for subsequent HNCN and HNC chemistry into the detailed GDFkin3.0_NCN mechanism for NO_x flame modeling. Two fuel-rich low-pressure CH₄/O₂/N₂-flames served as examples to quantify the impact of the additional chemical pathways. Although the overall NCN consumption by H₂ remains small, significant differences have been observed for NO yields with the updated mechanism. A detailed flux analysis revealed that HNC, mainly arising from HCN/HNC isomerization, plays a decisive role and enhances NO formation through a new HNC → HNCO → NH₂ → NH → NO pathway.

---

1 Introduction

Nitrogen oxides (NO_x) are atmospheric pollutants formed as byproducts in combustion processes. Especially under fuel rich conditions, NO is favorably formed over the so-called prompt-NO pathway, which is initiated by the reaction of small hydrocarbon radicals with molecular nitrogen from the combustion air. According to the traditional Fenimore mechanism,¹ it has been assumed for a long time that prompt-NO formation is mainly initiated by the reaction

CH(²Π) + N₂(¹Σ⁺) → N(⁴S) + HCN(¹Σ⁺). (1a)

Even though the formation of the products N + HCN is spin-forbidden and despite the fact that theoretical estimates^2,3 for the rate constant k_1a turned out to be inconsistent with the experimentally determined high temperature rate constants for the overall CH + N₂ reaction,^4,5reaction (1a) is still used in some flame modeling studies. Already in the year 2000, based on quantum-chemical and RRKM calculations, Moskaleva et al.⁶ suggested the alternative spin-conserved reaction channel

CH(²Π) + N₂(¹Σ⁺) → H(²S) + NCN(³Σ_g⁻) (1b)

and predicted NCN + H to be the main product of the reaction. In the meantime it has been experimentally proven that NCN radicals are in fact formed in flames^7–9 and that NCN is the main product of the reaction CH + N₂.¹⁰ Consequently, flame mechanisms for NO modeling have been updated with regard to NCN high temperature chemistry. Current versions of NCN submechanisms are the Konnov0.6¹¹ and the GDFkin3.0_NCN^12,13 mechanisms. The performance of the latter has been extensively validated and improved over the last few years by quantitative measurements and modeling of CH, NO and NCN concentration profiles in low-pressure CH₄/O₂/N₂ and C₂H₂/O₂/N₂ flames of various fuel/air equivalent ratios.^12,14 Recently, corresponding NCO, CN and HCN profiles have been measured as well.¹³ Whereas early versions of NCN submechanisms relied on rate constant estimates of Glarborg et al.,¹⁵ the more recent implementations are based on extensive rate constant data from the theoretical work performed by the M.C. Lin group. They reported RRKM and TST studies for the most important bimolecular NCN reactions NCN + O₂,¹⁶ O,¹⁷ OH¹⁸ and H¹⁹ as well as for the NCN forming reaction CH + N₂.^6,19 From the experimental point of view, most direct rate constant measurements of NCN reactions have been accomplished over the past few years in the shock tube laboratory of the authors (N.F. and G.F.). Beside our studies on NCN + O, H, M, NCN, NO, and NO₂,^20–22 only two other shock tube studies have been performed. Vasudevan et al.¹⁰ measured NCN absorption profiles during the pyrolysis of ethane/N₂ mixtures and Busch et al.^23,24 investigated the unimolecular decomposition reaction NCN + M → C + N₂ + M by C atom resonance absorption spectroscopy (ARAS). Ongoing work of one of the authors (N.L.) is concerned with the implementation, testing, and validation of the expanding – even though not yet complete – experimental database on NCN chemistry for flame modeling. Here, in order to assess the potential influence of the reaction NCN + H₂ on NO_x flame modeling, we rely on the GDFkin3.0_NCN submechanism as a well-validated starting point.

Surprisingly, despite rather high H₂ concentrations in the flame front, the title reaction

NCN + H₂ → products (2)

has not yet been implemented into flame mechanisms. Seemingly it was considered to be rather slow and therefore dispensable. However, neither experimental nor theoretical studies have been performed so far to confirm or falsify this assumption. In contrast, the rather slow NCN + O₂ reaction is included both in the Konnov0.6 and the GDFkin3.0_NCN mechanisms. Starting from early and too high rate constant estimates,¹⁵ this reaction was initially believed to be crucial for NCN modeling,²⁵ but later theoretical calculations of Zhu and Lin¹⁶ clearly showed that the reaction is activation controlled, slow, and therefore plays a less important role in NO_x formation in flames. As it turns out below, the rate constant of the reaction NCN + H₂ is about two orders of magnitude higher than for NCN + O₂. Therefore, an accurate rate constant determination and a thorough analysis of its impact for NO_x modeling as reported in this work is overdue.

2 Experimental

The used shock tube apparatus has been described in more detail elsewhere.²⁶ Briefly, the experiments have been performed in an overall 8.3 m long stainless steel shock tube with a 4.4 m long electropolished test section that could be evacuated to pressures of p ≈ 10⁻⁷ mbar by a combination of an oil-free turbo-molecular drag and a diaphragm pump. The test section and the driver section were separated by aluminum membranes of 30, 80 or 100 μm thickness. Hydrogen or hydrogen/nitrogen gas mixtures have been used as driver gas. The experimental conditions behind the incident and reflected shock waves were calculated from pre-shock conditions and the shock wave velocity, which was measured using four fast piezoelectronic sensors (PCB Piezotronics M113A21), by using a frozen-chemistry code.

Storage gas mixtures of 500 ppm to 1000 ppm NCN₃ in argon were prepared using the partial pressure method. The reaction mixtures were prepared using calibrated mass flow controllers (Aera, FC-7700CU; 10, 50, and 1000 sccm). Pure H₂ (Air Liquide, ≥99.999%) and the NCN₃ mixtures were further diluted with argon (Air Liquide, ≥99.999%) in a flow system and were passed into the test section of the shock tube. The section was flushed with the test gas mixture for about 5 min to minimize possible gas adsorption effects on the shock tube walls. High H₂ mole fractions of up to 9.6% were necessary in the reaction gas mixtures to achieve a fast NCN consumption due to reaction (2). At such high mole fractions, vibrational relaxation effects may compromise a simple frozen-chemistry calculation of the experimental conditions. Equilibration of the Boltzmann population of H₂ in its ν = 0 and ν = 1 vibrational states may cause a noticeable, gradual decrease of the temperature behind the shock wave. However, on the one hand the vibrational relaxation time of H₂ in argon is known to be rather short, about 9 μs at p = 700 bar and T = 1750 K,²⁷ and hence close to the time resolution of the experiments. On the other hand, due to the high vibrational quanta of H₂, the fraction of H₂ in the ν = 1 state and with it the overall temperature effect remains small. At a typical experimental temperature of T = 1750 K, the ratio H₂(ν = 1)/H₂(ν = 0) = 0.03. Calculation of shock wave conditions assuming fully and non-relaxed H₂ showed that even at the highest experimental temperatures and H₂ concentrations used in this work, the maximum expected temperature effect was ΔT < 5 K. This is within the 1% uncertainty of the temperature calculation from the shock wave velocity. Consequently, due to the fast relaxation and the overall small temperature effect, it could be safely assumed that H₂ relaxation did not interfere with the rate constant measurements.

NCN precursor

It has been shown by Dammeier et al.^28,29 that the thermal decomposition of cyanogen azide (NCN₃) serves as a quantitative source of NCN radicals. NCN₃ thermal decomposition yields NCN in its first electronically excited singlet state, which is rapidly converted to the triplet ground state by collision induced intersystem crossing (CIISC).

NCN₃ + M → ¹NCN + N₂ + M (3)

¹NCN + M → ³NCN + M (4)

Rate constants for reaction (3) and (4) have been adopted from previous work and are listed in Table 1. As it is known that the CIISC process (4) strongly depends on the collision partner and hence reaction mixture composition, its rate constant was allowed to vary within the error limits reported in ref. 29.

Table 1 Arrhenius parameters for the rate constants of all the included NCN reactions as used for simulating the experimental NCN profiles behind shock waves. k_i = ATⁿ exp[−E_a/RT], given in units of cm³, mol⁻¹, s⁻¹ and kJ. Except for reactions (3) and (4), all reactions have been duplicated for ¹NCN to take ¹NCN chemistry approximately into account. In addition to the listed reactions, the GDFkin3.0 mechanism¹² was used as a background mechanism

No.	Reaction	A	n	E a	Ref.
2	NCN + H2 → products	4.1 × 10^13		101	This work
3	NCN3 → ^1NCN + N2	4.9 × 10^9		71	ρ = 3 × 10^−6 mol cm^−3,^29
		7.5 × 10^9		71	ρ = 6 × 10^−6 mol cm^−3,^29
4	^1NCN → NCN	2.0 × 10^6		31	ρ = 3.5 × 10^−6 mol cm^−3,^29
5a	NCN + H → HCN + N	7.94 × 10^12	0.41	22.8	22
5b	NCN + H → CH + N2	4.2 × 10^15	−0.69	2.0	22
6	NCN + M ⇌ C + N2 + M	8.9 × 10^14		260	21
7	NCN + NCN ⇌ CN + CN + N2	3.7 × 10^12			21
8	NCN + C ⇌ CN + CN	1.0 × 10^14			21
9	NCN + N ⇌ N2 + CN	1.0 × 10^13			6
10	NCN + CN ⇌ C2N2 + N	1.25 × 10^14		33.5	6
11	NCN + H ⇌ HNCN	2.98 × 10^18	−9.28	27	760 Torr,^19

---

The extremely explosive and toxic precursor NCN₃ cannot be purified by freeze–pump cycles. It has therefore been synthesized directly in high purity in the gas phase, according to BrCN(g) + NaN₃(s) → NCN₃(g) + NaBr(s), using a method described in detail in ref. 22. After an 8 h reaction time the remaining BrCN impurities were usually <3% according to FTIR analysis. The pure NCN₃ was diluted in argon and was used within three days since NCN₃ tends to slowly form solid polymers. The actual initial NCN₃ concentrations in the reaction gas mixtures were determined from the NCN absorption signal plateaus behind the incident shock waves (for experiments behind the reflected shock wave) or by fitting the maximum of the NCN concentration profile (for experiments behind the incident shock wave). In all cases, the determined concentration was consistent with the concentration calculated from the expected NCN₃ mole fraction in the storage gas mixture.

NCN detection scheme

The narrow-bandwidth laser absorption setup for time-resolved radical detection behind shock waves has been described in detail elsewhere.²² Briefly, about 1 mW of UV radiation was generated by intra-cavity frequency doubling of a frequency-stabilized continuous-wave ring-dye laser (Coherent 899) operated with DCM-special as dye and pumped using 8 W at λ = 532 nm from a Nd:YVO₄ solid state laser (Coherent Verdi V10). The UV laser beam was split into a detection and a reference beam using a 50 : 50 beam splitter plate. The detection beam was focused, passed the shock tube through two quartz windows, and was coupled into an optical fiber connected to a balance photo-detector and amplifier (Thorlabs PDB 150A-EC). The reference beam intensity could be precisely adjusted using a variable neutral density filter to match the intensity of the detection beam. The resulting difference signal (ΔI) and the monitor signal of the detection beam (I₀) were stored by an analog input board (Measurement Computing PCI-DAS4020/12, 12 bit, 20 MHz) for further data processing.

Triplet NCN has been detected at [small nu, Greek, tilde] = 30381.11 cm⁻¹ (λ = 329.1302 nm) on the maximum of an absorption band stemming from the superposition of the ³Π₁ sub-band of the óΠ_u(000)–X̃³Σ_g(000) transition with the Q₁ band head of the vibronic ³Σ⁺(010)–³Π(010) transition.³⁰ NCN concentration–time profiles were calculated using the previously reported temperature-dependent absorption cross section, which has been measured with an accuracy of ±25% using the same apparatus at similar temperatures and pressures as used in this work.²⁸ As the (010) vibrational state becomes significantly populated at combustion temperatures, the absorption cross sections were comparatively high (e.g., σ(1500 K, base e) = 4.5 × 10⁷ cm² mol⁻¹). Hence, with a detection limit of 4 × 10⁻¹² cm³ mol⁻¹ (corresponding to 1.5 × 10⁻³ absorption at T = 1500 K, p = 500 mbar, and an electronic time-resolution of Δt ≈ 1 μs), NCN could be detected with high signal-to-noise ratios even at NCN mole fractions as low as a few ppm.

Numerical methods

Numerical simulations of NCN concentration–time profiles from the shock tube experiments were performed using the Chemkin-II program package³¹ in combination with GDFkin3.0_NCN as a detailed background mechanism. In order to be consistent with a previous shock tube work, rate constants for NCN reactions have been replaced or added according to our directly measured rate constant data set.^20–22 The most important reactions for modeling the shock tube experiments are listed in Table 1. For sensitivity analysis, the sensitivity coefficient σ(i,t) for reaction i at time t was normalized with respect to the maximum concentration [NCN]_max over the time history, σ(i,t) = 1/[NCN]_max × (∂[NCN]/∂ ln k_i).

Flame modeling was performed with the Chemkin/Premix code^31,32 and the detailed mechanism GDFkin3.0_NCN.¹² As will be further outlined below, the mechanism has been modified to take into account reaction (2) and subsequent chemistry of HNCN and HNC. Rate-of-production (ROP) and the N-atom flux analyses have been accomplished at the NCN peak locations using a homemade post processor that relies mostly on the Chemkin subroutines.³¹ Atom flux analysis has been performed with the program Kinalc, and the reaction fluxes were plotted using the included FluxViewer visualisation tool.³³ Thermodynamic data were adopted from GDFkin3.0¹² with updated NCN thermochemistry as described in ref. 13. Hence, in agreement with recent experimental work,²² the controversial value of the enthalpy of formation of NCN³⁴ was set to 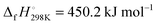. For HNCN and HNC, thermodynamic data were extracted from the Goos/Ruscic database.³⁵

Quantum chemical calculations were carried out using the Gaussian 09 suite of programs.³⁶ The transition state of the reaction NCN + H₂ → HNCN + H was located and verified by using a synchronous transit-guided quasi-Newton method (QST3 option) and an intrinsic reaction coordinate as follows.

3 Results and discussion

Shock tube experiments

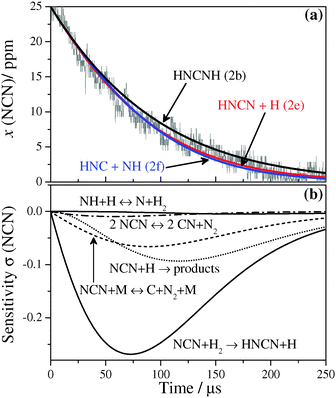
The rate constant of reaction (2), NCN + H₂, has been measured behind incident and reflected shock waves with reaction gas mixtures containing 3–27 ppm NCN₃ and 0.8–9.6% H₂ in argon. k₂ values have been obtained in the temperature and pressure ranges of 1057 K ≤ T ≤ 2475 K and 324 mbar ≤ p ≤ 1665 mbar, at two total densities of ρ ≈ 4.1 × 10⁻⁶ and 7.4 × 10⁻⁶ mol cm⁻³. Under these experimental conditions the reaction NCN + H₂ was always the most important reaction for NCN consumption. Experimental temperature limits were set by the thermal decomposition of NCN, which becomes the dominant reaction above 2500 K, and by the rate of reaction (2) itself, which becomes too slow at temperatures T < 1000 K to be measured with sufficient sensitivity.

Fig. 1a shows a typical NCN concentration–time profile behind the incident shock wave at T = 1582 K and a total density of ρ = 4.13 × 10⁻⁶ mol cm⁻³. The NCN profile reveals a rather slow NCN consumption with a half-life of t_1/2 ≈ 200 μs. Since there are no studies on the possible reaction channels of the reaction NCN + H₂, numerical simulations of the experimental NCN profiles have been performed assuming different sets of reaction products. Potential reaction products of reaction (2) include:

Fig. 1 (a) Typical experimental NCN concentration–time profile in comparison with numerical simulations. T = 1582 K, p = 544 mbar, ρ = 4.13 × 10⁻⁶ mol cm⁻³, [H₂] = 4.0%, [NCN₃] = 8.2 ppm, k_2e(NCN + H₂ → HNCN + H) = 1.8 × 10¹⁰ cm³ mol⁻¹ s⁻¹ (best fit, solid curve). (b) Corresponding sensitivity analysis of NCN.

^3NCN + ^1H2	→ ^1H2NCN	−317.2	(2a)
	→ ^1HNCNH	−304.2	(2b)
	→ ^3CH2 + ^1N2	−59.0	(2c)
	→ ^1HCN + ^3NH	38.4	(2d)
	→ ^2HNCN + ^2H	83.6	(2e)
	→ ^1HNC + ^3NH	100.5	(2f)
	→ ^2NH2 + ^2CN	174.7	(2g)

The formation of the thermodynamically most favorable products H₂NCN (2a) and HNCNH (2b) is spin-forbidden and hence their formation constitutes a presumably unimportant pathway. All other increasingly endothermic channels are spin-allowed and may become accessible at combustion temperatures. Except for reaction (2e), the assumed product sets require the formation of an unlikely collision complex on the triplet surface followed by several rearrangement steps. This is in particular the case for reaction (2c), where a feasible reaction pathway can hardly be imagined. Actually, reactions (2a) and (2g) may become important for the corresponding ¹NCN reaction as singlet radicals are known to prefer insertion reactions. For the triplet radical, however, reaction (2e) constitutes the by far most probable reaction channel. Next to the decomposition of a ³HNCNH intermediate, this reaction can take place as a direct activation controlled H abstraction reaction as well. It is known that H abstraction channels often become the dominating pathway at high temperatures even if complex-forming pathways are accessible.^26,37 Therefore, the most reasonable reaction products HNCN + H have been assumed for the target reaction NCN + H₂ in the first round of data evaluation. The effect of assuming different product sets will be further discussed below. The experimental NCN concentration–time profiles have been simulated based on a detailed mechanism assembled from our previous work (Table 1). Except for reactions (3) and (4), all reactions have been duplicated for ¹NCN to take ¹NCN chemistry approximately into account. Moreover, the reaction model was complemented by the extensive GDFkin3.0 mechanism.^12,13 Subsequent HNCN chemistry is only partly accounted for. Next to the reverse of reaction (2e), H + HNCN, only the thermal decomposition of HNCN has been included in the mechanism by the reverse of reaction (11). For the latter, the rate expression used for atmospheric pressure has been adopted from the recent work of Teng et al.;¹⁹ a formerly reported rate expression for the low pressure limit of the unimolecular decomposition reaction (−11) by Moskaleva and Lin,⁶ which is implemented into the Konnov0.6 mechanism, turned out to yield unrealistic high rate constant values. Other rate constant data for bimolecular HNCN loss reactions such as HNCN + C/CN/N are not available in the literature, however, these reactions are not expected to play significant roles for modeling the shock tube experiments.

In Fig. 1a, the solid curve represents the best numerical simulation of the NCN profile using k_2e = 1.8 × 10¹⁰ cm³ mol⁻¹ s⁻¹. Variation of k_2e by a factor of two yields the two dotted curves that fail to reproduce the experiment. The sensitivity analysis in Fig. 1b reveals that reaction (2e) is by far the most important reaction for NCN consumption. Only at reaction times t > 250 μs, the reaction NCN + H gains some influence. Its high temperature rate constant and branching ratio, however, have been directly measured recently.²² The sole other sensitive reaction, which is important to model the initial NCN formation at short reaction times, is the CIISC process (4). It has been studied in some detail by Dammeier et al.²⁹ and its rate constant value is dependent on the composition of the reaction gas mixture. Here, k₄ has been used as an adjustable parameter and was varied within the error limits reported in ref. 29 in order to model the initial increase of the NCN signal. Finally, an alternative rate constant determination by fitting the NCN decay assuming a simple pseudo-first order exponential decay without applying any reaction mechanism has been performed as well. As expected for negligible secondary chemistry, very similar rate constant values are obtained. For example, for the experiment shown in Fig. 1 a rate constant of k₂ = 1.9 × 10¹⁰ cm³ mol⁻¹ s⁻¹ has been obtained over the interval 25 μs ≤ t ≤ 250 μs, which is very close to the k_2e = 1.8 × 10¹⁰ cm³ mol⁻¹ s⁻¹ value from the numerical simulation mentioned above.

In order to analyze a possible influence of the assumed products of reaction (2), the experimental NCN concentration–time profiles have been simulated using different product sets. Fig. 2a illustrates an experimental NCN profile at a reflected shock wave temperature of T = 2123 K. Assuming reaction channel (2e) with the radical products HNCN + H yields a rate constant of k_2e = 1.3 × 10¹¹ cm³ mol⁻¹ s⁻¹ (red curve). The sensitivity analysis of the chosen high temperature experiment reveals that the influence of secondary chemistry is more pronounced than for the previously discussed T = 1582 K experiment (Fig. 1). For example, the thermal decomposition of NCN, NCN + M → C + N₂ + M starts to play a significant role. Its rate constant has been measured in two independent studies and highly consistent values have been reported.^21,24 Hence, a sensitive determination of k₂ is still possible. Next, the same value for the rate constant k₂ but the alternative recombination product HNCNH of channel (2b) has been used instead of the products HNCN + H. The resulting simulated curve predicts a somewhat too slow NCN decay (black curve). As no additional HNCNH chemistry has been included into the mechanism and hence HNCNH has been treated as a stable species, the difference between the two simulations reflects the impact of the secondary reactions resulting from the radical products formed in the case of channel (2e) products. Similar results are obtained when assuming reaction channel (2a). In contrast, simulations with the other potential radical forming reaction channels (2c), (2d), (2f) or (2g) yielded more or less the same k₂ values as for channel (2e). In Fig. 2a, the blue curve represents the simulation using the products of channel (2f), HNC + NH, as an example. Within error limits it is identical to the simulation using channel (2e).

Fig. 2 (a) Comparison of numerical simulations assuming HNCN + H (2e), HNC + NH (2f), or HNCNH (2b) as alternative products of the reaction NCN + H₂. T = 2123 K, p = 719 mbar, ρ = 4.08 × 10⁻⁶ mol cm⁻³, [H₂] = 1.5%, [NCN₃] = 25 ppm. k₂ = 1.3 × 10¹¹ cm³ mol⁻¹ s⁻¹ has been used for all three simulations. (b) Corresponding sensitivity analysis assuming the products HNCN + H.

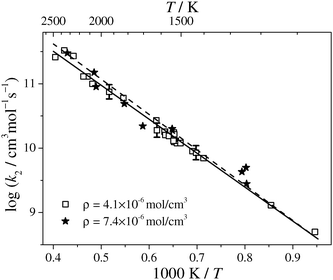
Total rate constant values for reaction (2) have been extracted from 36 shock tube experiments. The experimental conditions of all the experiments are listed in Table 2, an Arrhenius plot of the obtained k₂ values is given in Fig. 3. The symbols correspond to the results assuming HNCN + H as the reaction products. Within the scattering, the obtained data for the two different total densities of ρ ≈ 4.1 × 10⁻⁶ mol cm⁻³ (open squares) and 7.4 × 10⁻⁶ mol cm⁻³ (star symbols) agree, showing that the reaction is not significantly pressure dependent. The data points can be nicely represented by a two-parameter Arrhenius expression.

Table 2 Experimental conditions and the results for shock tube experiments with NCN₃/H₂/Ar reaction mixtures

T/K	p/mbar	ρ/10^−6 mol cm^−3	H2/%	NCN/ppm	k 2e/cm^3 mol^−1 s^−1	T/K	p/mbar	ρ/10^−6 mol cm^−3	H2/%	NCN/ppm	k 2e/cm^3 mol^−1 s^−1
Incident shock wave, ρ ≈ 4.06 × 10^−6 mol cm^−3						Reflected shock wave, ρ ≈ 4.12 × 10^−6 mol cm^−3
1057	324	3.69	2.81	13	5.0 × 10^8	1866	588	3.86	1.48	27	5.1 × 10^10
1171	371	3.81	2.81	10	1.3 × 10^9	1936	638	3.97	1.48	23	7.5 × 10^10
1402	466	4.00	2.81	10	7.0 × 10^9	2076	704	4.08	1.48	24	1.0 × 10^11
1433	489	4.10	6.34	4.5	8.5 × 10^9	2123	719	4.08	1.48	25	1.3 × 10^11
1449	498	4.13	7.48	5.3	9.0 × 10^9	2161	748	4.16	1.48	23	1.3 × 10^11
1503	510	4.08	9.63	3.2	1.2 × 10^10	2264	794	4.22	1.48	25	2.7 × 10^11
1520	518	4.10	3.38	6.8	1.2 × 10^10	2365	835	4.25	0.83	24	3.3 × 10^11
1525	520	4.10	3.64	7.6	1.3 × 10^10	2475	891	4.33	0.83	21	2.6 × 10^11
1533	526	4.13	5.06	6.0	1.7 × 10^10	Incident shock wave, ρ ≈ 6.48 × 10^−6 mol cm^−3
1534	523	4.10	3.15	5.6	1.3 × 10^10	1244	669	6.47	2.81	7	2.8 × 10^9
1534	525	4.11	3.17	4.2	1.4 × 10^10	1260	680	6.49	2.81	9	4.3 × 10^9
1535	527	4.13	4.31	8.6	1.8 × 10^10	Reflected shock wave, ρ ≈ 7.67 × 10^−6 mol cm^−3
1537	526	4.11	3.17	5.5	1.3 × 10^10	1247	652	6.29	2.93	10	5.0 × 10^9
1560	537	4.14	3.19	2.7	1.6 × 10^10	1543	916	7.14	2.93	12	2.0 × 10^10
1578	537	4.10	2.10	5.8	1.6 × 10^10	1705	1066	7.52	2.93	13	2.2 × 10^10
1579	539	4.11	2.36	8.3	1.8 × 10^10	1824	1178	7.77	2.93	10	4.9 × 10^10
1582	544	4.13	3.95	8.2	1.8 × 10^10	2044	1388	8.17	2.93	9.3	9.0 × 10^10
1623	558	4.13	2.81	10	1.9 × 10^10	2062	1405	8.19	2.81	12	1.5 × 10^11
1626	529	3.91	2.93	5	2.7 × 10^10	2330	1665	8.59	2.81	9.0	3.0 × 10^11

---

Fig. 3 Arrhenius plot of the rate constant for the reaction NCN + H₂ → products. Experimental data at two different total densities ρ ≈ 4.1 × 10⁻⁶ mol cm⁻³ (open squares) and ρ ≈ 7.4 × 10⁻⁶ mol cm⁻³ (star symbols) and corresponding Arrhenius fit (solid line) for an evaluation assuming radical products (channel (2c)–(g)) are shown. The dashed line depicts an Arrhenius fit obtained for an alternative data evaluation (corresponding data points are not shown) assuming stable reaction products (channels (2a) and (2b)).

The error bars in Fig. 3 exemplify the cumulative uncertainty of k₂ resulting from different error sources. Simulations show that a pessimistic ±25% error estimate for the initial NCN₃ concentration, which arises from the 25% error of the used NCN absorption cross section,²⁸ results in a ±6% uncertainty in k₂. Varying the most important background reactions within their error limits sum up to ±8%. Finally, the uncertainty of the H₂ concentration was ±2% and the statistical error of the Arrhenius fit of the scattered data amounts to ±8% (2σ standard error of the mean). A reasonable total error estimate in the middle of our temperature range at T ≈ 1750 K is therefore ±24%, corresponding to Δlog k₂ = ±0.11. The dashed line in Fig. 3 corresponds to the Arrhenius expression k₂/(cm³ mol⁻¹ s⁻¹) = 6.5 × 10¹³ × exp(−105 kJ mol⁻¹/RT) that has been obtained by assuming the unlikely formation of a stable reaction product (i.e., channel (2a) or (2b)). Such an evaluation yields data (not shown) that start to deviate from the evaluation assuming radical products (i.e., channels (2c)–(g)) at temperatures T > 1700 K with a maximum deviation of +30% at T = 2480 K.

A comparison with a similar reaction and quantum-chemical calculations show that the obtained activation energy is roughly consistent with a reaction that is dominated by an H abstraction pathway according to channel (2e). On the one hand, a comparable H abstraction reaction of the N-centered triplet species, ³NH, NH + H₂ → NH₂ + H, exhibits an activation energy, which is 33 kJ mol⁻¹ higher than the corresponding reaction enthalpy of 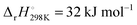.³⁸ Accordingly, an activation energy of E_a ≈ 84 kJ mol⁻¹ + 33 kJ mol⁻¹ = 117 kJ mol⁻¹ would be expected for reaction (2e). On the other hand, an estimate of the activation enthalpy of channel (2e) based on quantum-chemical calculations using G4 level of theory yields a similar result. This method provides a reaction enthalpy for channel (2e) of , which is close to the value of 84 kJ mol⁻¹ from thermodynamic data taken from the literature. The calculated energy of the H₂⋯NCN transition state (H₂ is bonded to one of the N atoms and is oriented essentially perpendicular to the slightly bended NCN moiety) yields ΔH^‡(T = 1750 K) = 101 kJ mol⁻¹. Accordingly, taking into account the simple transition state theory expression E_a ≈ ΔH^‡ + 2RT, an activation energy of about 130 kJ mol⁻¹ can be estimated for channel (2e) at T = 1750 K. However, a more detailed comparison with theory should be based on more advanced multi-reference quantum-chemical and kinetic calculations including tunneling corrections as well as a complete RRKM/master equation analysis of the possible role of additional complex-forming reaction pathways. Given that accurate energy calculation of NCN related species turned out to be very challenging,³⁴ such an analysis would have been beyond the scope of this paper.

Flame modeling

The reaction NCN + H₂ turns out to be comparatively fast. With a rate constant of k₂ = 3.2 × 10¹⁰ cm³ mol⁻¹ s⁻¹ at a typical flame temperature of T = 1700 K, it is about a factor of 300 faster than the reaction NCN + O₂. Therefore, in order to assess the potential influence of reaction (2) on NO_x formation in flames, reaction (2) as well as other NCN reactions have been implemented into the GDFkin3.0_NCN^12,13 flame mechanism. Arrhenius parameters of all reactions that have been added to the original mechanism are listed in Table 3. Simulations have been performed with HNCN + H, HCN + NH, and HNC + NH as the respective sole products of reaction (2).

Table 3 Arrhenius parameters for rate constants of NCN, HNCN and HNC reactions added to the GDFkin3.0_NCN mechanism¹³ for flame simulations. Rate constants are given as k_i = ATⁿ exp[−E_a/RT] in units of cm³, mol⁻¹, s⁻¹ and kJ

No.	Reaction	A	n	E a	Ref.
2	NCN + H2 → (d) HCN + NH, (e) HNCN + H, (f) HNC + NH	4.1 × 10^13		101	This work
6	NCN + M ⇌ C + N2 + M	8.9 × 10^14		260	21
7	NCN + NCN ⇌ CN + CN + N2	3.7 × 10^12			29
8	NCN + C ⇌ CN + CN	1.0 × 10^14			29
9	NCN + N ⇌ N2 + CN	1.0 × 10^13			6
10	NCN + CN ⇌ C2N2 + N	1.25 × 10^14		33.5	6
11	NCN + H ⇌ HNCN	1.78 × 10^41	−9.58	21.9	100 Torr,^19
12a	HNCN + O → NO + HNC	1.22 × 10^14	−0.05	0.3	39
12b	HNCN + O → NH + NCO	5.60 × 10^13	−0.05	0.3	39
12c	HNCN + O → CN + HNO	9.36 × 10^12	−0.05	0.3	39
13	HNCN + O2 → HO2 + NCN	1.26 × 10^8	1.28	101.3	39
14	HNCN + OH → H2O + NCN	1.04 × 10^5	2.48	−7.9	40
15	HCN (+M) → HNC (+M)	3.5 × 10^13		197.5	k ∞,^41
		1.60 × 10^26	−3.23	207.5	k 0,^41
16	HNC + H → HCN + H	7.8 × 10^13		15	42
17	HNC + O → NH + CO	4.6 × 10^12		9.2	41
18	HNC + OH → HNCO + H	2.8 × 10^13		15.5	41
19	HNC + CN → C2N2 + H	1.0 × 10^13			43

---

Consideration of HNCN + H as main products implies an update of the mechanism with respect to HNCN reactions as well. HNCN species may rapidly react with O atoms (reactions (12)) generating HNC species. Consequently, two new blocks of reactions have been added to account for possible HNCN and HNC chemistry. In order to be coherent with the experimental rate constant determination, some additional NCN consumption reactions, (6) to (11), have also been considered in the detailed mechanism. In the following, this updated mechanism is named up-GDFkin3.0_NCN (up-GDF for short) in contrast to the original mechanism GDFkin3.0_NCN (GDF for short). Calculations were performed to simulate species profiles in selected low pressure premixed flames where the reaction NCN + H₂ may play an important role in the prompt-NO pathway. Two fuel rich flames of CH₄/O₂/N₂ have been considered numerically. Both flames were simulated at low pressure (5.0 kPa) with the same total volumetric flow rate (300 L h⁻¹, under the standard conditions of temperature and pressure) and nitrogen dilution ratio (60%), but a different richness equal to ϕ = 1.3 and ϕ = 1.5, respectively. Imposed temperature profiles were identical for each flame. The temperature in the burned gas was limited to remain lower than 1850 K, hence thermal-NO contribution was reduced and prompt-NO formation was promoted.

Considering the original GDF mechanism, simulated temperature and species profiles of NO, NCN and H₂ are reported in Fig. 4. In the burned gases, NO mole fractions are equal to 24.5 and 38.3 ppm for ϕ = 1.3 and ϕ = 1.5, respectively. As shown in Fig. 4a, the NO mole fraction in the burned gases is hardly affected at ϕ = 1.3, but is increased by 8% at ϕ = 1.5 when the calculations are performed with the up-GDF mechanism instead. H₂ and NCN profiles are reported in Fig. 4b using the up-GDF mechanism. The profiles show that at the NCN peak location (height above burner, HAB (ϕ = 1.3) = 5.3 mm and HAB (ϕ = 1.5) = 6.8 mm) the mole fractions of H₂ with x(ϕ = 1.3) = 0.064 and x(ϕ = 1.5) = 0.091 are high. NCN peak mole fractions are quite similar in the two flames with peak values close to 145 ppb, but the shape of the NCN profile is much thinner at ϕ = 1.3.

Fig. 4 (a) NO profiles simulated for the low pressure flames (see text) at a richness of ϕ = 1.3 and ϕ = 1.5. The results are shown for both the GDF and up-GDF mechanisms. (b) Corresponding H₂ and NCN profiles simulated with the up-GDF mechanism.

N-atom flux analysis was performed after all the reactions have been declared in a non-reversible format. In this way the atom flux reveals the flux in both directions of reversible reactions (forward and backward) separately. Some results at the NCN peak locations for both flames are presented in Table 4. Only NCN losses in the direction of the prompt-NO formation pathway (forward flux) are included. As expected, the reaction NCN + H → HCN + N is the most important NCN loss reaction that dominates the NCN forward flux, followed by the reaction with O atoms (yielding CN + NO). Nevertheless, about 1.8% of the NCN radicals are consumed through reaction (2) at ϕ = 1.3 and 3.5% at ϕ = 1.5. The so-far neglected reaction with H₂ ranks third place and its contribution is even three orders of magnitude higher than for the reaction NCN + O₂. Note that the N-flux analysis reveals that next to reaction (2) also reaction (8), NCN + C, which was omitted in the original mechanism as well, becomes more important than other, already implemented bimolecular reactions such as NCN + OH/HO₂/NO/M that are negligible under the assumed flame conditions.

Table 4 N-atom flux analysis of the two CH₄/O₂/N₂ model flames. The table lists the forward fluxes associated with several NCN + X reactions on the prompt-NO formation pathway

Forward flux %	H^a	O	H2	C	H2O	OH	HO2	O2	NO	M
a For NCN + H (yielding either CH + N2 or HCN + N, with a relative ratio of 77/23) only the HCN + N forming channel contributes to the forward flux along the prompt-NO formation pathway.
ϕ = 1.3	69.21	25.68	1.76	1.36	1.33	0.44	0.21	<0.01	<0.01	<0.01
ϕ = 1.5	79.33	12.54	3.52	2.17	1.96	0.33	0.13	<0.01	<0.01	0.03

---

Although it turned out that the implementation of reaction (2) is important, its rather low contribution to the forward flux is in seemingly contrast to the mentioned significant change in the overall NO yield. Obviously, other reactions added to the updated mechanism must be responsible for this prominent effect. A complete reaction pathway diagram for the ϕ = 1.5 flame using the up-GDF mechanism is shown in Fig. 5. New reaction pathways that are absent in the corresponding diagram using the original GDF mechanism (not shown) are highlighted in red color. These pathways include the formation and loss reactions of the newly included species HNCN and HNC. Once formed, HNCN reacts quickly with O-atoms through reaction (12). According to theoretical calculations, the products of the reaction HNCN + O are mostly HNC + NO.³⁹ HNC then reacts with OH radicals yielding HNCO + H, and HNCO reacts with H atoms yielding NH₂ + CO. However, it becomes clear from the flux diagram that HNC radicals are formed primarily from HCN and only secondly from HNCN. In fact, the HCN/HNC isomerization according to reactions (15), which is close to its low-pressure limit, and the H atom initiated isomerization reaction (−16), HNC + H → HCN + H, represent 12% and 20% of the HCN consumption at ϕ = 1.3 and ϕ = 1.5, respectively. This finding is also reflected in the HCN profiles shown in Fig. 6 for the ϕ = 1.5 flame. HCN mole fraction peak values obtained with the updated mechanism decrease by 20%. According to the ROP, HCN is mainly consumed through the reaction HCN + O ⇌ NCO + H and reaction (−16), both being three times more important than the reactions HCN + OH ⇌ HOCN + H and HNC (+M) ⇌ HCN (+M). The combined effect of HNC formation from reactions (−16) and (12a) results in a substantial increase of HNCO by a factor of two (Fig. 6). This increase is followed by a comparable increase of the peak values of NH₂ as well.

Fig. 5 N-atom flux analysis at the NCN peak location in the ϕ = 1.5 CH₄/O₂/N₂ flame using the up-GDF mechanism. The pathways highlighted in red color are absent in a corresponding flux analysis using the original GDF mechanism.¹³

Fig. 6 Comparison of HCN, HNCO, and NH₂ profiles of the ϕ = 1.5 flame calculated with the original GDF (dashed curves) and the up-GDF (solid curves) mechanisms.

To sum up, although the implementation of reaction (2) has indeed a significant impact on NO formation through a new HNC → HNCO → NH₂ → NH → NO pathway, it is in fact the HCN/HNC isomerization and not the reaction NCN + H₂ that is mainly responsible for the distinct changes obtained with the up-GDF mechanism. Note that the rate constant of the H initiated isomerization reaction (16), H + HNC → HCN + H, is based on a theoretical QRRK estimate⁴² and, to the best of our knowledge, has not been experimentally confirmed yet. Therefore, our interesting preliminary finding calls for a more detailed analysis to better constrain and verify the role of the HNC initiated pathway for NO formation in flames.

The possible influence of the assumed products of reaction (2) for the NO formation in flames has also been analyzed. Whatever channel (d–f) of reaction (2) was assumed, simulated NO profiles are identical to each other. However, considering channel (2d), implementation of reactions (12–19) could be removed since HCN and NH species are already declared in GDF.¹³ In that case, simulated NO profiles would be identical to those obtained with the original GDF mechanism. Again, this clearly highlights the potential importance of the HCN/HNC isomerization pathway through reactions (15) and (−16).

4 Conclusion

The rate constant of reaction (2), NCN + H₂ → products, has been measured for the first time. Shock wave experiments with time-resolved NCN radical detection by narrow-bandwidth laser UV absorption were carried out under nearly pseudo-first order reaction conditions with H₂ as the excess component. The total rate constant has been measured at temperatures 1057 K ≤ T ≤ 2475 K and can be represented by the Arrhenius expression

No pressure dependence could be observed between p = 324 mbar and p = 1665 mbar. Quantum-chemical calculations show that the activation energy is roughly consistent with the formation of the products HNCN + H, hence the most likely direct abstraction pathway. Still, detailed quantum-chemical calculations in combination with RRKM/TST/ME modeling are desirable to further assess the role of complex-forming reaction pathways.

The detailed reaction mechanism GDFkin3.0_NCN has been updated to assess the potential influence of the so-far neglected reaction (2) on prompt-NO formation in flames. Next to reaction (2), HNC and HNCN submechanisms have been implemented as well to describe the subsequent chemistry of the reaction products. Two fuel-rich low-pressure methane flames served as a model case and it was shown that the contribution of reaction (2) on the overall NCN loss in the direction of prompt-NO is on the order of a few percent. Of course, the reaction may become even more important for other flame conditions and, therefore, needs to be included in detailed flame mechanisms. The flame simulation also highlights the fact that the reaction NCN + C ⇌ CN + CN, which was also omitted in the original GDFkin3.0_NCN mechanism should be considered in the future as well. As yet the rate constant for NCN + C has only been roughly determined experimentally, improved direct measurements are required. Moreover, as a pronounced impact of HCN/HNC isomerization on NO formation has been found in this study, a critical assessment and experimental verification of the role of this new HNC → HNCO → NH₂ → NH → NO prompt-NO formation pathway is important. A thorough validation of the updated mechanism going along with the implementation of other new experimental rate constant data that recently have become available for several bimolecular reactions of NCN is currently underway.

Acknowledgements

Financial support from the German Science Foundation (DFG-FR 1529/4) and the University Lille1 through a BQR International 2014 sponsorship is gratefully acknowledged. We also thank Johannes Dammeier for help and support with the shock tube experiments and Pascale Desgroux for fruitful discussion.

References

1. C. P. Fenimore, Formation of nitric oxide in premixed hydrocarbon flames, Proc. Combust. Inst., 1971, 13, 373–380.
2. Q. Cui and K. Morokuma, The spin-forbidden reaction CH(²Π) + N₂ → HCN + N(⁴S) revisited. I. Ab initio study of the potential energy surfaces, Theor. Chem. Acc., 1999, 102, 127–133.
3. Q. Cui, K. Morokuma, J. M. Bowman and S. J. Klippenstein, The spin-forbidden reaction CH(²Π) + N₂ → HCN + N(⁴S) revisited. II. Nonadiabatic transition state theory and application, J. Chem. Phys., 1999, 110, 9469–9482.
4. D. Lindackers, M. Burmeister and P. Roth, Perturbation studies of high temperature carbon and CH reactions with nitrogen and nitrogen oxide (NO), Proc. Combust. Inst., 1991, 23, 251–257.
5. A. J. Dean, R. K. Hanson and C. T. Bowman, High temperature shock tube study of reactions of CH and carbon-atoms with nitrogen, Proc. Combust. Inst., 1991, 23, 259–265.
6. L. V. Moskaleva and M. C. Lin, The spin-conserved reaction CH + N₂ → H + NCN: A major pathway to prompt NO studied by quantum/statistical theory calculations and kinetic modeling of rate constant, Proc. Combust. Inst., 2000, 28, 2393–2401.
7. G. P. Smith, Evidence of NCN as a flame intermediate for prompt NO, Chem. Phys. Lett., 2003, 367, 541–548.
8. J. A. Sutton, B. A. Williams and J. W. Fleming, Laser-induced fluorescence measurements of NCN in low-pressure CH₄/O₂/N₂ flames and its role in prompt NO formation, Combust. Flame, 2008, 153, 465–478.
9. N. Lamoureux, X. Mercier, C. Western, J. F. Pauwels and P. Desgroux, NCN quantitative measurement in a laminar low pressure flame, Proc. Combust. Inst., 2009, 32, 937–944.
10. V. Vasudevan, R. K. Hanson, C. T. Bowman, D. M. Golden and D. F. Davidson, Shock Tube Study of the Reaction of CH with N₂: Overall Rate and Branching Ratio, J. Phys. Chem. A, 2007, 111, 11818–11830.
11. A. A. Konnov, Implementation of the NCN pathway of prompt-NO formation in the detailed reaction mechanism, Combust. Flame, 2009, 156, 2093–2105.
12. N. Lamoureux, P. Desgroux, A. E. Bakali and J. Pauwels, Experimental and numerical study of the role of NCN in prompt-NO formation in low-pressure CH₄-O₂-N₂ and C₂H₂-O₂-N₂ flames, Combust. Flame, 2010, 157, 1929–1941.
13. N. Lamoureux, H. E. Merhubi, L. Gasnot, C. Schoemaecker and P. Desgroux, Measurements and modelling of HCN and CN species profiles in laminar CH₄/O₂/N₂ low pressure flames using LIF/CRDS techniques, Proc. Combust. Inst., 2015, 35, 745–752.
14. N. Lamoureux, X. Mercier, J. F. Pauwels and P. Desgroux, NCO quantitative measurement in premixed low pressure flames by combining LIF and CRDS techniques, J. Phys. Chem. A, 2011, 115, 5346–5353.
15. P. Glarborg, M. U. Alzueta, K. Dam-Johansen and J. A. Miller, Kinetic Modeling of Hydrocarbon/Nitric Oxide Interactions in a Flow Reactor, Combust. Flame, 1998, 115, 1–27.
16. R. S. Zhu and M. C. Lin, Ab Initio Study of the Oxidation of NCN by O₂, Int. J. Chem. Kinet., 2005, 37, 593–598.
17. R. S. Zhu and M. C. Lin, Ab Initio Study on the Oxidation of NCN by O (³P): Prediction of the Total Rate Constant and Product Branching Ratios, J. Phys. Chem. A, 2007, 111, 6766–6771.
18. R. S. Zhu, H. M. T. Nguyen and M. C. Lin, Ab Initio Study on the Oxidation of NCN by OH: Prediction of the Individual and Total Rate Constants, J. Phys. Chem. A, 2009, 113, 298–304.
19. W.-S. Teng, L. V. Moskaleva, H. Chen and M. C. Lin, Ab Initio Chemical Kinetics for H + NCN: Prediction of NCN Heat of Formation and Reaction Product Branching via Doublet and Quartet Surfaces, J. Phys. Chem. A, 2013, 117, 5775–5784.
20. J. Dammeier and G. Friedrichs, Direct Measurements of the Rate Constants of the Reactions NCN + NO and NCN + NO₂ Behind Shock Waves, J. Phys. Chem. A, 2011, 115, 14382–14390.
21. J. Dammeier, N. Faßheber and G. Friedrichs, Direct measurements of the high temperature rate constants of the reactions NCN + O, NCN + NCN, and NCN + M, Phys. Chem. Chem. Phys., 2012, 14, 1030–1037.
22. N. Faßheber, J. Dammeier and G. Friedrichs, Direct measurements of the total rate constant of the reaction NCN + H and implications for the product branching ratio and the enthalpy of formation of NCN, Phys. Chem. Chem. Phys., 2014, 16, 11647–11657.
23. A. Busch, M. Olzmann, Shock-Tube Study of the Thermal Decomposition of NCN, Proc. Eur. Combust. Meeting, 2009 Paper P810138, Vienna, Austria.
24. A. Busch, N. González-García, G. Lendvay and M. Olzmann, Thermal Decomposition of NCN: Shock-Tube Study, Quantum Chemical Calculations, and Master-Equation Modeling, J. Phys. Chem. A, 2015 DOI:10.1021/acs.jpca.5b01347.
25. A. E. Bakali, L. Pillier, P. Desgroux, B. Lefort, L. Gasnot, J. F. Pauwels and I. da Costa, NO prediction in natural gas flames using GDF-Kin 3.0 mechanism. NCN and HCN contribution to prompt-NO formation, Fuel, 2006, 85, 896–909.
26. M. Colberg and G. Friedrichs, Room Temperature and Shock Tube Study of the Reaction HCO + O₂ Using the Photolysis of Glyoxal as an Efficient HCO Source., J. Phys. Chem. A, 2006, 110, 160–170.
27. J. E. Dove and H. Teitelbaum, The vibrational relaxation of H₂. I. Experimental measurements of the rate of relaxation by H₂, He, Ne, Ar, and Kr, Chem. Phys., 1974, 6, 431–444.
28. J. Dammeier and G. Friedrichs, Thermal Decomposition of NCN₃ as a High-Temperature NCN Radical Source: Singlet-Triplet Relaxation and Absorption Cross Section of NCN(³Σ), J. Phys. Chem. A, 2010, 114, 12963–12971.
29. J. Dammeier, B. Oden and G. Friedrichs, A consistent model for the thermal decomposition of NCN₃ and the singlet–triplet relaxation of NCN, Int. J. Chem. Kinet., 2013, 45, 30–40.
30. N. Lamoureux, C. M. Western, X. Mercier and P. Desgroux, Reinvestigation of the spectroscopy of the A³Π_u–X³Σ_g⁻ transition of the NCN radical at high temperature: Application to quantitative NCN measurement in flames, Combust. Flame, 2013, 160, 755–765.
31. R. J. Kee, F. M. Ruply, J. A. Miller, Chemkin-II: A Fortran Chemical Kinetics Package for the Analysis of Gas- Phase Chemical Kinetics, Sandia Report SAND89-8009, Sandia National Laboratories, Livermore, California (Sept. 1989) http://www.sandia.gov/chemkin/index.html, accessed april 24, 2015.
32. R. Kee, J. Grcar, M. Smooke, J. Miller, Premix: A fortran program for modelling steady laminar one-dimensional premixed flames, Sandia report SAND85-8240, 1985.
33. KINALC: program for the kinetic analysis of combustion mechanisms, http://garfield.chem.elte.hu/Combustion/kinalc.htm, accessed april 24, 2015.
34. E. Goos, C. Sickfeld, F. Mau, L. Siedel, B. Ruscic, A. Burcat and T. Zeuch, Prompt NO formation in flames: The influence of NCN thermochemistry, Proc. Combust. Inst., 2013, 34, 657–666.
35. E. Goos, A. Burcat, B. Ruscic, Extended Third Millenium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables, (2009) http://garfield.chem.elte.hu/Burcat/burcat.html, accessed march 6, 2015.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009.
37. J. Dammeier, M. Colberg and G. Friedrichs, Wide temperature range (T = 295 K and 770–1305 K) study of the kinetics of the reactions HCO + NO and HCO + NO₂ using frequency modulation spectroscopy, Phys. Chem. Chem. Phys., 2007, 9, 4177–4188.
38. A. Fontijn, S. M. Shamsuddin, D. Crammond, P. Marshall and W. R. Anderson, Kinetics of the NH reaction with H₂ and reassessment of HNO formation from NH + CO₂, H₂O, Combust. Flame, 2006, 145, 543–551.
39. S. Xu and M. C. Lin, Ab initio chemical kinetics for the reactions of HNCN with O(³P) and O₂, Proc. Combust. Inst., 2009, 32, 99–106.
40. S. Xu and M. C. Lin, Ab Initio Chemical Kinetics for the OH + HNCN Reaction, J. Phys. Chem. A, 2007, 111, 6730–6740.
41. A. M. Dean and J. W. Bozzelli, in Combustion chemistry of nitrogen, ed. W. C. Gardiner, Gasphase Combustion Chemistry, Springer, New York, 2000.
42. R. Sumathi and M. T. Nguyen, A theoretical study of the CH₂N system: reactions in both lowest lying doublet and quartet states, J. Phys. Chem. A, 1998, 102, 8013–8020.
43. S. Petrie and Y. Osamura, NCCN and NCCCCN Formation in Titan’s Atmosphere: 2. HNC as a Viable Precursor, J. Phys. Chem. A, 2004, 108, 3623–3631.

---