Widely available active sites on Ni₂P for electrochemical hydrogen evolution – insights from first principles calculations

Abstract

We present insights into the mechanism and the active site for hydrogen evolution on nickel phosphide (Ni₂P). Ni₂P was recently discovered to be a very active non-precious hydrogen evolution catalyst. Current literature attributes the activity of Ni₂P to a particular site on the (0001) facet. In the present study, using Density Functional Theory (DFT) calculations, we show that several widely available low index crystal facets on Ni₂P have better properties for a high catalytic activity. DFT calculations were used to identify moderately bonding nickel bridge sites and nickel hollow sites for hydrogen adsorption and to calculate barriers for the Tafel pathway. The investigated surfaces in this study were the (101̄0), (1̄1̄20), (112̄0), (112̄1) and (0001) facets of the hexagonal Ni₂P crystal. In addition to the DFT results, we present experiments on Ni₂P nanowires growing along the 〈0001〉 direction, which are shown as efficient hydrogen evolution catalysts. The experimental results add these nanowires to a variety of different morphologies of Ni₂P, which are all active for HER.

---

1. Introduction

Water splitting by electrolysis or photocatalysis is attracting attention as a prospective sustainable source of hydrogen for energy storage applications.^1–3 The hydrogen evolution reaction (HER) is the cathode half reaction:

H⁺(aq) → 1/2H₂(g)

The most active and stable catalysts in acid environments for HER are currently based on precious metals.⁴ At low over-potentials, HER from Pt(111) is dominated by the Volmer–Tafel mechanism^5–7 which can be written as:

H⁺(aq) → H* (1)

2H* → H₂(g) (2)

This requires two H atoms to be adsorbed in proximity for fast diffusion and recombination. Alternatively the reaction may take place via a Volmer step (1), followed by the Heyrovski step:

H⁺(aq) + H* + e⁻ → H₂(g) (3)

Reaction (3) is considered to be relevant at high over-potentials only.⁷

In the last decade, several classes of non-precious materials have been found to be active catalysts for the HER. MoS₂ was proven as a promising non-precious HER catalyst material, which is stable in a wide pH range. However MoS_x catalysts are not as active as platinum and they are only active at undercoordinated edge sites.^8–11 Hydrodesulfurization (HDS) catalysts such as Mo₂C and MoB have recently attracted attention as hydrogen evolution catalysts with good stability in both acid and alkaline solution.^12,13 Ni₂P has also previously been subjected to experimental and theoretical studies for the catalysis of hydrodesulfurisation^13–16 water-gas-shift,¹⁷ and more recently for hydrogen evolution in acid.^18–20 The active sites and the details of the mechanism remain unknown for several of the newly discovered HER catalysts including Ni₂P. The observed Tafel slopes of the Ni₂P catalysts are similar to what is observed for MoS₂ edges, and the specific activity is one of the highest of the non-precious catalysts. Further experimental and theoretical studies can yield new insights for further design of electro-catalysts, which is the motivation of this study. In this paper, density functional theory (DFT) calculations are combined with experiments on high aspect ratio crystalline Ni₂P nanowires to understand the mechanism of HER from Ni₂P.

The trends in hydrogen evolution activity over various transition metals,^21,22 and various metal- and non-metal combinations have been investigated using DFT. The free energy of hydrogen adsorption, ΔG_H*, has been established as a descriptor for predicting the exchange current density,^21–24 of transition metal catalysts. The best catalysts have free binding energies close to 0.0 eV, which is explained by the Sabatier principle;²⁵ stronger binding results in hydrogen poisoning, leaving no free sites for adsorption. Weaker binding results in a high overpotential needed to adsorb protons. Transition metal catalysts have binding energies that are slightly coverage dependent. On Pt(111) the binding energy calculated with DFT varies from −0.12 eV at low coverage to 0.04 eV at one monolayer coverage.²¹ In addition, it has been shown by DFT calculations that platinum has no significant diffusion barrier between the adsorbing hollow sites on the (111) facet.²⁶

Liu and Rodriguez have published several studies on DFT calculations of hydrogen binding energies on the Ni₂P(0001) surface. In 2005, they predicted the hydrogen evolution activity of Ni₂P to be comparable to that of hydrogenase based on trends in adsorption energies. The ensemble of phosphor atoms available as proton acceptors next to moderately binding metal hollow sites and a weak binding Ni–P bridge is proposed to facilitate HER catalysis.¹⁸ The binding energies can be compared with the trends in HER exchange current density calculated by Nørskov et al.²¹ In these studies, the binding free energies are presented, which means that the calculated potential energy is corrected by +0.24 eV accounting for entropy and differences in zero point energy. When comparing the binding energies at the relevant coverage,^7,27 one observes that the metal hollow sites on Ni₂P will be fully occupied and that the Ni–P sites will need an overpotential of at least 0.31 V. This does not agree with the very high activity observed in new studies of hollow and multifaceted Ni₂P nanoparticle catalysts.^19,20,28,29 Another active site may therefore exist, and we investigate this using more detailed DFT calculations. In addition we report experiments showing that nano wires grown along the (0001) direction are highly active for HER, supporting the results of the present DFT calculations.

Calculation methods

Calculations were carried out using the GPAW code with projector augmented wave functions on a real space grid and ultra soft pseudopotentials.³⁰ The RPBE³¹ functional was used for the exchange–correlation contribution. The Ni₂P crystal structure³² was copied from The Materials Project,³³ and imported to The Atomic Simulation Environment (ASE).³⁴ Bulk lattice constants were converged to a = 5.151 Å and c = 3.408 Å using a third order polynomial fit to the energy versus the lattice constant.³⁵

A 1 × 1 supercell was used for the (0001) and (112̄1) surfaces, a 3 × 1 supercell was used for the (101̄0) surface and a 1 × 2 supercell was used for the ±(112̄0) surfaces. The (0001) surface had five atomic layers, the (112̄1) and (101̄0) slabs had four atomic layers, and the ±(112̄0) surfaces had three atomic layers. The dipoles across the unit cells were all less than 0.10 V.

A Monkhorst–Pack³⁶ sampling of 2 × 2 × 1 k-points was used for the large (112̄1) surfaces, 2 × 3 × 1 k-points were used for the ±(112̄0) surfaces, 3 × 2 × 1 k-points for the (101̄0) slabs and for the (0001) surface a 3 × 3 × 1 k-point sampling was used. The grid spacing was 0.18 Å in all calculations.

The slabs were relaxed using the Broyden–Fletcher–Goldfarb–Shanno LineSearch algorithm within ASE until the forces were below 0.01 eV Å⁻¹. A recalculation was later carried out with double the k-point sampling and a grid spacing of 0.12 Å for the most interesting slabs and adsorbate configurations. The resulting differences in adsorption energies did not exceed 0.02 eV, which is below the accuracy usually attributed to DFT.

The choice of facets and surface termination were based on calculations of the minimum energy configuration of all different ways to cut the crystal into the lowest index planes. Several STM and LEED studies^37–40 show that the Ni₂P surfaces can have a stable phosphor termination, but under the hydro-thermal treatment before testing, it is expected that they lose the phosphor layer and expose active metal sites, as on the structures investigated in our calculations. The chosen structures are (101̄0), (112̄0), (1̄1̄20), (112̄1) and the Ni₃P terminated (0001), as shown in Fig. 1 along with their (hkjl) indices from a top view.

Fig. 1 The Ni₂P unit cell and top views of the low index surfaces used in this study. The surface unit cells have been repeated once in the X and Y directions, apart from the (101̄0) direction, for which a 2 × 3 supercell is shown. Nickel atoms are represented by green spheres and phosphor atoms by yellow spheres.

The free adsorption energies are found from calculated potential energies by correcting for the gas phase entropy ΔS = −S₀(H₂) and the difference in zero point energy ΔZPE using the equation

ΔG = ΔE − TΔS + ΔZPE

where E denotes the ground state energy at 0 K obtained from DFT. The correction for ZPE and entropy makes an addition of 0.24 eV to the adsorption energy of a hydrogen atom.^21,41

The calculation of adsorption free energies and adsorbate coverages was carried out using the self consistent scheme as in the work reported by Skulason et al.⁷ The integral adsorption energy G_int(n) is

G_int = (G(N,n) − G(N,0) − nμ_H), where μ_H = 1/2G_H2 − eU

where G(N,n) is the free energy of a surface which includes N nickel atoms in the top layer and n adsorbed hydrogen atoms. Thus we use a definition of the coverage θ = n/N, where n is the number of hydrogen adsorbates and N is the number of Ni atoms on the surface. The configuration which is relevant at a given chemical potential of protons and electrons is the one with the minimum integral adsorption energy (G_int(n)). Using the computational hydrogen electrode approach⁴¹ with self-consistent coverage and adsorption free energies,²⁷ the adsorption phase diagram was calculated for every facet. The required over-potential to favor an intermediate step is given through the differential binding energy, which is given by:

ΔG_diff(n) = (G_int(n) − G_int((n − 1)))

We apply η = ΔG_diff(n)/e to find the minimum required over-potential to adsorb the intermediate,⁴¹ which enables a surface recombination reaction (the Tafel step). The barriers were calculated using the nudged elastic band (NEB) method with a climbing image.⁴²

2. Experimental methods

Materials

The commercially available materials were used as received: nickel acetylacetonate (Ni(acac)₂ for synthesis, VWR), oleic acid (suitable for cell culture, BioReagent, Aldrich), oleylamine (OA approximate C18-content 80–90%, Acros), trioctylphosphine (TOP 90%, technical grade, AcroSeal®, Acros), ethanol (absolute alcohol without additive ≥99.8%, Aldrich), n-hexane (HiPerSolv CHROMANORM® for HPLC 97%, VWR), sulfuric acid (H₂SO₄ volumetric 1 M, Aldrich), and Nafion® (117 solution, Aldrich). Water was first purified using a Millipore Milli-Q® Integral water purification system (18.2 MΩ cm resistivity). All syntheses were performed under strict air-free conditions using glove-box and Schlenk line techniques unless stated otherwise.

Synthesis of nickel phosphide nanowires

The synthesis was performed following a previous report.⁴³ A stock solution containing 0.75 mmol of Ni(acac)₂, 1.8 mmol of oleic acid and 10 mL of OA was heated at 120 °C. Then the stock solution was very slowly injected (0.05 mL min⁻¹) using a syringe pump into a stirred mixture containing 5 mL of OA and 2.4 mmol of TOP heated at 320 °C under reflux. The reaction mixture was kept at 320 °C under reflux until the stock solution was used up. Over the course of the reaction, the mixture color changes from transparent to dark yellow, orange and finally black. After cooling to room temperature, the products were washed using a mixture of hexane and ethanol, and separated by centrifugation. The supernatant was discarded and the washing step was repeated two more times. After the supernatant was discarded the nanowires were collected on a watch glass and dried in an oven at 50 °C overnight.

Physical characterization

X-ray diffraction (XRD) was carried out on a X'Pert Philips diffractometer in Bragg–Brentano geometry with Cu K_α1 radiation (λ = 0.1540 nm) and a fast Si–PIN multi-strip detector. The tube source was operated at 45 kV and 40 mA. The Scherrer equation was used to calculate the average crystallite size of the powder. The diffraction pattern was analyzed and compared with references in the international center of diffraction data (ICDD). Transmission electron microscope (TEM) images were taken on a Philips (FEI) CM12 with a LaB₆ source operated at 120 kV accelerating voltage. Specimens were prepared by ultrasonic dispersion of the samples in ethanol. The suspension was mixed with a micropipette by several suction–release cycles to ensure a representative and reproducible TEM sample is obtained. A few drops of the mixed suspension were deposited onto the carbon-coated grid.

Electrochemical measurements

Electrochemical measurements were recorded using a Gamry Instruments Reference 3000™ potentiostat. A traditional three-electrode configuration was used. For polarization and electrolysis measurements, a platinum wire was used as the auxiliary electrode and a double-junction Ag/AgCl (KCl saturated) electrode was used as the reference electrode. Both counter and reference electrodes were rinsed with distilled water and dried with compressed air prior to measurements. Potentials were referenced to a reversible hydrogen electrode (RHE) by adding a value of (0.2 + 0.059 × pH) V. The current was normalised over the geometric surface area of the electrode. Ohmic drop was corrected using the current interrupt method. A total electrolyte volume of ∼50 mL was used to fill the glass cell. All potentials were converted and referred to the RHE unless stated otherwise. The electrolyte used throughout all electrochemical experiments was a 1 M H₂SO₄ solution. During electrochemical experiments, the electrolyte was agitated using a magnetic stirrer rotating at 300 rpm. For all electrochemical experiments a glassy carbon electrode (∼0.071 cm²) was used as the working electrode. The cyclic voltammetry (CV) experiments were conducted in 1 M H₂SO₄ at 25 °C using a scan-rate of 5 mV s⁻¹ across a potential window of −0.3 to +0.1 V vs. RHE.

Pretreatment of the working electrode

Prior to loading of the catalyst, the working electrode was pretreated to achieve a better performance.⁴⁴ First, the electrode was manually polished using alpha alumina powder (CH Instruments, Inc.) with decreasing grain sizes (typically 0.3 and 0.05 μm) on a 73 mm diameter nylon polishing pad (MasterTex, Buehler). Between each polishing step the electrode was rinsed with deionized water and ultrasonicated in distilled water for 10 seconds. Then the electrode was dried using compressed air. This ultrasonication and drying cycle was repeated two more times: once in absolute ethanol and a second time with distilled water. This polishing process resulted in a shiny mirror finish. The bare working electrode was subjected to a constant potential of 2 V vs. RHE in 1 M H₂SO₄ under vigorous stirring at 25 °C over 1 hour. Then, the pretreated electrode was rinsed with absolute ethanol and dried with compressed air prior to catalyst deposition.

Electrode preparation

Before being deposited on the working electrode, the nanowires were annealed at 450 °C for 4 hours under 5% H₂/N₂ gas in order to remove any surfactant present on the nanowire surface.^19,43 The catalyst was loaded on a pretreated working electrode via drop-casting of 10 μL of the catalyst ink, equivalent to a loading of 1.42 mg cm⁻². The catalyst suspension was a 500 μL solution consisting of 5 mg of the catalyst, 400 μL of distilled water, and 100 μL of absolute ethanol. The slurry was ultrasonicated for 5 hours and mixed with a micropipette by several suction–release cycles prior to deposition to ensure that a representative and reproducible catalyst sample is obtained. The temperature of the ultrasonic bath was kept below 45 °C at all times to avoid any undesired heating effect. The nanowires are ultra-sonicated for 5 h to minimize aggregation. Once the catalyst was deposited, the electrode was dried in an oven at 50 °C for 10 minutes. 5 μL of 0.2% Nafion® solution in absolute ethanol was then drop-casted on the glassy carbon surface and the electrode was dried in air for 5 minutes prior to electrochemical measurements.

3. Results and discussion

XRD measurements were conducted on the annealed Ni₂P nanowires (Fig. 2). According to Scherrer's equation, the average crystallite size of the nanowires is 11 nm. Ni₂P is the predominant species in the sample, while small amounts of Ni₁₂P₅ and NiO are also present. Recently, Zhang et al. reported that pure Ni₁₂P₅ has a similar activity to that of Ni₂P for HER in acid.⁴⁵ We showed earlier that NiO is less active than Ni₂P; furthermore, NiO tends to dissolve at a reductive potential in acid. Thus, the HER activity of the nanowires (see below) can be mostly attributed to Ni₂P.

Fig. 2 (a) Representative TEM image of the annealed Ni₂P nanowires. (b) Focused SAED of nanowire crystallites indexed using JEMS© software. (c) and (d) Unfocused SAED patterns whose complementary information served to identify the growth direction of the nanowires.

The transmission electron microscope (TEM) image and selected area electron diffraction (SAED) patterns of the nanowires are shown in Fig. 2a–d. The nanowires are rather uniform and the width of the nanowires observed by TEM is in agreement with the crystallite size calculated from the XRD pattern. The focused SAED pattern (Fig. 2b) was indexed using the JEMS software program (P. Stadelmann, JEMS, EPFL). The line linking the (000n) spots is the (0001) direction. The nanowire can be observed on the SAED pattern when the focus is reduced (Fig. 2c and d). Comparison between the indexed (Fig. 2b) and unfocused SAED patterns (Fig. 2c and d) allows the determination of the growth direction. The results indicate that the nanowires grow along the c-axis, i.e., the 〈0001〉 direction.

Thus, the nanowires do not expose many (0001) facets, since the (000n) planes exist only in their cross section (see Fig. 3). The low index facets ±(112̄0) and (101̄0) are assumed to be widely available on the samples. These morphologies would be expected to exhibit a less than optimal performance if the ensemble on the Ni₃P terminated (0001) facet was the only active site.

Fig. 3 Model of a nanowire crystal. This illustrates the exposed facets. The (0001) plane of the unit cell is shown with solid lines, the coarsely dashed lines show a (101̄0) surface, and the finely dashed line shows the ±(112̄0) planes. Ni atoms are shown in green and phosphor atoms in yellow.

Fig. 4 shows the HER activity of the Ni₂P nanowires in 1 M H₂SO₄. The nanowires are excellent HER catalysts. This result combined with the calculations (see below) does not indicate that the (0001) ensemble is the only active site of HER from Ni₂P, although it is not possible to separate contributions from the various facets and sites in the experiments. The overpotential to drive a current density of 10 mA cm⁻² is 133 mV (Fig. 4a). Two Tafel slopes are observed. At η < 125 mV, the Tafel slope is about 60 mV dec⁻¹, while at η ≈ 125–275 mV, the Tafel slope is 126 mV dec⁻¹ (Fig. 4b). Despite the difference in sample preparation and morphology, the catalytic activity of the Ni₂P nanowires is very similar to the activity of hollow and multifaceted Ni₂P nanoparticles reported by Schaak et al.,¹⁹ that of polydispersed Ni₂P nanoparticles reported by our group²⁰ and that of high surface area Ni₂P nanoflakes reported by Han et al.²⁹ This suggests that widely available facets or sites of Ni₂P are active. This is contrary to MoS_x, where only specific morphologies are efficient because the edge sites need to be exposed.⁸ The facets with (ab −(a + b) 0) indices are propagating along the growth direction of the nanowires (see Fig. 3), and are thus expected to be abundant in the sample.

Fig. 4 (a) Polarization curve of Ni₂P nanowires in 1 M H₂SO₄ at 25 °C at a scan rate of 5 mV s⁻¹. (b) Tafel analysis of the polarization curve.

The DFT calculations show that the most strongly binding sites tend to be nickel bridge sites or nickel 3-fold hollow sites. The nickel bridge sites are found in continuous rows on the (101̄0) and (1̄1̄20) facets and adjacent to nickel hollow sites on the (112̄1) facet. (see ESI,† for geometries and adsorption energies.) Adsorption on Ni–P sites and on top P atoms was generally 0.2 eV to 0.4 eV less stable than the metal sites. Thus, adsorption on Ni–P sites and on top P atoms would require a higher over-potential.

It takes a high over-potential to favor a high coverage of atomic hydrogen on all the facets. Thus, Ni₂P is on the weak binding side of the Sabatier volcano. Adsorbates on Ni₂P interact strongly leading to a steeper increase in binding energy with increasing coverage (see ESI,† for the surface phase diagrams), compared to most transition metals including platinum.

The (0001) facet has the hollow site occupied at equilibrium, but as shown in Fig. 6, it requires a large over-potential of 0.41 V to stabilize the initial Ni–P bridge state for the Tafel step. It is also improbable that adsorbates from separate hollow sites on (0001) can combine since they are not neighbouring. This was confirmed by calculating the diffusion barriers on the (0001) and the (101̄0) facets (see ESI†). The (101̄0), (1̄1̄20) and (112̄1) facets only require an over-potential of 0.0 V, 0.06 V and 0.19 V, respectively, to stabilise neighbouring H* or H*, which are mobile in the row of nickel atoms. These results suggest that H* in Ni hollow sites on the (0001) facet do not contribute to the HER rate at low over-potentials. To investigate further, the barriers for the Tafel step were calculated as described in the following.

Previous calculations on Pt(111) suggest that the Tafel pathway is faster than the Heyrovski pathway at low over-potentials. If proton transfer is faster to H*(Ni₂P) than to H*(Pt(111)), it is possible that isolated metal hollow sites on the (0001) facet play a role. In the following, it is assumed that the surface coverage is in equilibrium with protons in solution, which means that the Tafel step is rate limiting. Calculation of the barrier for proton transfer (Volmer or Heyrovski step) is out of the scope of this paper, since it requires very precise information on the interfacial structure.⁴⁶

As shown in Fig. 5, the rate limiting HER barrier is G^TS, where G^TS is the energy of the transition state relative to the 2(H⁺ + e⁻) state. The initial states were the most stable configurations at the lowest possible over-potential according to the surface phase diagrams. As shown from calculations presented in Fig. 5, G^TS can be lowered by further increasing the over-potential until the free energy of protons in solution are at the Tafel transition state level. This agrees well with the exchange current density being a good indication for the activity at higher over-potentials.

Fig. 5 Free energy pathway of the Volmer–Tafel reaction on the (101̄0) facet. The configuration of every point is shown by the insets, where Ni is shown in green, P in yellow and H in white. The energy of the transition states is shown by the peak of the splines. These were calculated using the nudged elastic band method with a climbing image.⁴¹ This shows how G^TS is reduced by applying a higher over-potential.

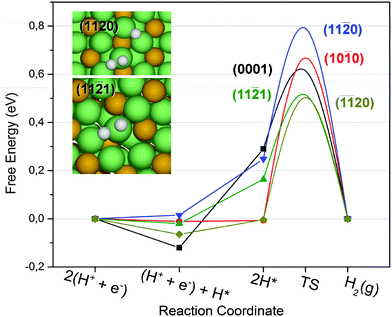
The results for a Tafel pathway are summarized in Fig. 6, with comparison between the studied facets. The adsorption energies, which are easy to calculate, are usually a good descriptor, since they are expected to scale with the transition state energies. In the case of a Tafel pathway, it is more accurate to use calculated G^TS to compare the activity from the different facets, since it is the highest barrier in the reaction pathway, which limits the rate.

Fig. 6 Free energy diagram assuming a Tafel mechanism. Calculated barriers for the Tafel step are shown by the peak of the splines for the configurations, which are most stable at 0 V vs. RHE. The insets show transition states of the two facets with the lowest Tafel barriers. Ni atoms are shown in green, P in yellow and H in white.

Observing the calculated G^TS in Fig. 6 for the Tafel steps, it is clear that the (1̄1̄20) facet and the (112̄1) facet should have the highest exchange current density and thus be the most active facets. The reason why these sites have the lowest combination barrier may be found in the geometry of the Ni atom binding the transition state. The transition states for (1̄1̄20) and (112̄1) are presented in the insets in Fig. 6. The atomic hydrogen moves from stable bridge sites on top of the nickel atom, which on these two facets is coordinated to six nickel atoms and two or three phosphor atoms. It is possible to imagine that a few defect sites, not investigated here, could be participating in the catalysis. However, the most active sites investigated in this study have binding energies very close to the optimal value and they are calculated to be very active. Other sites such as corners or kinks would only be relevant if they have a much higher activity than the low index facets. Furthermore, we expect that sites with lower coordination will bind too strongly, thus being less active according to the Sabatier principle.

4. Conclusion

In summary, the DFT calculations have shown that phosphor stabilized Ni-bridge sites found on several available facets of Ni₂P nanowires provide moderate binding to hydrogen atoms. The sites with highest exchange current density estimated from the Tafel transition state energy appear to be the Nickel bridge sites on either the (1̄1̄20) facet or the (112̄1) facet. The high activity measured from nanowires grown along the 〈0001〉 direction suggests that the active site of Ni₂P is unlikely the (0001) facet as previously speculated.¹⁸ Thus the experiments support the calculations, although contributions from various sites or facets cannot be completely isolated in the electrochemical measurements.

This work shows that Ni₂P has many very active sites for HER, which explains the good performance. An interesting outlook is the calculation of other metal phosphor compounds, to look for sites with slightly stronger hydrogen binding energies or less adsorbate repulsion, which could be promising candidates for new catalyst materials.

Acknowledgements

The work at EPFL is supported by EPFL and a grant from the Competence Center for Energy and Mobility (CCEM) in the framework of the Hytech project. At DTU, the work is funded by the Catalysis for Sustainable Energy (CASE) initiative and the Danish Council for Strategic Research via the NACORR project no. 12-132695.

References

1. A. Züttel, Hydrogen as a Future Energy Carrier, Wiley-VCH Verlag GmbH & Co. KGaA, 2008, pp. 1–6.
2. N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735.
3. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473.
4. S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184.
5. J. X. Wang, T. E. Springer and R. R. Adzic, J. Electrochem. Soc., 2006, 153, A1732–A1740.
6. K. Kunimatsu, T. Senzaki, M. Tsushima and M. Osawa, Chem. Phys. Lett., 2005, 401, 451–454.
7. E. Skulason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jonsson and J. K. Norskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250.
8. B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Norskov, J. Am. Chem. Soc., 2005, 127, 5308–5309.
9. T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102.
10. J. Kibsgaard, Z. Chen, B. N. Reinecke and T. F. Jaramillo, Nat. Mater., 2012, 11, 963–969.
11. J. R. McKone, B. F. Sadtler, C. A. Werlang, N. S. Lewis and H. B. Gray, ACS Catal., 2013, 3, 166–169.
12. H. Vrubel and X. Hu, Angew. Chem., Int. Ed., 2012, 51, 12703–12706.
13. C. G. Morales-Guio, L.-A. Stern and X. Hu, Chem. Soc. Rev., 2014, 43, 6555–6569.
14. P. Liu, J. A. Rodriguez, T. Asakura, J. Gomes and K. Nakamura, J. Phys. Chem. B, 2005, 109, 4575–4583.
15. G. H. Layan Savithra, E. Muthuswamy, R. H. Bowker, B. A. Carrillo, M. E. Bussell and S. L. Brock, Chem. Mater., 2013, 25, 825–833.
16. S. T. Oyama, T. Gott, H. Zhao and Y.-K. Lee, Catal. Today, 2009, 143, 94–107.
17. P. Liu, J. A. Rodriguez, Y. Takahashi and K. Nakamura, J. Catal., 2009, 262, 294–303.
18. P. Liu and J. A. Rodriguez, J. Am. Chem. Soc., 2005, 127, 14871–14878.
19. E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, J. Am. Chem. Soc., 2013, 135, 9267–9270.
20. L. Feng, H. Vrubel, M. Bensimon and X. Hu, Phys. Chem. Chem. Phys., 2014, 16, 5917–5921.
21. J. K. Nørskov, T. Bligaard, A. Logadottir, J. Kitchin, J. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26.
22. M. E. Bjorketun, A. S. Bondarenko, B. L. Abrams, I. Chorkendorff and J. Rossmeisl, Phys. Chem. Chem. Phys., 2010, 12, 10536–10541.
23. J. O. Bockris, A. K. Reddy and M. Electrochemistry, Electrodics in Chemistry, Engineering, Biology, and Environmental Science, Springer, 2000.
24. J. Greeley, J. K. Nørskov, L. A. Kibler, A. M. El-Aziz and D. M. Kolb, ChemPhysChem, 2006, 7, 1032–1035.
25. R. Parsons, Trans. Faraday Soc., 1958, 54, 1053–1063.
26. G. W. Watson, R. P. K. Wells, D. J. Willock and G. J. Hutchings, J. Phys. Chem. B, 2001, 105, 4889–4894.
27. J. Rossmeisl, J. K. Nørskov, C. D. Taylor, M. J. Janik and M. Neurock, J. Phys. Chem. B, 2006, 110, 21833–21839.
28. Y. Pan, Y. Liu, J. Zhao, K. Yang, J. Liang, D. Liu, W. Hu, D. Liu, Y. Liu and C. Liu, J. Mater. Chem. A, 2015, 3, 1656–1665.
29. A. Han, S. Jin, H. Chen, H. Ji, Z. Sun and P. Du, J. Mater. Chem. A, 2015, 3, 1941–1946.
30. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109.
31. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
32. E. Larsson, Ark. Kemi, 1965, 23, 335–365.
33. A. Jain, G. Hautier, C. J. Moore, S. P. Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295–2310.
34. S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66.
35. A. B. Alchagirov, J. P. Perdew, J. C. Boettger, R. C. Albers and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 026103.
36. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
37. D. Kanama, S. T. Oyama, S. Otani and D. F. Cox, Surf. Sci., 2004, 552, 8–16.
38. M. G. Moula, S. Suzuki, W.-J. Chun, S. Otani, S. T. Oyama and K. Asakura, Surf. Interface Anal., 2006, 38, 1611–1614.
39. Q. Li and X. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035414.
40. D. Guo, Y. Nakagawa, H. Ariga, S. Suzuki, K. Kinoshita, T. Miyamoto, S. Takakusagi, K. Asakura, S. Otani and S. T. Oyama, Surf. Sci., 2010, 604, 1347–1352.
41. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
42. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978.
43. Y. Chen, H. She, X. Luo, G.-H. Yue and D.-L. Peng, J. Cryst. Growth, 2009, 311, 1229–1233.
44. L.-A. Stern and X. Hu, Faraday Discuss., 2014, 176, 363–379.
45. Z. Huang, Z. Chen, Z. Chen, C. Lv, H. Meng and C. Zhang, ACS Nano, 2014, 8, 8121–8129.
46. J. Rossmeisl, K. Chan, R. Ahmed, V. Tripković and M. E. Björketun, Phys. Chem. Chem. Phys., 2013, 15, 10321–10325.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp01065a

---