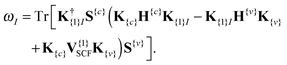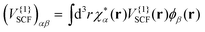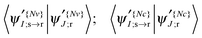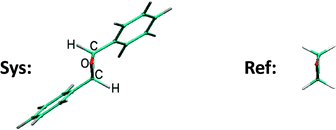Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identifying and tracing potential energy surfaces of electronic excitations with specific character via their transition origins: application to oxirane
Jian-Hao
Li
*,
T. J.
Zuehlsdorff
,
M. C.
Payne
and
N. D. M.
Hine
TCM Group, Cavendish Laboratory, J. J. Thomson Avenue, Cambridge CB3 0HE, UK. E-mail: jhl52@cam.ac.uk
First published on 1st April 2015
Abstract
We show that the transition origins of electronic excitations identified by quantified natural transition orbital (QNTO) analysis can be employed to connect potential energy surfaces (PESs) according to their character across a wide range of molecular geometries. This is achieved by locating the switching of transition origins of adiabatic potential surfaces as the geometry changes. The transition vectors for analysing transition origins are provided by linear response time-dependent density functional theory (TDDFT) calculations under the Tamm–Dancoff approximation. We study the photochemical CO ring opening of oxirane as an example and show that the results corroborate the traditional Gomer–Noyes mechanism derived experimentally. The knowledge of specific states for the reaction also agrees well with that given by previous theoretical work using TDDFT surface-hopping dynamics that was validated by high-quality quantum Monte Carlo calculations. We also show that QNTO can be useful for considerably larger and more complex systems: by projecting the excitations to those of a reference oxirane molecule, the approach is able to identify and analyse specific excitations of a trans-2,3-diphenyloxirane molecule.
I. Introduction
Kohn–Sham (KS) density functional theory (DFT)1–4 can accurately reproduce many properties of molecular and solid state systems5–7 as compared to experimental methods and higher-level theory, e.g. molecular structures, vibrational frequencies, atomisation energies and ionisation potentials. Meanwhile, its time-dependent extension, TDDFT,8–11 particularly in the linear response (LR) formalism,10 can deliver properties of excited states and optical absorption spectra of molecular systems. DFT and TDDFT calculations are increasingly able to treat large, complex biological systems, such as proteins, enzymes, and nucleic acids, due to the increasing availability of large computational facilities in recent years.12–15 However, there remain serious obstacles to such uses: the intrinsic cubic scaling of traditional KS-DFT with respect to the number of electrons; the explosion of the size of the available configurational phase space associated with large, flexible molecules; and the challenges of accurate electrostatics of solvated systems.16 When excited state properties are considered, further challenges come into play such as the proliferation of spurious charge transfer excitations, and the difficulty of identifying connected excited states on a PES.Recent advances in linear-scaling (LS)-DFT17–24 have made the study of very large molecular systems much more feasible. LS-DFT relies on the exponential decay of the density matrix, ρ(r,r′), with respect to |r − r′| in a system with a finite band-gap.25–27 In such systems, the density matrix, expressed using local orbitals, can be truncated by value or by range to render it local. In this work we use the ONETEP code,24 where a minimal number of local optimisable functions, called nonorthogonal generalised Wannier functions (NGWFs), are optimised in situ to best represent the density matrix of the system. Recently, linear-response TDDFT Tamm–Dancoff approximation (TDA) calculations have also become available in ONETEP, using a similar density matrix formalism.28 Such methods can provide valuable knowledge about the electronic excitations of very large molecular systems such as proteins and DNA segments. However, the low symmetry and complex geometry of biological systems exacerbates the aforementioned problem of tracing the PES of specific excited states. This work therefore focuses on quantified natural transition orbital (QNTO) analysis, recently proposed by Li et al.,29 which offers progress towards this goal.
QNTO analysis rewrites the transition vectors of an electronic excitation identified by a theoretical calculation, e.g. TDDFT, in terms of the natural transition orbitals (NTOs).11,30,31 The projection of hole (NTOn-H) and electron (NTOn-E) orbitals of the nth NTO pair onto a standard orbital basis set such as natural bond orbitals (NBOs)32–34 then helps quantify the transition origins of the NTOs of the excitation. Alongside the absorption energy and oscillator strength, knowledge of these transition origins helps provide a physical interpretation of the role of a given excitation dominated by single excitation character. Similar analysis may also be developed for single de-excitations, which is not as important in generic biological systems where de-excitations are usually negligible,11 signified by the good approximation of TDDFT/TDA to TDDFT. In addition, even in large and complex systems, electronic excitations may involve numerous electronic transitions between valence and conduction orbitals; using NTOs as the orbital basis, the number of dominant electronic transitions is often reduced to one or two, helping clarify what transition components contribute to the electronic excitations. QNTO analysis can help to assess the variation of transition origins determined by the different theoretical methods available in an electronic excitation calculation. For example, this approach has been used to assess the performance of different exchange–correlation functionals in predicting transition origins by comparing to a high-level theoretical calculation.29 The variations of transition origins caused by the presence of different molecular environments and/or different molecular geometries can also be investigated. For example, QNTO has been used to study the role of the DNA backbone in mediating the transition origins of electronic excitations of B-DNA.35
In the present paper, we introduce theoretical background to Linear-Response calculations in ONETEP (Section II), and show that QNTO analysis can be implemented with a non-orthogonal basis set such as the NGWFs used in ONETEP (Section III). In Section IV we then demonstrate two applications of LR-TDDFT/TDA/QNTO: (1) studying the photo-driven ring opening reaction of oxirane, and (2) identifying and comparing similar excitations between trans-2,3-diphenyloxirane and oxirane. We demonstrate that QNTO analysis can be readily used to locate state crossings that are otherwise unclear from plotting potential energy curves. The results are consistent with previous experimental and theoretical studies, showing that the present method is a feasible and reliable approach for investigating excited state related reactions.
II. LR-TDDFT in ONETEP
Linear-scaling DFT as implemented in ONETEP24,36 relies on a reformulation of the single-electron density matrix in terms of local orbitals, as follows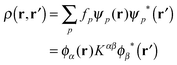 | (1) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) KS|ϕβ〉, with
KS|ϕβ〉, with ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) KS being the KS single-particle density operator. The nonorthogonal orbitals {ϕα} and their duals {ϕα} form a biorthonormal basis set such that 〈ϕα|ϕβ〉 = δβα.
KS being the KS single-particle density operator. The nonorthogonal orbitals {ϕα} and their duals {ϕα} form a biorthonormal basis set such that 〈ϕα|ϕβ〉 = δβα.
ONETEP employs a minimal number of NGWFs, each expressed in terms of periodic bandwidth limited delta functions (psincs) centred on the grid points of the simulation cell, with a spacing determined by a kinetic energy cutoff akin to that in a plane-wave code.37 NGWFs are localised to atom-centred spherical regions defined by a cutoff Rϕ. A total energy calculation proceeds by minimising the total energy simultaneously with respect to the matrix elements of the density kernel and the expansion coefficients of the NGWFs in terms of the psinc functions, via nested loops of conjugate gradients optimisations.38 NGWFs are initialised to pseudoatomic orbitals which solve the pseudopotential for a free atom.39 We confine our attention to closed-shell systems (even number of electrons) with non-fractional occupancy, and the total electronic energy of the real system is written as
| E0 = 2Tr[K{v}H{v}] + EDC | (2) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) {v}|ϕβ〉 with
{v}|ϕβ〉 with 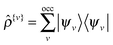 . The factor 2 accounts for the spin degeneracy and EDC is the standard “double-counting” correction. An FFT box technique36 is employed to allow one to construct matrix elements and density components in O(1) computational effort independent of system size.
. The factor 2 accounts for the spin degeneracy and EDC is the standard “double-counting” correction. An FFT box technique36 is employed to allow one to construct matrix elements and density components in O(1) computational effort independent of system size.
As described in detail in ref. 40, the minimisation is carried under the constraint of conserved total electron number,
| N = 2Tr[K{v}S{v}] | (3) |
| K{v} = K{v}S{v}K{v} | (4) |
Because the NGWFs are optimised in situ to describe the occupied part of the density matrix, they do not in general provide a good description of unoccupied states. Therefore, we instead generate and optimise in situ a second set of NGWFs, denoted as {χα}, obtained by minimising the bandstructure energy associated with a chosen range of low-energy conduction band states, having first projected out the valence states. The bandstructure energy to be minimised is written as
| E = 2Tr[K{c}H{c}] | (5) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) {c}|χβ〉. A full description of this procedure can be found in ref. 43.
{c}|χβ〉. A full description of this procedure can be found in ref. 43.
Recently Zuehlsdorff et al. proposed a formulation for linear-scaling LR-TDDFT/TDA (hereafter simply denoted as TDDFT) calculations, which uses the conduction and valence NGWFs as a basis for describing the response densities of electronic excitations.28 This approach adapts the Casida formulation for finding transition vectors, XI, and excitation energies ωI by using the TDDFT equation, AXI = ωIXI, to a nonorthogonal local orbital basis. The quantity sought is the sum of the energies of the Nω lowest excitations
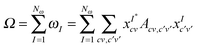 | (6) |
The transition density kernel, Kαβ{1}I = 〈χα|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) {1}|ϕβ〉 with
{1}|ϕβ〉 with 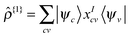 , defines the transition density according to
, defines the transition density according to
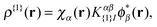 | (7) |
with V{1}SCF(r) being the Hartree and exchange–correlation response to the transition density as defined in eqn (9) of ref. 28.
The minimisation of eqn (6) proceeds as described in ref. 28. To avoid unwanted valence–valence transitions, we project out these unwanted components by constructing the kernel as
| K{1}I′ = K{c}S{c}K{1}IS{v}K{v} | (8) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) {c}|ζβ〉 = 〈ζα|Î −
{c}|ζβ〉 = 〈ζα|Î − ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) {v}|ζβ〉, giving
{v}|ζβ〉, giving| K{j} = S−1{j} − S−1{j}S{jv}K{v}S{jv}†S−1{j} | (9) |
We also note that in the TDDFT the KS-system is linked to the real-system by
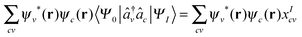 | (10) |
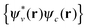 becomes likely as the orbital basis approaches completion44 and the simple assignment 〈Ψ0|â†vâc|ΨI〉 = xIcv may not be justified. Nevertheless, this assignment would become reasonable10 if the number of orbitals involved in 〈Ψ0|â†vâc|ΨI〉 is not too large, e.g. for low-lying excitations, and therefore the study of transition origins becomes possible via directly analysing xIcv or Kαβ{1}I from the TDDFT calculation.
becomes likely as the orbital basis approaches completion44 and the simple assignment 〈Ψ0|â†vâc|ΨI〉 = xIcv may not be justified. Nevertheless, this assignment would become reasonable10 if the number of orbitals involved in 〈Ψ0|â†vâc|ΨI〉 is not too large, e.g. for low-lying excitations, and therefore the study of transition origins becomes possible via directly analysing xIcv or Kαβ{1}I from the TDDFT calculation.
III. Quantified natural transition orbital (QNTO) analysis
In this section, we first introduce the basic formulation of QNTO analysis in terms of an orthonormal orbital basis such as KS-orbitals. We then detail how it is implemented in ONETEP within the NGWF representation. The standard notation ‘†’ is used throughout to denote conjugate transpose.A. Natural transition orbitals
The NTO basis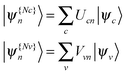 | (11) |
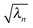 on the diagonal. In this representation the transition density operator is simplified to require summation over just one index:
on the diagonal. In this representation the transition density operator is simplified to require summation over just one index: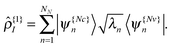 | (12) |
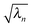 , which are ranked by magnitude.
, which are ranked by magnitude. 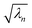 are called the singular values from the singular value decomposition (SVD) of XI = UDV†. We also see that the U and V respectively diagonalise XIX†I and X†IXI,
are called the singular values from the singular value decomposition (SVD) of XI = UDV†. We also see that the U and V respectively diagonalise XIX†I and X†IXI,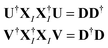 | (13) |
In TDDFT calculations in ONETEP, the local orbitals (NGWFs) are not an orthonormal basis. If the NTOs are expressed in terms of NGWFs as
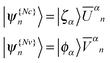 | (14) |
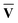 V† and the target for decomposition becomes
V† and the target for decomposition becomesK{1} = ŪD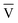 † † | (15) |
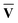 )†, where M†M = S{c} and N†N = S{v}. Once the singular vector matrices MŪ and N
)†, where M†M = S{c} and N†N = S{v}. Once the singular vector matrices MŪ and N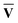 are obtained, we would then need to calculate M−1 and N−1 in order to solve for Ū and
are obtained, we would then need to calculate M−1 and N−1 in order to solve for Ū and 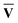 .
.
However, since the square root and inverse of a sparse matrix are in general much less sparse, their calculation would be very costly when dealing with large matrices. As an alternative approach, we can instead choose to diagonalise the XIX†I and X†IXI as shown in eqn (13). Since 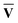 †S{v} =
†S{v} = 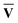 −1 and Ū†S{c} = Ū−1, the eigenvalue equations can be derived as
−1 and Ū†S{c} = Ū−1, the eigenvalue equations can be derived as
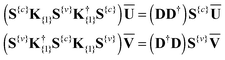 | (16) |
Note that in the SVD of XI = UDV†, the relative phase between each pair of left (NTOn-E) and right (NTOn-H) singular vectors are fixed: if the left vector is multiplied by (−1), the right vector must be multiplied by (−1) to remain a solution. Hence, the relative phase between each pair of eigenvectors needs to be determined after solving eqn (16). The following relation from eqn (15) can be used:
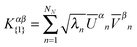 | (17) |
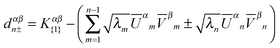 | (18) |
| Tr[dn+S{v}d†n+S{c}] < Tr[dn−S{v}d†n−S{c}] | (19) |
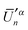 and
and 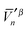 , produces the smaller value in eqn (19). If eqn (19) is not obeyed, we can multiply the whole vector
, produces the smaller value in eqn (19). If eqn (19) is not obeyed, we can multiply the whole vector 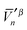 (or
(or 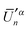 ) by (−1) to obtain a correct pair of
) by (−1) to obtain a correct pair of ![[V with combining overline]](https://www.rsc.org/images/entities/i_char_0056_0305.gif) β1 and Ūα1. As this is a separate operation from the calculation of
β1 and Ūα1. As this is a separate operation from the calculation of 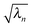 (eqn (16)), we can first solve for a number of eigenvalues n, where n ≤ NN, and subsequently define a number m, where (m ≤ n) of these where the associated singular vectors are of interest. This can reduce the computational effort compared to directly running an SVD algorithm given that many excitations will be dominated by just NTO1 or a small number of NTOn pairs.
(eqn (16)), we can first solve for a number of eigenvalues n, where n ≤ NN, and subsequently define a number m, where (m ≤ n) of these where the associated singular vectors are of interest. This can reduce the computational effort compared to directly running an SVD algorithm given that many excitations will be dominated by just NTO1 or a small number of NTOn pairs.
B. Interpretation of the transition origins of NTOn electron–hole pairs
After obtaining the NTO-based transition vector element to any NTOn, n ≤ NN, next we want to interpret the transition origins of each NTOn electron–hole pair from the projection to a standard orbital set. In the present work, we will in some places employ natural bond orbitals (NBOs)34 as the standard orbital set. By such a projection the composition of NTOn-H and NTOn-E can be quantitatively defined. We generate NBOs by applying the NBO 5.045 program as a postprocessing step after the ONETEP calculation. A relatively large atomic orbital (AO) basis set is used in ONETEP for generating NBOs, so that its quality is comparable to that of standard in situ optimised NGWFs. The electron spillage is thus reduced to a low level, typically 0.006% in the systems studied here, while the HOMO energy is typically within 0.03 eV of its value for NGWFs.Note that the transition vector, XI, can be based on different sets of reference orbitals in different calculations. Rewriting the transition vector using the unique NTO basis removes this reference dependence. Projection of NTOs onto a common orbital set such as NBOs then provides a unification of interpretative orbital set for these NTOs. For example, excitations in two systems of different environments and/or geometries can be compared and the precise contribution of an orbital of interest to an excitation can be computed. We may be interested in the hole orbital involved in a 1ππ* excitation of a molecule, and can compute its quantitative involvement in an excitation of the same molecule embedded in a chemical/physical environment with or without a covalent bond formed.
Two NTOs can be compared using the root mean square deviation, σ, of the projection coefficients with respect to a common standard orbital set35 such as the NBOs used in this work. The similarity of two NTOs can also be quantified by the magnitude of projection from one to the other. The projection sign can be arbitrary, as switching the overall phases of both NTOn-H and NTOn-E orbitals at the same time will result in them remaining a singular vector pair in eqn (15). We will use the latter method for comparing two NTOn-H(E) orbitals in the present work, while the projection to NBOs is only employed to help interpret the transition origins of NTOs.
The transition origins of each excitation can be seen as its fingerprint, helping to identify excitations of similar character. The adiabatic potential energy surfaces of electronic states can then be ‘reconnected’ on the basis of their character. If an electronic state of specific character changes its adiabatic energetic ordering from one geometry to the next, one would expect that at least one conical intersection (CX), key to many photochemical and photophysical processes,46–56 of electronic states has been passed between the two geometries. A by-product of analysing transition origins of a series of geometries along some coordinate(s) is, therefore, that one observes the influence of a CX (hyper-)point and locates the point where its projection onto the chosen path lies. Note that the current method is not by itself intended for locating the precise geometry of CX points, as to do that would require searching through the full internal coordinate space. In many well-defined cases, an appropriate series of geometries for analysing transition origins may be obtained by (constrained) geometry optimisation within the ground state or a chosen excited state,57 by molecular dynamics for the ground state or excited states,58via transition state search59etc. Overall, the method can be highly illustrative as to how a photo-absorption driven process/reaction might proceed.
We also note that due to the approximate nature of practical TDDFT functionals, the behaviour of TDDFT excitation energies around CXs may be incorrect,60e.g. they may have overly rapid energy variation. TDDFT can also give the wrong dimension of the branching plane.60 In other words, the PESs along some branching plane coordinates can be qualitatively wrong as the degeneracy is not lifted. While these issues of TDDFT on the study of CXs are still highly debated, TDDFT has, however, been able to offer a reasonable description of oxirane photochemistry61,62 which will be our focus in the present work. It has also been shown that TDA as implemented in the current work has some advantage over full TDDFT in the description of regions around intersections.62,63 It is known that the use of the TDA in TDDFT avoids the problems associated with singlet and triplet instabilities.64 The former can occur for systems which have strong static correlation, signified by the vanishing HOMO–LUMO gap, whereas the latter can occur for systems which have an unstable closed-shell ground state, reflected by a negative triplet excitation energy within the TDDFT/TDA.
Overall, since locating CXs is not the point of the present method, the ability to describe the immediate vicinity of a CX is not critical. As long as the influence of a CX on the excitation character of geometries reasonably distant from the CX itself in configuration space is qualitatively correct, then the method outlined will be useful. Note also that the current QNTO method is not limited to use with TDDFT; any electronic structure methods that provide a decomposition of excitations into single transitions of electrons can be combined with this approach, and TDDFT is particularly useful for the study of very large molecular systems.
As an example, we can examine the 2nd excitation of an oxirane molecule using TDDFT/QNTO. The geometry of the oxirane molecule, with CCO angle = 100°, is taken from a scan along the CCO angle which will be discussed in greater detail in Section IV. There are 9 valence (occupied) KS-orbitals in the calculation, and therefore the HOMO(LUMO) is indexed 9(10) etc. The transition density operator expressed in the KS-orbital basis results from summation over several pairs of orbitals:
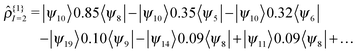 | (20) |
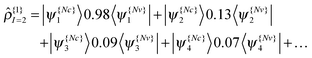 | (21) |
IV. Results and discussion
In this section, we discuss two applications of QNTO. In subsection A, we focus on tracing the PESs associated with the ring opening process of oxirane. In subsection B, we use QNTO to locate and compare similar excitations between trans-2,3-diphenyloxirane and those of oxirane. As discussed in Section III B, it is interesting to see how environmental factors can affect the transition origins of excitations of a molecule, which in turn may modify its reaction pathways. The study of trans-2,3-diphenyloxirane thus serves as an excellent example of the use of QNTO to identify specific excitations of the oxirane molecule embedded in a different environment.In all calculations a cut-off Coulomb approach65 has been employed to avoid the influence of periodic images from neighbouring simulation cells. A minimal set of 1 NGWF for H atom and 4 NGWFs for C and O atoms is used. All calculations are well-converged with respect to the variational parameters of the localisation radii: suitable values are 10 bohr for valence NGWFs and 16 bohr for conduction NGWFs. The kinetic energy cutoff for the grid spacing is well-converged at 1000 eV. Norm-conserving pseudopotentials are used to replace core electrons. For DFT and TDDFT calculations we make use of the (A)LDA functional in the Perdew–Zunger parameterisation66 throughout. While checking the accuracy of results using other higher level method may be desirable, we note that DFT/TDDFT calculations with the standard (semi-)local functionals LDA and PBE67 are capable of describing the photochemically relevant PESs of ring-opening reactions in qualitative agreement with high quality quantum Monte Carlo calculations.61,62 In addition, even though the use of Hartree–Fock exchange hybridised functionals such as PBE068 or asymptotically corrected functionals such as LB9469 may improve the DFT/TDDFT results, the results can deteriorate to be worse than that of pure PBE for structures near bond breaking region at large CCO angle where correlation effects become highly significant.61 Although further examinations of functionals such as range-separated hybrid ones that have been used for similar molecular systems7,29,70,71 may still be desirable, the (A)LDA is considered to be sufficient for the purpose of the present work.
A. Photoinduced ring opening of oxirane
The Gomer–Noyes mechanism, as depicted in Fig. 2, was postulated and experimentally confirmed72,73 as a way to explain the photoinduced ring opening process of the oxirane molecule. More discussions about this textbook molecule of stereochemistry can be found, for example, in ref. 74. In particular, the specific electronic states involved in the Gomer–Noyes mechanism have been examined in some detail through TDDFT excited state molecular dynamics (MD) simulations validated by high-quality quantum Monte Carlo calculations,61,62 and several states have been found to be involved in mediating the ring-opening reaction.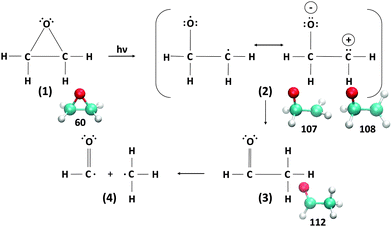 | ||
| Fig. 2 Gomer–Noyes mechanism. The underlying snapshots are from the CCO angle scans discussed in the text. | ||
Here, we perform a constrained ground state optimisation scan along the CCO bond angle of oxirane. We relax all internal coordinates except for a fixed CCO bond angle, which is set to values in the range 65° to 110°. For each oxirane geometry in the scan, a TDDFT calculation (vertical excitations) is performed followed by QNTO analysis to obtain the transition origins of the first few low-lying excitations.
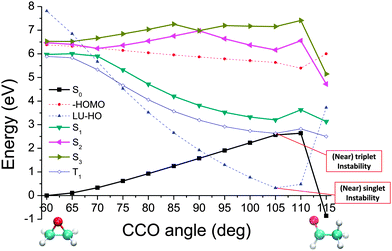
The potential energy curves of the low-lying singlet and triplet states are plotted in Fig. 3. For reference we also show the negative HOMO energy and the value of the HOMO–LUMO gap at each angle. A caveat is that the calculation quality would deteriorate for those excitations of energies higher than the negative HOMO energy. As this tends to be underestimated by the TDDFT/LDA,75 one may obtain fewer bound states than are present in the real system. In addition, as mentioned in Section III. B, a vanishing HOMO–LUMO gap and triplet excitation energy signifies a (nearly) singlet and triplet instability, respectively, whereas employment of TDA helps circumvent these problems and may be recommendable when using generic approximate functionals in TDDFT calculations.
We note that from the excitation energies alone there is no clear indication of where crossings, indicating nearby CX points, have been passed while progressing along these curves. This is where the utility of QNTO analysis can be seen, as discussed in Section III B. If the transition density operator for these systems is dominated by the NTO1 component (eqn (21)), the character of each excitation can be represented by the transition origins of just NTO1. The transition vector component for NTO1, 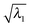 , along the scan are listed in Table 1. As can be seen, in most cases
, along the scan are listed in Table 1. As can be seen, in most cases 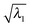 is higher than 0.99. For the first three excitations, the smallest
is higher than 0.99. For the first three excitations, the smallest 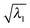 , 0.8477, is from the 3rd excitation of the oxirane geometry at CCO = 90°, which still captures about 72% of the density contribution. Thus, all the excitations on the oxirane geometries from the scan are dominated by the NTO1 transition, and when a switch of the NTO1 transition origins occurs, it shows that the excitation changes its character.
, 0.8477, is from the 3rd excitation of the oxirane geometry at CCO = 90°, which still captures about 72% of the density contribution. Thus, all the excitations on the oxirane geometries from the scan are dominated by the NTO1 transition, and when a switch of the NTO1 transition origins occurs, it shows that the excitation changes its character.
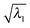 ) of the first eight excitations along the oxirane CCO scan (Fig. 3)
) of the first eight excitations along the oxirane CCO scan (Fig. 3)
| CCO | Excitation number | |||||||
|---|---|---|---|---|---|---|---|---|
| angle | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 60 | 0.9997 | 0.9999 | 0.9997 | 0.9981 | 0.9997 | 0.9985 | 0.9992 | 0.9961 |
| 65 | 0.9997 | 0.9997 | 0.9999 | 0.9980 | 0.9994 | 0.9986 | 0.9976 | 0.9980 |
| 70 | 0.9995 | 0.9997 | 0.9999 | 0.9976 | 0.9992 | 0.9916 | 0.9900 | 0.9983 |
| 75 | 0.9997 | 0.9998 | 0.9999 | 0.9964 | 0.9989 | 0.8737 | 0.8832 | 0.9947 |
| 80 | 0.9998 | 0.9999 | 0.9998 | 0.9921 | 0.9420 | 0.9874 | 0.9874 | 0.7348 |
| 85 | 0.9999 | 0.9998 | 0.9992 | 0.8237 | 0.7862 | 0.9972 | 0.9978 | 0.9560 |
| 90 | 0.9999 | 0.8798 | 0.8477 | 0.9971 | 0.9977 | 0.9926 | 0.9988 | 0.9789 |
| 95 | 0.9999 | 0.9800 | 0.9967 | 0.9963 | 0.9997 | 0.9954 | 0.9809 | 0.9996 |
| 100 | 0.9999 | 0.9843 | 0.9994 | 0.9996 | 0.9997 | 0.9859 | 0.9733 | 0.9877 |
| 105 | 0.9999 | 0.9868 | 0.9996 | 0.9997 | 0.9997 | 0.7387 | 0.7487 | 0.9853 |
| 110 | 0.9989 | 0.9503 | 0.9810 | 0.9067 | 0.9952 | 0.8161 | 0.7883 | 0.8233 |
| 115 | 0.9997 | 0.9959 | 0.9992 | 0.9993 | 0.9983 | 0.9909 | 0.9965 | 0.9877 |
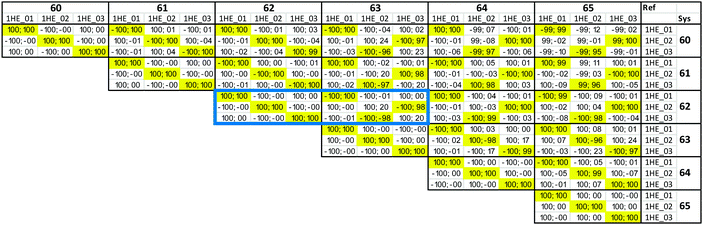
To put this in a form suitable for identifying electronic states of similar character section by section, we can construct a map (Fig. 4) showing the projections of the NTO1 pairs for each of the first three excitations (S1,S2,S3) at each geometry onto their equivalents at different geometries, forming a 3 × 3 block for each pair of geometries. We refer to the geometry listed down the row of the map as the ‘System’ (Sys) and compare it to a ‘Reference’ (Ref) geometry along the columns. To obtain a meaningful projection while accounting for the geometry change, the NTO1-H(E) orbitals are translated from the Sys-geometry to the Ref-geometry and renormalised before being used for projection. The optimised atom-centred NGWFs |ϕα;s〉 from the calculation in the Sys-geometry are translated to the corresponding atom centres in the Ref-geometry to produce NGWFs |ϕα;s→r〉. The NTO1-H orbital (eqn (14)) is then re-expressed in terms of these using the original coefficients ![[V with combining overline]](https://www.rsc.org/images/entities/i_char_0056_0305.gif) α1;s
α1;s
|ψ{Nv}1;s→r〉 = |ϕα;s→r〉![[V with combining overline]](https://www.rsc.org/images/entities/i_char_0056_0305.gif) α1;s. α1;s. | (22) |
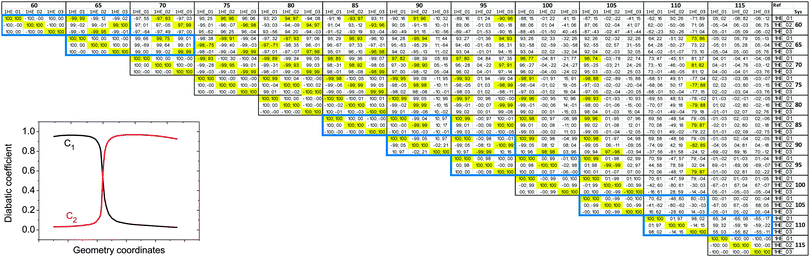 | ||
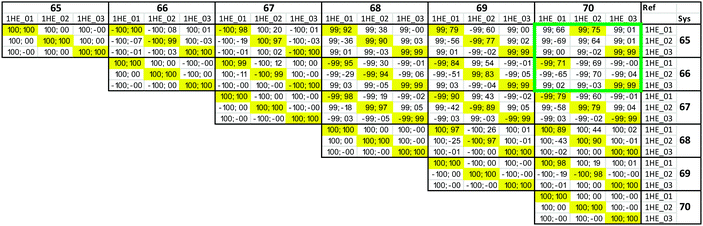
Fig. 4 Projection results for different pairs of NTO1-H(E) orbitals. Each row/column represents one of the first three excitations at each geometry at 5° intervals in a scan in the range CCO = 60°–115°. Each pair of CCO angles form a block in the map, which is divided into 9 cells for different pairing of excitations. The first and second number in a cell is the projection result (%) for NTO1-H and NTO1-E, respectively. A cell with yellow background indicates that both numbers are 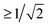 . The blocks marked by blue lines are where some character changes of excitations are observed one step off the diagonal blocks due to, for example, passing a CX. The small figure shows an example of adiabatic state behaviour near a CX.76Cn: (Diabatic) configuration coefficient for the two adiabatic states. . The blocks marked by blue lines are where some character changes of excitations are observed one step off the diagonal blocks due to, for example, passing a CX. The small figure shows an example of adiabatic state behaviour near a CX.76Cn: (Diabatic) configuration coefficient for the two adiabatic states. | ||
The translated orbital is then renormalised:
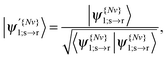 | (23) |
for I = 1, 2, 3 and J = 1, 2, 3.
In Fig. 4 one can immediately see which cells involve pairs of excitations with similar transition origins. We highlight those that have both projections greater than 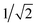 , indicating that the density contribution to one from the other is higher than 50%. One then sees where there are switches of transition origins of these adiabatic excited state curves, or changes of transition character of all excited states, from one block to another. The former case can indicate that there has been one or more CXs passed between the two excitations. The latter would be caused by a character change of the ground state itself. This can be due to the fact that a CX between S0 and S1 has been passed, e.g. 105° and 110°, or that the molecular structures have become drastically different, e.g. 105° and 65°.
, indicating that the density contribution to one from the other is higher than 50%. One then sees where there are switches of transition origins of these adiabatic excited state curves, or changes of transition character of all excited states, from one block to another. The former case can indicate that there has been one or more CXs passed between the two excitations. The latter would be caused by a character change of the ground state itself. This can be due to the fact that a CX between S0 and S1 has been passed, e.g. 105° and 110°, or that the molecular structures have become drastically different, e.g. 105° and 65°.
One can further subdivide the geometry scan to more accurately locate the position along the CCO angle coordinate where the character of the excitation changes. We demonstrate two such examples of switches of excitation which show subtly different behaviour. Fig. 5 shows an example where the switch of excitation character previously shown from the coarser map to occur between 60° and 65° is narrowed down to occurring abruptly between 62° and 63°. The corresponding potential energy curves for the two states involved, and the NTO1-H and NTO1-E orbitals before and after the switch, are plotted in Fig. 6, showing that the bands approach very closely around this point.
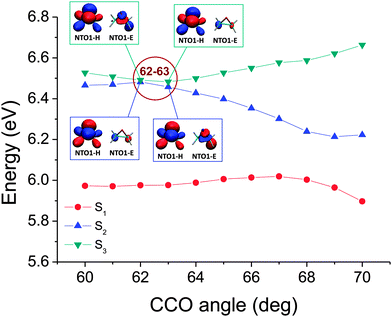 | ||
| Fig. 6 The corresponding potential energy curves for the map shown in Fig. 5. The NTO1-H(E) orbitals at 62° and 63° have also been plotted, with isovalue = 0.05 e bohr−3. While the NTO1-H remains the same for the 2nd and 3rd excitation, the NTO1-E orbitals can be seen to have switched their features between the 2nd and 3rd excitation at 62° and 63°, namely, the NTO1-E character of the 2nd(3rd) excitation at 62° corresponds to that of the 3rd(2nd) excitation at 63°. | ||
In other cases, however, when a more closely spaced geometry map is considered, the change of excitation character may be so smooth that no abrupt character switch occurring between two minimally-differentiated geometries can be found. An example is shown in Fig. 7. The two adiabatic excited state curves as plotted in Fig. 8 also do not come closer than 0.2 eV to each other. However, as the transition characters have switched for the two adiabatic excited states curves between CCO = 65°–70°, there must be a CX located nearby, i.e. on other (internal) coordinates, even if it does not occur exactly along the scanned coordinate. Thus, without analysing the electronic character, only from the plot of the energy, one would not necessarily know that molecular motions in this region of the scanned coordinate would be near a CX, and that an electronic state change from the upper surface to the lower surface could occur. However, note that from considering the overall shape of the energies in Fig. 3, it is not difficult to envisage that a crossing could have occurred between S1 and S2. For further analysis, the NTO1-H(E) orbitals of excitations from a geometry somewhat further away from those being considered can be used as a reference set, similar to a diabatic configurations set used for locating CXs.76 For the map shown in Fig. 7, the NTO1-H and NTO1-E orbitals of the first two excitations at CCO = 70° can provide an appropriate reference set. We thus project the NTO1-H and NTO1-E orbitals at varying geometries onto these reference orbitals, giving:
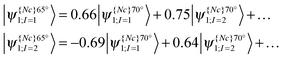 | (24) |
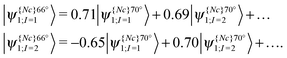 | (25) |
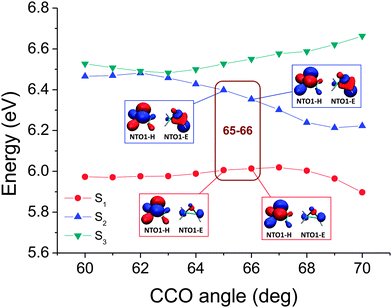 | ||
| Fig. 8 The corresponding potential energy curves for the map shown in Fig. 7. Unlike the case in Fig. 5, the switch of dominant NTO character cannot be seen from the plot of NTO1-H and NTO1-E, reflected also by the map (Fig. 7) where the projection results among 65°, 66°, and 67° cannot be seen to reveal a switch due to a smoother transition of dominant NTO1 character. | ||
We note that the exact point where the domination switches occur can be somewhat affected by the choice of reference orbitals used, although this does not in general prevent us from tracing down the CX to a small region in the scanned coordinate. In the language of diabatic configurations,76 the situation can be analysed by considering the matrix elements of a Hamiltonian Ĥ acting on a reduced subspace consisting of just two such configurations, denoted as |Φ1〉 and |Φ2〉. The switch of domination of two diabatic configurations as a given geometry path is traversed indicates that the surface H11 − H22 = 0 has been crossed, though the exact shape of the surface of H11 − H22 = 0 will be affected by the reference diabatic configurations used.
Evidence of a CX between S1 and S0, on the other hand, would be reflected in the map by the fact that a whole column of excitations would change transition character at the same time, because the ground state itself on which excitations are based has changed character. We are able to locate two such points in Fig. 4: between 107° and 108°, and between 111° and 112°, both related to the change of the ground state character expected from the Gomer–Noyes mechanism.
After locating the regions where two adiabatic excited state curves switch their characters, we can plot the adiabatic singlet states again, with the curves for the various excitations ‘re-connected’ based on their transition origins, as shown in Fig. 9. State labels of 1(n,3pz), 1(n,3s) and 1(n,σ*) are based on the symmetry at the CCO = 60° geometry and propagated to other geometries based on the connection of the states.
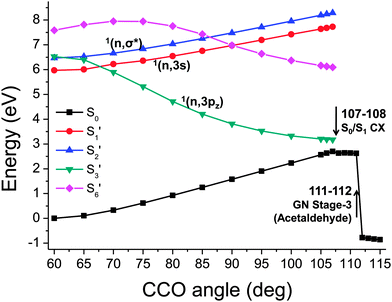 | ||
| Fig. 9 The 1st, 2nd, 3rd, and 6th singlet excitation potential energy curve (ranked at CCO = 60°) that is re-connected based on the similarity of transition origins. | ||
It then becomes clear that population of the S3′ state at CCO = 60° can directly lead to a crossing between S0 and S1. The energy decreases monotonically along with the widening CCO angle, which will result in a rapid ring opening reaction. This is consistent with the previous excited states MD study61 which found that the population of the 1(n,3pz) state would facilitate the occurrence of ring opening process. If the 1(n,3s) state is populated instead, it has to overcome an energy barrier to a widening of CCO angle before meeting a crossing with the 1(n,3pz) state which can then lead to the ring opening of oxirane. Thus, this chemical process is more difficult and would produce a lower quantum yield. We identify that the ground state is re-populated from the 1(n,3pz) state after oxirane passing the critical point between 107° and 108°.
Meanwhile, passing the critical point between 111° and 112° leads to another change of ground state character, which corresponds to a proton transfer process producing acetaldehyde, the product in the 3rd stage of the Gomer–Noyes mechanism (Fig. 2). This is also consistent with the MD study61 finding that the proton shift occurs after the oxirane has been de-excited to the ground state. Under thermally elevated conditions this proton shift will likely occur at lower CCO angles: here we address only the quasistatic constrained geometries. A follow-up reaction breaking the C–C bond, the final stage in Fig. 2, would then be possible while remaining in the ground state, given an appropriate combination of internal motion.61
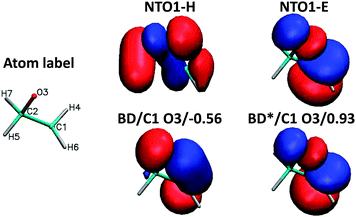
To demonstrate the chemical composition of these transitions, a decomposition of NTO1-H and NTO1-E into natural bond orbitals for the first three excitations at CCO = 60° is shown in Table 2. The AO basis used for generating NBOs is fairly large, producing 525 NBOs, but these are mostly of Rydberg (RY*) type. In practice, the lone-pair (LP) and bonding (BD) NBOs describe the majority of the NTO1-H excitation, which in all three cases is well-described by just five main NBOs. For the NTO1-E orbitals of the three excitations, however, a substantial contribution comes from RY* orbitals, which are highly dependent on the AO basis set used in generating NBOs. The LP and BD NBOs for NTO1-H, and the most relevant BD* NBOs for NTO1-E are shown in Fig. 10.
| N | NTO1-H | NTO1-E | ||||
|---|---|---|---|---|---|---|
| NBO type | Proj | NBO type | Proj | |||
| 1 | LP | O3 | 0.894 | BD* | C2 H7 | −0.168 |
| BD | C2 H7 | −0.215 | BD* | C1 H4 | −0.167 | |
| BD | C2 H5 | 0.213 | BD* | C1 H6 | −0.165 | |
| BD | C1 H6 | 0.199 | BD* | C2 H5 | −0.164 | |
| BD | C1 H4 | −0.198 | BD* | C1 O3 | 0.055 | |
| BD* | C2 H5 | 0.080 | BD* | C2 O3 | −0.048 | |
| Total | 0.976 | Total | 0.116 | |||
| 2 | LP | O3 | −0.894 | BD* | C1 C2 | −0.210 |
| BD | C2 H7 | 0.215 | BD* | C1 H4 | 0.124 | |
| BD | C2 H5 | −0.213 | BD* | C2 H5 | −0.123 | |
| BD | C1 H6 | −0.200 | BD* | C1 H6 | 0.121 | |
| BD | C1 H4 | 0.198 | BD* | C2 H7 | −0.119 | |
| BD* | C2 H5 | −0.080 | BD* | C1 O3 | 0.019 | |
| Total | 0.976 | Total | 0.104 | |||
| 3 | LP | O3 | 0.890 | BD* | C1 O3 | −0.306 |
| BD | C2 H7 | −0.219 | BD* | C2 O3 | 0.270 | |
| BD | C2 H5 | 0.218 | BD* | C2 H7 | −0.077 | |
| BD | C1 H6 | 0.203 | BD* | C1 H4 | −0.076 | |
| BD | C1 H4 | −0.202 | BD* | C1 H6 | −0.067 | |
| BD* | C2 H5 | 0.080 | BD* | C2 H5 | −0.065 | |
| Total | 0.977 | Total | 0.187 | |||
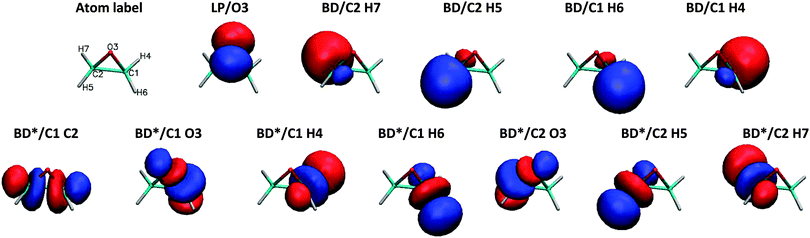 | ||
| Fig. 10 NBOs corresponding to Table 2. The lone pair on the oxygen (LP/O3) accounts for a large proportion of the NTO1-H for all three excitations. The 1st excitation is represented by NBOs denoted BD*/C2 H7, BD*/C1 H4, BD*/C1 H6, and BD*/C2 H5, whereas the 2nd excitation is represented by the same set of NBOs each with a reduced contribution, plus the more important BD*/C1 H2. The 3rd excitation is represented by BD*/C1 O3 and BD*/C2 O3. | ||
B. trans-2,3-Diphenyloxirane
In this subsection we focus on a significantly larger system, the trans-2,3-diphenyloxirane molecule, which contains the same CCO subsystem as oxirane as its central motif. We show that we can use the QNTO method to compare the excitations with those of an oxirane molecule. As would be expected, molecules with different physical/chemical environments can have distinct properties. For example, aryl substitution of oxirane can lead to a different ring opening mechanism.77 The fact that the trans-2,3-diphenyloxirane, referred to as the system (Sys) molecule, is formed by two aryl substitutions on oxirane makes it a good example for examining the influence of chemical environment on the excitations of the core oxirane moiety using TDDFT/QNTO.The structure of the Sys-molecule is first fully optimised without constraints. A equivalent geometry for the oxirane molecule, referred to as the reference (Ref) molecule, is then extracted from the optimised Sys-molecule by replacing the two aryl substitutents with hydrogen atoms and optimising the C–H bond lengths, at fixed bond angles (Fig. 11). The widespread problem that the energy of charge-transfer excitations is underestimated by local density functionals such as the LDA11 means in this case that we expect to find large numbers of charge-transfer excitations in the energy window of interest. In practice we find we need to calculate up to 100 excitations of the Sys-molecule so that the highest (100th) excitation energy calculated, 7.74 eV, exceeds the energy of the 8th excitation of the Ref-molecule (7.61 eV), which was the highest Ref-excitation studied in the current work.
The NTO1-H and NTO1-E orbitals for the excitations of Sys-molecule (Sys-excitations) and Ref-molecule (Ref-excitations) are then compared to each other to see if similar excitations can be identified between the first 8 Ref-excitations and the first 100 Sys-excitations. This is achieved by constructing, for each NTO1-H(E), a renormalised orbital based on just the component of each on the local orbitals of the 5 atoms common to both geometries (the oxirane core). We denote the NTO1-H(E) orbital of a Sys-excitation as |s〉, and the corresponding core orbital cNTO1-H(E) in the form |sc〉. Similarly, we define |r〉 and |rc〉 for the Ref-molecule. The |r〉 orbtitals are the NTO1-H(E) orbitals of the original reference oxirane geometry, whereas |s〉, |sc〉, and |rc〉 are constructed via a similar procedure to that used in constructing the projections of the previous section.
In particular, constructing |s〉 and |sc〉 requires a translation of the NTO1-H(E) from the Sys-molecule geometry to the Ref-molecule geometry. Using NTO1-H as an example, the set below are constructed:
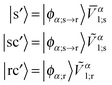 | (26) |
![[V with combining overline]](https://www.rsc.org/images/entities/i_char_0056_0305.gif) α1 in eqn (14) to zero for those NGWFs not centred on the core atoms; the subscript ‘s’ for Sys-excitations and ‘r’ for Ref-excitations indicate that the original NGWF coefficient matrices have been used.
α1 in eqn (14) to zero for those NGWFs not centred on the core atoms; the subscript ‘s’ for Sys-excitations and ‘r’ for Ref-excitations indicate that the original NGWF coefficient matrices have been used.
By evaluating the overlap 〈rc|sc〉 between an NTOn-H or NTOn-E orbital of the Sys-molecule and the corresponding NTO of the Ref-molecule, one can then tell whether there is a strong overlap of the character in the core region. In addition, the overlaps 〈sc|s〉 and 〈rc|r〉 allow one to determine how large a proportion of the total excitation is accounted for by the component within the core region.
In the general cases where excitations are dominated by the NTO1, one can then say that the two excitations from different molecules are similar if the following three conditions hold: (1) a Sys-excitation must have a substantial 〈sc|s〉 for both NTO1-H and NTO1-E, (2) a Ref-excitation must have a substantial 〈rc|r〉 for both NTO1-H and NTO1-E, and (3) the magnitude of 〈rc|sc〉 must be large.
We find that of all the 100 excitations of the larger system, there are 16 whose cNTO1-H and cNTO1-E respectively match with the cNTO1-H and cNTO1-E of one or more Ref-excitations. We choose a threshold of 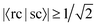 for both cNTO1-H and cNTO1-E. Overall there are 20 matching combinations, as some excitations overlap significantly with several excitations of the reference system. The 1st, 2nd, 4th, and 8th Ref-excitation are involved in these matching pairs.
for both cNTO1-H and cNTO1-E. Overall there are 20 matching combinations, as some excitations overlap significantly with several excitations of the reference system. The 1st, 2nd, 4th, and 8th Ref-excitation are involved in these matching pairs.
If the threshold is lowered to 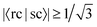 , the number of involved Sys-excitations becomes 25 and the number of matchings becomes 35. The 3rd and 7th Ref-excitation also now match with some Sys-excitations. All the 35 excitation matchings are listed in Table 3.
, the number of involved Sys-excitations becomes 25 and the number of matchings becomes 35. The 3rd and 7th Ref-excitation also now match with some Sys-excitations. All the 35 excitation matchings are listed in Table 3.
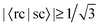 for both the NTO1-H and NTO1-E. The first and second number in a “(.)” is the projection result (%) for NTO1-H and NTO1-E, respectively. 00 denotes 100. Numbers shown in boldface are the excitations plotted in Fig. 12. Given the freedom of orbital shape outside the core region, it should not be surprising to see that the 2nd and 4th Ref-excitation match with multiple Sys-excitations
for both the NTO1-H and NTO1-E. The first and second number in a “(.)” is the projection result (%) for NTO1-H and NTO1-E, respectively. 00 denotes 100. Numbers shown in boldface are the excitations plotted in Fig. 12. Given the freedom of orbital shape outside the core region, it should not be surprising to see that the 2nd and 4th Ref-excitation match with multiple Sys-excitations
| Ref. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 〈rc|r〉 | (96;76) | (96;72) | (96;99) | (96;78) | (96;98) | (96;98) | (96;51) | (00;75) |
| Sys | 15 | 34 | 26 | 6 | 15 | 16 | ||
| 〈sc|s〉 | (80;38) | (78;81) | (79;32) | (81;15) | (80;38) | (32;39) | ||
| 〈rc|sc〉 | (−00;73) | (−00;−87) | (−00;65) | (−99;61) | (−00;−59) | (−90;74) | ||
| Sys | 24 | 43 | 39 | 14 | 24 | 21 | ||
| 〈sc|s〉 | (48;39) | (81;34) | (51;37) | (49;19) | (48;39) | (04;39) | ||
| 〈rc|sc〉 | (−00;74) | (00;84) | (−00;68) | (97;65) | (−00;−60) | (80;73) | ||
| Sys | 37 | 44 | 59 | 34 | 37 | 31 | ||
| 〈sc|s〉 | (81;65) | (65;87) | (39;43) | (78;81) | (81;65) | (50;24) | ||
| 〈rc|sc〉 | (00;−75) | (−00;−86) | (79;60) | (00;83) | (00;63) | (−92;−65) | ||
| Sys | 52 | 58 | (81) | 43 | 52 | 41 | ||
| 〈sc|s〉 | (47;66) | (13;39) | (51;62) | (81;34) | (47;66) | (32;63) | ||
| 〈rc|sc〉 | (−00;−75) | (−72;81) | (00;−58) | (−00;−76) | (−00;63) | (90;−78) | ||
| Sys | 57 | 44 | 57 | 46 | ||||
| 〈sc|s〉 | (61;38) | (65;87) | (61;38) | (04;65) | ||||
| 〈rc|sc〉 | (99;72) | (00;83) | (99;−60) | (75;−78) | ||||
| Sys | 65 | 58 | 79 | 64 | ||||
| 〈sc|s〉 | (28;64) | (13;39) | (42;53) | (29;65) | ||||
| 〈rc|sc〉 | (−66;68) | (72;−72) | (99;−61) | (−87;62) | ||||
| Sys | 79 | (71) | ||||||
| 〈sc|s〉 | (42;53) | (73;37) | ||||||
| 〈rc|sc〉 | (00;78) | (99;74) | ||||||
| Sys | 74 | |||||||
| 〈sc|s〉 | (03;57) | |||||||
| 〈rc|sc〉 | (−75;76) | |||||||
In Table 3, we see that 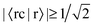 for both NTO1-H and NTO1-E of the 1st–6th and 8th Ref-excitation. As for 〈sc|s〉, of all the involved 25 Sys-excitations discussed above only the 34th Sys-excitation (hereafter denoted as Sys-34) satisfies
for both NTO1-H and NTO1-E of the 1st–6th and 8th Ref-excitation. As for 〈sc|s〉, of all the involved 25 Sys-excitations discussed above only the 34th Sys-excitation (hereafter denoted as Sys-34) satisfies 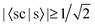 for both NTO1-H and NTO1-E. In other words, for the remaining 24 Sys-excitations there are ≥50% density contributions of NTO1-H and/or NTO1-E which come from outside of the core region. This would be unsurprising as there remain 22 atoms outside of the core region compared to 5 atoms in the core, and the de-localisation of the density contribution for many Sys-excitations is anticipated. If we lower the threshold to
for both NTO1-H and NTO1-E. In other words, for the remaining 24 Sys-excitations there are ≥50% density contributions of NTO1-H and/or NTO1-E which come from outside of the core region. This would be unsurprising as there remain 22 atoms outside of the core region compared to 5 atoms in the core, and the de-localisation of the density contribution for many Sys-excitations is anticipated. If we lower the threshold to 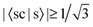 for both NTO1-H and NTO1-E, the Sys-37 and 44 also fall into the set. Some excitation properties of the Sys-34, 37, and 44 along with two more excitations, Sys-71 and 81, respectively for comparing with the Ref-08 and Ref-03, are listed in Table 4 and the NTO1-H(E) orbitals plotted in Fig. 12. It can be seen in Table 4 that the NTO1 transition vector component,
for both NTO1-H and NTO1-E, the Sys-37 and 44 also fall into the set. Some excitation properties of the Sys-34, 37, and 44 along with two more excitations, Sys-71 and 81, respectively for comparing with the Ref-08 and Ref-03, are listed in Table 4 and the NTO1-H(E) orbitals plotted in Fig. 12. It can be seen in Table 4 that the NTO1 transition vector component, 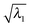 has generally decreased for the larger-sized Sys-molecule, although the NTO1 still accounts for at least 60% density contribution.
has generally decreased for the larger-sized Sys-molecule, although the NTO1 still accounts for at least 60% density contribution.
| Ref-01 | Ref-07 | Sys-37 | ||
| E (eV) | 6.04 | 7.46 | 6.55 | |
| f | 0.0253 | 0.0114 | 0.0070 | |
| NTO1 | 0.9997 | 0.9998 | 0.9876 | |
| Ref-02 | Ref-04 | Sys-34 | Sys-44 | |
| E (eV) | 6.52 | 6.62 | 6.44 | 6.75 |
| f | 0.0001 | 0.0199 | 0.0062 | 0.0489 |
| NTO1 | 0.9998 | 0.9982 | 0.9130 | 0.7740 |
| Ref-03 | Sys-81 | |||
| E (eV) | 6.57 | 7.36 | ||
| f | 0.0039 | 0.0332 | ||
| NTO1 | 0.9998 | 0.8154 | ||
| Ref-08 | Sys-71 | |||
| E (eV) | 7.61 | 7.20 | ||
| f | 0.0028 | 0.0054 | ||
| NTO1 | 0.9982 | 0.8851 | ||
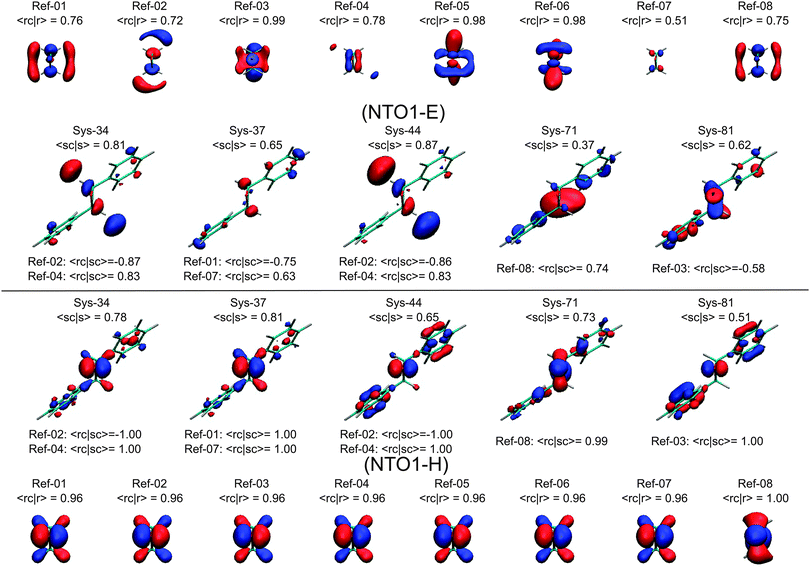 | ||
| Fig. 12 Plots of the NTO1-H(E) orbitals for the first eight Ref-excitations as well as several Sys-excitations that have a substantial overlap |〈rc|sc〉| to some Ref-excitations. Isovalue = 0.06 e bohr−3 for NTO1-H; for showing more details of the NTO1-E the isovalue is set to 0.03 e bohr−3. See Tables 3 and 4 and the text for more discussions. | ||
In Fig. 12 we see that the NTO1-H orbitals are essentially the same for the first 7 Ref-excitations. Moreover, the core parts of the Sys-excitations, Sys-34, 37, 44, and 81, fully coincide with the core parts of this NTO1-H orbital shared by the first 7 Ref-excitations, namely, |〈rc|sc〉| = 1.00. The differences between Sys-excitations and Ref-excitations mainly come from the more diffuse NTO1-E orbitals.
Strictly speaking, only the Sys-34 has a significant orbital component of NTO1-E coming from the core region, namely |〈sc|s〉|2 ≥ 0.5. In Table 4, it can be seen that the Sys-34 has an excitation energy that is close to those of the Ref-02 and Ref-04. The oscillator strength of Sys-34 also falls in between those of the Ref-02 and Ref-04. As for the orbital shape, the NTO1-E of the Sys-34 in Fig. 12 appears to be a mix between those of the Ref-02 and Ref-04, also reflected by a substantial |〈rc|sc〉| for both the Ref-02 and Ref-04.
The other Sys-excitations have a high proportion of NTO1-H and/or NTO1-E on the region outside the core, so comparing these Sys-excitations with the Ref-excitations would be misleading. In fact, the excitation energy can be close, as between the Ref-04 and Sys-44, or significantly different as between the Ref-03 and Sys-81. Nevertheless, the energies of similar-core excitations between the Sys- and Ref-molecule still fall reasonably close to each other, given the wide ranges of Sys- and Ref-excitation energies, i.e. 4.85–7.74 eV for the Sys-molecule and 6.04–7.61 eV for the Ref-molecule. Hence, the present method has been able to locate similar excitations of the two molecules among numerous other excitations, by appropriately tuning the thresholds of 〈rc|sc〉, 〈sc|s〉, and 〈rc|r〉.
It would be interesting to perform a similar study, and its ring opening reaction, using self-interaction error corrected or reduced functionals such as range-separated ones7,29 in the near future.78 For reducing charge-transfer contamination to local excitations, using some technique to confine electronic transitions to a small spatial range to counteract the de-localisation error from the LDA may also be a feasible approach.
V. Conclusions and future work
In this work we have developed QNTO analysis based on a non-orthogonal basis, as implemented in the linear-scaling DFT/TDDFT code ONETEP. We use the QNTO method to analyse the transition vectors of electronic excitations of various molecular systems offered by TDDFT calculations.We first studied the photo-induced ring-opening process of the oxirane molecule. Through a ground state scan along the reactive CCO angle of an oxirane molecule followed by TDDFT calculations (vertical excitations), a profile of several low-lying adiabatic excited state curves on which the excited state driven reaction may be carried can be constructed. However, these adiabatic excited state curves ranked by energies do not give us very much knowledge on how the reaction will proceed. We stress that the reaction process can be made much clearer if the excited state potential energy curves are labelled according to their excitation character instead of their energies. We demonstrated that the transition vectors of these low-lying excitations are dominated by the first NTO electron–hole pair (NTO1), and therefore the transition origins of NTO1 can be used to represent the character of these excitations. Based on this approach, we have successfully located several special geometrical points along the scanned CCO coordinate where the transition origins of two adiabatic excited state curves switch. By reconnecting the adiabatic excited state energy points (calculated by TDDFT) based on transition origins instead of energetic ordering, we are then able to depict how the excited state-driven ring-opening process can proceed. This picture is consistent with the previous excited state molecular dynamics study that found that the population of the 1(n,3pz) state facilitates the ring-opening process, while the population of 1(n,3s) state does not. We have demonstrated that the 1(n,3pz) state exhibits a monotonically-decreasing energy curve along the widening CCO angle, leading to a ring-opening reaction. For more complicated reactions with several coordinates involved and geometry strongly distorted, more geometries may be used, e.g. those from an excited state scan and molecular dynamics simulation, to help identify the photo-driven reaction pathways of interest. A promising future direction could be to apply this methodology to larger molecules with much more complex reaction pathways.
QNTO analysis has also been employed to study an aryl-substituted oxirane, the trans-2,3-diphenyloxirane molecule. The results demonstrate that the approach can be used to identify specific excitations among a large number of other excitations of a large/complex molecular system. By comparing the excitations of this larger molecule to those of oxirane, we have shown that a small number of mutually similar excitations can be identified and compared between the two molecules. The matching conditions that define similar excitations can be tuned by the magnitudes of: (1) the projection result of the core orbitals, cNTO1-H(E), between Sys-excitations and Ref-excitations; (2) the proportion of the cNTO1-H(E) accounting for the whole NTO1-H(E) in the Sys-excitation; (3) the proportion of the cNTO1-H(E) accounting for the whole NTO1-H(E) in the Ref-excitation. For example, a Sys-excitation can have a similar cNTO1-E to that of a Ref-excitation, but the cNTO1-E of the Sys-excitation only accounts for a tiny proportion to the whole NTO1-H(E) of Sys-excitation. In such a case, the orbital-section of the NTO1-E of Sys-excitation coming from outside of the core region cannot be ignored and the two excitations can not be assigned as similar excitations. The same approach for finding similar excitations through the transition origins would be particularly powerful when there are numerous excitations in a large molecular system. For example, those excitations that are located in a specific geometric region can be readily identified, helping to analyse the chemical properties of that region in a specific energy range of light absorption.
Acknowledgements
The authors would like to thank Louis Lee for very helpful discussions. All calculations in this work were carried out using the Cambridge HPC Service under EPSRC Grant EP/J017639/1. JHL acknowledges the support of Taiwan Cambridge Scholarship. TJZ acknowledges the support of EPSRC Grant EP/J017639/1 and the ARCHER eCSE programme. NDMH acknowledges the support of the Winton Programme for the Physics of Sustainability.References
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- R. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1994 Search PubMed.
- G. Giuliani and G. Vignale, Quantum Theory of the Electron Liquid, Cambridge University Press, Cambridge, 2005 Search PubMed.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2007, 128, 084106 CrossRef PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef.
- M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. K. U. Gross, Time-Dependent Density Functional Theory, Springer-Verlag, Berlin-Heidelberg, 2006 Search PubMed.
- M. E. Casida, in Recent Advances in Density Functional Methods, ed. D. P. Chong, World Scientific, Singapore, 1995, vol. 1 Search PubMed.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009 CrossRef PubMed.
- G. Lever, D. J. Cole, R. Lonsdale, K. E. Ranaghan, D. J. Wales, A. J. Mulholland, C.-K. Skylaris and M. C. Payne, J. Phys. Chem. Lett., 2014, 5, 3614 CrossRef.
- D. J. Cole, A. W. Chin, N. D. M. Hine, P. D. Haynes and M. C. Payne, J. Phys. Chem. Lett., 2013, 4, 4206 CrossRef.
- S. J. Fox, C. Pittock, C. S. Tautermann, T. Fox, C. Christ, N. O. J. Malcolm, J. W. Essex and C.-K. Skylaris, J. Phys. Chem. B, 2013, 117, 9478 CrossRef CAS PubMed.
- M. Todorovic, D. R. Bowler, M. J. Gillan and T. Miyazaki, J. R. Soc., Interface, 2013, 10, 20130547 CrossRef PubMed.
- G. Lever, D. J. Cole, N. D. M. Hine, P. D. Haynes and M. C. Payne, J. Phys.: Condens. Matter, 2013, 25, 152101 CrossRef PubMed.
- C. A. White and M. Head-Gordon, J. Chem. Phys., 1994, 101, 6593 CrossRef PubMed.
- V. Weber and M. Challacombe, J. Chem. Phys., 2006, 125, 104110 CrossRef PubMed.
- M. C. Strain, G. E. Scuseria and M. J. G. Frisch, Science, 1996, 271, 51 Search PubMed.
- E. Hernandez and M. J. Gillan, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10157 CrossRef.
- J. L. Fattebert and F. Gygi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115124 CrossRef.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103 CrossRef PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef.
- C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119 CrossRef PubMed.
- R. Baer and M. Head-Gordon, Phys. Rev. Lett., 1997, 79, 3962 CrossRef.
- S. Ismail-Beigi and T. A. Arias, Phys. Rev. Lett., 1999, 82, 2127 CrossRef.
- L. He and D. Vanderbilt, Phys. Rev. Lett., 2001, 86, 5341 CrossRef.
- T. J. Zuehlsdorff, N. D. M. Hine, J. S. Spencer, N. M. Harrison, D. J. Riley and P. D. Haynes, J. Chem. Phys., 2013, 139, 064104 CrossRef PubMed.
- J.-H. Li, J.-D. Chai, G. Y. Guo and M. Hayashi, Chem. Phys. Lett., 2011, 514, 362 CrossRef PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775 CrossRef PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1 CrossRef PubMed.
- L. P. Lee, D. J. Cole, M. C. Payne and C.-K. Skylaris, J. Comput. Chem., 2013, 34, 429 CrossRef PubMed.
- J.-H. Li, J.-D. Chai, G. Y. Guo and M. Hayashi, Phys. Chem. Chem. Phys., 2012, 14, 9092 RSC.
- C.-K. Skylaris, A. A. Mostofi, P. D. Haynes, O. Diéguez and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035119 CrossRef.
- C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Phys.: Condens. Matter, 2005, 17, 5757 CrossRef.
- A. A. Mostofi, P. D. Haynes, C.-K. Skylaris and M. C. Payne, J. Chem. Phys., 2003, 119, 8842 CrossRef PubMed.
- A. Ruiz-Serrano, N. D. M. Hine and C.-K. Skylaris, J. Chem. Phys., 2012, 136, 234101 CrossRef PubMed.
- P. D. Haynes, C.-K. Skylaris, A. A. Mostofi and M. C. Payne, J. Phys.: Condens. Matter, 2008, 20, 294207 CrossRef.
- P. D. Haynes, C.-K. Skylaris, A. A. Mostofi and M. C. Payne, Chem. Phys. Lett., 2006, 422, 345 CrossRef PubMed.
- N. D. M. Hine, P. D. Haynes, A. A. Mostofi, C.-K. Skylaris and M. C. Payne, Comput. Phys. Commun., 2009, 180, 1041 CrossRef PubMed.
- L. E. Ratcliff, N. D. M. Hine and P. D. Haynes, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165131 CrossRef.
- J. E. Harriman, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 29 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.9 (http://www.chem.wisc.edu/%E2%88%BCnbo5) & the NBO 5.9 Manual, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2011 Search PubMed.
- M. J. Bearpark, M. A. Robb and H. B. Schlegel, Chem. Phys. Lett., 1994, 223, 269 CrossRef CAS.
- D. R. Yarkony, J. Phys. Chem. A, 2001, 105, 6277 CrossRef CAS.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325 CrossRef CAS PubMed.
- A. M. Mebel, M. Baer and S. H. Lin, J. Chem. Phys., 2000, 112, 10703 CrossRef CAS PubMed.
- B. G. Levine and T. J. Martinez, Annu. Rev. Phys. Chem., 2007, 58, 613 CrossRef CAS PubMed.
- A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, J. Am. Chem. Soc., 2004, 126, 3234 CrossRef CAS PubMed.
- B. G. Levine, J. D. Coe and T. J. Martinez, J. Phys. Chem. B, 2008, 112, 405 CrossRef CAS PubMed.
- A. Raab, G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 110, 936 CrossRef CAS PubMed.
- S. Perun, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2006, 110, 13238 CrossRef CAS PubMed.
- B. K. Kendrick, C. A. Mead and D. G. Truhlar, Chem. Phys., 2002, 277, 31 CrossRef CAS.
- P. Celani, M. A. Robb, M. Garavelli, F. Bernardi and M. Olivucci, Chem. Phys. Lett., 1995, 243, 1 CrossRef CAS.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433 CrossRef CAS PubMed.
- E. Tapavicza, I. Tavernelli and U. Rothlisberger, Phys. Rev. Lett., 2007, 98, 023001 CrossRef.
- N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, Comput. Mater. Sci., 2003, 28, 250 CrossRef CAS.
- B. G. Levine, C. Ko, J. Quenneville and T. J. Martinez, Mol. Phys., 2006, 104, 1039 CrossRef.
- E. Tapavicza, I. Tavernelli, U. Rothlisberger, C. Filippi and M. E. Casida, J. Chem. Phys., 2008, 129, 124108 CrossRef PubMed.
- F. Cordova, L. J. Doriol, A. Ipatov, M. E. Casida, C. Filippi and A. Vela, J. Chem. Phys., 2007, 127, 164111 CrossRef PubMed.
- C. Hu, O. Sugino and K. Watanabe, J. Chem. Phys., 2014, 140, 054106 CrossRef PubMed.
- M. E. Casida, F. Gutierrez, J. Guan, F.-X. Gadea, D. Salahub and J.-P. Daudey, J. Chem. Phys., 2000, 113, 7062 CrossRef PubMed.
- N. D. M. Hine, J. Dziedzic, P. D. Haynes and C.-K. Skylaris, J. Chem. Phys., 2011, 135, 204103 CrossRef PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS PubMed.
- R. van Leeuwen and E. J. Baerends, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 2421 CrossRef.
- B. M. Wong, M. Piacenza and F. D. Sala, Phys. Chem. Chem. Phys., 2009, 11, 4498 RSC.
- M. Srebro, N. Govind, W. A. de Jong and J. Autschbach, J. Phys. Chem. A, 2011, 115, 10930 CrossRef CAS PubMed.
- E. Gomer and W. A. Noyes, Jr., J. Am. Chem. Soc., 1950, 72, 101 CrossRef.
- M. Kawasaki, T. Ibuki, M. Iwasaki and Y. Takezaki, J. Chem. Phys., 1973, 59, 2076 CrossRef CAS PubMed.
- J. Michl and V. Bonačić-Koutecký, Electronic Aspects of Organic Photochemistry, Wiley, New York, 1990 Search PubMed.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 11 CrossRef PubMed.
- G. J. Atchity and K. Ruedenberg, Theor. Chem. Acc., 1997, 97, 47 CrossRef.
- J. Friedrichs and I. Frank, Chem. – Eur. J., 2009, 15, 10825 CrossRef PubMed.
- J. Dziedzic, Q. O. Hill and C.-K. Skylaris, J. Chem. Phys., 2013, 139, 214103 CrossRef PubMed.
| This journal is © the Owner Societies 2015 |