Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modulated excitation extended X-ray absorption fine structure spectroscopy†
Gian Luca
Chiarello
*ab and
Davide
Ferri
c
aUniversità degli Studi di Milano, Dipartimento di Chimica, Via C. Golgi 19, I-20133 Milano, Italy. E-mail: gianluca.chiarello@unimi.it; Fax: +39 02 503 14300; Tel: +39 02 503 14281
bEmpa, Swiss Federal Laboratories for Materials Science and Technology, Ueberlandstrasse 129, CH-8600 Dübendorf, Switzerland
cPaul Scherrer Institut, CH-5232 Villigen PSI, Switzerland
First published on 13th March 2015
Abstract
The sensitivity of extended X-ray absorption fine structure spectroscopy (EXAFS) for minute structural changes can be enhanced by combination with the modulated excitation approach and making use of phase sensitive analysis. A modulated EXAFS experiment of a reversible periodic Pd to PdO partial oxidation has been simulated in order to understand the effect of the phase sensitive analysis on the shape and meaning of the resulting phase-resolved EXAFS spectra. In particular, the simulation comprises either a synchronous or a delayed sinusoidal variation of the EXAFS parameters, i.e. coordination number (N), interatomic distance (R) and Debye–Waller factor (σ2), of first Pd–Pd, first Pd–O, and second Pd–(O)–Pd coordination shells. The effect of these variations on the resulting phase-resolved Fourier transform EXAFS spectra is discussed. The results of the simulation are validated by an in situ EXAFS experiment at the Pd K-edge over 1.6 wt% Pd/Al2O3 undergoing reversible partial oxidation in a H2vs. O2 modulation at 573 K. It is shown that phase sensitive detection (PSD) is able to separate the minor contribution at ca. 2.8 Å corresponding to the growth of the Pd–(O)–Pd shell that is otherwise hidden under the static signal of the Pd–Pd shell of reduced Pd particles. The fitting of the phase-resolved EXAFS spectra suggests that the fast H2 to O2 switch leads the partial oxidation of the Pd surface with the formation of a PdO shell covering a metallic Pd core. Therefore, the dynamics of the full system can be described with greater detail than in conventional EXAFS. The intention of this work is to provide the tools and therefore a solid guidance to qualitatively and quantitatively understand the nature of the shape of phase-resolved FT-EXAFS spectra that may prove helpful in the analysis of a wide range of functional materials.
1. Introduction
The structure of the active surface species, e.g. the nature and geometry of adsorbates and of coordination sites on metal atoms, is a central issue to heterogeneous catalysis. X-ray Absorption Spectroscopy (XAS) has been largely employed in this context in an attempt to solve the oxidation state and the element specific local structure of the active sites, for example, on supported metal nano-particles while the catalytic event takes place.1 A vast improvement of knowledge on the structure of catalysts under working conditions has been achieved with both temporal and spatial resolution. However, XAS is intrinsically limited to bulk information due to the high penetration depth of the X-rays. Moreover, structural conclusions are usually derived from experiments performed under steady state conditions. Therefore, it may be difficult to ultimately discern the underlying red-ox dynamics of the catalyst in the catalytic cycle. Perturbation of the catalyst via modification of an external parameter can be used to enhance the catalyst performance2 and even more central to the spectroscopic investigations, it serves as an analytical expedient to obtain a deeper insight into reaction mechanisms. In this respect, Modulated Excitation Spectroscopy (MES),3–5 achieved through the periodic variation of the gas composition of feedstock, has been recently combined with time-resolved XAS.6–10 The combination revealed a powerful tool to convey enhanced sensitivity to XAS. MES exploits Phase Sensitive Detection (PSD) to increase the signal to noise ratio and to remove those parts of the spectra that are not affected by the external stimulation (e.g. the periodic change of the feedstock composition), significantly improving the active species response. This approach becomes particularly important for unveiling structural information of working nano-particles. Depending on the particle size, only a small fraction of atoms is usually involved in adsorption/reaction processes while their spectroscopic signature is often characterized by weak signals and hidden by the dominant static signals, e.g. of the nano-particle bulk. In the case of small particles of relevant (low) metal loadings of complex catalysts the noise will largely dominate the EXAFS signal. For metal oxide based catalysts, similar sensitivity improvements are anticipated.PSD is a function that transforms a set of time-resolved data I(t), with 0 < t < T (T being the stimulation period), into a new set of phase-resolved data I(φPSD), with 0° < φPSD < 360° (φPSD is the demodulation phase angle), according to the following equation:
 | (1) |
In previous reports considering supported Pd and Rh nano-particles,6–8,12,13 PSD was applied directly to the time-resolved XAS spectra. Though the method was demonstrated to be powerful for massively enhancing the EXAFS oscillations against the static response, a qualitative interpretation only of the region around the edge, the whiteline and ca. 150–200 eV above it was carried out.7,8,12 The result is that the ME-XAS is a valid alternative to the differential Δμ-XANES technique14,15 with the advantage of the higher signal to noise ratio and its intrinsic in situ nature (and no need for reference spectra in a vacuum). Contrary to the case of Rh where the catalyst structure oscillates between two boundary states, i.e. oxidized and reduced Rh, apparently without additional species, the phase-resolved spectra of Pd/Al2O3 exhibited a deviation from this behaviour. This was associated with the formation of Pd carbide species according to conventional EXAFS data fit.8 König et al.9 provided the first quantitative evaluation of phase-resolved EXAFS data after following the same procedure, thus demonstrating the great potential of this combination for elucidation of structural variations during reaction. Changes of coordination number and bond distances as low as 1% and 0.001 Å could be detected, respectively. The procedure for the isolation of transient structures additional to the two boundary states (oxidized and reduced metal) from phase-resolved EXAFS data was recently described by the same group.16 The massive enhancement of sensitivity provided by the method was further verified with the detection of sulfur containing species on Ru nano-particles while Ru changed from being partially oxidized to reduced.
Recently, Stötzel et al. have raised some doubts about the advantage of coupling ME with EXAFS followed by PSD data treatment.17 Thus, a more careful description of the possibilities at hand for application of PSD to XAS datasets is required even on a qualitative base. This has also been stimulated by the theoretical accounts of ME-XRD.18–20 As in the case of XRD, the interpretation of an EXAFS spectrum in the phase domain might turn into a more complex task than in the case of vibrational spectroscopy. During a modulation experiment, the periodic switch of e.g. gas composition affects the local structure around the absorber atom. Given the nature of the X-ray absorption process and thus of the EXAFS spectrum a greater number of variables are involved. The EXAFS spectrum in the k domain χ(k) is described by the well known equation,21
 | (2) |
As a complement to the previous reports where the XANES region was specifically treated,7,8,12,22 we proceed here to perform the phase sensitive analysis of time-resolved EXAFS data in the k space and discuss the effects of the variation of the structural parameters (N, R and σ2) on the shape and intensity of observable changes in the corresponding Fourier transform data set. In order to facilitate the interpretation of phase domain FT-EXAFS data, we will first analyze simulated EXAFS spectra at the Pd K-edge of an ideal Pd surface that undergoes reversible partial re-oxidation. This approach is not intended to simulate the real red-ox dynamics of catalytic Pd nano-particles. More sophisticated DFT calculations are necessary for this purpose. The aim of this simulation is rather the systematic evaluation of the effect of a periodic variation of the structural parameters on the shape of phase-resolved spectra. The effect of the variation of the three structural parameters on a single coordination shell or on different shells will be treated separately. Finally, the results of the simulation will be verified on a relatively simple experimental system for catalysis consisting of Pd nano-particles supported on Al2O3 subjected to reduction and re-oxidation cycles.
2. Experimental
2.1. Simulation of EXAFS spectra
In order to explore the reliability of the application of the PSD algorithm to EXAFS spectra a set of simulated time-resolved spectra at the Pd K-edge has been considered first. These spectra have been generated considering a metallic Pd surface subjected to a modulation experiment where the gas atmosphere is periodically switched from reducing (e.g. H2-rich) to oxidizing (e.g. O2-rich) with a full modulation period (T) of 100 s. Under these conditions, we can suppose that Pd is periodically partially oxidized in the presence of O2 and then reduced in the following H2-rich pulse. In a first approximation, the metal state can be described by considering only the first Pd–Pd scattering shell, whereas the oxidized state is well represented by both the first Pd–O and the second Pd–(O)–Pd scattering shells. Considering that the same number of atoms takes part to the periodic oxidation–reduction process (absence of disaggregation and re-construction),23 the oxidation proceeds reasonably from the surface to the bulk, thus provoking the decrease of the average coordination number of the Pd–Pd shell (this is particularly true in the case of Pd nanoparticles) and the simultaneous appearance of the Pd–O and Pd–(O)–Pd shells.The simulated EXAFS spectra at the Pd K-edge have been obtained using the scattering paths generated with the FEFF6 code.24 The structural parameters (N, R and σ2) of the three considered scattering paths (Pd–Pd, Pd–O and Pd–(O)–Pd) were varied as a sinusoidal function of the frequency ω, equal to the simulated modulation frequency (ω = 2π/T). All simulated and experimental spectra have been analyzed and processed using the IFFEFIT software package,25 including Athena for data normalization, background subtraction, k-weighting and Fourier transformation and Artemis for data fitting. All reported FT-EXAFS spectra are not phase corrected.
2.2. Modulated excitation quick-EXAFS experiment
Time-resolved quick-EXAFS spectra were collected at the Pd K-edge (24.35 keV) at the beamline BM23 of ESRF (Grenoble, France). The 1.6 wt% Pd/Al2O3 sample (141 m2 g−1; 13% Pd dispersion; Pd particles size of ca. 6 nm), kindly provided by Umicore, was tested using an in situ reactor cell designed for simultaneous XAS/DRIFTS measurements,26 though no DRIFT spectra have been considered for this work. The outlet gas composition was constantly monitored using mass spectrometry (MS).26,27 The sample was heated to 573 K under flowing 1 vol% O2/He (80 ml min−1). After 30 min at 573 K, the flow was changed to He until the MS signals were stable. At this point, the modulation experiment was started. A full modulation period (T = 155 s) consisted of a pulse of 1 vol% H2/He followed by an equal pulse of 1 vol% O2/He while recording 28 quick-EXAFS spectra (ca. 5.3 s per spectrum). The full ME-EXAFS experiment consisted of thirty consecutive periods. The first two periods were discarded in the data analysis in order to ensure that steady state conditions have been achieved. The PSD data are obtained using a homemade Matlab based routine including also the averaging of the time-resolved spectra over the modulation periods.3. Results and discussion
3.1. Interpretation of the phase resolved EXAFS spectra
The fundamental requirement in order to apply the PSD function (eqn (1)) is that the system undergoes a reversible transformation in response to the external stimulation. This is the case for many phenomena occurring at the surface or at the bulk of solid materials, such as adsorption/desorption of probe molecules or redox dynamics, which are often involved in catalytic or gas sensing mechanisms. Under this condition, a sinusoidal stimulation of frequency ω provokes a likewise sinusoidal system variation characterized by the same frequency ω, but with an amplitude and eventually a phase delay ϕ, both depending on the system response kinetics. Considering that an ideal Pd surface during the redox modulation experiment consisting of H2/O2 pulses Pd oscillates between two boundary structures, i.e. fully reduced and partially oxidized, with frequency ω. These two structures generate EXAFS spectra χt(k)i and χt(k)f, whose difference spectrum can be expressed as Δχt(k) = χt(k)f − χt(k)i. These two spectra are not necessarily the first and last spectra of a stimulation period. Moreover, at each k value, the temporal variation of the EXAFS signal intensity χk(t) oscillates between a maximum (χk,max) and a minimum (χk,min) value, hence with an amplitude equal to Δχk/2(Δχk = χk,max − χk,min).It must be noticed that the PSD function (eqn (1)) is applied to the signal variation recorded along the time at each k value χk(t), by varying the demodulation phase angle in the range 0° < φPSD < 360° with a step size of 10°. This operation transforms χk(t), recorded in the time domain, into a new set of 36 χk(φPSD), representing the phase domain. The new phase-resolved EXAFS spectrum at a given φPSD angle, χφ(k) is obtained by extending this procedure to all of the 0 < k < 14 values. The strength of PSD is to filter those contributions of the spectrum that are unaltered by the external stimulation, together with a considerable increase of the signal to noise ratio.8,9 As a result, a phase-resolved spectrum contains only those features of the active (responsive) species to the stimulation.
The signal intensity variation in the phase domain, χk(φPSD), can be calculated from eqn (1):3
 | (3) |
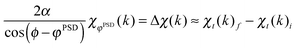 | (4) |
Because χt(k) are oscillating functions, there are points along the k-axis where χt(k)i and χt(k)f cross each other (Fig. 2A). In these points, Δχk = 0 and consequently χk(φPSD) = 0 for any φPSD (eqn (3)). These points are nodes of the phase resolved EXAFS spectra. The plots of all of the phase-resolved EXAFS spectra obtained in the phase domain 0° < φPSD < 360° result in a linear front (amplitude at each k value given by eqn (3)) of waves propagating along the k-axis, all crossing the k-axis at the nodes, giving rise to a typical envelope as the one displayed in the bottom panel of Fig. 2A. As shown in Fig. 3, the envelop can exhibit two characteristic shapes, “in phase” (Fig. 3A) or “out of phase” (Fig. 3B) (not to be confused with the “in-phase” spectrum), depending on the variation of the possible 3n EXAFS variables. Contrary to the “in phase”, the “out of phase” shape is generated when at least one of the possible 3n variables exhibits a different phase lag ϕi with respect to the others. A different phase delay can occur either between the structural parameters of a single shell (Ni, Ri and σi2) or of different shells. These two scenarios can be distinguished by means of the analysis of the Fourier transform of the phase-resolved EXAFS spectra, χφ(R). The FT-EXAFS spectra are calculated according to the equation:
 | (5) |
 | (6) |
 | ||
| Fig. 2 Effect of variation of coordination number N (according to Fig. S2, ESI†) of a single Pd–Pd first coordination shell on (A) the simulated k2-weighted χ(k) EXAFS spectra, (B) the FT-magnitude |χ(R)| and (C) the FT-real part Re[χ(R)]. Top panels: simulated time-resolved spectra where N varies from 12 (red curve) to 6 (blue curve) with a phase lag ϕ = 0° (R = 2.758 Å, σ2 = 0.003 Å2, ΔE° = 0 eV). Bottom panels: corresponding phase-resolved spectra, where the red curve is the “in-phase angle” (φPSD = ϕ = 0°). | ||
It is important to note that |χ(R)| always exhibits positive values, whereas its real and imaginary parts oscillate between positive and negative values. Moreover, Re[χφ=ϕ(R)] = −Re[χφ=ϕ+180°(R)], because the amplitude of the real and imaginary parts of the phase-resolved FT spectra as a function of φPSD are proportional to cos(ϕ – φPSD) (eqn (3)), whereas |χφ=ϕ(R)| = |χφ=ϕ+180°(R)|. In other words, the magnitude of the FT-EXAFS spectra in the range ϕ < φPSD < ϕ + 90° overlaps with those in the range ϕ + 90° < φPSD < 180° + ϕ (Fig. 2B), whereas the real and the imaginary parts of the latter set of spectra are the reciprocals of the former set (Fig. 2C). This observation is crucial to solve the dynamics of one coordination shell relative to another one, e.g. one shell appears while the other one disappears during a structural transformation, as will be described in the following sections.
3.2 Simulated EXAFS spectra at the Pd K-edge
The simple ME-EXAFS experiment considered here consists of alternate and repeated switches from H2 (i.e. reducing atmosphere) to O2 (i.e. oxidizing atmosphere) over an extended metallic Pd surface. This surface simulates for simplicity a metal nano-particle exposing extended facets as it is in the case of the nano-structured Pd supported catalyst (1.6 wt% Pd/Al2O3). Under such conditions, Pd periodically (either partially or fully) reduces and re-oxidizes. Depending on its extent, the oxidation process may cause a decrease of the average coordination number of the first Pd–Pd shell. The metal Pd nano-particle becomes increasingly smaller because the oxidation starts from the surface. Simultaneously, the oxidation leads to the formation of the two main PdO coordination shells, i.e. the first Pd–O and the second Pd–Pd (hereafter labeled as Pd–(O)–Pd) coordination shells. The decrease of the particle size can eventually produce a small decrease of the interatomic distance R because of lattice contraction and also an increase of the disorder (σ2). In a first approximation, the variation of these parameters (Ni, Ri and σi2) within the time I(t), resulting from a sinusoidal stimulation of frequency ω, can be represented using a sine function oscillating between a maximum (Imax) and a minimum (Imin) value with an amplitude equal to ΔI/2 (ΔI = Imax − Imin): | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = sin(α + 180°), the two parameters propagating as two anti-phase sine functions possess the same relative phase lag ϕi, but one of them has an absolute phase lag of ϕi + 180°. Moreover, the parameters can either possess the same or a different relative phase lag, ϕi. Both possibilities have been considered for the simulation. It should be pointed out that in the ME approach it is not crucial that the system response follows a perfect sine function. However, it is necessary that it is stationary along the time (i.e. it must be fully reversible) and a given event has to occur at the same frequency as that of the stimulation.
α = sin(α + 180°), the two parameters propagating as two anti-phase sine functions possess the same relative phase lag ϕi, but one of them has an absolute phase lag of ϕi + 180°. Moreover, the parameters can either possess the same or a different relative phase lag, ϕi. Both possibilities have been considered for the simulation. It should be pointed out that in the ME approach it is not crucial that the system response follows a perfect sine function. However, it is necessary that it is stationary along the time (i.e. it must be fully reversible) and a given event has to occur at the same frequency as that of the stimulation.
(1) N is directly proportional to the amplitude of χ(k). Fig. 2 shows the comparison of the simulated noise-free time-resolved χ(k), |χ(R)| and Re[χ(R)] of a single Pd–Pd shell (upper panels) with the corresponding phase-resolved spectra (lower panels), for a sinusoidal variation of only N (Fig. S1, ESI†) between 12 (red line in Fig. 2A) and 6 (blue line in Fig. 2A). In this case, the in-phase phase-resolved spectrum (red line in Fig. 2A) is simply equal to the time-resolved spectrum obtained with Nmax = 12 (same frequency and disorder, because R and σ2 have been kept constant) but with an amplitude reduced by a factor of 4.2 (i.e. 2.1Nmax/ΔN, with ΔN = 6). Thus, the fitting of the in-phase FT spectrum |χφ=ϕ(R)| gives R and σ2 of the time-resolved spectra and N = ΔN/2.1. Moreover, as shown in Fig. 4, the normalized (i.e. divided by the maximum value) time-resolved real part Re[χ(R)] is equal to the normalized phase-resolved Re[χφ(R)].
(2) σ2 affects the amplitude as well (Fig. S2 and S3, ESI†). However, the variation is k-dependent because σ2 appears in the exponential term exp(−2σ2k2) of eqn (1). As a consequence the amplitude of χ(k) decreases along the k-axis with increasing σ2. In particular, σ2 affects the shape of the FT-EXAFS spectrum. The variation of σ2 can be easily distinguished by the variation of N because it leads to a distortion of the real part with respect to that of the initial state. This effect can be better observed by comparing the normalized in-phase Re[χ(k)] (e.g. divided by the maximum value) with that of the initial state (Fig. S4, ESI†).
(3) In marked contrast, the change of interatomic distance R reflects upon both the amplitude and the frequency of the FT functions (Fig. S5 and S6, ESI†). As a consequence, the phase-resolved EXAFS spectrum is a difference of two waves (eqn (4)) having frequency R and R + ΔR. However, ΔR is usually lower than the achieved spatial resolution in EXAFS spectroscopy, because of the |χ(R)| peak broadening due to the limited k range (in this case 2 < k < 14 Å−1). Hence, the two peaks overlap in the phase-resolved FT spectra and the signals with frequency R and R + ΔR are additive in the real and imaginary parts of the FT. This latter property makes the normalized real part of the phase-resolved spectra slightly shifted along R and with lower (higher) amplitude at lower (higher) R compared to the normalized part of the initial state (Fig. 4).
The variation of R plays a dominant role in deciding the shape of the phase-resolved spectra. The differentiation of the synchronous variation of N is difficult if the two parameters possess the same relative phase lag, ϕN = ϕR (Fig. S7 and S8, ESI†). In contrast, if the two parameters have different phase lag (Fig. S9, ESI†), the phase-resolved χ(k) spectra generate an out of phase envelop (Fig. 3 and 5) and the final state with bond distance R + ΔR can be isolated in the FT spectra at φPSD = ϕN + 90° (green curves in Fig. 5). The out of phase envelop can be observed again in the real part of the phase-resolved FT spectra.
| Gas atmosphere | Shell |
S
0
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
N | R (Å) |
σ
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (Å2) d (Å2) |
ΔE0e (eV) |
|---|---|---|---|---|---|---|
| a Amplitude reduction factor (calculated by fitting of standard Pd foil and PdO). b Coordination number. c Interatomic distance. d Debye–Waller factor (mean square disorder). e Energy shift. f Fit of last time-resolved spectrum recorded in H2 and representing the initial state χ(k)i. g Fit of last time-resolved spectrum in H2 subtracted by the scaled phase-resolved spectrum at φPSD = 230°. h Fit of scaled phase-resolved spectrum at φPSD = 250°. and h Represent the structure of the final state in O2. | ||||||
| 1 vol% H2/He | Pd–Pdf | 0.74 | 11.4 ± 0.5 | 2.794 ± 0.003 | 0.012 ± 0.001 | 1.2 ± 0.3 |
| 1 vol% O2/He | Pd–Pdg | 0.74 | 7.7 ± 0.8 | 2.790 ± 0.008 | 0.013 ± 0.001 | 1.72 ± 0.7 |
| Pd–Oh | 0.70 | 2.0 ± 0.2 | 2.032 ± 0.007 | 0.003 ± 0.001 | 6.3 ± 0.9 | |
| Pd–(O)–Pd1h | 0.86 | 1.8 ± 0.6 | 3.049 ± 0.013 | 0.010 ± 0.003 | 6.3 ± 0.9 | |
| Pd–(O)–Pd2h | 0.60 | 3.4 ± 1.3 | 3.408 ± 0.011 | 0.009 ± 0.003 | 6.3 ± 0.9 | |
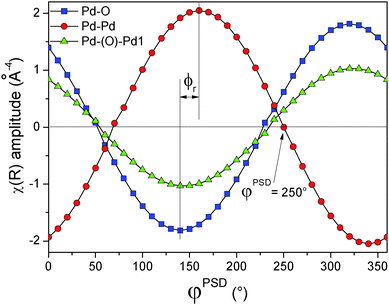
One more piece of information can be obtained from the analysis of the magnitude and the real part of the phase-resolved FT spectra. PSD provides access to the relative dynamics of the different shells, i.e. whether they appear simultaneously or delayed with respect to each other, or one appears while another one disappears. In case the evolution of shells is delayed, the considered shells are in ‘anti-phase’ and this is reflected in the variation of the real part as a function of the phase angle. This concept is clarified in Fig. 8A, where the phase angular variation of the characteristic interatomic distance R (obtained from the FT-spectra) for the three Pd–O, Pd–Pd and Pd–(O)–Pd shells is plotted. As mentioned above, because the magnitude of FT possesses only positive values the negative values can be obtained by considering the real (or alternatively the imaginary) part (Fig. 8B). In the case of the real part of FT, it is important to plot the intensity of a characteristic R, where that specific shell exhibits the maximum amplitude. For example, for the Pd–Pd shell R is chosen at 2.512 Å. However, if two shells are close to each other and they partially overlap, as it is in the case of Pd–Pd and Pd–(O)–Pd, it is important to select a characteristic R, where the two shells do not overlap. Following our example, R is 2.393 Å and 2.976 Å for Pd–Pd and Pd–(O)–Pd, respectively in Fig. 8B rather than 2.512 and 2.792 Å, respectively. For this purpose, it might also be useful to compare the imaginary part of the phase-resolved FT spectra. Fig. 8B shows that the Pd–O and Pd–Pd shells are in anti-phase, whereas the Pd–(O)–Pd shell is out-of-phase relative to the Pd–O shell and ϕr = −40°. The minus sign indicates that this shell appears with a time delay of td with respect to the Pd–O shell, in this case td = ϕrT/360° = −40° × 100 s/360° = −11.1 s. Therefore, the Pd–(O)–Pd shell starts to appear 11.1 s after the Pd–O shell, in agreement with the simulation.
3.3. Experimental ME-EXAFS spectra at the Pd K-edge
In order to demonstrate our approach, 1.6 wt% Pd/Al2O3 was subjected to 30 consecutive 1 vol% O2/He to 1 vol% H2/He switches at 573 K with a modulation period of 155 s.The first time-resolved spectra recorded at the beginning of the modulation experiment reveals that the Pd is oxidized (no contribution of the metallic Pd–Pd shell can be distinguished in the FT-EXAFS spectrum), as expected after the thermal pre-treatment at 573 K in 1 vol% O2/He (Fig. S11, ESI†). However, Pd readily reduces already after the first exposure to 1 vol% H2/He and steady state conditions were reached after the first two cycles. Thus, the time-resolved spectra recorded during the first two cycles were removed from the subsequent data processing.
The averaged time-resolved XANES spectra are shown in Fig. 9. A variation of the whiteline region upon oxidation is clearly visible. The linear combination analysis of the experimental spectra using those of bulk PdO and Pd foil as the reference spectra (inset of Fig. 9) shows that Pd undergoes a fast reduction in hydrogen, whereas the re-oxidation is slower and only 40% of the Pd(0) is oxidized to Pd(II) at the end of the oxygen pulse. The corresponding time-resolved FT-EXAFS spectra (Fig. 10A) recorded in hydrogen are dominated by a single contribution centered at 2.485 Å corresponding to the first Pd–Pd coordination shell of metallic Pd. The amplitude of the shell decreases, but does not disappear, after switching to O2. Simultaneously, a second contribution appears at 1.564 Å due to the formation of the first Pd–O shell, thus confirming the partial re-oxidation of Pd. The FT-EXAFS spectrum of bulk PdO (Fig. 10A) is characterized by the presence of a second broad signal due to the second Pd–(O)–Pd shell, which is composed of four Pd atoms located at 3.03 Å (Pd–(O)–Pd1 shell) and eight Pd atoms located at 3.42 Å (Pd–(O)–Pd2 shell). These two shells are so close to each other that they partially overlap, generating the broad peak of the FT-EXAFS spectrum centered at 3.1 Å with a shoulder at lower R. However, the contribution of this latter shell can be hardly solved in our experimental time-resolved FT-EXAFS spectra of Fig. 10A because of the superimposition with the residual but dominant Pd–Pd shell. The ME approach coupled with PSD is a powerful tool to solve this issue thus considerably improving the sensitivity of EXAFS spectroscopy as is described below.
The phase-resolved k3-weighted χ(k) spectra (Fig. S12, ESI†) exhibit a similar out of phase envelop to that of the simulated spectra of Fig. 3B, suggesting that some parameter possesses a different phase lag with respect to the others. Indeed, the Fourier transformation of the phase-resolved spectra (Fig. 10B) clearly shows the appearance of a peak at 2.82 Å. This signal is assigned to the Pd–(O)–Pd1 shell and varies as a function of the phase angle similarly to the simulated spectra in the middle panel of Fig. 6D, the case of the Pd–(O)–Pd shell having different phase lag compared to the Pd–Pd shell. This signal cannot be clearly distinguished in the time-resolved data of Fig. 10A, thus demonstrating the increased sensitivity of EXAFS by the use of PSD. The phase angular dependence of the three signals detected in the phase-resolved FT spectra at 1.56 Å (Pd–O), 2.48 Å (Pd–Pd) and 2.82 Å (Pd–(O)–Pd1) with assignment of the negative values on the basis of the FT real part (Fig. 10C), according to the procedure previously illustrated in Fig. 8, demonstrates (Fig. 11) that the signal generated by the Pd–Pd shell varies in opposition and with a different phase lag ϕr with respect to the other two shells. This behaviour reflects the red-ox dynamics of the Pd nano-particles, i.e. the periodic and alternate faster reduction than the re-oxidation, where the Pd–Pd shell decreases while the Pd–O shell is forming. The different phase lag of the Pd–Pd shell represents a key finding because it allows us to isolate the contribution of the Pd–(O)–Pd shell from that of the residual metallic Pd in the EXAFS spectrum at φPSD = 250° (Fig. 11 and the blue curve in Fig. 10B). Similarly, the spectrum at φPSD = 230° contains the contribution of the variation of the Pd–Pd shell only, filtered from that of PdO (Fig. 11 and the red curve in Fig. 10B).
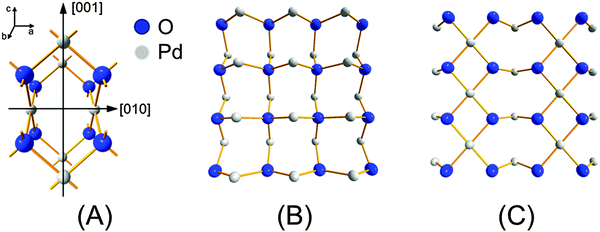
Fig. 12C demonstrates the most important finding of this work in agreement with the simulations shown above. The Fourier transform of the phase-resolved EXAFS spectrum at φPSD = 250° clearly displays the Pd–(O)–Pd1 and Pd–(O)–Pd2 shells which are otherwise hardly detectable in the time-resolved spectra. The contribution of the residual Pd–Pd shell has been removed by PSD. The fit of this spectrum provides the coordination number of the three Pd–O, Pd–(O)–Pd1 and Pd–(O)–Pd2 shells of 2.0, 1.8 and 3.4, respectively (Table 1). These values are evidently much lower than those of the bulk PdO (4, 4 and 8, respectively), indicating that oxidation has not been extensive in agreement with our simulation. However, they are consistent with a PdO surface with two Pd atomic layers. For example, if the (001) surface of PdO is considered (Fig. 13) the average coordination number of the shells is 2, 4 and 4, respectively, whereas for the (100) or the (010) surface it is 3, 2 and 4, respectively. These values are lower for smaller particles because the atoms at the edge and corners exhibit lower coordination. It is important to note that the main difference between the (001) and the (100) surface of PdO is that the ratio between the coordination number of the Pd–(O)–Pd2 and Pd–(O)–Pd1 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the former, whereas it is 2
1 in the former, whereas it is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the latter. The fitting results suggest that, being the experimental Pd–(O)–Pd2
1 in the latter. The fitting results suggest that, being the experimental Pd–(O)–Pd2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd–(O)–Pd1 ratio of 1.9, the (100) or the (010) surface are preferentially formed.31
Pd–(O)–Pd1 ratio of 1.9, the (100) or the (010) surface are preferentially formed.31
4. Conclusions
This work demonstrates that the modulated excitation approach combined with phase sensitive analysis can be successfully applied to extended X-ray absorption fine structure spectroscopy despite the high number of variables involved. Several additional qualitative and quantitative information can be extrapolated from the phase-resolved FT-EXAFS spectra with respect to the original time-resolved set of data, thus significantly improving the sensitivity of EXAFS spectroscopy. A first inspection of the phase-resolved χ(k) spectra reveals whether one or more variables (N, R or σ2), either within one shell or of a different shell, vary with a phase lag ϕ with respect to the other ones. The presence of a phase lag generates the typical out of phase envelop. The analysis of the real (or imaginary) part of the phase resolved FT-EXAFS spectra is crucial to recognize both (i) whether the phase lag occurs within one shell or in a different shell and (ii) to access the relative dynamics occurring during the modulation experiment, such as the formation/disappearance of a specific shell. The presence of one or more shells varying with a phase lag is a crucial point that allows extrapolation of the spectra of that specific shell/structure. One of the most important finding of this work is the possibility of isolating the contribution of the second Pd–(O)–Pd shell of PdO otherwise hidden from the residual first Pd–Pd shell of the metal Pd. This result could be in principle extended to any other minute structural change or intermediate species formed during a modulation experiment.Because the phase resolved EXAFS spectra are scaled difference spectra with reduced noise two different approaches have been here proposed for the quantitative analysis of the corresponding FT spectra. In particular, the FT-phase-resolved spectrum can be directly fitted only if a shell fully appears and disappears during the modulation (e.g. the Pd–O and Pd–(O)–Pd shells of the experimental example). By contrast, if a shell does not fully disappear (e.g. the Pd–Pd shell) the spectrum of the final state (e.g. in O2 atmosphere) can be obtained by subtracting the selected demodulated χφ(k) from the time-resolved χt(k)i spectrum of the initial state (e.g. in a H2 atmosphere) with the possible advantage of being isolated from the contribution of other structures.
Finally, the FT-EXAFS spectrum of PdO has been successfully isolated from that of the residual metallic Pd of partially oxidized Pd nanoparticles thanks to the application of PSD, thus allowing the fitting of the second Pd–(O)–Pd shell with enhanced accuracy. This result has shown that an oxide layer covering a metallic core is formed under a fast switch from reducing to oxidizing atmosphere at 573 K on 1.6 wt% Pd/Al2O3.
Therefore, we have demonstrated the potential of the modulated excitation approach applied to quantitative EXAFS. The approach becomes powerful when minute structural changes of functional materials under relevant conditions need to be analyzed.
List of symbols
| α | Amplitude correction factor |
| δ i (k) | Photoelectron phase shift |
| λ(k) | Photoelectron mean free path |
| σ i 2 | Debye–Waller factor |
| ϕ | Phase lag between the stimulation and the system response |
| φ PSD | Demodulation phase angle |
| χ t (k) | Time-resolved EXAFS spectrum |
| χ t (R) | Fourier transform of the time-resolved EXAFS spectrum |
| χ φ (k) | Phase-resolved EXAFS spectrum |
| χ φ (R) | Fourier transform of the phase-resolved EXAFS spectrum |
| |χ(R)| | Magnitude of the Fourier transform EXAFS spectrum |
| F i (k) | Photoelectron scattering amplitude |
| Im[χ(R)] | Imaginary part of the Fourier transform EXAFS spectrum |
| K | Demodulation index |
| k | Photoelectron wavenumber |
| N i | Coordination number |
| Re[χ(R)] | Real part of the Fourier transform EXAFS spectrum |
| R i | Interatomic distance |
| S 0 2 | Passive electron reduction factor |
| T | Stimulation period |
| W(k) | Window function |
| ω | Stimulation frequency |
Acknowledgements
The authors kindly acknowledge the financial support from the Competence Centre for Materials Science and Technology (CCMX) through project No 66, the Swiss National Science Foundation under project No. 200021-138068 and the University of Milano through project No. 17777 “Piano di Sviluppo 2014 linea B1”. The European Synchrotron Radiation Facility (ESRF, Grenoble, France) is acknowledged for providing the beamtime at beamline BM23. D.F. is grateful to Dr M. A. Newton for his precious and continued support and to Dr S. K. Matam, Dr S. Yoon and Dr Y. Lu for help during measurements.References
- S. R. Bare and T. Ressler, Adv. Catal., 2009, 52, 339–465 CAS.
- P. Silveston, R. R. Hudgins and A. Renken, Catal. Today, 1995, 25, 91–112 CrossRef CAS.
- D. Baurecht and U. P. Fringeli, Rev. Sci. Instrum., 2001, 72, 3782–3792 CrossRef CAS PubMed.
- T. Bürgi and A. Baiker, J. Phys. Chem. B, 2002, 106, 10649–10658 CrossRef.
- A. Urakawa, T. Bürgi and A. Baiker, Chem. Eng. Sci., 2008, 63, 4902–4909 CrossRef CAS PubMed.
- A. Eyssler, E. Kleymenov, A. Kupferschmid, M. Nachtegaal, S. K. Matam, P. Hug, A. Weidenkaff and D. Ferri, J. Phys. Chem. C, 2011, 115, 1231–1239 CAS.
- D. Ferri, M. A. Newton and M. Nachtegaal, Top. Catal., 2011, 54, 1070–1078 CrossRef CAS.
- D. Ferri, S. K. Matam, R. Wirz, A. Eyssler, O. Korsak, P. Hug, A. Weidenkaff and M. A. Newton, Phys. Chem. Chem. Phys., 2010, 12, 5634–5646 RSC.
- C. F. J. König, J. A. vanBokhoven, T. J. Schildhauer and M. Nachtegaal, J. Phys. Chem. C, 2012, 116, 19857–19866 Search PubMed.
- J. Stötzel, D. Lutzenkirchen-Hecht, R. Frahm, B. Kimmerle, A. Baiker, M. Nachtegaal, M. J. Beier and J. D. Grunwaldt, J. Phys.: Conf. Ser., 2009, 190, 012162 CrossRef.
- A. Haghofer, D. Ferri, K. Föttinger and G. Rupprechter, ACS Catal., 2012, 2, 2305–2315 CrossRef CAS.
- V. Marchionni, M. A. Newton, A. Kambolis, S. K. Matam, A. Weidenkaff and D. Ferri, Catal. Today, 2014, 229, 80–87 CrossRef CAS PubMed.
- G. L. Chiarello, M. Nachtegaal, V. Marchionni, L. Quaroni and D. Ferri, Rev. Sci. Instrum., 2014, 85, 074102 CrossRef PubMed.
- D. E. Ramaker and D. C. Koningsberger, Phys. Chem. Chem. Phys., 2010, 12, 5514–5534 RSC.
- C. S. Spanjers, T. P. Senftle, A. C. T. vanDuin, M. J. Janik, A. I. Frenkel and R. M. Rioux, Phys. Chem. Chem. Phys., 2014, 16, 26528–26538 RSC.
- C. F. J. König, T. J. Schildhauer and M. Nachtegaal, J. Catal., 2013, 305, 92–100 CrossRef PubMed.
- J. Stötzel, D. Lützenkirchen-Hecht, R. Frahm and J. D. Grunwaldt, J. Phys.: Conf. Ser., 2013, 430, 012126 CrossRef.
- R. Caliandro, D. Chernyshov, H. Emerich, M. Milanesio, L. Palin, A. Urakawa, W. vanBeek and D. Viterbo, J. Appl. Crystallogr., 2012, 45, 458–470 CrossRef CAS.
- D. Chernyshov, W. vanBeek, H. Emerich, M. Milanesio, A. Urakawa, D. Viterbo, L. Palin and R. Caliandro, Acta Crystallogr., Sect. A: Found. Crystallogr., 2011, 67, 327–335 CrossRef CAS PubMed.
- W. vanBeek, H. Emerich, A. Urakawa, L. Palin, M. Milanesio, R. Caliandro, D. Viterbo and D. Chernyshov, J. Appl. Crystallogr., 2012, 45, 738–747 CAS.
- D. C. Koningsberger and R. Prins, X-ray Absorption: principles, applications and techniques of EXAFS, SEXAFS and XANES, Wiley, 1988 Search PubMed.
- D. Ferri, M. A. Newton, M. DiMichiel, S. Yoon, G. L. Chiarello, V. Marchionni, S. K. Matam, M. H. Aguirre, A. Weidenkaff, F. Wen and J. Gieshoff, Phys. Chem. Chem. Phys., 2013, 15, 8629–8639 RSC.
- M. A. Newton, Chem. Soc. Rev., 2008, 37, 2644–2657 RSC.
- S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Phys. Rev. [Sect.] B, 1995, 52, 2995–3009 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- M. A. Newton, Top. Catal., 2009, 52, 1410–1424 CrossRef CAS.
- S. K. Matam, E. H. Otal, M. H. Aguirre, A. Winkler, A. Ulrich, D. Rentsch, A. Weidenkaff and D. Ferri, Catal. Today, 2012, 184, 237–244 CrossRef CAS PubMed.
- A. Jentys, Phys. Chem. Chem. Phys., 1999, 1, 4059–4063 RSC.
- A. L. Bugaev, A. A. Guda, K. A. Lomachenko, V. V. Srabionyan, L. A. Bugaev, A. V. Soldatov, C. Lamberti, V. P. Dmitriev and J. A. V. Bokhoven, J. Phys. Chem. C, 2014, 118, 10416 CAS.
- J. Wang, Q. Wang, X. Jiang, Z. Liu, W. Yang and A. I. Frenkel, J. Phys. Chem. C, 2015, 119, 854 CAS.
- D. T. Vu, K. A. R. Mitchell, O. L. Warren and P. A. Thiel, Surf. Sci., 1994, 318, 129–138 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp00609k |
| This journal is © the Owner Societies 2015 |