Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An OHD-RIKES and simulation study comparing a benzylmethylimidazolium ionic liquid with an equimolar mixture of dimethylimidazolium and benzene†
Lianjie
Xue
a,
George
Tamas
a,
Richard P.
Matthews
b,
Anthony J.
Stone
c,
Patricia A.
Hunt
b,
Edward L.
Quitevis
*a and
Ruth M.
Lynden-Bell
*c
aDepartment of Chemistry and Biochemistry, Texas Tech University, Lubbock, TX 79409, USA. E-mail: edward.quitevis@ttu.edu
bDepartment of Chemistry, Imperial College, London SW7 2AZ, UK
cDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: rmlb@cam.ac.uk; Fax: +44 (0)1223 336362; Tel: +44 (0)1223 336535
First published on 5th March 2015
Abstract
The principal difference between 1-benzyl-3-methyl-imidazolium triflimide [BzC1im][NTf2] and an equimolar mixture of benzene and dimethylimidazolium triflimide [C1C1im][NTf2] is that in the former the benzene moieties are tied to the imidazolium ring, while in the latter they move independently. We use femtosecond optical heterodyne-detected Raman-induced Kerr effect spectroscopy (OHD-RIKES) and molecular simulations to explore some properties of these two systems. The Kerr spectra show small differences in the spectral densities; the simulations also show very similar environments for both the imidazolium rings and the phenyl or benzene parts of the molecules. The low frequency vibrational densities of states are also similar in the model systems. In order to perform the simulations we developed a model for the [BzC1im]+ cation and found that the barriers to rotation of the two parts of the molecule are low.
1 Introduction
OHD-RIKES (optical heterodyne-detected Raman induced Kerr effect spectroscopy) is a nonlinear optical time-domain technique that gives information about the low frequency fluctuations in the polarizability of a liquid and is complementary to dielectric spectroscopy.1–3 Because of its ease of use and high quality of the data, it is one the most common methods for studying the low frequency intermolecular modes of liquids1–3 and in particular ionic liquids.4–32 By use of a Fourier-transform-deconvolution procedure,33,34 the OHD-RIKES time-domain data can be converted to a spectral density or Kerr spectrum, which is directly related to the depolarized Rayleigh/Raman spectrum of the liquid.35The low-frequency part of a Kerr spectrum is dominated by intermolecular motions, but is unable to discriminate between different types of motion such as librational (hindered rotation) and translational. Further one does not obtain any direct information about the local environments of different molecular species. Molecular simulation can complement these spectroscopic results by giving a molecular level picture of the local environments of molecules and the local molecular dynamics. Recently Quitevis and co-workers have compared the Kerr spectra of the neat ionic liquid 1,3-dimethylimidazolium triflimide, [C1C1im][NTf2], with its mixtures with benzene and with neat benzene.36 Simulations were used to show that the benzene response was at a lower frequency than that of the ionic liquid and that in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of this ionic liquid with benzene the benzene response moves to a higher frequency while the [C1C1im] response moves to a lower frequency. This is not unexpected as it implies that the ions move more freely on dilution with benzene while the benzene motion is impeded on dilution with an ionic liquid. Translational motion tends to be at a lower frequency than the librational motion. These results were based on an analysis of different contributions to the vibrational density of states.
1 molar mixture of this ionic liquid with benzene the benzene response moves to a higher frequency while the [C1C1im] response moves to a lower frequency. This is not unexpected as it implies that the ions move more freely on dilution with benzene while the benzene motion is impeded on dilution with an ionic liquid. Translational motion tends to be at a lower frequency than the librational motion. These results were based on an analysis of different contributions to the vibrational density of states.
This work on ionic liquid–benzene mixtures led Quitevis and coworkers to ask what would happen if the benzene and imidazolium were tied together as 1-benzyl-3-methyl-imidazolium [BzC1im]+ as shown in Fig. 1. Shirota et al.37 performed a study of the low-frequency Kerr spectra and physical properties of ionic liquids functionalized with phenyl moieties, including the [BzC1im][NTf2]. In this paper we describe the local molecular environments found in simulation and Kerr spectra of [BzC1im][NTf2]. The current study goes beyond the work of Shirota et al.37 in that we compare the results with those from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of C6H6 and [C1C1im][NTf2]. In order to do this, a force field for benzylimidazolium ions was needed; Section 3.1 describes how this was developed. The resulting local environments of the phenyl groups and the imidazolium rings are compared with those for the mixture in Section 5.1 while in Section 5.2 we compare the vibrational densities of states and the Kerr spectra.
1 mixture of C6H6 and [C1C1im][NTf2]. In order to do this, a force field for benzylimidazolium ions was needed; Section 3.1 describes how this was developed. The resulting local environments of the phenyl groups and the imidazolium rings are compared with those for the mixture in Section 5.1 while in Section 5.2 we compare the vibrational densities of states and the Kerr spectra.
2 Experimental
2.1 Sample preparation
The syntheses of [C1C1im][NTf2]36 and [BzC1im][NTf2]38,39 have been published previously. Prior to performing OHD-RIKES measurements, [C1C1im][NTf2] and [BzC1im][NTf2] were subjected for at least 1–2 days to further drying under vacuum. The water content of [C1C1im][NTf2] and [BzC1im][NTf2], as determined by Karl-Fischer titration prior to the preparation of the C6H6–[C1C1im][NTf2] mixture, was <100 μg g−1.The mixture was prepared by weighing a given amount of [C1C1im][NTf2] in an argon-filled glovebox and adding the required weight of benzene to make up an equimolar mixture. A syringe fitted with a 0.1 μm filter was used to deliver aliquots of the pure liquids and the mixtures, while still in the argon-filled glovebox, into 2 mm path-length quartz cuvettes fitted with vacuum stopcock valves to insure airtight sealing of the samples during OHD-RIKES measurements.
2.2 OHD-RIKES apparatus and procedures
The apparatus has been described previously.40,41 Briefly, a lab-built, self-modelocked Ti:sapphire laser, pumped by a Coherent Verdi V6 laser, generates a train of 38 ± 3 fs pulses at a repetition rate of 82 MHz. A (0°/45°/−45°) polarization configuration is used for the pump, probe and analyzer polarizers, with a λ/4-plate inserted in the probe beam before the sample. Stray birefringences, such as from the windows of the sample cell, are nulled by adjusting the λ/4-plate. A local oscillator (LO) field ELO is introduced for the signal field ES by slightly misaligning (±δ°) the probe polarizer.42 The two signals obtained in this way are given by| I± = |ELO2| + |ES|2 ± 2ℜ|ELOES*| | (1) |
The temperature of the sample is kept constant at 295 K by placing the sample cell in a lab-built, thermostated copper cell holder, with temperature control from a thermoelectric heater–cooler system. A data set is obtained by averaging at least 15 scans, with each scan being performed in 10 fs steps for time delays between −1 and 4 ps and in 50 fs steps for time delays greater than 4 ps to save the data collection time.
2.3 Analysis of the OHD-RIKES data
The OHD-RIKES signals in the 0.4–10 ps time range are fitted by the empirical decay functionr(t) = A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + A3 exp(−t/τ2) + A3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ3) + B exp(−t/τ3) + B | (2) |
In principle, the relative intensities of RSDs can be determined if the OHD-RIKES signals of each of the samples are measured under the same experimental conditions. In practice this is difficult to achieve because of having to make adjustments of the laser and tweak the alignment of the optics in the apparatus between runs. In our previous study36 a referencing technique was used. However in the current study, because the OHD-RIKES signals for all the systems were obtained in a single run in such a way that constant experimental conditions were maintained for all the data sets, the referencing technique was not used.
3 Simulation methods
3.1 Force field development for simulations
We use a standard type of force field with terms describing bond stretching, angle bending and dihedral motion within each molecular species together with partial charges and Lennard-Jones terms on each atomic site to describe intermolecular interactions. In earlier work45 on the adsorption of ethylene and ethane in various ionic liquids the experimental work was complemented by some simulations by Padua and co-workers on ionic liquids including [BzC1im][NTf2]. They used standard force fields and did not reconsider the charge or dihedral parameters. As we are here particularly concerned with the low frequency motions of the liquid, we examined the changes in energy with the dihedral rotations about the methylene group linking the phenyl and imidazolium rings as well as the partial charges.The partial charges of some of the configurations generated in the determination of the dihedral potential were determined by iterated stockholder analysis (ISA).46,47 In this method a calculated electronic charge density, (here obtained using density functional theory with PBE0 functional and asymptotic correction, and the Sadlej basis48), is partitioned between atoms using a spherical weight function for each atom, and the resulting density for each atom is spherically averaged to obtain a revised weight function. This procedure is iterated to obtain an optimum partition into atomic densities that are as nearly spherical as possible. Lillestolen and Wheatley46 showed that the method is guaranteed to converge, but their original grid-based method converged very slowly, and the basis-function-based method of Misquitta et al.47 converges very much more quickly. The method yields atomic multipole moments as well as charges, but the charges alone give a good account of the electrostatic potential. Fig. 2 shows the difference between the electrostatic potential from the full wave function and that generated at twice the van der Waals radii. It can be seen that the fit is good even though only site charges and not higher multipoles are included. The r.m.s. error over the surface is 0.03 V, about 1% of the potential, which varies between about 2 V and 3 V over the surface. The values of the partial charges vary by a small amount, of the order of 0.01e, with molecular conformation. For a classical simple point charge model one needs constant charges; we used an average of the charges obtained at the two geometries with energy minima (0 and 135°) truncated to two decimal places and adjusted to give a total charge of +1e.
 | ||
| Fig. 2 Difference between the model's electrostatic potential and that calculated from the full wave function on a surface at twice the Lennard-Jones radii. | ||
The bond stretching and angle bending terms for the methyl imidazolium moiety were taken from the CLAPS force field49,50 which is based on the OPLS force field.51,52 As the lowest vibrational frequency of benzene is 467 cm−1, the internal motions of the phenyl group are unlikely to affect the vibrational spectrum below 300 cm−1, and the phenyl ring was treated as a rigid body. The Lennard-Jones terms were initially taken from these force fields, but finally were scaled by 0.95 to obtain the correct pressure of the liquid at 300 K and the experimental density.
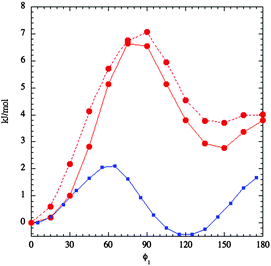
In order to obtain the variation of molecular energy with the dihedral angle, ϕ1, which describes the rotation of the imidazolium ring with respect to the bridging methylene group (see Fig. 3), conformations with fixed values of this angle were energy-minimised with respect to all other degrees of freedom. This was repeated for values of ϕ1 from 0 to 180° in steps of 15° in a relaxed scan. The quantum chemistry calculations were carried out at the MP2 level using a cc-pVTZ basis set as implemented in the Gaussian 09 software package53 Further details are given in the ESI.† The dihedral energy of this rotation is shown in Fig. 4 as red circles connected by a full red line. There is a global minimum at ϕ1 = 0°. Rotation of the imidazolium group leads to a global maximum of 6.8 kJ mol−1 near 80°, a secondary minimum of 2.8 kJ mol−1 near ϕ1 ≈ 140° and finally a secondary local maximum of about 3.8 kJ mol−1 at ϕ1 = 180°. As kT ≈ 2.5 kJ mol−1 at 300 K this barrier would be easily surmounted at room temperature for an isolated ion. This is what we found in the simulations (see below).
The second dihedral angle of interest, ϕ2, describes the rotation of the phenyl ring relative to the bridging methylene group (see Fig. 3). It was investigated in a similar way although the energy minimisations were carried out with the constraint that ϕ1 = 90°. This was done to avoid steric clashes between the phenyl and imidazolium rings. The results of this second set of calculations are shown in Fig. 5 as red circles connected by a full line. The dihedral energy for rotation of the phenyl group has a minimum at ϕ2 = ±90° and a maximum at ϕ2 = ±0°. The barrier is about 10 kJ mol−1 or 4kT at 300 K. The fitted function (open red circles) has no explicit dihedral terms connecting the phenyl group and the methylene group; the observed variation of energy with ϕ2 is solely due to other terms in the force field including electrostatic and dispersion interactions between the phenyl group and the rest of the molecule.
The dihedral terms in the force field for ϕ1 between the unique imidazolium carbon site and first phenyl carbon site (see Fig. 3) was expressed as the sum of three cosine terms
 | (3) |
 | ||
| Fig. 3 Dihedral angles: above: dihedral rotation ϕ1 in a conformation with ϕ1 = 0 and ϕ2 = 90°; below: dihedral rotation ϕ2 in a conformation with ϕ1 = 90° and ϕ2 = 0°. | ||
As the dihedral term between the phenyl group and the imidazolium nitrogen site was found to be described reasonably well with only a scaling of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 electrostatic and dispersion interactions by 0.5, no further dihedral term was included. The complete force field is given in the ESI.†
4 electrostatic and dispersion interactions by 0.5, no further dihedral term was included. The complete force field is given in the ESI.†
The distribution of conformers in the bulk depends on local intermolecular interactions as well as on the intramolecular potential. In simulations of bulk liquid we find that the observed free energies of both dihedral angles have considerably lower barriers than the single molecule energy results. These free energies A(ϕ) (determined from the observed probability distributions p(ϕ) by eqn (4)) are shown by full blue lines in Fig. 4 and 5.
A(ϕ) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(ϕ) p(ϕ) | (4) |
3.2 Simulations and analysis
Bulk simulations of liquid [BzC1im][NTf2] were then carried out using these potentials for the benzylimidazolium cation and the potential due to Ludwig and co-workers54,55 for the triflimide anion [NTf2] or (N(SO2CF3)2)−. This latter potential has a united CF3 group. These simulations were carried out using a modified version of DL_POLY.56 128 ion pairs in a periodically repeated box with sides of 4.014 nm were used and the electrostatics was treated by Ewald summation with a real space cutoff of 1.2 nm and convergence parameter = 2.3 nm−1. This corresponds to a precision of 10−5 in the energy. A time step of 2 fs was used and the temperature was 300 K. Simulations of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture under similar conditions were described in our previous paper36 and the results from that work used here.
1 mixture under similar conditions were described in our previous paper36 and the results from that work used here.
The vibrational densities of states are found by Fourier transforming the velocity autocorrelation functions of individual atomic sites. Here we report the density of states of the imidazolium ring and the phenyl group separately. These were calculated by taking the sum of the velocity autocorrelation functions for the 5 heavy atoms in the ring for the imidazolium density of states and the sum for the 6 carbon atoms in the phenyl group for the phenyl density of states and then Fourier transforming these two result separately. No cross terms are included. The local environment of the imidazolium ring in [BzC1im]+ was calculated by making 3-dimensional histograms of the probability densities of (a) ring centres, (b) phenyl groups centres and (c) nitrogen sites of [NTf2]− in local axis systems centred on each imidazolium. The local environment of the phenyl rings was calculated in a similar way. The resulting spatial distribution functions were plotted using the Aten software.57
4 Results from Kerr experiments
4.1 Time-domain responses
Fig. 6 shows the OHD-RIKES signals of pure C6H6, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] mixture, pure [C1C1im][NTf2], and pure [BzC1im][NTf2] in the 0–10 ps time range. Each of the signals have been normalized at the coherence spike (t = 0) for comparison purposes. In all cases, the OHD-RIKES signals are dominated by the instantaneous electronic response (i.e., the coherence spike), with the maximum relative amplitude of the non-instantaneous nuclear response equal to ∼0.87, 0.54, 0.407 and 0.33 for C6H6, C6H6–[C1C1im][NTf2] mixture, [BzC1im][NTf2] and [C1C1im][NTf2] respectively. Superimposed on the relaxational part of OHD-RIKES signals of [C1C1im][NTf2] and [BzC1im][NTf2] is a complex oscillatory component that arises from the coherently excited intramolecular modes of ions whose frequencies lie within the bandwidth of the fs pulse. In the case of [BzC1im][NTf2] there is also a deep oscillation at t ≈ 0.33 ps, with width Δt ≈ 0.17 ps. If we assume this feature to be the first period of an underdamped oscillation of an intramolecular mode, then we estimated its frequency to be ≈100 cm−1.
1 C6H6/[C1C1im][NTf2] mixture, pure [C1C1im][NTf2], and pure [BzC1im][NTf2] in the 0–10 ps time range. Each of the signals have been normalized at the coherence spike (t = 0) for comparison purposes. In all cases, the OHD-RIKES signals are dominated by the instantaneous electronic response (i.e., the coherence spike), with the maximum relative amplitude of the non-instantaneous nuclear response equal to ∼0.87, 0.54, 0.407 and 0.33 for C6H6, C6H6–[C1C1im][NTf2] mixture, [BzC1im][NTf2] and [C1C1im][NTf2] respectively. Superimposed on the relaxational part of OHD-RIKES signals of [C1C1im][NTf2] and [BzC1im][NTf2] is a complex oscillatory component that arises from the coherently excited intramolecular modes of ions whose frequencies lie within the bandwidth of the fs pulse. In the case of [BzC1im][NTf2] there is also a deep oscillation at t ≈ 0.33 ps, with width Δt ≈ 0.17 ps. If we assume this feature to be the first period of an underdamped oscillation of an intramolecular mode, then we estimated its frequency to be ≈100 cm−1.
 | ||
| Fig. 6 Semi-logarithmic plots of the OHD-RIKES signals of benzene, 50% mol benzene–50% mol [C1C1im][NTf2] mixture, [C1C1im][NTf2] and [BzC1im][NTf2] in the 0–10 ps time range: the signals have been normalized at the coherent spike at t = 0 and vertically offset by log-base 10 increments for clarity. The solid black lines through the data are fits of the OHD-RIKES decays in the 0.4–10 ps time range. The dashed lines are parts of the fits associated with the slow component τ3 and the constant B. Fit parameters are given in Table 1. | ||
The solid curves in Fig. 6 are fits of eqn (2) to the data in the 0.4–10 ps time range, with fit parameters listed in Table 1. The dashed lines correspond to the slow τ3 term or τ2 + τ3 terms (where the τ values are greater than 1 ps) plus the constant B. In addition to the fit parameters in eqn (2), the values of the average relaxation time for the fast part of the decay, defined by 〈τs〉 = (A1τ1 + A2τ2)/(A1 + A2), are also listed in Table 1. From Table 1 it can be seen that 〈τs〉 of the benzene–[C1C1im][NTf2] mixture has a much larger value (〈τs〉 = 0.61 ps) than that of [BzC1im][NTf2] (〈τs〉 = 0.15 ps) which indicates that the OHD-RIKES signal decays more slowly in the mixture.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] mixture, and [BzC1im][NTf2]a
1 C6H6/[C1C1im][NTf2] mixture, and [BzC1im][NTf2]a
| Liquid | A 1 | τ 1/ps | A 2 | τ 2/ps | A 3 | τ 3/ps | B | 〈τs〉 | χ 2 |
|---|---|---|---|---|---|---|---|---|---|
| a Fit range 0.4–10 ps. Errors in fit parameters A1, A2, τ1, τ2 ≈ ±5%; A3, τ3, 〈τs〉 ≈ ±12%. | |||||||||
| Pure C6H6 | 0.75 | 0.28 | 0.32 | 0.82 | 0.21 | 2.87 | 0 | 0.44 | 0.99962 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] 1 C6H6/[C1C1im][NTf2] |
0.16 | 0.42 | 0.02 | 1.62 | 0.017 | 4.53 | 0.004 | 0.55 | 0.99421 |
| Pure [C1C1im][NTf2] | 0.015 | 0.39 | 0.13 | 0.39 | 0.019 | 2.66 | 0.004 | 0.39 | 0.96558 |
| Pure [BzC1im][NTf2] | 0.98 | 0.13 | 0.05 | 0.53 | 0.01 | 3.72 | 0.001 | 0.15 | 0.98503 |
The value of τ3 = 6.4 ± 0.2 ps for the mixture is associated with the intermediate power-law region of the reorientational dynamics, which cannot be attributed solely to either C6H6 or the IL. However the value of τ3 of mixture is much larger than the value for [BzC1im][NTf2] (τ3 = 3.7 ± 0.2 ps).
4.2 Reduced spectral densities
Fig. 7 shows the RSDs of pure [C1C1im][NTf2], pure C6H6, the C6H6–[C1C1im][NTf2] mixture, and [BzC1im][NTf2] in the 0–450 cm−1 region. The RSDs shown in Fig. 7 and 8 were obtained from unnormalized OHD-RIKES time-domain signals and not the normalized OHD-RIKES signals shown in Fig. 6. As discussed above, because OHD-RIKES time domain signals for the four samples were measured in a single run, the referencing technique used in our previous study was not necessary. Thus the RSDs shown in Fig. 8a reflect actual relative intensities. It can be seen from the plot that the intensity of RSD of pure C6H6 is about 8 times of that of [C1C1im][NTf2]. And the intensity of RSD of the C6H6–[C1C1im][NTf2] mixture is about 3 times of that of [C1C1im][NTf2]. [BzC1im][NTf2] and the benzene–[C1C1im][NTf2] mixture have comparable RSD intensities. | ||
| Fig. 8 Comparison of Reduced spectral densities of the C6H6–[C1C1im][NTf2] mixture (black), and [BzC1im][NTf2] (red) (a) and normalised to the maximum value (b). | ||
The RSDs of pure C6H6, [C1C1im][NTf2] and the C6H6–[C1C1im][NTf2] mixture have been specifically discussed in our recent published paper.36 To see more clearly how the intermolecular spectrum of [BzC1im][NTf2] differs from that of C6H6–[C1C1im][NTf2], the RSDs of these systems in Fig. 7 are overlapped with each other and compared in Fig. 8. As can be seen in the Fig. 8a, C6H6–[C1C1im][NTf2] has a higher intensity than [BzC1im][NTf2], which suggests that the contribution of C6H6 to the mixture spectrum is stronger than that of the phenyl contribution in [BzC1im][NTf2]. Upon normalizing the spectra at their maxima in Fig. 8b, we find that the intermolecular spectrum of [BzC1im][NTf2] is broader and higher in frequency than that of the C6H6–[C1C1im][NTf2] mixture. The RSD intensity of [BzC1im][NTf2] between 150 and 250 cm−1 is higher than that of the C6H6–[C1C1im][NTf2] mixture and is comprised of two components at approximately 190 and 220 cm−1.
4.3 Multicomponent line-shape analysis
The featureless broad low frequency RSD spectrum contains contributions that arise from both intramolecular and intermolecular vibrational motions. The inter- and intramolecular dynamics overlap in this spectral region and cannot be distinguished unambiguously, so the RSDs in the 0–250 cm−1 region were fitted to an empirical multicomponent line shape model in order to gain further insight into these spectra. As described previously, in this model the lowest component is given by the Bucaro–Litovitz (BL) function | (5) |
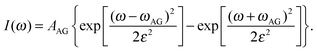 | (6) |
Fig. 9 shows multicomponent line shape fits of RSD in the 0–250 cm−1 region. The spectral parameters for the main band (first spectral moment M1 and full-width-at-half maximum Δω) and component bands (peak frequency, ωpk; peak width, Δω; and fractional area farea) that underlie the main band are shown in Table 2.
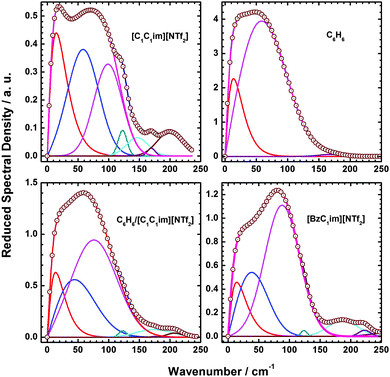 | ||
| Fig. 9 Multicomponent analysis of the mixture and [BzimC1][NTf2] Fits of the RSDs of pure [C1C1im][NTf2], neat benzene, 50% mol benzene/50% mol [C1C1im][NTf2] mixture, and [BzC1im][NTf2] in the 0–250 cm−1 range. (Note the scales of the ordinate axes of the plots are different.) The spectral parameters of the main band for each RSD as well as the underlying component bands are given in Table 2. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] mixture, and [BzC1im][NTf2]a
1 C6H6/[C1C1im][NTf2] mixture, and [BzC1im][NTf2]a
| Liquid | Main band | Component 1 | Component 2 | Component 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| M 1 | Δν | ν pk | Δν | f area | ν pk | Δν | f area | ν pk | Δν | f area | |
| a All frequencies and widths in cm−1 with errors ±1 cm−1. M1 is first moment; Δν is full width at half maximum; farea is fractional area. | |||||||||||
| Pure C6H6 | 61 | 97 | 13 | 28 | 0.17 | — | — | — | 59 | 85 | 0.82 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] 1 C6H6/[C1C1im][NTf2] |
64 | 113 | 15 | 32 | 0.27 | 58 | 60 | 0.41 | 99 | 54 | 0.32 |
| Pure [C1C1im][NTf2] | 65 | 104 | 14 | 28 | 0.14 | 54 | 87 | 0.05 | 62 | 91 | 0.80 |
| Pure [BzC1im][NTf2] | 69 | 110 | 14 | 30 | 0.12 | 38 | 57 | 0.25 | 88 | 67 | 0.63 |
The spectral parameters of C6H6, [C1C1im][NTf2] and the C6H6–[C1C1im][NTf2] mixture have been discussed in detail previously.36
The RSDs of the mixture and [BzC1im][NTf2] are both described well by a three-component model with components at similar frequencies. However the highest frequency component of [BzC1im][NTf2] is much stronger relative to that of the low and intermediate frequency components than in the mixture.
To compare the intramolecular interactions between the C6H6–[C1C1im][NTf2] mixture and [BzC1im][NTf2] further, Table 3 gives the frequencies, and relative intensities of the component bands, whereas the ESI† gives fit parameters corresponding to eqn (5) and (6).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] mixture and [BzC1im][NTf2]a
1 C6H6/[C1C1im][NTf2] mixture and [BzC1im][NTf2]a
| Liquid | Component 4 | Component 5 | Component 6 | Component 7 | ||||
|---|---|---|---|---|---|---|---|---|
| ν pk | f area | ν pk | f area | ν pk | f area | ν pk | f area | |
| a All frequencies in cm−1 with errors ±1 cm−1. farea is the fractional area. | ||||||||
| Pure [C1C1im][NTf2] | 122 | 0.16 | 147 | 0.37 | 169 | 0.04 | 200 | 0.44 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6H6/[C1C1im][NTf2] 1 C6H6/[C1C1im][NTf2] |
123 | 0.13 | 174 | 0.70 | 175 | 0.01 | 207 | 0.16 |
| Pure [BzC1im][NTf2] | 123 | 0.06 | 187 | 0.75 | 223 | 0.12 | 269 | 0.07 |
5 Results from simulations
5.1 Local environment of molecules in bulk
Fig. 10 shows that the local environment around a phenyl group in [BzC1im][NTf2] is much the same as around a benzene molecule in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [C1C1im][NTf2] with benzene. In both cases there is a high probability of finding either an imidazolium ring or another phenyl group in the volumes above and below the phenyl group or benzene molecule. The cutoffs are given as ratios to the average molecular number densities of each component. These are equal to 1.98 nm−3 and 1.81 nm−3 for [BzC1im][NTf2] and the 1
1 mixture of [C1C1im][NTf2] with benzene. In both cases there is a high probability of finding either an imidazolium ring or another phenyl group in the volumes above and below the phenyl group or benzene molecule. The cutoffs are given as ratios to the average molecular number densities of each component. These are equal to 1.98 nm−3 and 1.81 nm−3 for [BzC1im][NTf2] and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture respectively.
1 mixture respectively.
Fig. 11 shows the corresponding distributions around an imidazolium group. Here there is more of a difference between the united ion and the mixture. In the mixture the distribution is symmetrical with evidence of stacking of benzene and [C1C1im] ions in the z or polar direction (perpendicular to the imidazolium ring) with the anions distributed around the equator in three broad bands. This distribution is clearly perturbed by the benzyl substituent. The local distributions around both benzene and imidazolium ions have been seen in earlier simulations36,58 and in quantum mechanical ion pair studies.59,60
5.2 Simulation results for densities of states
The lower panel of Fig. 12 shows the computed densities of states for dimethyl imidazolium in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
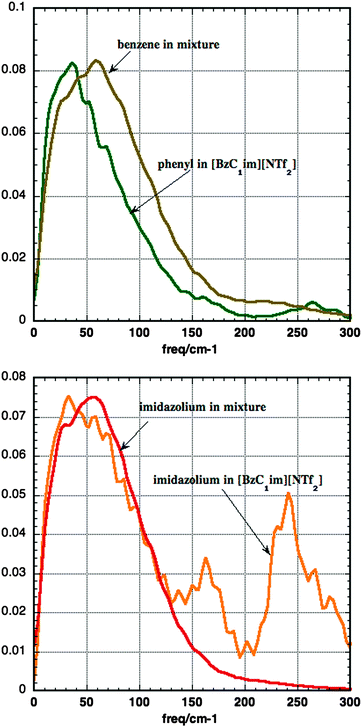
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture and for the imidazolium ring in [BzC1im][NTf2]. Below 100 cm−1 there is little difference between the densities of states, while at 150 cm−1 and above one sees low frequency internal modes in [BzC1im]+. The strong similarity of these two spectra can be correlated with the similarity in the local environment shown in Fig. 10. The upper panel of Fig. 12 shows the computed densities of states for benzene in a 1
1 mixture and for the imidazolium ring in [BzC1im][NTf2]. Below 100 cm−1 there is little difference between the densities of states, while at 150 cm−1 and above one sees low frequency internal modes in [BzC1im]+. The strong similarity of these two spectra can be correlated with the similarity in the local environment shown in Fig. 10. The upper panel of Fig. 12 shows the computed densities of states for benzene in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture and for the phenyl group in [BzC1im][NTf2]. The peak of the benzene density of states in the mixture is at a slightly higher frequency than the peak in the phenyl spectrum. This implies that the motion of the phenyl group is less impeded in [BzC1im][NTf2] than in the mixture. This is an unexpected result, which suggests that the packing around a benzene molecule in the mixture is tighter than that around the unwieldy [BzC1im]+ cation.
1 mixture and for the phenyl group in [BzC1im][NTf2]. The peak of the benzene density of states in the mixture is at a slightly higher frequency than the peak in the phenyl spectrum. This implies that the motion of the phenyl group is less impeded in [BzC1im][NTf2] than in the mixture. This is an unexpected result, which suggests that the packing around a benzene molecule in the mixture is tighter than that around the unwieldy [BzC1im]+ cation.
6 Discussion
The results shown in Fig. 7 and 8 show that the Kerr spectra of the C6H6–[C1C1im][NTf2] mixture and of neat [BzC1im][NTf2] are remarkably similar. The detailed comparison of the RSD plots in Fig. 8 and 9 show that the main difference is a decrease in the low frequency side of the main response compared to the high frequency side which shifts the maximum in [BzC1im][NTf2] to higher frequency. There is also an increased response around 160–250 cm−1 which is due to internal modes involving the relative motion of the phenyl and imidazolium groups which are absent in the mixture. The MP2 computed vibrational modes of the [BzC1im]+ cation below 270 cm−1 occur at 261, 202, 177, 67, 61, 45 and 24 cm−1 respectively. Computed vibrational frequencies are generally accepted to be accurate to 10%. The modes at 24, 45 and 61 cm−1 are relative torsional motions of the two rings while the mode at 67 cm−1 is methyl rotation. These overlap with the intermolecular modes in the liquid. The modes at 177 and 261 cm−1 relate to symmetric and antisymmetric rocking of the methyl and methylene substituents on the imidazolium ring and the mode at 202 cm−1 relates to relative rocking of the phenyl and imidazolium ring and it is these which give rise to the increased response around 160–250 cm−1 in the observed RSD and the imidazolium density of states in the simulation. Diagrams showing these motions are given in ESI.†The Kerr spectrum of the mixture is shifted to a lower frequency than that of pure [BzC1im][NTf2], and both the short and long time scales 〈τs〉 and τ3 found from the analysis of the signals in the time domain are longer for the C6H6–[C1C1im][NTf2] mixture than for pure [BzC1im][NTf2]. This difference in the time-domain Kerr responses is consistent with the frequency-domain frequencies (i.e., longer relaxation times, lower frequencies).
The Kerr signal in the time domain is due to the time correlation function of the anisotropic polarisability of the liquid as a whole. This is made up of contributions from individual molecules, interactions between molecules (such as the dipole-induced dipole terms), and cross terms between these two parts. At low frequencies these terms are affected by motions of molecules relative to each other. Hindered molecular rotation (libration) modulates the contributions from individual molecules, while hindered translation affects the interaction between molecules. All these motions are captured in the vibrational densities of states obtained from velocity correlation functions of individual atoms. These are easily calculated from a simulation. It is possible to simulate the Kerr response directly18,31,61,62 but we have not done so. As the Kerr response is a collective property of the liquid or solution it is noisier than the single particle vibrational densities of states and so more expensive to calculate. Further it would require a polarisable model which we do not use. Rather we calculate the vibrational densities of states in the liquid. The advantage of calculating the single particle vibrational densities of states is that different contributions can easily be distinguished; the disadvantage is that cross correlations are missing and that the strength of different contributions cannot be estimated. Thus the simulation results in Fig. 12 cannot be directly compared to the observed results in Fig. 8. For example it is possible that differences in the relative weighting of the phenyl and imidazolium rings in the mixture and in [BzC1im]+ causes the change in shape of the RSDs in Fig. 8. Shirota and co-workers37 speculate that coupling of the phenyl librations in [BzC1im]+ to the intraionic modes complicates the interpretation of the Kerr spectra. We can confirm the identification of the signal between 170 and 250 cm−1 in [BzC1im][NTf2] as being due to floppy internal modes which show in the phenyl, the CH2 and most strongly in the imidazolium response. It is surprising that the phenyl density of states in [BzC1im]+ peaks at a slightly lower frequency than that for C6H6 in the mixture, showing that the motion is less impeded when the phenyl group is tied to the imidazolium ring.
One can understand the similarities between the C6H6–[C1C1im][NTf2] mixture and [BzC1im][NTf2] to some extent by looking at the strong similarities in the spatial distribution functions in three dimensions shown in Fig. 10 and 11. The distributions around the benzene in the mixture and the phenyl group in [BzC1im][NTf2] both show stacking of imidazolium and benzene rings above and below a benzene moiety. Although the presence of the phenyl group in the latter compound does distort the stacking to some extent and changes the distribution of anions in the equatorial planes of the phenyl moieties, the changes are small. Thus it is not surprising that the local intermolecular motions are similar. The distributions around the imidazolium rings in the mixture and in [BzC1im][NTf2] are again similar, but the changes are perhaps more pronounced. Earlier we commented on the low values of the barriers to twisting the phenyl groups and imidazolium rings in this ion. It seems that although the phenyl and imidazolium parts of the ion are tied through a methyl group, they behave as if they are almost free.
It is difficult to interpret the difference between the Kerr spectra of the mixture and [BzC1im]+ in terms of these simulation results. In both cases the differences are small but the experimental and simulation results show opposite trends. In the multicomponent analyses of the experimental line shapes shown in Fig. 9 the difference between the mixture and [BzC1im]+ spectra arises from the relative strengths of the components rather than changes in their frequency. It is not possible to determine the relative strengths of different contributions from the simulations, so the changes in densities of states could be due to changes in the relative weighting. It is also possible that cross terms are important and also that the use of non-polarisable potentials is not adequate for this comparison.
7 Conclusions
We have performed OHD-RIKES experiments and simulations of [BzC1im][NTf2] and compared the results with an equimolar mixture of [C1C1im][NTf2] and benzene. The difference between these liquids is that in the first the benzene is tied to the imidazolium ring and in the second the benzene molecules are free to move relative to the cation. We found that the relative rotation of the two moieties of the [BzC1im]+ ion is nearly free with only small barriers. The local environments of both imidazolium rings and phenyl groups are similar as are the computed densities of states for intermolecular motion. The experimental Kerr spectra are more similar to each other than to either neat [C1C1im][NTf2] or neat C6H6, but that of [BzC1im][NTf2] has a stronger high frequency component, possibly due to internal modes involving relative motion of the imidazolium ring and the phenyl group.Acknowledgements
This research was supported by the National Science Foundation under Grant CHE-1153077 (ELQ). We thank the National Science Foundation for funding the purchase of the NMR instrumentation (CHE-1048553) used in this project.References
- S. Kinoshita, Y. Kai, T. Ariyoshi and Y. Shimada, Int. J. Mod. Phys. B, 2003, 10, 1229 CrossRef.
- J. T. Fourkas, in Ultrafast Infrared and Raman Spectroscopy, ed. M. D. Fayer, Marcel Dekker, Inc., New York, 2001, pp. 473–512 Search PubMed.
- N. Smith and S. R. Meech, Int. Rev. Phys. Chem., 2002, 21, 75–100 CrossRef CAS.
- B. R. Hyun, S. V. Dzyuba, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. A, 2002, 106, 7579–7585 CrossRef CAS.
- G. Giraud, C. M. Gordon, I. R. Dunkin and K. Wynne, J. Chem. Phys., 2003, 119, 464–477 CrossRef CAS PubMed.
- H. Cang, L. Jie and M. D. Fayer, J. Chem. Phys., 2003, 119, 13017–13023 CrossRef CAS PubMed.
- J. R. Rajian, S. Li, R. A. Bartsch and E. L. Quitevis, Chem. Phys. Lett., 2004, 393, 372–377 CrossRef PubMed.
- H. Shirota, A. M. Funston, J. F. Wishart and E. W. Castner Jr., J. Chem. Phys., 2005, 122, 184512 CrossRef PubMed.
- H. Shirota and E. W. Castner Jr., J. Phys. Chem. A, 2005, 109, 9388–9392 CrossRef CAS PubMed.
- H. Shirota and E. W. Castner Jr., J. Phys. Chem. B, 2005, 109, 21576–21585 CrossRef CAS PubMed.
- D. Xiao, J. R. Rajian, S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2006, 110, 16174–16178 CrossRef CAS PubMed.
- J. Li, I. Wang, K. Fruchey and M. D. Fayer, J. Phys. Chem. A, 2006, 110, 10384–10391 CrossRef CAS PubMed.
- D. Xiao, J. R. Rajian, A. Cady, S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2007, 111, 4669–4677 CrossRef CAS PubMed.
- H. Shirota, J. F. Wishart and E. W. Castner, J. Phys. Chem. B, 2007, 111, 4819–4829 CrossRef CAS PubMed.
- E. W. Castner Jr., J. F. Wishart and H. Shirota, Acc. Chem. Res., 2007, 40, 1217–1227 CrossRef PubMed.
- D. Xiao, J. R. Rajian, L. G. Hines Jr., S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2008, 112, 13316–13325 CrossRef CAS PubMed.
- D. Xiao, L. G. Hines Jr., S. Li, R. A. Bartsch, E. L. Quitevis, O. Russina and A. Triolo, J. Phys. Chem. B, 2009, 113, 6426–6433 CrossRef CAS PubMed.
- H. Shirota, K. Nishikawa and T. Ishida, J. Phys. Chem. B, 2009, 113, 9831–9839 CrossRef CAS PubMed.
- O. Russina, A. Triolo, D. Xiao, L. G. Hines Jr., R. A. Bartsch, E. L. Quitevis, L. Gontrani, R. Caminiti, N. V. Plechkova and K. R. Seddon, J. Phys.: Condens. Matter, 2009, 21, 424121 CrossRef.
- D. A. Turton, J. Hunger, A. Stoppa, G. Hefter, A. Thoman, M. Walther, R. Buchner and K. Wynne, J. Am. Chem. Soc., 2009, 131, 11140–11146 CrossRef CAS PubMed.
- D. Xiao, L. G. Hines Jr., R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2009, 113, 4544–4548 CrossRef CAS PubMed.
- T. Fujisawa, K. Nishikawa and H. Shirota, J. Chem. Phys., 2009, 131, 244519 CrossRef PubMed.
- D. Xiao, L. G. Hines Jr., M. W. Holtz, K. Song, R. A. Bartsch and E. L. Quitevis, Chem. Phys. Lett., 2010, 497, 37–42 CrossRef CAS PubMed.
- H. Shirota, H. Fukazawa, T. Fujisawa and J. F. Wishart, J. Phys. Chem. B, 2010, 114, 9400–9412 CrossRef CAS PubMed.
- B. G. Nicolau, A. Sturlaugson, K. Fruchey, M. C. C. Ribeiro and M. D. Fayer, J. Phys. Chem. B, 2010, 114, 8350–8356 CrossRef CAS PubMed.
- H. Fukazawa, I. Tateki and H. Shirota, J. Phys. Chem. B, 2011, 115, 4621–4631 CrossRef CAS PubMed.
- H. Shirota and I. Tateki, J. Phys. Chem. B, 2011, 115, 10860–10870 CrossRef CAS PubMed.
- P. Yang, G. A. Voth, D. Xiao, L. Hines, R. A. Bartsch and E. L. Quitevis, J. Chem. Phys., 2011, 135, 034502 CrossRef PubMed.
- F. Bardak, D. Xiao, L. Xue, L. G. Hines Jr., P. Son, R. A. Bartsch, E. L. Quitevis, P. Yang and G. A. Voth, ChemPhysChem, 2012, 13, 1687–1700 CrossRef CAS PubMed.
- H. Shirota, ChemPhysChem, 2012, 13, 1638–1648 CrossRef CAS PubMed.
- H. Shirota, J. Phys. Chem. B, 2013, 117, 7985–7995 CrossRef CAS PubMed.
- L. Xue, G. Tamas, E. Gurung and E. L. Quitevis, J. Chem. Phys., 2014, 140, 164512 CrossRef PubMed.
- D. McMorrow, Opt. Commun., 1991, 86, 236–244 CrossRef CAS.
- D. McMorrow and W. T. Lotshaw, J. Phys. Chem., 1991, 95, 10395–10406 CrossRef CAS.
- S. Kinoshita, Y. Kai, M. Yamaguchi and T. Yagi, Phys. Rev. Lett., 1995, 75, 148–151 CrossRef CAS.
- R. M. Lynden-Bell, L. Xue, G. Tamas and E. L. Quitevis, J. Chem. Phys., 2014, 141, 044506 CrossRef PubMed.
- H. Shirota, H. Matsuzaki, S. Ramati and J. F. Wishart, J. Phys. Chem. B, 2014 DOI:10.1021/jp509412z.
- S. V. Dzyuba and R. A. Bartsch, J. Heterocycl. Chem., 2001, 38, 265–268 CrossRef CAS.
- S. V. Dzyuba and R. A. Bartsch, ChemPhysChem, 2002, 3, 161–166 CrossRef CAS.
- E. L. Quitevis and M. Neelakandan, J. Phys. Chem. A, 1996, 100, 10005 CrossRef CAS.
- M. Neelakandan, D. Pant and E. L. Quitevis, J. Phys. Chem. A, 1997, 101, 2939 CrossRef.
- W. T. Lotshaw, D. McMorrow, N. Thantu, J. S. Melinger and R. Kitchenham, J. Raman Spectrosc., 1995, 26, 571 CrossRef CAS.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 8410–8424 CrossRef CAS PubMed.
- P. Yang, G. A. Voth, D. Xiao, L. Hines, R. A. Bartsch and E. L. Quitevis, J. Chem. Phys., 2011, 135, 034502 CrossRef PubMed.
- L. Moura, M. Mishra, V. Bernales, P. Fuentealba, A. A. Padua, C. C. Santini and M. F. Costa Gomes, J. Phys. Chem. B, 2013, 117, 7416–7425 CrossRef CAS PubMed.
- T. C. Lillestolen and R. Wheatley, Chem. Commun., 2008, 5909–5911 RSC.
- A. J. Misquitta, A. J. Stone and F. Fazeli, J. Chem. Theory Comput., 2014, 5405–5418 CrossRef CAS.
- A. J. Sadlej, Theor. Chim. Acta, 1991, 79, 123–140 CrossRef CAS.
- J. Canongia Lopes and A. Pádua, J. Phys. Chem. B, 2004, 108, 16893 CrossRef.
- J. Canongia Lopes and A. Pádua, Theor. Chem. Acc., 2012, 131, 1129 CrossRef PubMed.
- W. Jorgensen, D. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. Kaminski, R. Friesner, J. Tirado-Rives and W. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. Kodderman, D. Paschek and R. Ludwig, ChemPhysChem, 2007, 8, 2464 CrossRef PubMed.
- T. Kodderman, D. Reith and R. Ludwig, ChemPhysChem, 2013, 14, 3368 CrossRef PubMed.
- W. Smith, T. Forester and I. Todorov, The DL POLY Classic User Manual, STFC Daresbury Laboratory, 2012 Search PubMed.
- T. Youngs, J. Comput. Chem., 2010, 31, 639–648 CAS.
- J. B. Harper and R. M. Lynden-Bell, Mol. Phys., 2004, 102, 85–94 CrossRef CAS.
- R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3238 RSC.
- R. P. Matthews, C. Ashworth and P. A. Hunt, J. Phys.: Condens. Matter, 2014, 26, 284112 CrossRef PubMed.
- M. Elola, B. Ladanyi, A. Scodinu, B. Loughnane and J. Fourkas, J. Phys. Chem. B, 2005, 109, 24085–24099 CrossRef CAS PubMed.
- Z. Hu, X. Huang, H. V. R. Annapureddy and C. J. Margulis, J. Phys. Chem. B, 2008, 112, 7837–7849 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Force field for simulations; further experimental spectral parameters; details of ab initio vibrations. See DOI: 10.1039/c5cp00550g |
| This journal is © the Owner Societies 2015 |