 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
H/D exchange in reactions of OH− with D2 and of OD− with H2 at low temperatures
Dmytro
Mulin
a,
Štěpán
Roučka
*a,
Pavol
Jusko
a,
Illia
Zymak
a,
Radek
Plašil
a,
Dieter
Gerlich
b,
Roland
Wester
c and
Juraj
Glosík
a
aDepartment of Surface and Plasma Science, Faculty of Mathematics and Physics, Charles University in Prague, Czech Republic. E-mail: Stepan.Roucka@mff.cuni.cz; Tel: +420 22191 2344
bDepartment of Physics, Technische Universität Chemnitz, Germany
cInstitute for Ion Physics and Applied Physics, University of Innsbruck, Austria
First published on 23rd February 2015
Abstract
Using a cryogenic linear 22-pole rf ion trap, rate coefficients for H/D exchange reactions of OH− with D2 (1) and OD− with H2 (2) have been measured at temperatures between 11 K and 300 K with normal hydrogen. Below 60 K, we obtained k1 = 5.5 × 10−10 cm3 s−1 for the exoergic reaction (1). Upon increasing the temperature above 60 K, the data decrease with a power law, k1(T) ∼ T−2.7, reaching ≈1 × 10−10 cm3 s−1 at 200 K. This observation is tentatively explained with a decrease of the lifetime of the intermediate complex as well as with the assumption that scrambling of the three hydrogen atoms is restricted by the topology of the potential energy surface. The rate coefficient for the endoergic reaction (2) increases with temperature from 12 K up to 300 K, following the Arrhenius equation, k2 = 7.5 × 10−11 exp(−92 K/T) cm3 s−1 over two orders of magnitude. The fitted activation energy, EA-Exp = 7.9 meV, is in perfect accordance with the endothermicity of 24.0 meV, if one accounts for the thermal population of the rotational states of both reactants. The low mean activation energy in comparison with the enthalpy change in the reaction is mainly due to the rotational energy of 14.7 meV contributed by ortho-H2 (J = 1). Nonetheless, one should not ignore the reactivity of pure para-H2 because, according to our model, it already reaches 43% of that of ortho-H2 at 100 K.
1 Introduction
Interactions of ions with neutral particles and the formation of new molecules play an important role in natural and technical plasmas. The various ways to form interstellar molecules, including gas phase processes involving cations, radicals and gas-grain interactions, have attracted a lot of attention in the last four decades. The role of anions in the interstellar medium has been discussed for the first time by Dalgarno and McCray already in 1973.1 However, the interest in anions diminished because, due to a lack of spectroscopic data, they could not be detected. This has changed recently when the first anions were observed in the interstellar medium,2–4 reactivating the interest in theory5,6 and experiments7–13 with anion-molecule reactions, including associative detachment reactions. Also photodetachment of electrons from anions including interstellar anions has been reported.14–17 The anions are interesting not only due to their role in astrochemistry, but they also play an important role in plasma physics, in technical discharges, in radiation chemistry etc.18–20Experimental and theoretical studies of gas phase reactions provide a good basis for understanding the detailed dynamics of fundamental chemical reactions. Here, reactions of hydrogen atoms or molecules are of particular importance, because at low temperature, the influence of specific molecular quantum states can be probed.9–11,21–23 Furthermore, theoretical treatments of the reactive scattering process, while still challenging, become feasible for few-atom systems.24,25 A particular class of reactions is the hydrogen/deuterium isotopic exchange,26 which forms products that are chemically equivalent to the reactants and whose energies vary only by their change in vibrational zero-point energy.
We recently studied H/D isotope effects in the reactions H−(D−) + H and O− + H2(D2) using the AB-22-pole ion trap apparatus10,27,28 and we measured the temperature dependencies of their reaction rate coefficients for temperatures from 11 K up to 300 K. In the present study we investigate the H/D exchange process at a low temperature in a more complex collision system, OH− + H2 and its isotopic variants, where isotopic exchange occurs via the H3O− complex and requires several chemical rearrangement steps. As such, this system is different from H/D exchange in many cation–molecule reactions.26
The first experimental observation of the long-lived H3O− anion has been reported in 1983 by Kleingeld and Nibbering.29 One of the formation mechanisms is ternary association of OH− + H2, with He or H2 as a third body. A ternary rate coefficient of 10−30 cm6 s−1 was measured at 88 K,30 which increases for OD− + D2 to 3 × 10−29 cm6 s−1 at 15 K.31 The stability of this anion made it possible to probe the transition state of OH + H2 → H2O + H by starting the neutral reaction via photodetachment from the anion.32–34 These very interesting experiments stimulated state of the art calculations including accurate potential energy surfaces of H3O− and the neutral H3O complex.32,33
The endothermic proton transfer reaction OH− + H2 → H− + H2O proceeds via the H3O− collision complex. The enthalpy change in this reaction is in the range ΔH = 0.37–0.46 eV, the uncertainty of ΔH reflects values given in previous publications.30,32,33,35,36 Collisions of H− with H2O were studied in the first anion-molecule experiment.37 Crossed molecular beam experiments indicated that the reaction proceeds via a direct mechanism at collision energies above 0.7 eV.38 In a 4 K 22-pole ion trap, this reaction could be promoted by exciting the first vibrational state of the anion with 2.85 μm IR radiation.36
A common way to probe reaction dynamics and to learn more about the H3O− collision complex is to use isotope labelling and to look for scrambling of the chemically equivalent atoms. In the following, we will discuss the two isotope exchange reactions, which have been studied experimentally before,38–42
| OH− + D2 → OD− + HD, ΔH = −17.2 meV, | (1) |
| OD− + H2 → OH− + HD, ΔH = 24.0 meV. | (2) |
The reaction enthalpies at 0 K given in eqn (1) and (2) were calculated from electron affinities of OH and OD,44,45 zero point energies of H2, D2, and HD,46 and from zero point energies of OH and OD47,48 in the Born–Oppenheimer approximation. However, at sub-meV accuracy, the isotopic electronic shifts of the energy eigenvalues need to be accounted for. It has been shown for several isotope exchange reactions with H2 and D2 that the change of enthalpy due to adiabatic correction of the Born–Oppenheimer approximation is on the order of 1 meV.49–51 In particular, spectroscopic studies of OH and OD suggest that the isotopic shift of the electronic ground state potential energy surface in this system can be up to 2.5 meV (see note 78 in Ruscic et al.52). To our knowledge, there are no published results concerning the OH/OD isotopic shift, so in the worst case, the error of the above determined endothermicities can be up to 2.5 meV.
For a better understanding of the collision complex, Fig. 1 provides a sketch of the stationary points of different isotopic and isomeric configurations of the H2DO− system involved in reaction (2). It has already been discussed39,40 that, for H/D exchange, the system has to pass through three minima, separated by submerged transition states (TSs). The energies shown in Fig. 1 are corrected for zero point energies. As already mentioned above, the endothermicity of 24.0 meV is known with good precision. The values for the deuterated intermediates are estimated from H3O− energies calculated by Zhang et al.33 corrected for the rather uncertain zero point energies reported by Wang et al.35 Inspection reveals that, during the approach of the reactants, first an OH−·(H2) complex is formed, which can undergo rearrangement to the most stable form of H3O−, a H− ion bound to a perturbed H2O molecule. With exception of the zero point energies, the exit channel is symmetric. It is not so easy to predict, where scrambling of H and D atoms actually occurs, most probably in the transition states where both the H2 bond and one of the HO bonds are weakened. Extending this picture to all dimensions one may expect that the outcome of complex formation in the first minimum, isotope exchange around the minimum, and break-up either back to reactants or to products may be predictable with a statistical model. However, the submerged barriers, centrifugal barriers, and the rather rigid structures in the potential minima may hinder full scrambling. In total the probability for H/D exchange may depend on the relative orientation of the reactants during the approach, on the initial rotational states of both reactants, on the relative velocity, and certainly also on the total orbital angular momentum of the collision complex.
 | ||
| Fig. 1 Right panel: stationary points of the potential energy surface for the reaction OD− + H2 → OH− + HD. The energies are corrected for zero point energies, for details, see the text. The arrows (with dashed lines) indicate the binding energies of the intermediate complexes OD−·(H2), OH−·(HD) and H−·(DOH). Left panel: rotational energy levels47,53 of OD− and H2. The two arrows indicate the energies required for forming ground state products. | ||
To compare quantitatively rotational excitation of both reactants with the endothermicity of reaction (2), we included in the left panel of Fig. 1 the energies of two lowest rotational states of H2 with para (JH2 = 0) and ortho (JH2 = 1) nuclear spin configuration as well as the four lowest rotational states of the OD− ion.53
2 Experimental
The experiments have been carried out using the AB-22PT instrument.54,55 The principle of operating a 22-pole ion trap has been described many times so only a few essential details will be given here. For detailed descriptions, discussions of specific features, and comparisons between 22-pole trap experiments see ref. 10, 54, 56–61.The 22-pole trap was operated at an RF frequency of 27 MHz, the amplitude has been set to values up to 40 V (peak to peak). The temperature has been varied from 11 K to 300 K. The instrument uses ultra-high vacuum technology, the background number density of residual gas in the trap volume was at most 108 cm−3 at 11 K. High purity H2 or D2 gases were used in the experiments as reactants and He as buffer gas. Hydrogen or deuterium was used in its “normal” composition, i.e., with an ortho![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) para ratio of 3
para ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. Tests have indicated that this population does not change while passing the gas into the cooled trap via the inlet system.62,63
1, respectively. Tests have indicated that this population does not change while passing the gas into the cooled trap via the inlet system.62,63
OH− or OD− ions are produced in the electron impact storage ion source using a mixture of N2O and H2 or D2.27,28 The desired ions are then selected by a quadrupole mass filter and guided into the trap, where they are stored. A He–D2 or a He–H2 gas mixture is introduced directly into the trap volume. After various well-defined trapping times the trap is opened, the ions are mass selected using a second quadrupole mass spectrometer, and finally counted using an MCP detector. The actual reactant density is adjusted so that the decay of the number of trapped reactant ions due to the reaction is statistically significant. For the fast exothermic reaction (1), the D2 number density was varied between 1010 cm−3 and 1012 cm−3 while for the slow endoergic reaction (2) the H2 number density has been increased up to 1013 cm−3.
Helium buffer gas was added to the trap volume to cool the reactant ions. The actual density of He was such that reactant ions would have at least 10 collisions with He prior to collision with a molecule of reactant gas. This ensures that the kinetic and internal temperatures of OH− or OD− ions are thermalized at temperature of the He buffer gas prior to the reaction.
The temperature of trapped ions thermalized by the buffer gas was studied and discussed in many experimental studies. It was found that trap imperfections or patch potentials may lead to acceleration of the ions (i.e., higher kinetic energies). It was concluded several times for the present trap that the interaction temperature is close to the trap temperature (see e.g.ref. 57 and 63). In some previous studies the ion temperature was obtained by measuring the temperature dependence of reaction rate coefficients where this dependence could be extrapolated, e.g. the rate of the ternary association reaction of He+ + He + He.57 In the present experiments, the reaction of OD− with H2 is endothermic and has an Arrhenius-type temperature dependence of the reaction rate coefficient. Relying on the endothermicity allows us to estimate that the collision temperature deviates from the trap temperature T22PT by less than 5 K.
In the experimental studies of reactions (1) or (2), a small amount of H2 or D2, respectively, always leaks into the trap from the ion source, and the product ions react with these gases viareactions (2) or (1), respectively. In this way products are reconverted back to reactant ions. Note that these reactions are not the reverse reactions of (1) or (2), the presence of HD is negligible. Although the number density of gas from the ion source is very small compared to the reactant number density (see Table 1), it is necessary to include its influence in the data analysis, especially for the endothermic reaction (2). Consequently, the reaction rate coefficients for reactions (1) and (2) are determined by fitting the time dependence of the measured number of ions with the solution of the balance equations
 | (3) |
 | (4) |
| T 22PT (K) | [D2] (cm−3) | [He] (cm−3) | [H2]SIS (cm−3) |
|---|---|---|---|
| 25 | 2.1 × 1011 | 6.0 × 1012 | ≈6 × 109 |
| 60 | 6.0 × 1010 | 2.4 × 1012 | ≈3 × 109 |
| 100 | 4.7 × 1010 | 4.1 × 1012 | ≈1 × 109 |
3 Results and discussion
3.1 Reaction OH− + D2
As a typical result, Fig. 2 shows the decline of primary ions, NOH−, and the increase of products, NOD−, at three temperatures. For normalizing, the numbers of ions are divided by the sum NOH− + NOD−. This sum did not change with time indicating that there is no loss of ions or that there are no other products. The experimental conditions for these results are summarized in Table 1. Note that the number density of He buffer gas is at least 10 times higher than that of the reactant gas D2. The density of the perturbing H2 gas, originating from the ion source, is more than 10 times lower. The monoexponential decay of the primary ions in Fig. 2 indicates that reconversion of products can be neglected in the case of the exothermic reaction (1). The binary character of reaction (1) was checked by varying the number density [D2] from 2 × 109 cm−3 up to 4 × 1011 cm−3. The data plotted in Fig. 3 for 3 temperatures confirm the linear relationship r1 = k1[D2]. | ||
| Fig. 2 Normalized number of primary ions (OH−, closed symbols) and product ions (OD−, open symbols) as a function of storage time. Operating conditions were T22PT = 25, 60, 100 K, the densities of D2, He, and H2 are listed in Table 1. | ||
 | ||
| Fig. 3 Rate r1 of the reaction (1) as a function of deuterium number density [D2] at trap temperatures T22PT = 20, 125, 150 K. | ||
The measured temperature dependence of the rate coefficient k1 for reaction (1) is shown in Fig. 4. As already mentioned, normal D2 is used as the reactant. For comparison, the Langevin collisional rate coefficient k1L for OH− + D2 capture is indicated. The measurements were conducted in the range of trap temperatures T22PT from 11 K up to 200 K. The data show that above 60 K the reaction is getting slower with increasing temperature. The previous thermal data from the selected ion flow tube (SIFT) of Grabowski et al.39 and the flow drift tube (FDT) obtained by Viggiano and Morris40 are included in the graph. High temperature data obtained in high pressure mass spectrometer experiment (HPMS) are also plotted.41 We did not include FDT data at elevated collisional energy (KECM) because of unclear internal excitation of the ions.40 In their FDT study, Viggiano and Morris40 measured k1 both as a function of the D2 temperature and of KECM (kinetic energy in the center of mass for collision between D2 and OH− ions). They observed a significant negative dependence on the temperature but only a slight dependence on the kinetic energy. Therefore they concluded that the negative temperature dependence must be due to the increasing rotational temperature of D2. To illustrate the influence of the rotational population of deuterium in our temperature range, Fig. 4 shows a simple model rate coefficient (dash-dotted line), calculated with the assumptions that only the rotational ground state can react and this with the Langevin rate coefficient k1L. At first sight there seems to be a similarity in the temperature dependence of this function to the measured data; however, the decline of our experimental data is much steeper. In our temperature range, it must be due to the increase of the energy contributed from all degrees of freedom. This leads to a decrease of the life time of the collision complex in the first minimum (see Fig. 1). In this context we note that the comparison of k1L with the data measured below 60 K also leads to the supposition that, even at these low energies, many collision complexes decay back to reactants rather quickly. To gain more insight into the detailed dynamics of this reaction, more detailed experiments as well as theoretical studies are needed.
 | ||
| Fig. 4 Measured temperature dependence of the rate coefficient k1 for H/D exchange reaction (1). The calculated Langevin collisional rate coefficient is indicated as k1L. The assumption that exclusively the rotational ground state of D2 can react leads to the dash-dotted line (see text). Thermal FDT data of Viggiano and Morris,40 SIFT data of Grabowski et al.,39 and HPMS data of Mautner et al.41 are also included. The dashed line shows k1(T) calculated from eqn (5) with the parameters given there. | ||
Negative temperature dependencies have been observed for many binary reactions proceeding via formation of the intermediate complex. For such reactions it was deduced that the temperature dependence of the rate coefficient can be approximated by a power law dependence64–70 in analogy with the mechanism of ternary reactions described by Bates71 and Herbst.72
To describe the studied reaction (1), we are going to use a semi-empirical method given e.g. by Glosik et al.70 The general conclusion of this semi-empirical description is that the reaction rate coefficient k1 can be described by the dependence:
 | (5) |
 | ||
| Fig. 5 Plot of (k10/k1 − 1) versus T for the data shown in Fig. 4 emphasizing on the power law Tm. Data with a statistical error above 100% in this representation are not shown. | ||
The empirical model leading to eqn (5) can also be derived from RRKM theory and the exponent m can be explained with the number of “active” degrees of freedom of both the reactants and of the intermediate complex. However, looking at Fig. 1, it is not obvious, where the rate limiting bottlenecks really are. In any case, the fit through the data plotted in Fig. 4 and the linearity of the plot in Fig. 5 may be significant. The extrapolation of our fit towards higher temperatures gives a reasonable prediction for previous data, see Fig. 4 and 5. The discrepancy between the empirical curve and the data of Mautner et al.41 at higher temperatures must be due to direct mechanisms, which is not accounted for in eqn (5). Similar behavior has been observed before for several ion molecule reactions.65 The significant contribution of the present study is the coverage of a large interval at low temperatures.
3.2 Reaction OD− + H2
Examples of the measured time evolutions of normalized numbers of primary OD− and product OH− ions at four different temperatures are plotted in Fig. 6. The actual densities of H2, He and D2 in the trap are listed in Table 2. High number densities of H2 are necessary to obtain a significant decay of the number of primary OD− anions because at low temperatures the endothermic reaction (2) is slow. Note that, in comparison with the density of reactant H2, the density of D2 from the SIS is at least 100 times lower. In spite of this, back conversion of the OH− products via exothermic H/D exchange with D2 dominates at low temperatures. Therefore, the influence of reconversion cannot be neglected. Non-monoexponential decay is a clear indication of this fact. From this we can observe an approach towards equilibrium already at t > 50 ms at 12 K (see Fig. 6). The reconversion is the factor limiting the accuracy of k2. | ||
| Fig. 6 Normalized number of primary ions (OD−, closed symbols) and product ions (OH−, open symbols) as a function of storage time. The trap was at T22PT = 12, 21, 78, 200 K, the densities of D2, He and H2 in the trap are listed in Table 2. | ||
| T 22PT (K) | [H2] (cm−3) | [He] (cm−3) | [D2]SIS (cm−3) |
|---|---|---|---|
| 12 | 1.2 × 1013 | 3.4 × 1013 | ≈1 × 1010 |
| 21 | 6.7 × 1012 | 4.5 × 1013 | ≈1 × 1010 |
| 78 | 2.0 × 1012 | 2.3 × 1013 | ≈5 × 109 |
| 200 | 3.4 × 1011 | 2.5 × 1012 | ≈3 × 109 |
The temperature dependence of reaction (2) was studied in the range of trap temperatures T22PT from 11 K to 300 K. Varying the target density, it was confirmed that the products are formed via a bimolecular reaction. Our data shown in Fig. 7 were fitted by the Arrhenius function k2 = k2A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−EA-Exp/kBT), where k2A is pre-exponential factor and EA-Exp is the Arrhenius activation energy.73 From the fit we obtained k2A = 7.5 × 10−11 cm3 s−1 and EA-Exp = (7.9 ± 0.3) meV, corresponding to TA-Exp = EA-Exp/kB = (92 ± 3) K. The obtained function agrees with the data obtained in previous FDT experiments of Viggiano and Morris40 as well. To emphasize the low temperature region, Fig. 8 shows the data as the Arrhenius plot, revealing a linear decay over two orders of magnitude. Minor deviations are only at T22PT < 25 K.
exp(−EA-Exp/kBT), where k2A is pre-exponential factor and EA-Exp is the Arrhenius activation energy.73 From the fit we obtained k2A = 7.5 × 10−11 cm3 s−1 and EA-Exp = (7.9 ± 0.3) meV, corresponding to TA-Exp = EA-Exp/kB = (92 ± 3) K. The obtained function agrees with the data obtained in previous FDT experiments of Viggiano and Morris40 as well. To emphasize the low temperature region, Fig. 8 shows the data as the Arrhenius plot, revealing a linear decay over two orders of magnitude. Minor deviations are only at T22PT < 25 K.
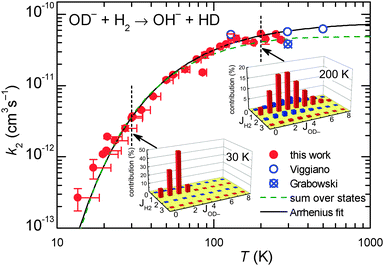 | ||
Fig. 7 Temperature dependence of the rate coefficient k2 (filled circles) for the endothermic reaction (2). The vertical error bars of the two points at the lowest temperatures include the estimated error caused by the oscillations of temperature and pressure. At temperatures above 20 K, these effects are negligible and only statistical errors are shown. The results have been fitted using an Arrhenius temperature dependence (solid line). Previous FDT data of Viggiano and Morris40 and SIFT data of Grabowski et al.39 are also plotted. The dashed curve is a fit with function (7) (see the text for details). The insets indicate the  in percent (eqn (6) and (7)) at 30 K and 200 K. in percent (eqn (6) and (7)) at 30 K and 200 K. | ||
 | ||
Fig. 8 Arrhenius plot of rate coefficient k2 for reaction (2) measured with normal H2. Shown are two almost identical fits, the two-parameter Arrhenius (solid line) and the sum over all relevant rotational states of the ion and of normal hydrogen (no ortho–para relaxation, dashed line). For details see the text. Previous FDT data of Viggiano and Morris40 and SIFT data of Grabowski et al.39 are also included in the plot. The plots marked with ok2 and pk2 are predictions for pure ortho- and para-hydrogen. In normal hydrogen, the contribution of para-hydrogen is only  . . | ||
For explaining the difference between the endothermicity of reaction (2), ΔH = 24.0 meV, and the obtained activation energy EA-Exp = (7.9 ± 0.3) meV, one is tempted to account simply for the rotational energy contributed from the hydrogen target. We use normal hydrogen with 75% in the ortho nuclear spin state. This means that, even at very low temperatures, 3/4 of the H2 molecules are rotationally excited with odd quantum numbers. If the rotational energy for J = 1, 14.7 meV, is available for promoting the reaction, the threshold onset is already lowered to 9.3 meV. For a more consistent comparison, one has to account for all rotational energies provided by both reactants (see Fig. 1). Introducing a state specific rate coefficient  for each combination of rotational states, JH2, JOD− and accounting for their thermal populations
for each combination of rotational states, JH2, JOD− and accounting for their thermal populations 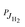 and
and  , the thermal rate coefficient can be calculated using the sum
, the thermal rate coefficient can be calculated using the sum
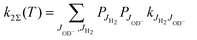 | (6) |
 | (7) |
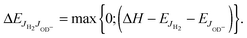 | (8) |
 and
and  , have been calculated using the rotational constants from Huber and Herzberg,47 Rehfuss et al.53 Using ΔH = 24.0 meV as fixed and putting eqn (7) into eqn (6), the averaged rate coefficient k2Σ(T) is completely determined with the exception of one free parameter, k20. Accounting for the temperature dependence of the rotational population of OD− and the constant 1
, have been calculated using the rotational constants from Huber and Herzberg,47 Rehfuss et al.53 Using ΔH = 24.0 meV as fixed and putting eqn (7) into eqn (6), the averaged rate coefficient k2Σ(T) is completely determined with the exception of one free parameter, k20. Accounting for the temperature dependence of the rotational population of OD− and the constant 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 population of even and odd J of normal H2, the experimental data could be fitted leading to k20 = 4.9 × 10−11 cm3 s−1. Comparison of this result (dashed line) with the data points in Fig. 7 and 8 reveals good agreement over a wide range of T. The small deviations at low temperatures are most probably due to experimental uncertainties in the translational and rotational temperatures (they may differ slightly). It cannot also be excluded that ΔH is slightly smaller. The problem of determining the endothermicity with sub-meV accuracy from the difference of zero point energies has been discussed above.
3 population of even and odd J of normal H2, the experimental data could be fitted leading to k20 = 4.9 × 10−11 cm3 s−1. Comparison of this result (dashed line) with the data points in Fig. 7 and 8 reveals good agreement over a wide range of T. The small deviations at low temperatures are most probably due to experimental uncertainties in the translational and rotational temperatures (they may differ slightly). It cannot also be excluded that ΔH is slightly smaller. The problem of determining the endothermicity with sub-meV accuracy from the difference of zero point energies has been discussed above.
Based on our simple model, specific rate coefficients can be calculated for various conditions of the trapping experiment. The two insets in Fig. 7 show the relative contributions as a function of the two rotational states (JH2,JOD−). At 30 K, the largest rate coefficient is predicted for (1,2) while at 200 K, also contributions from JH2 = 0 and 2 show up. Summing exclusively over even or odd rotational states of H2 leads to rate coefficients for pure ortho or pure para hydrogen, respectively. The results are shown in Fig. 8 as ok2 and pk2. The lowest curve in this plot, pfpnk2, shows the contribution of para-H2 in the present experiment, where normal-H2 has been used (pfn = 0.25). Such predictions are important for preparing experiments with para-enriched H2 or for estimating the product signal for a hydrogen beam, passing a trapped OD− cloud.
4 Conclusion
We have studied the temperature dependence of proton–deuteron exchange for the two reactions (1) and (2). The experiments have been carried out using the AB-22PT instrument, the cold head of which can reach nominal temperatures as low as 10 K. Both the He buffer gas and the hydrogen reactant gas have been leaked into the trap directly resulting in a nearly thermalized system.Isotope scrambling via the 0.2 eV bound intermediate H3O− is rather inefficient. This can be concluded from a comparison of the measured rate coefficients for the two isotopic combinations (1) and (2) with each other as well as with the corresponding capture values (Langevin: k1L = 1.16 × 10−9 cm3 s−1 and k2L = 1.55 × 10−9 cm3 s−1). Only at low temperatures, reaction (1) reaches almost 70% of ⅔k1L (the pre-factor accounts for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of H
2 ratio of H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D). Reaction (2) is always slower than (1) and increases only to 5% of ⅔k2L. All this may indicate steric hindrance during complex formation or weak coupling between the various H3O− intermediates.
D). Reaction (2) is always slower than (1) and increases only to 5% of ⅔k2L. All this may indicate steric hindrance during complex formation or weak coupling between the various H3O− intermediates.
More information has been gained from the change of reactivity with increasing temperature. The measured negative temperature dependence of the exoergic reaction (1) has been approximated using the function k1 ≈ k10/(1 + (T/130 K)2.7). This power law and its similarity to the T dependence of three body association reactions leads to the supposition that a decrease of the complex lifetime may be responsible for the fall-off of the experimental data. A different explanation, proposed by Viggiano and Morris,40 postulates that rotation of D2 hinders the reaction. This idea has been partly supported by Lee and Farrar42 who concluded that the reaction needs favorable alignments of OH− and D2. This may be easier to reach with non-rotating deuterium. We have tested this idea by comparing our data with a simple simulation assuming that exclusively D2 (J = 0) reacts. As can be seen from the dash-dotted line in Fig. 4, the resulting temperature dependence is not falling off steeply enough.
So far our results have not been detailed enough for extracting state specific rate coefficients 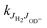 ; however, the results for the endoergic reaction (2) give additional hints. For modeling the increase of k2(T) we have assumed that each combination of rotational states of the two reactants contributes with the same rate coefficient multiplied with a state specific Arrhenius factor (see eqn (7) and (8)). The dashed line in Fig. 7 shows that this leads to a very good fit of our data with only one free parameter, k20. It is also in accord with previous data.39,40
; however, the results for the endoergic reaction (2) give additional hints. For modeling the increase of k2(T) we have assumed that each combination of rotational states of the two reactants contributes with the same rate coefficient multiplied with a state specific Arrhenius factor (see eqn (7) and (8)). The dashed line in Fig. 7 shows that this leads to a very good fit of our data with only one free parameter, k20. It is also in accord with previous data.39,40
In spite of our new results and their good agreement with the simple models, many questions remain open and ask for more experimental and theoretical activities. An obvious task is to use pure HD as target gas and to study reactions (1) and (2) in their reverse direction. The use of para-enriched hydrogen for separating J = 0 and J = 1 contributions already has been mentioned and work is in progress. For testing the dependence of k1 on the rotation of the D2 molecule, the AB-22PT instrument can be operated with a cold effusive D2 beam instead of leaking the gas directly into the trap.54 The combination neutral beam–trap allows one to control the rotational population of the ions separately from that of the neutrals.
For a deeper understanding of the reaction dynamics, theoretical investigations are required. Potential energy surfaces are available.33,34,38 First hints to a possible orientation dependence during the approach of the reactants may be obtained from trajectory calculations. Trajectories, started somewhere in the three potential minima, may provide information on the efficiency of H/D scrambling. To look closer to the H3O− transitions state, the spectroscopic characterization of this stable molecular anion is of great interest. Moreover, photofragmentation of the 0.2 eV bound H3O− may start selected half-collisions, complementary to the neutral reactions initiated by photo detachment of the electron from H3O−.34
Acknowledgements
The 22-pole ion trap instrument has been developed in Chemnitz and since 2009 it has been operated in the Faculty of Mathematics and Physics of the Charles University in Prague. We thank Chemnitz University of Technology and the DFG for making this transfer possible. This work was partly supported by GACR Grant No. P209/12/0233, 14-14715P, UNCE Grant No. 204020/2012, SV Grant No. 260 090, GAUK Grant No. 572214, 692214, 659112, AKTION 7AMB14AT023.References
- A. Dalgarno and R. A. McCray, Astrophys. J., 1973, 181, 95–100 CrossRef CAS.
- M. C. McCarthy, C. A. Gottlieb, H. Gupta and P. Thaddeus, Astrophys. J., 2006, 652, L141 CrossRef CAS.
- J. Cernicharo, M. Guélin, M. Agundez, K. Kawaguchi, M. McCarthy and P. Thaddeus, Astron. Astrophys., 2007, 467, L37–L40 CrossRef CAS.
- S. Brunken, H. Gupta, C. A. Gottlieb, M. C. McCarthy and P. Thaddeus, Astrophys. J., 2007, 664, L43 CrossRef CAS.
- P. Botschwina and R. Oswald, J. Phys. Chem. A, 2010, 114, 4875–4880 CrossRef CAS PubMed.
- Z. Yang, B. Eichelberger, O. Martinez, M. Stepanovic, T. P. Snow and V. M. Bierbaum, J. Am. Chem. Soc., 2010, 132, 5812–5819 CrossRef CAS PubMed.
- N. J. Demarais, Z. Yang, O. Martinez, N. Wehres, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2012, 746, 32 CrossRef.
- Z. Yang, B. Eichelberger, M. Y. Carpenter, O. Martinez, Jr., T. P. Snow and V. M. Bierbaum, Astrophys. J., 2010, 723, 1325–1330 CrossRef CAS.
- H. Kreckel, H. Bruhns, M. Čížek, S. C. O. Glover, K. A. Miller, X. Urbain and D. W. Savin, Science, 2010, 329, 69–71 CrossRef CAS PubMed.
- D. Gerlich, P. Jusko, Š. Roučka, I. Zymak, R. Plašil and J. Glosík, Astrophys. J., 2012, 749, 22 CrossRef.
- K. Miller, H. Bruhns, M. Čížek, J. Eliášek, R. Cabrera-Trujillo, H. Kreckel, A. OConnor, X. Urbain and D. Savin, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 032714 CrossRef.
- C. A. Cole, N. J. Demarais, Z. Yang, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2013, 779, 181 CrossRef.
- E. S. Endres, O. Lakhmanskaya, D. Hauser, S. E. Huber, T. Best, S. S. Kumar, M. Probst and R. Wester, J. Phys. Chem. A, 2014, 118, 6705–6710 CrossRef CAS PubMed.
- S. Trippel, J. Mikosch, R. Berhane, R. Otto, M. Weidemuller and R. Wester, Phys. Rev. Lett., 2006, 97, 193003 CrossRef CAS.
- P. Hlavenka, R. Otto, S. Trippel, J. Mikosch, M. Weidemuller and R. Wester, J. Chem. Phys., 2009, 130, 061105 CrossRef CAS PubMed.
- T. Best, R. Otto, S. Trippel, P. Hlavenka, A. v. Zastrow, S. Eisenbach, S. Jézouin, R. Wester, E. Vigren, M. Hamberg and W. D. Geppert, Astrophys. J., 2011, 742, 63 CrossRef.
- S. S. Kumar, D. Hauser, R. Jindra, T. Best, Š. Roučka, W. D. Geppert, T. J. Millar and R. Wester, Astrophys. J., 2013, 776, 25 CrossRef.
- J. E. Parr and J. L. Moruzzi, J. Phys. D: Appl. Phys., 1972, 5, 514 CAS.
- Y. Okuyama, M. Sabo, H. Itoh and S. Matejcík, Eur. Phys. J.: Appl. Phys., 2013, 61, 7 CrossRef.
- M. Kučera, M. Stano, J. Wnorowska, W. Barszczewska, D. Loffhagen and Š. Matejčík, Eur. Phys. J. D, 2013, 67, 1–8 CrossRef.
- O. Martinez, Z. Yang, N. B. Betts, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2009, 705, L172 CrossRef CAS.
- Z. Yang, C. A. Cole, J. Oscar Martinez, M. Y. Carpenter, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2011, 739, 19 CrossRef.
- R. Otto, J. Mikosch, S. Trippel, M. Weidemuller and R. Wester, Phys. Rev. Lett., 2008, 101, 063201 CrossRef CAS.
- M. Cížek, J. Horáček and W. Domcke, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 2571–2583 CrossRef.
- T. González-Lezana, P. Honvault, P. G. Jambrina, F. J. Aoiz and J.-M. Launay, J. Chem. Phys., 2009, 131, 044315 CrossRef PubMed.
- D. Gerlich and S. Schlemmer, Planet. Space Sci., 2002, 50, 1287–1297 CrossRef CAS.
- P. Jusko, Š. Roučka, R. Plašil and J. Glosík, Int. J. Mass Spectrom., 2013, 352, 19–28 CrossRef CAS PubMed.
- P. Jusko, Š. Roučka, D. Mulin, I. Zymak, R. Plašil, D. Gerlich, M.
![[C with combining breve]](https://www.rsc.org/images/entities/char_0043_0306.gif) í
í![[z with combining breve]](https://www.rsc.org/images/entities/char_007a_0306.gif) ek, K. Houfek and J. Glosík, J. Chem. Phys., 2015, 142, 014304 CrossRef CAS PubMed.
ek, K. Houfek and J. Glosík, J. Chem. Phys., 2015, 142, 014304 CrossRef CAS PubMed. - J. C. Kleingeld and N. M. M. Nibbering, Int. J. Mass Spectrom., 1983, 49, 311–318 CrossRef CAS.
- T. M. Miller, A. A. Viggiano, A. E. S. Miller, R. A. Morris, M. Henchman, J. F. Paulson and J. M. V. Doren, J. Chem. Phys., 1994, 100, 5706–5714 CrossRef CAS PubMed.
- D. Hauser, O. Lakhmanskaya, S. Lee, Š. Roučka and R. Wester, New J. Phys., 2015 Search PubMed , submitted.
- E. de Beer, E. H. Kim, D. M. Neumark, R. F. Gunion and W. C. Lineberger, J. Phys. Chem., 1995, 99, 13627–13636 CrossRef CAS.
- D. H. Zhang, M. Yang, M. A. Collins and S.-Y. Lee, PNAS, 2002, 99, 11579–11582 CrossRef CAS PubMed.
- D. M. Neumark, Phys. Chem. Chem. Phys., 2005, 7, 433–442 RSC.
- D. Wang, J. Z. H. Zhang and C.-h. Yu, Chem. Phys. Lett., 1997, 273, 171–178 CrossRef CAS.
- P. Jusko, O. Asvany, A.-C. Wallerstein, S. Brunken and S. Schlemmer, Phys. Rev. Lett., 2014, 112, 253005 CrossRef.
- E. E. J. Muschlitz, J. Appl. Phys., 1957, 28, 1414–1418 CrossRef CAS PubMed.
- Y. Li, L. Liu and J. M. Farrar, J. Phys. Chem. A, 2005, 109, 6392–6396 CrossRef CAS PubMed.
- J. J. Grabowski, C. H. DePuy and V. M. Bierbaum, J. Am. Chem. Soc., 1983, 105, 2565–2571 CrossRef CAS.
- A. A. Viggiano and R. A. Morris, J. Chem. Phys., 1994, 100, 2748–2753 CrossRef CAS PubMed.
- M. M.-N. Mautner, J. R. Lloyd, E. P. Hunter, W. A. Agosta and F. H. Field, J. Am. Chem. Soc., 1980, 102, 4672–4676 CrossRef CAS.
- S. T. Lee and J. M. Farrar, J. Chem. Phys., 2000, 113, 581–595 CrossRef PubMed.
- M. Henchman and J. F. Paulson, Int. J. Radiat. Appl. Instrum., Part C, 1988, 32, 417–423 CAS.
- J. R. Smith, J. B. Kim and W. C. Lineberger, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 2036–2043 CrossRef CAS.
- P. A. Schulz, R. D. Mead, P. L. Jones and W. C. Lineberger, J. Chem. Phys., 1982, 77, 1153–1165 CrossRef CAS PubMed.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397 CrossRef CAS PubMed.
- K. Huber and G. Herzberg, Molecular Spectra and Molecular Structure: Constantso Diatomic Molecules, Van Nostrand Reinhold, New York, 1979, vol. IV Search PubMed.
- N. H. Rosenbaum, J. C. Owrutsky, L. M. Tack and R. J. Saykally, J. Chem. Phys., 1986, 84, 5308–5313 CrossRef CAS PubMed.
- L. I. Kleinman and M. Wolfsberg, J. Chem. Phys., 1973, 59, 2043–2053 CrossRef CAS PubMed.
- L. I. Kleinman and M. Wolfsberg, J. Chem. Phys., 1974, 60, 4740–4748 CrossRef CAS PubMed.
- A. Adohi-Krou, F. Martin, A. J. Ross, C. Linton and R. J. L. Roy, J. Chem. Phys., 2004, 121, 6309–6316 CrossRef CAS PubMed.
- B. Ruscic, A. F. Wagner, L. B. Harding, R. L. Asher, D. Feller, D. A. Dixon, K. A. Peterson, Y. Song, X. Qian, C.-Y. Ng, J. Liu, W. Chen and D. W. Schwenke, J. Phys. Chem. A, 2002, 106, 2727–2747 CrossRef CAS.
- B. D. Rehfuss, M. W. Crofton and T. Oka, J. Chem. Phys., 1986, 85, 1785–1788 CrossRef CAS PubMed.
- D. Gerlich, G. Borodi, A. Luca, C. Mogo and M. A. Smith, Z. Phys. Chem., 2011, 225, 475–492 CrossRef CAS.
- G. Borodi, A. Luca and D. Gerlich, Int. J. Mass Spectrom., 2009, 280, 218–225 CrossRef CAS PubMed.
- I. Zymak, P. Jusko, Š. Roučka, R. Plašil, P. Rubovič, D. Gerlich and J. Glosík, Eur. Phys. J.: Appl. Phys., 2011, 56, 24010 CrossRef.
- R. Plašil, I. Zymak, P. Jusko, D. Mulin, D. Gerlich and J. Glosík, Philos. Trans. R. Soc., A, 2012, 370, 5066–5073 CrossRef PubMed.
- D. Gerlich and S. Horning, Chem. Rev., 1992, 92, 1509–1539 CrossRef CAS.
- D. Gerlich, Phys. Scr., 1995, 1995, 256 CrossRef.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- O. Asvany, S. Brunken, L. Kluge and S. Schlemmer, Appl. Phys. B: Lasers Opt., 2014, 114, 203–211 CrossRef CAS.
- M. Hejduk, P. Dohnal, J. Varju, P. Rubovič, R. Plašil and J. Glosík, Plasma Sources Sci. Technol., 2012, 21, 024002 CrossRef.
- I. Zymak, M. Hejduk, D. Mulin, R. Plašil, J. Glosík and D. Gerlich, Astrophys. J., 2013, 768, 86 CrossRef.
- J. Glosik, D. Smith, P. Španl, W. Freysinger and W. Lindinger, Int. J. Mass Spectrom., 1993, 129, 131–143 CrossRef CAS.
- J. Glosik, W. Freysinger, A. Hansel, P. Spanel and W. Lindinger, J. Chem. Phys., 1993, 98, 6995–7003 CrossRef CAS PubMed.
- J. Glosik, P. Zakouřil and W. Lindinger, Int. J. Mass Spectrom., 1995, 145, 155–163 CrossRef CAS.
- J. Glosik, P. Zakouřil, V. Skalský and W. Lindinger, Int. J. Mass Spectrom., 1995, 149–150, 499–512 CrossRef.
- J. Glosík, P. Zakouřil and W. Lindinger, J. Chem. Phys., 1995, 103, 6490–6497 CrossRef PubMed.
- P. Zakouřil, J. Glosik, V. Skalsky and W. Lindinger, J. Phys. Chem., 1995, 99, 15890–15898 CrossRef.
- J. Glosik, P. Zakouřil and A. Luca, Int. J. Mass Spectrom., 2003, 223–224, 539–546 CrossRef CAS.
- D. R. Bates, J. Phys. B: At. Mol. Phys., 1979, 12, 4135 CrossRef CAS.
- E. Herbst, J. Chem. Phys., 1979, 70, 2201–2204 CrossRef CAS PubMed.
- M. Menzinger and R. Wolfgang, Angew. Chem., Int. Ed. Engl., 1969, 8, 438–444 CrossRef CAS.
| This journal is © the Owner Societies 2015 |
