Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling proton tunnelling in the adenine–thymine base pair
A. D.
Godbeer
,
J. S.
Al-Khalili
* and
P. D.
Stevenson

University of Surrey, Guildford, Surrey GU2 7XH, UK. E-mail: j.al-khalili@surrey.ac.uk
First published on 20th April 2015
Abstract
The energies of the canonical (standard, amino-keto) and tautomeric (non-standard, imino-enol) charge-neutral forms of the adenine–thymine base pair (A–T and A*–T*, respectively) are calculated using density functional theory. The reaction pathway is then computed using a transition state search to provide the asymmetric double-well potential minima along with the barrier height and shape, which are combined to create the potential energy surface using a polynomial fit. The influence of quantum tunnelling on proton transfer within a base pair H-bond (modelled as the DFT deduced double-well potential) is then investigated by solving the time-dependent master equation for the density matrix. The effect on a quantum system by its surrounding water molecules is explored via the inclusion of a dissipative Lindblad term in the master equation, in which the environment is modelled as a heat bath of harmonic oscillators. It is found that quantum tunnelling, due to transitions to higher energy eigenstates with significant amplitudes in the shallow (tautomeric) side of the potential, is unlikely to be a significant mechanism for the creation of adenine–thymine tautomers within DNA, with thermally assisted coupling of the environment only able to boost the tunnelling probability to a maximum of 2 × 10−9. This is barely increased for different choices of the starting wave function or when the geometry of the potential energy surface is varied.
1 Introduction
In their seminal work,1 Watson and Crick proposed that the genetic code is stored in the form of hydrogen-bonds between the canonical purine and pyrimidine nucleic acid bases: adenine–thymine (A–T) and cytosine–guanine (C–G), which form the chains of the double helix structure of the DNA molecule. They recognised that tautomerization alters the hydrogen-bonding patterns and therefore could lead to mismatches in the canonical base pairs. The rare tautomer hypothesis of spontaneous mutagenesis thus states that mutations can arise through the spontaneous formation of high energy tautomers. However, accurate quantitative studies of the probability of proton transfer along the hydrogen bonds between the bases have only been possible in recent years once detailed knowledge of the potential energy surface felt by the protons could be accurately mapped. It is generally accepted that this surface is in the shape of an asymmetric double-well potential, allowing for the proton to be transferred either via classical over-the-barrier hopping or via quantum tunnelling through the barrier.The likelihood of quantum tunnelling occurring within DNA and the question of whether this is a significant contributor to spontaneous point mutations has been the subject of much research over the past few decades.2–15 It has become more prominent in recent years as more sophisticated computational methods for investigating the problem have become feasible. In addition, it is now known that the external environment, such as the presence of water molecules, also plays a role in the stability and structure of DNA. The question of interest in this study is the extent to which the environment might play a role in promoting or inhibiting proton transfer in the H-bonds in A–T and C–G base pairs.
Many studies have focussed on the hydrogen transfer itself without considering whether tunnelling is the cause. Some have claimed that tunnelling in DNA7,16,17 is either not possible or so unlikely as to be statistically negligible. Others claim it is a reasonable possibility.18 In the case of DNA base pairs, Löwdin2 correctly declared in 1963 that once a DNA replication event had occurred, the protons in the connecting hydrogen bonds would be in one of several quantum states, some or all of which could lead to potential tunnelling events, affecting any future replication events.
The canonical forms of the DNA base pairs are very stable, as would be required of the molecules responsible for the storage of the genetic information of life. However, one early study by Parker and Van Everv4 calculated the energy levels of both standard DNA base units (A–T and G–C) and a non-standard DNA base unit (G–T). They estimate that if the proton is initially in the ground state of the double well potential, then tunnelling across from the deeper well to the shallow well is extremely unlikely due to the large asymmetry. By using a simple semi-classical WKB approximation they conclude that the only way to promote tunnelling is through incoming radiation that can excite the proton to higher energy levels.
This conclusion was supported and expanded upon by Villani in a series of papers between 2005 and 2012, investigating whether the tautomeric Watson–Crick configurations are stable enough to exist for reasonable lengths of time.18–21 He identifies that mapping a potential energy surface is a suitable approach to model hydrogen atom transfer, and that a double hydrogen transfer that preserves electro-neutrality, as is the case with A–T and the tautomeric A*–T*, requires a double well with relatively large asymmetry. Florián et al. had earlier studied the stability of the canonical and tautomeric structures in 19947 and concluded that the difference in energy between the potential energy barrier and the A*–T* configuration is very small and thus A*–T* reverts to A–T very quickly.
In his 2007 paper, Villani shows using a two-dimensional model that the probability of the A*–T* tautomer existing at any given time is around 4 × 10−4, although the probability of other tautomers that exhibit charge separation occur with a slightly higher probability.19 In the four-dimensional model (with the four degrees of freedom being the two lengths of the hydrogen bonds, and the two out-of-plane positions of the hydrogen atoms in the hydrogen bridges), the probability is closer to 3 × 10−3, but this does not change his main conclusion that A*–T* does not appear often enough to be considered “a mutation point in the DNA chain”.
One of the most comprehensive studies of the suitability of various theoretical frameworks for solving the adenine–thymine system was published by Bende in 2009.22 Various types of DFT calculations using different exchange–correlation functionals were compared to results from ab initio MP2 (second-order Møller–Plesset perturbation theory),23,24 which is more precise but more computationally expensive than DFT. An important conclusion of this work is that DFT produces very good results for this type of system when using certain functionals such as BLYP,25,26 B3LYP,27 and BHLYP,28 with the latter two performing the best. Lower-level functionals such as PBE29,30 and KMLYP31 did not perform so well, particularly in the case of the hydrogen bond lengths and interaction energies. The choice of exchange–correlation functional is very important when using DFT to find energies and optimise molecular geometries.
A further illuminating study was carried out by Brovarets and Hovorun in 2013,17 which also compares MP2 and various types of DFT calculation, but in addition considers tunnelling and its potential impact on the appearance of adenine–thymine tautomers within DNA strands. They showed that the tautomerisation of A–T to A*–T* via double hydrogen transfer is both concerted and asynchronous; that is, the reaction pathway (found using the Hessian-based predictor-corrector integration algorithm32–34) does not feature an intermediate step, but the hydrogen atoms move one at a time.
Curiously, they demonstrate a step-wise double hydrogen transfer where the hydrogen atom on the N–N bridge moves across first, followed by that of the O–N bridge, counter to what Villani had found three years earlier.20 It is possible that there are various reaction pathways and that different models lead to different pathways being more prominent. Crucially, however, Brovarets and Hovorun also considered the effect of the surrounding environment: when modelling the hydrophobic interfaces of protein–nucleic acid interactions using a low dielectric constant (ε = 4), the stability and lifetime of A*–T* was not improved significantly enough for A*–T* to occur very often. This is counter to various studies35–38 that put the instance rate of A*–T* tautomers at between 10−3 and 10−6. Hence, they conclude that tautomerisation cannot be a source of spontaneous mutations during the DNA replication process, in agreement with Florián et al.7 In addition, they claim that the appearance of A*–T* tautomers does not occur via proton tunnelling but instead by above-barrier vibrations.
In 2010, Pérez et al. studied the stability of the Watson–Crick base pair tautomers and found that, although previous studies based on classical mechanics had declared them stable, when taking into account quantum effects, they were found to be dynamically metastable (i.e. stable enough to have reasonable lifetimes).39 In that work, several versions of density functional theory were used, as well as methods such as MP2 and Hartree–Fock. They showed that Hartree–Fock performs poorly for DNA base pairs and, in agreement with Bende,22 DFT using hybrid functionals such as PBE0 and B3LYP produce good results.
2 The H-bonds in A–T
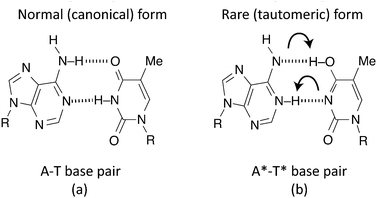
A double hydrogen bond exists between A and T, with C being joined to G via a triple hydrogen bond. This makes the A–T bond somewhat easier to model (Fig. 1(a)). When DNA undergoes replication, the weak hydrogen bonds between the bases of the nucleotides break and are free to recombine with new nucleotides in the nucleoplasm, assisted by the enzyme DNA polymerase.40 However, if the canonical forms of the nucleotides become tautomeric due to a proton tunnelling event in the hydrogen bond, the base pair is said to consist of new nucleotides, known as A* and T* (Fig. 1(b)). If a DNA strand splits, A* will no longer combine with T and it is far more energetically favourable for it to combine with C instead. Likewise, T* will almost certainly combine with G. If this error makes it past the error correction processes such that neither new DNA strand matches the original, a mutation is said to have occurred.Such a hydrogen bond can be modelled as a superposition of quantum states inside a double well potential. To get from a canonical to a tautomeric state a proton transfer would have to take place. Various studies attempt to describe this process as either a double proton transfer2,5,7,11 or a single proton transfer,6,8,10 in order to explain these mutations. Once in a tautomeric state, DNA replication of this base pair could result in a codon error (see Fig. 2).
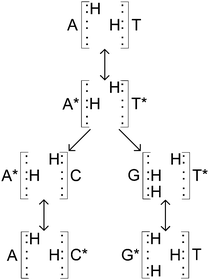 | ||
| Fig. 2 Adapted from Löwdin.2 Canonical A–T base pair undergoing tautomerisation and then replication. Neither new base pair is of the usual A–T or C–G forms. | ||
In this work, we employ density functional theory to model the 1-D potential energy surface felt by one of the two protons in the double H-bond of the A–T base pair. A full two-dimensional map of the reaction pathway would be ideal but also computationally prohibitive; fortunately, a one-dimensional map appears sufficient for such a proton transfer.39 Once this static double-well potential is found it is used to solve the time-dependent generalised Liouville equation, including a dissipative term to model the action of the environment (e.g. H2O molecules) surrounding the base pair. We assume that if one of the two protons moves across then so will the second one, whether together or sequentially in a two-step process, to create the tautomeric form, A*–T*. It has been found that using ab initio constrained molecular dynamics calculations41 that double potential transfer in the A–T base pair is a stepwise and most likely asynchronous process. However, whether the double proton transfer occurs in a concerted or step-wise fashion is of little importance when utilising a one-dimensional reaction pathway because the “secondary” hydrogen atom will always move to preserve electroneutrality. Thus, the movement of a single proton is the rate-determining action that should be investigated.20,17,39,42
3 Mapping the potential energy surface
The differences between the various density functional theory (DFT) methods hinge on their choice of exchange–correlation functional. In the absence of a perfect method for calculating geometries and energies, the most suitable functional in terms of performance and computational complexity must be chosen. For this work, we have used B3LYP,27 a hybrid generalised gradient approximation (GGA) functional derived from the GGA functional BLYP, which itself combines Becke's exchange functional25 with the correlation functional by Lee, Yang, and Parr.26 There is evidence in the literature to suggest that hybrid GGA functionals like B3LYP are well suited to a system like adenine–thymine19–22,39,42,43 (and indeed match well with results from higher level methods such as MP2). It should be noted, however, that B3LYP has been demonstrated to underestimate hydrogen bond strengths for A–T.44 In addition, DFT functionals in general tend to underestimate barrier energies compared to other methods.45–47The structure of the canonical form of A–T is listed in the S22 database,48 which was calculated using MP2 with the cc-pVTZ basis set.49 The structure data was converted to a format readable by CASTEP50 and then a geometry optimisation was performed using the “precise” preset for plane-wave energy cut off, with BLYP norm-conserving pseudopotentials.51 Since the tautomeric form, A*–T*, is not available in the S22 database, it was necessary to estimate its form before a geometry optimisation could be performed. To do this, the B3LYP optimised geometry for A–T was adjusted to create a starting geometry for A*–T*. The lengths and the angles of the hydrogen bond ions were estimated based on the average of values reported in literature, then those hydrogen bonds were fixed in place whilst the rest of the geometry was optimised. Lastly, that result was used as the starting structure for a final pass during which all ions were free to move. Both the canonical and tautomeric optimised geometries are shown in Fig. 3 and the difference in energy between the two forms, ΔE = EA*–T* − EA–T was found to be 4613.5 cm−1 (0.572 eV or 13.19 kcal mol−1). This is compared to existing results in literature in Table 1.
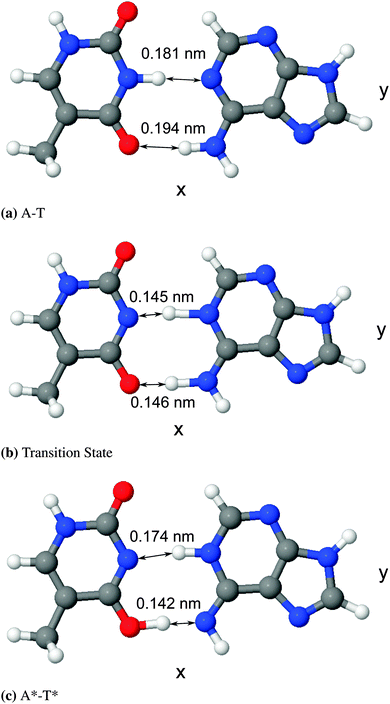 | ||
| Fig. 3 Diagrams of optimised geometries generated using the software package J mol,52,53 with bond lengths displayed. | ||
| Source | ΔE (cm−1) | E B (cm−1) |
|---|---|---|
| This work | 4597 | 8066 |
| Villani (2005)18 | 4517 | — |
| Bende (2009)22 | 4759–5243 | — |
| Yue-Jie Ai et al. (2010)43 | 4597 | 4759–4920 |
| Florián et al. (1994)7 | 3307 | 3388 |
| 5243–6614 | 6614–7017 | |
| Guallar et al. (1999)54 | 7872 | 7864 |
| Gorb et al. (2004)16 | 4194–5727 | 4033–6049 |
| Cerón-Carrasco et al. (2009)55 | 3780–5070 | — |
| Pérez et al. (2010)39 | 2984–3468 | 3307–4355 |
| Gobbo et al. (2012)42 | 5001 | 5650–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
| Herrera and Torro-Labbe (2004)56 | 4200–7000 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700–17 700–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
It is important to note that the z-axis positions for all of the ions are essentially static for both states (unsurprising given that the molecule is very “flat”). The relative change in y-axis positions for the protons in the hydrogen bonds is ∼5% that of the change in x-axis positions. This suggests that a one-dimensional potential, varying along the x-axis, can accurately describe the transition state between these two molecular forms, in agreement with other authors.18,39
Once minimum energies and optimised geometries were known for stable versions of both A–T and A*–T*, it was necessary to find the height and shape of the barrier between them to complete the double well potential picture. There are a few different methods to perform a transition state search, in order to calculate a minimum energy pathway or potential energy surface of a geometry transition. The most powerful one offered by CASTEP is the complete LST/QST,57 which combines the linear synchronous transit (LST) and quadratic synchronous transit (QST) methods. Initially, a single LST interpolation is performed, bracketing the maximum energy between the reactants and product, which is followed by continual energy minimisations in “directions conjugate to the reaction pathway” until a true energy minimum is reached. This approximation is then used to perform QST “constrained minimisations” to much more accurately refine the transition state. Once this is complete the cycle is repeated beginning with another LST maximisation until a stationary point is found, which represents the transition state barrier.
Next, a fourth-order polynomial fit was carried out to map the full shape of the potential with five boundary conditions: the two well minima energies, the barrier maximum, and the two well minima ζ-axis positions, where ζ is the dimensionless reduced position co-ordinate of the proton along the x-axis defined as ζ = x/a, where a is half the distance between the two well minima positioned such that they are equidistant from x = 0, placing them at ζ = ±1. (Note that, due to the asymmetry in the potential, the peak of the barrier may not be exactly at ζ = 0.) The nature of a fourth order polynomial is similar to that of a quartic well and produces the high well walls necessary for outer-box boundary conditions. The resulting polynomial is described in eqn (1) and appears alongside the energies found during the CASTEP transition state search in Fig. 4. Note that the 8065.73 factor is to convert eV to cm−1.
| V(ζ) = 8065.73(−4464.49 + 0.429ζ − 1.126ζ2 − 0.143ζ3 + 0.563ζ4) | (1) |
 | ||
| Fig. 4 Polynomial fit applied to the results of CASTEP's transition state search for stable and optimised forms of A–T & A*–T*. | ||
In Fig. 4 the potential energy scale has been adjusted such that the energy of the canonical state EA–T = 0 since only the relative energies of the barrier and minima, and the well shape, are important.
4 Time evolution of the density matrix
The density matrix operator describing a single proton in a 1-D double-well potential is defined as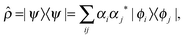 | (2) |
| Ĥ0|ϕi〉 = Ei|ϕi〉, | (3) |
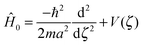 | (4) |
In order to model an open (dissipative) system, coupling to the environment (in the limit of weak coupling to a Markovian bath) can be included in the generalised Liouville equation that include a dissipative (Lindblad) term on the right hand side58,59
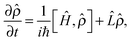 | (5) |
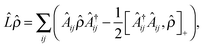 | (6) |
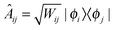 | (7) |
Substituting the above back into eqn (5) leads to diagonal and off-diagonal density matrix elements
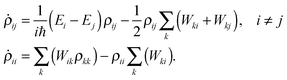 | (8) |
| Ĥ = Ĥ0 + Ĥb + ΔĤ, | (9) |
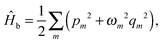 | (10) |
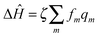 is the interaction between the system and bath, with coupling constant, fm.
is the interaction between the system and bath, with coupling constant, fm.
The transition probability Wij between states i and j is defined as
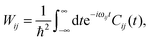 | (11) |
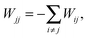 | (12) |
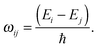 | (13) |
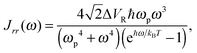 | (14) |
The power spectral density function can be transformed to give two correlation functions, one for the active bath displacement
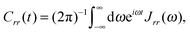 | (15) |
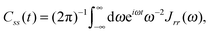 | (16) |
| Ctun(t; d2) = ed2ℏ−2(Css(t)−Css(0)), | (17) |
| d = |ζii′ − ζjj′|. | (18) |
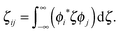 | (19) |
Finally, the correlation function
| Cij(t) = (ζij′)2Crr(t)Ctun(t; d2) | (20) |
Unfortunately, transition probabilities are not trivial to calculate for this system because the difference between each energy eigenvalue is relatively large, and as the difference in energy between eigenstates i and j increases, the smaller the values for Crr(t) and Css(t) become around t = 0. For numerical integration, many of these smaller values must be summed, and they are less prominent compared with the already small values at more extreme values of t. Fortunately, an analytical approach for calculating these correlation functions using the residue theorem can be used to solve the troublesome integrals, Css(t) and Crr(t).
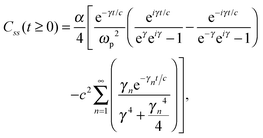
The analytic solutions of Css(t) and Crr(t) are shown below:
 | (21) |
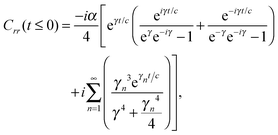 | (22) |
 | (23) |
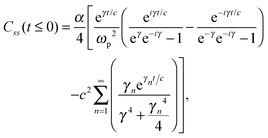 | (24) |
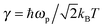 , c = ℏ/kBT,
, c = ℏ/kBT, 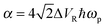 , and γn = 2πn. With analytic solutions for Crr(t) and Css(t), the expression for Cij(t) also becomes analytic. However, there is a single case, at Crr(t = 0), where the infinite sum is divergent, leading to numerical difficulty when solving the Fourier transform integral over time in eqn (11). However, there is a way around this. The infinite sum in eqn (21) and (22) only contributes to the real part of Crr(t). With this in mind, it is useful to find a means of solving the FT integral for Wij without requiring the real component of Cij(t).
, and γn = 2πn. With analytic solutions for Crr(t) and Css(t), the expression for Cij(t) also becomes analytic. However, there is a single case, at Crr(t = 0), where the infinite sum is divergent, leading to numerical difficulty when solving the Fourier transform integral over time in eqn (11). However, there is a way around this. The infinite sum in eqn (21) and (22) only contributes to the real part of Crr(t). With this in mind, it is useful to find a means of solving the FT integral for Wij without requiring the real component of Cij(t).
To this end, Wij is split into its real and imaginary constituents as follows:
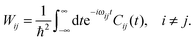 | (25) |
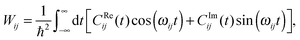 | (26) |
Eqn (26) still includes the real component of Cij(t) and so doesn't solve the divergent-sum problem entirely. However, there are several useful identities and relations that can be employed to solve this. Since ωij = ℏ−1(Ei − Ej) = −ωij, then Cij(t) = Cij(t). Also, the transition probabilities between energy eigenstates must conform to the principle of detailed balance,63
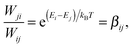 | (27) |
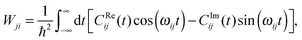 | (28) |
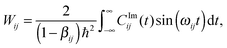 | (29) |
5 Results
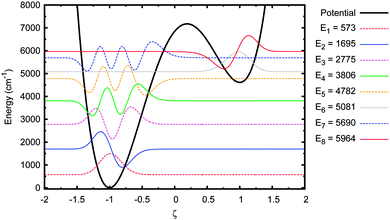
The energy eigenstates for the adenine–thymine double potential well, shown in Fig. 4, were calculated using the DSTEV function included in the LAPACK library.65 The first eight eigenstates are shown in Fig. 5.The most important feature to note here is that the first five eigenstates are wholly localised in the deeper well on the left (i.e. the canonical state). The 6th eigenstate is the first that is localised in the shallower well (the tautomeric state). The 5th and 6th eigenstates have sufficiently close energy eigenvalues to be considered a tunnel doublet. The same is true for the 7th and 8th eigenstates. The 12th energy eigenstate (not shown in figure), at 7407 cm−1 (or 0.92 eV), is the first one above the barrier, which means there are six eigenstates below the barrier with energies high enough to allow for tunnelling between the wells.
With the eigenstates known, the time evolution of the density matrix can be computed using eqn (5). The proton is chosen to be initially in the ground state and the initial wave function is thus (|ψ(t = 0)〉 = |ϕ1〉). This is a reasonable choice since the ground state probability amplitude in such an asymmetric double well is almost entirely in the deep well anyway, where we would wish to start the proton in. Of course it should be noted here that without a dissipative Lindblad term in eqn (5) there would be no tunnelling since this is a stationary state. The effect of the dissipative term is therefore to allow transitions between eigenstates and it is only the coupling to the higher states (6th to 11th) that leads to any significant probability of finding the proton in the shallow well.
The values of several parameters in the Lindblad term are now required. The temperature of the environment, appearing in the spectral density function, was fixed at 320 K. The other two parameters, ΔVR and ωp, relate to the properties of the heat bath of harmonic oscillators. However, without experimental data for this system it is difficult to choose appropriate values and it is instructive to carry out computations over a range of values. Fortunately, since the double hydrogen-bond in the A–T system shares its properties with that of a much simpler and better studied molecule, the benzoic acid dimer,66–68 it was decided to use parameters from the latter (ΔVR = 44 cm−1, ℏωp = 186 cm−1)69 as a benchmark around which to explore.
The time evolution was computed over a range of 10 ns and repeated for ΔVR = 10, 20, 44, 100, 400 cm−1 and ℏωp = 20, 100, 500 cm−1. The probability of tunnelling is plotted over time in Fig. 6. Each sub-figure is for a specific value of ωp with curves for different values of ΔVR. The probability of the wave function being in the shallow well at each time interval required for outputted results was calculated from the diagonal elements of the density matrix in the position basis, |ψ(ζ)|2, then normalising this wave function and integrating over the relevant range along the ζ-axis that covers the width of the shallow well. We feel that this is a more informative quantity to calculate in our approach than the equivalent tunnelling times (for example using a semi-classical WKB approach) or transition rates (using Fermi's golden rule).
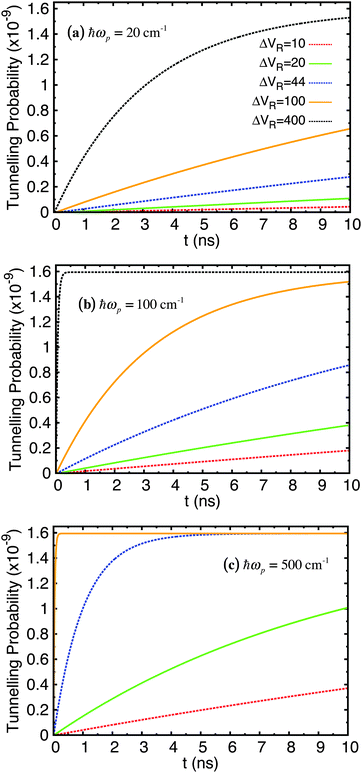 | ||
| Fig. 6 Tunnelling probability in adenine–thymine nucleobase pair for |ψ(t = 0)〉 = |ϕ1〉, T = 320 K, and varying Lindblad parameters. ΔVR has units cm−1. | ||
The key feature of these plots is that the probability of finding the proton in the shallow well increases over time (very slowly in comparison with rate of tunnelling itself – several nanoseconds compared typically with around a tenth of a picosecond), but this probability reaches a plateau of around 1.6 × 10−9 for all parameters used; in fact, the only parameter that affects the maximum tunnelling probability is temperature. We showed in a previous study68 that for the case of the benzoic acid dimer the tunnelling rate is reduced at lower temperatures since the weaker coupling to the environment means it is less likely that there will be strong transitions between eigenstates, particularly those at energies above the bottom of the shallow well. Secondly, both ωp and ΔVR affect how quickly the system reaches equilibrium.
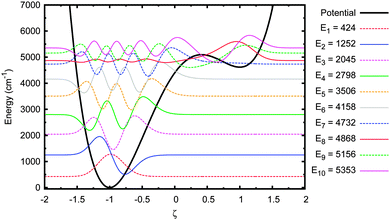
Next we investigated the sensitivity of the tunnelling probability to the A–T well geometry. Firstly, the height of the barrier above to the deeper well, EB, was reduced by 30%. This adjusted potential and its energy eigenstates are shown in Fig. 7. The first 7 eigenstates are now wholly localised in the deeper well, with the 7th & 8th and 9th & 10th states forming tunnel doublets. The 8th eigenstate is the lowest in the shallow well, but even this state is partially in the deep well because the barrier is so close in energy to the shallow well minimum. The tunnelling probability in this potential are shown in Fig. 8.
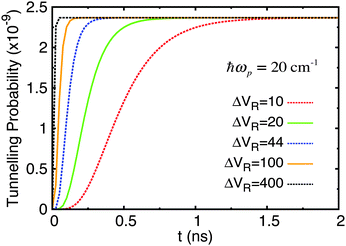 | ||
| Fig. 8 Tunnelling probability in adenine–thymine nucleobase pair for |ψ(t = 0)〉 = |ϕ1〉, T = 320 K, and varying Lindblad parameters. The height of the potential barrier compared to the deeper well minimum has been reduced by 30%. ΔVR has units cm−1. This figure should be compared with Fig. 6(a). | ||
There are two important differences to note here. Firstly, the time it takes for an equilibrium to be reached is much reduced in all cases, being rarely greater than 100 ps. Secondly, the maximum tunnelling probability has increased slightly to 2.4 × 10−9.
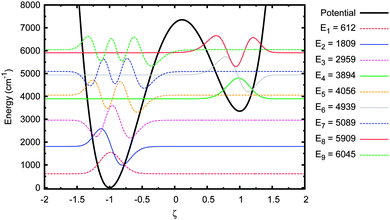
Next, the original adenine–thymine potential was adjusted by increasing the depth of the shallow well compared to the potential barrier, EB − ΔE, by 50%. This adjusted potential and its energy eigenstates are shown in Fig. 9. There are now 3 pairs of tunnel doublets (states 4 & 5, 6 & 7, and 8 & 9) and there are more localised eigenstates in the shallow well, starting with the 4th. The tunnelling probability results for this new potential are shown in Fig. 10.
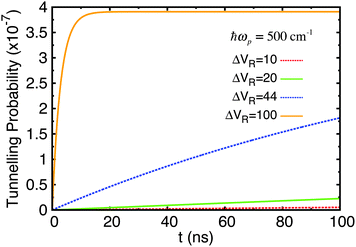 | ||
| Fig. 10 Tunnelling probability in adenine–thymine nucleobase pair for |ψ(t = 0)〉 = |ϕ1〉, T = 320 K, and varying Lindblad parameters. The depth of the shallow well compared to the potential barrier has been increased by 50%. ΔVR has units cm−1. This figure should be compared with Fig. 6(c). | ||
Now, the time taken to reach equilibrium is dramatically increased compared to the standard adenine–thymine model, being approximately an order of magnitude greater. However, the tunnelling probability is increased significantly to almost 4 × 10−7. This still represents a very low chance of tunnelling having taken place, but is nearly 250 times higher than for the original adenine–thymine potential.
Finally, it was decided to alter the initial (t = 0) wave function from the ground state to a Boltzmann distribution in order to simulate an “average” starting wave function based on the density of states:70
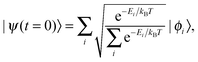 | (30) |
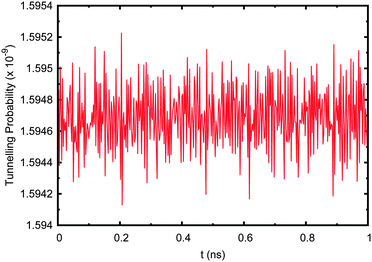 | ||
| Fig. 11 Tunnelling probability in adenine–thymine nucleobase pair when the starting wave function, ψ(t = 0), is set to a Boltzmann distribution with no environment coupling. | ||
Now the tunnelling probability oscillates rapidly due to the complex nature of the wave function. The probability of tunnelling is still extremely low at ∼1.6 × 10−9, which is due to the fact that the first energy eigenstate (being localised to the deep well) is by far the largest contributor, having a coefficient of 0.9936. Including the effect of the environment makes no difference to the resulting tunnelling probability and is negligible compared to the complex oscillations due to interference between the system's eigenfunctions.
It is worth noting that even when starting the proton in the highest excited state below the bottom of the shallow well (|ψ(t = 0)〉 = |ϕ5〉), mimicking similar tests carried out by Gobbo et al.,42 the transitions between eigenstates due to the environmental coupling bring the tunnelling probability down to 1.6 × 10−9. This takes approximately 70 ns with default parameters, during which time the tunnelling probability briefly reaches a peak of 8 × 10−5. Whilst this is much higher than when the proton is in the ground state (which is to be expected since the barrier is relatively lower), it still cannot account for a large percentage of occurring tautomers.
6 Summary and conclusions
An improved method for discovering transition probabilities was devised and applied to the adenine–thymine potential. These were calculated and applied in order to find that the tunnelling probability, even with an environment present, is very low in this model. It thus seems unlikely that the instance rate of A*–T* is due to proton tunnelling in any significant way, with other mechanisms being more important. The effect of changing the asymmetry and barrier height of the potential is small, although the former is the more potent factor of the two. In addition, altering the mass parameter to simulate a deuterated molecule has a minimal effect on the tunnelling probability and thus it seems unlikely that any change in the instance rate of A*–T* due to deuteration is because of tunnelling.The main purpose of this study has been to add to the body of work on the influence of quantum tunnelling on proton transfer within DNA base pair H-bonds. Although previous studies have looked at the stability, lifetimes, and instance rates of tautomeric Watson–Crick adenine–thymine base pairs within DNA,2,7,16–21,35–39,42,71 few have look specifically at tunnelling, particularly in the absence of external radiation exciting the protons to higher energies where tunnelling would be more likely. Even the notion that base pair tautomers exist for any meaningful length of time within DNA is yet to be settled, with some indications that A*–T* is metastable and others that it reverts to the canonical A–T form too quickly to have any influence during DNA replication.
The adenine–thymine potential was created using DFT with the B3LYP functional. The results obtained compared favourably with those in the existing literature, particularly in the case of the energy difference between the canonical state and tautomeric state. An initial wave function was set up in both the ground state (|ψ(t = 0)〉 = |ϕ1〉) and in a Boltzmann distribution, then transition probabilities were calculated using an improved, mostly analytical, method to include the dissipative effects of coupling to an external heat bath. The density matrix was then allowed to evolve in time and it was found that tunnelling was promoted by the environmental coupling, but by a very low amount (2 × 10−9). It was confirmed in an earlier work68 that the effect of the dissipative Lindblad term is to induce thermally assisted tunnelling, but (crucially) not to encourage classical over the barrier hopping. This was determined in that work, which was applied to proton tunnelling in the benzoic acid dimer molecule, by comparing the probability of finding the proton in the shallow well in two eigenstate basis calculations. In the first, a large basis set of energy eigenstates was used, which included many eigenstates with energies above the barrier. In the second, a smaller basis set was used, restricted to just those eigenstates below the barrier, some of which could support tunnelling if their energies were above the base of the shallow well. Hardly any change to the tunnelling probability was found between the two calculations, implying that tunnelling is the dominant mechanism (namely, that the only way for the proton to find its way to the shallow well was via quantum tunnelling rather than classical over the barrier hopping. The reason for this is that the transition probabilities Wij between eigenstates that link to the above barrier states were negligibly small. This is key because it demonstrates that the primary effect of dissipation is not to allow classical over-the-barrier hoping but to increase the likelihood of tunnelling below the barrier. We have made the assumption that this argument also holds for the case of proton transfer in A–T. However, it may be that further work is necessary to confirm this.
To test the sensitivity of the outcomes to the input parameters, various adjustments were made to the potential and environment parameters. The only environment parameter to actually affect the maximum tunnelling rate was temperature, thus confirming that future adjustments to the other parameters would not drastically affect the conclusions of this work. Despite this, it would be interesting to generate more accurate parameters for the nucleoplasm environment using experimental data and then repeat the procedure. In terms of the potential itself, both the depth of the shallow well and the height of the barrier were adjusted and it was found that the asymmetry was by far the most important factor (even more so than the particle mass) for determining the increase in tunnelling probability in this model. Therefore, the range of barrier heights in the literature, which is fairly large (3200–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 or 0.4–2.3 eV), is unlikely to be critical; even if the barrier height is dropped significantly (by 30%), the affect on tunnelling rates remains relatively small.
600 cm−1 or 0.4–2.3 eV), is unlikely to be critical; even if the barrier height is dropped significantly (by 30%), the affect on tunnelling rates remains relatively small.
A comparison between the method used here, where first a static potential is generated via a DFT approach and then the time-dependent master equation for an open quantum system is solved, with a fully time-dependent DFT approach would be of interest and could prove useful in testing our conclusions. Finally, even if quantum tunnelling really does not play an important role in point mutations in DNA, there is still the potential for utilising the tools developed here in other biochemical processes, such as those involving proton transfer promoted by enzyme catalysis.
References
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 964–967 CrossRef CAS.
- P.-O. Löwdin, Rev. Mod. Phys., 1963, 35, 724–732 CrossRef.
- P.-O. Löwdin, Advances in Quantum Chemistry, Academic Press, 1966, vol. 2, pp. 213–360 Search PubMed.
- B. R. Parker and J. V. Everv, Chem. Phys. Lett., 1971, 8, 94–99 CrossRef CAS.
- W. Sokalski, H. Romanowski and A. Jaworski, Adv. Mol. Relax. Interact. Processes, 1977, 11, 29–41 CrossRef CAS.
- A. O. Colson, B. Besler and M. D. Sevilla, J. Phys. Chem., 1992, 96, 9787–9794 CrossRef CAS.
- J. Florián, V. Hrouda and P. Hobza, J. Am. Chem. Soc., 1994, 116, 1457–1460 CrossRef.
- M. Hutter and T. Clark, J. Am. Chem. Soc., 1996, 118, 7574–7577 CrossRef CAS.
- K. Brameld, S. Dasgupta and W. A. Goddard, J. Phys. Chem. B, 1997, 101, 4851–4859 CrossRef CAS.
- J. Bertran, A. Oliva, L. Rodríguez-Santiago and M. Sodupe, J. Am. Chem. Soc., 1998, 120, 8159–8167 CrossRef CAS.
- V. L. Golo and Y. S. Volkov, Int. J. Mod. Phys. C, 2003, 14, 133–156 CrossRef CAS.
- E. K. Ivanova, N. N. Turaeva and B. L. Oksengendler, 2011, arXiv:1105.8282.
- P. Ball, Nature, 2011, 474, 272–274 CrossRef CAS PubMed.
- D. Jacquemin, J. Zúñiga, A. Requena and J. P. Cerón-Carrasco, Acc. Chem. Res., 2014, 2467–2474 CrossRef CAS PubMed.
- A. Kumar and M. D. Sevilla, Chem. Rev., 2010, 110, 7002–7023 CrossRef CAS PubMed.
- L. Gorb, Y. Podolyan, P. Dziekonski, W. A. Sokalski and J. Leszczynski, J. Am. Chem. Soc., 2004, 126, 10119–10129 CrossRef CAS PubMed.
- O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2013, 32, 127–154 Search PubMed.
- G. Villani, Chem. Phys., 2005, 316, 1–8 CrossRef CAS PubMed.
- G. Villani, Chem. Phys., 2007, 336, 143–149 CrossRef CAS PubMed.
- G. Villani, Phys. Chem. Chem. Phys., 2010, 12, 2664–2669 RSC.
- G. Villani, Chem. Phys., 2012, 394, 9–16 CrossRef CAS PubMed.
- A. Bende, Theor. Chem. Acc., 2010, 125, 253–268 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. K. Kang and C. B. Musgrave, J. Chem. Phys., 2001, 115, 11040–11051 CrossRef CAS PubMed.
- H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924 CrossRef CAS PubMed.
- C. Dykstra, G. Frenking, K. Kim and G. Scuseria, Theory and Applications of Computational Chemistry: The First Forty Years, Elsevier Science, 2011, pp. 195–249 Search PubMed.
- H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69 CrossRef CAS.
- S. Basu, R. Majumdar, G. Das and D. Bhattacharyya, Indian J. Biochem. Biophys., 2005, 42, 378–385 CAS.
- A. Shukla, Chemical Basis of Inheritance, Discovery Publishing House Pvt. Limited, 2009, p. 51 Search PubMed.
- M. Williams and L. Maher, Biophysics of DNA-Protein Interactions: From Single Molecules to Biological Systems, Springer, 2010 Search PubMed.
- T. A. Kunkel and K. Bebenek, Annu. Rev. Biochem., 2000, 69, 497–529 CrossRef CAS PubMed.
- A. Pérez, M. E. Tuckerman, H. P. Hjalmarson and O. A. von Lilienfeld, J. Am. Chem. Soc., 2010, 132, 11510–11515 CrossRef PubMed.
- A. Stanford, Foundations of biophysics, Academic Press, 1975 Search PubMed.
- S. Xiao, L. Wang, Y. Liu, X. Lin and H. Liang, J. Chem. Phys., 2012, 137, 195101 CrossRef PubMed.
- J. P. Gobbo, V. Saur, D. Roca-Sanjun, L. Serrano-Andrs, M. Merchn and A. C. Borin, J. Phys. Chem. B, 2012, 116, 4089–4097 CrossRef CAS PubMed.
- Y.-J. Ai, F. Zhang, G.-L. Cui, Y. Luo and W.-H. Fang, J. Chem. Phys., 2010, 133, 064302 CrossRef PubMed.
- T. van der Wijst, C. F. Guerra, M. Swart and F. M. Bickelhaupt, Chem. Phys. Lett., 2006, 426, 415–421 CrossRef CAS PubMed.
- B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2001, 105, 2936–2941 CrossRef CAS.
- M. N. Glukhovtsev, R. D. Bach, A. Pross and L. Radom, Chem. Phys. Lett., 1996, 260, 558–564 CrossRef CAS.
- R. L. Bell, D. L. Taveras, T. N. Truong and J. Simons, Int. J. Quantum Chem., 1997, 63, 861–874 CrossRef CAS.
- B. Energy and G. Database, Adenine–Thymine Watson–Crick Complex, 2006 Search PubMed.
- P. Jurecka, J. Sponer, J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristall., 2005, 220, 567–570 CrossRef CAS.
- R. Sabatini, Quantum Espresso - Pseudopotentials, 2014 Search PubMed.
- Jmol, Jmol: an open-source Java viewer for chemical structures in 3D, 2014.
- A. Herráez, How to Use Jmol to Study and Present Molecular Structures, http://Lulu.com, 2007.
- V. Guallar, A. Douhal, M. Moreno and J. M. Lluch, J. Phys. Chem. A, 1999, 103, 6251–6256 CrossRef CAS.
- J. P. Cerón-Carrasco, A. Requena, J. Ziga, C. Michaux, E. A. Perpte and D. Jacquemin, J. Phys. Chem. A, 2009, 113, 10549–10556 CrossRef PubMed.
- B. Herrera and A. Toro-Labbe, J. Chem. Phys., 2004, 121, 7096–7102 CrossRef CAS PubMed.
- N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, Comput. Mater. Sci., 2003, 28, 250–258 CrossRef CAS.
- V. Gorini, A. Kossakowski and E. C. G. Sudarshan, J. Math. Phys., 1976, 17, 821–825 CrossRef PubMed.
- G. Lindblad, Commun. Math. Phys., 1976, 48, 119–130 CrossRef.
- C. Scheurer and P. Saalfrank, J. Chem. Phys., 1996, 104, 2869–2882 CrossRef CAS PubMed.
- K. Lendi and R. Alicki, Quantum Dynamical Semigroups and Applications (Lecture Notes in Physics), Society for Industrial and Applied Mathematics, 11th edn, 1987, vol. 286 Search PubMed.
- H. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, USA, 2002 Search PubMed.
- R. Meyer and R. R. Ernst, J. Chem. Phys., 1990, 93, 5518–5532 CrossRef CAS PubMed.
- P. Rebentrost, M. Mohseni, I. Kassal, S. Lloyd and A. Aspuru-Guzik, New J. Phys., 2009, 11, 033003 CrossRef.
- E. Anderson, Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney and D. Sorensen, LAPACK Users' Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, 3rd edn, 1999 Search PubMed.
- C. Foces-Foces, L. Infantes, F. Aguilar-Parrilla, N. S. Golubev, H.-H. Limbach and J. Elguero, J. Chem. Soc., Perkin Trans. 2, 1996, 349–353 RSC.
- M. J. Wjcik, K. Szczeponek and M. Boczar, Int. J. Mol. Sci., 2003, 4, 422–433 CrossRef PubMed.
- A. D. Godbeer, J. S. Al-Khalili and P. D. Stevenson, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 012102 CrossRef.
- A. Stockli, B. H. Meier, R. Kreis, R. Meyer and R. R. Ernst, J. Chem. Phys., 1990, 93, 1502–1520 CrossRef CAS PubMed.
- A. Durrant, Quantum Physics of Matter, Taylor & Francis, 2000 Search PubMed.
- E. S. Kryachko, Int. J. Quantum Chem., 2002, 90, 910–923 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |