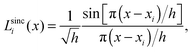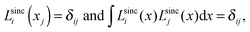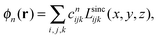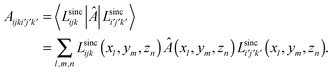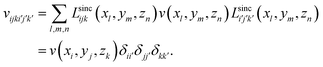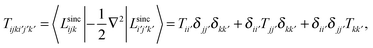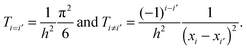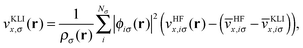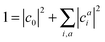Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Configuration interaction singles based on the real-space numerical grid method: Kohn–Sham versus Hartree–Fock orbitals†
Jaewook
Kim‡
,
Kwangwoo
Hong‡
,
Sunghwan
Choi
,
Sang-Yeon
Hwang
and
Woo
Youn Kim
*
Department of Chemistry, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 305-701, Korea. E-mail: wooyoun@kaist.ac.kr
First published on 1st April 2015
Abstract
We developed a program code of configuration interaction singles (CIS) based on a numerical grid method. We used Kohn–Sham (KS) as well as Hartree–Fock (HF) orbitals as a reference configuration and Lagrange-sinc functions as a basis set. Our calculations show that KS-CIS is more cost-effective and more accurate than HF-CIS. The former is due to the fact that the non-local HF exchange potential greatly reduces the sparsity of the Hamiltonian matrix in grid-based methods. The latter is because the energy gaps between KS occupied and virtual orbitals are already closer to vertical excitation energies and thus KS-CIS needs small corrections, whereas HF results in much larger energy gaps and more diffuse virtual orbitals. KS-CIS using the Lagrange-sinc basis set also shows a better or a similar accuracy to smaller orbital space compared to the standard HF-CIS using Gaussian basis sets. In particular, KS orbitals from an exact exchange potential by the Krieger–Li–Iafrate approximation lead to more accurate excitation energies than those from conventional (semi-) local exchange–correlation potentials.
Introduction
Rapidly growing interest in computational materials design1–5 and quantum biology6 has encouraged development of innovative methods for accurate electronic structure calculations of large systems.7–12 Though quantum chemistry using atom-centred basis functions such as Gaussian basis sets shows unrivalled performance for small and medium size molecules in terms of computation costs, they face the limit of their capabilities in dealing with large systems. Apparently, grid-based methods are promising alternatives, because their computational costs can be reduced through massive parallelization as well as linear scaling algorithms7–10,13–15 and their accuracy can be systematically improved by single parameter control without optimizing system- or method-dependent parameters.Most available codes using numerical grid basis sets adopt density functional theory (DFT) for ground state calculations and time-dependent DFT for excited state calculations.7–10,16 Though (time-dependent) DFT offers a cost-effective way to describe large systems with reliable accuracy in many cases, it fails even qualitatively for strongly-correlated systems,17,18 since it relies on a single-determinant approach.
Strong correlation effects of electrons can readily be captured by using multiconfiguration (MC) methods. To our best knowledge, however, no traditional wave function theory has been used in real-space numerical grid methods. The so-called post-Hartree–Fock (post-HF) approaches may not be adequate for numerical grid basis sets, since the nonlocal HF exchange operator greatly reduces the sparsity of the Hamiltonian matrix and consequently increases computational costs. The optimized effective potential (OEP) method which constructs a local potential from the nonlocal HF exchange energy can be employed to circumvent such a numerical burden. Then, one is able to use the framework of a conventional Kohn–Sham (KS) DFT method but that a local exchange potential is replaced by an orbital-dependent exact exchange (EXX) potential. For practical purposes, the Krieger–Li–Iafrate (KLI) approximation,19–23 the localized HF method,24–26 and the common energy denominator approximation27,28 have been developed to implement EXX in a cost-effective manner.
MC methods require virtual orbitals in addition to occupied orbitals. KS orbitals obtained from EXX may show similar or better performance for application to MC methods than HF orbitals. In our previous work, we investigated the features of KLI orbitals through comparison to HF orbitals and conventional KS orbitals obtained from local density approximation (LDA) and generalized gradient approximation (GGA).29 Since the KLI potential has been derived from the HF exchange term, occupied orbitals of KLI are similar to those of HF in terms of energy and shape. However, their virtual orbitals have no such similarity. KLI virtual orbitals are the result of an n-electron system as usual KS orbitals and thus their energies are relatively closer to vertical excitation energies.29–31 In contrast, HF yields virtual orbitals of an (n + 1)-electron system and thus their energies are regarded as electron affinities. In addition, the KLI potential has the correct −1/r asymptotic behaviour, while LDA and GGA potentials exponentially decay due to self-interaction errors.29,32 As a result, the KLI potential well describes Rydberg-like states with a number of bound virtual orbitals, whereas HF or conventional KS orbitals have few bound states.29 In fact, KLI orbitals are relatively closer to the so-called exact KS orbitals.29–31 Therefore, we expect that these distinct features of KLI orbitals certainly offer benefits for excited state calculations using MC methods.
There have been preceding research studies on MC methods using KS orbitals. For instance, the accurate excitation energies of atoms and small molecules could be obtained using (multi-reference) configuration interaction (CI) methods.33–39 Gutlé et al. reported that a coupled-cluster singles and doubles method using approximated OEP orbitals produced quantitatively similar correlation energies for atoms compared to the HF version.40 CI with configurations obtained from constrained DFT described various excited state properties of molecules in a qualitatively correct manner, where KS theory fails.41
It should be noted that the aforementioned KS-MC methods are based on atom-centred basis sets. Yanai et al. devised the linear response TD-HF method using multiresolution multiwavelet basis sets.42 However, the extension of such an approach to double or higher excitations will be an intractable task due to the increased dimensionality of response function accordingly. In this work, we, for the first time, developed a CI method based on real-space numerical grids using the traditional matrix approach, which can be straightforwardly extended to higher levels. For comparison, we used KLI, GGA, and HF orbitals to build a reference configuration. Specifically, the CI code includes only single excitations as a prototype and was implemented in our KS-DFT code that uses Lagrange-sinc functions (LSFs) as a basis set. We already reported the details of our KS-DFT code and its accuracy for ground state calculations of molecules in comparison to the results of widely-used Gaussian basis sets.29,43 Here, we briefly explain the features of the LSFs as a basis set and the KLI approximation, and then describe details of the CIS implementation using LSFs. We compared between KLI-, GGA-, and HF-CIS results for excited state calculations of molecules and finally draw conclusions with future outlook on the extension of the present CI method to double and higher excitations.
Method
Lagrange-sinc functions as a basis set
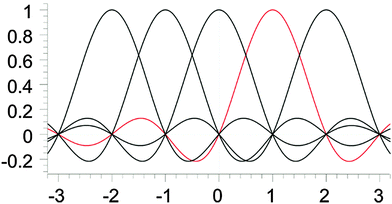
A sinc function localized on a grid point xi (e.g., the red curve in Fig. 1) is given bywhere h is a scaling factor. The roots of a sinc function form a set of grid points with uniform spacing h. Sinc functions localized on those grid points have the following intriguing attributes: cardinality and orthonormality written as
respectively. In fact, there is a family of functions, namely the Lagrange functions that share the above two attributes. Therefore, sinc functions localized on grid points with uniform spacing h are called the Lagrange-sinc functions (LSFs), while the grid is named as the Lagrange-sinc mesh. For more details of the Lagrange functions, we refer to ref. 44 and 45.
The LSFs can be used as a basis set to represent HF or KS orbitals;
| Lsincijk(x,y,z) ≡ Lsinci(x)Lsincj(y)Lsinck(z). |
Due to the cardinality of LSFs, the matrix of any local potential v(r) has non-zero values only in its diagonal elements;
Since LSFs are analytically differentiable, the matrix elements of the kinetic energy operator can also be obtained analytically;
where for the x-direction as an example, we have
It should be noted that the overlap matrix between LSFs is an identity matrix due to the orthonormality of LSFs.
LSFs apparently have beneficial features for application in electronic structure calculations. Compared to the finite difference method which shares the same uniform grid, LSFs guarantee more accurate kinetic energy thanks to the analytic expression for derivatives. However, the use of pseudopotentials is essential for cost-effective calculations. We have implemented a KS-DFT code using LSFs as a basis set with norm-conserving pseudopotentials.43 Our previous work showed that accuracy of the Lagrange-sinc basis set can be systematically improved for atomization energies, ionization energies, electron affinities, and polarizabilities of atoms and molecules. In particular, we demonstrated that it is suitable to describe highly diffuse and polarized orbitals. For more details of implementation and its accuracy, we refer to ref. 43.
Krieger–Li–Iafrate approximation
The KLI approximation has been regarded as a practical approach to obtain a local EXX potential. We implemented this method in our code and addressed the distinct features of KLI orbitals compared to HF or conventional LDA/GGA orbitals.29 Here, we provide a brief review on the KLI approximation but for more details we refer to ref. 23 and 29.The HF exchange energy, EHFx, can be written as
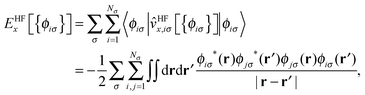 | (1) |
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) HFx,iσ is the HF exchange potential operator, which can be formulated by rearranging eqn (1) as follows:
HFx,iσ is the HF exchange potential operator, which can be formulated by rearranging eqn (1) as follows: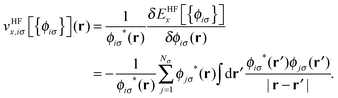 | (2) |
where
![[v with combining overline]](https://www.rsc.org/images/entities/i_char_0076_0305.gif) HFx,iσ ≡ 〈ϕiσ|
HFx,iσ ≡ 〈ϕiσ|![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) HFx,iσ|ϕiσ〉 and
HFx,iσ|ϕiσ〉 and ![[v with combining overline]](https://www.rsc.org/images/entities/i_char_0076_0305.gif) KLIx,iσ ≡ 〈ϕiσ|
KLIx,iσ ≡ 〈ϕiσ|![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) KLIx,iσ|ϕiσ〉. It should be noted that unlike the original OEP integral equation, the KLI potential can be obtained using simple linear algebra with only occupied orbitals.19,20
KLIx,iσ|ϕiσ〉. It should be noted that unlike the original OEP integral equation, the KLI potential can be obtained using simple linear algebra with only occupied orbitals.19,20
CIS based on Lagrange-sinc functions
We implemented a CIS method using KS orbitals in our code. We use a Slater determinant composed of ground state KS orbitals, |Φ0〉, as a reference configuration. Then, we performed CIS calculations almost in the same manner by the traditional HF-CIS method. For instance, a single excitation configuration |Φai〉 can be generated by promoting one electron from an occupied orbital ϕi to a virtual orbital ϕa. Because we use numerical grid methods and pseudopotentials, the generation of single excitation configurations should be carried out within an active orbital space which includes only valence orbitals in the occupied space and a finite number of virtual orbitals truncated by an energy threshold. It should also be noted that KS orbitals are not the eigenfunctions of the Fock operator and thus unlike the HF-CI method, Brillouin's theorem does not hold for namely the KS-CI method as shown in eqn (3).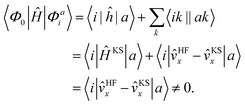 | (3) |
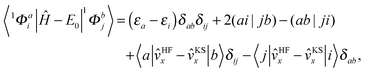 | (4) |
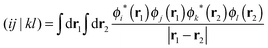 | (5) |
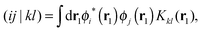 | (6) |
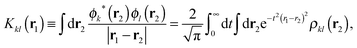 | (7) |
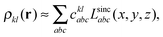 | (8) |
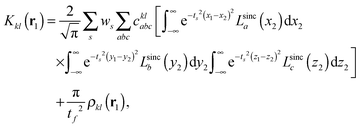 | (9) |
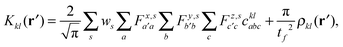 | (10) |
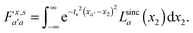 | (11) |
Calculation details
We performed a series of CIS calculations to obtain the excitation energies of H2, formaldehyde, formamide, and benzene. The bond length of H2 was set to 1.5 Bohr, while the geometries of the other molecules were obtained from ref. 52 and 53. For comparison, we used both KS-CIS and HF-CIS methods with various basis sets. KS orbitals for CIS calculations have been calculated using the KLI exchange-only potential and the PBE54 exchange–correlation potential. Because virtual orbitals are more diffuse than occupied orbitals, their energies and shapes would be more sensitive to the choice of basis set than those of occupied orbitals. Therefore, we studied the effects of simulation box size and grid spacing on CIS results. Also, we investigated the dependence of the CIS results on active space size that is denoted by the notation, (n-electrons, m-orbitals), used in conventional post-HF methods.We used our KS-DFT code to obtain KLI and PBE orbitals. To perform HF-CIS calculations using a numerical grid basis set, we first obtained HF orbitals from the Octopus program,7 which uses the finite difference method, and then put them in our code for the remaining calculations. We applied an identical grid setting with a sphere-shape simulation box and identical norm-conserving pseudopotentials at the PBE level55 to obtain KLI, PBE, and HF orbitals. We also carried out HF-CIS calculations using (aug)-cc-pVNZ (N = D, Q) basis sets as implemented in the Gaussian 09 package56 and compared the results with those of the grid basis sets. All orbital figures were drawn with the isovalue of 0.014.
Results
Energy convergence
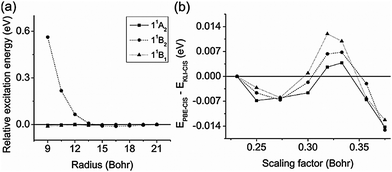
We first investigated the convergence of CIS excitation energies as a function of the radius of a spherical simulation box and the scaling factor h. As a test set, we used the three valence excitation energies of formaldehyde (11A2, 11B2, and 11B1) obtained from KLI-CIS with the active space (12,24).Hereafter, all calculations were done using a spherical simulation box with the radius of 15.0 Bohr and the scaling factor of 0.3 Bohr.
Excitation energies from KLI-, PBE-, and HF-CIS
We compared the excitation energies of formaldehyde, benzene, formamide, and hydrogen molecules obtained from KLI-, PBE-, and HF-CIS methods.Fig. 3 shows the convergence of CIS excitation energies as a function of active space size with respect to the best known values computed by multireference methods (see the caption of Table 2). Fig. 3(a) shows that the absolute deviations of PBE- and KLI-CIS excitation energies for formaldehyde readily converge to certain values with small deviations (<0.05 eV) as more than 30 virtual orbitals are included in the active space, whereas the HF-CIS results converge slowly (see Tables S1 and S2, ESI† for the complete data). We extended the convergence test of active space size for formaldehyde, benzene, formamide, and hydrogen molecules. In Fig. 3(b), the mean absolute deviation (MAD) values of PBE- and KLI-CIS converge rapidly, while that of HF-CIS converges slowly, implying that KS-CIS requires a smaller active space than HF-CIS for the same accuracy.
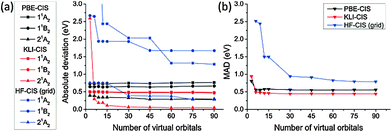 | ||
| Fig. 3 (a) The convergence of the excitation energies of formaldehyde obtained from PBE-, KLI- and HF-CIS as a function of the number of virtual orbitals in the active space. (b) The convergence of the mean absolute deviation (MAD) of the three valence excitation energies for four molecules (see Table 2). The reference values were obtained from ref. 52 and 53 (see the caption of Table 2). All values were calculated using radius = 15.0 Bohr and scaling factor h = 0.3 Bohr. | ||
More intriguingly, the results of each method converge to different values. It is understandable by considering that the ground state determinants from each method are not orthogonal to each other and hence their CIS spaces span different subspaces of a given Hilbert space. Therefore, the accuracy of truncated CI methods should depend on the reference configuration obtained from ground state calculations. Fig. 3(b) demonstrates that KLI provides better reference configurations than PBE and HF.
From the convergence test in Fig. 3, we chose the active spaces shown in Table 1 for more detailed study on the individual excited states of each molecule in the following sections. In Table 1, the active space names, “45”, “6”, and “3”, denote the number of virtual orbitals in the given active space. In the case of “45”, the conventional expressions for the active spaces of formaldehyde, benzene, formamide, and hydrogen molecules correspond to (12,51), (30,60), (18,54), and (2,46), respectively. For comparison, the active spaces for Gaussian basis sets are also given in Table 1.
| 45 | 6 | 3 | aug-cc-pVQZ | aug-cc-pVDZ | cc-pVQZ | cc-pVDZ | |
|---|---|---|---|---|---|---|---|
| a The active space sizes are denoted by (n-electrons, m-orbitals). | |||||||
| Formaldehyde | (12,51) | (12,12) | (12,9) | (16,252) | (16,64) | (16,170) | (16,38) |
| Benzene | (30,60) | (30,21) | (30,18) | (42,752) | (42,192) | (42,510) | (42,114) |
| Formamide | (18,54) | (18,15) | (18,12) | (24,378) | (24,96) | (24,255) | (24,57) |
| Hydrogen molecule | (2,46) | (2,7) | (2,4) | (2,92) | (2,18) | (2,60) | (2,10) |
| Excited state | Best estimation | HF-CIS (grid) | HF-CIS (Gaussian) | KLI-CIS | PBE-CIS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 45 | 6 | 3 | aug-cc-pVQZ | aug-cc-pVDZ | cc-pVQZ | cc-pVDZ | 45 | 6 | 3 | 45 | 6 | 3 | ||||
| a The “Best estimation” means the best known values computed by multireference methods which were obtained from ref. 52 and 53 for benzene, formaldehyde, and formamide, and from ref. 57–59 for hydrogen molecule. “45”, “6”, and “3” denote the size of active space used for each molecule (Table 1). For details, see the text. HF-CIS (Gaussian) means the HF-CIS results obtained using the Gaussian 09 package with Dunning basis sets. We note that all occupied and virtual orbitals of each molecule were used for CIS calculations using the Gaussian 09 package. Mean absolute deviations were calculated with respect to the “Best estimation” values. | ||||||||||||||||
| Formaldehyde | 11A2 | n → π* | 3.88 | 5.91 | 9.23 | 9.50 | 4.51 | 4.49 | 4.52 | 4.48 | 4.37 | 4.38 | 4.38 | 4.62 | 4.62 | 4.61 |
| 11B1 | σ → π* | 9.10 | 10.78 | 11.75 | 11.77 | 9.64 | 9.69 | 9.65 | 9.66 | 9.58 | 9.59 | 9.59 | 9.73 | 9.74 | 9.74 | |
| 21A1 | π → π* | 9.30 | 9.68 | 10.05 | 10.05 | 9.43 | 9.49 | 9.62 | 9.95 | 9.36 | 9.59 | 11.89 | 9.59 | 9.69 | 9.69 | |
| Benzene | 11B1u | π → π* | 6.54 | 6.79 | 11.53 | 11.59 | 6.15 | 6.16 | 6.20 | 6.35 | 6.71 | 6.89 | 6.93 | 6.82 | 6.98 | 7.02 |
| 11B2u | π → π* | 5.08 | 6.29 | 11.78 | 11.81 | 5.99 | 6.00 | 6.04 | 6.18 | 6.17 | 6.14 | 6.14 | 6.18 | 6.14 | 6.14 | |
| 11E1u | π → π* | 7.13 | 7.35 | 7.59 | 11.69 | 7.51 | 7.78 | 8.08 | 8.36 | 7.40 | 7.45 | 9.49 | 7.14 | 7.15 | 9.57 | |
| Formamide | 11A′′ | n → π* | 5.63 | 7.98 | 8.51 | 8.52 | 6.45 | 6.44 | 6.49 | 6.48 | 6.40 | 6.42 | 6.42 | 6.79 | 6.81 | 6.81 |
| 21A′ | π → π* | 7.39 | 8.90 | 9.33 | 9.40 | 8.43 | 8.46 | 8.74 | 9.09 | 8.47 | 8.64 | 8.94 | 8.82 | 8.91 | 9.17 | |
| 31A′ | π → π* | — | 9.26 | 9.59 | 9.62 | 8.87 | 8.89 | 10.04 | 11.07 | 8.90 | 9.23 | 9.61 | 9.28 | 9.39 | 11.15 | |
| Hydrogen molecule | B1Σu+ | σg → σu | 12.32 | 12.52 | 13.31 | 13.31 | 12.28 | 12.25 | 12.89 | 13.56 | 12.27 | 12.36 | 12.65 | 12.33 | 12.37 | 12.38 |
| EF1Σg+ | σg → σg | 12.79 | 12.66 | 13.06 | 13.06 | 12.65 | 12.72 | 15.76 | 21.43 | 12.58 | 12.66 | 12.66 | 12.62 | 12.69 | 12.69 | |
| C1Πu | σg → πu | 12.85 | 12.91 | 13.51 | — | 13.62 | 15.39 | 20.56 | 39.89 | 12.64 | 12.70 | 12.70 | 12.63 | 12.86 | 12.86 | |
| Mean absolute deviation | 0.91 | 2.51 | — | 0.53 | 0.72 | 1.56 | 3.98 | 0.44 | 0.49 | 0.94 | 0.55 | 0.56 | 0.81 | |||
To understand such differences, we invoke the features of KLI, PBE, and HF orbitals. As learned from our previous work,29 the energy gaps between occupied and virtual orbitals from KLI are relatively closer to vertical excitations. PBE orbital energies are overall upshifted compared to those of KLI, but their energy gaps are similar to those of KLI. However, HF has substantially large energy gaps. Furthermore, HF virtual orbitals are much more diffuse than KLI and PBE counterparts. As shown in eqn (4), CIS adds the energy correction from the two-centre integrals between single excitation configurations to the corresponding orbital energy gap. Therefore, KLI-CIS readily gives accurate excitation energies even with small correction from the two-centre integral, while HF-CIS needs large corrections. As a result, as long as we use the same size of active space, KLI-CIS will give us more accurate results than HF-CIS.
The comparison between aug-cc-pVDZ and cc-pVQZ manifests the importance of diffuse basis functions to obtain accurate excitation energies. For grid basis sets, the accuracy for diffuse states can be systematically tuned by controlling the size of the simulation box.43 If a sufficiently large simulation box is used, grid basis sets may perform better for diffuse states than Gaussian basis sets. In Table 2, however, the MADs of the grid-based HF-CIS are larger than those of aug-cc-pVNZ. This can be understood from the fact that the active space in the grid-based HF-CIS is much smaller than that in the Gaussian basis sets [cf.Fig. 3(b)].
We also found that the excitation energies from KS-CIS are relatively insensitive to the size of active space compared to HF-CIS. For example, the MAD of HF-CIS decreases by 1.60 eV as the active space size increases from “6” to “45”, whereas that of KS-CIS decreases by 0.05 eV for the same change. This is another important aspect for practical applications.
In order to further uncover the difference between KS-CIS and HF-CIS, we closely examine individual excitations of each molecule especially by focusing on their CIS coefficients and corresponding orbital shapes in the following section.
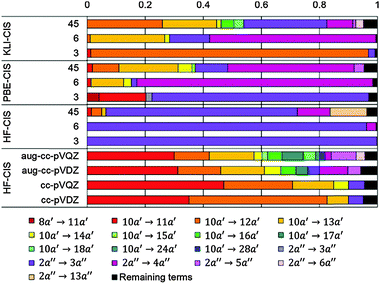
CIS coefficients of individual excitations
A singlet excited state wavefunction using CIS can be written aswhere c0 is zero in the case of HF-CIS by virtue of Brillouin's theorem (for Brillouin's theorem of KS-CIS, we refer to ref. 29). Due to the normalization condition of wavefunction, the coefficients satisfy the following relation.
Thus, without loss of generality, we investigated the absolute squared values of CIS coefficients to analyse individual excitations instead of the coefficients themselves.
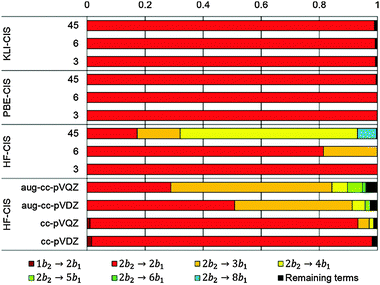
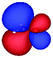
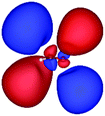
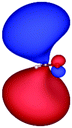
Table 3 shows those orbitals involved in the excitation to the 11A2 state. The highest occupied molecular orbitals (HOMOs) denoted as 2b2 from KLI and HF have very similar shapes at least to the naked eye. In contrast, as stressed above, their virtual orbitals are substantially different in shape and size. In particular, the 2b1 orbital from KLI is more compact than those from HF. Moreover, the energy gap (4.19 eV) between 2b2 and 2b1 from KLI is much smaller, that is closer to the best estimation value (3.88 eV), than those from HF (13.17 or 13.64 eV). As a result, HF-CIS needs to add more virtual orbitals with the same symmetry to improve accuracy (Fig. 4). In general, KLI gives a number of bound virtual orbitals with negative energies and compact shapes, whereas HF produces unbound virtual orbitals with positive energies and diffuse shapes.29 Thus, the excitation to the 11B1 and 21A1 states also shows similar trends as depicted in Fig. S3 (ESI†).
| 2b2 (HOMO) | 2b1 | 3b1 | 4b1 | |
|---|---|---|---|---|
| a The values below each orbital figure indicate corresponding orbital energies (unit: eV). | ||||
| KLI (h = 0.3 Bohr) |

|
|

|
|
| −11.83 | −7.64 | −2.89 | −1.44 | |
| HF (h = 0.3 Bohr) |

|
|
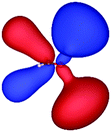
|
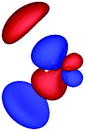
|
| −12.03 | 1.14 | 1.19 | 2.76 | |
| HF (aug-cc-pVQZ) |

|
|

|

|
| −12.13 | 1.51 | 3.12 | 4.82 | |
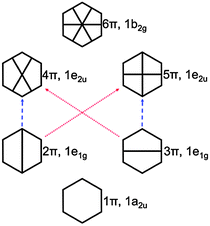 | ||
| Fig. 5 π orbital diagram of benzene. The red and blue dashed arrows indicate the excitations to the 11B2u and 11B2u states, respectively (see also Fig. S4, ESI†). | ||
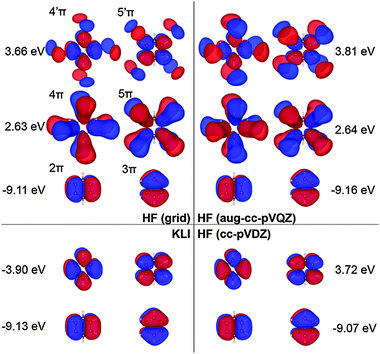 | ||
| Fig. 7 Selected π molecular orbitals and corresponding energies of benzene calculated using KLI and HF. | ||
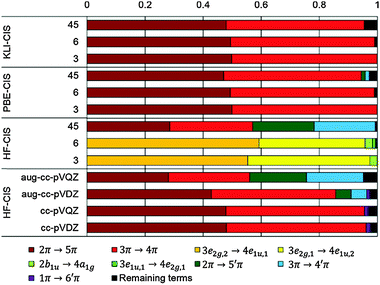
In the case of KS-CIS, the 11B1u state is represented by mainly two π → π* excitations as shown in Fig. 6: 2π → 5π and 3π → 4π. In constrast, HF-CIS (grid) has no such excitation characteristics within the small active spaces (“3” and “6”), leading to the large deviations in the excitation energies (Table 2). For the active space “45”, more configurations especially involving nπ → n′π excitations in addition to the two π → π* excitations contribute to the corresponding excitation energy, and then the excitation energy of HF-CIS (grid) is comparable to that of KS-CIS. This indicates that for HF-CIS (grid) the two configurations are not sufficient to achieve a similar accuracy to KLI-CIS and thus more configurations should be added. A similar trend is observed for the Gaussian basis sets.
Fig. 7 shows the orbitals involved in the excitation to the 11B1u state. Like the case of formaldehyde, KLI and HF have similar occupied π orbitals (2π,3π), but considerably different virtual orbitals with strong dependence on the basis set size. The relatively small Gaussian basis set (cc-pVDZ) gives compact 4π and 5π orbitals that are similar to those from KLI. However, HF with a larger basis set such as aug-cc-pVQZ or numerical grid yields much more diffuse orbitals. KLI (5.23 eV) has smaller energy gaps between (2π,3π) and (4π,5π) than HF (grid: 11.74 eV and aug-cc-pVQZ: 11.8 eV). Therefore, HF-CIS (“45” and aug-cc-pVQZ) compensates the large energy gap by adding the contribution from the 2π → 5′π and 3π → 4′π excitations to the 2π → 5π and 3π → 4π excitations.
Conclusions
Real-space numerical grid methods are promising for accurate electronic structure calculations of large molecules, because their computational costs can be reduced through massive parallelization as well as linear scaling algorithms and their accuracy can be systematically improved toward complete basis set limits. In particular, those methods are inherently good for excited state calculations in which large basis sets including diffuse functions are essential. We developed a CIS method using Lagrange-sinc functions localized on a uniform grid. The nonlocal HF exchange operator reduces the sparsity of the Hamiltonian matrix, giving rise to high computational costs. Therefore, the traditional HF-based CIS seems impractical for grid-based methods. Instead, we proposed a KS-based CIS in particular with an exact exchange potential. KLI and PBE orbitals as well as HF orbitals were used to build a reference configuration and their relative accuracy for excitation energies of molecules has been assessed.Since the grid-based method uses an iterative diagonalization scheme, the size of active space should be determined in a way to compromise between computational costs and accuracy. For our test molecules with the active space using all occupied orbitals and 45 virtual orbitals, KLI-CIS shows smallest deviations (MAD = 0.44 eV) in excitation energy calculations with respect to the known best estimation values, followed by PBE-CIS (MAD = 0.55 eV), while HF-CIS (MAD = 0.91 eV) causes significantly large deviations. We also found that excitation energies from KLI-CIS are less sensitive to the size of active space, whereas the results from HF-CIS are very sensitive. Such differences originate from the unique features of KLI orbitals; HF-like occupied orbitals, but KS-like virtual orbitals. Compared to HF, KLI yields many bound virtual orbitals with more compact shapes and smaller energy gaps between occupied and virtual orbitals. As a result, for H2, benzene, and formaldehyde, KLI-CIS needs mostly a specific single configuration for non-degenerate excitations and multiconfigurations for degenerate excitations, whereas HF-CIS demands multiconfigurations for any excitation. However, for formamide, both KLI-CIS and HF-CIS require multiconfigurations to obtain accurate excitation energies which may be due to its multiple-excitation character. Consequently, the size of active space should be cautiously determined as a convergence parameter especially for HF-CIS.
The size of active space is directly related to computational costs of multiconfiguration methods. For CI singles and doubles (CISD) calculations, the number of configurations is approximately proportional to Nocc2Nvir2. Based on the CIS results in this work, we expect that KLI-CISD should be more cost-effective because it needs smaller active space to achieve similar accuracy than HF-CISD. For benzene as an example, KLI-CISD with the active space “45” and “6” have 315 and 2644 times smaller number of configurations than HF-CISD with aug-cc-pVQZ, respectively (cf.Table 1). Hence, we believe that KLI-based multiconfiguration methods combined with numerical grid basis sets will provide a new promising way for accurate electronic structure calculations of large systems.
Acknowledgements
This work was supported by Basic Science Research Programs (NRF-2012R1A1A1004154), the EDISON Program (NRF-2012M3C1A6035359), and the MIR center (No. 20090083525) through the NRF funded by the Korea government [MSIP]. The authors would like to acknowledge the support from KISTI supercomputing center for computing time (KSC-2013-C1-028). W.Y.K. is also grateful for financial support from Chung-Am Fellowship and EWon assistant professorship.Notes and references
- I. Samish, C. M. MacDermaid, J. M. Perez-Aguilar and J. G. Saven, Annu. Rev. Phys. Chem., 2011, 62, 129–149 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- S. Martí, J. Andrés, V. Moliner, E. Silla, I. Tuñón and J. Bertrán, Chem. Soc. Rev., 2008, 37, 2634–2643 RSC.
- L. Wang, G. Nan, X. Yang, Q. Peng, Q. Li and Z. Shuai, Chem. Soc. Rev., 2010, 39, 423–434 RSC.
- V. Nanda and R. L. Koder, Nat. Chem., 2010, 2, 15–24 CrossRef CAS PubMed.
- N. Lambert, Y.-N. Chen, Y.-C. Cheng, C.-M. Li, G.-Y. Chen and F. Nori, Nat. Phys., 2013, 9, 10 CrossRef CAS PubMed.
- X. Andrade, J. Alberdi-Rodriguez, D. A. Strubbe, M. J. T. Oliveira, F. Nogueira, A. Castro, J. Muguerza, A. Arruabarrena, S. G. Louie, A. Aspuru-Guzik, A. Rubio and M. A. L. Marques, J. Phys.: Condens. Matter, 2012, 24, 233202 CrossRef PubMed.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- S. Mohr, L. E. Ratcliff, P. Boulanger, L. Genovese, D. Caliste, T. Deutsch and S. Goedecker, J. Chem. Phys., 2014, 140, 204110 CrossRef PubMed.
- C. K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119 CrossRef PubMed.
- J. I. Iwata, D. Takahashi, A. Oshiyama, T. Boku, K. Shiraishi, S. Okada and K. Yabana, J. Comput. Phys., 2010, 229, 2339–2363 CrossRef CAS PubMed.
- L. Kronik, A. Makmal, M. L. Tiago, M. M. G. Alemany, M. Jain, X. Huang, Y. Saad and J. R. Chelikowsky, Phys. Status Solidi, 2006, 243, 1063–1079 CrossRef CAS PubMed.
- F. Bottin, S. Leroux, A. Knyazev and G. Zérah, Comput. Mater. Sci., 2008, 42, 329–336 CrossRef CAS PubMed.
- E. Di Napoli and M. Berljafa, Comput. Phys. Commun., 2013, 184, 2478–2488 CrossRef CAS PubMed.
- Y. Zhou and Y. Saad, Numer. Algorithm., 2008, 47, 341–359 CrossRef.
- A. Sitt, L. Kronik, S. Ismail-Beigi and J. R. Chelikowsky, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 054501 CrossRef.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- A. J. Cohen, P. Mori-Sanchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 101 CrossRef CAS.
- J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 5453–5458 CrossRef.
- J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Lett. A, 1990, 148, 470–474 CrossRef.
- J. B. Krieger, Y. Li and G. J. Iafrate, in Density Functional Theory, ed. E. K. U. Gross and R. M. Dreizler, Springer US, 1995, pp. 191–216 Search PubMed.
- G. J. Iafrate and J. B. Krieger, J. Chem. Phys., 2013, 138, 094104 CrossRef CAS PubMed.
- F. Della Sala and A. Görling, J. Chem. Phys., 2001, 115, 5718–5732 CrossRef CAS PubMed.
- F. Della Sala and A. Görling, J. Chem. Phys., 2002, 116, 5374–5388 CrossRef CAS PubMed.
- F. Della Sala and A. Görling, J. Chem. Phys., 2003, 118, 10439–10454 CrossRef CAS PubMed.
- O. Gritsenko and E. J. Baerends, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 042506 CrossRef.
- M. Grüning, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2002, 116, 6435–6442 CrossRef PubMed.
- J. Kim, K. Hong, S. Choi and W. Y. Kim, Bull. Korean Chem. Soc., 2015, 36, 998–1007 Search PubMed.
- R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432–4441 CrossRef CAS.
- E. J. Baerends, O. V Gritsenko and R. van Meer, Phys. Chem. Chem. Phys., 2013, 15, 16408–16425 RSC.
- Y.-H. Kim, M. Stadele and R. M. Martin, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 3633–3640 CrossRef CAS.
- S. Grimme, Chem. Phys. Lett., 1996, 259, 128–137 CrossRef CAS.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645 CrossRef CAS PubMed.
- P. Bour, Chem. Phys. Lett., 2001, 345, 331–337 CrossRef CAS.
- L. Veseth, J. Chem. Phys., 2001, 114, 8789 CrossRef CAS PubMed.
- T. Hupp, B. Engels, F. Della and G. Andreas, Chem. Phys. Lett., 2002, 360, 175–181 CrossRef CAS.
- T. Hupp, B. Engels and A. Görling, J. Chem. Phys., 2003, 119, 11591 CrossRef CAS PubMed.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- C. Gutlé, J. L. Heully, J. B. Krieger and A. Savin, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 012504 CrossRef.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- T. Yanai, R. J. Harrison and N. C. Handy, Mol. Phys., 2005, 103, 413–424 CrossRef CAS PubMed.
- S. Choi, K. Hong, J. Kim and W. Y. Kim, J. Chem. Phys., 2015, 142, 094116 CrossRef PubMed.
- D. Baye, Phys. Status Solidi, 2006, 243, 1095–1109 CrossRef CAS PubMed.
- K. Varga and S. T. Pantelides, Phys. Status Solidi, 2006, 243, 1110–1120 CrossRef CAS PubMed.
- L. Genovese, T. Deutsch, A. Neelov, S. Goedecker and G. Beylkin, J. Chem. Phys., 2006, 125, 074105 CrossRef PubMed.
- S. A. Losilla, D. Sundholm and J. Jusélius, J. Chem. Phys., 2010, 132, 024102 CrossRef CAS PubMed.
- J. Jusélius and D. Sundholm, J. Chem. Phys., 2007, 126, 094101 CrossRef PubMed.
- H.-S. Lee and M. E. Tuckerman, J. Chem. Phys., 2008, 129, 224108 CrossRef PubMed.
- G. Beylkin and L. Monzón, Appl. Comput. Harmon. Anal., 2005, 19, 17–48 CrossRef PubMed.
- M. M. Mehine, S. A. Losilla and D. Sundholm, Mol. Phys., 2013, 111, 2536 CrossRef CAS PubMed.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 129, 104103 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- THEOS, http://theossrv1.epfl.ch/Main/Pseudopotentials, accessed Jan. 19, 2015.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- W. Kolos and L. Wolniewicz, J. Chem. Phys., 1965, 43, 2429–2441 CrossRef CAS PubMed.
- W. Kolos and L. Wolniewicz, J. Chem. Phys., 1969, 50, 3228 CrossRef CAS PubMed.
- L. Wolniewicz and K. Dressler, J. Chem. Phys., 1988, 88, 3861 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: KLI virtual orbitals of formaldehyde; CIS excitation energies and CIS coefficients for three valence excited states of formaldehyde, benzene, formamide, and hydrogen molecules. See DOI: 10.1039/c5cp00352k |
| ‡ Jaewook Kim and Kwangwoo Hong contributed equally to this work. |
| This journal is © the Owner Societies 2015 |