Open Access Article
Open Access ArticlePrediction of a stable associated liquid of short amyloidogenic peptides
Jurriaan A.
Luiken
and
Peter G.
Bolhuis†
*
van 't Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: P.G.Bolhuis@uva.nl
First published on 12th March 2015
Abstract
Amyloid fibril formation is believed to be a nucleation-controlled process. Depending on the nature of peptide sequence, fibril nucleation can occur in one step, straight from a dilute solution, or in multiple steps via oligomers or disordered aggregates. What determines this process is poorly understood. Since the fibril formation kinetics is driven by thermodynamic forces, knowledge of the phase behavior is crucial. Here, we investigated the phase behavior of three short peptide sequences of varying side-chain hydrophobicity. Replica exchange molecular dynamics simulations of a mid-resolution model indicate that the weakly hydrophobic peptide forms fibrils directly from solution, whereas the most hydrophobic peptide forms a dense liquid phase before crystallizing into ordered fibrils at low temperatures. For the medium hydrophobic peptide we found evidence of a novel additional transition to a liquid phase consisting of clusters of aligned peptides, implying a three-step nucleation process. We tested the robustness of this prediction by applying Wertheim's theory and statistical associating fluid theory to a hard-sphere model dressed with isotropic and anisotropic attractions. We found that the ratio of interaction strengths strongly affects the phase behavior, and under certain conditions indeed gives rise to a stable polymerized liquid phase. The peptide clusters in the associated liquid tend to be slow and long-lived, which may give the oligomer droplet more time to act as a toxic oligomer, before turning into a fibril.
1 Introduction
The aggregation of freely soluble peptides and proteins into well-organized amyloid fibrils occurs both in vivo and in vitro, and, perhaps surprisingly, even for globular proteins.1 Besides its important role in the neurodegenerative diseases such as Alzheimer's, Parkinson's, etc.,2–5 peptide self-assembly plays a functional role in organisms such as bacteria6,7 and, moreover, may be utilized in the fabrication of nanostructures, medicine and other biotechnological applications.8,9 The mechanism of amyloid fibril formation is poorly understood, but is of considerable interest because early amyloid aggregates are considered to be toxic.4 Experimental data10 point to a common shared mechanism of nucleation and growth for the self-assembly of peptides. Unfortunately, current techniques cannot provide detailed molecular information on nucleation and growth processes. Intermediate oligomeric species may be too short-lived11 and many independent stochastic events contribute to the self-assembly,12 thereby complicating a comprehensive description. Molecular simulations can give insight into such processes, and aggregation of various peptides has been successfully studied in the past using a variety of CG models and sampling techniques.13–25 Yet, investigation of the fibril nucleation process itself remains difficult due to the long time scales involved.As a simple first approximation to the aggregation process, the classical nucleation theory (CNT)26–28 describes the formation of a (spherical) critical nucleus of an ordered (fibril) phase within the monomer solution. However, recent studies29,30 have shown that the kinetics of amyloid fibril formation cannot be fully described by CNT. Indeed, fibril growth may occur along the fibril axis through monomer addition, as well as along the thickening axis through protofilament association,31 whereas CNT assumes the growth of nuclei to be strictly one-, two- or three-dimensional. The growth direction is a direct consequence of the interplay of directional and non-directional interactions.32,33 For peptides, the combination of a non-directional interaction, due to hydrophobic forces, and directional interactions such as hydrogen bonding, leads to a complex non-classical nucleation behavior. The relative strength of these interactions is determined by the amino acid sequence, and strongly affects the followed nucleation pathway. For weakly hydrophobic peptides, aggregation is dominated by bond formation and peptides may fibrilize directly in solution, a process known as one-step nucleation (1SN). In 1SN growth occurs via the dock–lock mechanism,34–36 where monomers first dock to the end of a growing fibril, and then lock into place. For strongly hydrophobic peptides, fibril formation is preceded by the hydrophobic collapse of peptides into a disordered oligomer, known as two-step nucleation (2SN). In the 2SN pathway, peptides associate into droplets to form nuclei from which further crystallization takes place.37 The free energy barrier associated with the formation of such nuclei is a function of the energy of monomer activation to an aggregation prone state,38,39 the nucleus surface and the free energy change associated with transferring a monomer from the bulk to the nucleus. Short peptides with a low activation energy form one-dimensional chains, and as such have a low free energy barrier for the formation of nuclei.
The nucleation behavior is in first place determined by the thermodynamics of the system; therefore we focus here on the phase behavior of amyloidogenic peptides. This has two aims: first, to provide a basis for understanding the kinetic nucleation process. Second, we examine the possibility of an associated liquid phase, an additional intermediate between a disordered oligomer and the fully formed fibril, in which chains of aligned peptides coexist in a liquid droplet. Employing replica exchange molecular dynamics (REMD) of a coarse-grained (CG) protein model we provide evidence for such an associated peptide liquid as a stable intermediate during two-step nucleation. We studied three segments of varying hydrophobic strength, each of which follow a different aggregation pathway to the fibril state, namely GNNQQNY from the Sup35 protein, the hydrophobic core segment KLVFFAE of Amyloid-β, and VEALYL from the human insulin B chain. As expected, we found that with increasing hydrophobicity the fibril mechanism switches from one- to two-step nucleation. However, in the 2SN pathway, where monomers readily collapse into disordered oligomers due to hydrophobic interactions, we found evidence for a transition to a liquid of associated peptides. The aligned peptide clusters in the associated fluid state have slow intrinsic dynamics, making them long lived. It is well known that oligomeric intermediates are involved in several neurodegenerative diseases, such as Alzheimer's disease;40 therefore this finding might be relevant for understanding the toxicity of early amyloid oligomers.
Since the protein force field is coarse-grained, it is important to assess the robustness of our prediction. We do so by establishing the phase behavior of a simple patchy particle model employing Wertheim's theory41–44 and statistical associating fluid theory.45,46 This allows for the prediction of the phase diagrams as a function of the hydrophobic strength. We found that the phase diagrams predicted are in agreement with the SN1 and SN2 nucleation scenarios. Moreover, we are able to identify within the theory the existence of the associated liquid state, for certain conditions and interaction strengths, thus showing that the findings obtained using the coarse-grained protein model are robust.
The remainder of the paper is organized as follows. In Section 2, we introduce the simulation details, as well as the statistical mechanical theory. In Section 3, we first present and discuss the results of the REMD simulations, followed by a discussion of the predicted phase diagrams. We end with concluding remarks.
2 Methods
2.1 Simulations
As full atom simulations of fibril formation are notoriously difficult to converge, we conducted REMD simulations using the CG model by Bereau and Deserno.47 This model offers full sequence specificity and is of higher resolution than most other models, and includes the important back-bone hydrogen bonds. Furthermore, the model is not biased towards any particular secondary structure, but parameterized such that both α-helical and β-sheet structures are equally accessible, thereby making the model more generic and realistic. This is partly achieved by including dipole interactions between carbonyl and amide groups involved in bonding, which are often ignored in CG models.48 Finally, the model is publicly available and easy to implement within the ESPResSo49 MD package.We employed the ESPResSo MD package using Langevin dynamics with a 2 fs timestep. N ∈ {8,12,20} peptides were solvated in a cubic, periodic simulation box with lengths L = 36.8, 42.2 and 50.0 Å, respectively, corresponding to a concentration of ∼0.25 M for all systems. The chosen concentration is sufficiently low for a thermodynamically stable gas phase at high temperatures, but high enough to avoid diffusion problems. For GNNQQNY we distributed 24 replicas from 240 to 600 K using a geometric spacing method,50 optimized the temperature distribution aiming for a flat acceptance rate of 25%, and simulated for 480 ns with 6 ps between each exchange. For both VEALYL and KLVFFAE we distributed 16 replicas between 240 and 420 K. Initiating from the solution, we simulated for 2 μs with increased swap time (50 ps) to grant the system more time to relax between exchanges. We analyzed the equilibrated data using weighted histogram analysis (WHAM),51 WORDOM52 for a nematic order parameter analysis53 and home-written scripts for cluster analysis.
To obtain more insight into the early steps of aggregation we study the dimerization process of each peptide, by performing additional REMD simulations for a small system (L = 34.8 Å) containing two peptides. We spaced 16 replicas geometrically between 240 and 420 K, set the replica swap time to 10 ps and simulated for 800 ns in total.
2.2 Statistical mechanical theory
Given two types of interactions: (i) an isotropic attraction due to side chain hydrophobicity and (ii) a directional interaction that favors alignment of strands in a β-sheet, we turn to a highly simplified model that captures the essential physics of the peptide self-assembly process, and study this model using statistical associating fluid theory (SAFT).45,46 We start by viewing the peptides as simple hard spheres of diameter σ with two patches on opposite sides. The hydrophobic interactions of peptides in water are known to decay with distance as the van der Waals-dispersion force.54 Therefore we employ a van der Waals potential to represent the hydrophobic interaction between peptides: | (1) |
 to favor alignment of strands in a β-sheet:
to favor alignment of strands in a β-sheet: | (2) |
 | (3) |
Here, εhb is the interaction strength due to hydrogen bonding and σhb is the hydrogen bond equilibrium distance. For the orientational part of the potential we follow the model of Kern and Frenkel,55 where a patch A with orientational unit vector êA on particle i interacts with a patch B with orientation êB on particle j if the inter-particle vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij intersects both patches:
ij intersects both patches:
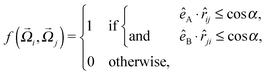 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij denotes the unit vector along
ij denotes the unit vector along ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij and α is the solid angle of a patch (Fig. 1, left). By applying SAFT we can derive all thermodynamic properties of a system containing such particles. SAFT was developed using Wertheim's thermodynamic perturbation theory (WTPT),41–44 and has been successful in describing the phase behavior of a wide range of fluids at high and low pressures.56,57 In first-order WTPT, the free energy contributions from the isotropic interaction potential and the presence of bonding sites may be added as perturbations to the Helmholtz free energy density of a hard-sphere fluid:
ij and α is the solid angle of a patch (Fig. 1, left). By applying SAFT we can derive all thermodynamic properties of a system containing such particles. SAFT was developed using Wertheim's thermodynamic perturbation theory (WTPT),41–44 and has been successful in describing the phase behavior of a wide range of fluids at high and low pressures.56,57 In first-order WTPT, the free energy contributions from the isotropic interaction potential and the presence of bonding sites may be added as perturbations to the Helmholtz free energy density of a hard-sphere fluid:| f = fhs + fhp + fhb, | (5) |
 | ||
Fig. 1 Left: two patches of solid angle α with orientation êA and êB interact when ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij intersects both patches. Right: schematic of the hydrogen bonding (hb) and hydrophobic interactions (hp) in the solid, similar to the lattice model described in ref. 31. ij intersects both patches. Right: schematic of the hydrogen bonding (hb) and hydrophobic interactions (hp) in the solid, similar to the lattice model described in ref. 31. | ||
For the hard-sphere reference state we use the Carnahan–Starling approximation,58 for which the free energy density and pressure are given by
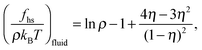 | (6) |
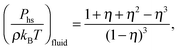 | (7) |
 | (8) |
 | (9) |
where the equilibrium constant for the reaction between two non-bonded patches is equal to 2Δ, and is defined by
 | (10) |
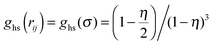 is the contact value of the reference hard-sphere fluid distribution function in the Carnahan–Starling approximation. The term in brackets denotes an angle average of the Mayer f function over all orientations
is the contact value of the reference hard-sphere fluid distribution function in the Carnahan–Starling approximation. The term in brackets denotes an angle average of the Mayer f function over all orientations  and
and  , which becomes a prefactor equal to the fraction of orientations at which the particles can interact, given by the product of the interacting surface fraction of each particle:
, which becomes a prefactor equal to the fraction of orientations at which the particles can interact, given by the product of the interacting surface fraction of each particle:  . Note that we only integrate over the attractive contributions to the hydrogen bonding potential. Using the law of mass action,
. Note that we only integrate over the attractive contributions to the hydrogen bonding potential. Using the law of mass action, | (11) |
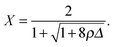 | (12) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) :
: | (13) |
While polymerization is taken care of by SAFT, fibrillization is not. Here we model the fibril as an FCC crystal phase, for which we use a simple equation of state (EOS) for hard-sphere FCC crystals obtained from the Lennard-Jones–Devonshire cell theory.61–63 The free energy density and pressure are given by
 | (14) |
 | (15) |
 is the FCC close-packing fraction. Following Daanoun et al.,64 we add free energy density perturbations by calculating the average interaction with the nearest neighbors in the solid:
is the FCC close-packing fraction. Following Daanoun et al.,64 we add free energy density perturbations by calculating the average interaction with the nearest neighbors in the solid: | (16) |
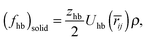 | (17) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ij = (ηcp/η)1/3 is the reduced nearest-neighbor distance in the solid. To mimic bonding interactions in a fibril, we assume that particles will always be hydrogen bonded with the two nearest-neighbors along the fibril axis; therefore zhb = 2 and
ij = (ηcp/η)1/3 is the reduced nearest-neighbor distance in the solid. To mimic bonding interactions in a fibril, we assume that particles will always be hydrogen bonded with the two nearest-neighbors along the fibril axis; therefore zhb = 2 and  . As opposed to the fluid, where hydrophobic interactions in our model are considered fully isotropic, peptides in the solid will interact primarily along the fibril axis and the thickening axis. This view of the fibril is similar to the lattice models used in ref. 31, 65 and 66. For the hydrophobicity solid perturbations we therefore include nearest-neighbor interactions only in two dimensions, i.e. zhp = 6 in the plane of an FCC lattice (Fig. 1, right).
. As opposed to the fluid, where hydrophobic interactions in our model are considered fully isotropic, peptides in the solid will interact primarily along the fibril axis and the thickening axis. This view of the fibril is similar to the lattice models used in ref. 31, 65 and 66. For the hydrophobicity solid perturbations we therefore include nearest-neighbor interactions only in two dimensions, i.e. zhp = 6 in the plane of an FCC lattice (Fig. 1, right).
To compare with the theoretical predictions we must determine the relative strength λ of the hydrogen bonding and hydrophobic interactions. Although we cannot determine the exact value of λ for peptides, we can estimate their hydrophobicity by comparing the side-chain interaction strength parameters used in the force field. These parameters are listed in Table 1. GNNQNNY is by far the least hydrophobic peptide according to the force field parameters, and VEALYL is slightly more hydrophobic than KLVFFAE.
| Segment | Residue | ||||||
|---|---|---|---|---|---|---|---|
| GNNQQNY | GLY(2.13) | ASN(1.70) | ASN(1.70) | GLN(1.85) | GLN(1.85) | ASN(1.70) | TYR(4.31) |
| KLVFFAE | LYS(1.00) | LEU(7.76) | VAL(5.40) | PHE(7.58) | PHE(7.58) | ALA(2.73) | GLU(1.36) |
| VEALYL | VAL(5.40) | GLU(1.36) | ALA(2.73) | LEU(7.76) | TYR(4.31) | LEU(7.76) | |
3 Results and discussion
3.1 Dimerization
Although the main aim of this paper is to study the formation of larger clusters and their conversion into a fibril, we first investigate the thermodynamics of dimerization as it precedes the formation of larger clusters in both the gas and liquid phases. Previous studies aiming at elucidating the dimerization process used REMD with other force fields,67 as well as path sampling techniques.68
Fig. 2 shows the heat capacity at constant volume, CV, versus temperature, obtained from the dimer REMD simulations. A peak in the CV is a good indication of a phase transition. The 2-peptide GNNQNNY system undergoes a dimerization transition at around 261 K, whereas KLVFFAE forms its dimer around 300 K. The dimerization transition of VEALYL is initiated at low temperatures, but the full transition is likely to occur at even lower temperatures (T < 240 K). Fig. 3 shows the Landau free energy F = −kBTln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (
(![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) for each replica, obtained from the normalized probability distribution
) for each replica, obtained from the normalized probability distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (
(![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) for the distance between the peptides' center of mass
) for the distance between the peptides' center of mass ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . The three dimers prefer to align in a parallel fashion (see insets in Fig. 3), which in previous work47 has been partly attributed to the lack of explicit electrostatic interactions in the CG model at the N- and C-termini. At low temperature the average interstrand distance in the GNNQQNY and VEALYL dimers is approximately 5 Å, while for KLVFFAE the strands are in slightly closer proximity at 4 Å, as the hydrophobic phenylalanine residues keep the center of the chains closely together. At low temperatures VEALYL exhibits two different metastable states (Fig. 3b). The state corresponding to the leftmost minimum consists of fully aligned VEALYL peptides. In the other state peptides are tightly bound via hydrophobic and hydrogen-bond interactions between the strongly hydrophobic C-terminal leucine and tyrosine residues, whereas the rest of the chain forms no hydrogen bonds. For high temperatures we notice that the KLVFFAE and VEALYL peptides remain in close proximity (
. The three dimers prefer to align in a parallel fashion (see insets in Fig. 3), which in previous work47 has been partly attributed to the lack of explicit electrostatic interactions in the CG model at the N- and C-termini. At low temperature the average interstrand distance in the GNNQQNY and VEALYL dimers is approximately 5 Å, while for KLVFFAE the strands are in slightly closer proximity at 4 Å, as the hydrophobic phenylalanine residues keep the center of the chains closely together. At low temperatures VEALYL exhibits two different metastable states (Fig. 3b). The state corresponding to the leftmost minimum consists of fully aligned VEALYL peptides. In the other state peptides are tightly bound via hydrophobic and hydrogen-bond interactions between the strongly hydrophobic C-terminal leucine and tyrosine residues, whereas the rest of the chain forms no hydrogen bonds. For high temperatures we notice that the KLVFFAE and VEALYL peptides remain in close proximity (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ∼ 7 Å), even in the unbound state, whereas for GNNQQNY the chains fully dissociate (
∼ 7 Å), even in the unbound state, whereas for GNNQQNY the chains fully dissociate (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ∼ 17 Å). Strong non-directional side-chain interactions of VEALYL and KLVFFAE (Table 1) keep the peptide in a disordered aggregate state even at high temperatures, while the GNNQQNY dimer, lacking such strong interactions, dissolves completely. This also explains the relatively strong heat capacity peak of GNNQQNY, as the potential energy difference between the bound and solvated states is far greater than between the bound and disordered aggregate states. In Appendix A we provide an additional free energy analysis using in-register contacts and the nematic order parameter.
∼ 17 Å). Strong non-directional side-chain interactions of VEALYL and KLVFFAE (Table 1) keep the peptide in a disordered aggregate state even at high temperatures, while the GNNQQNY dimer, lacking such strong interactions, dissolves completely. This also explains the relatively strong heat capacity peak of GNNQQNY, as the potential energy difference between the bound and solvated states is far greater than between the bound and disordered aggregate states. In Appendix A we provide an additional free energy analysis using in-register contacts and the nematic order parameter.
 | ||
| Fig. 2 Heat capacity versus temperature for the dimers of GNNQQNY (green line), VEALYL (red line) and KLVFFAE (black line). | ||
Clearly, the side-chain hydrophobicity plays an important role in the formation of small oligomers. How this influences the fibril formation will be discussed in the following sections by performing the REMD simulations with 8 or more peptides.
3.2 The GNNQQNY peptide
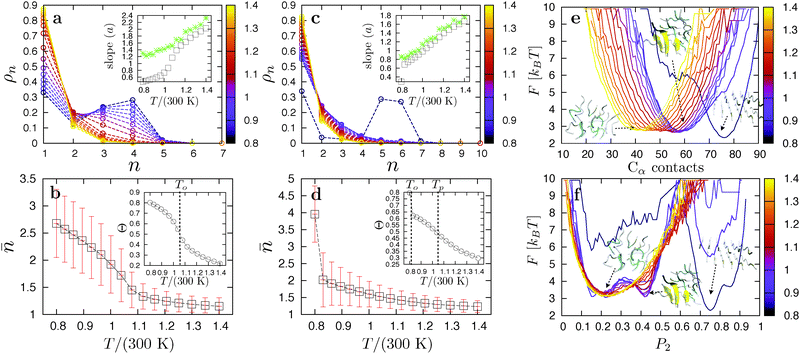
Fig. 4a shows the heat capacity curves from the REMD simulation for the weakly hydrophobic GNNQQNY peptides for N ∈ {8,12,20}. The observed single peak corresponds to fibril formation directly from the soluble phase (snapshot 2 in Fig. 4), in agreement with the findings in ref. 47. At the ordering temperature To, solvated GNNQQNY peptides dock to each other through their tyrosine residues. As the overall hydrophobic interactions are not strong enough to induce a hydrophobic collapse into a liquid state, the peptides lock into place and form fibrils in one step (1SN) from solution. These fibrils consist of one parallel aligned layer of peptides in the case of N = 8, and two parallel layers for N = 12 and 20 (snapshot 1). Analysis of the replica flow (see Appendix B), a measure of the diffusivity of replicas through temperature space, indicates that there is very little exchange of replicas at the phase boundary. We attribute this to a large jump in potential energy between the soluble and fibril phases. The small shoulder in the heat capacity peak for N = 20 in Fig. 4a is an indication of this poor flow.3.3 The VEALYL peptide
The aggregation thermodynamics of the strongly hydrophobic VEALYL peptides is markedly different. Here, hydrophobic interactions drive the collapse of freely soluble peptides to a disordered liquid phase (snapshot 4 in Fig. 4) at the condensation temperature Tc/(300 K) ≫ 1.4, outside the replica temperature interval. The peak in the heat capacity curves in Fig. 4b represents the ordering transition at temperature To from the disordered liquid to fibril phase. At the ordering temperature (and the used concentration), VEALYL nucleation is thus likely to proceed via a condensation-ordering mechanism (2SN).33 We report a good flow of replicas around the transition temperature, in large part due to the liquid phase lying closer in energy to both the fibril and soluble phases. Around the ordering temperature To, VEALYL peptides dock through their hydrophobic C-terminal leucine residues and form fibrils consisting of multiple parallel β-sheets, hooked into each other to form a hydrophobic core along the fibril axis (snapshot 3).Focusing on the transition from the disordered oligomer to a fibril, we performed a cluster analysis. Two peptides belong to the same cluster if they form at least five contacts, defined as two Cα atoms from different peptides being closer than 5.5 Å. Fig. 5a and b show the cluster size distributions ρn and average cluster size ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , respectively, for all replicas of the 12-peptide system. The degree of association increases as the temperature is lowered, and the average cluster size in the liquid slowly grows until the fibril is fully formed at To. If the cluster distribution is truly exponential, ln
, respectively, for all replicas of the 12-peptide system. The degree of association increases as the temperature is lowered, and the average cluster size in the liquid slowly grows until the fibril is fully formed at To. If the cluster distribution is truly exponential, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρn should be linear with an ideal slope a, where a = −ln(1 − 1/
ρn should be linear with an ideal slope a, where a = −ln(1 − 1/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ). We may arrive at this expression from the calculation of
). We may arrive at this expression from the calculation of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) using an exponential distribution ρn ∝ e−an:
using an exponential distribution ρn ∝ e−an:
 | (18) |
 as a function of temperature. This quantity is useful to characterize the transition to a polymerized phase, as it passes through an inflection point at the polymerization temperature.69,70 However, for VEALYL the aggregation fraction (Fig. 5b inset) does not reach an inflection point above the ordering temperature To, and no such transition is observed.
as a function of temperature. This quantity is useful to characterize the transition to a polymerized phase, as it passes through an inflection point at the polymerization temperature.69,70 However, for VEALYL the aggregation fraction (Fig. 5b inset) does not reach an inflection point above the ordering temperature To, and no such transition is observed.
3.4 The KLVFFAE peptide
KLVFFAE peptides are slightly less hydrophobic than VEALYL, with the strongest hydrophobic residues (phenylalanine) in the middle of the segment rather than at the end. Again, strong side-chain interactions drive the collapse of peptides into disordered droplets (snapshot 7 in Fig. 4) at high temperatures Tc/(300 K) ≫ 1.4. For N = 8 and 12 we identify two peaks in Fig. 4c: a strong peak corresponding to an ordering transition to a one- and two-layered fibril (snapshot 5) at low temperatures, respectively, and an additional peak around Tp ∼ 315 K corresponding to a polymerization transition. The molecular structure of a polymerized droplet, which consists of multiple randomly oriented β-sheets, is shown in snapshot 6. There is a clear separation between the transitions, indicating that this is a thermodynamically stable intermediate in the aggregation pathway of KLVFFAE peptides. The heat capacity per peptide CV/N around the polymerization transition is shown in the inset of Fig. 4. For the 20-peptide system only the polymerization transition is shown, as the simulations did not converge to the fibril structure. We stress that the polymerization transition is very far away from the condensation transition Tc/(300 K) ≫ 1.4, so that it is not likely to be related to critical fluctuations.We now take a closer look at the ordering and polymerization transition for N = 12 using a cluster and order parameter analysis. Fig. 5d shows the average cluster size as a function of temperature for N = 12. As with VEALYL the association inside the droplet increases gradually with decreasing temperature. However, the ordering temperature for KLVFFAE is much lower, and the aggregation fraction, plotted in the inset, passes through an inflection point at Tp > To. The cluster size distributions in Fig. 5c appear exponential for all but the lowest temperature (corresponding to the fibril). Indeed, the slope a plotted in the inset shows almost ideal behavior. The heat capacity peak at Tp in Fig. 4d is therefore the result of a continuous polymerization transition from a disordered droplet. From the cluster analysis we obtain the free energy curves F = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (NCα) as a function of the total number of Cα contacts, where
(NCα) as a function of the total number of Cα contacts, where ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (NCα) is the normalized probability of being in a state with NCα contacts. The results are plotted for the 12-peptide KLVFFAE system in Fig. 5e. The free energy curves show a gradual increase of the minimum from 41 contacts for the disordered oligomer at 420 K, to 59 for the fully polymerized oligomer at 249 K. A strong shift to 76 contacts occurs at To, corresponding to the formation of a two-layered fibril.
(NCα) is the normalized probability of being in a state with NCα contacts. The results are plotted for the 12-peptide KLVFFAE system in Fig. 5e. The free energy curves show a gradual increase of the minimum from 41 contacts for the disordered oligomer at 420 K, to 59 for the fully polymerized oligomer at 249 K. A strong shift to 76 contacts occurs at To, corresponding to the formation of a two-layered fibril.
Another parameter to quantify order inside aggregates is the nematic order parameter  , where N is the number of peptides, ẑi represents the unit vector pointing from the second to second-to-last Cα atom on peptide i, and
, where N is the number of peptides, ẑi represents the unit vector pointing from the second to second-to-last Cα atom on peptide i, and ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) is the director.53,71 The value of P2 ranges from
is the director.53,71 The value of P2 ranges from  to 1, specifying complete disorder and order, respectively. The free energy curves are calculated in the same way as above, and are shown for the 12-peptide KLVFFAE system in Fig. 5f. The free energy plots reveal a shift of the minimum from 0.23, matching the expectation value
to 1, specifying complete disorder and order, respectively. The free energy curves are calculated in the same way as above, and are shown for the 12-peptide KLVFFAE system in Fig. 5f. The free energy plots reveal a shift of the minimum from 0.23, matching the expectation value 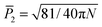 (≈0.23 for N = 12) for a random array of 12 peptides,72 to 0.42 for the polymerized phase, and 0.90 for the fibril.
(≈0.23 for N = 12) for a random array of 12 peptides,72 to 0.42 for the polymerized phase, and 0.90 for the fibril.
These findings support the existence of a stable intermediate polymerized phase consisting of multiple aligned peptides packed disorderly within the droplet. The aggregation behavior of KLVFFAE can be summarized as follows: when cooling a dilute peptide solution at high temperature, non-directional hydrophobic interactions induce condensation to a liquid. Meanwhile, hydrogen bond interactions drive the association of peptides in the liquid, yielding a polymerized phase with increased order below the polymerization temperature. Close to the ordering temperature To, these peptide clusters are kinetically trapped and must first dissolve into the disordered liquid and reassemble to form the fibril. Interestingly, as there is no preference for an anti-parallel or parallel arrangement during association,73 the presence of a polymerization transition could imply an increased likelihood of misfolded states during the nucleation pathway. Peptide association in the oligomer droplets may therefore slow down the nucleation process considerably.
3.5 Theoretical phase diagrams
As the force field calculations are specific, our aim is to show that the above results are a robust consequence of the interplay between non-directional hydrophobic interactions and directional hydrogen bond interactions. To do so, we consider a simple Kern–Frenkel-like model55 in which every peptide is thought of as an attractive hard-sphere of diameter σ dressed with two patches that interact with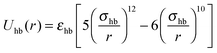 when their inter-particle vector intersects both patches, and Uhb = 0 otherwise. Here, r is the inter-particle distance, and εhb and σhb are the hydrogen bonding strength and the equilibrium distance, respectively. The hydrophobic interactions are modeled as
when their inter-particle vector intersects both patches, and Uhb = 0 otherwise. Here, r is the inter-particle distance, and εhb and σhb are the hydrogen bonding strength and the equilibrium distance, respectively. The hydrophobic interactions are modeled as  , where εhp is the interaction strength. The ratio of interaction strengths λ = εhb/εhp is the governing parameter for the phase behavior. We applied statistical associating fluid theory (SAFT)45,46 in conjunction with Wertheim's first-order thermodynamic perturbation theory (WTPT)41–44 to derive the thermodynamic properties of this system. The Carnahan–Starling equation of state (EOS) provides the hard-sphere fluid reference. The fibril phase is approximated as an FCC crystal, for which the reference EOS is given by simple cell theory.61–63 See Section 2.2 for a detailed description of the theory. We set a wide patch angle α = π/6 and bonding distance εhb = 1.08. Given these values, the gas–liquid coexistence curve always becomes metastable with respect to the solid in the limit of high λ, i.e. it meets the condition that weakly hydrophobic peptides will follow the 1SN pathway.
, where εhp is the interaction strength. The ratio of interaction strengths λ = εhb/εhp is the governing parameter for the phase behavior. We applied statistical associating fluid theory (SAFT)45,46 in conjunction with Wertheim's first-order thermodynamic perturbation theory (WTPT)41–44 to derive the thermodynamic properties of this system. The Carnahan–Starling equation of state (EOS) provides the hard-sphere fluid reference. The fibril phase is approximated as an FCC crystal, for which the reference EOS is given by simple cell theory.61–63 See Section 2.2 for a detailed description of the theory. We set a wide patch angle α = π/6 and bonding distance εhb = 1.08. Given these values, the gas–liquid coexistence curve always becomes metastable with respect to the solid in the limit of high λ, i.e. it meets the condition that weakly hydrophobic peptides will follow the 1SN pathway.
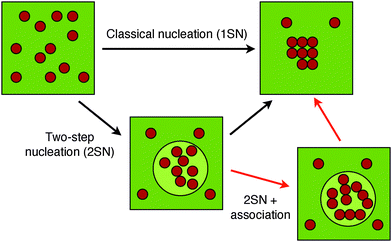
The phase diagrams for peptides with increasing λ ∈ {0.5,2.5,5} as a function of the reduced number density ρ* = ρσ3 and reduced temperature T* = kBT/εhb are plotted in Fig. 6a–c. The phase diagrams show a gas–liquid binodal characteristic of a van der Waals fluid, and a liquidus and a solidus along which the liquid and solid coexist. Here, the gas phase (g) corresponds to a dilute peptide solution, the liquid phase (l) to the disordered aggregate state induced by hydrophobicity, and the solid (s) to the fibril. Also shown is the polymerization line signifying the inflection point of the aggregation fraction Θ versus temperature. Note that varying λ changes only the relative hydrophobic strength of the peptide; the contribution from the backbone hydrogen bonding is considered constant. The phase diagrams for λ < 0.6 (Fig. 6a) show a stable gas–liquid binodal. For temperatures below the critical point a solution prepared in the coexistence region will separate into a gas-like dilute monomer solution in equilibrium with a disordered liquid phase. Following the arrows in the diagram, further cooling will result in the transition to a fibril at the triple point. Therefore, in line with the REMD results for VEALYL, strong hydrophobic interactions promote a two-step condensation-ordering mechanism. In contrast, for much weaker hydrophobicities (λ > 4.2, Fig. 6c), the phase diagrams show a shift of the liquidus to lower densities. As with GNNQQNY, the hydrophobic interactions are too weak to drive the formation of a liquid. The gas–liquid coexistence curve is now metastable (dotted lines) with respect to the solid, and nucleation of fibrils proceeds in one step directly from solution. An interesting phase diagram for peptides of intermediate hydrophobicity (0.6 < λ < 4.2) is shown in Fig. 6b. Here, the gas–liquid binodal is stable with respect to the liquidus, but in the liquid phase region we now find an additional transition to a polymerized liquid (l*). This polymerization transition is continuous, and is identified by an inflection point in the aggregation fraction at the polymerization temperature Tp, as well as by a peak in the heat capacity CV,70 both of which have been identified in our REMD simulations of the KLVFFAE peptide. Thus, given that the non-directional interactions are strong enough to drive the hydrophobic collapse of monomers into a liquid, yet are comparable to the bonding strength, a condensation–polymerization-ordering transition is the preferred nucleation pathway. While the theory is very simple, the prediction is robust against perturbations such as the precise interactions, the patch width and the topology of the solid phase. The effect of λ on the aggregation behavior of the three main transition temperatures Tc, Tp and To is summarized in Fig. 6d. Starting from a soluble phase, we enter the phase diagrams at ρ* = 0.15. Following the arrows in Fig. 6a we then reach the coexistence curves at the corresponding transition temperatures. For λ < 0.6 condensation takes place at high temperatures, and since here Tp < To the liquid will crystallize before it can polymerize. Decreasing the isotropic interaction strength to 0.6 < λ < 4.2, we found that both the condensation and ordering temperature drop substantially. In fact, the ordering temperature is now lower than the polymerization temperature, and the ordering step is preceded by a condensation step and a polymerization step. Lastly, for λ > 4.2 the gas–liquid binodal becomes metastable and there is no longer a triple point, allowing fibrils to form directly from solution.
4 Conclusions
We predicted the phase behavior of three short amyloidogenic peptides with varying hydrophobic strength. The weakly hydrophobic GNNQQNY shows a direct transition from the soluble (gas) phase to the fibril state, in line with the 1SN nucleation scenario. The hydrophobic VEALYL peptide, in contrast, shows behavior consistent with the 2SN route: first a collapse to a compact cluster, followed by reorganization into a fibril. Surprisingly, our simulations indicate that the KLVFFAE peptide, with a hydrophobicity between that of VEALYL and GNNQQNY, exhibits a previously unrecognized associated liquid phase in which small clusters of aligned peptides coexist. This result cannot follow from studying the dimerization process alone, and requires the simulation of larger systems. Analysis of a simple patchy particle model using statistical associating fluid theory shows that such a behavior is robust, and is a consequence of the interplay between non-directional hydrophobic interactions and directional hydrogen bond interactions. Since both simple and more complex CG models predict the associated fluid phase to be stable under certain conditions, it is possible and even likely that a fibril nucleation process following the 2SN route, under conditions that the fibril is thermodynamically stable, will first encounter the associated phase, before crystallizing into a fibril (see Fig. 7).In the newly predicted associated liquid phase the aligned clusters are kinetically trapped and must either dissolve into the disordered liquid and reassemble, or diffuse and align with other clusters, to form the fibril. Both processes are slow and may considerably slow down the dynamics of nucleation. This suggests that, once formed, these polymerized oligomer droplets can be relatively long lived, and may therefore prolong the existence of early oligomers in the nucleation process. Because early oligomers are considered toxic,4,40 the polymerized phase may be relevant for understanding the early stages of neurological disorders such as Alzheimer's disease. To further understand the implications of the polymerized phase, one should also take into account the environment of the oligomers. For instance, the presence of molecular crowders may have broad implications for the kinetics and thermodynamics of aggregation.74,75 Previous crystallography studies,76 supported by simulations,77 have shown that for several short amyloidogenic peptides, including GNNQQNY, multiple forms of close-packed amyloid structures exist. Thus, a comprehensive description of aggregation should include effects such as molecular crowding and oligomer polymorphism. How exactly the fibril nucleation occurs dynamically remains an open question. We intend to address this question with path sampling technology in future work.
Appendix A: Additional free energy plots
We calculated two additional order parameters related to dimerization: the in-register contacts NCα, where a contact is defined as two Cα atoms on the same residue of different peptides being in closer proximity than 5.5 Å; and the nematic order parameter P2 (see Section 3.4).The free energy curve for GNNQQNY in Fig. 8a increases steeply with the number of in-register contacts at high temperatures, indicative of a solvated state. For temperature T/(300 K) = 0.8 (240 K) the free energy curve for VEALYL shows a metastable minimum at NCα ≈ 5 contacts (Fig. 8c). As described in the main text, the full transition to the dimer is likely to occur below 240 K. The free energy curves for KLVFFAE (Fig. 8e) contain a single minimum for all temperatures, corresponding to a disordered aggregate state at high temperatures, and to a parallel aligned arrangement at low temperatures. The nematic order parameter P2 (Fig. 8b, d and f) is randomly distributed for high temperatures, as expected, and becomes narrowly distributed around P2 ∼ 0.9, corresponding to the aligned state.
For completeness, we included plots of the free energy versus total Cα contacts and P2 for the 12-peptide system of GNNQQNY (Fig. 9a and b) and VEALYL (Fig. 9e and f), the cluster size distribution (Fig. 9c) and the average number of contacts of the 12-peptide GNNQQNY system (Fig. 9d). At low temperature we observe a second minimum in the free energy versus P2 in Fig. 9b, which corresponds to an imperfect alignment of the second layer of peptides (inset in Fig. 9c) due to a rotating or sliding motion.
Appendix B: Replica flow
The replica flow f(Ti),78 defined as the fraction of replicas that diffused from the lowest to highest temperature versus the temperature index i, is a measure of the diffusivity of a replica in temperature space plotted from f(T1) = 1 to f(TN) = 0 with N being the number of replicas. We use it here to monitor the reliability of the REMD simulations. Plots of the replica flow are shown in Fig. 10.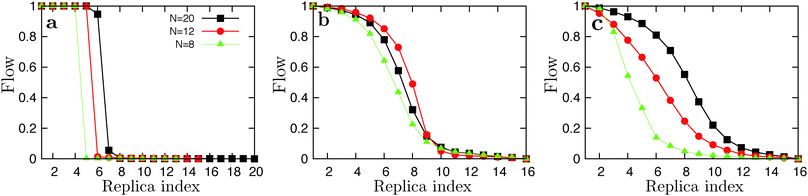 | ||
| Fig. 10 Plots of the replica flow versus index from the low temperature simulations for GNNQQNY (a), VEALYL (b) and KLVFFAE (c). | ||
Using a geometric progression temperature set we report poor replica flows for the GNNQQNY system. We applied the feedback-optimized parallel tempering approach introduced in ref. 78, but in general too few round-trips are made through temperature space within the available computation time to provide sufficient statistics on the flow function for the algorithm to be effective. We then applied the constant-rate method where, using WHAM, we calculated the theoretical acceptance rate based on the energy histograms of the previous simulations and calculated a new temperature distribution, aiming for a flat acceptance rate of 25%. We ended up with fewer replicas over the desired temperature range, and more closely spaced replicas around the transition temperature. For N = 20 GNNQQNY there was, at first, no exchange (flow) at the phase boundary at all, and the measured heat capacity is infinite. To this end, we decreased the temperature interval to fit 20 replica's around the transition temperature, with T1 = 240 and Tf = 363 K, using a geometric progression. The corresponding replica flow is plotted in Fig. 10a (black line). For VEALYL and KLVFFAE a geometric progression of temperatures, in combination with longer swap times (50 ps), was generally sufficient to obtain a good replica flow. For N = 8 KLVFFAE the REMD simulations did not converge to the one-layered fibril structure at low temperatures, but rather to the two-layered fibril which has a higher potential energy. To this end, we initiated simulations from a parallel one-layered fibril for all replicas. Here we find a large difference in potential energy of the one-layered fibril compared to the polymerized droplet, which resulted in a poor flow around the ordering transition (Fig. 10c, green line). The flow of replicas near the polymerization temperatures was good in all cases.
Acknowledgements
This work is part of the research programme VICI 700.58.442, which is financed by the Netherlands Organization for Scientific Research (NWO).References
- F. Chiti and C. M. Dobson, Nat. Chem. Biol., 2009, 5, 15–22 CrossRef CAS PubMed.
- C. Haass and D. J. Selkoe, Nat. Rev. Mol. Cell Biol., 2007, 8, 101 CrossRef CAS PubMed.
- F. Chiti, P. Webster, N. Taddei, A. Clark, M. Stefani, G. Ramponi and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3590 CrossRef CAS.
- F. Chiti and C. M. Dobson, Annu. Rev. Phys. Chem., 2006, 75, 333–366 CAS.
- C. M. Dobson, Protein Pept. Lett., 2006, 13, 219–227 CrossRef CAS.
- L. P. Blanco, M. L. Evans, D. R. Smith, M. P. Badtke and M. R. Chapman, Trends Microbiol., 2012, 20, 66–73 CrossRef CAS PubMed.
- T. P. J. Knowles and M. J. Buehler, Nat. Nanotechnol., 2011, 6, 469–479 CrossRef CAS PubMed.
- R. Mezzenga, P. Schurtenberger, A. Burbidge and M. Michel, Nat. Mater., 2005, 4, 729–740 CrossRef CAS PubMed.
- O. G. Jones and R. Mezzenga, Soft Matter, 2012, 8, 876–895 RSC.
- J. E. Gillam and C. E. MacPhee, J. Phys.: Condens. Matter, 2013, 25, 373101 CrossRef CAS PubMed.
- Y. Li and C. J. Roberts, J. Phys. Chem. B, 2009, 113, 7020–7032 CrossRef CAS PubMed.
- T. P. J. Knowles, D. A. White, A. R. Abate, J. J. Agresti, S. I. A. Cohen, R. A. Sperling, E. J. de Genst, C. M. Dobson and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 14746 CrossRef CAS PubMed.
- P. H. Nguyen and P. Derreumaux, Acc. Chem. Res., 2014, 47, 603–611 CrossRef CAS PubMed.
- P. H. Nguyen and P. Derreumaux, J. Phys. Chem. B, 2013, 117, 5831–5840 CrossRef CAS PubMed.
- J. Nasica-Labouze, M. Meli and P. Derreumaux, PLoS Comput. Biol., 2011, 7, e1002051 CAS.
- A. D. Simone and P. Derreumaux, J. Chem. Phys., 2010, 132, 165103 CrossRef PubMed.
- Y. Lu, P. Derreumaux, Z. Guo, N. Mousseau and G. Wei, Proteins, 2009, 75, 954–963 CrossRef CAS PubMed.
- D. Matthes, V. Gapsys and B. L. de Groot, J. Mol. Biol., 2012, 421, 390–416 CrossRef CAS PubMed.
- M. Mompeán, C. González, E. Lomba and D. V. Laurents, J. Phys. Chem. B, 2014, 118, 7312–7316 CrossRef PubMed.
- A. Srivastava and P. V. Balaji, PLoS One, 2014, 9, e96660 Search PubMed.
- G. Wei, W. Song, P. Derreumaux and N. Mousseau, Front. Biosci., 2008, 13, 5681–5692 CrossRef CAS PubMed.
- B. Barz, D. J. Wales and B. Strodel, J. Phys. Chem. B, 2014, 118, 1003–1011 CrossRef CAS PubMed.
- X. Qi, L. Hong and Y. Zhang, Biophys. J., 2012, 102, 597–605 CrossRef CAS PubMed.
- U. F. Röhrig, A. Laio, N. Tantalo, M. Parrinello and R. Petronzio, Biophys. J., 2006, 91, 3217–3229 CrossRef PubMed.
- G. Favrin, A. Irbäck and S. Mohanty, Biophys. J., 2004, 87, 3657–3664 CrossRef CAS PubMed.
- P. G. Debenedetti, Metastable Liquids, Princeton University Press, Princeton, 1996 Search PubMed.
- Homogeneous Nucleation Theory, Academic Press, NY, 1974 Search PubMed.
- Nucleation: Basic Theory with Applications, Butterworth-Heinemann, Oxford, 2000 Search PubMed.
- R. J. Bingham, L. G. Rizzi, R. Cabriolu and S. Auer, J. Chem. Phys., 2013, 139, 241101 CrossRef CAS PubMed.
- R. Cabriolu, D. Kashchiev and S. Auer, J. Chem. Phys., 2012, 137, 204903 CrossRef PubMed.
- H. D. Nguyen and C. K. Hall, J. Biol. Chem., 2005, 280, 9074–9082 CrossRef CAS PubMed.
- S. Whitelam, Phys. Rev. Lett., 2010, 105, 088102 CrossRef.
- M. Cheon, I. Chang, S. Mohanty, L. M. Luheshi, C. M. Dobson, M. Vendruscolo and G. Favrin, PLoS Comput. Biol., 2007, 3, e173 Search PubMed.
- W. P. Esler, E. R. Stimson, J. M. Jennings, H. V. Vinters, J. R. Ghilardi, J. P. Lee, P. W. Mantyh and J. E. Maggio, Biochemistry, 2000, 39, 6288–6295 CrossRef CAS PubMed.
- P. H. Nguyen, M. S. Li, G. Stock, J. E. Straub and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 111–116 CrossRef CAS PubMed.
- M. Schor, J. Vreede and P. G. Bolhuis, Biophys. J., 2012, 103, 1296–1304 CrossRef CAS PubMed.
- S. Auer, C. M. Dobson, M. Vendruscolo and A. Maritan, Phys. Rev. Lett., 2008, 101, 258101 CrossRef.
- A. M. Morris, M. A. Watzky and R. G. Finke, Biochim. Biophys. Acta, Proteins Proteomics, 2009, 1794, 375–397 CrossRef CAS PubMed.
- C. Frieden and D. W. Goddette, Biochemistry, 1983, 22, 5836–5843 CrossRef CAS.
- D. M. Walsh and D. J. Selkoe, J. Neurochem., 2007, 25, 569–580 Search PubMed.
- M. S. J. Wertheim, J. Stat. Phys., 1984, 35, 19 CrossRef.
- M. S. J. Wertheim, J. Stat. Phys., 1984, 35, 35 CrossRef.
- M. S. J. Wertheim, J. Stat. Phys., 1986, 42, 477 CrossRef.
- M. S. J. Wertheim, J. Stat. Phys., 1986, 42, 459 CrossRef.
- G. Jackson, W. G. Chapman and K. E. Gubbins, Mol. Phys., 1988, 65, 1–31 CrossRef CAS.
- W. G. Chapman, K. E. Gubbins and G. Jackson, Ind. Eng. Chem. Res., 1990, 29, 1709–1721 CrossRef CAS.
- T. Bereau and M. J. Deserno, J. Chem. Phys., 2009, 130, 235106 CrossRef PubMed.
- N. Y. Chen, Z. Y. Su and C. Y. Mou, Phys. Rev. Lett., 2006, 96, 078103 CrossRef.
- H. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174, 704–727 CrossRef CAS PubMed.
- C. Predescu, M. Predescu and C. J. Ciobanu, J. Phys. Chem. B, 2005, 109, 4189 CrossRef CAS PubMed.
- A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1988, 61, 2635 CrossRef CAS.
- M. Seeber, M. Cecchini, F. Rao, G. Settani and A. Caflisch, Bioinformatics, 2007, 23, 2625–2627 CrossRef CAS PubMed.
- M. Cecchini, F. Rao, M. Seeber and A. J. Caflisch, J. Chem. Phys., 2004, 121, 10748–10756 CrossRef CAS PubMed.
- J. Israelacvhili and R. Pashley, Nature, 1982, 300, 341–342 CrossRef.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS PubMed.
- S. Huang and M. Radosz, Ind. Eng. Chem. Res., 1990, 29, 2284 CrossRef CAS.
- I. G. Economou, Ind. Eng. Chem. Res., 2002, 41, 953–962 CrossRef CAS.
- N. F. Carnahan and K. E. J. Starling, J. Chem. Phys., 1969, 51, 635 CrossRef CAS PubMed.
- E. A. Müller and K. E. Gubbins, Ind. Eng. Chem. Res., 2001, 40, 2193 CrossRef.
- F. Sciortino, E. Bianchi, J. F. Douglas and P. Tartaglia, J. Chem. Phys., 2007, 126, 194903 CrossRef PubMed.
- J. E. Lennard-Jones and A. F. Devonshire, Proc. R. Soc. London, Ser. A, 1937, 163, 53 CrossRef CAS.
- J. E. Lennard-Jones and A. F. Devonshire, Proc. R. Soc. London, Ser. A, 1937, 165, 11 Search PubMed.
- J. E. Lennard-Jones and A. F. Devonshire, Proc. R. Soc. London, Ser. A, 1937, 169, 317 CrossRef.
- A. Daanoun, C. F. Tejero and M. Baus, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 2913 CrossRef CAS.
- J. Zhang and M. J. Muthukamar, J. Chem. Phys., 2009, 130, 035102 CrossRef PubMed.
- R. Cabriolu, D. Kashchiev and S. Auer, J. Chem. Phys., 2010, 133, 225101 CrossRef PubMed.
- G. Wei, N. Mousseau and P. Derreumaux, Prion, 2007, 1, 3–8 CrossRef.
- A. S. Reddy, M. Chopra and J. J. de Pablo, Biophys. J., 2010, 98, 1038–1045 CrossRef CAS PubMed.
- S. C. Greer, Adv. Chem. Phys., 1996, 94, 261 CrossRef CAS.
- S. C. Greer, Annu. Rev. Phys. Chem., 2002, 53, 173 CrossRef CAS PubMed.
- M. Cecchini, R. Curcio, M. Pappalardo, R. Melki and A. Caflisch, J. Mol. Biol., 2006, 357, 1306 CrossRef CAS PubMed.
- T. P. Doerr, D. Herman, H. Mathur and P. L. Taylor, Europhys. Lett., 2002, 59, 398 CrossRef CAS.
- F. Baftizadeh, F. Pietrucci, X. Biarnés and A. Laio, Phys. Rev. Lett., 2013, 110, 168103 CrossRef.
- D. C. Latshaw, M. Cheon and C. K. Hall, J. Phys. Chem. B, 2014, 118, 13513–13526 CrossRef CAS PubMed.
- A. V. Martinez, E. Maolepsza, E. Rivera, Q. Lu and J. E. Straub, J. Chem. Phys., 2014, 141, 22D530 CrossRef PubMed.
- M. R. Sawaya, S. Sambashivan, R. Nelson, M. I. Ivanova, S. A. Sievers, M. I. Apostol, M. J. Thompson, M. Balbirnie, J. J. W. Wiltzius, H. T. McFarlane, A. O. Madsen, C. Riekel and D. Eisenberg, Nature, 2007, 447, 453–457 CrossRef CAS PubMed.
- W. M. Berhanu and A. E. Masunov, Biopolymers, 2012, 98, 131–144 CrossRef CAS PubMed.
- H. G. Katzgraber, S. Trebst, D. A. Huse and M. Troyer, J. Stat. Mech.: Theory Exp., 2006, 6, 1742 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2015 |