Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Asymmetric polarization and hysteresis behaviour in ferroelectric P(VDF–TrFE) (76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) 24) copolymer thin films spatially resolved via LIMM†
24) copolymer thin films spatially resolved via LIMM†
T.
Putzeys
* and
M.
Wübbenhorst
*
Dept. of Physics and Astronomy, Soft Matter and Biophysics section, KU Leuven, Leuven, Belgium. E-mail: tristan.putzeys@fys.kuleuven.be; michael.wubbenhorst@fys.kuleuven.be
First published on 17th February 2015
Abstract
The concept of charge-polarization coupling in the ferroelectric copolymer PVDF–TrFE (poly[vinylidene fluoride-co-trifluoroethylene]) has been revisited by employing high resolution (<50 nm) pyroelectric depth profiling (LIMM). By virtue of probing the pyroelectric activity over the film thickness in the presence of a variable, external electrical field, the local ferroelectric response and spatially resolved hysteresis could be obtained. A large asymmetry was found between the positive and negative electrode–polymer interface. Differences in amplitude of polarization, contribution of interface charges and length scale of the polarization-free zone near the electrodes suggest a higher availability of compensation charges at the negative electrode that finally stabilize the local polarization. The resulting asymmetries in the polarization distribution are hence attributed to excess charges as a result of electron injection as a specific charge generation mechanism at the negative electrode.
1 Introduction
The exceptional piezo-, pyro- and ferroelectric properties of PVDF (polyvinylidene fluoride) and its most common copolymer P(VDF–TrFE) (poly[vinylidene fluoride-co-trifluoroethylene]) have stimulated numerous studies for many years that aimed at understanding its structural, morphological and electrical properties.1–6 After application of a high electrical field, PVDF exhibits pyro7,8- and piezoelectric9 properties. PVDF is a semicrystalline polymer consisting of linear chains with the sequence (CH2–CF2), as illustrated in Fig. 1. The difference in electronegativity between the fluorine and hydrogen substituent at opposite sides of the polymer chain results in a large dipole moment oriented perpendicular to the chain direction.10PVDF usually crystallizes in the non-polar α-phase (phase II).11 A conversion into the macroscopically polar β-phase (phase I), which shows ferroelectric properties, is possible by stretching at elevated temperatures12 or by applying a high external electrical field.13 This procedure is not easily applicable in all geometries.
This drawback can be overcome by copolymerizing VDF with the trifluoroethylene (TrFE) monomer resulting in the random copolymer P(VDF–TrFE) that crystallizes in a polar phase similar to the ferroelectric β-phase of a PVDF homopolymer.13 The presence of TrFE increases the size of the unit cell and the inter-planar distance, reducing all intermolecular interactions including dispersion forces and dipole–dipole interactions.14 As a result, both the coercive field and the Curie temperature are decreased depending on the VDF-fraction and thus allow easier electrical poling at room temperature. If the statistical copolymer contains VDF and TrFE at a ratio of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, the highest spontaneous polarization can be achieved,15 a composition that is close to the material studied in this work (76
25, the highest spontaneous polarization can be achieved,15 a composition that is close to the material studied in this work (76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24). The copolymer is semicrystalline and will contain both crystalline (crystallites) and non-crystalline (amorphous) phases, of which the crystalline phase leads to a ferroelectric response.
24). The copolymer is semicrystalline and will contain both crystalline (crystallites) and non-crystalline (amorphous) phases, of which the crystalline phase leads to a ferroelectric response.
Its ferroelectric properties find their origin in the large density of carbon–fluorine dipoles, each having a dipole moment of 1.79 Debye.16 A large spontaneous polarization is achieved by parallel packing of the polymer chains in their all-trans conformation in a polar crystal lattice (β-form crystals). Polarization reversal occurs by collectively rotating chain sequences around their chain axis under a sufficiently high electrical field, the coercive field.1 Though ferroelectricity is a collective phenomenon associated with a long range dipolar order, it should be emphasised that the ferroelectric properties of P(VDF–TrFE) also rely on short-range van der Waals interactions that stabilize the parallel packing and all-trans configuration.17
While the importance of the dipole orientation for the polarization formation was recognized immediately,18 the role of charges proved more difficult to elucidate.19,20,22 Using a series of experiments involving blocking electrodes, the necessity of free charges and charge injection for a remnant polarization in PVDF was demonstrated by Eisenmenger et al.21 A stable polarization in the bulk of PVDF after removing the external electrical field is only achieved when electrically conducting electrodes are used.22 By analysing the gasses emitted during poling the authors concluded that hydrogen and fluorine ions are created and trapped.23 The proposed charge-trapping model assumes the interaction between space charges and dipolar polarization by means of an enhanced trapping probability near polarized crystalline regions, resulting in local charge compensation areas near the crystallite surfaces.22 In this picture, the interplay between dipolar polarization and charge trapping for stabilizing this polarization finally leads to inhomogeneous polarization and space charge distributions in the P(VDF–TrFE) copolymer, especially at low poling fields.24
It is the aim of the present paper to revisit the idea of charge–polarisation coupling in the ferroelectric P(VDF–TrFE) polymer by studying spatial polarization profiles with high spatial resolution in the thickness direction of thin films. For this purpose we have employed a photothermal depth profiling technique known as Laser Intensity Modulation Method (LIMM)25,26 that yields details of the polarization distribution at sub-μm resolution near the metal–polymer interface.
LIMM is a particularly useful method for the investigation of spatially resolved polarization and charge distributions in ferroelectric materials.27,28 The technique probes a sample using thermal waves of different frequencies. The resulting pyroelectric current spectrum can be deconvoluted or transformed to a polarization depth profile.29 In this study we have used thermal waves at frequencies up to 25 MHz, which gives access to an unmatched spatial resolution down to 30 nanometers.
In addition to a higher spatial resolution, we have performed unique in situ LIMM measurements to reveal changes in the polarisation distribution while an external electrical field was applied. In this way, spatially resolved ferroelectric switching could be monitored with simultaneous information about the polarization profile. Finally, in order to disentangle pyroelectric contributions arising from the amorphous (temporarily polarized) fraction and the crystalline fraction, we have studied the influence of the temperature on the polarisation distribution at temperatures from −50 °C, well below the glass transition temperature of P(VDF–TrFE), up to 125 °C, slightly above the Curie temperature.30,31 Variation of these parameters allows for separation and identification of various contributions to the polarization distribution at the electrode interface of P(VDF–TrFE) thin films.
From these polarization profiles we have reconstructed spatially resolved ferroelectric hysteresis curves with special attention to the asymmetry at the polymer–anode and polymer–cathode interface. This pyroelectric reconstruction allows us to overcome potential artefacts associated with the conventional Tower–Sawyer method32 and yields both temperature and field dependent length-scale information on the polarization. Though asymmetry and inhomogeneity in the polarization profile of P(VDF–TrFE) copolymer have been observed earlier,33–35 the current study provides detailed spatially resolved, temperature and in situ field dependent polarisation data, that confirm the prominent role of negative charges, most likely generated by charge injection, as a major ingredient to achieve a stable remnant polarization in PVDF-based ferroelectric polymers.
2 Experimental
2.1 Sample preparation
Thin film samples were prepared in a metal–insulator–metal (MIM) geometry by subsequent vapour deposition and spin coating, resulting in a flat polymer film sandwiched between aluminium films, which serve both as electrodes and optical absorber. The three major preparation steps of the sample are displayed in Fig. 2. The aluminium electrodes are also used to apply the external bias field.After thermal evaporation of a 70 nm aluminium layer onto a clean glass substrate, a 2%, 3% or 4% w/w solution of P(VDF–TrFE) (76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24) dissolved in methyl-ethyl-ketone was spincoated at 1500 rpm, resulting in layers of 1000, 1500 or 2000 nm. The thickness of the polymer was verified by ellipsometry (Sentech LaserPro). Thermal evaporation was again used to apply the top electrode, resulting in the complete sample arrangement sketched in Fig. 2 (right).
24) dissolved in methyl-ethyl-ketone was spincoated at 1500 rpm, resulting in layers of 1000, 1500 or 2000 nm. The thickness of the polymer was verified by ellipsometry (Sentech LaserPro). Thermal evaporation was again used to apply the top electrode, resulting in the complete sample arrangement sketched in Fig. 2 (right).
2.2 Experimental setup
The basic experimental LIMM-setup has widely been described in the literature and comprises, in its original version proposed by Lang and Das-Gupta,26 a HeNe laser, a frequency generator, an opto-acoustic modulator, a current amplifier and a lock-in amplifier. In this work, a state-of-the-art set-up is used, which was specifically designed to extend the frequency range up to 25 MHz, allowing temperature control at low temperatures and the application of an external bias field.All results in this study were obtained using a 10 mW LISA-laser red laser module HL25/M2 modulated with the sine output of a Tektronix AFG3021 frequency generator. The current was amplified using a Femto-Messtechnik current amplifier HCA-5M-500K and correlated with the sine wave using a Stanford Research Systems SR844 RF lock-in amplifier.
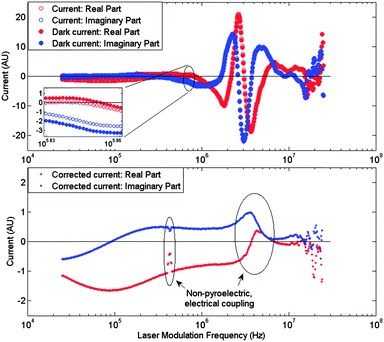
Despite careful electrical shielding, the measured spectrum is heavily distorted by correlated and uncorrelated sources as evidenced in a representative spectrum in Fig. 3 (top). To reduce these contributions, a shutter was installed between the laser and the sample's absorbing electrode. After measuring the pyroelectric response at a particular frequency, the shutter closes and the dark current value is obtained for that frequency. Subtracting the resulting dark-current spectrum from the measured LIMM spectrum results in a dark-current corrected spectrum as displayed in Fig. 3 (bottom). This method does not eliminate mechanical resonances and associated piezoelectric current contributions.
Varying the external electrical field was achieved by electrically connecting the voltage output of a Keithley237 Source-Measure unit to the sample electrodes with a Tektronix 2220 Voltage Probe. A 100 nF ceramic capacitor was used to block the DC contribution from the external poling field. The current setup is limited to ±100 Volts, which corresponds to 100 MV m−1 for a 1000 nm sample. Temperature control was realized via a thin film Pt100 resistance thermometer mounted on the sample glass substrate and a resistive heating coil driven by a PID (Red Lion) temperature controller. Cooling occurred by heating liquid nitrogen to generate cold nitrogen gas to pass through copper tubing connected to the sample holder. All equipment was computer controlled via a Matlab program and GPIB and USB communication, allowing automation of the measurements.
2.3 Pyroelectric response and scale transform method
The frequency-dependent pyroelectric response of a material can be attributed to both the spontaneous polarization P(x) and the space charge distribution p(x) with corresponding current contributions of (αp + αL − αε)dP(x)/dx and (αL − αε)p(x) with αp the pure dipolar pyroelectric effect, αL the thermal expansion coefficient of the sample and αε the temperature coefficient of the electrical permitivity.36,37 In practical situations, where it is unfeasible to assume the polarization is locally compensated by charges, it is difficult to distinguish between space charge and polarization distributions based only on the pyroelectric spectrum. For convenience, results in this paper are presented in terms of an effective local polarization, combining the two contributions into what shall further be addressed to as the local polarization.The scale transform method is used to obtain the polarization distribution profile from the acquired pyroelectric current spectrum. It is a direct and time-efficient means of obtaining the depth profile. The scale transform method, as described by Ploss et al.,38 attributes the local polarization, P, at a depth z to the difference between the real and imaginary part of the pyroelectric current, eqn (2.1), at a frequency that corresponds to the thermal diffusion length equal to the depth z, eqn (2.2).
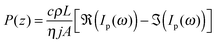 | (2.1) |
 | (2.2) |
Due to uncertainties regarding the optical absorbance and αp, αL, αε coefficients, we will further discuss polarization distributions using intercomparable arbitrary units (AU).
3 Results and discussion
3.1 Polarization distribution under external field
Using the LIMM-method, polarization profiles were obtained for different values of external electric field using the scale transform method. Starting from a virgin sample of the copolymer, the field was increased from 0 up to 90 MV m−1 in steps of 30 MV m−1. The field was then decreased likewise to −90 MV m−1, exceeding the coercive field (Ec) of 50 MV m−1 and thus reversing the sign of polarization, and built back up to 90 MV m−1 to complete the hysteresis loop.The resulting polarization profiles are displayed in Fig. 4, where a position of 0 nm corresponds to the position of the electrode/polymer boundary of the initially positive electrode while the right limit corresponds to the counter electrode. In the centre of the film (at 500 nm) there is a slight mismatch between the left and right profiles due to destructive interference of thermal waves. Fig. 5 displays the best fitting results of the same data set using a Monte-Carlo deconvolution method for the first 8 external fields on a logarithmic length scale, to allow a more detailed analysis. The first increase from 0 to 30 MV m−1 shows an increase at both electrode regions, though a noticeably larger amplitude is observed at the positive electrode region. At 60 MV m−1, above the coercive field, the negative electrode displays a 30 percent larger polarization than at the positive electrode. A further increase in external field does not lead to an increase in polarization near the positive electrode, suggesting a saturation of polarization, but does result in a further increase near the negative electrode. Decreasing the external field to 0 MV m−1 changes little to either polarization profile or amplitude. A further decrease to −30 MV m−1 reduces the amplitude of local polarization at both electrodes, with the largest relative decrease at the negative electrode. Starting from −60 MV m−1, the pattern repeats.
The results suggest a saturation of the polarization build-up at the positive electrode for fields exceeding 60 MV m−1 while an additional mechanism at the negative electrode remains active up to 90 MV m−1. This additional polarization contribution can be rationalised by excess charges in the region near the negative electrode, which suggests the idea of electron injection, our work hypothesis, at high fields.
3.2 Local ferroelectric hysteresis
An integration of the obtained local polarization over the entire depth of the thin film sample at each field displays a hysteresis in the total polarization of the sample, similar to those obtained via other means, such as the Tower–Sawyer (TS) method.1Fig. 6 shows the result of such an integration for both the entire polarization profile and a spatial limitation to either electrode half. A complete integration reveals a hysteresis curve corresponding to literature examples of the same blend.1 The spatial distribution obtained via the LIMM allows more selective information on the hysteresis. By limiting the integration to one half of the thin film thickness, the asymmetries discussed earlier are also visible in the P–E-plot, with a persistent larger response near the negative electrode above Ec.A specific advantage of measuring the polarization distribution instead of the total polarization is that ferroelectric hysteresis curves can be reconstructed for different spatial regions. In Fig. 7 three sample depth regions are selected. In the first 100 nm the asymmetry is most pronounced, with a lower signal strength at the positive poling electrode and a stronger field dependence at the negative electrode. Between 100 to 200 nm from the electrode, the field dependence is similar, showing a larger negative polarization response. Near the middle of the sample, at a depth of 200–450 nm, the hysteresis curve is more symmetric, though the negative polarization remains larger. These results emphasize the origin of the asymmetry to the near-electrode region of the sample. Previous work has indicated the importance of charge injection21 when poling the P(VDF–TrFE) copolymer, meaning it is reasonable to assume a difference in charge trapping at the crystalline interfaces between the two electrode regions.
We hypothesize that at the negative electrode an additional mechanism of electron-trapping in the interface coulomb-trap takes place, a process that is not present at the positive electrode and would explain a weaker response and an earlier saturation above the coercive field.
According to Rollik et al.,41 there are several contributing mechanisms in poled P(VDF–TrFE) that lead to a pyroelectric response. By measuring the local polarization near the Curie temperature and at temperatures below the glass transition, it is possible to discern between, respectively, the contributions of the interface polarization and the polarization of the non-crystalline phase.
3.3 Interface charge contribution
Poling of the sample results in both a polarization of the crystalline phase, as well as an interface polarization.41 This interface polarization leads to a significant pyroelectric response due to inhomogeneously distributed excess charges and differences in the thermal expansion coefficient of the crystalline and noncrystalline phases. Heating the sample to a sufficiently high temperature, near the Curie temperature, enables the charges to get released from the crystallite surfaces, effectively short-circuiting and reducing the interface polarization. Upon cooling, only the repeatable pyroelectric response of the crystalline phase is observed.To this end, a 1500 nm thin film of PVDF–TrFE was prepared by poling at a field of 60 MV m−1 at room temperature for a period of two hours, after which the contacting electrodes were short circuited for one additional hour. The sample was placed in a low vacuum cell and the temperature was first increased from 25 °C to 125 °C at a rate of 2 °C per minute, and then allowed to cool down again to room temperature (25 °C). During the heating and cooling, the evolution of the pyroelectric signal at both the positive and negative poling electrode was measured at 100 kHz, corresponding to a thermal diffusion depth of 560 nm.
The results displayed in Fig. 8, suggest a Curie temperature near 120 °C for the heating run and about 80 °C for the cooling run, in line with the findings of Furukawa et al.1 The onset of the phase transition is noticeable as a slightly larger pyroelectric response, due to the large difference in polarization between the paraelectric and ferroelectric phase. After heating and cooling, the sample has reduced its pyroelectric response by a factor of 2. The origin of the reduction is twofold; above the Curie temperature of 120 °C a number of crystallites has switched to the paraelectric phase and no longer contribute to the pyroelectric response; the other cause is the reduction of crystalline/amorphous interface surface charges, reducing their contribution to the response. It is reasonable to assume that an equal amount of crystallites have changed to the paraelectric phase at both electrode interfaces, which implies that the asymmetry in pyroelectric change must be sought in a difference in interface surface charges.
Further support for this idea comes from the observation that the negative electrode (cf.Fig. 8, open circles) shows a slightly stronger response during heating, but ends up with a smaller response after. The positive electrode (filled circles) retains a larger response upon cooling than the negative electrode. These results indicate a higher initial interface charge concentration at the negative poling electrode.
The discontinuity in pyroelectric response between the heating and cooling run at 125 °C is due to a time delay of 2 hours. During this time, a pyroelectric spectrum was recorded, displayed in Fig. 9, revealing a nearly uniform distribution at 125 °C in comparison to the initial and final distribution at room temperature, 25 °C. A clearly distinct characteristic of the polarization profile at the elevated temperature of 125 °C, is a region with opposed pyroelectric response in the first 75 nm near the electrode. This negative response cannot be of ferroelectric origin and thus implies the existence of a reversed internal field in the near-electrode region caused by macroscopically distributed excess charges. The implied excess charge concentration would originate from trapped crystallite interface charges that were released and redistributed during the ferro- to paraelectric transition above Tc. These excess charges are re-trapped in interface coulomb traps upon cooling to room temperature, resulting in a partial recovery of the ferroelectric polarization response in the bulk and the vanishing of the opposing pyroelectric response at the polymer–electrode interface, as seen in distribution (3) of Fig. 9.
The injection of electrons at the negative electrode provides additional free charge carriers, which, in turn, reduce the local electrical field, resulting in a polarization-free zone near the electrodes. It is likely that the width of this zone is related to the spatial extension of the space charge zone and thus scales somehow with the Debye screening length. The width of this polarization-free zone should also display a weaker temperature dependence when a large concentration of local free charge is present. To test this idea, polarization profiles were obtained at different temperatures to compare the width of the polarization-free zone during poling at a field of 90 MV m−1. In Fig. 10 it is observed that at elevated temperatures, from 95 to 115 °C the width of the polarization-free zone increases the most for the positive electrode. This can be explained by assuming that effective switching of the crystalline phase starts from a depth related to Debye screening length (eqn (3.1)),42 where λ is the Debye length, ε the relative permitivity, ε0 the permitivity of vacuum, kb the Boltzmann constant, T the temperature, e the elementary charge, n the free charge concentration and z the charge number. It is obvious that an increase in temperature will result in a larger screening length λ and thus polarization-free zone, a trait that is visible at both poling electrodes.
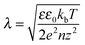 | (3.1) |
A larger increase of λ at the positive electrode compared to the negative electrode can be ascribed to a higher concentration of free charges n− at the negative electrode, which is consistent with the hypothesis of an additional charge generation mechanism at the negative electrode, i.e. the injection of electrons at fields exceeding 60 MV m−1.
3.4 Contribution from the amorphous phase
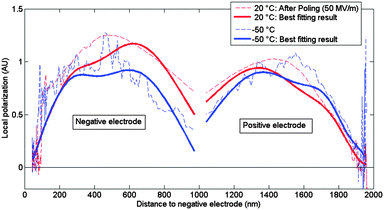
While the crystalline phase retains its remnant part of the polarization after removal of the external field, the corresponding polarization charges give rise to a strong internal field that polarizes the non-crystalline phase of the material.43,44 This induced polarization will also contribute to the pyroelectric activity of the sample. By cooling the poled thin film well below the glass transition temperature to −50 °C, large dipolar fluctuations within the amorphous fraction gets largely reduced (freezing of segmental mobility), which results in substantially reduced contribution of the induced polarization in the amorphous phase and its pyroelectric contribution accordingly.Fig. 11 shows the resulting polarization profiles for a 2000 nm thin film of P(VDF–TrFE) poled at room temperature with an external field of 50 MV m−1. At room temperature, the usual asymmetry is observed with a 20 percent larger response from the negative electrode as opposed to the positive electrode. Upon cooling to −50 °C, a large drop in response is observed at the negative electrode, nearly approaching the same pyroelectric amplitude as the positive electrode, which retains almost its full response. The larger drop in local polarization near the negative electrode suggests a 20 percent larger contribution of induced polarization to the initial response. The trapping of injected electrons near the crystallite interface could be responsible for a higher polarization of the amorphous fraction. Moreover, the contribution at the positive region merely shifts closer to the electrode. Interestingly, the width of the polarization-free zone does not change for lower temperatures at the negative poling electrode, while this “gap” decreases at the positive side. This observation is in line with the results of the previous subsection where the width of the polarization-free zone at the positive electrode was found to have a greater temperature dependence than at the negative side.
A final, interesting detail shown in Fig. 11 concerns the oscillating behaviour of the polarization distribution obtained via the scale transform (dashed line) at −50 °C. These oscillations were identified as mechanical resonances of the thin film structure,40 which become prominent in the glassy state of the polymer film due to an enhanced Young's modulus (>GPa) and reduced mechanical losses in the measurement range of 25 kHz to 25 MHz.
4 Conclusions and outlook
Using the LIMM technique on samples of PVDF–TrFE with an electrical DC bias field, we are able to spatially resolve the local ferroelectric hysteresis curve via the local polarization. A pronounced asymmetry is observed between the positive and negative poling electrode region, where the positive electrode region saturated earlier and consistently had a lower local response for fields exceeding the coercive field. By measuring the polarization profile at temperatures near the Curie temperature and well below the glass transition, we were able to discern the contribution of interface surface charges and of the amorphous fraction to the pyroelectric response at both electrode regions. We hypothesize that the negative electrode has a more efficient charge generation mechanism related to electron injection, resulting in a larger concentration of free space charges and a larger local response. The difference in “excess” space charge concentration also leads to a different temperature dependence of the Debye length and the related width of the polarization-free zone.The poled copolymer thin film is also suspected to be capable of Second Harmonic Generation (SHG), an optical frequency conversion mechanism in non-centrosymmetric materials, based on the work of Siegfried Bauer et al. on PVDF films.45 Future work will focus on the evolution of the SHG response upon variation of an external field and the influence of the proposed electron injection on the nonlinear optical properties.
The observed difference in width of the polarization-free zone between the positive and negative poling electrode could be relevant for a rational design of memory-,46 sensor- and photonic47-applications based on thin films of PVDF and copolymers.
Acknowledgements
The authors would like to thank Simona Bauer-Gogonea for providing the PVDF–TrFE (76/24) copolymer pellets (Piezotech S.A., France).The authors acknowledge financial support from the Research Council of the KU Leuven, project OT/11/065.
Notes and references
- T. Furukawa, T. Nakajima and Y. Takahashi, IEEE Trans. Dielectr. Electr. Insul., 2006, 13, 1120 CAS.
- K. Omote, H. Ohigashi and K. Koga, J. Appl. Phys., 1997, 81, 2760 CrossRef CAS PubMed.
- F. G. Shin, H. L. W. Chan, B. Ploss and C. L. Choy, IEEE Trans. Dielectr. Electr. Insul., 2000, 7, 517 CrossRef.
- R. Gregorio Jr., C. Y. Iguchi and W. N. dos Santos, Polym. Test., 2007, 26, 788 CrossRef PubMed.
- M. Sharma, G. Madras and S. Bose, Phys. Chem. Chem. Phys., 2014, 16, 23421 RSC.
- Z. Li, X. Zhang and G. Li, Phys. Chem. Chem. Phys., 2014, 16, 5475 RSC.
- J. G. Bergman Jr., J. H. McFee and G. R. Crane, Appl. Phys. Lett., 1971, 18, 203 CrossRef PubMed.
- A. M. Glass, J. H. McFee and J. G. Bergman Jr., J. Appl. Phys., 1971, 42, 5219 CrossRef CAS PubMed.
- H. Kawai, Jpn. J. Appl. Phys., 1969, 8, 975 CrossRef CAS.
- L. Pauling, The nature of chemical bonding, Cornell university press, Ithaca, NY, 3rd edn, 1960, p. 644 Search PubMed.
- A. J. Lovinger, in Developments in Crystalline Polymers, ed. D. C. Basset, Elsevier Applied Science, London, 1982, vol. 1 Search PubMed.
- V. Sencadas, Rb. Gregorio Jr. and S. Lanceros-Méndez, J. Macromol. Sci., Part B: Phys., 2009, 48, 514 CrossRef CAS.
- R. G. Kepler and R. A. Anderson, J. Appl. Phys., 1978, 49, 1232 CrossRef CAS PubMed.
- H. S. Nalwa, Ferroelectric polymers chemistry, physics and applications, Marcel Dekker, Inc., New York, 1995, p. 63 Search PubMed.
- T. Yamada and T. Kitayama, J. Appl. Phys., 1981, 52, 6859 CrossRef CAS PubMed.
- M. B. Smith, Organic chemistry: an acid-base approach, CRC press, Taylor & Francis group, 2011, ISBN 13:978-1-4200-7921-0 Search PubMed.
- T. Furukawa, Phase Transitions, 1989, 18, 143 CrossRef CAS.
- M. Womes, E. Bihler and W. Eisemenger, IEEE Trans. Electr. Insul., 1989, 24, 461 CrossRef CAS.
- R. Ruf, S. Bauer and B. Ploss, Ferroelectrics, 1992, 127, 1545 CrossRef CAS.
- G. M. Sessler, D. K. Das-Gupta, A. S. DeReggi, W. Eisenmenger, T. Furukawa, J. A. Giacometti and R. Gerhard-Multhaupt, IEEE Trans. Electr. Insul., 1992, 27, 872 CrossRef CAS.
- W. Eisenmenger, H. Schmidt and B. Dehlen, Braz. J. Phys., 1999, 29, 295 CrossRef CAS PubMed.
- E. Bihler, G. Neumann, G. Eberle and W. Eisenmenger, Annu. Rep. Conf. Electr. Insul. Diel. Phenom., 1990, IEEE pub 90CH2919-9, 140.
- E. Bihler, K. Holdik and W. Eisenmenger, IEEE Trans. Electr. Insul., 1987, 22, 207 CrossRef.
- M. Wübbenhorst, T. Petzsche and C. Ruscher, Ferroelectrics, 1988, 81, 373 CrossRef.
- S. B. Lang and D. K. Das-Gupta, Ferroelectrics, 1984, 60, 23 CrossRef CAS.
- S. B. Lang and D. K. Das-Gupta, J. Appl. Phys., 1986, 59, 2151 CrossRef CAS PubMed.
- F. Feller, D. Geschke and A. P. Monkman, Polym. Int., 2002, 51, 1184 CrossRef CAS.
- N. Leister, D. Geschke and M. V. Kozlovsky, Mol. Cryst. Liq. Cryst., 1998, 309, 201 CrossRef CAS.
- S. B. Lang and D. K. Das-Gupta, Ferroelectrics, 1981, 39, 1249 CrossRef CAS.
- A. J. Lovinger, T. Furukawa, G. T. Davis and M. G. Broadhurst, Ferroelectrics, 1983, 50, 227 CrossRef.
- K. Koga and H. Ohigashi, J. Appl. Phys., 1986, 56, 2142 CrossRef PubMed.
- J. F. Scott, J. Phys.: Condens. Matter, 2008, 20, 021001 CrossRef.
- F. I. Mopsik and A. S. DeReggi, Appl. Phys. Lett., 1984, 44, 65 CrossRef CAS PubMed.
- K. Holdik and W. Eisenmenger, Proc. ISE, 1985, 5, 553–558 Search PubMed.
- G. Eberle, E. Bihler and W. Eisenmenger, IEEE Trans. Electr. Insul., 1991, 26, 69 CrossRef CAS.
- B. Ploss, R. Emmerich and S. Bauer, J. Appl. Phys., 1992, 72, 5363 CrossRef CAS PubMed.
- M. Wübbenhorst and P. Wünsche, Prog. Colloid Polym. Sci., 1991, 85, 23 Search PubMed.
- B. Ploss and O. Bianzano, Proc. ISE, 1994, 8, 206 Search PubMed.
- S. B. Lang and R. Fleming, IEEE Trans. Dielectr. Electr. Insul., 2009, 16, 809 CrossRef.
- M. Wübbenhorst and J. van Turnhout, Proc. ISE, 1994, 8, 182 Search PubMed.
- D. Rollik, S. Bauer and R. Gerhard-Multhaupt, J. Appl. Phys., 1999, 85, 3282 CrossRef CAS PubMed.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, 1992, ISBN 9780521426008 Search PubMed.
- S. N. Fedosov and H. Von Seggern, J. Appl. Phys., 2008, 103, 014105 CrossRef PubMed.
- S. N. Fedosov and H. Von Seggern, J. Appl. Phys., 2004, 96, 2173 CrossRef CAS PubMed.
- S. Bauer, G. Eberle, W. Eisenmenger and H. Schlaich, Opt. Lett., 1993, 18, 16 CrossRef CAS.
- Z. Hu, M. Tian, B. Nysten and A. M. Jonas, Nat. Mater., 2009, 8, 62 CrossRef CAS PubMed.
- S. Bauer, J. Appl. Phys., 1996, 80, 5531 CrossRef CAS PubMed and references therein.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp06033d |
| This journal is © the Owner Societies 2015 |