 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Site-dependence of van der Waals interaction explains exciton spectra of double-walled tubular J-aggregates
Jörg
Megow
*a,
Merle I. S.
Röhr
b,
Marcel
Schmidt am Busch
c,
Thomas
Renger
c,
Roland
Mitrić
b,
Stefan
Kirstein
d,
Jürgen P.
Rabe
de and
Volkhard
May
d
aInstitut für Chemie, Universität Potsdam, Karl-Liebknecht-Straße 24-25, D-14476 Potsdam, F. R. Germany. E-mail: megow@uni-potsdam.de
bInstitut für Physikalische und Theoretische Chemie, Universität Würzburg, Emil-Fischer-Straße 42, D-97074 Würzburg, F. R. Germany
cInstitut für Theoretische Physik, Johannes Kepler Universität Linz, Altenberger Straße 69, AT-4040 Linz, Austria
dInstitut für Physik, Humboldt-Universität zu Berlin, Newtonstraße 15, D-12489 Berlin, F. R. Germany
eIRIS Adlershof, Humboldt-Universität zu Berlin, Zum Großen Windkanal 6, D-12489 Berlin, F. R. Germany
First published on 15th January 2015
Abstract
The simulation of the optical properties of supramolecular aggregates requires the development of methods, which are able to treat a large number of coupled chromophores interacting with the environment. Since it is currently not possible to treat large systems by quantum chemistry, the Frenkel exciton model is a valuable alternative. In this work we show how the Frenkel exciton model can be extended in order to explain the excitonic spectra of a specific double-walled tubular dye aggregate explicitly taking into account dispersive energy shifts of ground and excited states due to van der Waals interaction with all surrounding molecules. The experimentally observed splitting is well explained by the site-dependent energy shift of molecules placed at the inner or outer side of the double-walled tube, respectively. Therefore we can conclude that inclusion of the site-dependent dispersive effect in the theoretical description of optical properties of nanoscaled dye aggregates is mandatory.
I. Introduction
The investigation of electronic exciton energy transfer (EET) in huge supramolecular systems is of enormous interest for the understanding of processes taking place in both biological1–3 and artificial4,5 light harvesting antennae systems and therefore a topic of recent research. As an example chlorosomes from green sulfur bacteria which cover thousands of pigment molecules have been investigated only recently.6–8Various artificial light harvesting systems have been established and explored experimentally9,10 and were also investigated theoretically, such as giant molecular macrocycles11,12 or large complexes of tetrapyrrole type molecules.13,14 However, an appropriate theoretical treatment of such systems still remains challenging. In this work we focus on the appropriate description of the structural and optical properties of the tubular dye aggregate (TDA) of the amphiphilic cyanine dye named C8S3,15 formed in aqueous solution, which have been discussed in several studies.4,16–18
Former cryogenic transmission electron microscope (cryo-TEM) images suggested that the dyes are arranged within a double layer structure similar to lipid membranes facing the hydrophilic groups, and hence the chromophoric units, towards the liquid medium inside and outside of the tube and hiding the hydrophobic alkyl chains from the aqueous environment.4,16 This building principle is illustrated in Fig. 1 and 2.
 | ||
| Fig. 1 Initial model of the C8S3 TDA. One molecular ribbon of the outer cylinder is highlighted in color. The whole outer cylinder is drawn in grey and the inner one in light grey. (The figure was created using VMD.28) | ||
 | ||
| Fig. 2 MD aggregate after 7 ns of simulation. Upper panel: the side view according to Fig. 1. Lower panel: the top view of the C8S3 TDA with the dye molecules in the inner cylinder and the outer cylinder being highlighted. The spheres around the highlighted molecules have a radius of 2 nm. They indicate a volume that includes all dye molecules that contribute more than 99% to the dispersive energy shift. Note that more dye molecules are within this sphere for the molecules at the inner wall than those at the outer wall. (The figures were created using VMD.28) | ||
In previous studies investigating the double-walled tubular J-aggregates the linear optical spectra were explained theoretically using a parameterized Frenkel exciton Hamiltonian.19–21 Therefore, the tubes were modelled using two telescoped tubes of dye molecules. For each cylinder independently a regular and destortion free lattice of dyes was assumed with two molecules per unit cell where every dye was represented by an extended dipole.5,18,22 All energy shifts in the spectra were attributed to excitonic coupling while solvent shifts or dispersive interactions were implicitly taken into account, but assumed to be site-independent. By the adjustment of mutual orientations, distances, and tilt angles, the absorption spectra were modelled in great detail. Also an assignment of bands that correspond to the inner and outer cylinders was provided. Notice that in those studies the structures of the inner and outer cylinder were assumed to be uncorrelated.
In contrast, highly sophisticated image reconstruction techniques revealed details of the structure of the tube wall indicating an organization of the dyes in ribbons that are helically winding within the wall.17 The appearance of these ribbons requires a strong correlation between the arrangement of dyes within the inner and outer tubes, which is not fulfilled by the model described above. On the other hand, the computation of optical spectra based on molecular dynamics (MD) simulations was approached, as reported in ref. 23, for a single-walled tube which resulted in a too wide absorption line shape.
In this contribution we provide two new approaches to refine the aggregate structure and description of spectra. First, the structure is modelled employing MD simulations. The starting configuration is resolved to best approximate the appearance of highly resolved cryo-TEM images (cf.Fig. 1). A detailed model down to atomic resolution has been obtained that can be handled numerically and is stable over timescales of nanoseconds. Second, the linear absorption spectrum is calculated based on the MD structure taking into account transition densities of resonant excitonic interactions but also a full description of dispersive energies due to non-resonant interactions. The huge number of molecules within the slightly disordered aggregates account for the disorder effects in the spectra. The results lead us to a new interpretation of the shift, and splitting into two fundamental bands of the absorption spectrum.
Considering bulk systems, the change in the molecular excitation energy due to an environmental influence is known as the gas-to-crystal shift. Electrostatic and inductive site energy shifts depend on the difference in charge density between the excited and ground states of the molecule. If the latter is small, the leading contribution to the site energy shift is due to mutual polarization of different atoms (molecules), the van der Waals interaction or dispersive interaction. It was first proposed by London24 to explain the attractive interaction between noble gas atoms (exhibiting closed electronic shells). Due to the Coulomb coupling between electrons in different atoms (molecules) a dynamic correlation in electronic motion stabilizes the coupled system and leads to reduction in energy. Since excited state wavefunctions are often more extended than the ground state ones, the dispersive shifts of excited state energies are usually larger than those of electronic ground states leading to a redshift of the transition energy.36 It is important to note that the dispersive shift also includes the interaction with all other molecules of the environment.
Usually, dispersion effects of the surrounding medium are taken into account by assuming a single value for the molecular excitation (site) energy in order to place the whole absorption spectrum in the correct wavelength region. This implies the use of a constant transition energy shift. In the case of a nano-structured system the polarizability of the environment may strongly depend on the molecular position. Accordingly, the excitation energy shift does not remain constant but becomes site-dependent. If this shift overcomes the strength of the resonant EET (excitonic) coupling it significantly affects the spectrum of excitation energies. We note that such site-dependent dispersive energy shifts have been calculated for aggregates of Rydberg atoms in ref. 25. Here, we utilize a method that is applicable to molecular aggregates.
It will be shown in the following that the separation of the two low-energy absorption bands as reported in ref. 5 is mostly due to different dispersive shifts of the molecular excitation energy in the inner and outer walls of the TDA. On the other hand, the resonant excitonic coupling is found to have less impact on the separation of these two bands.
II. Results
To obtain a consistent explanation of the absorption spectrum of TDA, our subsequent considerations will be based on a spatial structure that is obtained by MD simulations starting from a configuration resembling highly resolved cryo-TEM images.17 The simulated system included 828 C8S3 molecules, 74116 water molecules and 9242 methanol molecules in a box of 17 × 17 × 12.6 nm with periodic boundary conditions.26 The simulations are extended up to 7 ns. Here, it is essential to ensure that the solvent density inside the tube coincides with that outside. After an equilibration time of a few 100 ps the structural parameters of TDA were found to stay constant, indicating the stable structure of the aggregate. In Fig. 2 the structure resulting after 7 ns of simulation is shown.In the case of a TDA of C8S3, due to the curvature the environment in the proximity of the dye molecules has a different composition in terms of the number of dye molecules per volume. This mainly depends on the molecule either being located in the outer wall or in the inner wall. This effect is shown in the lower panel of Fig. 2 by circles showing the close environment of two dyes within the top view of a MD simulated aggregate. These circles with a radius of about 2 nm around the center of the molecular transition dipole moments indicate the close environment of the dyes which contributes most (>99%) to the dispersive energy shift.
A. TDA structure
According to the cryo-TEM data, the whole TDA structure consists of six ribbons, turned around a common axis, forming an inner and an outer cylinder (see Fig. 1). Both cylinders have the same periodicity (twists per aggregate length), which is 12.7 nm−1. The width of a single ribbon amounts to 20.1 Å for the outer cylinder and 19.5 Å for the inner cylinder (they differ due to the different screw angles). The extension of a single C8S3 molecule along the transition dipole axis is 20.8 Å. We assumed an orientation of the molecules with dipole moments parallel to the cylinder surface which is confirmed by our MD simulations. These ribbons then wind up with a screw angle θ and the molecules have to be tilted against the z-axis of the tube by an angle β (see Fig. 3). According to the MD simulations, θ amounts to 18.3° for the outer cylinder and 23.0° for the inner cylinder. β amounts to 34.5° for the outer cylinder and 44.3° for the inner cylinder. We note that no exact value for β can be extracted from the cryo-TEM images.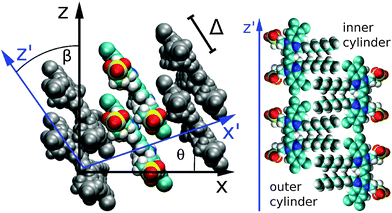 | ||
| Fig. 3 Internal structure of the C8S3 TDA. Left panel: molecular ribbon with two molecules forming a unit cell. The internal coordinate system is drawn in blue. Right panel (schematic): orientation of the C8S3 dyes in the outer (left) and inner (right) cylinders. (The figures were created using VMD.28) | ||
The mean distance of neighboring molecules is 5 Å within both cylinders, measured as the distance between the molecular centers of the π-electron system. The closest distance between two molecules is about 4 Å. The distance between neighboring molecules varies due to the angle between them. We also tried simulations with closely packed molecules. They were not stable since some of the atoms came too close to each other. The distance between the two cylinders amounts to 13 Å (measured with respect to the centers of the molecular π-electron systems).
Our model assumes two molecules per unit cell. Therefore, a mutual displacement Δ as indicated in Fig. 3 was introduced by hand with a value of Δ = 9 Å. Δ was chosen in order to obtain the corrected absorption spectrum (see below) and is the only free parameter in our model. Due to the displacement Δ our model includes two molecules per unit cell. The structural stability of the TDA for such a mutual molecular displacement has been confirmed by extended MD simulations. We note that using Δ = 0, a structural model consistent with that reported in ref. 17 results in an H-aggregate-like absorption spectrum.
For comparison, a MD simulation, based on the structural model presented in ref. 5 was employed. It is specific for that model that the molecular structures of the inner and outer walls differ and furthermore are completely independent of each other, i.e. there is no correlation between the respective molecular positions. Additionally, the molecules are arranged in a Herringbone-like structure, also resulting in 2 molecules per unit cell. However, by performing MD simulations, this model turned out to be unstable, since the tubes disintegrated with time. Therefore, we conclude that the strong correlation between inner and outer tubes as provided by the model of the two-layer ribbons reduces the system's free energy and stabilizes the structure significantly.
B. Frenkel exciton Hamiltonian
Having determined the TDA structure we can turn to the computation of the resulting excited electronic states. Singly excited states of the TDA as detected in linear absorption measurements can be deduced from the standard Frenkel-exciton Hamiltonian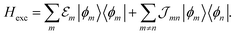 | (1) |
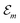 (excitation energy of molecule m). The off-diagonal part is formed by the excitonic coupling
(excitation energy of molecule m). The off-diagonal part is formed by the excitonic coupling 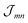 which resonantly transfers excitation energy from one dye molecule to the other. ϕm is the molecular product state with molecule m in the first excited state φme and all other molecules in the ground state φng. Restriction to a single excited state becomes possible since higher excited states are energetically sufficiently far away. The overall ground state ϕ0 is a product of all φng. A ground state part E0|ϕ0〉〈ϕ0| does not appear in the Hamiltonian since we set
which resonantly transfers excitation energy from one dye molecule to the other. ϕm is the molecular product state with molecule m in the first excited state φme and all other molecules in the ground state φng. Restriction to a single excited state becomes possible since higher excited states are energetically sufficiently far away. The overall ground state ϕ0 is a product of all φng. A ground state part E0|ϕ0〉〈ϕ0| does not appear in the Hamiltonian since we set 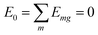 .
.
The excitonic coupling 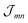 coincides with
coincides with 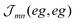 which is a particular example of the general two-molecule Coulomb matrix element
which is a particular example of the general two-molecule Coulomb matrix element 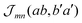 . The electronic quantum numbers a and a′ belong to molecule m, and b and b′ to molecule n. The matrix element appears as the Coulomb interaction of charge density
. The electronic quantum numbers a and a′ belong to molecule m, and b and b′ to molecule n. The matrix element appears as the Coulomb interaction of charge density 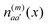 of molecule m and charge density
of molecule m and charge density 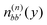 of molecule n. If, for example, a ≠ a′ the density
of molecule n. If, for example, a ≠ a′ the density 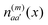 is exclusively determined by the electronic transition density
is exclusively determined by the electronic transition density 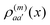 .31 For concrete computations the continuous charge densities are replaced by discrete atomic centered partial charges and partial transition charges.37 The unscreened excitonic coupling is between +30 and +40 meV for neighboring molecules within the same ribbon. It is between −40 and −30 meV for neighboring molecules of two adjoined ribbons. Since each molecule couples strongly to four molecules of adjacent ribbons (cf.Fig. 3) the J-aggregate character dominates.
.31 For concrete computations the continuous charge densities are replaced by discrete atomic centered partial charges and partial transition charges.37 The unscreened excitonic coupling is between +30 and +40 meV for neighboring molecules within the same ribbon. It is between −40 and −30 meV for neighboring molecules of two adjoined ribbons. Since each molecule couples strongly to four molecules of adjacent ribbons (cf.Fig. 3) the J-aggregate character dominates.
C. Curvature induced dispersion shifts
The minimal version of the exciton Hamiltonian introduced so far has to be improved by consideration of further couplings among the molecules which may change the site energies as well as the matrix elements of the excitonic coupling.27 Electrostatic couplings due to permanent charge distributions in the ground and excited states of the dye molecules result in the shift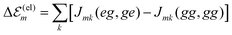 of site-energy
of site-energy  (contributions due to solvent molecules are incorporated in the k-sum29).
(contributions due to solvent molecules are incorporated in the k-sum29).
The charge densities of the ground and excited states polarize the environmental molecules, a polarization that reacts back on the considered molecules and introduces the site energy shift  . A third type of site energy shift arises from the mutual Coulomb coupling of transition densities and is termed dispersive site energy shift
. A third type of site energy shift arises from the mutual Coulomb coupling of transition densities and is termed dispersive site energy shift  .31,32 Introducing the dispersive change in the molecular energy of the state φma referred to as ΔE(disp)ma we obtain (remember a = g, e)27
.31,32 Introducing the dispersive change in the molecular energy of the state φma referred to as ΔE(disp)ma we obtain (remember a = g, e)27
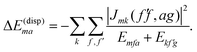 | (2) |
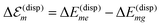 .
.
Hence, the site energies 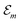 are shifted in total by
are shifted in total by
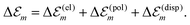 | (3) |
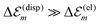 . While
. While 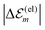 is in the order of 10 meV,
is in the order of 10 meV, 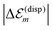 is in the order of over 500 meV. This result is understood by noting the comparably similar charge densities of the ground and excited electronic states (differential dipole moment is about 1 D30). Since we expect
is in the order of over 500 meV. This result is understood by noting the comparably similar charge densities of the ground and excited electronic states (differential dipole moment is about 1 D30). Since we expect 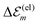 is in the same order of magnitude as
is in the same order of magnitude as 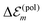 , we get
, we get 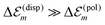 . Therefore, we neglect
. Therefore, we neglect 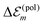 in our calculations.
in our calculations.
In order to determine the energy shifts of every individual molecule within the aggregate the expression, eqn (2), has to be transformed into a tractable form to compute its dependence on the mutual position of the coupled molecules. Here, we follow ref. 27. Accordingly, in the first step Jmk(ag, f′f) is replaced by an expression of two interacting extended dipoles with charges ±q(fa) and ±q(f′g). Electronic structure computations indicate that these dipoles are oriented along the elongated part of the cyanine dye. Assuming uniform extension of all extended dipoles we may write 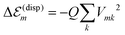 , where Vmk represents all geometrical factors, i.e. the Coulomb interaction of both extended dipoles but with unit charges. Concrete values of the latter are included in the factor
, where Vmk represents all geometrical factors, i.e. the Coulomb interaction of both extended dipoles but with unit charges. Concrete values of the latter are included in the factor 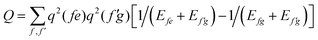 , where Efe(Ef′e) and Efg(Ef′g) are the transition energies between the first excited and ground states of the isolated monomers, respectively, and the higher excited states.
, where Efe(Ef′e) and Efg(Ef′g) are the transition energies between the first excited and ground states of the isolated monomers, respectively, and the higher excited states.
By further proceeding in line with ref. 27 we do not determine the Q-factor by a direct computation, which would not be accurate enough, but by using experimental data on transition energy shifts in non-polar solvents. If the solvent is described by a dielectric continuum with refractive index n, the shift can be approximately obtained as,33,36
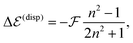 | (4) |
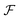 is available and if we know n for a random arrangement of C8S3 molecules we can determine the site-energy shift. Noting the previously published spectra of a similar compound34 we may deduce
is available and if we know n for a random arrangement of C8S3 molecules we can determine the site-energy shift. Noting the previously published spectra of a similar compound34 we may deduce 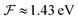 , and a gas-phase transition energy follows as Egp = 2.64 eV. Moreover, we take nTDA ≈ 1.78.35 According to ref. 27 and 36 we have to chose the long wavelength limit of the refractive index resulting in
, and a gas-phase transition energy follows as Egp = 2.64 eV. Moreover, we take nTDA ≈ 1.78.35 According to ref. 27 and 36 we have to chose the long wavelength limit of the refractive index resulting in 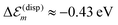 . Identifying this value with
. Identifying this value with 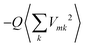 , averaged over all molecules m, we deduce Q = 7.61 eV Å2.
, averaged over all molecules m, we deduce Q = 7.61 eV Å2.
This value of Q is further used to calculate the dispersive site-energy shifts of all molecules within the TDA. The used approximation leads to a significant fluctuation of the individual energy shifts. This is mainly caused by the extended dipole approximation, which is a good approximation on average. However, individual couplings may vary by up to 30%. Therefore, we average the shifts for the inner and outer cylinders separately. This way, the artificial fluctuation due to the utilization of the extended dipole approximation disappears.
The solvent effect on the dispersive site-energy shift 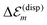 (eqn (4)) was neglected because of the small refractive index of the solvent (n ≈ 1.33) and the comparably restricted contact area between the solvent and the dye molecules. For comparison, a dissolved monomer is shifted by about 0.3 eV (cf.eqn (4)). The C8S3 molecules within the tube, however, show a smaller dispersive shift, since they are mostly surrounded by other C8S3 molecules (cf.Fig. 2). Assuming that a molecule within a wall interacts with less than half of the solvent molecules than a monomer in solution one obtains an upper limit of below 0.15 eV for the solvent dispersive shift of C8S3 molecules within an aggregate. The dispersion shift due to solvent interaction is somewhat larger for molecules in the outer cylinder, since they have contact with more solvent molecules due to geometric reasons. Assuming that this solvent interaction shift will be about 10–15% larger for molecules in the outer cylinder one obtains a reduction of the mutual energy splitting of the two J-aggregate bands by 0.02 eV (6 nm) at most.
(eqn (4)) was neglected because of the small refractive index of the solvent (n ≈ 1.33) and the comparably restricted contact area between the solvent and the dye molecules. For comparison, a dissolved monomer is shifted by about 0.3 eV (cf.eqn (4)). The C8S3 molecules within the tube, however, show a smaller dispersive shift, since they are mostly surrounded by other C8S3 molecules (cf.Fig. 2). Assuming that a molecule within a wall interacts with less than half of the solvent molecules than a monomer in solution one obtains an upper limit of below 0.15 eV for the solvent dispersive shift of C8S3 molecules within an aggregate. The dispersion shift due to solvent interaction is somewhat larger for molecules in the outer cylinder, since they have contact with more solvent molecules due to geometric reasons. Assuming that this solvent interaction shift will be about 10–15% larger for molecules in the outer cylinder one obtains a reduction of the mutual energy splitting of the two J-aggregate bands by 0.02 eV (6 nm) at most.
Having discussed the change in the site energies due to dispersion of the environment we briefly comment on a related alternation of the excitonic coupling, i.e. we introduce screening to the non-diagonal elements of eqn (1). Similar to the site-energy shift it results from an environmental dispersion (see e.g.ref. 38) which, in general, reduces the excitonic coupling 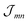 between two molecules to
between two molecules to 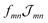 .14,38 The prefactor fmn can be approximated by a constant 1/ε = 1/n2 where n is the optical refractive index.14 From the dispersive shifts of the inner and outer cylinders we calculated the respective refractive indices nout and nin for both cylinders. This was realized assuming the measured refractive index n = 1.78 being an average value n = (Noutnout + Ninnin)/(Nout + Nin), Nout = 468 and Nin = 360 being the number of molecules in the outer and inner cylinders, respectively. We obtain n = 1.89 for the inner cylinder and n = 1.69 for the outer cylinder. From the respective indices we obtain screening factors for the coupling of two molecules within a certain cylinder. We note that this site-dependent screening factors, used for reasons of consistency, change our result only slightly, which can be explained by the rather small contribution of the excitonic couplings to the overall energy shifts.
.14,38 The prefactor fmn can be approximated by a constant 1/ε = 1/n2 where n is the optical refractive index.14 From the dispersive shifts of the inner and outer cylinders we calculated the respective refractive indices nout and nin for both cylinders. This was realized assuming the measured refractive index n = 1.78 being an average value n = (Noutnout + Ninnin)/(Nout + Nin), Nout = 468 and Nin = 360 being the number of molecules in the outer and inner cylinders, respectively. We obtain n = 1.89 for the inner cylinder and n = 1.69 for the outer cylinder. From the respective indices we obtain screening factors for the coupling of two molecules within a certain cylinder. We note that this site-dependent screening factors, used for reasons of consistency, change our result only slightly, which can be explained by the rather small contribution of the excitonic couplings to the overall energy shifts.
For the coupling between two molecules located in different cylinders we take n = 1.78, getting fmn = 0.35 for the outer cylinder, fmn = 0.28 for the inner cylinder and fmn = 0.32 for molecules located in different cylinders, i.e. a noticeable reduction of the excitonic coupling. The somewhat larger screening factor for the outer cylinder results in a slightly decreased energy distance of the two J-aggregate peaks. The 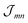 values were calculated via a coupling of transition partial charges (which have been somewhat rescaled to reproduce the measured transition dipole moment37).
values were calculated via a coupling of transition partial charges (which have been somewhat rescaled to reproduce the measured transition dipole moment37).
D. Optical spectra
After determining the site-energies and excitonic couplings which define the exciton Hamiltonian Hex, eqn (1), in an appropriate way,39 the respective diagonalization results in exciton energies and wave functions. To account for a large spatial delocalization of the exciton wave function, the TDA which constitutes the Hamiltonian Hex has been formed by five fragments of 12.7 nm length used in the MD simulations (a further increase of the number of fragments only induces a minor effect on the exciton spectrum). Since after 7 ns of MD simulations all molecular positions deviate from the ordered structure (see Fig. 1) structural disorder is accounted for. Moreover, the huge amount of molecules which contribute to Hex and thus to the exciton spectrum introduce a self-averaging effect. Since it operates when computing the absorption line-shape (sum of the squared excitonic transition dipole moments times the energy conserving δ-function) further disorder averaging is not necessary. Homogeneous broadening was introduced by replacing sharp transitions into the various exciton levels by individual Lorentz-curves with a linewidth of 3 nm (FWHM).The respective results together with measured data are presented in Fig. 4. If dispersive effects are neglected only a single TDA band results, which is shifted slightler to longer wavelengths compared with the monomer absorption. The small red shift of about 10 meV (2 nm) is due to the screened excitonic coupling (it is about −10 meV between neighboring molecules belonging to adjacent ribbons). Calculating the absorption spectra separately for the outer and inner TDA cylinders (yet neglecting dispersive effects) confirms almost vanishing splitting between the two exciton bands. Including, however, the site-dependent dispersion results in a line-shape that exhibits two separate bands and agrees quite well with the measured curves.
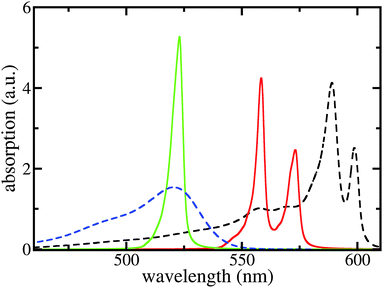 | ||
| Fig. 4 Linear absorption spectra of the C8S3 TDA and the respective dye monomers. Black dashed line: measured TDA absorption according to ref. 5, blue dashed line: measured monomer absorption; green solid line: calculated TDA absorption neglecting the site-dependent dispersion; and red solid line: completely calculated TDA absorption spectrum. No free parameters used, except for the slip Δ in order to build the structure. | ||
The calculated red shift of the exciton bands is too small by 0.1 eV (about 30 nm) compared to the experimentally measured shift (see Fig. 4). This 0.1 eV offset can be related not only to the ignored energy shift due to solvent dispersion but also to the uncertainty when determining the linear factor 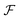 and the gas-phase transition energy Egp. This small unexplained shift has to be compared to the total energy shift of more than 0.5 eV relative to Egp = 2.64 eV for which reason it can be accepted.
and the gas-phase transition energy Egp. This small unexplained shift has to be compared to the total energy shift of more than 0.5 eV relative to Egp = 2.64 eV for which reason it can be accepted.
The treatment of solvent dispersion would also result in a slightly smaller energy difference between the two J-aggregate peaks (0.02 eV at most).
Although the two long wavelength peaks of TDA absorption are nicely reproduced in their spectral position and height, there is a considerable discrepancy at around 550 nm. We briefly demonstrate that this discrepancy may be overcome by including C8S3 intra-molecular vibrations. Fig. 5 shows the respective results where a single representative and broadened vibrational mode per dye molecule has been used. Here, the 0.1 eV offset seen in Fig. 4 and supposedly caused by the neglection of solvent dispersive shifts is corrected. The coincidence of the computed monomer spectrum with the measured one as shown in the inset of Fig. 5 justifies the used vibrational energy of 0.1 eV, the Huang–Rhys factor of 0.74, and the line-broadening of ≈35 nm (it differs somewhat between the 0 → 0 and 0 → μ > 0 transitions).
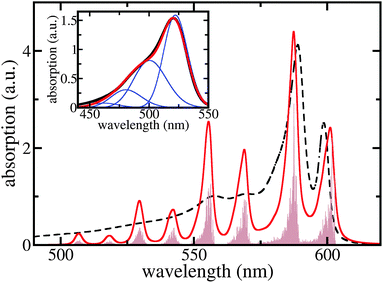 | ||
| Fig. 5 Linear absorption spectra of the C8S3 TDA including a single representative intramolecular vibration per monomer (for details, see text). Brown filled area: stick spectrum, red curve: ≈3 nm broadened stick spectrum, and black dashed curve: measured absorption (cf.Fig. 4). The offset of 0.1 eV due to solvent dispersive shifts is included here. Inset: C8S3 monomer absorption. Red curve: computed absorption spectrum, black curve: measured spectrum, and blue curves: single vibrational level contributions. | ||
To calculate the whole TDA exciton spectrum by including a single vibrational mode per dye molecule we followed ref. 40 and employed the so-called single particle approximation suggested therein (cf. also ref. 27). In this case, exciton states are introduced as 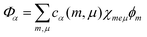 , where χmeμ is the total vibrational wave function with μ = 1…3 vibrational excitations in the excited state of molecule m. The expansion coefficients cα(m,μ) are obtained via the diagonalization of the Hamiltonian, eqn (1), which, however, has been extended upon introducing vibrational contributions in the site energies and excitonic couplings. Now, vibrational satellites appear in the wavelength region at around 550 nm which corresponds to absorption bands observed experimentally. The remaining differences between the calculated spectrum and the experimental data may be caused by the restriction to a single vibrational mode per C8S3 monomer. At this point we cannot exclude that other configurations are possible that lead to additional exciton bands and thus would reproduce more details of the spectra without involving vibrational modes. However, we can state that vibrational modes seem to strongly contribute to the spectra, which is due to the rather large Huang–Rhys factor. We can state further that our model is consistent regarding cryo-TEM figures, optical spectra, electronic structure calculations and MD simulations.
, where χmeμ is the total vibrational wave function with μ = 1…3 vibrational excitations in the excited state of molecule m. The expansion coefficients cα(m,μ) are obtained via the diagonalization of the Hamiltonian, eqn (1), which, however, has been extended upon introducing vibrational contributions in the site energies and excitonic couplings. Now, vibrational satellites appear in the wavelength region at around 550 nm which corresponds to absorption bands observed experimentally. The remaining differences between the calculated spectrum and the experimental data may be caused by the restriction to a single vibrational mode per C8S3 monomer. At this point we cannot exclude that other configurations are possible that lead to additional exciton bands and thus would reproduce more details of the spectra without involving vibrational modes. However, we can state that vibrational modes seem to strongly contribute to the spectra, which is due to the rather large Huang–Rhys factor. We can state further that our model is consistent regarding cryo-TEM figures, optical spectra, electronic structure calculations and MD simulations.
Finally, we would like to comment on a recent work where an environmentally induced heavy-tailed Lévi disorder is utilized to explain an additional low energy fluorescence band for drop-cast samples of 1-D J-aggregates.41 Such a low energy band (90 meV below the general fluorescence band) in principle could also be attributed to a local conformation induced dispersion effect.
III. Conclusions
A novel structure model for a C8S3 TDA together with site-dependent dispersive effects leads to a conclusive interpretation of the general features of the respective linear absorption spectra. Molecules in the inner and outer cylinders of the TDA interact with different environments, and accordingly their dispersive shifts differ. For the considered C8S3 TDA the excitonic coupling is particularly small due to screening and, thus, the observed absorption line splitting is mostly determined by environmental dispersive effects. This splitting, but not the overall shift of the spectrum, would vanish if the dyes formed an uncurved double-walled layer. Accordingly, we consider a long-wavelength absorption line splitting in TDAs a general feature, due to the curvature-induced site-dependent dispersive effect. While we ascribe the energy splitting of the main peaks mainly to an interaction of higher transition densities (non-resonant excitonic coupling), in previous work the splitting was attributed to (resonant) excitonic coupling.5,19,20,21 It can be concluded that the site-dependence of dispersive energies is of key-importance to understand the optical properties of nanostructured molecular dye systems, such as nano-tubular light harvesting dye aggregates. We strongly suspect that this reasoning holds for nanoscaled molecular aggregates in general.Acknowledgements
Financial support from the Deutsche Forschungsgemeinschaft through Sfb 951 and project ME 4215/2-1 (J.M.) and from the Austrian Science Fund (FWF) through project P 24774-N27 (T.R.) is gratefully acknowledged.References
- L. Zhang, D.-A. Silva, Z. Houdao, A. Yue, Y. J. Yan and X. Huang, Nat. Commun., 2014, 5, 4170 CAS.
- J. Strümpfer, M. Sener and K. Schulten, J. Phys. Chem. Lett., 2011, 3, 526 Search PubMed.
- G. D. Scholes and C. Smyth, J. Chem. Phys., 2014, 140, 110901 CrossRef PubMed.
- D. M. Eisele, S. Kirstein, J. Knoester, J. P. Rabe and D. A. Vanden Bout, Nat. Nanotechnol., 2009, 4, 658 CrossRef CAS PubMed.
- D. M. Eisele, C. W. Cone, E. A. Bloemsma, S. M. Vlaming, C. G. F. van der Kwaak, R. J. Silbey, M. G. Bawendi, J. Knoester, J. P. Rabe and D. A. Vanden Bout, Nat. Chem., 2012, 4, 655 CrossRef CAS PubMed.
- T. Fujita, J. C. Brookes, S. K. Saikin and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2012, 3, 2357 CrossRef CAS PubMed.
- J. M. Linnanto and E. I. Korppi-Tommola, J. Phys. Chem. B, 2013, 117, 11144 CrossRef CAS PubMed.
- J. Huh, S. K. Saikin, J. C. Brookes, S. Valleau, T. Fujita and A. Aspuru-Guzik, J. Am. Chem. Soc., 2014, 136, 2048 CrossRef CAS PubMed.
- F. Würthner, T. E. Kaiser and C. R. Saha-Möller, Angew. Chem., Int. Ed., 2011, 50, 3376 CrossRef PubMed.
- H. Lin, R. Camacho, Y. Tian, T. E. Kaiser, F. Würthner and I. G. Scheblykin, Nano Lett., 2010, 10, 620 CrossRef CAS PubMed.
- S. Liu, D. Schmitz, S.-S. Jester, N. J. Borys, S. Höger and J. M. Lupton, J. Phys. Chem. B, 2013, 117, 4197 CrossRef CAS PubMed.
- A. V. Aggarwal, A. Thiessen, A. Idelson, D. Kalle, D. Würsch, Th. Stangl, F. Steiner, S.-S. Jester, J. Vogelsang, S. Höger and J. M. Lupton, Nat. Chem., 2013, 5, 964 CrossRef CAS PubMed.
- E. A. Ermilov, S. Hackbarth, S. Al-Omari, M. Helmreich, N. Jux, A. Hirsch and B. Röder, Opt. Commun., 2005, 250, 95 CrossRef CAS.
- J. Megow, T. Renger and V. May, ChemPhysChem, 2014, 15, 478 CrossRef CAS PubMed.
- 5,6-Dichloro-2-[3-[5,6-dichloro-1-octyl-3-(2-sulfopropyl)-benzimidazol-2-ylidene]-propenyl]-1-octyl-3-(2-sulfopropyl)-benzimidazolium hydroxide.
- H. v. Berlepsch, S. Kirstein, R. Hania, A. Pugžlys and C. Böttcher, J. Phys. Chem. B, 2007, 111, 1701 CrossRef PubMed.
- H. v. Berlepsch, K. Ludwig, S. Kirstein and C. Böttcher, Chem. Phys., 2011, 385, 27 CrossRef.
- K. A. Clark, C. W. Cone and D. A. Vanden Bout, J. Phys. Chem. C, 2013, 117, 26473 CAS.
- C. Didraga, A. Pugžlys, P. R. Hania, H. v. Berlepsch, K. Duppen and J. Knoester, J. Phys. Chem. B, 2004, 108, 14976 CrossRef CAS.
- A. Pugžlys, R. Augulis, P. H. M. van Loosdrecht, C. Didraga, V. A. Malyshev and J. Knoester, J. Phys. Chem. B, 2006, 110, 20268 CrossRef PubMed.
- S. M. Vlaming, E. A. Bloemsma, M. L. Nietiadi and J. Knoester, J. Chem. Phys., 2011, 134, 114507 CrossRef CAS PubMed.
- D. M. Eisele, D. H. Arias, X. Fu, E. A. Bloemsma, C. P. Steiner, R. A. Jensena, P. Rebentrost, H. Eisele, A. Tokmakoff, S. Lloyd, K. A. Nelson, D. Nicastro, J. Knoester and M. G. Bawendi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E3367 CrossRef CAS PubMed.
- F. Haverkort, A. Stradomska, A. H. de Vries and J. Knoester, J. Phys. Chem. A, 2014, 118, 1012 CrossRef CAS PubMed.
- F. London, Trans. Faraday Soc., 1937, 33, 8 RSC.
- H. Zoubi, A. Eisfeld and S. Wüster, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 053426 CrossRef.
- The MD simulations have been carried out using NAMD42 together with the AMBER force field43 as well as the GAFF parameter sets.44 The MD simulations are carried out in a periodic box, the electrostatic interactions were computed using the particle mesh Ewald method.45 The temperature was heated to 300 K and 7 ns of MD simulation with a time-step of 0.5 fs was carried out.
- J. Megow, T. Körzdörfer, M. Sparenberg, T. Renger, S. Blumstengel, F. Henneberger and V. May, arXiv:1411.2818 [cond-mat.mtrl-sci].
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- J. Megow, A. Kulesza, Z. Wang Qu, T. Ronneberg, V. Bonačić-Koutecký and V. May, Chem. Phys., 2010, 377, 10 CrossRef CAS.
- The partial charges have been computed (see ref. 39). The differential dipole moment Δd was fitted to the result of hole burning experiments for similar cyanine dyes (0.7 D < |Δd| < 1.1 D).46 We chose Δd = 1 D and we note that other values within the range will change the absorption spectrum only slightly.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VHC, 2011 Search PubMed.
- T. Renger and F. Müh, Phys. Chem. Chem. Phys., 2013, 15, 3348 RSC.
- N. S. Bayliss, J. Chem. Phys., 1950, 18, 292 CrossRef CAS.
- L. Wenyuan, Z. Fushi, T. Yingwu and S. Xinqi, Acta Phys.-Chim. Sin., 1985, 1, 12 Search PubMed.
- V. V. Shelkovnikov and A. I. Plekhanov, Optical and Resonant Non-Linear Optical Properties of J-Aggregates of Pseudoisocyanine Derivatives in Thin Solid Film, in Macro To Nano Spectroscopy, ed. D. J. Uddin, InTech, 2012 Search PubMed.
- T. Renger, B. Grundkötter, M. E.-A. Madjet and F. Müh, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13235 CrossRef PubMed.
- M. E. Madjet, A. Abdurahman and T. Renger, J. Phys. Chem. B, 2006, 110, 17268–17281 CrossRef CAS PubMed.
- J. Adolphs, F. Müh, M. E.-A. Madjet and T. Renger, Photosynth. Res., 2008, 95, 197–209 CrossRef CAS PubMed.
- The geometry of the monomeric cyanine dye has been optimized at the DFT level; the absorption energy of the first excited state has been calculated in the frame of TDDFT employing the long-range corrected hybrid CAM-B3LYP functional47 and the TZVP atomic orbital basis set48 for all atoms. Atomically centered partial charges (electronic ground and first excited states) and transition charges (only for heavy atoms) have been fitted to the electrostatic potential of the respective charge/transition charge densities by using the CHELPG procedure.49.
- F. C. Spano, J. Chem. Phys., 2002, 116, 5877 CrossRef CAS.
- A. Merdasa, Á. J. Jiménez, R. Camacho, M. Meyer, F. Würthner and I. G. Scheblykin, Nano Lett., 2014, 14, 6774 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- D. A. Case, et al., AMBER 8, University of California, San Francisco, CA, 2004 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- A. Chowdhury, S. Wachsmann-Hogiu, P. R. Bangal, I. Raheem and L. A. Peteanu, J. Phys. Chem. B, 2001, 105, 12196–12201 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361 CrossRef.
| This journal is © the Owner Societies 2015 |
