Sensing sulfur-containing gases using titanium and tin decorated zigzag graphene nanoribbons from first-principles

Abstract

Atom implantation in graphene or graphene nanoribbons offers a rich opportunity to tune the material structure and functional properties. In this study, zigzag graphene nanoribbons with Ti or Sn adatoms stabilised on a double carbon vacancy site are theoretically studied to investigate their sensitivity to sulfur-containing gases (H₂S and SO₂). Due to the abundance of oxygen in the atmosphere, we also consider the sensitivity of the structures in the presence of oxygen. Density functional theory calculations are performed to determine the adsorption geometry and energetics, and nonequilibrium Green's function method is employed to compute the current–voltage characteristics of the considered systems. Our results demonstrate the sensitivity of both Ti- and Sn-doped systems to H₂S, and the mild sensitivity of Ti-doped sensor systems to SO₂. The Ti-doped sensor structure exhibits sensitivity to H₂S with or without oxidation, while oxidation of the Sn-doped sensor structure reduces its ability to adsorb H₂S and SO₂ molecules. Interestingly, oxygen dissociates on the Ti-doped sensor structure, but it does not affect the sensor's response to the H₂S gas species. Oxidation prevents the dissociation of the H–S bond when H₂S adsorbs on the Ti-doped structure, thus enhancing its reusability for this gas species. Our study suggests the potential of Ti- and Sn-doped graphene in selective gas sensing, irrespective of the sensing performance of the bulk oxides.

---

1 Introduction

Graphene nanoribbons (GNRs), strips of graphene with widths on the nanometer scale, have attracted immense interest owing to their unique physical properties. Using simple chemical methods, GNRs have been fabricated with widths of a few nanometers^1–6 and it has been demonstrated that they exhibit tunable energy bandgaps that can be manipulated by changing the width of the nanoribbon.⁷ Furthermore, they exhibit unique ballistic electron transport properties¹ and very large magnetoresistance,² making them more appealing for applications in nanoelectronics than single-walled carbon nanotubes.¹ GNRs are particularly interesting for molecular gas sensing applications compared to graphene because they can be more easily doped and chemically and structurally modified than graphene.⁸

Effective gas sensing requires an interaction between the gas molecule and the GNR, where the interaction should ideally be around 1 eV (weak chemisorption)⁸ to allow for nondestructive photodesorption (gas desorption by lasers that do not disturb the structure of the sensor surface).⁹ A gas molecule can interact with a GNR either through (a) binding to the the edge,^10–12 (b) binding to defect sites in defective GNR or (c) binding to a chemisorbed species on the GNR.¹³ The latter approach has more potential for offering selective sensing because different dopants are expected to exhibit a different reactivity to the various gas species. In this respect, numerous studies have been dedicated to exploring the possibilities of improving graphene sensing abilities by substitutional doping. Dopants, such as boron and nitrogen, have been used to improve gas sensing of CO, NO, NO₂, and NH₃ (ref. 9) and, when doped on carbon nanotubes, for detecting hazardous gases.¹⁴ Al-doped graphene can be sensitive to most of the common gases in air, but it is strongly reactive.¹⁵ This is problematic in sensor reuse.⁹ Sulfur-doped graphene has been shown to have an enhanced sensitivity to NO₂ and NO.¹⁵ Transition metal adatoms are expected to be even more appealing owing to their inherent diversity of chemical properties. Given the ability to perform fine deposition of adatoms into the graphene surface,¹⁶ transition metal adatoms adsorbed on pristine, single vacancy (SV) and double vacancy (DV) graphene sheets have been studied;^17,18 such decorated graphene sheets show more interesting physics, as well as potential diverse applications. Metal adatoms bind more strongly to DV graphene than SV graphene¹⁷ or to pristine graphene¹⁸ (except for lithium), suggesting that a more stable sensing system can be obtained in the adatom-DV configuration.¹⁹ This would suggest that DV graphene is a better choice with respect to sensor recycling. Furthermore, it is possible that combining transition metals with DV GNRs will enhance the sensitivity of GNRs by favouring the adsorption–desorption processes, leading in turn to greater responses and faster response/recovery times.²⁰

A large body of experimental literature has sought to address the sensing capabilities of the transition metal oxides. The seminal review by Eranna et al.²¹ reports a matrix for matching metal oxides against their most favorable gases (see Table 23 in ref. 13). This can also be utilized to identify specific selectivity characteristics of some metal oxides. For example, titanium appears not to respond to sulfur gases while it exhibits significant sensitivity to NH₃, CO, CO₂, and other organic gases. Bulk tin oxides, however, are known to be good sensors for all gases considered by Eranna et al.,²¹ including H₂S and SO₂ gas species. Graphene oxide–tin dioxide nanocomposites were found to be sensitive to NO₂,²⁰ and graphene sheets decorated with tin dioxide were found to be highly selective to propanol.²² Several experimental studies were recently published on the enhanced performance of fullerene–TiO₂–SnO₂ composite structures.^20,22,23 For example, Zhang et al.²³ investigated the performance of TiO₂–carbon nanotube composites as potential SO₂ gas sensors. A theoretical study of titanium adatoms on graphene provided qualitative insight into the applicability of graphene–titanium systems as sensors for water, as well as a nondestructive sensor for nitrogen.²⁴ The authors emphasized the importance of adding an oxygen molecule to the graphene–titanium system to resemble the actual experimental conditions, given that oxygen, present in abundance in the atmosphere, will be very reactive to titanium. That study, however, did not investigate transport properties to evaluate its performance as a resistive sensor, nor consider adsorption of Ti in DV graphene.

In the present work, we study the sensitivity of a titanium or tin atom adsorbed in a double-vacancy zigzag graphene nanoribbon (DV ZGNR) to sulfur-containing gases with and without oxidation, and compare the sensitivity of the titanium-doped DV ZGNR system (Ti/DV ZGNR) to the tin-doped DV ZGNR system (Sn/DV ZGNR). Note that bulk titanium oxide is known to be a poor sensor to these gaseous species.²¹ To our knowledge, the present work is the first contribution towards theoretically predicting the performance of stabilized transition metal decorated graphene ribbons as resistive sensors by computing current–voltage characteristics. We restrict our study to the sulfur-containing gas species H₂S and SO₂ which are known for their remarkable toxicity and corrosivity, as well as pungent smell. The object of our work is to address the following three questions: (1) does the presence of adsorbed oxygen gas improve the sensitivity of the system to the two gas species? (2) Does oxygen improve the reusability of the sensor system to the gas species (that is, avoiding sensor contamination)? (3) Does the adatom/DV ZGNR configuration offer titanium higher sensitivity potential over tin, in contrast to the situation in bulk-oxide structures?

2 Computational details

We perform density functional theory (DFT) calculations with the SIESTA code,²⁵ using the generalized gradient approximation for the exchange–correlation functional as developed by Perdew, Burke and Ernzerhof (PBE).²⁶ SIESTA uses basis sets comprised of numerical atomic orbitals, and approximates the atomic potential in terms of Troullier–Martins²⁷ norm-conserving pseudopotentials. The valence electron configuration of the Ti pseudopotential is 3d²4s², and that of Sn is 5p²5s². The calculated lattice constants are 2.95 Å for hcp titanium 4.92 Å for Fm3m tin and 2.48 Å for graphene in agreement with other ab initio calculations. The auxiliary basis uses a real-space mesh with a kinetic energy cutoff of 200 Ry, and basis functions are radially confined using an energy shift of 0.005 Ry (see ref. 25 for details).

We use a single-ζ plus polarization (SZP) basis set in the relaxation calculations. In the transport calculations, we use single-ζ for C and H atoms, and SZP for the Ti, Sn and O atoms in order to achieve a balance between computational accuracy and finite computational resources. To check the accuracy of using an SZP basis set for these calculations, we compared the adsorption energy of the Ti adatom on the DV ZGNR and the system's geometry to the results obtained using a spin-unrestricted double-ζ plus polarization (DZP) basis set. We found that the adsorption energy with the DZP basis set is only about 2% lower than with the SZP basis set, and the difference in ionic positions is negligible. In addition, the differences between the relative change in current when using a SZP or DZP basis set is negligible.¹⁰

Calculations of the doped DV ZGNRs involves a two-step procedure. In the first step, we perform relaxation of the ionic positions of the doped DV ZGNR structures with the adsorbed gases. The portion of the system subjected to full relaxation is shown in the middle grey-shaded region in Fig. 1 (the scattering region). The atomic positions of the other two regions (left and right electrodes) are fixed during the coordinate optimization iterations. For each gas species, we have tried two initial horizontal configurations (which are symmetric to two other possible configurations), in an attempt to obtain the global minimum structure, which was then used in our transport calculations. As for the Ti- and Sn-doped structures with adsorbed oxygen and H₂S/SO₂, we tried two initial configurations where the H₂S/SO₂ molecule was placed close to the metal atom.

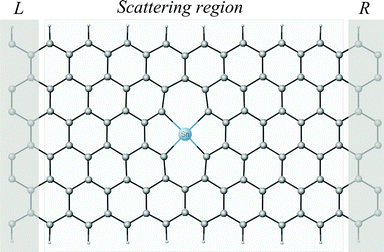Fig. 1 Atomic structure of the Sn/DV ZGNR system containing two electrodes and the scattering region. L: left electrode. R: right electrode.

In the second step, we performed transport calculations based on the nonequilibrium Green's function (NEGF) method as implemented in the TRANSIESTA code.²⁸ TRANSIESTA is a well established implementation of the NEGF transport approach that has been successfully applied in systems with graphene sheets and nanoribbons.^10,29–32

The graphene nanoribbons used in the present work are ZGNR(6), where the 6 indicates the number of zigzag lines across the width of the unit cell. The size of the DV ZGNR supercell is 30 Å × 30 Å × 24.83 Å (118 C atoms and 20 H atoms), and the metal adatom is adsorbed in the DV site. The DV ZGNR system is composed of a scattering region ∼20 Å in length, which is placed between two electrodes, each composed of 14 atoms (12 C atoms and 2 H atoms). The H atoms passivate the terminal carbon atoms on both edges of the DV ZGNR in order to avoid the effect of dangling bonds on transport properties. Fig. 1 depicts the Sn/DV ZGNR system with shaded areas showing the electrode and scattering regions. NEGF theory treats the two short electrodes as effectively semi-infinite leads. The length of the scattering region is long enough to avoid abrupt change in electronic structure due to strain induced by the presence of the adatom²⁹ (thus averaging the resulting strain over a longer region along the propagation direction). We use a spacing between the structure and its neighbouring images of >15 Å in the x and y directions to eliminate interaction between the periodic images (as described in ref. 15 and 17), as well as to prevent clustering of metal atoms which occurs whenever they are brought close to each other (the aggregation problem).²²

We addressed the applicability of our system to wider ZGNRs by comparing the LDOS of Ti-doped DV ZGNR(6) and DV ZGNR(8), and found that the difference of the interaction between the dopant and edge states for these two models is negligible.

Atomic relaxation was performed by allowing all ionic coordinates to move, whilst keeping electrode atoms fixed. This scheme is necessary when performing NEGF computations for two reasons. First, freezing the electrode atoms replicates realistic conditions in molecular transport experiments, in which the electrodes are forced into static positions. Second, if the electrode unit cell atoms are allowed to move, they will not be valid as repeating unit cells for the semi-infinite electrode structure. The adsorption and formation energies are calculated using the following formulae,

E^M_ad = E_{M/DV ZGNR} − E_{DV ZGNR} − E^M_free, (1)

E^gas_ad = E_{gas:M/DV ZGNR} − E_{M/DV ZGNR} − E_gas, (2)

E^gas_{ad oxidized} = E_{gas:oxidized M/DV ZGNR} − E_{oxidized M/DV ZGNR} − E_gas, (3)

E_form = E_ZGNR − E_{DV ZGNR} − 2E_C, (4)

where E^M_ad is the adsorption energy for the metal atom (M = Ti or Sn) on the DV ZGNR, E_{M/DV ZGNR} (E_{oxidized M/DV ZGNR}) is the total energy of the (oxidized) M/DV ZGNR structure, E_{DV ZGNR} is the total energy of the DV ZGNR structure, E^M_free is the total energy of the free metal atom, E^gas_ad is the adsorption energy of a gas molecule on M/DV ZGNR, E^gas_{ad oxidized} is the adsorption energy of the gas molecule on top of the oxidized structure, E_form is the formation energy of the DV in the ZGNR, E_{gas:M/DV ZGNR} (E_{gas:M/oxidized DV ZGNR}) is the total energy of the structure (oxidized structure) with the adsorbed gas molecule, E_C is the total energy of a C atom in pure graphite, and E_gas is the total energy of the isolated gas molecule.

We address sensor reusability here by calculating the adsorption energy of the gas molecule to the adatom/DV ZGNR structure, as well as monitoring the bond length between the sulfur atom of the gas molecule and the adatom. Gas adsorption that involves bond-breaking reactions indicates poor reusability, because the adsorbed gas will irreversibly change the chemistry of the structure (sensor chemical poisoning).

All calculations are performed without spin polarization. This choice was made after performing spin-polarized calculations of the Ti/DV ZGNR structure where we found that the magnetic moment is concentrated around the edge C atoms (∼0.29 μ_B per atom) of the DV ZGNR structure, and a smaller magnetic moment on the Ti atom (∼0.17 μ_B) and the carbon atoms surrounding it. The Sn atom in the Sn/DV ZGNR system has a magnetic moment ∼0 μ_B.

Resistive sensitivity can be quantitatively determined by computing the current–voltage (I–V) diagrams of the structure under bias voltage from the transport properties of the structure, and monitoring the resistance of the structure in the presence of the gas species compared to its resistance without the gas species. We compute the electronic structure of the combined electrodes-scattering structure using a real-space mesh cutoff 200 Ry, and a 1 × 1 × 100 k-point grid (note that z is along the transport direction). The current I is computed according to the Landauer-Buttiker formula,³³

where L and R denote left and right electrodes, respectively, T(E,V_bias) is the transmission function, which is a function of the energy (E) and V_bias, the voltage applied across the electrodes. f_L/R is the Fermi–Dirac distribution function and μ_L/R is the electrochemical potential. T(E,V_bias) is the trace of the square of the transmission amplitude t, and it takes the form

T(E,V_bias) = Tr[t^†t] = Tr[Γ_RG_CΓ_LG^†_C], (6)

where Γ_R/L is the imaginary part of the self-energy, and G_C is the Green's function.

3 Results and discussion

3.1 Adsorption energy and atomic structure

Fig. 2 shows the atomic geometries of the energetically favorable structures with and without adsorbed gases, for both the oxidized (including an O₂ molecule) and the unoxidized cases. Fig. 3 displays a tree diagram of the corresponding adsorption/formation energies defined in eqn (1)–(4), starting from the initial pristine ZGNR, then forming a DV ZGNR (thus a positive energy of formation), and finishing with the adsorption of various gas species on the (oxidized or unoxidized) Ti/DV ZGNR and Sn/DV ZGNR systems. Note that the energy cost of a double vacancy in the ZGNR(6) system in the present work (here 6.82 eV cf.eqn (4)) is slightly smaller than the 7.00 eV in an infinite graphene sheet (compared to 7.32 eV in ref. 37), favoring chemical and structural modification.⁸ The difference in formation energy may be attributed to the edges of the nanoribbons, which allows for greater ionic freedom during relaxation.

Fig. 2 Relaxed atomic geometries for (a) adsorbed Sn (inset shows side view), (b) H₂S and (c) SO₂ adsorbed on Sn/DV ZGNR, (d) oxidized Sn/DV ZGNR, (e) H₂S and (f) SO₂ adsorbed on oxidized Sn/DV ZGNR, (g) Ti adsorbed on DV ZGNR (inset shows side view), (h) H₂S and (i) SO₂ adsorbed on Ti/DV ZGNR, (j) oxidized Ti/DV ZGNR, (k) H₂S and (l) SO₂ adsorbed on oxidized Ti/DV ZGNR. Except for carbon and hydrogen atoms (depicted by medium and small grey spheres, respectively), the atom labels are printed on the atoms. Note in (h) the strong interaction between Ti and the H₂S molecule leads to dissociation of one of the H–S bonds, and the hydrogen atom bonds to a neighbouring edge carbon atom. The frame surrounding the SO₂ molecule in (f) is for visual convenience.

Fig. 3 Adsorption energies of Ti and Sn atoms on DV ZGNR (eqn (1)), adsorption energies of the gas molecules on adatom/DV ZGNR (eqn (2)) and the adsorption energies of the gas molcules on top of the oxidized structures (eqn (3)), and formation energy for DV ZGNR from pristine ZGNR (eqn (4)). N₂, O₂, H₂S, and SO₂, denote adsorbed nitrogen, oxygen, H₂S, and SO₂ molecules, respectively. Similarly, O₂ + H₂S and O₂ + SO₂ denote adsorbed H₂S and SO₂ on top of the O₂ molecule/adatom (oxidized system), respectively.

3.1.1 The Sn/DV ZGNR system. The Sn adatom adsorbs in the DV site in the plane of the nanoribbon (see Fig. 2(a)) with an adsorption energy of −3.59 eV (cf.eqn (1)) and a Sn–C bond length of 2.08 Å. Adsorption of the O₂ molecule at the Sn/DV ZGNR structures increases the O–O bond length of the molecule from 1.32 Å to 1.45 Å (see Fig. 2(d)) with an adsorption energy of −1.77 eV (cf.eqn (2)) and an Sn–O distance of 2.53 Å. This value is larger than the corresponding bond length in our bulk SnO₂ calculation, which is 2.15 Å. For the case of SO₂ adsorbed on Sn/DV ZGNR, the adatom attracts both O atoms to form a rhombic structure of Sn–O–S–O–Sn (S–Sn bond length is 2.97 Å, average O–Sn bond length is 2.35 Å, see Fig. 2(c)) with an adsorption energy of −1.78 eV (cf.eqn (2)). The S–O bond length in adsorbed SO₂ on the unoxidized structure slightly increases from 1.57 Å in an isolated SO₂ molecule to 1.62 Å in Sn/DV ZGNR.

Adsorption of H₂S on Sn/DV ZGNR causes a negligible change in the S–H bond length, and the S-Sn bond length is 2.78 Å (see Fig. 2(b)), which is slightly less than the Sn–S bond length in adsorbed SO₂. The corresponding adsorption energy of H₂S is −1.43 eV, less than the adsorption of SO₂ and O₂.

Considering now the adsorption of H₂S and SO₂ at the oxidized structures, we found that the adsorption of H₂S becomes more favorable than SO₂, where the adsorption energy of the former is −1.35 eV (see Fig. 2(e)) and the latter is considerably lower, namely −0.35 eV (cf.eqn (3)). SO₂ is bonded to one of the oxygen atoms in the adsorbed oxygen molecule, where the distance between S and the closest oxygen atom is 2.15 Å (compared to S–O bond length of 1.53 Å in the SO₂ molecule adsorbed on the oxidized structure) while the S–Sn distance is 4.78 Å. The adsorption of SO₂ on the oxidized Sn/DV ZGNR has insignificant effect on the transport properties of the structure, as we will see later.

3.1.2 The Ti/DV ZGNR system. For Ti/DV ZGNR, the Ti atom is located 1.58 Å above the plane of the DV ZGNR (see Fig. 2(g)) and has an adsorption energy of −5.94 eV. The resulting average Ti–C bond length is 2.10 Å. Adsorption of the O₂ molecule at the Ti/DV ZGNR structure increases the O–O bond length of the molecule from 1.32 Å to 3.37 Å, i.e. the O₂ molecule dissociates and the O atoms chemisorb on the surface. The adsorption energy is −6.92 eV (relatively high due to oxygen dissociation). The Ti–O bond length is 1.88 Å, which is slightly less than the average Ti–O bond length in rutile TiO₂ of 2.03 Å,³⁴ and the C–O distance is 1.39 Å (the closest C atom to the O atom).

In the unoxidised Ti/DV ZGNR structure, the equilibrium position of the adsorbed SO₂ molecule resembles a rhombic structure of Ti–O–S–O–Ti (Ti–S distance is 2.78 Å, the average Ti–O bond length is 2.14 Å, see Fig. 2(i)), with an adsorption energy of −1.32 eV, about 0.4 eV less than that in the Sn/DV ZGNR system. The S–O bond length in adsorbed SO₂ slightly increases from 1.57 Å for an isolated SO₂ molecule to 1.67 Å. The situation for H₂S is quite different. While adsorption on the Sn/DV ZGNR system leaves the S–H bond length almost unchanged, the Ti/DV ZGNR structure breaks one of the H–S bonds (the distance increases from 1.44 Å in an isolated H₂S molecule to 2.62 Å at the surface, see Fig. 2(h)), with a relatively high adsorption energy of −2.35 eV. This signifies the chemical poisoning of the sensor. Note that the broken H–S bond corresponds to the formation of a C–H bond at one of the closest C neighbours to the Ti atom.

Interestingly, the chemical poisoning problem does not occur for the case of adsorbed H₂S on the oxidized Ti/DV ZGNR structure (see Fig. 2(k)). The S–Ti distance in H₂S adsorbed on oxidized Ti/DV ZGNR is 2.77 Å (with an adsorption energy of −0.57 eV), compared to the S–Sn bond length of 4.27 Å when H₂S is adsorbed on oxidized Sn/DV ZGNR (with a higher adsorption energy, namely −1.35 eV). H₂S adsorbed on unoxidized Ti/DV ZGNR induces significant atomic displacements, in the direction normal to the ZGNR plane, of the C atoms surrounding the Ti atom. However, this behaviour is suppressed in the case of the oxidized Ti/DV ZGNR structure. That the H₂S molecule does not dissociate on this surface enhances the sensor's reusability. Moreover, the oxygen molecule binds very strongly to the Ti/DV ZGNR structure with an adsorption energy of −6.92 eV, indicating that reusability in Ti/DV ZGNR applies to the oxidized structure as well. An interesting observation is that both gas species bond more strongly to oxidized Sn/DV ZGNR than to oxidized Ti/DV ZGNR (as seen from the adsorption energies). SO₂ binds weakly to the oxidized Ti/DV ZGNR structure with an adsorption energy of only −0.01 eV and a S–Ti distance of 3.75 Å. As we will see later, this weak bonding deminishes the effect of the presence of SO₂ in the oxidized Ti/DV ZGNR structure on its transport properties.

3.1.3 Nitrogen adsorption. In addition to oxygen, we also studied nitrogen adsorption in our calculations (due to nitrogen's relative abundance in air). We find that nitrogen binds weakly to Sn/DV ZGRN but is stronger for the Ti/DV ZGNR system (−0.14 eV and −1.21 eV, respectively). Since oxygen binds more strongly to the metal/DV ZGNR system than nitrogen, we restricted our investigation to oxidation.

3.2 Current–voltage characteristics

The sensitivity of the proposed systems is characterized using the I–V curves presented in Fig. 4(a) and (b) for bias voltages ranging from 0 to 1 V. V is the bias voltage, and the current I is computed using eqn (5). We investigate the sensor response for the voltage range below 1 V since operation at low voltage is favorable at such small scales. The adsorption of O₂ on the Sn/ZGNR system makes the system virtually saturated with respect to an additional H₂S or SO₂ molecule, therefore the effect of the adsorption of any of the two sulfur gases on the transport properties of the Sn/ZGNR system is negligible. Fig. 4 shows that both systems display improved sensitivity which is manifested by enhanced transport upon adsorption of each of the two gas species, but sensitivity in the Ti/DV ZGNR system is higher than that of Sn/ZGNR. This is contrary to the situation in bulk oxides, in which Sn oxides are known to display stronger sensitivity to sulfur-containing gases than Ti oxides.²¹ Moreover, while Sn/ZGNR is more sensitive to SO₂ than H₂S (Fig. 4(a)), Ti/DV ZGNR is more sensitive to H₂S than SO₂ (Fig. 4(b)). Regarding the sensitivity towards SO₂, it is clear that it is chiefly driven by the presence of oxygen, rather than sulfur, atoms. This can be seen in (Fig. 4(b)), where the system is less sensitive to SO₂ than the other gases, while the effect of adsorbing SO₂ is close to that of adsorbing O₂.

Fig. 4 I–V characteristics for (a) Sn/DV ZGNR and (b) Ti/DV ZGNR systems. The label “pure” denotes the system without any gases. O₂ + gas denotes the adsorption of the gas molecule on the oxidized structure.

Fig. 4(b) shows that the Ti/DV ZGNR system can be used as a selective sensor for H₂S and O₂, but is a poor sensor to SO₂. Interestingly, oxidation in Ti/DV ZGNR does not affect its sensitivity to H₂S. Also note that oxidiation diminishes the role of the S atom in influencing the electronic properties of the system, as seen by the similarity between the sensitivity of the Ti/DV ZGNR system towards SO₂ in the oxidized and the non-oxidized states.

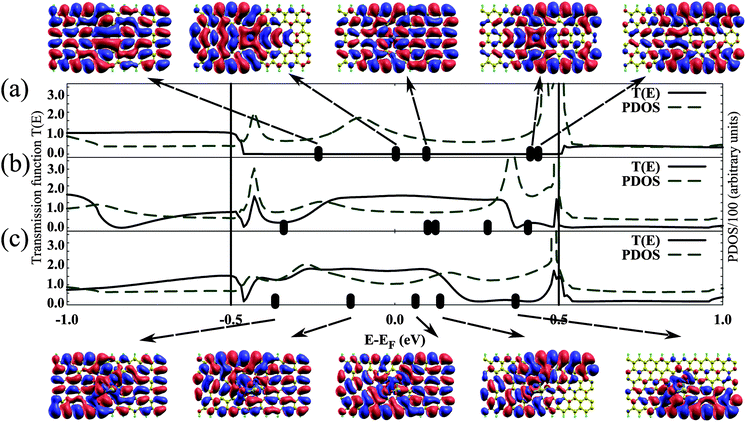
In order to understand the enhanced conductivity of the Ti/DV ZGNR system upon adsorption of H₂S, we studied the transmission functions (T(E), defined in eqn (6)) and the partial density of states (PDOS) of Ti/DV ZGNR (showing the density of states of the atoms in the scattering region) at bias voltage 1.0 V in Fig. 5. We chose V_bias = 1.0 V, since the effect of the adsorption of a H₂S on conductivity of the Ti/DV ZGNR system becomes very obvious as shown in Fig. 4(b), where the current in the Ti/DV ZGNR + H₂S is above 40 μA, while the current in the Ti/DV ZGNR system alone is of the order of a few μA. Therefore, choosing 1.0 V affords a more conclusive statement about the utility of the Ti/DV ZGNR as a sensor for H₂S. Indicated on the x-axis of the plots in Fig. 5(a)–(c) are the locations of the molecular projected self-consistent Hamiltonian eigenenergies, and arrows show the corresponding molecular projected self-consistent Hamiltonian eigenstates (MPSH) isosurfaces. For the case of the Ti/DV ZGNR system without any adsorbed gases, the T(E) of eigenchannels lying within the bias window (the range of energies from −V_B/2 to V_B/2, where V_B is the applied bias voltage which is 1.0 V) is very low, so the contribution of orbitals which exhibit strong coupling between the scattering region and the electrodes, such as LUMO + 1 and HOMO, to the electric current is minimal. The two eigenstates LUMO + 2 and LUMO + 3 are weakly coupled to the electrode, as can be seen in the MPSH isosurface at the top-right of Fig. 5, so they do not contribute to conductance. The adsorption of H₂S strongly influences the electronic properties of the system, as can be seen in Fig. 5(b), where LUMO + 1, LUMO + 2, LUMO + 3 states contribute to transmission. This is in contrast to the transport in pristene GNRs which is dominated by edge states.³⁵ The adsorption of a single H₂S on the oxidized Ti/DV ZGNR system has a slightly different PDOS from that of the un-oxidized Ti/DV ZGNR system with an adsorbed H₂S (Fig. 5(b)), and shows significant transmission within the bias window. In Fig. 5(c), we show the MPSH orbitals that contribute to transmission at the bottom of the figure, where the strong coupling between the scattering region and the electrodes is clear in the isosurfaces (except for the LUMO + 2 orbital which weakly couples the system to the left electrode, and has a very small transmission amplitude).

Fig. 5 Transmission function (T(E), solid, black) and partial density of states (PDOS, dotted, blue) calculated at bias voltages 1 V versus E − E_F (where E_F is the Fermi energy) for Ti/DV ZGNR (a) without any adsorbed gas molecule, (b) with adsorbed H₂S on the un-oxidized Ti/DV ZGNR, (c) with adsorbed H₂S on the oxidized Ti/DV ZGNR. The two vertical lines at −0.5 V and 0.5 V indicate boundaries of the voltage bias window. The small thick vertical lines show the position of the MPSH eigenenergies. For the MPSH isosurfaces, the isovalue 0.01.

4 Conclusion

We have used theoretical calculations to examine the atomic structure and gas sensitivity of Ti- and Sn-doped DV ZGNRs by combining density functional theory and the nonequilibrium Green's function method. We studied the possible enhancements of H₂S and SO₂ sensitivity and selectivity of Ti/DV ZGNR, given that bulk TiO₂ is known to be a poor sensor for sulfur-containing gases. Oxygen interacts strongly with Ti/DV ZGNR via chemisorption, where the molecule completely dissociates on the surface with an O–O distance of 3.37 Å. Oxidation reduces the adsorption energy of both gases on Ti/DV ZGNR considerably, whereas for Sn/DV ZGNR the adsorption of oxygen does not significantly reduces the adsorption energy of the subsequent H₂S, while it significantly reduces the adsorption energy of SO₂. Therefore, the oxidized Ti/DV ZGNR exhibits reusability with respect to both gases, while Sn/DV ZGNR exhibits reusability only with respect to SO₂. Both Ti/DV ZGNR and Sn/DV ZGNR structures exhibit sensitivity to H₂S. Oxidation does not affect the sensitivity of Ti/DV ZGNR to H₂S. However, it prevents the dissociation of the H–S bond when H₂S adsorbs on the Ti-based structure, making it more reusable for this gas species. Both Ti/DV ZGNR and Sn/DV ZGNR structures are poor sensors to SO₂, and Sn/DV ZGNR only exhibit very weak sensitivity to this gas. The present study suggests the applicability of nanosensing doped-graphene nanoribbon based structures as resistive sensors of hazardous gases by utilizing recent advances in experimental manipulation and control of graphene sheets and ribbons, even when the doped material may not exhibit sensitivity properties in the bulk structures.

Acknowledgements

We gratefully acknowledge computational resources provided by the Australian National Computational Infrastructure (NCI) and support from the Australian Research Council.

References

1. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229.
2. J. Bai, R. Cheng, F. Xiu, L. Liao, M. Wang, A. Shailos, K. L. Wang, Y. Huang and X. Duan, Nat. Nanotechnol., 2010, 5, 655.
3. J. Bai, X. Duan and Y. Huang, Nano Lett., 2009, 9, 2083.
4. S. Masubuchi, M. Ono, K. Yoshida, K. Hirakawa and T. Machida, Appl. Phys. Lett., 2009, 94, 082107.
5. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229.
6. J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh and X. Feng, Nature, 2010, 466, 470.
7. M. Y. Han, B. Ozyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
8. B. Huang, Z. Li, Z. Liu, G. Zhou, S. Hao, J. Wu, B. Gu and W. Duan, J. Phys. Chem. C, 2008, 112, 13442.
9. Y. Zhang, Y. Chen, K. Zhou, C. Liu, J. Zeng, H. Zhang and Y. Peng, Nanotechnology, 2009, 20, 185504.
10. R. Chowdhury, S. Adhikari, P. Rees, S. P. Wilks and F. Scarpa, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045401.
11. B. Huang, Z. Li, Z. Liu, G. Zhou, S. Hao, J. Wu, B.-L. Gu and W. Duan, J. Phys. Chem. C, 2008, 112, 13442.
12. Y. Liu, X. Dong and P. Chen, Chem. Soc. Rev., 2012, 41, 2283.
13. H. Terrones, R. Lv, M. Terrones and M. S. Dresselhaus, Rep. Prog. Phys., 2012, 75, 062501.
14. E. Llobet, Sens. Actuators, B, 2013, 179, 32.
15. J. Dai, J. Yuan and P. Giannozzi, Appl. Phys. Lett., 2009, 95, 232105.
16. K. Pi, K. M. McCreary, W. Bao, W. Han, Y. F. Chiang, Y. Li, S.-W. Tsai, C. N. Lau and R. K. Kawakami, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075406.
17. X. Y. Cui, R. K. Zheng, Z. W. Liu, L. Li, B. Delley, C. Stampfl and S. P. Ringer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125410.
18. K. M. Fair, X. Y. Cui, L. Li, C. C. Shieh, R. K. Zheng, Z. W. Liu, B. Delley, M. J. Ford, S. P. Ringer and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014102.
19. Y. Gan, L. Sun and F. Banhart, Small, 2008, 4, 5.
20. G. Neria, S. G. Leonardia, M. Latinob, N. Donatoc, S. Baekd, D. E. Contee, P. A. Russoe and N. Pinnad, Sens. Actuators, B, 2013, 179, 61.
21. G. Eranna, B. C. Joshi, D. P. Runthala and R. P. Gupta, Crit. Rev. Solid State Mater. Sci., 2004, 29, 111.
22. H. Song, L. Zhang, C. He, Y. Qu, Y. Tian and Y. Lv, J. Mater. Chem., 2011, 21, 5972.
23. X. Zhang, J. Zhang, Y. Jia, P. Xiao and J. Tang, Sensors, 2012, 12, 3302.
24. M. I. Rojas and E. P. M. Leiva, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 155415.
25. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. N. Troullier and J. L. Martins, Solid State Commun., 1990, 74, 613.
28. M. Brandbyge, J. L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
29. M. Topsakal, V. M. K. Bagci and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205437.
30. K. Saloriutta, Y. Hancock, A. Karkkainen, L. Karkkainen, M. J. Puska and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205125.
31. J. A. Fürst, M. Brandbyge, A. P. Jauho and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195405.
32. Z. Li, H. Qian, J. Wu, B. L. Gu and W. Duan, Phys. Rev. Lett., 2008, 100, 206802.
33. S. Datta, in Electronic Transport in Mesoscopic Systems, ed. H. Ahmed, M. Pepper and A. Broers, Cambridge University Press, Cambridge, England, 1995.
34. A. Rubio-Ponce, A. Conde-Gallardo and D. Olguin, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035107.
35. J. Baringhaus, M. Ruan, F. Edler, A. Tejeda, M. Sicot, I. A. Taleb, A.-P. Li, Z. Jiang, E. H. Conrad, C. Berger, C. Tegenkamp and W. A. de Heer, Nature, 2014, 506, 349.

---