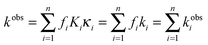Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interplay between water uptake, ion interactions, and conductivity in an e-beam grafted poly(ethylene-co-tetrafluoroethylene) anion exchange membrane†
Tara P.
Pandey
a,
Ashley M.
Maes
a,
Himanshu N.
Sarode
a,
Bethanne D.
Peters
a,
Sandra
Lavina
b,
Keti
Vezzù
bc,
Yuan
Yang
d,
Simon D.
Poynton
e,
John R.
Varcoe
e,
Soenke
Seifert
f,
Matthew W.
Liberatore
a,
Vito
Di Noto
b and
Andrew M.
Herring
*a
aDepartment of Chemical and Biological Engineering, Colorado School of Mines, Golden, CO 80401, USA. E-mail: aherring@mines.edu
bDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, I-35131 Padova, Italy
cVeneto Nanotech, Via San Crispino 106, I-35129 Padova, Italy
dDepartment of Chemistry and Geochemistry, Colorado School of Mines, Golden, CO 80401, USA
eDepartment of Chemistry, University of Surrey, Guildford GU2 7XH, UK
fX-Ray Science Division, Argonne National Laboratory, Argonne, IL 60439, USA
First published on 23rd December 2014
Abstract
We demonstrate that the true hydroxide conductivity in an e-beam grafted poly(ethylene-co-tetrafluoroethylene) [ETFE] anion exchange membrane (AEM) is as high as 132 mS cm−1 at 80 °C and 95% RH, comparable to a proton exchange membrane, but with very much less water present in the film. To understand this behaviour we studied ion transport of hydroxide, carbonate, bicarbonate and chloride, as well as water uptake and distribution. Water uptake of the AEM in water vapor is an order of magnitude lower than when submerged in liquid water. In addition 19F pulse field gradient spin echo NMR indicates that there is little tortuosity in the ionic pathways through the film. A complete analysis of the IR spectrum of the AEM and the analyses of water absorption using FT-IR led to conclusion that the fluorinated backbone chains do not interact with water and that two types of water domains exist within the membrane. The reduction in conductivity was measured during exposure of the OH− form of the AEM to air at 95% RH and was seen to be much slower than the reaction of CO2 with OH− as the amount of water in the film determines its ionic conductivity and at relative wet RHs its re-organization is slow.
1. Introduction
Anion exchange membranes (AEM) are being investigated as an alternative to proton exchange membranes (PEM) in energy conversion devices such as fuel cells, electrolyzers, redox flow batteries, etc.1,2 AEM fuel cells have potential advantages over PEM fuel cells for the direct oxidation of hydrocarbon fuels, such as reduced fuel cross-over, which improves performance with liquid fuels, and higher reaction kinetics at the electrodes under basic conditions, allowing the use of less expensive non-precious metal catalysts and more complex fuels.3–5 As water is a reactant and the ultimate source of oxygen in the products of a direct fuel cell, the study of its transport in AEMs is crucial to their application. Compared to PEMs such as Nafion™, AEMs are still in need of improvements in terms of ionic and water transport, chemical stability, and mechanical properties to develop materials capable of practical fuel cell operations.6 To enable next generation AEMs, it is, therefore, important that the properties of the current AEMs under consideration for fuel cell applications be thoroughly studied.One class of AEMs that has been found to have consistent and desirable properties are synthesized via grafting of cationic functional groups on to preformed polymer sheets, taking advantage of material properties of commercially available polymer films.7–10 Radiation grafted AEMs based on poly(ethylene-co-tetrafluoroethylene) [ETFE] films were the first membranes formed by this synthetic method to demonstrate promising conductivities while maintaining good mechanical characteristics. In this report, we study water uptake properties and ionic transport performance of a quaternary ammonium ETFE radiation grafted polymer membrane (ETFE-g-PVBTMA) AEM, Fig. 1.8,11 Previous characterization of this material has demonstrated that the hydration conditions significantly affect the anionic conductivity.12
 | ||
| Fig. 1 Radiation grafted ETFE-g-PVBTMA membrane consisted of a mixture of both para and meta structures. | ||
Sustained high ionic conductivity is a crucial material property for a competitive fuel cell electrolyte. The most important anion for ionic transport through AEMs is hydroxide (OH−) due to its basicity enabling fast anode kinetics, its small size13 and therefore, high ionic mobility in water as compared to other anions.14 However, rapid reaction of OH− with atmospheric CO2 makes conductivity measurement of the pure OH− form of AEMs a major characterization challenge.1 When the OH− form of an AEM is exposed to atmospheric CO2, the membrane counter-ions become a mixture of carbonate, bicarbonate, and residual OH−, which show reduced overall ionic conductivity.10,15,16
Yanagi et al. observed a sharp decrease in OH− ion concentration in a dynamic OH− concentration measurement as a function of time at ambient conditions.17 For this reason, few studies reporting OH− conductivity in AEMs can guarantee measurement of pure OH− transport within the membrane, making comparison of results problematic. Many researchers report OH− conductivity of membranes measured in water with ambient air exposure, while others report OH− conductivity measured in various concentrations of hydroxide salt solutions.18 AEM fuel cells can also be operated with carbonate ions as the anion transported from cathode to anode. However, Ohmic losses will be higher due to the lower ion mobility of the larger anion and the reactivity of the catalysts at the electrodes will be reduced due to the reduced basicity. This situation is still an improvement over the formation of insoluble carbonate salt formation in alkali fuel cells with liquid electrolytes, which is detrimental to operation and requires operation without exposure to CO2.19,20
In this study the water absorption kinetics and structure in the membranes are elucidated through environmentally controlled FT-IR experiments. Analysis of peak intensity and position migration during hydration gives an understanding of the polymer structure interactions with water. The in-plane conductivity of the AEM was measured in different counter anionic forms including OH− (with no exposure to CO2) as a function of temperature and relative humidity. A dynamic in-plane conductivity study of the OH− form of the membrane during reaction with atmospheric CO2 was also conducted. We also report the self-diffusion coefficients of F− ions in the material that give insights into the ionic channel tortuosity of the membrane. The similar ionic size of F− and OH− ions made F− an acceptable model anion replacing OH− in NMR self-diffusion studies.21,22
2. Experimental
2.1 Materials
The detailed synthetic route of the polymeric membrane is published elsewhere.7,8 The AEM was received in the Cl− form and exchanged to other counter-ions as needed. The procedure for F− exchange has been previously reported.22 Carbonate and bicarbonate forms of the samples were prepared by soaking membranes in 1 M aqueous solutions of sodium carbonate and sodium bicarbonate, respectively. Samples were rinsed repeatedly and then soaked in 18 MΩ cm deionized (DI) water for 12 h. The OH− form of the membrane was prepared using a unique preparation and testing procedure designed to prevent exposure to atmospheric CO2. Samples were converted to OH− form while contained in a CO2 free glovebox. The Cl− form of the membranes were soaked in 1 M aqueous solution of KOH for 12 h, then rinsed and soaked with ultra high purity (UHP) N2 purged DI water until the solution was stable at a neutral pH = 7.0. The sample was then loaded in an airtight cell inside the glovebox before it was taken to the conductivity measurement apparatus.2.2 Chemical characterization
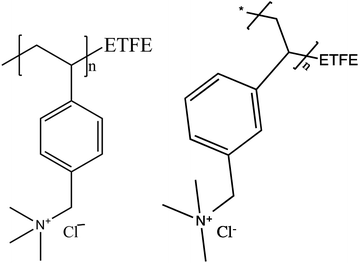
A Dynamic Vapor Sorption (DVS)-advantage instrument by Surface Measurement System™ was used to measure the sorption and desorption of water vapor by the AEM at 30 °C as function of relative humidity. The samples were equilibrated for 3.0 h at 0% RH to measure dry weight and then equilibrated for 1.5 h each at 20, 40, 60, 80 and 95% RH before further water uptake measurements. Experimental conditions were selected to mimic temperature and humidity conditions during FT-IR experiments. The liquid water uptake by the AEM in different anionic forms was studied by measuring the wet and dry membrane weight. The anion exchanged and rinsed membrane samples were kept in DI water for 24 h before wet weight measurements. The membrane samples were vacuum dried at 60 °C for 12 h before dry weight measurements.Water uptake (WU) and λ (the number of water molecules per quaternary ammonium group) are calculated as: WU = 100% × (mrh − mdry)/mdry and λ = WU/100/(IEC × MWH2O) where mrh is the mass of membrane at specific %RH and mdry is the mass of membrane at 0% RH, and IEC is ion exchange capacity of the membrane (1.78 ± 0.02 meq g−1 for this ETFE-g-PVBTMA AEM).11
A FTIR spectroscopy (Nexus™470 FT-IR) was used for collection of IR spectra at a range of temperature and relative humidity (RH) conditions. A liquid N2 cooled MCT detector in attenuated total reflection (ATR) mode was used to collect spectra with 256 scans and a resolution of 8 cm−1. The RH of the test environment was controlled using a custom designed environmental control set up (Fig. S1, ESI†). Humidity was controlled inside the sample oven by adjusting the ratio of the flow of dry and water-saturated N2 (N2 bubbled through DI water) using mass flow controllers (MKS Instrument Inc.). The flow rate of each gas stream was controlled through Labview® software. The sample was heated in the ATR accessory (Specac, Inc.) while the humidity bottle and all gas flow lines were heated using a 4 channel E&M temperature controller.
Self-diffusion coefficients of anions (19F) were determined with a pulsed field gradient stimulated echo (PGSTE) NMR technique as described previously.22
2.3 Quantum mechanical calculations of FT-IR spectra
Optimal geometries and infrared spectra of meta- and para-molecule configuration models of [benzyltrimethylammonium][Br] side groups of the polymer matrix were obtained by density functional theory methods (DFT). DFT calculations were performed on the basis of an all-electron DFT code using the DMol3 program as part of the Material Studio package with double numerical plus polarization basis set and a gradient-connected (GCA) BLYP functional. The internal modes were identified by animating the vibrational modes using the features available in the DMol3 package.23,242.4 Conductivity measurements
The in-plane ionic conductivity of the membrane was measured with varied anionic counter-ions using electrochemical impedance spectroscopy (EIS). Impedance spectra were collected over a frequency range of 0.3 Hz–100 kHz using a 4-probe test cell with Pt electrodes connected to a VMP3potentiostat (BioLogic). In the standard experiments, test cells were placed in a TestEquity (Solatron 1007 H Model) environmental chamber to control the relative humidity and the temperature of the sample environment. The OH− conductivity measurements were conducted under UHP N2 gas flow at different temperature and RH using a BekkTech conductivity cell.25 For the real time conductivity measurements collected during bicarbonate–carbonate formation, the pure form of OH− membrane was exposed to CO2(g) while impedance spectra were collected by switching from UHP N2 to compressed air.The impedance spectra collected using EIS were fit to the Randall circuit using EC-Lab software to obtain the membrane resistances. The conductivity (mS cm−1) was calculated from the measured membrane resistance from: σ = l/Rwt where l is the distance between two electrodes (l = 4.25 mm), R is the resistance (Ω); w and t are the width and thickness of the membrane.
2.5 Small angle X-ray scattering (SAXS)
SAXS measurements were made at Advanced Photo Source, Argonne National Laboratory on beamline 12-ID-B as described previously.263. Results and discussion
3.1 Studies on equilibrated samples
Of the other anions studied HCO3− had a higher anionic conductivity than CO32− and Cl−, Fig. 2. The in-plane conductivity in HCO3− forms of the AEM observed was slightly higher than the reported through-plane ionic conductivity of the membrane at similar temperature.11 The Cl− form membrane had the lowest ionic conductivity, however, 2.5 mS cm−1 at 80% RH and 30 °C: this still represents a fairly mobile anion. The anionic conductivity of Cl− being lower than both the CO32− and the HCO3− is counter-intuitive as the hydration radius of Cl− is smaller than that of both the other anions (Table 1).
| Anions | OH− | HCO3− | CO32− | Cl− | |
|---|---|---|---|---|---|
| 95% RH Ea (kJ mol−1) | 19 ± 2 | 29 ± 1 | 29 ± 2 | 24 ± 4 | |
| 80% RH Ea (kJ mol−1) | 19 ± 3 | 27.3 ± 0.7 | 26.6 ± 0.7 | 32.6 ± 0.4 | |
| λ | Literature, anion solvation (in H2O, 27 °C) | 4.013,31 | 6.932 | 8.732 | 629 |
| Measured (in membrane, 95% RH, 30 °C) | 4.4 ± 0.1 | 3.5 ± 0.1 | 4.2 ± 0.1 | 3.7 ± 0.2 | |
| Measured (in membrane, liquid water) | 14 ± 2 | 15 ± 2 | 20 ± 4 | 19 ± 3 | |
| Hydrated radius (Å) | 3.0013 | 5.633 | 3.9434,35 | 3.3234 | |
To get further insights into the differences in the anionic conductivities of the various anions in this AEM, we measured the water uptake from both vapor and liquid water. Water uptake for the Cl− exchanged film is relatively easy to measure as it is not necessary to protect the film from atmospheric CO2(g). The films swells little, and after steady water uptake with increasing RH obtains a λ value (number of waters per charge carrier) = 3.7 was obtained at 95% RH (Fig. 3). The λ values at both 80% and 95% RH are far lower than the 6, the commonly accepted hydration value for Cl− in solution.29 This explains the low anionic conductivity of Cl− in these films when equilibrated with water vapor: insufficient water is present in the membrane to solvate the anion and so its mobility is impaired. The story is also the same for HCO3− and CO32−. When the films with these anions are equilibrated with water vapor, insufficient water is present in the AEM to solvate the anion, Table 1. The higher anionic conductivities of these anions when compared to Cl− could be because they are in equilibrium with some OH− anions in aqueous solution and that transport of OH− is contributing to the overall ionic conductivity of the film. When λ was measured for the various films in liquid water the values where very much higher, 14 ± 2 for OH−, 15 ± 2 for HCO3−, 20 ± 4, for CO32−, and 19 ± 3 for Cl−, Table 1. Clearly in liquid water the film is equilibrated with sufficient water to solvate the anions present in the film.
 | ||
| Fig. 3 λ values and gravimetric water uptake for the ETFE-g-PVBTMA AEM in the Cl− form as a function of %RH at 30 °C. | ||
The data presented in Fig. 2 show a slight non-linear dependence in the Arrhenius plot. This indicates that the data instead fit with Vogel–Tammann–Fulcher (VTF) behavior, in which polymer segmental motion enhances ion transport across the membrane.30 However, the deviations for these data were small and when the data were fit to the Arrhenius equation and compared to a VTF fit, the Ea values obtained where within error, Table 1. The lowest Ea was observed in the OH− form of the membrane, 19 kJ mol−1 at both 95% and 80% RH. Ea for CO32− and HCO3− conductivity were within 1 standard deviation of each other at both RHs studied, ca. 28 kJ mol−1. For Cl−, we observed 24 and 33 kJ mol−1 at 95% and 80% RH, respectively. OH− anion in this AEM, when equilibrated with water vapor, does have sufficient water to be hydrated and so it is of no surprise that the Ea we measured was the lowest observed for the anions studied; this anion is also capable of conduction via an additional, Grotthuss hopping, mechanism. HCO3− and CO32− have higher Ea values that are independent of RH, which could reflect their larger ionic radii or that ionic transport is dominated by a small amounts of OH− anion present. Cl− anions can only move by a vehicular mechanism, which leads to an Ea for conductivity, that is dependent on RH due to the water being available to solvate the anion decreasing with RH (and so hinder its movement).
 | ||
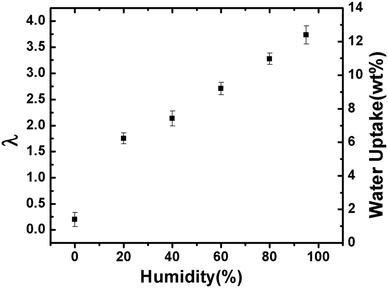
| Fig. 4 Self diffusion coefficient of F− ions through the AEM at 100% RH as a function of diffusion time (Δ). | ||
If the mean squared displacement of the F− ions is short, i.e., short Δ compared to the space available for diffusion, ions do not encounter the wall effects. As the Δ increases, the restrictions of the solid wall of the channel become more effective for ionic diffusion. At longer Δs, the diffusion coefficient reaches a constant value (D∞) which is no longer time dependent.
Consider α = Db/D∞, where α reflects the degree of structured tortuosity of diffusion path exhibited by a specific diffusion pathways. For Δ > 100 ms, the diffusion is not time limited and we can assume DΔ=200ms = D∞. The calculated tortuosity value close to 1 indicates straight ionic channels. The hypothesis of straight ionic channels is compatible with the fabrication method of this AEM that used e-beams that were applied in a direction that was normal to the polymer sheet; this demonstrates a possible advantage of functionalizing membranes using the e-beam grafting method in the through plane direction.
Since the gradient is only applied in the z direction, displacement of F− ions can be calculated using 〈z2〉 = 2Dt.36 It is evident from the Fig. 5 that as Δ is increased, the total displacement increases fairly linearly showing a low restriction to F− diffusion in the channels of the AEM. Certain ionic liquids have shown similar unrestricted behavior in extruded Nafion® 117 (N117).37Ea for F− self-diffusion at Δ = 100 ms was calculated using the temperature range 30 °C to 55 °C. The obtained activation energy value of 17.4 kJ mol−1 is comparable to the activation energy of in-plane conductivity of membranes in the OH− form and water diffusion in Nafion® N117.38 The surface to volume ratio (S/V) of a cylindrical pore can be calculated by applying the Mitra equation of diffusion to time dependent diffusion experiments.39 It was found that the S/V ratio varies largely from 0.012 to 0.042 μm−1 with increasing temperature. This variability (deviation from Mitra equation) can be accounted for as the Mitra equation is valid only for small diffusion times, when the ions don't encounter the curvature or tortuosity of the AEM's channels. As stated earlier, the network of cavities and the tortuous path of the channel are responsible for the exact value of self-diffusion of F− ions.
 | ||
| Fig. 6 FT-IR ATR spectra of ETFE-g-PVBTMA AEMs at selected RHs between 0–95%. The spectra are normalized to the polymer backbone δ(CH) peak at 1323 cm−1 for presentation and analysis purposes. | ||
The profiles of Fig. 6 are the result of overlapping of spectral features that are typical of water molecules embedded in membranes and the vibrational modes of polymer matrix. The vibrational modes of water molecules consist of stretching and bending vibrations respectively in the regions 3600–3100 cm−1 and 1800–1500 cm−1. The intensity of these modes increases with RH (as expected). Peaks in the regions 3100–2800 cm−1 and lower than 1500 cm−1 are associated with the host-polymer vibrational modes.
The spectra are assigned correlatively, and the polar side group assignment is confirmed by DFT calculations, which were performed as described in the experimental section. The DFT calculations included ETFE-g-PVBTMA side chains of both meta (m) and para (p) benzyl trimethyl ammonium groups as shown in Fig. 7. Peak assignments are summarized in Table 2.
 | ||
| Fig. 7 View of the meta (m) and para (p) molecular configurations of [benzyltrimethylammonium][Br] described in VTF models. | ||
| FT-IR ATR experimental frequenciesa | meta model | para model | Assignmentb | Ref. | ||
|---|---|---|---|---|---|---|
| Calculated frequencies | Mode description | Calculated frequencies | Mode description | |||
| a Relative intensities are reported in parentheses; vs very strong; s strong; m medium; w weak; vw very weak; sh shoulder. b ν: stretching; δ: bending; r: rocking; sc: scissoring; ip: in-plane; oop: out-of-plane; a: antisymmetric mode; s: symmetric mode; hy: hydroxyl groups of water involved in hydrogen bonds; δ(H2O)n: bending associated to bulk water; δ(H2O)2: bending associated to water dimmers; [N+]: referred to tri-methyl-ammonium group; [bkb]: vibration localized mainly on the carbon chain representing the polymer backbone; [ring]: vibration involving phenyl ring; δ[ETFE] bending of the fluorinated backbone; δ(C–CH2–N): bending of the angle between phenyl ring, CH2 bridging to N and N atom; [link]: referred to the C atom bridging phenyl side group to the main backbone. | ||||||
| 3405(vs) | ν a(OH) | 40 | ||||
| 3240(sh) | ν hy(OH) | 40 | ||||
| 3024(w) | 3027(21) | ν(CH3)[N+] | 3028(20) | ν(CH3)[N+] | ν(CH3) [N+] | 41 |
| 2924(w) | 2917(86) | ν(CH3)[N+] | 2905(107) | ν(CH3)[N+] | ν a(CH2) | 40 |
| 2858(vw) | 2898(54) | ν(CH2)[N+] | 2872(79) | ν(CH2)[N+] | ν s(CH2) | 40 |
| 1643(w) | δ(H2O)n | 42 | ||||
| 1558(vw) | δ(H2O)2 | 42 | ||||
| 1485(w) | 1483(22) | {δ(CH2) + δ(CH3)}[N+] | 1482(16) | {δ(CH2) + δ(CH3)}[N+] | {δ(CH2) + δ(CH3)}[N+] | 41 |
| 1454(m) | 1454(14) | sc(CH2)[bkb] | 1458(37) | {δ(CH2) + δ(CH3)}[N+] | {δ(CH2) + δ(CH3)}[N+] | 41 |
| 1380(vw) | 1385(6) | {δ(CH2) + δ(CH3)}[N+] | 1391(4) | {δ(CH2) + δ(CH3)}[N+] | δ s(CH3) | 41 |
| 1379(6) | {δ(CH) + δ(CH2)}[bkb] | 1382(3) | {δ(CH) + δ(CH2) }[bkb] | |||
| 1323(w) | 1305(11) | {δ(CC) + δ(CH) + δ(CH2)}[bkb] + δ(ring) | 1315(16) | {ν(CC) + δ(CH)}ip[ring] + {δ(CH) + δ(CH2) + ν(CC)}[bkb] | δ[ETFE] + ν(CC) + ν(CH) + δ(ring) + ν(CF) | 43 |
| 1250(s) | 1251(2.1) | {δ(CH2) + δ(CH3)}[N+] | 1249(1) | {δ(CH2) + δ(CH3)}[N+] | ν(CC) | 41 |
| 1242(sh) | ||||||
| 1173(vs) | 1178(38) | δ ip(CH)[ring] + ν(CC)[bkb] | 1173(32) | {δ(CH) + ν(CC)}ip[ring] + {ν(CC) + ν(CF)}[bkb] + δ(CH)[link] | δ(CH)[ring] + ν(CF2) | 41 |
| 1115–1119(w) | 1115(426) | ν(CF) | 1116(4) | δ(CH3)[N+] | δ(CH3)[N+] + ν(CC) + ν(CF) + δ(CH) | 41 |
| 1053(vs) | 1053(0.1) | δ(NCH)[N+] | 1066(37) | {ν(CC) + ν(CF) + δ(CH)}[bkb] | ν(CN)[N+] | 41 |
| 976(w) | 980(36) | δ oop(CH)[ring] + δ(C–CH2–N) | 979(5) | {δ(CH2) + δ(CH3)}[N+] | δ(C–CH2–N) + δ(CH3)[N+] | 41 |
| 935(vw) | 941(74) | δ(CH)oop[ring] + ν(CN) + ν(CF) | 942(10) | δ(CH)oop[ring] | δ(CCH) | 41 |
| 887(vw) | 888(5) | δ(CH)oop[ring] + ν(CN) + r(CH2)[bkb] | 890(20) | r(CH2)[bkb] + ν(CN) | r(CF2 + CC + CCC) | 41 |
| 798(vw) | 799(3) | {δ(CH) + δ(CC)}oop[ring] | 811(5) | δ(CH)oop[ring] | δ(CCH) | 41 |
| 741(vw) | 751(24) | δ(CH)oop[ring] + δ(CCC)ip[ring] + r(CH2)[bkb] | 748(9) | {δ(CH) + δ(CC)}oop[ring] + ν(CN) + ν(CF) | δ(CCH) | 41 |
| 690(vw) | 687(2) | {δ(CH) + δ(CCC)}oop[ring] + ν(CN) + ν(CF) | 672(25) | {δ(CH) + δ(CCC)}oop[ring] + ν(CN) + ν(CF) | δ[N+(CH3)3] | 41 |
| 652(vw) | 636(18) | δ(CCC)ip[ring] | 643(1) | δ(CCC)ip[ring] | δ(ring) | 41 |
| 598(vw) | 597(18) | sc(CF2) | 620(3) | δ(CCC)ip[ring]+ν(CF) | δ(CCF) | 41 |
| 552(vw) | 552(3) | δ(CF) | 551(1) | sc(CF2) + r(CH2) + δ(CH)oop[ring] + ν(CN) | 41 | |
The results indicate that as the concentration of water is raised, the peaks associated to the water domains embedded in materials and the stretching and bending modes of –CH2–N(CH3)3 groups are both significantly influenced. These observations demonstrate: firstly, that the secondary structure of the backbone host polymer, in accordance with other studies,30 is not influenced by the vapor–solid interactions and secondly, that the H2O absorption process occurs by a number of processes such as insertion–diffusion and aggregation of H2O molecules along the hydrophilic domains. These events are selective modulation of only the polar side groups of the host materials. Further confirmation is obtained by analyzing the dependence on RH% of the difference FT-IR ATR spectra shown in Fig. 6. These spectra are obtained by first normalizing the profile to the band at 1323 cm−1 and then subtracting the RH = 0% spectrum from those recorded at RH > 0%. Note that the intensities of the ν(OH) stretching and δ(H2O) bending modes that are associated with the water domains present in AEM, 3405 cm−1 and 1640 cm−1 respectively, both show the same behavior of ΔI versus RH (inset Fig. 8).
In addition, Fig. 7 and 8 show the modes diagnostic of H2O⋯TMA+ cation interactions, observed at 3023 cm−1 and in the region from 1660 to 1500 cm−1. The mode at 3023 cm−1 is assigned to the ν(CH3)[N+] stretching mode of the TMA+ groups (Fig. 9a). The two peaks at 1643 and 1558 cm−1 (Fig. 9b) correspond to the bending vibrations of water molecules forming in bulk membranes: water aggregates [(H2O)n] and water dimer [(H2O)2]. In accordance with other studies on Nafion®, δ[(H2O)2] corresponds to the bending vibrations of water in dimer form.42 These water dimer molecules represent the water forming the solvation shell of the TMA+ groups. The dependence on RH of the ν(–N(CH3)3) and δ[(H2O)2] peak frequencies (Fig. 9c) show that these two modes are strictly correlated together, indicating that the –CH3 groups of the TMA+ cations are directly interacting with a water molecule solvation shell that mostly consists of water dimers. Indeed, as RH increases, δ[(H2O)2] decreases due to a reduction of the bending constant force from the extension of inter-dimer interactions in TMA+ solvation shell. Conversely, the ν(–N(CH3)3) rises due to an increase of the force constant of the C–H bond. It is expected that the [(H2O)2] solvation shells are interconnected with bulk [(H2O)n] water aggregates.
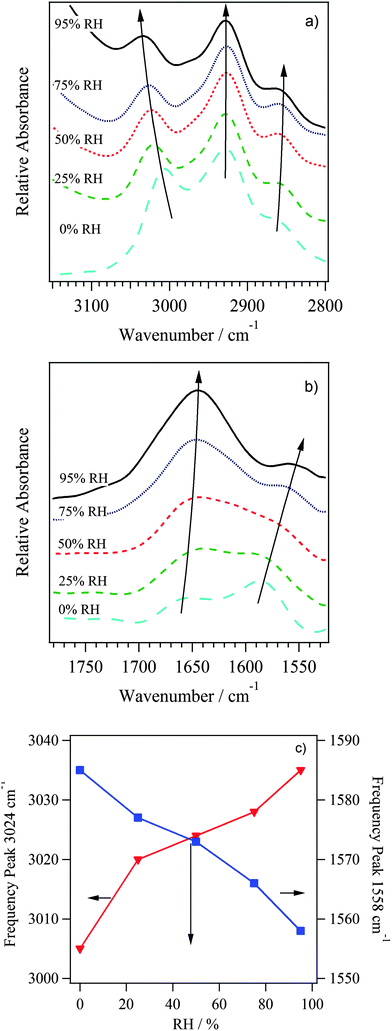 | ||
| Fig. 9 Detailed view of regions (a, b) that were highlighted in Fig. 8. (c) Shift in frequencies of ν(–N(CH3)3) and δ[(H2O)2] peaks with RH, demonstrating correlation. | ||
Taken all together, vibrational studies allowed us to detect that: (a) the secondary structure of host polymer is not dependant on the RH; and (b) the overall water amount adsorbed in bulk membranes is distributed in two domains (water aggregates and water dimers) coordinating the polar side chains of host polymer; and (c) water dimers are interacting with host polymer through C–H⋯OH2 interactions, where C–H belongs to –CH3 groups of the quaternary ammonium groups.
3.2 Transient measurements on the AEM
 | ||
| Fig. 11 Dependence with time of the Ib/I0 intensity ratios (the intensity of the band at 3405 cm−1, ν(OH) vibrational mode, respectively for the sample at t and at t = ∞ s) and of the percent relative humidity (blue circles). Ib and I0 are intensity values measured at t = 0 and t = ∞ s, where t = 0 s is time of gas flow change from dry to saturated N2. Fit line corresponds to eqn (10) that is derived in the main text below. | ||
In order to visualize the behavior of Fig. 11, keeping in mind the conclusions in the above section from the FT-IR vibration assignments, the polymer membrane can be imagined as illustrated in Fig. 12.
There are many sites (labeled Mi) in the bulk membrane that can potentially uptake water from the bulk gas environment with water activity, [a], forming domains of water aggregates (labelled Di). Molecules forming Di can then proceed to solvate cationic structures attached to the polymer chains, thus interacting with the salted site and forming a solvation shell (labelled Ci).
To understand the interactions between gas-phase water and the various domains present in the membrane, a formalism is developed as follows. At any time, there is a distribution of potential Mi domains, Di aggregates, and Ci solvation shells. Thus, the process of absorption, diffusion, aggregation and solvation can be described for every ith site (i = 1, 2, 3…n) with the following reaction steps:
 | (1) |
Furthermore, the overall reaction rate for the process described by eqn (1) can be written in terms of the disappearance of reactant:
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 fi is the fraction of the ith sites, [Mi] is the concentration at equilibrium of the potential ith sites, and [Di] is the concentration of the ith water aggregate in the bulk membrane at the equilibrium. The fractions of each type of site must satisfy the following condition:
fi is the fraction of the ith sites, [Mi] is the concentration at equilibrium of the potential ith sites, and [Di] is the concentration of the ith water aggregate in the bulk membrane at the equilibrium. The fractions of each type of site must satisfy the following condition: 
Assuming that at different [a], the numbers of sites holding water are negligible as compared to the potential sites to be filled in the bulk (i.e. [Di] ≪ [Mi]), we obtain:
 | (6) |
and where
If we consider that the following relation for the water activity is also valid for each time:
| [a]0 = [a] + [a]b | (7) |
| [a]b = [a]0{1 − eξt} | (8) |
It is evident that for t → ∞ [a]b → [a]0 = [a]∞ where [a]∞ is the maximum concentration that can be absorbed at time t → ∞.
Finally, eqn (8) can be defined in terms of experimental values by relating the intensity of FT-IR peaks to the water activity ([a]) with a Beer–Lambert law:
| I = εl[a] | (9) |
By substituting eqn (9) into eqn (8) for each condition of [a], we obtain a direct description of our experimental data:
 | (10) |
Here, Ib and I0 are the intensity of ν(OH) peak at 3405 cm−1 at t and t = ∞, respectively. The fitting results shown in Fig. 9 show that eqn (10) is very closely mimicking the experimental data, resulting in a rate constant of ξ = 9.05 ± 0.4 × 10−4 s−1, which fully describes the water uptake processes in this AEM. This value is of the same order of magnitude as rate constants of water uptake seen in perfluorinated PEMs such as Nafion®.44 This model allowed us to understand the role of the two kinds of absorption sites in the overall process of water uptake in the studied AEM and will allow future quantitative comparison of the water absorption dynamics between AEMs.
All together, the analyses of water absorption through FT-IR lead to conclusion that two types of water domains exist within the radiation-grafted AEM. In the first type of domain, water is solvating the polar groups, interacting closely with the side chains and influencing the vibration modes of the polymer-bound quaternary ammonium cations. This close binding of water is kinetically described by the kinetic constant (κ) in the model presented above. The FT-IR peak around 1580 cm−1 is evidence of dimer pairs of water molecules. This peak shifts toward lower frequencies as RH increases thus demonstrating that the solvation shells of [(H2O)2)] pairs are directly correlated with the C–H stretch shift to higher frequencies of the quaternary ammonium methyl groups. As water is added, the dimers interact more strongly with the hydrogen atoms of the –CH3 of the quaternary ammonium groups, thus increasing the C–H force constant and the methyl groups' C–H stretching frequency. This evidence allows us to hypothesize that dimer water molecules are closely interacting with the side chains through the TMA+ groups, forming the solvation shell. In the second type of domain, water exists in aggregates within the membrane bulk. The absorption of water into these aggregates is described by the equilibrium constant K. Evidence of these water aggregates appears as the FT-IR band at 1650 cm−1, with behavior like bulk liquid water. As expected this peak does not shift in frequency with increased hydration of the membranes confirming that interactions of water molecules with the host polymer are negligible.
 | ||
| Fig. 13 In-plane conductivity versus time of an ETFE-g-PVBTMA AEM initially in the OH− form when exposed to compressed air in a RH and temperature controlled environment. Dotted lines represent the ionic conductivity of the AEM in pure anion forms. All measurements performed at 60 °C and 95% RH. Solid red line corresponds to the fit of data with eqn (15). | ||
Membrane degradation was not observed when comparing the FT-IR before and after the conductivity measurements, so the decrease in performance was attributed to the reaction of CO2 and OH− to form HCO3− and/or CO32− anions according to the reactions (R1) and (R2).32
| OH− + CO2 → HCO3− | (R1) |
| OH− + HCO3− ↔ CO32− + H2O | (R2) |
The decrease in conductivity appears to follow the trend of a first order reaction, leading to the hypothesis that the reaction of OH− anions predominantly proceeds through reaction (R1). This was tested by developing a kinetic model of the depletion of the concentration of OH− in the membrane ([OH−]) and related this to measured conductivity (σ). Full derivation is included as ESI.†
The rate expression of (R1) leads to:
| [OH−] = [OH−]0·e−k·pCO2t | (11) |
The conductivity of each ion can be defined using the Nernst–Einstein equation:
 | (12) |
 | (13) |
Knowing that the measured conductivity at any time (σ) is the sum of the conductivity of each ionic species present, we can use eqn (12) and (13) and a reactant balance to write:
| σ = σ02·[OH−]0 + (σ01 − σ02)[OH−] | (14) |
Finally, inserting eqn (11) and combining the constant terms, conductivity is defined as:
| σ = a + b·e−kobst | (15) |
Yanagi and Fukuta have shown that the ionic charge density of OH− decreases when exposed to ambient conditions, reducing the ionic conductivity compared to pure OH− form of a Tokuyama A201 AEM membrane. Their study observed the reaction of OH− in the membrane with air to form the combination of CO32− and HCO3− in <30 min.17 Previous researchers have assumed that exposure to CO2 quickly reduces the conductivity of OH− form AEMs to the values similar to the CO32− and HCO3− forms.45–47 The decrease in conductivity of the OH− form of the AEM when exposed to air was slower in this study as compared to the OH− conversion time seen in a previous ATR kinetic study in a poly(ethyleneimine) AEM.45 This is almost certainly because of the re-organization of water in the film, the measurement performed at 95% RH and the film in the CO32−/HCO3− forms must loose water as compared to the hydroxide form, not surprisingly under such humid conditions, this proves to be slow process.
The ratio of the diffusion constants of the ions can also be written in terms of the experimental constants as:
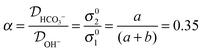 | (16) |
4. Conclusions
The chemical and ionic conductivity characteristics of an electron-beamed radiation, ETFE-g-PVBTMA anion exchange membrane (AEM) were investigated to determine the effect of counter-ion species and the material's interaction with water. The method of fabrication of this film, e-beam irradiation normal to the plane of a rigid engineering plastic, followed by post functionalization, gives rise to a unique microstructure. In-plane conductivities were measured using EIS with the EFTE-g-PVBTMA membrane in HCO3−, CO32−, Cl− and OH− anion forms. The stability of the AEM was tested by IR studies and no degradation was observed after OH− conductivity measurements. The high OH− conductivity (0.112 ± 0.020 S cm−1 at 95% RH and 0.062 ± 0.003 S cm−1 at 80% RH, both at 60 °C) shows a performance that approaches that of perfluorosulfonic acid proton-exchange membranes, such as Nafion™. This is because the material has limited swelling, but as we have shown the vapor equilibrated sample at 95% RH has just enough water, corresponding to a λ = 4 to enable rapid transport of OH−. Additionally the e-beam grafting synthesis technique results in the formation of straight, low tortuosity paths in the AEM, shown by the constant self-diffusion coefficient values of F− ions in the AEM, measured over a range of diffusion times.The analyses of water absorption using FT-IR led to the conclusion that the fluorinated backbone chains do not interact with water and that two major types of water domains exist within the AEM. In the first type of domain, water is solvating the polar (cationic) groups, interacting closely with the polymer side chains and influencing the vibration modes of the polymer bound quaternary ammonium cations. The shift towards lower frequencies of the peak related to [(H2O)2)] water dimer pairs (ca. 1580 cm−1) as the RH was increased is correlated with the shift to the higher frequencies of the C–H stretch mode (ca. 1580 cm−1) related to the methyl groups of the polymer bound quaternary ammonium cations. This close binding of water is described by the kinetic constant (κ) in the model derived in this paper. In the second type of domain, water exists in aggregates within the membrane bulk. The absorption of water into these aggregates is described by the equilibrium constant K in the derived model. Evidence of these water aggregates appears in FT-IR at 1650 cm−1, with bulk liquid water like behaviour; i.e. no shift in peak frequency with changes in RH.
The reduction in conductivity was measured during exposure of OH− form AEM to (CO2 containing) air. The OH− conductivity dropped with time and approached the conductivity value measured with a HCO3− AEM. The kinetic model derived for this conductivity decrease revealed that OH− reacts primarily to create HCO3− ions, with a quasi 1st order reaction rate constant of 1.063 × 10−5 ± 0.011 × 10−5 s−1. The calculated ratio of diffusion coefficients (α) of 0.35 matches closely to the ratio of the mobility of each ion in dilute aqueous solutions (α0). This evidence is in agreement with other studies demonstrating that the overall conductivity of in ETFE radiation-grafted AEMs occurs by the ion exchange between delocalization bodies. In this case, the long-range charge exchange takes place through the water aggregates present in the AEM.
Acknowledgements
The authors would like to thank the Army Research Office for support of this research under the MURI program, grant W911NF-11-1-0462, and The Colorado School of Mines NMR facility funded by National Science Foundation under the an MRI grant CHE-0923537. The anion-exchange membranes were fabricated and characterized using funds from EPSRC Grant EP/I004882/1. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.Notes and references
- M. A. Hickner, A. M. Herring and E. B. Coughlin, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1727–1735 CrossRef CAS.
- J. R. Varcoe, P. Atanassov, D. R. Dekel, A. M. Herring, M. A. Hickner, P. A. Kohl, A. R. Kucernak, W. E. Mustain, K. Nijmeijer, K. Scott, T. Xu and L. Zhuang, Energy Environ. Sci., 2014, 7, 3135–3191 CAS.
- J. R. Varcoe and R. C. T. Slade, Fuel Cells, 2005, 5, 187–200 CrossRef CAS.
- G. Couture, A. Alaaeddine, F. Boschet and B. Ameduri, Prog. Polym. Sci., 2011, 36, 1521–1557 CrossRef CAS PubMed.
- G. Merle, M. Wessling and K. Nijmeijer, J. Membr. Sci., 2011, 377, 1–35 CrossRef CAS PubMed.
- M. R. Hibbs, M. A. Hickner, T. M. Alam, S. K. McIntyre, Cy H. Fujimoto and C. J. Cornelius, Chem. Mater., 2008, 20, 2566–2573 CrossRef CAS.
- H. Herman, R. C. T. Slade and J. R. Varcoe, J. Membr. Sci., 2003, 218, 147–163 CrossRef CAS.
- J. R. Varcoe, R. C. T. Slade, E. Lam How Yee, S. D. Poynton, D. J. Driscoll and D. C. Apperley, Chem. Mater., 2007, 19, 2686–2693 CrossRef CAS.
- M. Mamlouk, J. A. Horsfall, C. Williams and K. Scott, Int. J. Hydrogen Energy, 2012, 37, 11912–11920 CrossRef CAS PubMed.
- J. Fang, Y. Yang, X. Lu, M. Ye, W. Li and Y. Zhang, Int. J. Hydrogen Energy, 2012, 37, 594–602 CrossRef CAS PubMed.
- O. I. Deavin, S. Murphy, A. L. Ong, S. D. Poynton, R. Zeng, H. Herman and J. R. Varcoe, Energy Environ. Sci., 2012, 5, 8584–8597 CAS.
- J. R. Varcoe, Phys. Chem. Chem. Phys., 2007, 9, 1479–1486 RSC.
- M. E. Tuckerman, A. Chandra and D. Marx, Acc. Chem. Res., 2006, 39, 151–158 CrossRef CAS PubMed.
- E. Cussler, Diffusion – mass-transfer in fluid systems, 1997 Search PubMed.
- J. Yan and M. A. Hickner, Macromolecules, 2010, 43, 2349–2356 CrossRef CAS.
- J. A. Vega, C. Chartier and W. E. Mustain, J. Power Sources, 2010, 195, 7176–7180 CrossRef CAS PubMed.
- H. Yanagi and K. Fukuta, ECS Trans., 2008, 16, 257–262 CAS.
- L. An, T. S. Zhao, Q. X. Wu and L. Zeng, Int. J. Hydrogen Energy, 2012, 37, 14536–14542 CrossRef CAS PubMed.
- M. Unlu, J. Zhou and P. A. Kohl, Electrochem. Solid-State Lett., 2009, 12, B27–B30 CrossRef CAS PubMed.
- J. F. Zhou, M. Unlu, J. A. Vega and P. A. Kohl, J. Power Sources, 2009, 190, 285–292 CrossRef CAS PubMed.
- K. N. Grew and W. K. S. Chiu, J. Electrochem. Soc., 2010, 157, B327–B337 CrossRef CAS PubMed.
- Y.-L. S. Tse, H. N. Sarode, G. E. Lindberg, T. A. Witten, Y. Yang, A. M. Herring and G. A. Voth, J. Phys. Chem. C, 2013, 118, 845–853 Search PubMed.
- B. Delley, J. Chem. Phys., 1990, 92, 508 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS PubMed.
- R. Janarthanan, J. L. Horan, B. R. Caire, Z. C. Ziegler, Y. Yang, X. Zuo, M. W. Liberatore, M. R. Hibbs and A. M. Herring, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1743–1750 CrossRef CAS.
- Y. Liu, J. Wang, Y. Yang, T. M. Brenner, S. Seifert, Y. Yan, M. W. Liberatore and A. M. Herring, J. Phys. Chem. C, 2014, 118, 15136–15145 CAS.
- J. Fang, Y. X. Yang, X. H. Lu, M. L. Ye, W. Li and Y. M. Zhang, Int. J. Hydrogen Energy, 2012, 37, 594–602 CrossRef CAS PubMed.
- S. Slade, S. A. Campbell, T. R. Ralph and F. C. Walsh, J. Electrochem. Soc., 2002, 149, A1556–A1564 CrossRef CAS PubMed.
- D. H. Powell, A. C. Barnes, J. E. Enderby, G. W. Neilson and P. S. Salmon, Faraday Discuss. Chem. Soc., 1988, 85, 137–146 RSC.
- V. Di Noto, M. Piga, G. A. Giffin, K. Vezzù and T. A. Zawodzinski, J. Am. Chem. Soc., 2012, 134, 19099–19107 CrossRef CAS PubMed.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- K. Leung, I. M. B. Nielsen and I. Kurtz, J. Phys. Chem. B, 2007, 111, 4453–4459 CrossRef CAS PubMed.
- B. W. Connors and B. R. Ransom, J. Physiol., 1984, 355, 619–633 CrossRef CAS.
- E. R. Nightingale, J. Phys. Chem., 1959, 63, 1381–1387 CrossRef CAS.
- M. Falk and T. A. Ford, Can. J. Chem., 1966, 44, 1699–1707 CrossRef CAS.
- T. M. Alam and M. R. Hibbs, Macromolecules, 2014, 47, 1073–1084 CrossRef CAS.
- J. Hou, Z. Zhang and L. A. Madsen, J. Phys. Chem. B, 2011, 115, 4576–4582 CrossRef CAS PubMed.
- T. Ohkubo, K. Kidena and A. Ohira, Macromolecules, 2008, 41, 8688–8693 CrossRef CAS.
- P. P. Mitra, P. N. Sen, L. M. Schwartz and P. Ledoussal, Phys. Rev. Lett., 1992, 68, 3555–3558 CrossRef CAS.
- V. Munchow, V. Di Noto and E. Tondello, Electrochim. Acta, 2000, 45, 1211–1221 CrossRef CAS.
- D. L. Vien, N. B. Colthup, W. G. Fateley and J. G. Grasselli, The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules, Academic Press, Inc., San Diego, CA, 1991 Search PubMed.
- V. Di Noto, R. Gliubizzi, E. Negro and G. Pace, J. Phys. Chem. B, 2006, 110, 24972–24986 CrossRef CAS PubMed.
- P. C. Painter, M. M. Coleman and J. L. Koenig, The theory of vibrational spectroscopy and its applications to polymeric materials, John Wiley and Sons, Inc., New York, 1982 Search PubMed.
- J. Benziger, A. Bocarsly, M. Cheah, P. Majsztrik, B. Satterfield and Q. Zhao, in Fuel Cells and Hydrogen Storage, ed. A. Bocarsly and D. M. P. Mingos, Springer, Berlin Heidelberg, 2011, ch. 41, vol. 141, pp. 85–113 Search PubMed.
- A. M. Maes, T. P. Pandey, M. A. Vandiver, L. K. Lundquist, Y. Yang, J. L. Horan, A. Krosovsky, M. W. Liberatore, S. Seifert and A. M. Herring, Electrochim. Acta, 2013, 110, 260–266 CrossRef CAS PubMed.
- L. A. Adams, S. D. Poynton, C. Tamain, R. C. T. Slade and J. R. Varcoe, ChemSusChem, 2008, 1, 79–81 CrossRef CAS PubMed.
- N. Li, T. Yan, Z. Li, T. Thurn-Albrecht and W. H. Binder, Energy Environ. Sci., 2012, 5, 7888–7892 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Schematic of a custom built environment control system for FTIR spectroscopy and ATR-FTIR spectra of AEM before and after ionic conductivity measurements. See DOI: 10.1039/c4cp05755d |
| This journal is © the Owner Societies 2015 |