 Open Access Article
Open Access ArticleComment on “How to interpret Onsager cross terms in mixed ionic electronic conductors” by I. Riess, Phys. Chem. Chem. Phys., 2014, 16, 22513
Han-Ill
Yoo
*a,
Manfred
Martin
b and
Juergen
Janek
c
aDepartment of Materials Science and Engineering, Seoul National University, Seoul 151-744, Korea. E-mail: hiyoo@snu.ac.kr
bInstitute of Physical Chemistry, RWTH Aachen University, 52056 Aachen, Germany
cInstitute of Physical Chemistry, Justus Liebig-University of Giessen, 35392 Giessen, Germany
First published on 4th March 2015
Abstract
Here we show that the Onsager cross terms for ion–electron interactions are not an artifact, but the necessity to phenomenologically and completely describe the mass/charge transport of a mixed ionic–electronic conductor in terms of mobile charged components which are the only experimentally operable species. The use of an appropriate comprehensive defect model may help to reduce the cross terms (which depend on the choice of formal charge of the mobile defects), but it cannot obviate them if long-range Coulombic interactions are in action among the defects.
According to irreversible thermodynamics,1–3 all the isothermal transport phenomena of a mixed ionic electronic conductor (MIEC), e.g., A1−δOν, having one of the ionic components, e.g., O2− (= i) and holes h+ (= h) as mobile charged components, must be phenomenologically completely described as
 | (1) |
| Lih = Lhi | (2) |
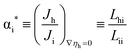 | (3) |
Recently, Chatzichrostodoulou et al.7 have measured all the L-coefficients in the system Ce0.8Pr0.2O2−δ at 800 °C by the semi-blocking method which was first proposed by Wagner3 and first implemented experimentally by Miyatani.8 Using the formal charge numbers zi = −2 for oxygen ions and zh = +1 for holes, they have found that αi* decreases from a value close to +1 to near 0 as the oxygen activity decreases from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aO2 = 0.0 to −2.5.
aO2 = 0.0 to −2.5.
In a recent paper, Riess9 discusses the Onsager cross terms and concludes implicitly that the dependence of the cross terms on the choice of formal charge number makes the cross terms an “artifact”. Obviously, this conclusion is incorrect, and in the following we clarify the meaning of the cross terms.
On the work by Chatzichrostodoulou7 “and references cited therein”:
(1) Riess9 first claims that “… in most cases Lih = 0.”
This statement could be misleading. Until now, the attempt to measure Lih has been made only on nine or so limited numbers of systems and the general conclusion is that Lih ≠ 0, the magnitude of which depends on the thermodynamic state of the system, see ref. 3, 8 and 10–18. Even though the mobile ionic defects are fully ionized, Lih ≠ 0 if there are long-range inter-defect interactions, see below and the Appendix. A correct statement would rather be that Lih can become small by mathematical transformation if short-range interactions (associations) lead to an ionic defect with a smaller charge number, e.g., the formation of  by the association of
by the association of  and e′, and if this is the majority defect. If the concentrations of
and e′, and if this is the majority defect. If the concentrations of 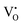 and
and  are comparable, the cross term becomes appreciable in order to account for the deviation of the effective charge from the integer formal charge, see eqn (4) below.
are comparable, the cross term becomes appreciable in order to account for the deviation of the effective charge from the integer formal charge, see eqn (4) below.
(2) Riess9 claims that there is “… no explanation for a mutual effect [Lih ≠ 0]… Indeed there is none.”
This claim ignores all of the earlier works on this subject. It is Wagner3 who first set up the thermodynamic equations of motion for an MIEC in terms of the mobile charged components, eqn (1), first proposed the experiments to determine the L-coefficients, and first considered the physicochemical origin of the mutual effect. He says that “appropriate models of lattice defects are considered in order to see under which condition the cross coefficients may be ignored or yield significant contributions.” And he clearly points out that the “finite cross coefficients are due to coupling of transport processes” not only in the short range (i.e., defect association), but also in the long range. For example, as a transfer of 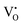 corresponds to a coupled transfer of
corresponds to a coupled transfer of  and e′, one would have αi* = 1 if
and e′, one would have αi* = 1 if  and e′ were in the majority. Otherwise, one would have to consider the “long-range energetic interaction among charged defects according to Coulomb’s law” which “results in a coupling of the motions of the individual defects due to Debye, Hückel, Onsager and Fuoss for aqueous solutions.”
and e′ were in the majority. Otherwise, one would have to consider the “long-range energetic interaction among charged defects according to Coulomb’s law” which “results in a coupling of the motions of the individual defects due to Debye, Hückel, Onsager and Fuoss for aqueous solutions.”
Later, Yoo et al.6 showed that the cross coefficients include the contributions of any possible defect “d” (structure elements) with different effective charges: in the absence of long-range interactions, one has a non-vanishing charge-of-transport,
 | (4) |
In order to rationalize the influence of long range interactions, Janek et al.20,21 subsequently applied the Debye–Hückel–Onsager–Fuoss theory22,23 to solid-state MIECs. The major conclusion is that αi* corresponds to the number of holes or electrons in the electronic charge cloud surrounding the central ionic defect. This may be written for the systems, e.g., 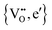 (as in CeO2−δ) or
(as in CeO2−δ) or  (as in Co1−δO) as
(as in Co1−δO) as
 | (5) |
 .20 It has later been found that eqn (5) explains the results more convincingly than eqn (4) for Co1−δO24 and TiO2−δ.25
.20 It has later been found that eqn (5) explains the results more convincingly than eqn (4) for Co1−δO24 and TiO2−δ.25
The present status of understanding is, thus, evenhandedly that the non-vanishing cross effect is partly due to short-range interactions, eqn (4), and partly due to long-range interactions, eqn (5), but that the latter take precedence with increasing defect concentrations.3 (Of course,  because then electronic–ionic defect associations are rendered negligible and κ−1 → ∞ as well.) In this light, Riess's claim9 is incorrect and misleading as well. We would like to add that, for materials with high defect concentrations, even the distinction of short- and long-range interactions becomes arbitrary and the more important consideration becomes that of the phenomenological cross terms. It is necessary to get a complete description of the charge transport.
because then electronic–ionic defect associations are rendered negligible and κ−1 → ∞ as well.) In this light, Riess's claim9 is incorrect and misleading as well. We would like to add that, for materials with high defect concentrations, even the distinction of short- and long-range interactions becomes arbitrary and the more important consideration becomes that of the phenomenological cross terms. It is necessary to get a complete description of the charge transport.
(3) Riess9 subsequently states, “It turns out that the appearance of finite cross terms and the ability to measure them are due to an incomplete description of the system at hand.” For the system, e.g., Ce0.8Pr0.2O2−δ for which the ionic defects are known to be  and
and  in addition to electrons or holes, “if only two,” say,
in addition to electrons or holes, “if only two,” say, 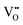 and electrons (or holes), “are considered” as charge carriers, “the missing information manifests itself as cross terms (Lih) in the theory and leads to misinterpretation of the measurement.”
and electrons (or holes), “are considered” as charge carriers, “the missing information manifests itself as cross terms (Lih) in the theory and leads to misinterpretation of the measurement.”
This is a typical misunderstanding arising when one does not properly take into account the detailed inter-relationship between the description of the charged component or building-unit level, eqn (1), and that of the defect or structure-element level. When the fluxes and forces of all possible structure elements including regular and irregular ones are reduced, in due thermodynamic course, to the independent ones, one eventually ends up with eqn (1) on the charged component level, see the Appendix. All the defect-level information is, thus, condensed into the three independent, measurable coefficients Lii, Lih (= Lhi) and Lhh, with no information missing, see ref. 3 and 6. We would like to note that a comprehensive analysis of transport coefficients, emphasizing the description of the systems with irregular SE or defects of variable charges, but neglecting long range interactions, has also been provided by Maier.27,28
It has to be emphasized that the inter-relationships between a measurable transport property and the L-coefficients are irrespective of the choice of mobile charged components, e.g., {O−,h+} instead of {O2−,h+}. In particular, the effective charge number of mobile ions, zi* = zi + αi*, is invariant, in contrast to zi and αi*.6,19 This is because the entropy creation or energy dissipation rate should remain invariant, and hence, the L-coefficients are only to be transformed in accordance with this invariance.1,2,19 In more practical terms: indeed one can choose the formal charge number of ions such that a short range order is anticipated and the cross terms become smaller, but they will still include long range interactions, which, of course, can be small for dilute defect concentrations.
It is further emphasized that what can be experimentally observed or measured is the transport of the charged components, never that of the structure elements themselves. It is because our system can interact electrochemically with the surroundings only by exchanging charged components or building units (e.g., 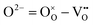 ): our system can never communicate by exchanging defects or structure elements themselves (e.g.,
): our system can never communicate by exchanging defects or structure elements themselves (e.g.,  ) due to the structure condition of the system.3,26 Therefore, the cross coefficients are a physical necessity and reality as well on the level of the charged components, not an artifact arising from a deficient choice of defect carriers.
) due to the structure condition of the system.3,26 Therefore, the cross coefficients are a physical necessity and reality as well on the level of the charged components, not an artifact arising from a deficient choice of defect carriers.
(4) Riess9 finally consummates his argument by saying, “When an appropriate, comprehensive defect model is considered for the MIEC, no cross terms are required.”
It is an inherent problem with the defect chemistry and formal description of MIECs that one never knows a priori the “appropriate, comprehensive defect model” for a system under study without observing the related phenomena on the charged component level. Thus, this consummation is just in vain or of no practical significance.
Furthermore, even if such a model were at hand, the cross terms are still required as long as there is a long-range interaction among defects as described by eqn (5), see the Appendix. They are actually unavoidable particularly as defect concentrations increase typically over 10−4 in mole fractions.3 Thus, the author's statement9 is incorrect.
It may help the author9 to understand the situation better to read Wagner:3 if αi* is known with sufficient precision, then “one obtains additional information for a discussion of the merits of different models of defects to be used in conjunction with other experimental data…”
In conclusion, Riess's interpretation9 of the Onsager cross terms is essentially based on the independent migration of differently charged ionic defects and electrons or holes, eventually leading to eqn (4). This interpretation is nothing new because it has already been fully explored, as well as being not totally correct because of the unavoidable long-range interactions among charged defects leading to eqn (5). The careless notion of the cross coefficients as “artifacts” is physically incorrect and will mislead the uninformed reader.
Appendix: Reduction of the transport equations from the structure element level to the charged component level
Here we will show, by assuming a simple defect structure without sacrificing any generality, how the transport equations on the structure element level are to be reduced to those on the charged component level, eqn (1), in due thermodynamic course.Suppose that we know a priori the defect structure of a mixed conducting oxide, say AO1−δ, comprising oxygen vacancies with all possible effective charges and electrons. The mobile structure elements (SE) may then be listed in the Kroger-Vink notation as:
 | (A.1) |
 stands for the electrons in the conduction band (C) and
stands for the electrons in the conduction band (C) and 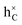 for the holes in C, the electronic regular SE corresponding to the ionic regular SE,
for the holes in C, the electronic regular SE corresponding to the ionic regular SE,  . These SEs will be henceforth labelled k = 1, 2,…,6 in order.
. These SEs will be henceforth labelled k = 1, 2,…,6 in order.
Irreversible thermodynamics stipulates that the energy dissipation (Tσ) due to entropy generation (σ) at a certain temperature (T) can be written as
 | (A.2) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) km denote the coupling transport coefficient on the SE level,
km denote the coupling transport coefficient on the SE level,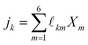 | (A.3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -coefficients, which are subject to redundancies due to the constraints upon the SE fluxes jk and local quasi-chemical equilibria.
-coefficients, which are subject to redundancies due to the constraints upon the SE fluxes jk and local quasi-chemical equilibria.
Firstly, they are
 | (A.4) |
 | (A.5) |
 | (A.6) |
 | (A.7) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -coefficients in eqn (A.3) are subject to 12 inter-relationships in eqn (A.4), and another 12 in eqn (A.7). These 24, however, are not independent of each other at all: as the summations over m of eqn (A.4) and those over k of eqn (A.7) are the same, 4 out of these 24 are rendered redundant, and hence, only 16 out of 36 survive. As these 16 are for the 4 independent fluxes, they further satisfy the Onsager reciprocity [1,2,4] or
-coefficients in eqn (A.3) are subject to 12 inter-relationships in eqn (A.4), and another 12 in eqn (A.7). These 24, however, are not independent of each other at all: as the summations over m of eqn (A.4) and those over k of eqn (A.7) are the same, 4 out of these 24 are rendered redundant, and hence, only 16 out of 36 survive. As these 16 are for the 4 independent fluxes, they further satisfy the Onsager reciprocity [1,2,4] or![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) km = km = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) mk mk | (A.8) |
The thermodynamic forces are also reduced to those of mobile charged components O2− (=i) and e− (=e), or holes h+ (=h) via internal quasi-chemical equilibria:
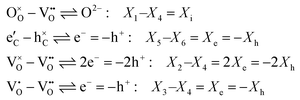 | (A.9) |
 | (A.10) |
| β1 = β4 = β6 = 0; β2 = 2; β3 = β5 = 1 | (A.11) |
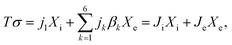 | (A.12) |
 | (A.13) |
 | (A.14) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) km as:
km as: | (A.15) |
Let us finally examine the ionic charge-of-transport,  . By replacing
. By replacing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1m for the regular SE k = 1 with those for the irregular structural elements or defects by using eqn (A.5) and (A.7), one gets
1m for the regular SE k = 1 with those for the irregular structural elements or defects by using eqn (A.5) and (A.7), one gets
 | (A.16) |
 for k ≠ m, eqn (A.16) takes the form,
for k ≠ m, eqn (A.16) takes the form, | (A.17) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) kk ∝ Dkck, one can immediately recognize that eqn (A.17) is nothing but eqn (4) in the text. The ionic charge-of-transport
kk ∝ Dkck, one can immediately recognize that eqn (A.17) is nothing but eqn (4) in the text. The ionic charge-of-transport  would, thus, phenomenologically correspond to the kinetic average of the number of electrons (βk) or holes (−βk) associated with all kinds of ionic defects, were it not for long-range interactions among defects (i.e.,
would, thus, phenomenologically correspond to the kinetic average of the number of electrons (βk) or holes (−βk) associated with all kinds of ionic defects, were it not for long-range interactions among defects (i.e., ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) km ≠ 0 for k ≠ m).
km ≠ 0 for k ≠ m).
Acknowledgements
The authors thank B. Luerssen for creating the TOC graph.References
- S. R. de Groot, Thermodynamics of Irreversible Processes, North-Holland Publishing Company, Amsterdam, 1951 Search PubMed.
- R. E. Howard and A. B. Lidiard, Rep. Prog. Phys., 1964, 27, 161 CAS.
- C. Wagner, Prog. Solid State Chem., 1975, 10, 3 CrossRef.
- L. Onsager, Phys. Rev., 1931, 37, 405 CrossRef CAS.
- A. Cukrowski, Acta Phys. Hung., 1989, 66, 159 Search PubMed.
- H.-I. Yoo, H. Schmalzried, M. Martin and J. Janek, Z. Phys. Chem., 1990, 168, 129 CrossRef CAS.
- C. Chatzichrostodoulou, W.-S. Park, H.-S. Kim, P. V. Hendriksen and H.-I. Yoo, Phys. Chem. Chem. Phys., 2010, 12, 9637 RSC.
- S. Miyatani, Solid State Commun., 1981, 38, 257 CrossRef CAS.
- I. Riess, Phys. Chem. Chem. Phys., 2014, 16, 22513 RSC.
- D.-K. Lee and H.-I. Yoo, Phys. Rev. Lett., 2006, 97, 255901 CrossRef.
- N. Ait-Younes, F. Millot and P. Gerdanian, Solid State Ionics, 1984, 12, 431 CrossRef CAS.
- H.-I. Yoo and M. Martin, Ceram. Trans., 1991, 24, 108 Search PubMed.
- J.-H. Lee and H.-I. Yoo, J. Electrochem. Soc., 1994, 141, 2789 CrossRef CAS PubMed.
- J.-H. Lee, M. Martin and H.-I. Yoo, Electrochemistry, 2000, 68, 482 CAS.
- J.-O. Hong and H.-I. Yoo, J. Mater. Res., 2002, 17, 1213 CrossRef CAS.
- W.-S. Park, I. Yang and H.-I. Yoo, ECS Trans., 2008, 13, 327 CAS.
- T. Lee and H.-I. Yoo, Solid State Ionics, 2013, 241, 5 CrossRef CAS PubMed.
- H.-S. Kim and H.-I. Yoo, Phys. Chem. Chem. Phys., 2014, 16, 16595 RSC.
- H.-I. Yoo, J.-H. Lee, M. Martin, J. Janek and H. Schmalzried, Solid State Ionics, 1994, 67, 317 CrossRef CAS.
- J. Janek, M. Martin and H.-I. Yoo, Ber. Bunsen-Ges., 1994, 98, 655 CrossRef CAS.
- J. Janek and M. Martin, Ber. Bunsen-Ges., 1994, 98, 665 CrossRef CAS.
- P. Debye and E. Huckel, Phys. Z., 1923, 24, 185 CAS; P. Debye and E. Huckel, Phys. Z., 1923, 24, 305 Search PubMed.
- L. Onsager and R. M. Fuoss, J. Phys. Chem., 1932, 36, 2689 CrossRef CAS.
- H.-I. Yoo and J.-H. Lee, J. Phys. Chem. Solids, 1996, 57, 65 CrossRef CAS.
- H.-I. Yoo and D.-K. Lee, Solid State Ionics, 2008, 179, 837 CrossRef CAS PubMed.
- H. Schmalzried, Chemical Kinetics of Solids, VCH, Weinheim, 1995, ch. 2 Search PubMed.
- J. Maier and G. Schwitzgebel, Phys. Status Solidi B, 1982, 113, 535 CrossRef CAS.
- J. Maier, Z. Phys. Chem., 1984, 140, 191 CrossRef CAS.
Footnote |
| † Eqn (1) employs h+, instead of e−. One can easily transform Je to Jh simply by taking Je = −Jh, Xe = −Xh and −βm as the number of holes associated with the SE m. |
| This journal is © the Owner Societies 2015 |
