Ultrafast hydrogen bond dynamics and partial electron transfer after photoexcitation of diethyl ester of 7-(diethylamino)-coumarin-3-phosphonic acid and its benzoxaphosphorin analog

Abstract

The solvation dynamics after optical excitation of two phosphono-substituted coumarin derivatives dissolved in various solutions are studied by fluorescence up-conversion spectroscopy and quantum chemical simulations. The Kamlet–Taft analysis of the conventional absorption and emission spectra suggests weakening of the solvent–solute H-bonds upon optical excitation, which is in contrast to the results gained by the quantum simulations and earlier studies reported for coumarin derivatives without phosphono groups. The simulations give evidence that the solvent reorganisation around the excited fluorophore leads to partial electron transfer to the first solvation shell. The process occurs on a timescale between 1 and 10 ps depending on the solvent polarity and leads to a fast decay of the time-resolved emission signal. Using the ultrafast spectral shift of the time-dependent fluorescence we estimated the relaxation time of the H-bonds in the electronically excited state to be about 0.6 ps in water, 1.5 ps in ethanol and 2.8 ps in formamide.

---

1 Introduction

The nature of hydrogen bonds (H-bonds) in solution is of particular interest due to their fundamental importance in many branches of science.^1–6 The physical and chemical properties of H-bonding in the electronic ground state have been investigated by diverse experimental and theoretical methods.^7–14 Upon electronic excitation of H-bonded systems, the hydrogen donor and acceptor molecules reorganize themselves in the electronically excited state due to the new charge distribution in the system. Fluorescent molecules can serve as fast and sensitive probes for their local environment, since the solvation shell alters the transition energies of the solute.^15–21 Since optical transitions are instantaneous compared with solvent motions, the absorption energy provides information on the solvation shell of the ground state, while the emission frequency is sensitive to the solvation properties of the electronically excited state. The Kamlet–Taft analysis²² allows the estimation of the absorption/emission frequencies in different solvents using the corresponding empirical values for their polarity π*, their ability to donate H-bonds to the solute (α, donor acidity) or to accept H-bonds from the solute (β, acceptor basicity): ν = ν₀ + s·π* + a·α + b·β. Here ν₀ is the peak frequency of the undissolved fluorophore. The coefficients s, a and b can be extracted via a linear fit of spectral data obtained in various solvents. The absolute values of these coefficients give qualitative information on the strength of the accepted (a) or donated H-bonds (b). The change in these molecular properties during the solvation process following optical excitation can be traced by the comparison of s, a and b extracted from absorption and emission spectra. Merging these coefficients with computer simulations and time-resolved spectroscopy provides a detailed microscopic picture of the solvation dynamics in the electronically excited state.^16,23,24

The aim of the present study is to investigate the solvation properties and H-bonding dynamics around P=O groups in electronically excited molecules. The P=O bond is an important component of the phosphate backbone of DNA, phospholipids in cell membranes²⁵ and the energy transport system in living cells via adenosine triphosphate.²⁶ It is obvious that the H-bonding around electronically excited P=O groups is crucial for the photo-induced dynamics of various biosystems. Comparably small molecules of the coumarin derivatives allow studying the attached functional groups after electronic excitation.^{17,23,24,27–29} Here we use diethyl ester of 7-diethylaminocoumarin-3-phosphonic acid (compound 1, see Fig. 1) and its P-analog, diethyl ester of 7-(diethylamino)-2-ethoxy-2-oxo-2H-1,2-oxaphosphorin-3-phosphonic acid (compound 2, see Fig. 1), which allow us to study the dynamics of P=O⋯H bonds. The absorption and emission spectra of both compounds are recorded in eleven solvents and analyzed via the Kamlet–Taft method. The performed quantum chemical simulations of compound 1 dissolved in water indicate the delocalization of the electron density from coumarin to the solvent. This partial electron transfer seems to be facilitated by the phosphono groups and enhanced by the H-bonds with the solvent. The electron transfer time and H-bonding dynamics after optical excitation are studied by femtosecond fluorescence up-conversion spectroscopy.

Fig. 1 Structure of the investigated chemical compounds 1 and 2. The structures of coumarins 3 and 4 are taken from ref. 23, 24 and are shown only for comparison.

2 Experimental

Both compounds 1 and 2 were synthesized as described by Bojilova et al.³⁰ and Petkova et al.³¹ The conventional absorption measurements have been performed on a UV/Vis absorption spectrometer Lambda 19 (PerkinElmer) using UV grade fused silica glass cuvettes with a thickness of 1 mm (Suprasil, Hellma). The solvents used in the present study have been purchased from: Merck (formamide 99.5% and methanol for spectroscopy, dimethyl sulfoxide (DMSO) 99.9%, dimethyl formamide (DMF) 99.8%, 2-propanol 99.9%, and acetone 99.9%); VWR Prolabo Chemicals (acetic acid 99.9% and ethyl acetate (EA) 99.9%); Sigma Aldrich (acetonitrile 99.5%) and Roth AG (ethanol 99.5%). For the aqueous samples, deionized and purified water (TKA Smart2Pure, Thermo Scientific) has been used. The sample concentration was 2 × 10⁻⁴ M. Steady-state fluorescence data have been recorded on a spectrofluorometer Jasco FP-6500 using 10 mm thick glass cuvettes (Suprasil, Hellma). The concentrations have been reduced by a factor of 10 compared to the absorption measurements. The excitation wavelengths of the spectrofluorometer have been set at the corresponding absorption maxima.

Time-resolved emission data were obtained using the sum-frequency generation technique (fluorescence up-conversion). The femtosecond laser source is a Ti:sapphire long-cavity oscillator (Femtosource Scientific XL, Femtolasers) pumped by a continuous wave frequency-doubled solid-state laser (Finesse, Laser Quantum). The laser system provides pulses with a duration of 60 fs at 800 nm, with a repetition rate of 5.2 MHz and an average output power of 1 W. Frequency-doubled pulses at 400 nm are used for excitation. The sample was contained in a 1 mm thick flowing quartz cell (Suprasil, Hellma). The emission was collected using a 2 inch off-axis parabolic mirror, passed through an optical long-pass filter (LC-3RD/410LP-50, Cut-On 410 nm, Laser Components), and was focused into a 0.2 mm BBO crystal using a second parabolic mirror, identical to the first one. 10% of the 800 nm beam were overlapped with the focused fluorescence signal in the BBO crystal, thus serving as a gating pulse for the sum-frequency generation. Up-converted light (at about 300 nm) was passed through a monochromator (SA HR250, Jobin Yvon) and detected by a single-photon counter (H8259-01, Hamamatsu Photonics). Frequency-resolved optical gating³² (FROG and XFROG) techniques are used for characterization of pump and gate pulses giving rise to a time resolution of the setup of approximately 200 fs. The emitted signals are measured in parallel and perpendicular polarization configurations I_|| and I_⊥ relative to the excitation beam. Both signals are used to determine the isotropic fluorescence intensity I_Fl(t_D) = (I_||(t_D) + 2·I_⊥(t_D))/3 and fluorescence anisotropy r(t_D) = (I_||(t_D) − I_⊥(t_D))/(I_||(t_D) + 2·I_⊥(t_D)).

3 Computational details

We performed quantum-chemical simulations of compound 1 dissolved in water applying the density functional theory (DFT) and time-dependent (TD) DFT by using the Gaussian09 suite of programs.³³ The long-range corrected hybrid exchange–correlation functional CAM-B3LYP XC^34,35 coupled to the 6-31+G** basis set has been employed and the polarizable continuum model (PCM) was used.³⁶ It describes the solvent as a homogeneous dielectric medium, which is polarized by the solute. Despite the fact that DFT in general leads to large errors as soon as charge transfer states are involved, there are exchange–correlation functionals, which are able to describe such systems with charge transfer states with satisfying accuracy. Moreover, the same functional as used in this work was successfully applied to study at least the intramolecular charge transfer in coumarin molecules.^37,38 The vertical excitations were calculated at the TDDFT level of theory using state specific approaches in PCM.³⁹ The geometry of the studied molecular cluster, consisting of compound 1 and solvent molecules, was optimized in the ground state and the excited state. Since the PCM alone is not able to reproduce solvent effects for protic solvents,³⁸ a mixed discrete-continuum approach was exploited to study the photo-physical properties of compound 1 in water.

4 Steady-state absorption and fluorescence

The absorption and emission spectra of compounds 1 and 2 dissolved in eleven solvents have been recorded. They show a similar shape, while their peak position depends on the solvent properties. Representative spectra recorded in three solvents are illustrated in Fig. 2. The energies of maximal absorption and fluorescence are summarized in Table 1 together with the corresponding solvent polarity π* and donor acidity α. The results obtained by the Kamlet–Taft analysis are shown in Table 2. Here the parameter b is neglected, since both compounds under investigation do not possess chemical groups donating H-bonds to the solvent.²³ The correlation coefficient R² from the Kamlet–Taft model indicates the similarity between measured and calculated absorption and emission frequencies.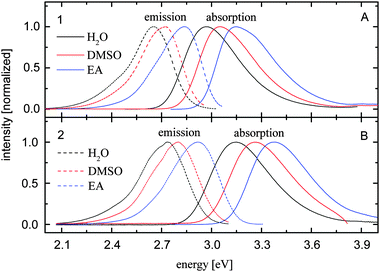

Fig. 2 Normalized steady-state absorption (solid lines) and fluorescence spectra (dashed curves) of compounds 1 (A) and 2 (B) dissolved in water, DMSO and ethyl acetate (see insets).

Table 1 Kamlet–Taft parameters, π* and α, of the used solvents, together with the energies of absorption (ν_abs in [eV]) and emission maxima (ν_em in [eV]) for compounds 1 and 2 dissolved in the corresponding solvent

Solvent	π*	α	ν ^(1)abs	ν ^(1)em	ν ^(2)abs	ν ^(2)em
Water	1.09	1.17	2.97	2.66	3.15	2.74
Formamide	0.97	0.71	2.99	2.66	3.19	2.75
Acetic acid	0.64	1.12	3.06	2.73	3.26	2.83
Methanol	0.60	0.93	3.05	2.73	3.24	2.80
DMSO	1.00	0	3.05	2.73	3.26	2.80
Ethanol	0.54	0.83	3.06	2.74	3.26	2.82
DMF	0.88	0	3.08	2.74	3.29	2.82
2-Propanol	0.48	0.76	3.07	2.76	3.29	2.86
Acetonitrile	0.75	0.19	3.09	2.74	3.30	2.82
Acetone	0.71	0.08	3.12	2.78	3.33	2.86
EA	0.55	0	3.15	2.83	3.38	2.92

---

Table 2 Results yielded by the Kamlet–Taft analysis of the conventional absorption (abs.) and emission (em.) spectra of compounds 1 and 2. ν₀ is the transition energy in vacuum, s is the solvent polarity coefficient, a is the hydrogen bonding coefficient and R² is the correlation coefficient in the Kamlet–Taft model. The corresponding data reported for coumarins 3²³ and 4²⁴ are shown for comparison

	ν 0 [eV]	s [meV]	a [meV]	R ^2
1 abs.	3.23	−169	−78	0.92
1 em.	2.90	−177	−65	0.89
2 abs.	3.47	−196	−96	0.92
2 em.	3.00	−195	−58	0.85
3 abs.	3.05	−162	−53	0.94
3 em.	2.93	−347	−130	0.89
4 abs.	3.21	−128	−43	0.93
4 em.	2.89	−349	−133	0.97

---

The estimated absorption maximum of isolated compound 1 is 3.23 eV, while the value for compound 2 is 3.47 eV. As discussed above, the solvation shells around the molecules reduce their absorption energies. The influence of the solvent polarity on the absorption frequency is described by the parameter s for absorption (s_abs), summarized in Table 2. The extracted value for compound 1 (−169 meV) is larger than those reported for coumarins 3 and 4,^23,24 whose structures are shown in Fig. 1 (see also Table 2). Various theoretical and experimental studies on coumarins 3 and 4 and other similar compounds indicate an intramolecular charge transfer upon optical excitation (from the diethylamino groups to the accepting groups at positions 2 and 3).^40–42 A missing electron acceptor group at position 3 in coumarin 4 and the slightly better electron acceptor properties of the P=O group with respect to the CN group are in accordance with the extracted sensitivities to the solvent polarity (s_abs). The presence of a second P=O group at position 2 in compound 2 leads to an even higher value of s_abs (−196 meV). Due to the formation of H-bonds donated by the solvent, the absorption frequencies of all four compounds are additionally decreased. The downshift increases going from compound 4 to 3, 1 and 2 in accordance with the number of H-bonds accepted by the different fluorophores (see parameter a for absorption in Table 2, a_abs).

Most interestingly, the Kamlet–Taft analysis of the emission maxima measured in compounds 1 and 2 shows a significant variation in the data reported for 3 and 4 (see Table 2).^23,24 In the last two molecules, the sensitivity of the fluorescence frequency to solvent polarity and H-bonding is more than twice stronger than that of the absorption. The higher impact of the solvent polarity agrees with the larger dipole moment of the excited molecules. Intramolecular charge transfer caused by the optical excitation increases the electron density on the C=O group and improves its ability to accept H-bonds from the solvent. Gustavsson et al.⁴¹ and Zhao et al.¹⁷ suggested that the strength of the H-bonds to the C=O group covers the weakening or breaking of the H-bond to the positively charged N-atom. The features are manifested by the significant increase of the parameters s and a for emission (i.e. s_em and a_em) after equilibration of the solvent cavity around the excited molecules. In contrast, the data measured in compounds 1 and 2 show that equilibration of the solvation shell around the excited fluorophores reduces the influence of the H-bonding on the fluorescence frequency (a_em < a_abs), while the effect of the solvent polarity is almost the same as in the ground state (s_em ≈ s_abs). It seems that the total strength of the H-bonds between the solvent and the dye molecule is weakened upon electronic excitation. The effect is stronger in compound 2, which gives evidence that additional electron density at the phosphono group dramatically changes the solvent response. In order to elucidate this phenomenon, we performed quantum chemical simulations on compound 1 dissolved in water.

5 Computational results

Since compound 1 has a variety of sites serving as proton acceptors in H-bond formation with the solvent molecules, we started using a single probe water molecule to estimate the relative H-bond strength on each site. Our data show that the shortest H-bond is formed between a water molecule and the P=O group. Changing the accepting site from P=O to C=O, P–O–C or N, the relative binding energy of the individual H-bonds decreases by 2.6 kJ mol⁻¹, 10.7 kJ mol⁻¹ or 14 kJ mol⁻¹, respectively. The results for the H-bonds to C–O–C are missing, since after optimization this bond migrates to the C=O accepting site.

In order to estimate the total influence of the solvent–solute interactions, we modeled a molecular cluster consisting of compound 1 and totally 7 water molecules. This is the smallest system where each of the H-bond acceptor sites is saturated by at least one water molecule. The cluster is placed in the PCM environment. The calculated absorption and emission energies (3.37 and 3.11 eV) exceed the experimentally measured values, however, the simulated Stokes shift of 0.26 eV is in agreement with the experiment (0.31 eV). The lengths of the H-bond donated by the solvent to the fluorophore in ground and excited states are summarized in Table 3. Most interestingly, the H-bond to the N-atom vanishes upon optical excitation, while the strength of the other H-bonds increases in the electronically excited state. These observations are in accordance with earlier simulations on other coumarins,^16,17,29 but they are in clear contradiction to the results extracted by the Kamlet–Taft analysis discussed just above. It seems that the Kamlet–Taft method is not applicable for fluorophores containing phosphono groups like compounds 1 and 2. A detailed picture of the electron density distribution before and after optical excitation could elucidate this phenomenon.

Table 3 Calculated lengths (R_HB) of different H-bonds accepted by compound 1 in water (7 H₂O molecules + PCM) for the molecular ground state (GS) and excited state (ES) geometry

H-bond acceptor	R HB (pm) (GS)	R HB (pm) (ES)
N	204.2	358.0
C–O–C	209.6	197.3
C=O	194.8	193.3
P=O	186.6	185.9
P=O	201.3	200.0
P–O–C	199.9	199.0
P–O–C	210.0	206.3

---

Fig. 3A shows the highest occupied molecular orbital (HOMO) of compound 1 solvated in water (isovalue = 0.04). The lowest unoccupied molecular orbital (LUMO) of the system is presented in Fig. 3B. The solvation shell in both pictures is optimized to the ground state (GS) of fluorophores and the optical transition from A to B corresponds to absorption (noted by a blue arrow). Comparison of both molecular orbitals indicates an intramolecular charge transfer from the amino group to the carbon skeleton and the attached phosphono group. Note that both orbitals have small contributions from the anti-bonding orbitals of the water molecules engaged in H-bonding with the P–O–C fragment. The green arrow indicates the relaxation of the solvent molecules around the new charge distribution in the electronically excited state (ES). The process reduces the energy difference between the ES and the GS, which is manifested in the frequency downshift of the fluorescence. Most interestingly, after relaxation of the solvation shell, the solvent molecules have an even higher contribution to the charge density of the HOMO and LUMO (Fig. 3C and D). The calculated natural bond orbital (NBO) charge of the fluorophore, as a sum of NBO charges of all atoms of the molecule, decreases by 0.10 e after excitation. These findings give evidence for partial electron transfer to the first solvation shell. Since a significant contribution to the frontier orbitals comes from the water molecules around the phosphono group, we can suggest that this group plays a crucial role in this phenomenon. Recent studies showed the importance of excited state H-bonding in the photo-induced electron transfer (PET),^16,43,44 which has been found to be ultrafast for several coumarin compounds in neat aromatic amine solvents.¹⁹ It can be expected that an additional electron density on the solvation shell influences the interaction between those solvent molecules, thus leading to a local change in the solvent dielectric properties. Since the emission energy of the fluorophore is dominated by interactions with its first solvation shell, these dielectric changes could locally alter the solvent parameters π* and α distorting the Kamlet–Taft analysis.

Fig. 3 Kohn–Sham molecular orbitals corresponding to the HOMO and the LUMO of compound 1 dissolved in water. The HOMO (A and D) and the LUMO (B and C) for solvation shells optimized with the fluorophore in the ground state (GS) and the excited state (ES). Note the significant electron density on the solvent molecules after relaxation of the solvation shell (right panel).

6 Time-resolved data

The ultrafast dynamics of compounds 1 and 2 dissolved in DMSO, ethanol, formamide and water have been studied by fluorescence up-conversion spectroscopy. Normalized isotropic signals measured for compound 1 in ethanol are shown as an example in Fig. 4A. The data obtained at higher emission energies indicate ultrafast signal decay, whereas the relaxation dynamics of the lower energetic part is significantly slower. We also observe a downshift of the emission maximum for longer delay times. Similar relaxation dynamics was observed for all eight samples. Note that the signal transients measured at energies close to the excitation (3.1 eV, 400 nm) include some coherent artifact due to sum-frequency generation between scattered pump radiation and the gate beam. The contribution of this artifact changes among the different samples (see Fig. 6).

Fig. 4 (A) Normalized fluorescence signals measured for compound 1 dissolved in ethanol at a few selected detection energies. (B) Contour plot of the fluorescence intensity as a function of emission energy and delay time. The contour values are given in the color scale in (C). The delay time is given on a linear scale up to 2 ps and on a logarithmic scale for longer delay times. (C) Transient spectral data for different delay times. Experimental data points, calculated solid lines.

Fig. 4B shows the normalized fluorescence intensity as a function of the photon energy and the delay time. The data indicate a spectral shift of the fluorescence maximum during the first 10 ps. This data set provides the transient fluorescence spectra at fixed delay times. Such transient spectra are depicted in Fig. 4C (experimental points) for a few selected delay times. The solid curves are calculated assuming that the transient fluorescence spectra S_fl(E,t_D) are similar to the steady-state spectrum S_fl(E), but their amplitudes, peak positions and spectral widths are time-dependent parameters:

S_fl(E,t_D) = A(t_D)·S_fl(w(t_D)·(E − E_max) + E_max − ΔE(t_D))

Here, A(t_D) scales the steady-state amplitude, w(t_D) modifies the spectral width and ΔE(t_D) describes the spectral down-shift of the fluorescence maximum compared to the steady state value E_max. The fitting procedure is schematically illustrated by the sketch in Fig. 5A. Despite the limited number of detected emission energies, the good agreement between calculated and measured spectra should be noted. The agreement supports the correctness of the used fitting procedure. The transient spectra measured at each delay time t_D are modeled with only three parameters A(t_D), w(t_D) and ΔE(t_D) according to the equation. For the following discussion, we define the spectrally integrated fluorescence IF(t_D) = A(t_D)·w(t_D) and the solvation correlation function C(t_D) = ΔE(t_D)/Δν_Stokes.²⁴ The integrated fluorescence is proportional to the total emission signal at delay time t_D and gives evidence for the transient population of the excited state. In contrast, C(t_D) provides information on the solvent response of the changed electron density in the excited state. The data points in Fig. 5B and C illustrate the parameters IF(t_D) and C(t_D), respectively, extracted from the transient emission spectra measured for compound 1 in ethanol. In the second step, both time-dependent parameters are fitted with a multi-exponential model (see solid lines in Fig. 5B and C).

Fig. 5 (A) Sketch illustrating the applied data analysis. Steady-state (dashed line) and calculated transient spectrum (solid curve) of compound 1 in ethanol. The scaling factors for transient amplitudes A(t_D), spectral widths at half maximum w(t_D), as well as the spectral shift ΔE(t_D) are extracted by matching calculated spectra with measured transient spectra. (B and C) Extracted spectrally integrated fluorescence intensity IF(t_D) and the solvation correlation function C(t_D).

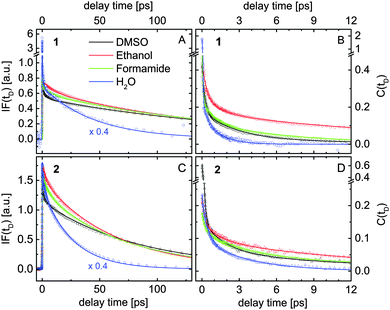Fig. 6 Results extracted by fitting the transient data measured for compounds 1 (A and B) and 2 (C and D) dissolved in four different solvents (see inset) according to the model illustrated in Fig. 5A. (A and C) Spectrally integrated fluorescence signals IF(t_D). (B and D) The solvation correlation function C(t_D).

Fig. 6A and B show the extracted evolution of IF(t_D) and C(t_D) for compound 1 dissolved in water, formamide, ethanol and DMSO. The corresponding results obtained for compound 2 are presented in Fig. 6C and D. For a better view, the IF-signals measured in water are scaled by a factor of 0.4. The coherent artifact in the transient data measured for compound 1 in water is responsible for the signal spikes observed at zero delay time (blue data in Fig. 6A and B). The temporal evolution of IF(t_D) extracted in various samples is dominated by two constants T_tr and T_fl, summarized in Table 4. Taking into account the results of the quantum calculations, the shorter time constant T_tr is assigned to a partial electron transfer from the fluorophore to the solvent molecules. The transient spectral dynamics discussed below support this assignment. T_tr decreases for a higher solvent polarity π*. In compound 2, the electron transfer process is slower.

Table 4 Time constants for the fit of the solvation correlation function C(t_D) and the spectrally integrated fluorescence signals IF(t_D). All values are given in picoseconds

Solvent	Water	Ethanol	Formamide	DMSO
T tr 1	1.1 ± 0.2	10.7 ± 1	6.7 ± 0.7	3.8 ± 0.4
T tr 2	2.1 ± 0.2	10.4 ± 1	7.1 ± 0.7	6.2 ± 0.5
T fl 1	45 ± 5	149 ± 10	158 ± 10	177 ± 10
T fl 2	27 ± 3	67 ± 5	71 ± 5	85 ± 5
T hb 1	0.6 ± 0.2	1.5 ± 0.2	2.8 ± 0.3	4.1 ± 0.4
T hb 2	0.5 ± 0.2	1.6 ± 0.2	2.9 ± 0.3	2.9 ± 0.3
T diff 1	2.3 ± 0.2	19 ± 2	14 ± 2	20 ± 2
T diff 2	3.7 ± 0.4	19 ± 2	18 ± 2	20 ± 2

---

The fluorescence lifetimes T_fl measured for compound 2 are twice shorter than those in 1 (see Table 4). Several investigations have shown that the fluorescence in coumarin dyes depends on the relative orientation of the amino group with respect to the aromatic rings. This behavior has been attributed to the formation of a twisted intramolecular charge transfer state (TICT) leading to a fast non-radiative de-excitation.^38,45,46 Our calculations show that such a TICT quenches the emission of both investigated compounds. We found that the additional phosphono group in compound 2 reduces the NBO charge of the N atom by 0.01 e, which lowers the rotation energy by almost 30% compared to compound 1. This energy was estimated from the energy difference between the ground state and the excited state, where the amino group is rotated with respect to its equilibrium. Note that these calculations were performed in the PCM environment without any explicit solvent molecules. Nevertheless, this finding agrees with the observed faster fluorescence decay in compound 2. The twisting of the amino group requires reorganization of the surrounding solvent molecules, which leads to an increase of T_fl going from water to ethanol, formamide and DMSO (see Table 4).

The relaxation dynamics of the solvation correlation function C(t_D) measured in various solutions are dominated by three different time constants. The initial spectral shift occurs with time constants between 30 fs and 350 fs among the different samples, which are comparable to the time resolution of the setup and therefore not shown in Table 4. The ultrafast solvent response causes a significant part of the fluorescence downshift. Molecular dynamics simulations also suggest that inertial ultrafast components (100–250 fs for aprotic DMSO⁴⁷ and 30 fs for water⁴⁸), e.g. small angle rotations of the first solvation shell, take place within this time scale.⁴¹

The second time constant, T_hb, of the solvation correlation function increases going from water to ethanol and formamide (see Table 4). The observed broadening of the transient fluorescence spectra within this time constant (data not shown) indicates growing delocalization of the charge distribution into the first solvation shell. Similar features have been reported for ultrafast fluorescence spectroscopy on charge transfer to solvent (CTTS) in aqueous iodide,⁴⁹ where the solvation dynamics lead to a down-shift and broadening of the emission spectrum. In protic solvents, the time constant T_hb decreases with the H-bond donor acidity α, which gives evidence that it is related to the reorganization of the H-bond network around the excited fluorophore. However, since the Coulomb interactions with the dipole moments of the excited fluorophores also affect the fast solvation dynamics, T_hb should only be used as a qualitative benchmark of the H-bond dynamics. Hence we used the same time constant to denote the fast reorganization of the solvation cavity in aprotic DMSO, which is purely electrostatic. The shorter time constant of compound 2 dissolved in DMSO (2.9 ps) compared to that of compound 1 in the same solvent (4.1 ps) agrees with the larger excited state dipole moment of compound 2 with respect to compound 1 (see s_em in Table 2).

The long-tail spectral shift with time constant T_diff was attributed to diffusional spectral relaxation due to reorganization of the second and third solvation shells. The extracted values are in qualitative agreement with the characteristic times for the spectral evolution reported by transient spectroscopy on CTTS systems in various solvents.^50,51 Our data show that the last spectral relaxation step typically includes only 5% of the observed Stokes shift and is faster in water than in formamide, ethanol and DMSO.

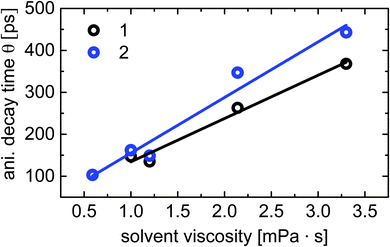
The fluorescence anisotropy r(r), determined from the polarization resolved emission signals, shows a mono-exponential decay with a time constant Θ (data not shown). This time constant could be attributed to the rotational correlation time Θ = ηV/RT, where η is the solvent viscosity, V denotes the rotating volume of the solute, R is the gas constant and T is the temperature.⁵² This model assumes a spherical rotating dipole located in a solution. The anisotropy decay times versus the solvent viscosity measured for compounds 1 and 2 at room temperature (T = 295 K) are shown in Fig. 7. Using a simple linear fit (solid lines in Fig. 7), we were able to calculate the rotating volumes of the fluorophores. The molar concentrations for the time-resolved measurements have been identical for all solvents and compounds. The estimated rotating volume of compound 1 is V₁ = (253 ± 25) cm³ mol⁻¹ and that of 2 is approximately V₂ = (325 ± 37) mm³ mol⁻¹. These values are in excellent agreement with the molecular volumes of 263 cm³ mol⁻¹ for compound 1 and 330 cm³ mol⁻¹ for compound 2 extracted by our quantum simulations.

Fig. 7 Anisotropy decay time Θ measured for compounds 1 (black) and 2 (blue) dissolved in water, ethanol, formamide and DMSO versus the solvent viscosity (experimental points and linear fit). The data measured for compound 2 in methanol are also shown in the figure.

7 Conclusions

We report on the solvation properties and H-bonding dynamics around two phosphono-substituted 7-aminocoumarins (compounds 1 and 2) in the electronically excited state using steady-state and time-resolved fluorescence spectroscopy, as well as quantum chemical simulations. The conventional absorption and fluorescence spectra recorded for compounds 1 and 2 dissolved in several different solvents were analyzed using the Kamlet–Taft technique. This simple empirical analysis leads to weakening of the solvent–solute H-bonds upon optical excitation, which is in contrast to similar results published for coumarin derivatives without phosphono groups. Furthermore, the quantum simulations on the molecular cluster of compound 1 and seven water molecules placed in the PCM environment indicate breaking of the H-bond to the N-atom upon photoexcitation, while the H-bonds to carbonyl and phosphono groups are strengthened. These results are in accordance with the reported studies on other 7-aminocoumarins. Most interestingly, our simulations give evidence for partial electron transfer to the first solvation shell, where the phosphono group seems to be involved. The time-resolved data support this suggestion. The local change in the dielectric properties of the solvent due to the partial electron transfer could be the reason that the Kamlet–Taft analysis is not applicable for these compounds.

The solvation dynamics was studied by fluorescence up-conversion spectroscopy with a time-resolution of 200 fs. We applied a simple method for fitting the steady-state spectrum to the transient spectra using a time-dependent spectral shift and scale factors for amplitude and width to extract the evolution of the solvation correlation function and the spectrally integrated fluorescence intensity. Using the ultrafast spectral shift we estimated the relaxation time of the H-bonds in the electronically excited state to be about 0.6 ps in water, 1.5 ps in ethanol and 2.8 ps in formamide. The fast decay of the spectrally integrated fluorescence signal was assigned to the partial electron transfer to the solvent. The process occurs on timescales between 1 and 10 ps depending on the solvent polarity. A twisted intramolecular charge transfer explains the variation in the measured fluorescence lifetimes of both compounds in different solvents. Additionally, the fluorescence anisotropy decay has been found to correlate linearly with the solvent viscosity.

Acknowledgements

We thank Dr Jasper Werhahn and Martin Wörle for the experimental support and the helpful discussions. The authors are grateful to the FP7 project BeyondEverest. We also thank the Leibniz-Rechenzentrum der Bayerischen Akademie der Wissenschaften for providing computing resources.

References

1. J. N. Wilson and E. T. Kool, Org. Biomol. Chem., 2006, 4, 4265–4274.
2. A. W. Czarnik, Acc. Chem. Res., 1994, 27, 302–308.
3. A. R. Fersht, et al. , Nature, 1985, 314, 235–238.
4. R. V. Ulijn and A. M. Smith, Chem. Soc. Rev., 2008, 37, 664–675.
5. C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511–544.
6. M. C. Etter, J. Phys. Chem., 1991, 95, 4601–4610.
7. E. T. J. Nibbering and T. H. Elsaesser, Chem. Rev., 2004, 104, 1887–1914.
8. H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517.
9. R. Laenen, C. Rauscher and A. Laubereau, Phys. Rev. Lett., 1998, 80, 2622–2625.
10. S. Woutersen, U. Emmerichs and H. J. Bakker, Science, 1997, 278, 658–660.
11. T. Head-Gordon and G. Hura, Chem. Rev., 2002, 110, 2651–2670.
12. J. D. Smith, C. D. Cappa, K. R. Wilson, B. Messer, R. C. Cohen and R. J. Saykally, Science, 2004, 306, 851–853.
13. J. C. Werhahn, S. Pandelov, S. S. Xantheas and H. Iglev, J. Phys. Chem. Lett., 2011, 2, 1633–1638.
14. J. Lindner, P. Vöhringer, M. S. Pshenichnikov, D. Cringus and D. A. Wiersma, Chem. Phys. Lett., 2006, 421, 329–333.
15. C. Chudoba, E. T. J. Nibbering and T. Elsaesser, Phys. Rev. Lett., 1998, 81, 3010–3013.
16. G.-J. Zhao and K.-L. Han, Acc. Chem. Res., 2011, 45, 404–413.
17. G.-J. Zhao and K.-L. Han, J. Phys. Chem. A, 2007, 111, 2469–2474.
18. G.-J. Zhao and K.-L. Han, J. Phys. Chem. A, 2007, 111, 9218–9223.
19. N. Barman, D. Singha and K. Sahu, Phys. Chem. Chem. Phys., 2014, 16, 6159–6166.
20. F. Santoro, V. Barone, T. Gustavsson and R. Importa, J. Am. Chem. Soc., 2006, 128, 16312–16322.
21. K. Winkler, J. R. Lindner, V. Subramaniam, T. M. Jovin and P. Vöhringer, Phys. Chem. Chem. Phys., 2002, 4, 1072–1081.
22. M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887.
23. H. Turki, S. Abid, R. El Gharbi and S. Fery-Forgues, C. R. Chim., 2006, 9, 1252–1259.
24. K. Das, B. Jain and H. S. Patel, J. Phys. Chem. A, 2006, 110, 1698–1704.
25. K. J. Tielrooij, D. Paparo, L. Piatkowski, H. J. Bakker and M. Bonn, Biophys. J., 2009, 97, 2484–2492.
26. S. J. Ferguson, D. Nicholls and S. Ferguson, Bioenergetics 3, Academic, 2002.
27. N. Trendafilova, G. Bauer and T. Mihaylov, Chem. Phys., 2004, 302, 95–104.
28. I. Georgieva, N. Trendafilova, A. Aquino and H. Lischka, J. Phys. Chem. A, 2005, 109, 11860–11869.
29. A. DeFusco, N. Minezawa, L. V. Slipchenko, F. Zahariev and M. S. Gordon, J. Phys. Chem. Lett., 2011, 2, 2184–2192.
30. A. Bojilova, R. Nikolova, C. Ivanov, N. A. Rodios, A. Terzis and C. P. Raptopoulou, Tetrahedron, 1996, 52, 12597–12612.
31. N. I. Petkova, R. D. Nikolova, A. G. Bojilova, N. A. Rodios and J. Kopf, Tetrahedron, 2009, 65, 1639–1647.
32. R. Trebino and D. J. Kane, J. Opt. Soc. Am. A, 1993, 10, 1101–1111.
33. M. J. Frisch, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
34. Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433.
35. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
36. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
37. D. Yang, Y. Liu, D. Shi and J. Sun, Comput. Theor. Chem., 2012, 984, 76–84.
38. A. Pedone, J. Chem. Theory Comp., 2013, 9, 4087–4096.
39. G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107.
40. D. S. English, K. Das, K. D. Ashby, J. Park, J. W. Petrich and E. W. Castner, J. Am. Chem. Soc., 1997, 119, 11585–11590.
41. T. Gustavsson, L. Cassara, V. Gulbinas, G. Gurzadyan, J.-C. Mialocq, S. Pommeret, M. Sorgius and P. van der Meulen, J. Phys. Chem. A, 1998, 102, 4229–4245.
42. M. S. Zakerhamidi, A. Ghanadzadeh, H. Tajalli, M. Moghadam, M. Jassas and R. H. nia, Spectrochim. Acta Mol. Biomol. Spectros., 2010, 77, 337–341.
43. N. Barman, D. Singha and K. Sahu, J. Phys. Chem. A, 2013, 117, 3945–3953.
44. G.-J. Zhao, J.-Y. Liu, L.-C. Zhou and K.-L. Han, J. Phys. Chem. B, 2007, 111, 8940–8945.
45. B. Raju and T. Varadarajan, J. Photochem. Photobiol. A, 1995, 85, 263–267.
46. S. Nad, M. Kumbhakar and H. Pal, J. Phys. Chem. A, 2003, 107, 4808–4816.
47. E. A. Carter and J. T. Hynes, J. Chem. Phys., 1991, 94, 5961–5979.
48. M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1988, 89, 5044–5069.
49. F. Messina, O. Bräm, A. Cannizzo and M. Chergui, Nat. Commun., 2013, 4, 2119.
50. V. H. Vilchiz, X. Chen, J. A. Kloepfer and S. E. Bradforth, Radiat. Phys. Chem., 2005, 72, 159–167.
51. H. Iglev, A. Trifonov, A. Thaller, I. Buchvarov, T. Fiebig and A. Laubereau, Chem. Phys. Lett., 2005, 403, 198–204.
52. J. R. Lakowicz, Principles of fluorescence spectroscopy, Springer, 2009.

---