 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long-lived nuclear spin states far from magnetic equivalence†
Gabriele
Stevanato
,
Soumya
Singha Roy
,
Joe
Hill-Cousins
,
Ilya
Kuprov
,
Lynda J.
Brown
,
Richard C. D.
Brown
,
Giuseppe
Pileio
and
Malcolm H.
Levitt
*
School of Chemistry, University of Southampton, University Road, Southampton, UK. E-mail: mhl@soton.ac.uk
First published on 23rd January 2015
Abstract
Clusters of coupled nuclear spins may form long-lived nuclear spin states, which interact weakly with the environment, compared to ordinary nuclear magnetization. All experimental demonstrations of long-lived states have so far involved spin systems which are close to the condition of magnetic equivalence, in which the network of spin–spin couplings is conserved under all pair exchanges of symmetry-related nuclei. We show that the four-spin system of trans-[2,3-13C2]-but-2-enedioate exhibits a long-lived nuclear spin state, even though this spin system is very far from magnetic equivalence. The 4-spin long-lived state is accessed by slightly asymmetric chemical substitutions of the centrosymmetric molecular core. The long-lived state is a consequence of the locally centrosymmetric molecular geometry for the trans isomer, and is absent for the cis isomer. A general group theoretical description of long-lived states is presented. It is shown that the symmetries of coherent and incoherent interactions are both important for the existence of long-lived states.
1 Introduction
Clusters of coupled nuclear spins may form long-lived states (LLS) with decay time constants TLLS much longer than the conventional spin–lattice relaxation time T1.1–22 Such long-lived states have been used to enhance the study of slow processes such as diffusion and flow by NMR, and to enhance the contrast in ligand binding investigations.21,22 Long-lived states hold particular promise for extending the range of nuclear hyperpolarization experiments,23–28 in which the small (∼10−5) thermal polarization of nuclear spins is temporarily enhanced by many orders of magnitude. In the case of spin systems containing only two nuclear spins-1/2, the long-lived state is known as singlet order.10 This represents the difference in population between the singlet state of the spin-1/2 pair, which is antisymmetric with respect to spin exchange, and the mean population of the triplet states, which are symmetric with respect to exchange. Singlet order is immune to intra-pair dipolar relaxation, which is often the dominant mechanism for the T1 process. Singlet order lifetimes TLLS exceeding ∼60T1 have been reported.13 Long-lived singlet order may also be observed for spin-1/2 isotopes of different type (heteronuclear singlet order).29In systems of more than two coupled spins-1/2, the existence of long-lived singlet order (and LLS in general) depends strongly on the geometrical arrangement of the nuclei, and the relative magnitudes of spin–spin couplings and chemical shift differences. This problem was examined both theoretically14 and numerically.30 Multiple-spin states that are protected against intramolecular relaxation mechanisms were predicted to exist, in the case that the rigid geometrical arrangement of nuclei displays local inversion symmetry.30 However, no experimental demonstrations of such geometrically imposed long-lived states were provided.
The absence of local geometrical centrosymmetry does not preclude the existence of long-lived spin orders when either the geometrical remoteness of the central spin pair from the other members of the spin system is provided,16–19,25–27 or in the presence of fast intramolecular dynamics.31
In the following discussion, we provide a clear experimental demonstration of a geometrically-imposed long-lived nuclear spin state in an asymmetrically substituted derivative of 13C2-fumarate (trans-[2,3-13C2]-but-2-enedioate). As discussed below, this system exhibits local centrosymmetry but is far from the regime of magnetic equivalence. The confirmed existence of a long-lived state in this system verifies the analyses in ref. 14 and 30, and shows that near-magnetic-equivalence is not a necessary condition for generating and observing long-lived nuclear spin states.
A theoretical framework accounting for the symmetry properties of the coherent and fluctuating terms in the hamiltonian is introduced for predicting the existence of long-lived spin order. This theory emphasizes the interlocking symmetries of both the coherent and fluctuating parts of the nuclear spin Hamiltonian, as opposed to recent work which only takes the coherent spin interactions into account.16–19
2 Near magnetic equivalence
Consider a pair of nuclei denoted Ij and Ik, with chemical shifts δj and δk, so that their chemical shift frequencies in a magnetic field B0 are given by ω0j = −γjB0(1 + δj) where γj is the magnetogyric ratio of Ij, and similarly for Ik. Their mutual J-coupling is denoted Jjk. The nuclei are considered to be chemically equivalent if the symmetry of the molecule ensures equal chemical shifts δj = δk. If there are no other nuclei in the system, chemical equivalence also implies magnetic equivalence. However, if there are other nuclei {Il…} in the system, with finite couplings to one or both of Ij and Ik, then a chemically-equivalent pair of nuclei is only magnetically equivalent if all out-of-pair couplings are equal, i.e. Jjl = Jkl ∀ l ∉ {j,k}.32We define a pair of nuclei Ij and Ik to exhibit near magnetic equivalence if the following condition holds:
| (ω0j − ω0k)2 + π2(Jjl − Jkl)2 ≤ π2Jjk2 ∀ l ∉ {j,k} | (1) |
The condition (1) is depicted graphically in Fig. 1. The horizontal axis indicates the difference in chemically shifted resonance frequencies of the two spins in the pair, while the vertical axis represents the difference of out-of-pair J-couplings to other spins in the same molecule. The dashed circle indicates the intra-pair J-coupling. Spin pairs may be characterized as being chemically equivalent (corresponding to points on the vertical axis) or magnetically equivalent (point at the origin). Spin pairs with parameters within the dashed circle present near magnetic equivalence.
 | ||
| Fig. 1 Pictorial representation of the concepts of chemical and magnetic equivalence for a pair of spins labelled j and k. The label l identifies homonuclear spin species coupled with the pair. The dashed circle has a radius |πJjk|. The filled circle indicates the point of exact magnetic equivalence. Points on the vertical axis (gray) correspond to systems whose nuclei are chemically equivalent. The filled hexagon represents a spin system whose nuclei are chemically equivalent but slightly magnetically inequivalent.16–19 The filled square indicates a spin system formed by two nuclei which are slightly chemically inequivalent.9,11 The open square, falling well outside the dashed circle, represents spin systems in the regime of strong magnetic inequivalence, as studied in this work. | ||
There have been extensive investigations of isolated spin-1/2 pairs with slightly different chemical shifts, represented by the filled square in Fig. 1. In some cases, the chemical shift difference is sufficiently small that the near-magnetic-equivalence condition (1) is satisfied without intervention in high magnetic fields.9,12 In other cases is satisfied by transporting the sample into a region of low applied magnetic field6,8 or by applying resonant radiofrequency fields.33 In the regime of near magnetic equivalence, long-lived order may be accessed by carefully timed pulse trains9,34 or by continuous radiofrequency fields of suitable amplitude.20,35 Appropriate modifications of the terms ω0j and ω0k in eqn (1) should be used in these cases.
It is also possible to attain near-magnetic-equivalence by a deviation in the vertical direction, corresponding to small differences in J-couplings to spins outside the pair, providing that eqn (1) is still satisfied. This has been demonstrated for chemically equivalent systems (points along the vertical axis).16–19
In this publication we demonstrate the existence of long-lived order in a four-spin-1/2 system which does not conform to condition (1). This spin system displays strong magnetic inequivalence with parameters represented by an open square falling well outside the dashed circle in Fig. 1. By comparing two strongly magnetic inequivalent isomers, one exhibiting local centrosymmetry of a four-spin system, and one without centrosymmetry, we show that only the centrosymmetric system displays a long-lived state. In this special case, the long-lived state is geometrically imposed by the local centrosymmetry of the rigid molecular structure, as suggested in ref. 14 and 30. These cases highlight the important role of symmetry in both the coherent and fluctuating spin Hamiltonian, in determining the existence of LLS.
3 Experimental
3.1 Samples
The molecular structures of the samples used in this study are shown in Fig. 2. Both materials are di-esters of [2,3-13C2]-but-2-enedioate which contains a central spin system comprising two 13C nuclei and two 1H nuclei; the fumarate derivative (panels (a) and (c)) has a trans double bond, while the maleate derivative (panes (b) and (d)) has a cis double bond. In both cases, the two ester groups are different, causing the two 13C sites (and their attached protons) to have slightly different chemical shifts. As discussed below, this slight chemical asymmetry is necessary for accessing the long-lived state. All ester groups are deuterated in order to reduce their relaxation contributions.In the following discussion, the [2,3-13C2]-fumarate derivative in Fig. 2a [1-(ethyl-d5) 4-(propyl-d7)(E)-but-2-enedioate-2,3-13C2] is referred to as 13C2-AFD (asymmetric fumarate diester); the [2,3-13C2]-maleate derivative in Fig. 2b [1-(ethyl-d5) 4-(propyl-d7)(Z)-but-2-enedioate-13C2] is referred to as 13C2-AMD (asymmetric maleate diester).
13C2-AFD contains a 4-spin-1/2 system displaying a local centre of inversion, midway between the two 13C nuclei (Fig. 2c); the local 4-spin-1/2 system in 13C2-AMD, on the other hand, displays a reflection plane but is not locally centrosymmetric (Fig. 2d).
The samples were synthesized as described in the ESI.† In both cases 30 mg of the diester were dissolved in 0.5 ml of CD3OD, added to a Wilmad low pressure/vacuum 5 mm NMR tube, degassed thoroughly using the freeze and pump technique (5 cycles), and hermetically sealed.
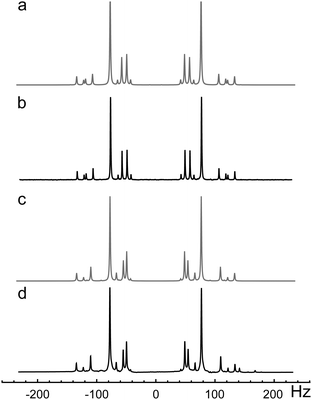 | ||
| Fig. 3 NMR 1D-spectra of 13C2-AFD: (a) simulated 13C spectrum; (b) experimental 13C spectrum. (c) Simulated 1H spectrum; (d) experimental 1H spectrum. | ||
3.2 NMR experiments
All NMR experiments were performed at a magnetic field of 11.75 T on a Bruker 500 MHz Avance III spectrometer using a Bruker 5 mm triple-resonance liquid-state probe. | ||
| Fig. 4 NMR 1D-spectra of 13C2-AMD: (a) simulated 13C spectrum; (b) experimental 13C spectrum. (c) simulated 1H spectrum; (d) experimental 1H spectrum. | ||
The 13C and 1H 1D-NMR spectra were fitted using Spinach simulation software (Fig. 3 and Fig. 4).36,37 The obtained chemical shift and coupling parameters are given in Table 1.
| 13C2-AFD | 13C2-AMD | ||
|---|---|---|---|
| Simulation | J 23 | 71.0 ± 0.6 Hz | 71.6 ± 0.8 Hz |
| J 13 = J24 | −2.8 ± 0.03 Hz | −1.16 ± 0.02 Hz | |
| J 12 = J34 | 166.7 ± 0.2 Hz | 166.5 ± 0.2 Hz | |
| J 14 | 15.7 ± 0.2 Hz | 11.95 ± 0.4 Hz | |
| Δδ23 | 62 ± 5 ppb | 92 ± 4 ppb | |
| Δδ14 | 7 ± 0.9 ppb | 1.8 ± 0.2 ppb | |
| Experiment | Δ(13C) | 3.5 ms | 3.7 ms |
| Δ(1H) | 16 ms | 21 ms | |
| n 1(13C) | 14 | 14 | |
| n 2(13C) | 7 | 7 | |
| n 1(1H) | 6 | 18 | |
| n 2(1H) | 3 | 9 | |
| ω nutev(1H)/2π | 520 Hz | 520 Hz | |
| ω nutev(13C)/2π | 700 Hz | 700 Hz | |
| T 1(13C) | 6.0 ± 0.1 s | 6.0 ± 0.1 s | |
| T 1(1H) | 6.0 ± 0.1 s | 4.5 ± 0.1 s | |
The spin systems in both 13C2-AMD and 13C2-AFD are far from magnetic equivalence. The coupling difference |J12 − J13| is more than twice |J23|, well outside the near-magnetic-equivalence condition expressed in eqn (1).
Experimental investigation of the long-lived states in the four-spin-1/2 systems of 13C2-AFD and 13C2-AMD was accomplished by the double-resonance pulse sequences shown in Fig. 5. These pulse sequences are based on the magnetization-to-singlet (M2S) and singlet-to-magnetization (S2M) pulse sequences used to study LLS in homonuclear 2-spin-1/2 systems8,9 and in near-equivalent heteronuclear systems.16–19 In the current case, each of the M2S and S2M sequences may be performed on either the 13C or the 1H channel, giving rise to the four pulse sequence combinations reported in Fig. 5.
 | ||
| Fig. 5 Pulse sequences used to access the Δgu state in 13C2-AFD and 13C2-AMD. Excitation and detection of Δgu is done using M2S and S2M pulse sequences, respectively. M2S and S2M are run on the same RF channel in (a) and (b) or on different channels in (c) and (d). The exact scheme of an M2S sequence is shown in (e). The S2M pulse sequence is obtained by running M2S in reverse time order. The echo duration is given by τe ∼ 1/(2J14) when the sequence is applied to the 1H channel, and τe ∼ 1/(2J23) when using the 13C channel. The number of loops is always n1 = 2n2. During the variable evolution time τev a weak continuous wave irradiation of 800 μW is applied on both RF channels (ωnutev(13C)/2π = 700 Hz, ωnutev(1H)/2π = 520 Hz) to impose chemical equivalence. A WALTZ-16 decoupling sequence38 is applied to the 1H channel during detection of the 13C signal; WALTZ-16 is applied to the 13C channel when the 1H signal is detected. | ||
All four sequence variants access the same collective state denoted Δgu, as reported by the simulation in Fig. 6 performed using SpinDynamica.39 This operator represents the population difference between spin states that are symmetric (g) and antisymmetric (u) with respect to simultaneous exchanges of the 1H and the 13C nuclei, as described below. In the case of 13C2-AFD this four-spin state is long-lived. In all cases, the M2S sequence converts either 1H or 13C magnetization into Δgu. This state evolves during a variable evolution interval τev, during which an unmodulated irradiation field (∼800 μW) is applied on both RF channels (nutation frequencies reported in Table 1). This suppresses the small chemical shift difference induced by the different ester substituents.33 An S2M sequence, applied on either the 1H or 13C channel, converts the state Δgu into observable transverse magnetization, which is then detected.
 | ||
Fig. 6 Simulated trajectories for the transfer of longitudinal magnetization into carbon transverse magnetization I2x + I3x in blue, proton transverse magnetization I1x + I4x in red and Δgu spin order in black under the pulse sequence in Fig. 5a for 13C2-AFD. The spin system is assumed to evolve under the influence of 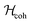 with parameters reported in Table 1 and τev = 0.5 s. No relaxation was included in the simulations. with parameters reported in Table 1 and τev = 0.5 s. No relaxation was included in the simulations. | ||
A WALTZ-16 decoupling sequence38 is applied on the 1H channel during 13C observation, to collapse the spectrum into a single peak. Conversely, the 1H NMR signal is detected in the presence of 13C WALTZ-16 decoupling.
The signal amplitudes for the two compounds, using the four different pulse sequence variants, are plotted against τev in Fig. 7. The decay time constants reported in Table 2 are consistent among the four different experiments. The experimental points were fitted using a single exponential decay curve when exciting and detecting the spin system on different RF channels. A double exponential decay curve was instead applied when excitation and detection occured on the same RF channel. Further details and the fitting functions are reported in the ESI.† In the case of 13C2-AFD, the state Δgu is found to have a decay time constant of ∼10T1, marking the existence of a four-spin LLS protected against dipole–dipole relaxation and the other mechanisms contributing to the rapid decay of longitudinal magnetization. In the case of 13C2-AMD, where a local centre of inversion is absent, the state Δgu decays faster than T1 and hence cannot be designated as a long-lived state. The experimental results confirm the link between local molecular geometry and the existence of LLS in multi-spin systems.
 | ||
| Fig. 7 Experimental results are shown for pulse sequence in (a) Fig. 5a, (b) Fig. 5b, (c) Fig. 5c and (d) Fig. 5d. Black triangles refer to 13C2-AFD, and gray circles to 13C2-AMD. The dashed lines are best fits to bi-exponential decays in (a) and (b) and single exponential decays in (c) and (d). The time constants for 13C2-AFD are: (a) 61.01 ± 0.1 s; (b) 63.2 ± 2.5 s; (c) 59.9 ± 3.2 s; (d) 61.6 ± 2.0 s. The time constants for 13C2-AMD are: (a) 2.5 ± 0.2 s; (b) 2.1 ± 0.1 s; (c) 2.5 ± 0.2 s; (d) 2.7 ± 0.2 s. | ||
| Pulse sequence | 13C2-AFD/s | 13C2-AMD/s |
|---|---|---|
| M2S(13C)–S2M(13C) | 61.0 ± 1.0 | 2.5 ± 0.2 |
| M2S(1H)–S2M(1H) | 63.2 ± 2.5 | 2.1 ± 0.1 |
| M2S(13C)–S2M(1H) | 59.9 ± 3.2 | 2.5 ± 0.2 |
| M2S(1H)–S2M(13C) | 61.6 ± 2.0 | 2.7 ± 0.2 |
4 Theory
A nuclear spin system experiences a spin Hamiltonian containing coherent and fluctuating contributions: | (2) |
 is associated with the frequencies and amplitudes of the NMR peaks, while
is associated with the frequencies and amplitudes of the NMR peaks, while  leads to relaxation. In solution NMR, the symmetry of
leads to relaxation. In solution NMR, the symmetry of  is associated with chemical and magnetic equivalence; the symmetry of
is associated with chemical and magnetic equivalence; the symmetry of  is responsible for the existence of long-lived forms of spin order. The existence of LLS in near magnetic equivalent multi-spin systems has been recently analysed in terms of the symmetry of the coherent Hamiltonian alone.17,19 As shown below, this can be misleading. The interplay of the various symmetries is now described. Although the discussion will be conducted for the specific cases described in this paper, the general principles may be used to analyze a wide variety of molecular geometries.
is responsible for the existence of long-lived forms of spin order. The existence of LLS in near magnetic equivalent multi-spin systems has been recently analysed in terms of the symmetry of the coherent Hamiltonian alone.17,19 As shown below, this can be misleading. The interplay of the various symmetries is now described. Although the discussion will be conducted for the specific cases described in this paper, the general principles may be used to analyze a wide variety of molecular geometries.
4.1 Symmetry of the coherent hamiltonian
We write the coherent Hamiltonian as follows: | (3) |
 respects the idealized symmetry of the molecular spin system and
respects the idealized symmetry of the molecular spin system and  is a small perturbation due to the asymmetric remote substituents. In isotropic liquids, each of these is a superposition of Zeeman and J-coupling terms, i.e.
is a small perturbation due to the asymmetric remote substituents. In isotropic liquids, each of these is a superposition of Zeeman and J-coupling terms, i.e. and
and  , where in the current cases
, where in the current cases | (4) |
 | (5) |
 | (6) |
 | (7) |
 and
and  respect the local symmetry of the four-spin system, while the terms
respect the local symmetry of the four-spin system, while the terms  and
and  contain the small symmetry-breaking terms induced by the remote asymmetric ester groups. In the experiments described here, the asymmetric term
contain the small symmetry-breaking terms induced by the remote asymmetric ester groups. In the experiments described here, the asymmetric term  is exploited during the M2S and S2M sequences to access the state Δgu. However, during the evolution interval τev, the effect of
is exploited during the M2S and S2M sequences to access the state Δgu. However, during the evolution interval τev, the effect of  is suppressed by the applied RF field.
is suppressed by the applied RF field.
Spin permutation operators denoted (i1i2…in) may be defined, which lead to a cyclic permutation of n spin labels when applied to a spin state or a spin operator.40 Different spin permutations may be multiplied. Examples are:
| (12)I1zI3z(12)† = I2zI3z | (8) |
| (12)(34)I1zI3z(34)†(12)† = I2zI4z | (9) |
 , is defined here as the group of spin permutation operations which commutes with
, is defined here as the group of spin permutation operations which commutes with  .
.
In the current case, the group  consists of just two operations, for both molecules:
consists of just two operations, for both molecules:
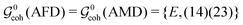 | (10) |
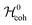 is concerned). The fact that the permutation (14) does not appear in the group
is concerned). The fact that the permutation (14) does not appear in the group 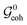 as an isolated element, but as a product with a different permutation (23), indicates that spins I1 and I4 are magnetically inequivalent.
as an isolated element, but as a product with a different permutation (23), indicates that spins I1 and I4 are magnetically inequivalent.
The group  has two irreducible representations denoted Ag and Bu, with opposite parity under the operation (14)(23).
has two irreducible representations denoted Ag and Bu, with opposite parity under the operation (14)(23).
In the absence of any symmetry breaking interactions, the NMR spectral peaks are generated by transitions within the Ag or Bu manifolds.
![[Doublestruck B]](https://www.rsc.org/images/entities/i_char_e165.gif) ST = {ST}23 ⊗ {ST}14 ST = {ST}23 ⊗ {ST}14 | (11) |
| (ij)|ψij〉 = p(ij)|ψij〉 | (12) |
As different spin permutations may be multiplied, a four-spin state can be either symmetric (g) or antisymmetric (u) under the homonuclear spin permutation (ij)(kl), that is p(ij)(kl) = +1 (for g) or p(ij)(kl) = −1 (for u).
States belonging to ![[Doublestruck B]](https://www.rsc.org/images/entities/i_char_e165.gif) ST can be classified (see Table 2) according to the magnetic quantum number M and their parities under the homonuclear spin permutations:
ST can be classified (see Table 2) according to the magnetic quantum number M and their parities under the homonuclear spin permutations:
| (I1z + I2z + I3z + I4z)(|ψ14〉 ⊗ |ψ23〉) = M(|ψ14 ⊗ |ψ23〉) (14)(|ψ14〉 ⊗ |ψ23〉) = p(14)(|ψ14 ⊗ |ψ23〉) (23)(|ψ14〉 ⊗ |ψ23〉) = p(23)(|ψ14 ⊗ |ψ23〉) (14)(23)(|ψ14〉 ⊗ |ψ23〉) = p(14)p(23)(|ψ14〉 ⊗ |ψ23〉) = p(14)(23)(|ψ14〉 ⊗ |ψ23〉) | (13) |
| Γspin = 10Ag ⊕ 6Bu | (14) |
![[Doublestruck B]](https://www.rsc.org/images/entities/i_char_e165.gif) ST in eqn (11) used for describing both 13C2-AFD, 13C2-AMD. Each ket is classified according to its parity under exchange of the two 13C nuclei, exchange of the two 1H nuclei, and simultaneous exchange of both homonuclear pairs. The last column indicates the total magnetic quantum number
ST in eqn (11) used for describing both 13C2-AFD, 13C2-AMD. Each ket is classified according to its parity under exchange of the two 13C nuclei, exchange of the two 1H nuclei, and simultaneous exchange of both homonuclear pairs. The last column indicates the total magnetic quantum number
![[Doublestruck B]](https://www.rsc.org/images/entities/i_char_e165.gif) ST
ST
|
p (23) | p (14) | p (14)(23) | M |
|---|---|---|---|---|
| |T123T114〉 | g | g | g | 2 |
| |T023T114〉 | g | g | g | 1 |
| |T123T014〉 | g | g | g | 1 |
| |T123T−114〉 | g | g | g | 0 |
| |T023T014〉 | g | g | g | 0 |
| |T−123T114〉 | g | g | g | 0 |
| |T023T−114〉 | g | g | g | −1 |
| |T−123T014〉 | g | g | g | −1 |
| |T−123T−114〉 | g | g | g | −2 |
| |S023S014〉 | u | u | g | 0 |
| |T123S014〉 | g | u | u | 1 |
| |T023S014〉 | g | u | u | 0 |
| |T−123S014〉 | g | u | u | −1 |
| |S023T114〉 | u | g | u | 1 |
| |S023T014〉 | u | g | u | 0 |
| |S023T−114〉 | u | g | u | −1 |
4.2 Symmetry of the fluctuating hamiltonian
Consider now the fluctuating spin interactions which cause relaxation. An example of such interactions is given by the dipole–dipole interaction between the nuclei, which may be written as follows: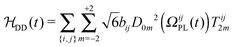 | (15) |
At an arbitrary time point t, molecular vibrations distort the molecular geometry away from its equilibrium configuration, breaking the geometrical symmetry. Hence, in general, the instantaneous value of 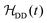 (and other fluctuating terms) does not display symmetry. However, since rapid vibrations are usually too fast to cause significant NMR relaxation, the relevant spin Hamiltonian for relaxation purposes may be locally averaged over molecular vibrations (typically on the sub-picosecond timescale), denoted here
(and other fluctuating terms) does not display symmetry. However, since rapid vibrations are usually too fast to cause significant NMR relaxation, the relevant spin Hamiltonian for relaxation purposes may be locally averaged over molecular vibrations (typically on the sub-picosecond timescale), denoted here  . This vibrationally averaged spin Hamiltonian reflects the geometrical symmetry of the equilibrium molecular structure, and displays the corresponding spin permutation symmetry.
. This vibrationally averaged spin Hamiltonian reflects the geometrical symmetry of the equilibrium molecular structure, and displays the corresponding spin permutation symmetry.
In general,  may be calculated from eqn (15) by using nuclear coordinates from the equilibrium molecular geometry, but with small adjustments to the interaction strengths caused by vibrational averaging.
may be calculated from eqn (15) by using nuclear coordinates from the equilibrium molecular geometry, but with small adjustments to the interaction strengths caused by vibrational averaging.
As previously done for  we will consider in this section the nuclear spin permutations that are symmetry operations for
we will consider in this section the nuclear spin permutations that are symmetry operations for  in both molecular systems.
in both molecular systems.
In the case of 13C2-AFD, the permutation (14)(23) is a symmetry operation for the vibrationally-averaged dipole–dipole spin Hamiltonian because of the inversion geometry of the local molecular structure. The double permutation always exchanges pairs of nuclei with parallel internuclear vectors, so that the spatial interaction tensors are identical for all molecular orientations. Similar considerations apply for other interaction terms such as the chemical shift anisotropy.
The group of the vibrationally-averaged fluctuating Hamiltonian is therefore given by
 | (16) |
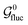 contains the group of spin permutation operators that commute with 〈
contains the group of spin permutation operators that commute with 〈 〉vib. In the case of the cis isomer, the equilibrium geometry is not sufficient to impose symmetry on the vibrationally averaged spin Hamiltonian. We therefore get a trivial symmetry group in this case,
〉vib. In the case of the cis isomer, the equilibrium geometry is not sufficient to impose symmetry on the vibrationally averaged spin Hamiltonian. We therefore get a trivial symmetry group in this case, | (17) |
![[Doublestruck B]](https://www.rsc.org/images/entities/i_char_e165.gif) ST. In the case of 13C2-AFD (Fig. 8b), the matrix representation of 〈HDD〉vib is block-diagonal in this basis, since the vibrationally averaged dipole–dipole Hamiltonian has the same symmetry as
ST. In the case of 13C2-AFD (Fig. 8b), the matrix representation of 〈HDD〉vib is block-diagonal in this basis, since the vibrationally averaged dipole–dipole Hamiltonian has the same symmetry as  (eqn (10) and (16)). In the case of 13C2-AMD (Fig. 8d), on the other hand, off-diagonal elements connecting different irreducible representations appear, since 〈HDD〉vib has a lower symmetry than
(eqn (10) and (16)). In the case of 13C2-AMD (Fig. 8d), on the other hand, off-diagonal elements connecting different irreducible representations appear, since 〈HDD〉vib has a lower symmetry than  (eqn (17)).
(eqn (17)).
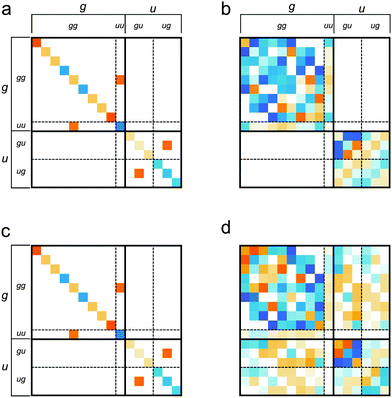 | ||
Fig. 8 Matrix plot representations of  and and  hamiltonians for 13C2-AFD in panels (a), (b) and for 13C2-AMD in panels (c) and (d) respectively. hamiltonians for 13C2-AFD in panels (a), (b) and for 13C2-AMD in panels (c) and (d) respectively.  hamiltonian is block diagonal for 13C2-AFD (panel (b)). The basis is hamiltonian is block diagonal for 13C2-AFD (panel (b)). The basis is ![[Doublestruck B]](https://www.rsc.org/images/entities/i_char_e165.gif) ST, and the ordering follows the convention adopted in Table 3. ST, and the ordering follows the convention adopted in Table 3. | ||
The sole consideration of the symmetry properties of the coherent hamiltonian (Fig. 8a and c) to infer the existence of LLS could be deceptive. The symmetry group for  is identical for both 13C2-AFD and 13C2-AMD (eqn (10)) but a long-lived order is expected only in one case.
is identical for both 13C2-AFD and 13C2-AMD (eqn (10)) but a long-lived order is expected only in one case.
In general, if the molecular structure is rigid, and the equilibrium geometry of the local spin system is centrosymmetric, the group  has dimension 2. If the molecule is rigid but non-centrosymmetric,
has dimension 2. If the molecule is rigid but non-centrosymmetric, 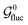 has dimension 1. The symmetry properties of the coherent and fluctuating hamiltonians can be combined to derive the correct symmetry properties for the Liouvillian superoperator.
has dimension 1. The symmetry properties of the coherent and fluctuating hamiltonians can be combined to derive the correct symmetry properties for the Liouvillian superoperator.
4.3 Idealized Liouvillian group and long-lived states
We define the idealized Liouvillian group of the spin system as the intersection of the groups and
and  :
: | (18) |
 | (19) |
 | (20) |
 . Hence the spin evolution must preserve a population difference between states belonging to different irreducible representations of
. Hence the spin evolution must preserve a population difference between states belonging to different irreducible representations of  . Such a population difference is a constant of motion and does not evolve, providing that the realistic spin interactions conform exactly the idealized symmetry assumed in the theoretical model. In practice, deviations from ideal symmetry invariable cause slow relaxation, but the lifetime of such a state may nevertheless be long compared to the relaxation of most other states.
. Such a population difference is a constant of motion and does not evolve, providing that the realistic spin interactions conform exactly the idealized symmetry assumed in the theoretical model. In practice, deviations from ideal symmetry invariable cause slow relaxation, but the lifetime of such a state may nevertheless be long compared to the relaxation of most other states.
Suppose that  has
has 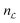 irreducible representations. There are
irreducible representations. There are  combinations of populations which do not evolve, in the ideal case. However one of these constants of motion is the total spin system population, which is trivially conserved in all circumstances, for a closed system.
combinations of populations which do not evolve, in the ideal case. However one of these constants of motion is the total spin system population, which is trivially conserved in all circumstances, for a closed system.
Hence the number of non-trivial long-lived states (NLLS) is given by  − 1.
− 1.
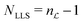 | (21) |
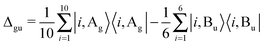 | (22) |
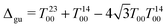 | (23) |
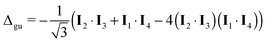 | (24) |
 (see eqn (19)). In the case of 13C2-AMD, the idealized Liouvillian group is one-dimensional even in a regime of perfect chemical equivalence (see eqn (20)) and there is no long-lived state, except for the trivial mean of all spin state populations that is always a conserved quantity for an isolated spin system.
(see eqn (19)). In the case of 13C2-AMD, the idealized Liouvillian group is one-dimensional even in a regime of perfect chemical equivalence (see eqn (20)) and there is no long-lived state, except for the trivial mean of all spin state populations that is always a conserved quantity for an isolated spin system.
4.4 Torsional angle dependence of the decay rate
The dependence of the LLS on the equilibrium molecular geometry is now investigated. The arrangements of the four nuclear spins in 13C2-AMD and 13C2-AFD may be obtained from each another by rotating one of the heteronuclear 13CH single bonds around the axis passing through the 13C2 double bond.The standard approach in LLS analysis consists in the diagonalization of the Liouvillian superoperator that can be set up to include all the relevant relaxation mechanisms. We will restrict our considerations to the relaxation induced by the intra-molecular dipole–dipole interaction (eqn (25)) for simplicity. When the dimension of the Hilbert space is N the Liouvillian superoperator has a set of N2 eigenvalues–eigenoperators pairs {Lq,Qq}. In general  is not hermitian so the eigenvalues may be complex.
is not hermitian so the eigenvalues may be complex.
 | (25) |
| Lq = −λq + iωq | (26) |
Numerical simulation performed with SpinDynamica39 in Fig. 9b shows the dependence of the smallest non-zero rate constant λmin on the torsional angle θ. It was assumed the J coupling parameters to be independent of the torsional angle and equal to those reported in Table 1 for 13C2-AFD. This approximation appears to be reasonable given the small difference in parameters as obtained by fitting the 1D-NMR spectra and listed in Table 1. The relaxation superoperator takes into account all dipole–dipole couplings in the 4-spin system and assumes rigid molecular geometry and isotropic molecular tumbling with a correlation time τC = 15 ps. As expected, a long-lived state with infinite relaxation time is predicted only when θ = 180°, which is the geometric equilibrium configuration for 13C2-AFD.
4.5 Symmetry breaking
Since applied fields are symmetric for all spins, the LLS described by eqn (22) can only be accessed by breaking the idealized Liouvillian symmetry . In the current case, the symmetry-breaking occurs naturally through the term
. In the current case, the symmetry-breaking occurs naturally through the term  , which is associated with the asymmetric ester substituents. The true symmetry group of the coherent Hamiltonian is therefore given by
, which is associated with the asymmetric ester substituents. The true symmetry group of the coherent Hamiltonian is therefore given by  , instead of the idealized group
, instead of the idealized group  in eqn (10). The true Liouvillian group is given by
in eqn (10). The true Liouvillian group is given by | (27) |
 for both molecular systems. In the case of 13C2-AFD, the symmetry-breaking perturbation generates terms connecting the irreducible representations of
for both molecular systems. In the case of 13C2-AFD, the symmetry-breaking perturbation generates terms connecting the irreducible representations of  , allowing experimental access to the LLS, through pulse sequences such as M2S, S2M, and relatives.8,9,20 In the study described here, the symmetry-breaking perturbation induced by the asymmetric ester substituents is large enough to provide experimental access to the LLS, but sufficiently small that a theoretical description based on the idealized Liouvillian group
, allowing experimental access to the LLS, through pulse sequences such as M2S, S2M, and relatives.8,9,20 In the study described here, the symmetry-breaking perturbation induced by the asymmetric ester substituents is large enough to provide experimental access to the LLS, but sufficiently small that a theoretical description based on the idealized Liouvillian group 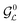 provides a good approximation.
provides a good approximation.
Following the notation used throughout the script where 1H nuclei are labelled 1 and 4, and 13C nuclei are labelled 2 and 3, the theory developed could be also applied to the molecular AA‘XX’ 4-spin systems discussed for example in ref. 17, 18 and 25–27. The coherent spin Hamiltonian displays near-magnetic-equivalence, and the central spin pair is sufficiently remote from other participating spins that the symmetry group {E,(14),(23),(14)(23)} is a reasonable approximation for both the coherent and the fluctuating Hamiltonians. This group has four irreducible representations, leading to three non-trivial long-lived states. Two of these may be accessed without breaking the chemical equivalence.
5 Conclusions
We have demonstrated the existence of a long-lived nuclear spin state in a multiple spin system, far from the usual conditions of near magnetic equivalence. A state of this kind is only supported by molecules with centrosymmetric local molecular geometry, such as fumarate. A group theoretical description of the conditions leading to long-lived states in multiple spin systems has been given. This theoretical approach is likely to be useful for understanding a variety of related problems, such as long-lived states in chemically equivalent spin systems16–19,26,27 and long-lived states in rapidly rotating methyl groups.31The existence of long-lived states in fumarate derivatives may also have practical relevance to hyperpolarized NMR studies of fumarate metabolism, in the context of in vivo cancer detection.41,42 We are currently exploring the possibility of generating the long-lived population imbalance between the Ag and Bu manifolds directly through solid-state dynamic nuclear polarization (DNP), as has been demonstrated for singlet order in spin-pair systems.43
Acknowledgements
This research was funded by EPSRC (UK) and the European Research Council. We are grateful to Salvatore Mamone, Jean-Nicolas Dumez, Michael C. D. Tayler and Kevin Brindle for discussions and suggestions, and to Ole G. Johannessen for instrumental support.References
- M. Carravetta, O. Johannessen and M. Levitt, Phys. Rev. Lett., 2004, 92, 153003 CrossRef.
- M. Carravetta and M. H. Levitt, J. Am. Chem. Soc., 2004, 126, 6228–6229 CrossRef PubMed.
- M. Carravetta and M. H. Levitt, J. Chem. Phys., 2005, 122, 214505 CrossRef PubMed.
- R. Sarkar, P. R. Vasos and G. Bodenhausen, J. Am. Chem. Soc., 2007, 129, 328–334 CrossRef PubMed.
- G. Pileio and M. H. Levitt, J. Magn. Reson., 2007, 187, 141–145 CrossRef PubMed.
- G. Pileio, M. Carravetta, E. Hughes and M. H. Levitt, J. Am. Chem. Soc., 2008, 130, 12582–12583 CrossRef PubMed.
- M. C. D. Tayler, S. Marie, A. Ganesan and M. H. Levitt, J. Am. Chem. Soc., 2010, 132, 8225–8227 CrossRef PubMed.
- G. Pileio, M. Carravetta and M. H. Levitt, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17135–17139 CrossRef PubMed.
- M. C. D. Tayler and M. H. Levitt, Phys. Chem. Chem. Phys., 2011, 13, 5556–5560 RSC.
- M. H. Levitt, Annu. Rev. Phys. Chem., 2012, 63, 89–105 CrossRef PubMed.
- G. Pileio, J. T. Hill-Cousins, S. Mitchell, I. Kuprov, L. J. Brown, R. C. D. Brown and M. H. Levitt, J. Am. Chem. Soc., 2012, 134, 17494–17497 CrossRef PubMed.
- G. Pileio, S. Bowen, C. Laustsen, M. C. D. Tayler, J. T. Hill-Cousins, L. J. Brown, R. C. D. Brown, J. H. Ardenkjaer-Larsen and M. H. Levitt, J. Am. Chem. Soc., 2013, 135, 5084–5088 CrossRef PubMed.
- J.-N. Dumez, J. T. Hill-Cousins, R. C. D. Brown and G. Pileio, J. Magn. Reson., 2014, 246, 27–30 CrossRef PubMed.
- A. K. Grant and E. Vinogradov, J. Magn. Reson., 2008, 193, 177–190 CrossRef PubMed.
- W. S. Warren, E. Jenista, R. T. Branca and X. Chen, Science, 2009, 323, 1711–1714 CrossRef PubMed.
- Y. Feng, R. M. Davis and W. S. Warren, Nat. Phys., 2012, 8, 831–837 CrossRef PubMed.
- Y. Feng, T. Theis, T.-L. Wu, K. Claytor and W. S. Warren, J. Chem. Phys., 2014, 141, 134307 CrossRef PubMed.
- K. Claytor, T. Theis, Y. Feng and W. Warren, J. Magn. Reson., 2014, 239, 81–86 CrossRef PubMed.
- K. Claytor, T. Theis, Y. Feng, J. Yu, D. Gooden and W. S. Warren, J. Am. Chem. Soc., 2014, 136, 15118–15121 CrossRef PubMed.
- S. J. DeVience, R. L. Walsworth and M. S. Rosen, Phys. Rev. Lett., 2013, 111, 173002 CrossRef.
- N. Salvi, R. Buratto, A. Bornet, S. Ulzega, I. Rentero Rebollo, A. Angelini, C. Heinis and G. Bodenhausen, J. Am. Chem. Soc., 2012, 134, 11076–11079 CrossRef PubMed.
- R. Buratto, D. Mammoli, E. Chiarparin, G. Williams and G. Bodenhausen, Angew. Chem., Int. Ed., 2014, 53, 11376–11380 CrossRef PubMed.
- P. R. Vasos, A. Comment, R. Sarkar, P. Ahuja, S. Jannin, J.-P. Ansermet, J. a. Konter, P. Hautle, B. van den Brandt and G. Bodenhausen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18469–18473 CrossRef PubMed.
- P. Ahuja, R. Sarkar, S. Jannin, P. R. Vasos and G. Bodenhausen, Chem. Commun., 2010, 46, 8192–8194 RSC.
- L. Buljubasich, M. B. Franzoni, H. W. Spiess and K. Münnemann, J. Magn. Reson., 2012, 219, 33–40 CrossRef PubMed.
- M. B. Franzoni, L. Buljubasich, H. W. Spiess and K. Münnemann, J. Am. Chem. Soc., 2012, 134, 10393–10396 CrossRef PubMed.
- Y. Zhang, P. C. Soon, A. Jerschow and J. W. Canary, Angew. Chem., Int. Ed., 2014, 53, 3396–3399 CrossRef PubMed.
- T. Theis, M. Truong, A. M. Coffey, E. Y. Chekmenev and W. S. Warren, J. Magn. Reson., 2014, 248C, 23–26 CrossRef PubMed.
- M. Emondts, M. P. Ledbetter, S. Pustelny, T. Theis, B. Patton, J. W. Blanchard, M. C. Butler, D. Budker and A. Pines, Phys. Rev. Lett., 2014, 112, 077601 CrossRef.
- H. J. Hogben, P. J. Hore and I. Kuprov, J. Magn. Reson., 2011, 211, 217–220 CrossRef PubMed.
- B. Meier, J.-N. Dumez, G. Stevanato, J. T. Hill-Cousins, S. S. Roy, P. H kansson, S. Mamone, R. C. D. Brown, G. Pileio and M. H. Levitt, J. Am. Chem. Soc., 2013, 135, 18746–18749 CrossRef PubMed.
- M. H. Levitt, Spin dynamics. Basics of Nuclear Magnetic Resonance, 2001 Search PubMed.
- G. Pileio and M. H. Levitt, J. Chem. Phys., 2009, 130, 214501 CrossRef PubMed.
- G. Pileio, M. Carravetta and M. H. Levitt, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17135–17139 CrossRef PubMed.
- T. Theis, Y. Feng, T.-l. Wu and W. S. Warren, J. Chem. Phys., 2014, 140, 014201 CrossRef PubMed.
- H. J. Hogben, M. Krzystyniak, G. T. P. Charnock, P. J. Hore and I. Kuprov, J. Magn. Reson., 2011, 208, 179–194 CrossRef PubMed.
- I. Kuprov, J. Magn. Reson., 2011, 209, 31–38 CrossRef PubMed.
- A. Shaka, J. Keeler and R. Freeman, J. Magn. Reson., 1983, 53, 313–340 Search PubMed.
- M. H. Levitt, Spin Dynamica, 2013 Search PubMed.
- P. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, Academic Press, London, 2 edn, 2006, p. 721 Search PubMed.
- M. Karlsson, A. Gisselsson, S. K. Nelson, T. H. Witney, S. E. Bohndiek, G. Hansson, T. Peitersen, M. H. Lerche and K. M. Brindle, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19801–19806 CrossRef PubMed.
- K. M. Brindle, S. E. Bohndiek, F. a. Gallagher and M. I. Kettunen, Magn. Reson. Med., 2011, 66, 505–519 CrossRef PubMed.
- M. C. D. Tayler, I. Marco-Rius, M. I. Kettunen, K. M. Brindle, M. H. Levitt and G. Pileio, J. Am. Chem. Soc., 2012, 134, 7668–7671 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp05704j |
| This journal is © the Owner Societies 2015 |


