The n → π* interaction: a rapidly emerging non-covalent interaction

Abstract

This perspective describes the current status of a recently discovered non-covalent interaction named as the n → π* interaction, which is very weak and counterintuitive in nature. In this review, we have provided a brief overview of the widespread presence of this interaction in biomacromolecules, small biomolecules and materials, as well as the physical nature of this interaction explored using various experimental and theoretical techniques. It has been found that this interaction is equally important to other non-covalent interactions for the stability and specific structures of biomolecules and materials. An in-depth understanding of this interaction can help in designing more efficient functional materials as well as drugs. The review also provides a future outlook in terms of exploring the detailed functional role of this interaction in biological processes and its direct spectroscopic evidence, which other commonly known non-covalent interactions (conventional hydrogen bonding, π-hydrogen bonding, π-stacking, etc.) have.

---

Santosh K. Singh

Santosh K. Singh obtained his BSc in Chemistry from St. Xavier’s college, Ranchi in 2011. He joined the Integrated PhD program at the Indian Institute of Science Education and Research (IISER) Pune in the same year. Currently, he is pursuing his PhD under the supervision of Dr Aloke Das at IISER Pune. His research interest is the detailed understanding of the n → π* interaction, which is a recently discovered non-covalent interaction.

Aloke Das

Aloke Das obtained his PhD from the Indian Institute of Technology Kanpur in 2002. He worked with Professor Tapas Chakraborty for his PhD work on optical spectroscopy of aromatic clusters in a supersonic jet. After finishing his PhD, he moved to Purdue University to do postdoctoral research with Professor Timothy S. Zwier and worked on the conformation-specific UV and IR spectroscopy of flexible aromatic hydrocarbons, which are isomeric products in fuel combustion processes. During 2004–2007, he worked with Professor Erwin D. Poliakoff at the Louisiana State University to study vibrationally resolved VUV photoelectron spectroscopy of polyatomic molecules in the gas phase using synchrotron radiation at the Advanced Light Source of the Lawrence Berkeley National Laboratory. In 2007, he joined the Indian Institute of Science Education and Research (IISER) Pune as an Assistant Professor in the Department of Chemistry and presently, he is an Associate Professor there. His research includes the molecular level understanding of non-covalent interactions through gas phase laser spectroscopy of molecules and complexes relevant to biomolecules and materials using laser desorption as the vaporization source.

---

1. Introduction

Non-covalent interactions are the backbone of biomolecular and material structures, as well as biological processes.^1–14 Thus, an in-depth understanding of these weak interactions may lead to the design of efficient functional materials and drugs. These non-bonding interactions generally have a broad range of classifications depending on their nature, origin and strength. Hydrogen bonding is the most versatile and well understood non-covalent interaction documented in the literature.^1–5 Intermolecular interactions involving π-systems, which are also very popular and well studied, are π-stacking, π-hydrogen bonding and cation–π interactions.^9–21 However, quite recently, two more non-covalent interactions involving π-electrons, namely anion–π and n → π* interactions, have been recognized by the scientific community.^22–85 Neither of these interactions were appreciated earlier in spite of their widespread presence in biology and materials, because the attractive interaction between an electron rich species and the π-electron cloud is counterintuitive in nature. Although the name “anion–π interaction” was conceived by Frontera, Deya, and co-workers²⁴ in 2002, the interaction between an anion and electron deficient aromatic ring was reported in the literature much earlier.⁸⁶

Both n → π* and anion–π interactions seem to be similar in nature, but the origin of these two attractive interactions is very much different. The anion–π interaction originates mostly from electrostatics (anion-quadrupole) combined with smaller but important contributions of induction (anion-induced polarization) and dispersion.^{22–25,28–31} On the other hand, it has been found from a few studies that dispersion forces play a significant role in the stability of the n → π* interaction, but this conclusion demands more detailed investigation in this direction.^32–35 The cation–π interaction, which is another ion–π interaction, is mainly stabilized by both electrostatics and induction, with a smaller but significant contribution of dispersion.^15–17 In some cases with extended π-systems (buckybowls) or alkali and alkaline earth metal cations, the induction effect has a leading contribution in the stabilization of the cation–π interaction.^18,21

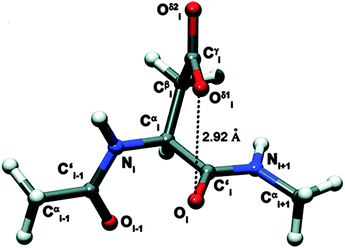
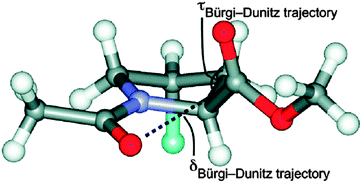
The n → π* interaction is generally classified into two categories: n → π*_Am (amide) and n → π*_Ar (aromatic).³⁶ The n → π*_Am interaction is widely present in the backbones of proteins and peptoids^37–49 where the lone pair of electrons on the oxygen atom of a carbonyl group is delocalized into the π* orbital of a neighbouring carbonyl group.^41–49 In the case of the n → π*_Ar interaction, lone pair electrons on an oxygen or nitrogen atom are delocalized into the π* orbital of an aromatic ring.^50–53Fig. 1 shows examples of n → π*_Am as well as n → π*_Ar interactions and the geometrical parameters used for the characterization of the Burgi–Dunitz trajectory.

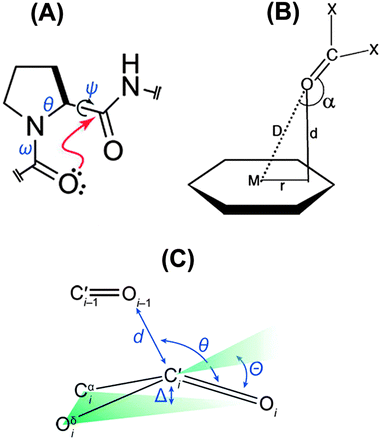Fig. 1 (A) Example of n → π*_Am interaction. Angles θ, ψ and ω are Ramachandran angles. Adapted in part with permission from ref. 44. Copyright [2014] American Chemical Society. (B) Example of n → π*_Ar interaction. Adapted in part with permission from ref. 63. Copyright [2007] American Chemical Society. (C) Geometrical parameters which are used to characterize the Burgi–Dunitz trajectory. Adapted in part with permission from ref. 44. Copyright [2014] American Chemical Society.

The n → π*_Ar interaction is also termed as the lone pair (lp)⋯π interaction. Both types of this n → π* interaction follow the Burgi–Dunitz trajectory of approach of a nucleophile to an electrophilic system.^54–56 To have an n → π*_Am interaction, an O⋯C=O distance (d) of ≤3.2 Å and ∠O⋯C=O (θ) of 109 ± 10° are required [see Fig. 1(C)]. It has been noticed that the donor carbonyl distorts the plane of the acceptor carbonyl group, which rises above the plane of its substituents and moves towards the oxygen atom of the donor carbonyl group. Such deviation from planarity can be measured as degree of pyramidalization (Δ), which is a signature of n → π*_Am interactions in proteins.^43,44 In the case of the n → π*_Ar interaction, a distance (d) of 2.8–3.8 Å between the oxygen or nitrogen atom and aromatic ring centroid as well as an angle (α) of ≤90° between the plane containing the oxygen or nitrogen atom and aromatic plane are required [see Fig. 1(B)]. The lp⋯π (n → π*_Ar) interaction was first discovered in Z-DNA by Egli and co-workers in 1995.^{35,53,58–60} Since then, there have been tremendous efforts to recognize the n → π* interaction in biomolecules, as well as in materials, through extensive search of the X-ray crystal structures in the Cambridge Structural Database (CSD) and Protein Data Bank (PDB).^62–68 Analysis of the CSD reveals that the occurrence of the lp⋯π interaction is much more frequent than that of the anion–π interaction. However, the field of the anion–π interaction is much more mature than that of the n → π* interaction. This fact indeed demands a few reviews on the n → π* interaction in the literature and this is the motivation for the present perspective.

The most significant and detailed contribution to our current understanding of the n → π* interaction has come from the recent studies of Raines and co-workers.^44,69–76 They have investigated the trans/cis ratios in polypeptides, peptoids, and thiopeptoids through NMR spectroscopy and demonstrated that the preferential stability of one of the conformers over the other one is due to the n → π* interaction. From extensive analysis of the protein crystal structures in the PDB, they have found that the n → π* interaction, which is present in the backbone of about 45% of amino acid residues of proteins, plays a significant role in the stability of the structures of proteins.⁴¹ The present perspective provides an overview of the recent advancement as well as future outlook on the understanding of this rapidly emerging realm of the n → π* interaction.

2. n → π* interaction in biomolecules

2.1. Role of the n → π* interaction in nucleic acids

Egli and co-workers have identified several nucleic acids where significant n → π* interactions are present.^53,63,65 They have analyzed crystal structures of three forms of Z-DNA: mixed spermine/magnesium, magnesium, and spermine. Z-DNA does not have the proper base stacking that A-DNA and B-DNA have. However, it has been found that the O₄ oxygen of the deoxyribose sugar of the cytidine moiety at each GC site of Z-DNA points directly towards the guanine ring of the guanidium (G) moiety. Fig. 2 exhibits the crystal structure of Z-DNA, showing that the cytidine sugar unit is placed over the guanine base while the stacking interaction between the guanine and cytosine bases is mostly disrupted. The distance between the oxygen atom of the sugar and one of the carbons of the guanine ring in the Z-DNA has been found to be 2.98 Å, which is less than the sum of the van der Waals radii of oxygen and carbon atoms. The angle between the O₄ atom and the exocyclic C–N bond, i.e. ∠O₄⋯C–N, is 105°. It has been demonstrated from this geometrical arrangement of the oxygen atom of the sugar unit and the guanine ring that an attractive n → π* interaction between one of the lone pairs of the O₄ atom and the π* orbitals of the guanine ring provides stability in the Z-DNA, in spite of the poor base stacking present there.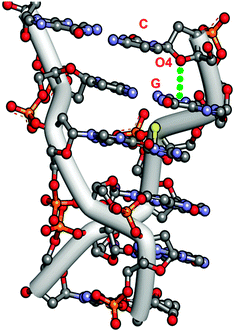

Fig. 2 Crystal structure of Z-DNA [PDB ID-131D].

The significance of the n → π* interaction is observed not only in Z-DNA but also in RNA.^63,65 Egli and co-workers have pointed out that there is a possibility of an n → π* interaction at the U-turns of RNA. U-turns are actually structural motifs found in diverse three dimensional structures of RNA. At a U-turn, the RNA backbone makes a sharp turn of about 120° from the standard helical conformation between the first and second nucleotides of a UNR sequence, where U is uridine, N is any base and R is usually adenine or guanine.⁶³

It is interesting to note that U-turns are stabilized by two hydrogen bonds and an n → π* interaction between an oxygen atom of the phosphate group of the third residue and the face of the nucleobase of the first nucleotide. Such a U-turn is observed in the crystal structure of t-RNA^Phe (see Fig. 3A). The GUAA (guanine–uridine–adenine–adenine) tetraloop in hammerhead ribozyme also makes a U-turn where the oxygen atom of the phosphate group of the first adenine is found to be in close contact with the guanine ring. Egli and co-workers have also reported an n → π* interaction between the oxygen of water molecules and the aromatic ring of unstacked nucleobases in the crystal structure of an RNA pseudoknot obtained from beet western yellow virus (see Fig. 3B).⁶⁵ The distance between the oxygen of the water molecule and the ring centroid of cytosine (C8) is 2.93 Å and the dihedral angle between the plane defined by the water molecule and the plane of the ring is 91°. It has been found that the n → π* interaction may have functional importance in the frameshifting activity of the RNA pseudoknot.

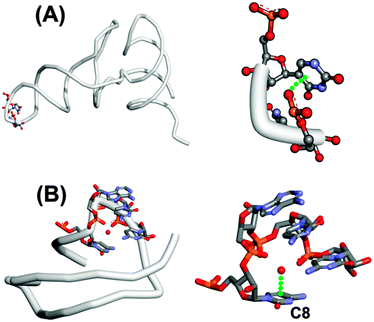Fig. 3 (A) Structure of t-RNA and its U-turn, showing the possibility of an n → π* interaction [PDB ID-1EHZ]. (B) Structure of RNA pseudoknot and its U-turn, showing the possibility of an n → π* interaction between water and cytosine (C8) nucleobase [PDB ID-2A43].

In order to understand whether such close contacts between the oxygen of one nucleobase or the phosphates and aromatic ring of other nucleobases can stabilize the structure of Z-DNA, and the U-turns of t-RNA and hammerhead ribozyme, Egli and co-workers have performed ab initio calculations on model systems and a few of them have been shown in Fig. 4.⁶³ These model systems are built based on the crystallographic co-ordinates, and single point energies are calculated for each system at the DFT/6-31G* level of theory. The interaction energy for the n → π* interaction between the oxygen of the ribose sugar of cytosine and the guanine ring in Z-DNA has been found to be insignificant [ΔE(lp–π)], although it shows stabilization of about −2 kcal mol⁻¹ in the presence of Mg²⁺ coordinated to N7 of guanine (Fig. 4A). Protonation of O6 of guanine further increases the interaction energy to −5.6 kcal mol⁻¹. The interaction between the oxygen of the phosphate group and the ring of uracil in the U-turn of t-RNA has been found to be stable and the interaction energy has been calculated to be −4.8 kcal mol⁻¹ (Fig. 4B). The authors have found that the n → π* interaction can have a significant contribution towards the stabilization of the structure if the nucleobase is protonated. The n → π* interactions in the structures of DNA and RNA can be a signature of the polarization or protonation state of a nucleobase.⁶³

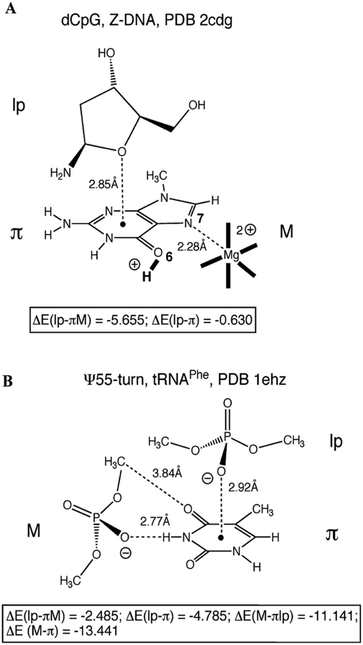Fig. 4 (A) Oxygen of the 2-deoxyribose sugar of cytidine interacting with the guanine nitrogenous base of an adjacent guanidine in Z-DNA. (B) Ψ-turn in t-RNA^Phe, with interaction between the oxygen atom of phosphate and a cytosine nitrogenous base. ΔE(lp–π) represents the binding energy of the system in kcal mol⁻¹ in the absence of modulators (M) like a metal ion, protonation of bases, and other non-covalent interactions with surrounding phosphates with the surrounding moieties. ΔE(lp–πM) represents the binding energy of the system in kcal mol⁻¹ in the presence of modulators (M). Adapted in part with permission from ref. 63. Copyright [2007] American Chemical Society.

Sankararamakrishnan and co-workers have analyzed high resolution crystal structures of DNA and RNA to find close contacts between the oxygen atom of one base and aromatic centre of another base.⁶² They have analyzed 77 crystal structures of DNA having 110 base sequences and 55 crystal structures of RNA containing 76 base sequences. It has been found that the n → π* interaction is possible in 91 base pairs in DNA and 18 base pairs in RNA. The authors have reported that oxygen–aromatic close contacts between the base pairs are very less frequent in RNA compared to in DNA. They have performed ab initio calculations on all the 91 base pairs in DNA showing close contacts between an oxygen atom and the centre of an aromatic ring by taking the co-ordinates of the atoms from the crystal structures. It has been found that such close contacts are indeed attractive in nature.

2.2. Role of the n → π* interaction in proteins

2.2.1. n → π* interactions in the backbones of proteins. It has been found that the n → π* interaction, similarly to the hydrogen bonding interaction, plays a significant role in the stability of the backbones of proteins. The search for the significance of the n → π* interaction in proteins began after its recognition in the stability of the collagen triple helix in 2002.³⁸ Collagen consists of three polypeptide chains connected through hydrogen bonds and forms an extended triple helical structure. Each polypeptide chain consists of a Xaa–Yaa–Gly repeating sequence, where Xaa is usually proline (Pro) and Yaa is either proline or 4R-hydroxyproline (4R-Hyp). Although the Xaa_i−1–Pro_i peptide bond can have possibilities of both trans and cis conformations, the peptide bonds in the collagen triple helix predominantly exist in the trans form.³⁸ A section of collagen triple helix crystal structure showing the pro-Hyp-gly sequence has been shown in Fig. 5.

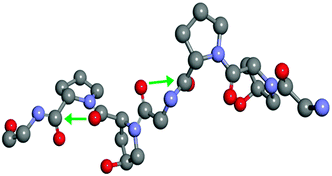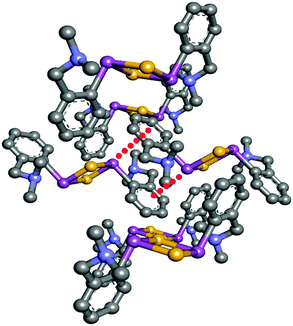
Fig. 5 Section of collagen triple helix showing the Pro-Hyp-Gly sequence (green arrows shows the n → π* interaction).

Raines and co-workers have performed NMR spectroscopy and computational studies on three model compounds (AcProOMe, Ac-4R-Flp-OMe, and Ac-4S-Flp-OMe) to understand the role of the n → π* interaction in the stability of the collagen triple helix.³⁸Fig. 6 shows the structures of the trans conformers of the three model compounds. They have found through NMR spectroscopy studies that the equilibrium constant (K_trans/cis) between the trans and cis conformations is greater than 1 for all three of the compounds. The results obtained from theoretical calculations performed on these model compounds correlate well with the experimental results. The trans conformation allows closer approach of the amide oxygen to the carbonyl group of the ester, following the Burgi–Dunitz trajectory. It has been found from the Natural Bond Orbital (NBO) analysis of these model compounds that there is a significant overlap between the lone pair orbital on the amide oxygen and the empty π* orbital of another adjacent carbonyl group in the trans conformation. The second order perturbative energy for this interaction in the trans exo form of Ac-4R-Flp-OMe has been calculated to be 1.38 kcal mol⁻¹. The crystal structure of Ac-4R-Flp-OMe shown in Fig. 7 also has a good resemblance to the theoretically calculated structure. These results indicate that the trans conformation of the Xaa_i−1–Pro_i peptide bonds in the collagen triple helix are stabilized by n → π* interactions between the lone pair of the carbonyl oxygen of position i − 1 and the antibonding orbital of the carbonyl group of position i. (For labelling notation see Fig. 1C.)

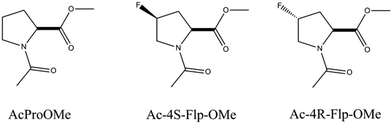Fig. 6 Structures of the trans conformer of three model compounds designed to understand the role of the n → π* interaction in the collagen triple helix.³⁸ Flp stands for fluoroproline.

Fig. 7 Crystal structure of Ac-4R-Flp-OMe. Adapted with permission from ref. 38. Copyright [2002] American Chemical Society.

But does the n → π* interaction exist in other secondary structures of proteins too? To answer this question, Raines and co-workers created a computational library of allowed conformations of proteins using a model peptide of four alanine residues (AcAla₄NHMe) capped with an acetyl group at the N terminus and –NHMe group at the C terminus.⁴¹ They performed NBO analysis on the computationally generated allowed conformations to predict the ones that could have an n → π* interaction, and those conformations were depicted on a Ramachandran type plot based on the Φ and Ψ values for the residue pairs. This study was followed by PDB analysis of a high resolution (≤1.6 Å) and non-redundant subset of 1731 protein crystal structures to search for close contact between the carbonyl groups as observed in the collagen triple helix. The allowed distance between the oxygen of the carbonyl group of residue i − 1 and the carbon of the carbonyl group of residue i as well as the O_i−1⋯C_i=O_i angle were set to ≤3.2 Å and 99°–119°, respectively, for the search. It has been found that there are abundant n → π* interactions in the allowed regions of the Ramachandran plot. Further, the computational search of the possible conformations of proteins which can give rise to an n → π* interaction correlates well with the actual PDB search.⁴¹

Christian Fufezan followed a similar procedure to determine the significance of the n → π* interaction in the structural stability of proteins.⁶⁶ The author performed PDB analysis of a non-redundant set of 5296 protein crystal structures using python module p3d with similar search criteria for the n → π* interaction to those applied by Raines and co-workers.⁴¹ About 45.1% of all the residues in the non-redundant dataset satisfied the search criteria. Simulations on model peptides were also performed to search for the possible conformations showing an n → π* interaction.

Both the studies by Raines and co-workers and those of Christian Fufezan show that the regions for the n → π* interaction identified through computational methods correspond well to those searched for through PDB analysis. The Ramachandran plots generated in these studies show that the highest propensity for the n → π* interaction is in left and right handed α-helices. However, the presence of the n → π* interaction between the i − 1 and i residues in β-strands is insignificant. Nevertheless, the n → π* interaction can exist in twisted β-strands, which are also known as twisted β-sheets or β-bulges. Raines and co-workers have pointed out two common types of β-bulges, namely G1 and wild types, having a significant amount of n → π* interaction.⁴¹ This interaction is also observed in 3₁₀ helices and polyproline II helices.⁴¹

The n → π* interaction is responsible not only for the stability but also the function of proteins. Raines and co-workers have found a series of four n → π* interactions between consecutive residues in the selectivity filter of the K⁺ channel from Streptomyces lividans.⁴¹ They have observed that the n → π* interaction is present only in the region responsible for the filtering of K⁺ ions, while this interaction is nearly absent in that region at high concentrations of K⁺ ions. They pointed out that the n → π* interactions could stabilize the conformation of the filter region of the protein at low concentrations of K⁺ ions.

2.2.2. n → π* interactions involving the side chains of proteins. The n → π* interaction exists not only in the backbone but also in the side chains of proteins. Sankararamakrishnan and co-workers have analyzed high resolution crystal structures of about 500 proteins and reported that the oxygen atom of the backbone carbonyl group interacts frequently with side chain carbonyl groups, as well as aromatic centers.^50,64,68 Thus, both n → π*_Am and n → π*_Ar types of interactions are present in proteins. Four amino acid residues containing aromatic side chains are histidine, tyrosine, phenylalanine and tryptophan. It has been found that there are 249 examples where a close contact of about 3.5 Å between an aromatic center and backbone carbonyl oxygen is present.⁶⁴ On the other hand, the occurrence of the interaction between a side chain carbonyl oxygen and aromatic center is very less frequent (37 examples). Fig. 8(A) shows an example of an n → π*_Am interaction between the backbone carbonyl oxygen atom of an alanine residue and the aromatic center of a phenylalanine residue in the protein bacterial luciferase enzyme (PDB ID:1LUC).⁶⁴ A similar interaction between the side chain carbonyl oxygen of glutamine and the aromatic center of tyrosine present in the protein Serratia marcescens endonuclease (PDB ID:1QL0) is shown in Fig. 8(B).⁶⁴ It has been reported that the aromatic residue that is involved most frequently in this interaction is histidine.⁶⁴

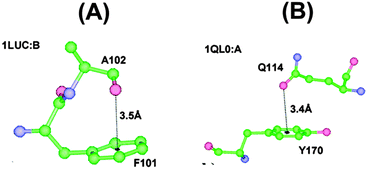Fig. 8 n → π*_Ar interaction between (A) the oxygen atom of Ala residue and aromatic center of Phe residue (PDB ID:1LUC) and (B) the oxygen atom of Glu residue and aromatic ring of Tyr residue (PDB ID:1QL0). Adapted in part with permission from ref. 64. Copyright [2007] American Chemical Society.

Close contact between the carbonyl groups of the backbone and side chain of the same amino acid residue aspartic acid (Asp) has been identified by Sankararamakrishnan and co-workers from an exhaustive search of high resolution protein crystal structures in the PDB.⁶⁸ They have found that these intra-residue close contacts between the carbonyl groups are present in about 102 Asp residues. Fig. 9 shows an example of this interaction in an Asp residue of the protein epidermolytic toxin A (PDB ID:1AGJ).⁶⁸ The authors have also recognized n → π* interactions between water oxygen atoms and the π-clouds of aromatic residues in proteins through the detailed analysis of high resolution crystal structures of proteins as well as quantum chemistry calculations of model compounds based on protein structures in the presence of different orientations of water molecules.⁵⁰

Fig. 9 Crystal structure of an aspartic acid residue interacting through a n → π* interaction [PDB ID-1AGJ]. Adapted in part with permission from ref. 68. Copyright [2010] American Chemical Society.

2.2.3. Co-operativity between hydrogen bonding and n → π* interactions. NBO analysis performed by Raines and co-workers on a model α-helix peptide shows that the n → π* interaction is present due to delocalization of the p-rich lone pair of the oxygen atom of the carbonyl group of residue i − 1 over the π* orbital of the carbonyl group of residue i.⁴¹ Interestingly, the s-rich lone pair of the same oxygen is delocalized over the σ* antibonding orbital of the N–H bond of residue i + 4 to form a N–H⋯O=C hydrogen bond. They have called it kinship of a hydrogen bond and a n → π* interaction in an α-helix. Raines and co-workers have also performed PDB analysis and found several crystal structures of proteins in which the oxygen atom of the side chain of an asparagine residue is involved in hydrogen bonding with a hydrogen bond donor as well as a n → π* interaction with a carbonyl group of the backbone of the protein.⁷³Fig. 10 shows the involvement of the lone pair orbitals of the oxygen atom of the side-chain of an asparagine residue in the hydrogen bond with the N–H group of residue i + 2 and the n → π* interaction with the carbonyl group of the main chain. The n → π* interaction contributes about 0.5 kcal mol⁻¹ in the stabilization of the α-helix. Here the presence of the n → π* interaction reduces the O_i−1⋯C_i=O_i distance, which favours the hydrogen bond formation. Thus the existence of the n → π* interaction increases the strength of the hydrogen bond and this is called positive co-operativity.⁷³

Fig. 10 The lone pair orbital of the oxygen of the side-chain of an asparagine residue is involved in a hydrogen bond with the N–H of residue i + 2 as well as an n → π* interaction with the carbonyl group of the main chain. Adapted in part with permission from ref. 73. Copyright [2013] American Chemical Society.

Very recently, Das and co-workers have studied the interplay between n → π*_Ar and N–H⋯N hydrogen bonding interactions in the complexes of 7-azaindole and 2,6-substituted fluoropyridines.³⁴ They have found that the strength of the hydrogen bond in these complexes decreases due to the presence of the n → π*_Ar interaction. This negative co-operativity is mostly due to subtle competition between the weak n → π*_Ar (about 0.5 kcal mol⁻¹) and strong hydrogen bonding (about 4 kcal mol⁻¹) interactions. It is interesting to point out that the weak interaction present here can govern the final geometry of these complexes despite the presence of the strong hydrogen bonding interaction. It is also intriguing to note in this case that the lone pairs on two different nitrogen atoms take part in the hydrogen bonding and n → π*_Ar interactions, while there is participation by two lone pairs on the same oxygen atom in the two non-covalent interactions in an α-helix. Fig. 11 shows the initial and final structures of 7-azaindole⋯2,6-difluoropyridine calculated at the M05-2X/cc-pVTZ level of theory. The optimized structure exhibits both N–H⋯N hydrogen bonding and n → π*_Ar interactions.

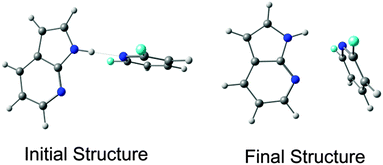Fig. 11 Initial and final structures of 7-azaindole⋯2,6-difluoropyridine calculated at the M05-2X/cc-pVTZ level of theory (reproduced from ref. 34).

3. Significance of the n → π* interaction in materials

The n → π* interaction plays a significant role in the structures of not only biomacromolecules but also materials.^78–85 There are quite extensive reports in the literature which show the existence of the n → π* interaction as well as its role in the supramolecular self assembly of molecules to give rise to specific structures of materials. Reedijk and co-workers have named this interaction as a new supramolecular bond.⁶⁷ They have synthesized a [Zn₄(oxodentriz)Cl₈](CH₃CN)₂(H₂O) complex in acetonitrile at room temperature and determined the crystal structure, which shows that the nitrogen atom of acetonitrile is in close contact with the aromatic ring of triazine (see Fig. 12).⁷⁸ The distance between the nitrogen atom of the acetonitrile molecule and the center of the triazine ring is 3.25 Å and the angle of approach of the nitrogen atom of the acetonitrile molecule towards the center of the triazine ring is 75.2°. These favourable geometrical parameters indicate the presence of an lp⋯π interaction between the nitrogen atom of acetonitrile and heteroaromatic ring triazine.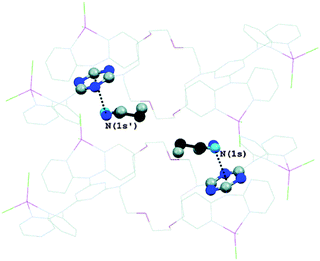

Fig. 12 Crystal structure of the complex [Zn₄(oxodentriz)Cl₈](CH₃CN)₂(H₂O) showing the lp⋯π interaction between the nitrogen of acetonitrile and the triazine ring. Adapted with permission from ref. 78. Copyright [2006] American Chemical Society.

Further, Reedijk and co-workers have designed two triazine-based compounds which self assemble to form structures stabilized by both C–H⋯π and lp⋯π interactions.⁷⁹ The crystal packing of the self assembled structure of one of the compounds has been shown in Fig. 13, which shows that each molecular unit interacts with four neighbouring molecules by means of two Cl⋯π and two weak C–H⋯π interactions. Later, the same group reported the crystal structure of a co-ordination complex, [Cu(Hspet)(NO₃)₂](NO₃)·0.5H₂O, synthesized from the reaction of the ligand 2,4,6-tris-N-[N-2-(methylsulfanyl)-N-(pyridine-2-ylmethyl)ethanamine]-1,3,5-triazine (spet) with copper II nitrate.⁸¹ This crystal structure is depicted in Fig. 14, and it shows that the third substituent nitrogen atom (N19) of the 1,3,5-triazine ring is in close contact with the triazine ring of the adjacent co-ordination molecule, and the N19 atom of the latter co-ordination molecule is also in close contact with the centroid of the triazine ring of the former co-ordination molecule. Thus, a double lp⋯π interaction holds the two complexes together in their crystal packing.⁸¹

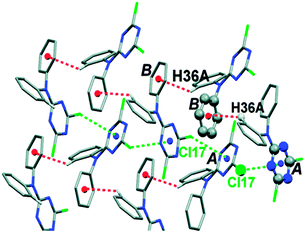Fig. 13 Crystal packing of a triazine-based compound stabilized by C–H⋯π and lp⋯π interactions. Adapted in part with permission from ref. 79. Copyright [2007] American Chemical Society.

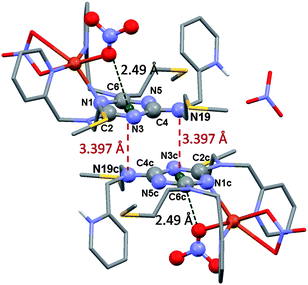Fig. 14 Crystal structure of the [Cu(Hspet)(NO₃)₂](NO₃)·0.5H₂O complex showing lp⋯π interactions between nitrogen (N19) atoms and 1,3,5-triazine rings. Reproduced from ref. 81 with permission from The Royal Society of Chemistry.

Mukhopadhyay and co-workers have designed two co-ordination complexes of nickel II malonate, namely (C₅H₇N₂)₄[Ni(C₃H₂O₄)₂(H₂O)₂](ClO₄)₂ and (C₅H₇N₂)₄[Ni(C₃H₂O₄)₂(H₂O)₂](PF₆)₂.⁸² The crystal structure of the complex containing ClO₄ (Fig. 15) shows that the malonate is bonded to nickel through an oxygen atom of the malonate and all the anionic monomeric units [Ni(C₃H₂O₄)₂(H₂O)₂]²⁻ are interlinked with each other through hydrogen bonding. The oxygen atom (O3) of the non-coordinating carbonyl group of malonate is in close contact (3.2 Å) with the center of the 2-aminopyridine ring. Such close contact is favorable for lp⋯π interactions. The 2-amino pyridine ring is further stacked over the other aminopyridine ring, resulting in a π⋯π stacking interaction. The perchlorate anion is sandwiched between two aminopyridine rings. The aminopyridine ring which interacts with the perchlorate anion through an anion⋯π interaction further interacts with the oxygen atom (O3) of a carbonyl group of the malonate moiety through an lp⋯π interaction. Thus, the lp⋯π interaction, π⋯π stacking and anion⋯π interaction together form a chain of non covalent interactions which stabilize the supramolecular network of the (C₅H₇N₂)₄[Ni(C₃H₂O₄)₂(H₂O)₂](ClO₄)₂ complex. The crystal structure of the (C₅H₇N₂)₄[Ni(C₃H₂O₄)₂(H₂O)₂](PF₆)₂ complex also shows a lp⋯π interaction between the oxygen atom of the malonate moiety and the 2-aminopyridine ring. The above examples demonstrate that the lp⋯π interaction, in combination with other non-covalent interactions, plays an important role in the self-assembly of the molecules to form large multidimensional structures.

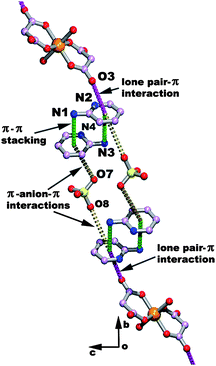Fig. 15 The lone pair⋯π interaction between an oxygen and aminopyridine ring in the crystal packing of the (C₅H₇N₂)₄[Ni(C₃H₂O₄)₂(H₂O)₂] (ClO₄)₂ complex. (Reproduced from ref. 82 with permission from The Royal Society of Chemistry).

Reedijk and co-workers have performed an extensive search of the Cambridge Structural Database (CSD) to identify lp⋯π interactions in materials.⁶⁷ They have analyzed 263 007 crystal structures and each one of them contains at least one neutral six membered aromatic ring. The authors have found fluorine⋯π close contacts in 5716 crystal structures where the mean fluorine⋯centroid distance varies from 3.012 Å to 3.242 Å, and the angle containing the plane of the ring, centroid of the ring, and lone pair donor atom lies between 60°–90°. Lp⋯π interactions with other halogen atoms have also been identified. Cl⋯π close contact has been observed in 3078 crystal structures, while Br⋯π and I⋯π interactions are present in 343 and 31 crystal structures, respectively. Close contact between the oxygen atom of an ether group and an aromatic ring (O⋯π) has been observed in 3703 crystal structures, while C=O⋯π close contact has been found in 5069 crystal structures. In fact, they have observed lp⋯π interactions in a large number of crystal structures and their observation has helped in the recognition of lp⋯π interactions in materials. Not only oxygen, nitrogen and halogen atoms act as lone pair donors in lp⋯π interactions, but also other elements in the periodic table have been demonstrated as potential lone pair donors.

Caracelli and co-workers have reviewed several crystal structures where antimony (Sb) and bismuth (Bi) participate in the lp⋯π interaction.⁸³ They have performed CSD analysis to find such structures. It has been found that the metal lp⋯π interaction is independent of other supramolecular binding motifs like hydrogen bonding, π⋯π stacking, etc. Thus, the structure can be stabilized by only Sb⋯π interactions or Bi⋯π interactions. A representative structure having Sb⋯π interactions obtained from the CSD search is shown in Fig. 16 This structure shows that the lp⋯π interaction between the metal atom (Sb) and aromatic ring can lead to the formation of small one-dimensional or large three-dimensional structure. The authors have also found the existence of the Sb(lp)⋯π interaction in biomolecules. Sb is found in the FAD (flavine adenine dinucleotide) active site of chains A and B of trypanothione reductase.⁸³

Fig. 16 Two dimensional crystal structures showing Sb(lp)⋯π interactions [CSD ref code-GAJPIR]

Another type of lp⋯π interaction involving a sulfur atom and an aromatic ring, i.e. sulphur⋯π interaction, has been found to be very important for the stabilization of protein structures. Sherrill and co-workers have studied the benzene⋯H₂S complex as a prototype for the sulphur⋯π interaction and reported that the configuration with the sulphur atom facing towards the π-cloud is favorable.^87,88 The presence of sulphur⋯π interactions in solid state crystal structures has also been reported recently.^89,90 Very strong sulphur⋯π interactions have been demonstrated in the complexes of H₂S and polycyclic aromatic hydrocarbons.⁹¹

4. Significance of the n → π* interaction in small molecules

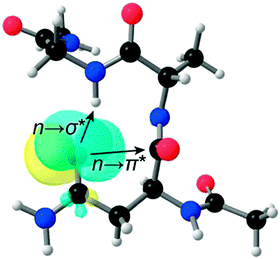
The significance of the n → π* interaction is observed even in small molecules like N-acyl homoserine lactones, aspirin, poly-(lactic acid), γ-aminobutyric acid (GABA) and peptoids.^{36,44,70,71,77}N-Acyl homoserine lactone (see Fig. 17A) acts as a signalling molecule and is released in response to the population density of a bacterial colony, a phenomenon which is known as quorum sensing.⁴⁴ It binds to LuxR-type receptor proteins and causes changes in growth, virulence, antibiotic resistance and other phenotypes. N-Acyl homoserine lactones have two carbonyl groups adjacent to each other, as in proline residue (see Fig. 17).⁴⁴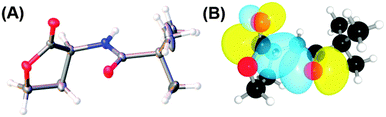

Fig. 17 (A) Crystal structure of N-trimethylacetyl homoserine lactone and (B) NBO view of donor (n) and acceptor (π*) orbitals in the optimized geometry of N-trimethylacetyl homoserine lactones. Adapted with permission from ref. 44. Copyright [2014] American Chemical Society.

Raines and co-workers have argued that N-acyl homoserine lactones, similarly to the proline residue, can exhibit an n → π* interaction between the proximal carbonyl groups.⁴⁴ They were able to crystallize N-trimethyl homoserine lactone, which is not a natural N-acyl homoserine lactone, but can mimic the natural one. Natural N-acyl homoserine lactones cannot be crystallized easily due to the presence of a large alkyl group. The crystal structure of N-trimethyl homoserine lactone shows that the distance between the N-acyl carbonyl oxygen and carbon of the lactone carbonyl group is 2.73 Å and the angle of approach of the donor oxygen towards the acceptor carbonyl group is 90.6°. These geometrical parameters are very close to the Burgi–Dunitz trajectory for the attack of a nucleophile on an electrophile. This indicates that there is a possibility of an n → π* interaction between the donor oxygen of the N-acyl carbonyl group and the acceptor π* orbital of the lactone carbonyl group. The authors have further performed DFT calculations to obtain the most stable geometry of N-trimethyl homoserine lactone and carried out NBO analysis of this structure. NBO analysis shows significant overlap between the lone pair orbital (n) of the donor oxygen and the acceptor π* orbital of the lactone carbonyl group with an interaction energy of 0.64 kcal mol⁻¹. They have examined the crystal structure of bound N-acyl homoserine lactones with their LuxR receptors and found that the bound-state conformation of N-acyl homoserine lactones changes due to the formation of a hydrogen bond between the N-acyl carbonyl oxygen and the tyrosine residue of the receptor prohibiting an n → π* interaction.⁴⁴ Thus, there is a competition between the hydrogen bonding and n → π* interaction at the time of binding of the N-acyl homoserine lactone with its receptor. Any factor which can attenuate the strength of the n → π* interaction will increase the binding affinity of N-acyl homoserine lactones with their receptors. Thus, the n → π* interaction has valuable significance in governing the biological activity of N-acyl homoserine lactones.

γ-Amino butyric acid (GABA) is an inhibitory neurotransmitter in the brain and spinal cord. Lopez and co-workers have identified the most stable conformation of GABA using laser ablation (LA) molecular beam Fourier transform microwave spectroscopy (LA-FTMW) combined with ab initio calculations.⁷⁷ Microwave spectroscopic data show evidence of the nine conformers of GABA in the gas phase, which differ in the folding and orientation of the functional groups present in the molecule. Out of the nine conformers, five conformers have folded form with intramolecular non-covalent interactions between the functional groups, while the remaining four structures with no intramolecular non-covalent interactions are called extended conformations. Among the five folded conformations, three show the possibility of intramolecular hydrogen bonding and two show the possibility of an n → π* interaction between the donor lone pair (n) orbital of nitrogen and acceptor (π*) orbital of the carbonyl group. Thus, the n → π* interaction also contributes to the conformation of an important inhibitory neurotransmitter.

Raines and co-workers have found the presence of the n → π* interaction in poly-(lactic acid) (PLA), a versatile polyester.⁷⁰ They have examined the crystal structure of α-PLA and found that its backbone torsional angles, i.e. Φ and Ψ, are similar to those of the strands of the collagen triple helix. Fig. 18 shows the structure of α-PLA. NBO analysis of the crystal structure of α-PLA at the B3LYP/6-311++G(2d,p) level of theory shows that the energy for each n → π* interaction is 0.44 kcal mol⁻¹. This indicates that the n → π* interaction has significance in stabilizing the structure of polyesters, which are similar to polyamides. The authors have pointed out that poly-(lactic acid) is similar to polyalanine and the only difference is that the amide is replaced by an ester bond, resulting in the absence of a N–H hydrogen bond donor in poly-(lactic acid). The existence of the n → π* interaction even in the absence of hydrogen bonding indicates that this interaction can exist independently and it is not just a short contact imposed by the geometric constraint due to the hydrogen bonding patterns. Thus, the n → π* interaction can exist in proteins and its presence is independent of the hydrogen bonding patterns.

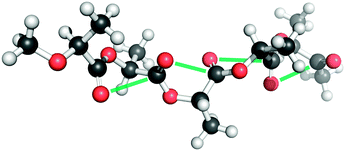Fig. 18 Structure of α-PLA showing n → π* interactions. (Reproduced from ref. 70 with permission from The Royal Society of Chemistry).

The n → π* interaction is also found to regulate the conformations of peptoids. Blackwell and co-workers have designed small peptoids to study these interactions.³⁶Fig. 19A shows the general structure of a peptoid, while structures of peptoids representing n → π*_Am and n → π*_Ar interactions have been depicted in Fig. 19B and C, respectively. In the case of the peptoid in Fig. 19B, the trans-amide is more stable than the cis-amide, while the peptoid in Fig. 19C shows a propensity for the cis-amide compared to the trans-amide. The authors have determined the preferential stability of one of the conformers of these peptoids by measuring K_cis/trans using NMR spectroscopy and this conformational preference could be only due to the presence of the n → π* interaction. Raines and co-workers have found the significance of the n → π* interaction in the structure as well as chemical and biological functions of the well known analgesic medicine aspirin.⁷¹ Aspirin is an O-acetylated form of salicylic acid. The authors have found that the crystal structure of aspirin shows close contact between the oxygen atom of the alcohol group of the carboxylic acid and the carbon atom of the carbonyl group of the ester (see Fig. 20A) in a Burgi–Dunitz trajectory fashion. The crystal structure also shows significant pyramidalization of the acceptor carbonyl group, which is the key signature of the n → π* interaction. The pyramidalization parameter (Δ) has been found to be 0.011 Å. They have found six low energy conformations of aspirin by performing ab initio calculations. Interestingly, the lowest energy conformer shows an n → π* interaction between the oxygen atom of the carbonyl group of the carboxylic acid and the carbonyl group of the ester. The interaction energy of the n → π* interaction calculated through NBO analysis of this conformer has been found to be 1.73 kcal mol⁻¹. The second lowest energy conformer resembles the crystal structure of aspirin where the donor oxygen atom is of the alcohol group of the carboxylic acid. The NBO analysis of this conformer also shows an n → π* interaction of 0.95 kcal mol⁻¹ in energy. Fig. 20B shows these two structures that have an n → π* interaction. It has been found that aspirin needs to pass through a paraffin-like channel without any hydration to perform its pharmacological activity.⁷¹ The authors have explained that the intramolecular n → π* interaction in aspirin may shield the donor oxygen from interaction with solvent and help its passage through the hydrophobic channel. Thus, it is interesting to point out that the n → π* interaction could facilitate the chemical and pharmacological functions of aspirin.

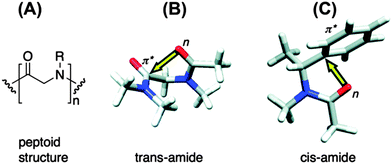Fig. 19 (A) General structure of a peptoid. (B) Structure of a peptoid showing an n → π*_Am interaction. (C) Structure of a peptoid showing an n → π*_Ar interaction. Adapted with permission from ref. 36. Copyright [2007] American Chemical Society.

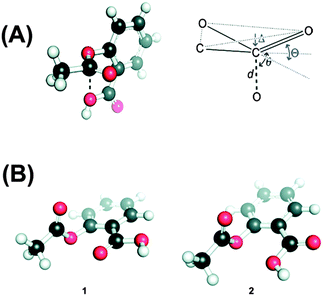Fig. 20 (A) Crystal structure of aspirin and Burgi–Dunitz parameters in aspirin. (B) Two low energy conformers of aspirin obtained through ab initio study. Adapted with permission from ref. 71. Copyright [2011] American Chemical Society.

5. Physical nature of the n → π* interaction

5.1. The n → π*_Ar or lp⋯π interaction

Among the various ion–π interactions, in general, the cation–pi interaction is quite obvious and easy to realize but neither anion–π nor lp⋯π interactions are straightforward. These two interactions (anion–π and lp⋯π) are generally found to be favorable when the or aromatic ring is electron deficient or π–acidic. However, it has been reported recently that both lp⋯π and anion–π interactions can be favorable in the case of electron rich π-clouds.^{27,33,35,91,92}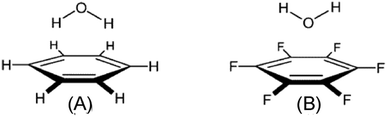

5.1.1. The lp⋯π interaction in complexes of electron deficient aromatic rings. The very first theoretical study on the lp⋯π interaction was performed on the C₆F₆⋯H₂O complex by Dougherty and co-workers in 1999.⁵⁷ They found that water binds to hexafluorobenzene through the oxygen atom pointing towards the face of the π system. On the other hand, benzene interacts with water through π-hydrogen bonding between a hydrogen atom of the water and the π-cloud of the benzene ring. The structures of C₆H₆⋯H₂O and C₆F₆⋯H₂O calculated at the cp-MP2/6-31G** level of theory have been provided in Fig. 21. Benzene and hexafluorobenzene have a quadrupole moment that is equal in magnitude but opposite in sign. The electrostatic potential above and below the ring is negative in benzene while the same is positive in hexafluorobenzene. As the lone pair electrons on the oxygen atom of water are attracted towards the electron deficient aromatic ring in the C₆F₆⋯H₂O complex, the authors have argued that the lp⋯π interaction in the complex originates from electrostatics. Besnard and co-workers have also reported the same geometry of the C₆F₆⋯H₂O complex from ab initio calculations.⁵⁸ The binding energy of the C₆F₆⋯H₂O complex has been calculated to be about −2 kcal mol⁻¹ at the MP2 level of theory. Alkorta and co-workers have performed an ab initio study on complexes of hexafluorobenzene with small electron rich moieties (FH, HLi, CH₂, NCH, and CNH) at the HF, MP2 and B3LYP levels of theory.⁵⁹ In the case of all of these complexes, geometrical minima have been found when the electron rich atoms of these small molecules point directly towards the face of the hexafluorobenzene. It seems from these studies on the complexes of hexafluorobenzene that lone pair electrons on the electronegative atoms can interact only with electron deficient aromatic rings through electrostatic interaction.

Fig. 21 Calculated structures of (A) C₆H₆⋯H₂O complex stabilized by O–H⋯π hydrogen bonding and (B) C₆F₆⋯H₂O complex stabilized by an lp⋯π interaction. Adapted with permission from ref. 57. Copyright [1999] American Chemical Society.

5.1.2. The lp⋯π interaction in complexes of electron rich aromatic rings. The question now should be asked whether the lp⋯π interaction can occur between a lone pair containing atom and an electron rich aromatic ring. If this interaction is possible with an electron rich aromatic ring, electrostatics cannot be the major driving force. There are a few theoretical calculations reported in the literature to address this issue. It is indeed interesting that the lp⋯π interaction is favorable between the oxygen atom of H₂O and polycyclic aromatic hydrocarbons (PAHs, i.e. anthracene, triphenylene, coronene, circumcoronene, etc.) although the same interaction is repulsive in the benzene⋯H₂O complex.^91,92 It has been also reported that the lp⋯π interaction in PAH⋯H₂S is much stronger than that in PAH⋯H₂O.⁹¹ Interestingly, this interaction is attractive even in the benzene⋯H₂S complex.⁹¹ Very recently, it has been demonstrated that substituted benzenes with electron donating groups have attractive lp⋯π interactions with dimethyl ether (Me₂O) and trimethyl ammonia (NMe₃) while similar interaction is absent with water and ammonia.^33,35 All of these results reveal that the increase in the dispersion in these systems switches on the lp⋯π interaction by overcoming the repulsive electrostatic interaction. Thus, it seems that a dispersion interaction is a key to having a lp⋯π interaction in the system. However, it is very difficult to conclude from these data that dispersion is the main contribution in the stability of the lp⋯π interaction.

In general, the introduction of bulky groups in the systems increases the dispersion contribution in the total interaction energy for all types of non-covalent interactions. Recently, Hoja et al. studied several dimers starting from a water dimer to a tertiary-butyl alcohol dimer by increasing the size of the alkyl substituent.⁹³ They have reported that the dispersion becomes very important in the stabilization of the hydrogen bonded (O–H⋯O) complexes as the substituents become bulkier. Cabaleiro-Lago and co-workers have shown that the anion–π interaction is also stable in electron rich aromatic systems, i.e. extended PAHs (buckybowls).²⁷ The dispersion interaction also becomes significant in the case of the cation–π interaction when the bulkiness of the cation increases.^19,20

In Section 2.2.3, the competition between the lp⋯π interaction and hydrogen bonding in the complexes of 7-azaindole and several 2,6-substituted fluoropyridines studied by Das and co-workers has been discussed.³⁴ They found that the binding energies of the 7-azaindole⋯2,6-substituted fluoropyridines calculated at the B3LYP level of theory are very much less than those obtained at the dispersion-corrected DFT and MP2 levels. Fig. 22 shows the plots of the binding energies of these complexes calculated at different levels of theory.³⁴ The discrepancy in the results obtained from the B3LYP and dispersion-corrected DFT levels indicates that the dispersion interaction has a significant role in the stability of these complexes.

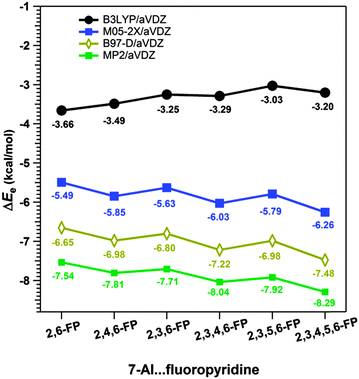Fig. 22 Binding energies of complexes of 7-azaindole with several 2,6-substituted fluoropyridines calculated at various levels of theory. (Reproduced from ref. 34.)

The most significant finding from the study of 7-azaindole⋯2,6-substituted fluoropyridines has come out through decomposition of the total interaction energy. It has been found that there is a significant increase in the dispersion component of the total interaction energy in 7-azaindole⋯2,6-substituted fluoropyridines with the increase in fluorine substitution on the pyridine ring. Fig. 23 shows the different components of the total interaction energy of these complexes, calculated at the M05-2X/cc-pVDZ level of theory. It is intriguing to note that the increase in the dispersion force compared to the electrostatic one is greater with the increase in fluorine substitution, although fluorine has a smaller size and less polarizability. Thus, the point is that the increase in fluorine substitution in the system cannot increase the dispersion contribution, unlike the case in benzene⋯NMe₃ or benzene⋯Me₂O complexes where the introduction of bulky methyl groups increases the dispersion. Indeed, it has been reported that there is hardly any change in the dispersion contribution with the increase in fluorine substitution in the case of the complexes of 7-azaindole and fluorosubstituted pyridines, which have planar double hydrogen bonded structures. The different components of the total interaction energy in the complexes of 7-azaindole with 2,3-difluoropyridine, 2,3,4-trifluoropyridine and 2,3,4,5-tetrafluoropyridine are depicted in Fig. 24. This observation clearly points out that the increase in the dispersion force with the increase in fluorine substitution in 7-azaindole⋯2,6-fluoropyridines is due to the lp⋯π interaction only. Thus, it could be stated that dispersion plays a major role in the stability of the lp⋯π interaction.

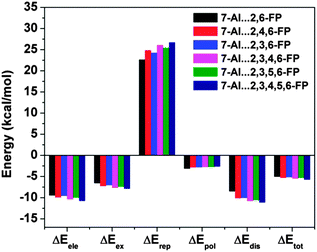Fig. 23 Different components of the total interaction energy of complexes of 7-azaindole with several 2,6-substituted fluoropyridines. (Reproduced from ref. 34.)

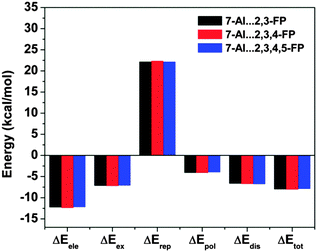Fig. 24 Different components of the total interaction energy of complexes of 7-azaindole with 2,3-difluoropyridine, 2,3,4-trifluoropyridine, and 2,3,4,5-tetrafluoropyridine. (Reproduced from ref. 34.)

The lp⋯π interaction in complexes of electron rich aromatic rings has also been explored through experiments by Gung and co-workers. They have designed triptycene scaffolds (see Fig. 25) which have anti and syn conformations.⁵¹ The syn conformation of triptycene allows close contact between the benzyl ring, attached to the C(9) carbon atom and oxygen atom of the OMe/RCOO (R = H, Me, Et, i-Pr, CF₃) group attached to the C(1) carbon atom. Both electron withdrawing groups (NO₂, CN, CF₃, F, Br, Cl) and electron donating groups (Me, MeO, Me₂N) have been used as a substituent (X) on the benzyl ring, attached to the C(9) carbon atom, keeping the substituents (MeO or ester group) at the C(1) carbon atom fixed. The authors have measured the NMR spectra of these triptycene scaffolds at low temperature to determine the ratio of syn and anti conformers in each of these cases. The syn to anti ratio reflects the degree of interaction of the arene ring with the oxygen atom of the OMe or ester group attached to the C(1) carbon atom. The ratio has been found to be 2 : 1 when no interaction is present between the C(1) and C(9) substituents. Therefore a ratio greater than 2 : 1 will indicate the preference of the syn over anti conformation due to the presence of the attractive arene–oxygen interaction.

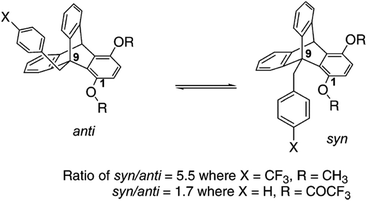Fig. 25 Structures of anti and syn conformations of the triptycene scaffold. Adapted with permission from ref. 51. Copyright [2005] American Chemical Society.

Gung and co-workers have observed that the syn/anti ratio with OMe as the substituent at C1 is greater than 2 (∼2.4) even if the aromatic ring is electron rich, i.e. X = Me, MeO. The highest syn/anti ratio (3.5–5.5) is observed when X is an electron withdrawing group like CF₃, Cl, etc.⁵¹ They have initially concluded that the origin of the attraction could be electrostatic as the interaction between the arene and oxygen atom increases with the decrease in electron density of the aromatic ring. To explain the observed value of the syn/anti ratio greater than 2 in the presence of the electron donating substituent, they have pointed out that the oxygen atom of the methoxy group is close to the edge of the aromatic ring, which has a belt of positive electrostatic potential. Therefore the syn conformation, even in the case of the arene ring with an electron donating substituent, is preferentially stable over the anti conformation.

In a later study, Gung and co-workers replaced the OMe group in triptycene with a methylmethoxy group (MOM) to place the oxygen atom of the methoxy group close to the centre of the aromatic ring in the syn conformation, and studied the system with low temperature NMR spectroscopy (see Fig. 26).³² Keeping the MOM group fixed at C1, the substituent X of the arene ring has been varied from electron withdrawing to electron donating groups. They have observed a syn/anti ratio of 7–8 in the case of the electron withdrawing groups (X) and a ratio of 3–4 even in the case of the electron donating group. The syn/anti ratio has been found to be 25 and 6.8 when the arene ring is hexafluorobenzene and benzene, respectively. Here the authors have pointed out that the syn conformation of trypticene with electron donating substituents on the arene ring is still preferred over the anti conformation in spite of the unanticipated close proximity between the oxygen atom and electron rich aromatic ring in the former. These results indicate that there is an attractive interaction between the oxygen atom of the MOM group and the electron rich aromatic ring. The above observation cannot be rationalized on the basis of the electrostatic potential of the ring. Thus, eventually the authors have concluded that the major driving force for such an interaction cannot be electrostatic.

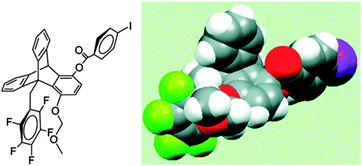Fig. 26 Structure of the syn conformation of the triptycene scaffold where the OMe group is replaced with a methylmethoxy group (MOM). The structure is depicted as a three dimensional molecular model. Adapted with permission from ref. 32. Copyright [2008] American Chemical Society.

5.2. The n → π*_Am interaction

To unearth the origin of the n → π*_Am interaction, Raines and co-workers have studied the nature of the carbonyl–carbonyl interaction in proteins using the model system shown in Fig. 27.³⁷ The model system contains a pyrrolidine ring with acetyl substitution at the C2 position and acetyl or thioacetyl substitution at the N1 position. This model system can exist in both trans and cis conformations. However, close contact between the adjacent carbonyl groups in the Burgi–Dunitz trajectory fashion can occur only in the trans conformation. Further, this model system mimics the proline amino acid residue in proteins. When the acetyl group is substituted at the N1 position, the trans/cis ratio has been observed to be 4.6, i.e. the trans conformer is more stable. Here the authors have asked the question whether the nature of the carbonyl–carbonyl interaction is due to charge–charge, dipole–dipole or n → π* electronic delocalization (see Fig. 28). In order to understand the source of this interaction, they have replaced the oxygen donor (O_i−1) with a sulphur donor (S₋₁) in their model system and measured the equilibrium constant (K_trans/cis) between trans and cis conformations through NMR studies. There will be a decrease in the trans/cis ratio if a charge–charge interaction is responsible for the close contact of the two carbonyl groups since sulphur is less electronegative than oxygen. On the other hand, an increase in the trans/cis ratio will indicate that the origin of the carbonyl–carbonyl interaction is due to dipole–dipole or n → π* electronic delocalization because C=S has a larger dipole moment than C=O and sulphur, being a softer base than oxygen, is more efficient in donating an electron pair than oxygen.

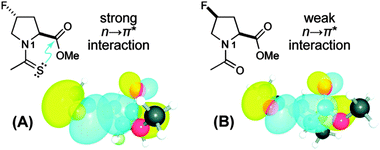Fig. 27 Structures of substituted prolines designed to study the n → π*_Am interaction. (A) Substitution of thioacetyl group at N1 and (B) substitution of acetyl group at N1. NBO views of the overlap of their respective n and π* orbitals are shown below. Adapted with permission from ref. 37. Copyright [2009] American Chemical Society.

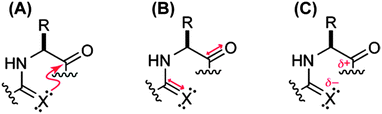Fig. 28 Carbonyl–carbonyl interaction (C=O⋯C=O) can be due to (A) n → π* electronic delocalization, (B) dipole–dipole or (C) charge–charge interaction. Adapted with permission from ref. 37. Copyright [2009] American Chemical Society.

Raines and co-workers have observed an increase in the trans/cis ratio when the oxygen donor has been replaced by sulphur.³⁷ This result indicates that the preferential stability of the trans conformer over cis is not due to a charge–charge interaction and is rather due to a dipole–dipole interaction or n → π* electronic delocalization. Delocalization of electrons is possible when there is an appreciable overlap between the donor and acceptor orbitals. To have proper orbital overlap, the distance between the donor and acceptor atoms should be less than the sum of the van der Waals radii of both the atoms. As the n → π* interaction is more sensitive to the distance between the donor and acceptor atoms in comparison to the dipole–dipole interaction, an increase in the distance between these two interacting atoms will affect the strength of the n → π* interaction. Generally, an electron withdrawing group substituted at the C4 carbon atom (where the C4 carbon atom is in the S-configuration) of the pyrrolidine ring (see Fig. 27), influences the pyrrolidine ring to be in C^γ-endo puckered conformation. In this conformation, the distance between the O_i−1 or S_i−1 donor and C_i=O_i acceptor increases and it is greater than the sum of the van der Waals radii of oxygen/sulphur and carbon. This indicates that proper orbital overlap is not possible in the 4S configuration but dipole–dipole interaction is possible. Thus, the authors argued that an increase in the trans/cis ratio upon replacement of the oxygen donor by sulphur in the C^γ-endo puckered configuration of the pyrrolidine ring will indicate that the dipole–dipole interaction is the driving force for the carbonyl–carbonyl interaction. They have observed that the value of K_trans/cis for the endo puckered conformation of the pyrrolidine ring with a 4S EWG is similar with both oxygen and sulphur as donors. This indicates that the trans conformation is not stabilized by dipole–dipole but rather the n → π* interaction is the origin of the stabilization.

To have a favourable dipole–dipole interaction between two carbonyl groups, two interacting dipoles should have proper orientation, i.e. they should be orthogonal to each other.⁷² In other words, it restricts all the four atoms to a fixed orientation. On the other hand, close contact between two carbonyl groups for the n → π* interaction demands proper orbital overlap between O_i−1 and C_i=O_i and this does not restrict the positions of all the four atoms. In the case of the n → π* interaction, only the donor atom (O_i−1) and acceptor carbonyl group (C_i=O_i) are required to be in favourable orientation and the positive pole of the donor carbonyl group, i.e. C_i−1, is not restricted. It has been found that the two adjacent carbonyl dipoles in an α-helix are in a repulsive orientation but there is still close contact between them. Raines and co-workers have demonstrated that the secondary structures of proteins exhibit close contact between the adjacent carbonyl groups and there is an orientation preference on the O_i−1⋯C_i=O_i angle but not the C=O⋯C=O dihedral angle.⁷² This indicates that the positive pole of the donor carbonyl group is not restricted in terms of its orientation. In order to further clarify whether a dipole is required for the intimate interaction between two carbonyl groups, the close contacts between a monopole (halide ion, X⁻¹) and carbonyl group in the crystal structures of small molecules containing a halide ion and carbonyl group have been analyzed.⁷² It was observed that the distance between the halide ion and the carbon of the carbonyl group, as well as the X⁻¹⋯C=O angle, fall mainly within the Burgi–Dunitz trajectory. This suggests that a dipole is not required for close contact between two carbonyl groups.

All the theoretical as well as experimental studies described above indicate that the nature of the n → π*_Am interaction is neither charge–charge nor dipole–dipole, but is rather the delocalization of lone pair electrons on the donor atom into the antibonding orbital (π*) of the acceptor carbonyl group. Further, Raines and co-workers have studied the trans/cis ratio of the amide bond in N-formylproline phenylester to understand the energetics of the n → π* interaction.⁴²Fig. 29 shows the cis and trans conformers of N-formylproline phenylester. The trans conformer, having an n → π* interaction, is more stable than the cis when X (substitution) is an electron withdrawing group, while the cis conformer is more stable than the trans when X is an electron donating group. It has been found that the substituents modulate the electrophilicity of C_i=O_i, which affects the strength of the n → π* interaction. This suggests that the electron withdrawing group decreases the energy of the π* orbital of C_i=O_i, making it more electrophilic, and thus allows closer overlap of the lone pair orbital of the oxygen with the π* orbital of the C_i=O_i carbonyl group. Thus, the strength of the n → π* interaction is affected substantially due to the electronic effect of the substituents attached close to the acceptor C_i=O_i group.

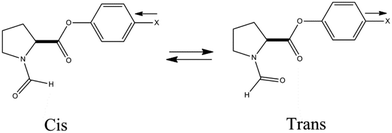Fig. 29 Structures of cis and trans conformations of N-formylproline phenylester (ref. 42).

Raines and co-workers have also studied the effect on the strength of the n → π* interaction on changing the substituent attached to the donor carbonyl group (C_i−1=O_i−1) and the nature of the donor atom.^37,69 The donor oxygen (O_i−1) of N-acetylproline methylester was replaced by sulphur (S_i−1) to give N-thioacetylproline methylester. NMR experiments show that the trans/cis ratio of N-thioacetylproline methylester is 2 times greater than that measured for N-acetylproline methylester. NBO analysis also shows that the interaction energy of the n → π* interaction is more when the donor atom is sulphur compared to when it is an oxygen atom. Sulphur, being a better electron pair donor, enhances the n → π* interaction. Thus, stronger electron pair donor atoms can enhance the n → π* interaction and favor one of the conformers over the other one.

6. Conclusions and outlook

In comparison to the commonly known non-covalent interactions in the literature, the n → π* interaction is quite new to the scientific community and it demands extensive exploration from experimental as well as theoretical points of view. The n → π* interaction, being very weak and counterintuitive in nature, was overlooked by scientists for a long time. We have reviewed here the recent discovery of this special non-covalent interaction and the rapid growth in its understanding through experiment and theory. It has been found that the n → π* interaction is widely present in biomolecules, i.e. proteins and nucleic acids, as well as in materials. This review describes the detailed literature studies on the propensity of the n → π* interaction in biomolecules and materials from PDB and CSD searches, respectively, the physical nature of this interaction, the interplay of this interaction with other non-covalent interactions, and experimental as well as theoretical evidences of the n → π* interaction.

It has been found that the n → π* interaction is as important as other non-covalent interactions for the stability of the structures of biomolecules and materials, although the former is generally very weak (∼0.5–1 kcal mol⁻¹) in strength. It is revealed from recent studies that the n → π* interaction can even modulate the overall structural motifs in the presence of strong hydrogen bonding interactions. Till now, experimental approaches to determine the presence of the n → π* interaction were limited to only NMR spectroscopy and X-ray crystallographic studies. NMR spectroscopy experiments on small model compounds show preferential population of the conformer having an n → π* interaction over the conformer without an n → π* interaction. X-ray crystallographic studies confirm the presence of the n → π* interaction in biomolecules and materials in terms of the Burgi–Dunitz trajectory, but there is no direct spectroscopic evidence for the n → π* interaction through probing the vibrational frequencies of the functional groups involved in the interaction. Generally, a shift in the X–H stretching frequency is a signature for the X–H⋯Y (both X and Y are generally electronegative atoms) hydrogen bond formation. In the future, it will be interesting to probe the stretching frequency of the carbonyl group in peptides or peptoids using IR spectroscopy to obtain direct spectroscopic proof for the n → π* interaction. As this non-covalent interaction is very weak compared to other relatively strong non-covalent interactions (i.e. hydrogen bonding), isolated gas phase spectroscopy in supersonic jet or matrix isolation infrared spectroscopy will be ideal to determine the strength of this interaction accurately. Although there are thorough literature studies on conventional hydrogen bonding, π-stacking and π-hydrogen bonding interactions in isolated gas phase, similar studies on the n → π* interaction are scarce in the literature, which is definitely due to unfamiliarity and the weak nature of this interaction. In fact, gas phase spectroscopy of small model compounds is highly desirable to check the results available on the n → π* interaction from quantum chemistry calculations.

There are very limited theoretical studies in the literature to determine the physical origin of the n → π* interaction. It has been demonstrated that an increase of dispersion in the system favors the n → π* interaction, overcoming repulsive electrostatic interactions. However, it cannot be stated with certainty that dispersion is the main source of stabilization for this interaction. Further theoretical studies, including energy decomposition analysis, are required for this purpose. In the future, theoretical studies should be aimed at molecular systems without bulky groups (i.e. alkyl) or extended conjugation, which contribute to dispersion. One recent work indeed shows that the dispersion contribution in an n → π* bound complex increases with increasing fluorine substitution, which itself does not introduce dispersion in the system.³⁴ This result indicates that the enhancement of the dispersion contribution could be due to the n → π* interaction.

Although the widespread presence of the n → π* interaction in biomolecules and materials is well documented in the literature, the functional role of this interaction in biological processes, i.e. protein–DNA interactions, protein–protein interactions, protein–ligand binding, and drug–DNA interactions, has not been explored yet. Thus, future studies should include detailed analysis of the crystal structures of protein–DNA, protein–protein complexes, etc. to trace the role of the n → π* interaction in these processes. It has been already pointed out that the n → π* interaction governs the chemical and biological activity of the drug aspirin, the regio-selective phosphorylation of anhydroribonucleoside, and the pharmacological activity of N-acyl homoserine lactones by inhibiting hydrolysis.^44,71,76 In a nutshell, detailed understanding of this interaction will be helpful in crystal engineering as well as drug design to obtain effective functional materials and drugs. The requirement of the development of force fields that will account for this counterintuitive interaction, leading to the refinement of the theoretical results of protein modelling, has been already recommended by Raines and co-workers.⁴¹

Acknowledgements

We would like to thank the Indian Institute of Science Education and Research (IISER) Pune for providing financial support to perform this research. S. K. S. acknowledges IISER Pune for his research fellowship. Financial support from the Department of Science and Technology (DST), India (Grant No. SR/S1/PC/0054/2010) is also acknowledged. The authors wish to acknowledge the anonymous reviewers for their constructive suggestions to improve the manuscript.

Notes and references

1. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, New York, 1999.
2. J.-M. Lehn, Supramolecular Chemistry: Concepts and Perspectives, John Wiley & Sons, New York, 1996.
3. J. W. Steed and J. L. Atwood, Supramolecular Chemistry: A Concise Introduction, John Wiley & Sons Inc, New York, 2000.
4. G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer-Verlag, Berlin, 1991.
5. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenber, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
6. W. Saenger, Principles of Nucleic Acid Structure, Springer-Verlag, New York, 1984.
7. G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356.
8. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967.
9. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250.
10. L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842.
11. J. B. O. Mitchell, C. L. Nandi, I. K. McDonald, J. M. Thornton and S. L. Price, J. Mol. Biol., 1994, 239, 315–331.
12. L. Serrano, M. Bycroft and A. R. Fersht, J. Mol. Biol., 1991, 218, 465–475.
13. S. K. Burley and G. A. Petsko, Science, 1985, 229, 23–28.
14. G. R. Desiraju, Angew. Chem., Int. Ed., 1995, 34, 2311–2327.
15. D. A. Dougherty, Acc. Chem. Res., 2013, 46, 885–893.
16. J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324.
17. D. A. Dougherty, Science, 1996, 271, 163–168.
18. J. A. Carrazana-García, J. Rodríguez-Otero and E. M. Cabaleiro-Lago, J. Phys. Chem. B, 2012, 116, 5860–5871.
19. E. M. Cabaleiro-Lago, J. Rodríguez-Otero and Á. Peña-Gallego, J. Chem. Phys., 2011, 135, 214301.
20. A. A. Rodriguez-Sanz, E. M. Cabaleiro-Lago and J. Rodriguez-Otero, Org. Biomol. Chem., 2014, 12, 2938–2949.
21. I. Soteras, M. Orozco and F. J. Luque, Phys. Chem. Chem. Phys., 2008, 10, 2616–2624.
22. H. T. Chifotides and K. R. Dunbar, Acc. Chem. Res., 2013, 46, 894–906.
23. A. Frontera, P. Gamez, M. Mascal, T. J. Mooibroek and J. Reedijk, Angew. Chem., Int. Ed., 2011, 50, 9564–9583.
24. D. Quiñonero, C. Garau, C. Rotger, A. Frontera, P. Ballester, A. Costa and P. M. Deyà, Angew. Chem., Int. Ed., 2002, 41, 3389–3392.
25. A. Robertazzi, F. Krull, E.-W. Knapp and P. Gamez, CrystEngComm, 2011, 13, 3293–3300.
26. A. Campo-Cacharrón, E. M. Cabaleiro-Lago, I. González-Veloso and J. Rodríguez-Otero, J. Phys. Chem. A, 2014, 118, 6112–6124.
27. A. Campo-Cacharrón, E. M. Cabaleiro-Lago and J. Rodríguez-Otero, J. Comput. Chem., 2014, 35, 1533–1544.
28. D. Kim, P. Tarakeshwar and K. S. Kim, J. Phys. Chem. A, 2004, 108, 1250–1258.
29. S. E. Wheeler and K. N. Houk, J. Phys. Chem. A, 2010, 114, 8658–8664.
30. G. J. Jones, A. Robertazzi and J. A. Platts, J. Phys. Chem. B, 2013, 117, 3315–3322.
31. M. Mascal, A. Armstrong and M. D. Bartberger, J. Am. Chem. Soc., 2002, 124, 6274–6276.
32. B. W. Gung, Y. Zou, Z. Xu, J. C. Amicangelo, D. G. Irwin, S. Ma and H. C. Zhou, J. Org. Chem., 2008, 73, 689–693.
33. J. C. Amicangelo, B. W. Gung, D. G. Irwin and N. C. Romano, Phys. Chem. Chem. Phys., 2008, 10, 2695–2705.
34. S. K. Singh, S. Kumar and A. Das, Phys. Chem. Chem. Phys., 2014, 16, 8819–8827.
35. T. Yang, J. J. An, X. Wang, D. Y. Wu, W. Chen and J. S. Fossey, Phys. Chem. Chem. Phys., 2012, 14, 10747–10753.
36. B. C. Gorske, B. L. Bastian, G. D. Geske and H. E. Blackwell, J. Am. Chem. Soc., 2007, 129, 8928–8929.
37. A. Choudhary, D. Gandla, G. R. Krow and R. T. Raines, J. Am. Chem. Soc., 2009, 131, 7244–7246.
38. M. L. DeRider, S. J. Wilkens, M. J. Waddell, L. E. Bretscher, F. Weinhold, R. T. Raines and J. L. Markley, J. Am. Chem. Soc., 2002, 124, 2497–2505.
39. R. W. Newberry, B. VanVeller, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2013, 135, 7843–7846.
40. C. L. Jenkins and R. T. Raines, Nat. Prod. Rep., 2002, 19, 49–59.
41. G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620.
42. J. A. Hodges and R. T. Raines, Org. Lett., 2006, 8, 4695–4697.
43. A. Choudhary and R. T. Raines, Protein Sci., 2011, 20, 1077–1081.
44. R. W. Newberry and R. T. Raines, ACS Chem. Biol., 2014, 9, 880–883.
45. M. D. Shoulders, F. W. Kotch, A. Choudhary, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2010, 132, 10857–10865.
46. C. Caumes, O. Roy, S. Faure and C. Taillefumier, J. Am. Chem. Soc., 2012, 134, 9553–9556.
47. B. C. Gorske, J. R. Stringer, B. L. Bastian, S. A. Fowler and H. E. Blackwell, J. Am. Chem. Soc., 2009, 131, 16555–16567.
48. J. R. Stringer, J. A. Crapster, I. A. Guzei and H. E. Blackwell, J. Am. Chem. Soc., 2011, 133, 15559–15567.
49. B. C. Gorske, R. C. Nelson, Z. S. Bowden, T. A. Kufe and A. M. Childs, J. Org. Chem., 2013, 78, 11172–11183.
50. A. Jain, V. Ramanathan and R. Sankararamakrishnan, Protein Sci., 2009, 18, 595–605.
51. B. W. Gung, X. Xue and H. J. Reich, J. Org. Chem., 2005, 70, 7232–7237.
52. A. Nijamudheen, D. Jose, A. Shine and A. Datta, J. Phys. Chem. Lett., 2012, 3, 1493–1496.
53. M. Egli and R. V. Gessner, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 180–184.
54. H. B. Burgi, J. D. Dunitz and E. Shefter, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1517–1527.
55. H. B. Bürgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067.
56. H. B. Bürgi, J. M. Lehn and G. Wipff, J. Am. Chem. Soc., 1974, 96, 1956–1957.
57. J. P. Gallivan and D. A. Dougherty, Org. Lett., 1999, 1, 103–106.
58. Y. Danten, T. Tassaing and M. Besnard, J. Phys. Chem. A, 1999, 103, 3530–3534.
59. I. Alkorta, I. Rozas and J. Elguero, J. Org. Chem., 1997, 62, 4687–4691.
60. J. C. Amicangelo, D. G. Irwin, C. J. Lee, N. C. Romano and N. L. Saxton, J. Phys. Chem. A, 2013, 117, 1336–1350.
61. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2000, 122, 3746–3753.
62. A. Jain, R. N. V. Krishna Deepak and R. Sankararamakrishnan, J. Struct. Biol., 2014, 187, 49–57.
63. M. Egli and S. Sarkhel, Acc. Chem. Res., 2007, 40, 197–205.
64. A. Jain, C. S. Purohit, S. Verma and R. Sankararamakrishnan, J. Phys. Chem. B, 2007, 111, 8680–8683.
65. S. Sarkhel, A. Rich and M. Egli, J. Am. Chem. Soc., 2003, 125, 8998–8999.
66. C. Fufezan, Proteins: Struct., Funct., Bioinf., 2010, 78, 2831–2838.
67. T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501–1515.
68. T. K. Pal and R. Sankararamakrishnan, J. Phys. Chem. B, 2010, 114, 1038–1049.
69. A. Choudhary, C. G. Fry and R. T. Raines, ARKIVOC, 2010, 251–262.
70. R. W. Newberry and R. T. Raines, Chem. Commun., 2013, 49, 7699–7701.
71. A. Choudhary, K. J. Kamer and R. T. Raines, J. Org. Chem., 2011, 76, 7933–7937.
72. K. J. Kamer, A. Choudhary and R. T. Raines, J. Org. Chem., 2013, 78, 2099–2103.
73. G. J. Bartlett, R. W. Newberry, B. VanVeller, R. T. Raines and D. N. Woolfson, J. Am. Chem. Soc., 2013, 135, 18682–18688.
74. C. E. Jakobsche, A. Choudhary, S. J. Miller and R. T. Raines, J. Am. Chem. Soc., 2010, 132, 6651–6653.
75. A. Choudhary, R. W. Newberry and R. T. Raines, Org. Lett., 2014, 16, 3421–3423.
76. A. Choudhary, K. J. Kamer, M. W. Powner, J. D. Sutherland and R. T. Raines, ACS Chem. Biol., 2010, 5, 655–657.
77. S. Blanco, J. C. López, S. Mata and J. L. Alonso, Angew. Chem., Int. Ed., 2010, 49, 9187–9192.
78. T. J. Mooibroek, S. J. Teat, C. Massera, P. Gamez and J. Reedijk, Cryst. Growth Des., 2006, 6, 1569–1574.
79. Z. Lu, P. Gamez, I. Mutikainen, U. Turpeinen and J. Reedijk, Cryst. Growth Des., 2007, 7, 1669–1671.
80. M. Barcelo-Oliver, C. Estarellas, A. Garcia-Raso, A. Terron, A. Frontera, D. Quinonero, E. Molins and P. M. Deya, CrystEngComm, 2010, 12, 362–365.
81. J. S. Costa, A. G. Castro, R. Pievo, O. Roubeau, B. Modec, B. Kozlevcar, S. J. Teat, P. Gamez and J. Reedijk, CrystEngComm, 2010, 12, 3057–3064.
82. A. Das, S. R. Choudhury, C. Estarellas, B. Dey, A. Frontera, J. Hemming, M. Helliwell, P. Gamez and S. Mukhopadhyay, CrystEngComm, 2011, 13, 4519–4527.
83. I. Caracelli, I. Haiduc, J. Zukerman-Schpector and E. R. T. Tiekink, Coord. Chem. Rev., 2013, 257, 2863–2879.
84. R. Gyepes, S. Pacigová, J. Tatiersky and M. Sivák, J. Mol. Struct., 2013, 1041, 113–121.
85. I. Alfaro-Fuentes, H. López-Sandoval, E. Mijangos, A. M. Duarte-Hernández, G. Rodriguez-López, M. I. Bernal-Uruchurtu, R. Contreras, A. Flores-Parra and N. Barba-Behrens, Polyhedron, 2014, 67, 373–380.
86. K. Hiraoka, S. Mizuse and S. Yamabe, J. Phys. Chem., 1987, 91, 5294–5297.
87. T. P. Tauer, M. E. Derrick and C. D. Sherrill, J. Phys. Chem. A, 2004, 109, 191–196.
88. A. L. Ringer, A. Senenko and C. D. Sherrill, Protein Sci., 2007, 16, 2216–2223.
89. C.-Q. Wan, J. Han and T. C. W. Mak, New J. Chem., 2009, 33, 707–712.
90. F. Zhou, R. Liu, P. Li and H. Zhang, New J. Chem., 2015, 39, 1611–1618.
91. E. M. Cabaleiro-Lago, J. A. Carrazana-García and J. Rodríguez-Otero, J. Chem. Phys., 2009, 130, 234307.
92. M. Rubeš, P. Nachtigall, J. Vondrášek and O. Bludský, J. Phys. Chem. C, 2009, 113, 8412–8419.
93. J. Hoja, A. F. Sax and K. Szalewicz, Chem. – Eur. J., 2014, 20, 2292–2300.

---