Large protonation-gated photochromism of an OPE-embedded difurylperfluorocyclopentene†
Received
12th November 2014
, Accepted 23rd January 2015
First published on 23rd January 2015
Abstract
A recently reported protolytic gating effect on the ring closing reaction of an oligo(phenylene ethynylene) (OPE) embedded difurylperfluorocyclopentene (S) with a dimethylaminophenyl chain link in each of the side arms, was quantitatively analyzed in detail. The reaction system (So, SoH+, SoH22+, Sc, ScH+, ScH22+) comprising three protolytic forms in both open and closed configuration, is characterized by four protolytic equilibrium constants and six photochemical quantum yields of ring closing and ring opening. The absorption spectra, conductivity, and effective photochemical quantum yields were measured in acetonitrile as functions of solvent acidity varied by addition of trifluoroacetic acid and triethylamine and characterized by an effective pHnon-aq. Based on the derivation of a rigorous method for assessing the individual quantum yields of ring closure and ring opening of the six species, it was shown that it is specifically the second protonation step that is responsible for a more than 10-fold increase in the quantum yield of ring closure.
Introduction
Molecules that can be reversibly switched between two well-defined states through optical activation are of special interest for molecular electronics applications. Diarylethenes (DAEs) are particularly suited for this task since they are thermally stable and highly fatigue resistant. During the switching process, DAEs with 5-membered heterocycles connected by the ethene-1,2-diyl-bridge in the 3- and 3′-position, respectively, are converted by a 6π-electrocyclic reaction between two states differing in the π-electron delocalization across the molecule. As borne out by the valence bond structures, in the open state, electronic communication from one substituent attached in 2-position of the aryl moiety with a substituent attached in the 2′-position of the other aryl moiety is not possible. In the closed state, the substituents attached in 2- and 2′-position of the aryl rings electronically communicate efficiently over the π-system that now spans the whole molecule (Scheme 1). In recent years, efforts have been made to integrate these molecules into mechanically controlled break junction setups, for measuring the conductance difference between the two forms.2,3 It was shown that the conjugated ring-closed isomer of diarylperfluorocyclopentenes can exhibit up to 38 times higher conductance compared to its ring-open isomer.4 In a recent study aimed at a better understanding of the switching mechanism and the charge transport along these molecules, we presented a family of switchable molecular wires having electron withdrawing or electron donating side chains on long conjugated oligophenylene–ethynylene side arms (OPE).1 We demonstrated that the electron density in these OPEs influences the efficiency of the photochromic process, as quantified by the quantum yields of ring opening and ring closing. One member of the family, equipped with strongly electron donating N,N-dimethylamino groups on the side arm, showed extensive reversible modulation of the quantum yield of ring closing upon protonation. On another note, molecular switches also can be used for a direct control of their environment by changes in their physical and chemical properties upon photoisomerization. After Lehn's seminal work on the photomodulation of a pKa-value,5 Raymo and coworkers have systematically exploited the photomodulation of pH by spiropyranes to establish logical gates on a molecular basis.6–8 Furthermore, the control of catalytic activity9 or the switching of material properties in thin film devices10,11 have represented a main focus of investigations in the area of DAEs.
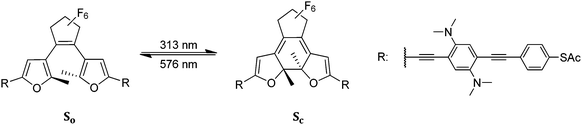 |
| | Scheme 1 Reversible photochromism of the bisfurylperfluorocyclopentyl-derived molecular switch with a dibasic phenylenediamine group inserted in each of the conjugated OPE side arms. So (open form) and Sc (closed form). | |
Gated photochromism (GP) in its pure definition denotes a situation where chemical or environmental changes of either of two interconvertible photochromic forms of a compound causes it to become non-photochromic.12 Contrary to the IUPAC definition, in practice GP often is not a strict on/off phenomenon because of the co-existence of various protolytic species in both photochromic forms. Kobatake et al. demonstrated that, upon protonation, an acid-sensitive DAE having a phenyl-diethylamino side group could be switched from a thermally irreversible to a thermally reversible photochromic system.13 A similar effect for a DAE based on 2-ethynyl-pyridyl substituents was reported by Yumoto et al.14 Upon protonation of the pyridyl moiety, the DAE became unswitchable by visible light, and thus was locked in the ring closed isomer. This effect was not observed if the quaternized pyridyl moiety was connected by a non-conjugated alkyl linker, a fact that clearly demonstrates the long range influence of the remote protonation on the switching core if transmitted by a conjugated linker. The trend that modulation of the electron donating abilities of para-N,N-diethylamino-phenyl groups in the 5-position of the DAE significantly affects the switching behavior was first observed by Irie and Uchida.15,16 Strong electron donors such as the para-N,N-dimethylamino-phenyl group reduced the quantum yield of the ring closing reaction. However, after addition of trifluoroacetic acid (TFAH), resulting in the formation of a protonated species, which the authors assigned to the doubly protonated molecular switch, the protonated DAE smoothly underwent cyclization and cycloreversion. A separation of quantum yields of the mono- and di-protonated form was not attempted. The idea of a “multi-addressable” switching system was pursued by Liu and Chen17 who studied a dithiophenylethene (DTE) symmetrically conjugated to a 2-(8-hydroxyquinoline) substituent on each of both thiophene rings, thereby introducing at the same time two basic functions with the nitrogen heteroatoms as potential protonation sites and also two chelating functions in a cooperation of the nitrogens in the ring and neighboring hydroxyl groups. Both functions, when addressed, cause a moderate change of the ring closing quantum yield of the DTE unit. A more detailed analysis attempting to separate e.g. the effects of single and double protonation as well as a pK-determination was not pursued.
In a recent paper by Cipolloni et al.18 a benzobis(imidazol) bearing two aniline substituents and thus functioning as a four-basic chromophore was inserted between two DTE units. Combining the 5 protolytic stages with 3 ring-closing stages (open–open, open–closed, closed–closed) this system would bear the potential of realizing a 15-stage switch. Although the pK-values were not exactly determined, the sequence of protonations and the predominant form at various pH values were assigned. The average quantum yields of ring-closing and opening determined as a function of pH exhibited a pronounced minimum at the point of double protonation. A precise separation of the photochemical quantum yields of all 5 protolytic forms was not feasible. Since the central benzobis(imidazol) chromophore is also fluorescent, the pH-dependent behavior was also observable in the emission quantum yields.19
More recently, Massaad et al. reported the first quantitative GP study of a 1,2-bis(5-carboxy-2-methylthien-3-yl)cyclopentene DAE.20 In this case, the DAE was a dicarboxylic acid. Its quantum yield of ring closing was found to be slightly sensitive to the presence of tetrabutyl ammonium hydroxide, whereas its cycloreversion was not affected. On the other hand, a photomodulation of the pKa of more than one pKa-unit was observed, the closed isomer being more acidic. The theoretical method of evaluation applied in this work, as well as in another interesting paper by Kutsunugi et al.21 on protolytic gating involving a bis(dibenzothienyl)ethene with the central double bond bridged by a dimethylaminophenyl thiamide function capable of double protonation at the amino group and the thiamide nitrogen, will be further referred to below in relation to our own work.
In this paper, we present a detailed quantitative study of the protonation-gated photochromic behavior of the long, conjugated molecular switch So in solution (Scheme 1). This compound is characterized by its extended π-system with the photoreactive chromophore embedded between two conjugated side arms comprising phenylenediamine groups in each side arm for efficient pH-gating. The overall length of ca. 3 nm in the closed state and the thiol endgroups render So a switchable molecular wire (SMW). Upon treatment of So with TFAH, the tetra-basic molecular switch considerably changes its photophysical behavior. A more than tenfold increase in the ring-closing quantum yield, accompanied by a high conversion rate at the photo stationary state (PSS) was observed in the presence of 70 equiv. of TFAH. The modulation is fully reversible upon addition of an equimolar amount of triethylamine (TEA). By modeling the coupled protolytic equilibria in the So–Sc–TFAH–TEA system on the basis of the concept of an effective pHnon-aq, we succeeded in assessing the relative fractions of mono- and di-protonated species as functions of the TFAH and TEA concentrations and in assigning individual quantum yields of photoswitching to the two protolytic species. Thereby, we clearly demonstrate that double protonation of the SMW is required to achieve the drastic quantum yield increases that are observed.
Experimental
All sample solutions were air-saturated and no special measures were taken to exclude moisture during the experiments. Trifluoroacetic acid (TFAH) from Sigma-Aldrich and spectroscopic grade MeCN from Merck were used as received. The synthesis of the investigated molecular switch is reported in ref. 1.
1. Continuous irradiation in solution
A high-pressure mercury lamp (Osram HBO 200 W/2) was used. The light was passed through a heat filter (optical length 5 cm, filled with a saturated aqueous solution of CuSO4), a collimating lens and an electronic shutter. Irradiation experiments were performed in a setup with a 313 nm or 576 nm interference filter (Schott), a thermostated optical cell holder with a cell of 1 cm path length (Hellma QS) equipped with a magnetic stirring bar and filled with 3 mL of sample solution. At 313 nm, the photon irradiance I0 was determined by azobenzene actinometry,22,23 at 576 nm by mesodiphenylhelianthrene actinometry.24 UV-vis absorption spectra were recorded before and after irradiation on a Cary 50 UV-vis spectrophotometer. Quantum yields of the photoreactions were determined according to the method of Gauglitz.22,23,25
2. Acid–base titration experiments with So
These experiments were carried out in Quartz cuvettes and monitored by UV-vis spectroscopy. In each experiment, a sample of the SMW in its open form in MeCN (3 mL, c = 1.25 × 10−5 M) was used. The titrations were carried out with a micropipette, and the cuvette was shaken after each addition. Stock solutions in MeCN of either TFAH (“St-TFAH”; c = 3.75 × 10−1 M) or TEA (“St-TEA”; c = 3.75 × 10−1 M) were used for titrations. The concentration was chosen such that 1 μl of each stock solution equals 10 equivalents of either acid or base with respect to the content of So in the UV-cuvette. For the forward titration, St-TFAH was used. The back titration was carried out with St-TEA on a sample pre-treated with 7 μL of St-TFAH. The basicity of the ring-closed isomer was estimated by adding 7 μL of St-TFAH to the sample before it was irradiated at 313 nm to yield a PSS, where 97% of the switch is present in the closed form.26 This solution was then back titrated with St-TEA in portions of 10 equivalents. For determining the pHnon-aq dependence of the quantum yields, pHnon-aq values were set by adding suitable amounts of St-TFAH to freshly prepared samples.
3. Conductometric test of protonation constants
Modeling the observed spectral changes during the titration with TFAH, indicated the formation of free ions. Conductometric titrations were performed in order to yield independent evidence of free-ion formation during the titration. A regime of higher concentrations of the SWM So (1.00 × 10−4 M in MeCN) compared to the UV-vis spectroscopic analyses was chosen in order to yield higher conductivity values matching the sensitivity range of the conduction bridge. The measurements were performed under ambient conditions at room temperature. The conductance of a stirred solution of SMW So in MeCN (20 mL) was monitored during the addition of aliquots of 10 equiv. of TFAH (53.3 μL St-TFAH).
Results and discussion
1. Equilibrium constants of protonation
Details of the light induced switching between the non-conjugated open ring isomer So and the conjugated ring closed isomer Sc (cf.Scheme 1) have been reported in ref. 1. In summary, the absorption maximum of the ring open isomer in MeCN was found at 331 nm. Upon irradiation with 313 nm light, an absorption band in the visible developed with a maximum at 589 nm. However, the degree of conversion to the closed ring isomer in the PSS was rather low (46%), due to a rather small quantum yield ϕo–c (0.4%) for the ring closing process. Upon addition of 70 equiv. of TFAH to the solution, this quantum yield increased by more than a factor of 10 up to a value of 5% and conversion to the closed SMW in the PSS was almost complete (97%) under such conditions. The protonation dependent gating effect was found to be fully reversible upon addition of equimolar amounts of TEA. Such back titrated samples showed the same photophysical behavior as untreated samples, indicating that the furan rings of the molecular switch are stable under non-nucleophilic but acidic conditions. Furthermore, it was observed that the other molecular switches investigated in our previous study that did not have NMe2 groups showed neither an enhancement of the ring closing quantum yield nor decomposition in the presence of TFAH.1 Thus, it can be concluded that the behavior of the molecular switch S is uniquely controlled by protonation/deprotonation of the molecule at the NMe2 groups in the side arms. NMR spectra of the protonated So and Sc are provided in the SI of ref. 1. The ring opening quantum yield ϕc–o was not affected by the presence of acid or base.1
Two distinct sites sensitive to protonation are located at each phenylenediamine in the side arms of So. In view of the Coulomb repulsion energy, it can be assumed that a second protonation will be unlikely to occur at the second NMe2 group at the same site. Instead, the phenylenediamine of the other side arm will be protonated. Consequently, the following protonation scheme was adopted, where TFAH stands for the undissociated trifluoroacetic acid and TFA− for its anion:
| |  | (1) |
| | 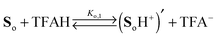 | (2) |
| |  | (3) |
| |  | (4) |
The symbols
SoH
+ and (
SoH
+)′ in
eqn (1) and (2) denote the two forms with single protonation at the left or right OPE arm, respectively. Since both sides of the molecule are spectroscopically and chemically identical, these two equilibria can be treated as one but with double statistical weight. Thus, the equations for the protonation equilibria can be reduced to
| |  | (5) |
| |  | (6) |
The cartoon shown in
Scheme 2 illustrates the situation.
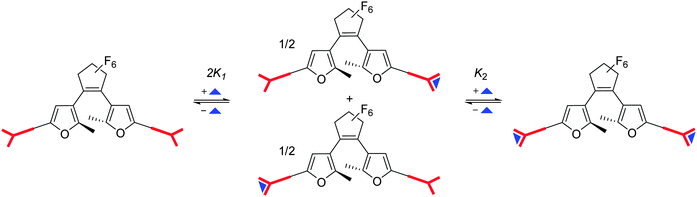 |
| | Scheme 2 Cartoon illustrating the protonation processes. The red “Y” represents the dibasic phenylenediamine and the blue triangle a proton. | |
The effect of protonation is clearly represented by a change of the absorption spectra during titration with TFAH (Fig. 1). The spectral change is characterized by several isosbestic points and almost linear relationships between the absorbance values at different wavelengths (cf. ESI,† Fig. S1), which generally is taken as an indication that there are only two different forms involved in the observed conversion. In the following, we describe the evaluation of the equilibrium constants for the conversion between three protolytic forms So, SoH+ and SoH22+ and the assignment of individual spectra to these species. Actually, the apparent bimodal character of the spectral change can be accounted for by the fact that the spectrum of SoH+ as such very closely corresponds to a linear combination of the spectra of So and SoH22+ (cf. Fig. S2, ESI†).
 |
| | Fig. 1 UV-vis spectra recorded during the titration of So (3 mL, 1.25 × 10−5 M, MeCN) with TFAH (3.75 × 10−1 M, MeCN). 10 equiv. aliquots TFAH (1 μl) were used for each step. The inset shows the volume corrected titration curve extracted at 330 nm. | |
Applying the law of mass action to eqn (5) and (6) and taking into account the stoichiometric relations in the titrated reaction mixture, a system of eqn (S1)–(S5) (ESI†) was obtained. It was solved with the help of a Mathematica computer program27 for various trial values of K1 and K2, to yield the equilibrium concentrations of TFAH, TFA−, So, SoH+ and SoH22+. Two representative examples of the calculated equilibrium compositions as a function of the amount of acid are shown in Fig. 2.
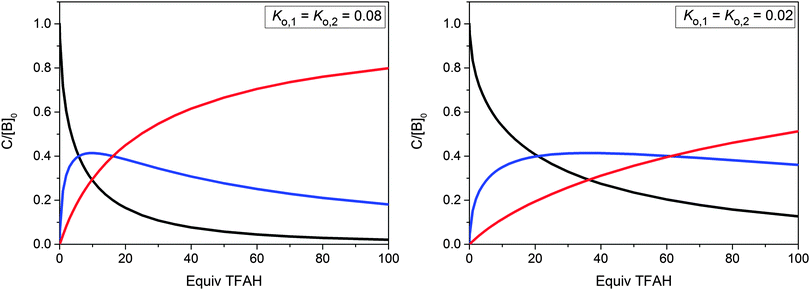 |
| | Fig. 2 Calculated equilibrium concentrations of So (black), SoH+ (blue) and SoH22+ (red) as functions of added acid ([TFAH]0) for two representative values of Ko,1 = Ko,2. Concentrations are given in units of [So]tot = 1.25 × 10−5 M. The horizontal scale represents the number of added TFAH equivalents. | |
Values for K1 and K2 were assumed to be equal since it is plausible that the first protonation in one half of the molecule does not significantly influence the second protonation step in the other half. In any case, for similar values of K1 and K2 it would be difficult to assess their difference from the limited information at hand.28
Each measured spectrum A(λ, [TFAH]0) during the stepwise titration of So with TFAH (Fig. 1) represents the superposition of the weighted individual spectra of the three protolytic forms So, SoH+ and SoH22+ at this specific point of the titration:
| |  | (7) |
The concentrations of the various protolytic forms [
SoHnn+]([TFAH]
0) are functions of the total concentration [TFAH]
0 of the acid. The wavelength dependent coefficients
ASo(
λ),
ASoH+(
λ) and
ASoH22+(
λ) represent the individual spectra of the [
SoHnn+] if present in the total concentration [
So]
tot.
Based on the calculated concentrations of the three protolytic forms in dependence of [TFAH]0 for certain values of Ko,1 and Ko,2, the measured spectra were used to fit the three absorbances Ai for each wavelength. The [TFAH]0 dependence of the measured spectra can be fitted well with the described procedure such that the differences between measured and simulated spectra were always found below 1%. However, a rather wide range of preset trial values for Ko,1 = Ko,2 gave equally good results for the fit. Therefore, the quality of the fit does not represent a sufficient criterion to determine the most realistic values for Ko,1 = Ko,2. In Fig. S2 (ESI†), four representative examples of simulated spectra of the individual protolytic forms for different K-values are shown. For higher values of Ko,1 = Ko,2, the SoH+ spectrum is closer to the So spectrum, whereas for lower values of K1 = K2, the SoH+ spectrum is closer to the SoH22+ spectrum. If it is assumed that the spectrum of the mono protonated form should be in the middle between the spectra of So and SoH22+, one would expect the values of K1 and K2 to range between 0.06 and 0.1. This conclusion is confirmed by conductometric titration experiments and by the analysis of the acidity dependence of the photochemical quantum yield (vide infra).
2. Conductometric validation of protonation constant
Neat MeCN showed a specific conductivity of 0.3 μS cm−1. Adding TFAH to neat MeCN did not result in an increase of conductivity, indicating no dissociation of this acid in this solvent. The specific conductivity of a 10−4 M solution of So in dry MeCN was determined to be 2.1 μS cm−1. Upon the addition of TFAH, the specific conductivity increased asymptotically to reach saturation at 24.3 μS cm−1 (7 added aliquots, Fig. 3). The observed saturation in the measurement of conductivity correlates with the saturation observed in the UV-vis spectra during titration. Under the prevailing experimental conditions, the charge carriers are represented by the ions SoH+, SoH22+ and TFA−. According to eqn (5) and (6), protonation of So or SoH+ yields the equivalent amount of anions TFA− assuming that, according to their charges, the molar conductances of SoH+, TFA− and SoH22+ (TFA−)2 are in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the specific conductance κ of the solution should be described by eqn (8)
2, the specific conductance κ of the solution should be described by eqn (8)| | | κ = κ0 + Λ[SoH+] + 2Λ[SoH22+] | (8) |
where κ0 is the initial value of the specific conductivity and Λ is the molar conductivity of the salt SoH+ TFA−. The conductivity of a solution of So before addition of TFAH indicates that a small fraction of the sample is already protonated as a remnant of its preparation method. In Fig. 3, the observed variation of κ as a function of equivalents of TFAH is shown together with theoretical curves for κ according to eqn (8) using various values of Ko,1 = Ko,2 together with pertinent best fit values of Λ. The diagram shows that Ko,1 values in the range of 0.5 and 0.08 fit the observed conductivity curve very well. The assumed molar conductivities of about 140 Ω−1 cm2 mol−1 are of an order of magnitude perfectly reasonable for ions of the present size in MeCN.29
 |
| | Fig. 3 Conductometric titration curve of a 1.0 × 10−4 M sample solution of So in MeCN. Black points: experimental data with error bars; colored curves: simulations according to eqn (8) assuming Ko,1 = Ko,2 = 0.05 and Λ = 155 Ω−1 cm2 mol−1 (blue curve), Ko,1 = Ko,2 = 0.06 and Λ = 146 Ω−1 cm2 mol−1 (red curve), Ko,1 = Ko,2 = 0.08 and Λ = 138 Ω−1 cm2 mol−1 (green curve). | |
These experiments confirm that ion pairs between the protonated compound SoH+ and the anion TFA− in MeCN dissociate rather completely. The same is probably true when the dimethylaminophenylthioamide modified DAE described by Kutsunugi et al.21 reacts with TFAH in MeCN. This issue was under discussion in that work.
3. Equilibrium constants of protonation of the closed form Sc
Since the electronic structure of the closed-ring isomer Sc differs from its ring-open counterpart So, it can be expected that both forms show different basicity. The basicity of the open form So is characterized by the equilibrium constants Ko,1 and Ko,2 given in the previous sections. The ring closed isomer Sc is not readily prepared by irradiation in the UV, due to the too low quantum yield of ring closure of So. But in previous experiments, it has been found that So undergoes photochemical ring closure much more efficiently in the protonated state. Furthermore, the PSS for the protonated form lies almost exclusively on the side of the closed form (97%), indicating that the quantum yield of ring closure strongly increases on protonation,1 without a concomitant increase of the quantum yield of the reverse photoreaction.
To determine the protolytic equilibria of Sc, in principle one can start with the photochemically converted acidified solution and then add a base such as TEA. However, in such mixtures the acid base equilibria of Sc corresponding to those of So described by eqn (1)–(4) are coupled to further equilibria between TFAH and TEA, which turned out not to be simple since they also involve non-dissociated ion pairs. In order to avoid the complication of having to unravel these additional equilibria, it was useful to apply the concept of pH in non-aqueous solutions which we here define as (cf. ESI†)
| |  | (9) |
As detailed in the ESI,
† the degree of protonation of
So as well as of
Sc is uniquely determined by the value of pH
non-aq. But the converse is also true: the value of pH
non-aq is a unique function of the degree of protonation of the two forms of
S. Hence our strategy to determine the pH
non-aq in the mixed acid–base solutions, was as follows: forward titration of a solution of
So by TFAH, followed by back titration with TEA. From the forward titration, we can assess the value of the total absorbance at a given total concentration [TFAH]
0 of the acid, for which we know the pH
non-aq according to our previous analysis of the protonation equilibria of
So according to
eqn (1)–(4). Then, from the total absorbance of the mixed protolytic forms of
So measured during the back titration, we can assess the pH
non-aq values as a function of total concentrations of TFAH and TEA. In the next experiment, we follow the same procedure, but after the end of the forward titration, irradiate the solution to the PSS, yielding the closed form almost quantitatively. During the subsequent back titration we determine the absorbances of the mixtures of the protolytic forms of
Sc as a function of pH
non-aq which now is known from the first titration run carried out exclusively with the open form.
The spectra obtained during back titration of So pretreated with 70 equiv. TFAH are depicted in Fig. 4.
 |
| | Fig. 4 Spectral series of the back titration of an acidic sample (70 equiv. TFAH) of So (3 mL, 1.25 × 10−5 M in MeCN) with 10 equiv. aliquots (1 μL) of TEA (3.75 × 10−1 M, MeCN). The inset shows a series of absorption values extracted at 374 nm for the forward and back titration of So with 10 equiv. aliquots of TFAH and TEA, respectively. | |
As evident from the inset of Fig. 4, the back titration of the acidified samples of So with TEA in MeCN does not simply yield the reverse curve of the forward titration with TFAH. This is due to the fact that not only the concentration of non-dissociated TFAH is diminished, but also free TFA− anions are created. Thus, there is a twofold effect in the law-of-mass-action according to eqn (1)–(4): (i) through the decrease of [TFAH] in the denominator, and (ii) through the increase of [TFA−] in the nominator. The change of pHnon-aq during the back titration, obtained in the way described above, is shown in Fig. 5. A reference value of 0.08 was adopted for Ko,1 = Ko,2 when calculating the concentrations of TFAH and TFA− needed for pHnon-aq determination according to eqn (9), because this value of Ko,1 = Ko,2 is in good agreement with all three criteria: spectral middle argument for SoH+, conductivity, and quantum yield (cf. below).
 |
| | Fig. 5 Variation of pHnon-aq during forward (red line) and back (blue open circles) titration. During the forward titration, pHnon-aq was calculated according to the definition in eqn (9) using the values of [TFAH] and [TFA−] resulting from calculations of the equilibria (1)–(4) with Ko,1 = Ko,2 = 0.08. The filled data points indicate the absorbance at 374 nm during forward (red) and back titration (blue). The horizontal axis denotes the number of added equivalents of TFAH (red) and subsequently of TEA (in blue). The rectangles demonstrate the procedure to convert the absorbance values during back titration into pHnon-aq values. For details cf. text. | |
Taking full advantage of the assignment of a pHnon-aq value to any of the titration stages, the fractions of the protolytic forms, ScH+ and ScH22+ during each stage of the titration can be obtained solely from the pertinent protonation constants and the pHnon-aq value (cf. ESI†). As in the case of the open form, the equilibrium constants for the first and second protonation by TFAH are treated as equal. Likewise, the statistical factor of 2 is included in the definition of K1,c. The equilibrium constants K1,c = K2,c have been determined in the same manner as shown for the open form. The fractions of the protolytic forms have been calculated according to eqn (S15)–(S17) given in the ESI.† Using these fractions, the absorbance at any wavelength is represented as given in eqn (10):
| | | Ac(λ,pHnon-aq) = ASc(λ)X(pHnon-aq) + AScH+(λ)Y(pHnon-aq) + AScH22+(λ)Z(pHnon-aq) | (10) |
where the coefficients
Ai are the specific absorbances referring to the total concentration and
X,
Y,
Z the fractions of the individual protolytic forms. Trial values for
K1,c =
K2,c were assumed and the
Ai,closed values were fitted against the titration data shown in
Fig. 6. Similar to the fitting procedure of the open form, the quality of the fit did not represent a sufficiently sharp criterion to determine the proper
K-values unequivocally since a wide range of equilibrium constants gives equally good fits. Adopting again the spectroscopic argument that at each wavelength the absorbance of
ScH
+ should be intermediate between the absorbance of the two other forms (
Sc and
ScH
22+), the best fit was found to be
K1,c =
K2,c = 0.043. Thus, within the present accuracy of determining the
K-values, the basicity of the ring-closed isomer does not significantly deviate from that of the ring-open isomer.
 |
| | Fig. 6 (a) Absorption spectra during back titration of Sc with TEA after its photochemical generation from So in a solution with 70 equivalents of TFAH. The inset shows the spectral region used for the analysis of the protonation equilibria. (b) The upper panel shows the pHnon-aq dependence of the absorbance of the closed form at 313 nm. For K1,c = K2,c = 0.043, the best fit values of the specific absorbances of Sc, ScH+ and ScH22+ obeying the criterion that AScH+ should be intermediate between AScand AScH22+ are ASc = 0.509, AScH+ = 0.541 and AScH22+ = 0.571. The lower panel depicts the pHnon-aq dependence at 583 nm with the fit of ASc = 0.266, AScH+ = 0.255 and AScH22+ = 0.255 calculated assuming the same K1,c = K2,c = 0.043 as in the upper panel. In this case we are close to an isosbestic point of all three forms. | |
4. pH dependent quantum yields
Depending on pHnon-aq, variable amounts of the three protolytic forms So, SoH+, and SoH22+ of S are present in the sample solution. For each of them, a forward and backward photoisomerization with a distinct quantum yield is possible. Isomer Sc is involved in protolytic equilibria, too, with its protolytic forms being denoted Sc, ScH+, and ScH22+. Consequently, there are four equilibrium constants and six individual quantum yields to be considered for a comprehensive description of the reactions in the sample solution (Scheme 3). Analyzing the photochemical kinetics of ring opening and closing at different pHnon-aq, it is possible to single out the six individual quantum yields and to distinguish the protolytic gating effect of the first and second stage of protonation. In general, when it comes to the determination of photochemical parameters from stationary photokinetics, particularly in the case of photoreversible reactions, there are two basic strategic philosophies: (i) one can set up all relevant rate equations, integrate them numerically and fit the unknown parameters to the observed kinetic curves (cf. e.g.ref. 21 and 30), or (ii) one can aim for an analytical solution as worked out by Gauglitz and coworkers.22,23 Simplifications can be achieved, by irradiating at isosbestic points and by exploiting directly the slopes of kinetic curves (cf. e.g.ref. 18), although the slope-based methods are less accurate, since they use fewer kinetic data points than when using a time-integrated simulation. Compared to numerical integration methods, the analytical integration method appears to be more general and more transparent and therefore will be the method of choice in our approach.
 |
| | Scheme 3 Reaction scheme of coupled protolytic and photochemical conversions with assignment of equilibrium constants Ko,1, Ko,2, Kc,1, Kc,2 and quantum yields ΦSo, ΦSoH+, ΦSoH22+ for the open and ΦSc, ΦScH+, and ΦScH22+ for the closed forms. | |
The time-dependence of the total concentration of all three open forms [So]tot is described by eqn (11).31
| |  | (11) |
Here
I0 denotes the photon flux density,
F the illuminated area of the cuvette,
V the (stirred) volume of the sample solution,
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
the optical path length,
A the total absorbance at the wavelength of irradiation and the various
ε parameters are the molar absorption coefficients of the respective open and closed species. As shown in Section 6 of the ESI
† (eqn (S20)–(S28)),
eqn (11) can be reduced to the form
| | 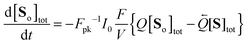 | (12) |
where the photokinetic factor
Fpk is given by
| |  | (13) |
Q is the pseudo quantum yield, comprising forward and backward reaction
| |  | (14) |
with
32| | ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) = ΦSoASoXSo + ΦSoH+ASoH+YSoH+ + ΦSoH22+ASoH22+ZSoH22+ = ΦSoASoXSo + ΦSoH+ASoH+YSoH+ + ΦSoH22+ASoH22+ZSoH22+ | (15) |
| | 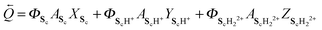 | (16) |
involving the definitions
| | 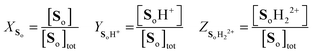 | (17) |
| |  | (18) |
| | ASo = εSo![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [So]tot ASoH+ = εSoH+ [So]tot ASoH+ = εSoH+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [So]tot ASoH22+ = εSoH22+ [So]tot ASoH22+ = εSoH22+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [So]tot [So]tot | (19) |
| | ASc = εSc![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [Sc]tot AScH+ = εScH+ [Sc]tot AScH+ = εScH+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [Sc]tot AScH22+ = εScH22+ [Sc]tot AScH22+ = εScH22+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [Sc]tot [Sc]tot | (20) |
[
So]
tot and [
Sc]
tot denote the sum of concentrations of all protolytic forms of
So and
Sc, respectively.
It should be noted that unless the absorption coefficients of the reacting species involved are all equal, the use of “average quantum yields” (i.e. omitting the absorption coefficients in eqn (15) and (16)) in photokinetic equations, is not exact.32
From eqn (12) it can be deduced that in the photostationary (PSS) state (d[So]/dt = 0) the following equation holds:
| |  | (21) |
and similarly, combining
eqn (21) with
eqn (14):
| | ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) [S]tot = Q[Sc]tot,pss [S]tot = Q[Sc]tot,pss | (22) |
Using
eqn (21),
eqn (12) can be rewritten as
| |  | (23) |
Since the total concentration of the open form
So (as well as of the closed form) is linearly related to the absorbance
A at any wavelength,
eqn (23) is also valid in the form
| |  | (24) |
Of course, the observation wavelength should be best chosen far from an isosbestic point, in order to render changes of
A relatively high.
This form of the photokinetic rate law corresponds exactly to that one which the approximate analytical method by Gauglitz,22,23 employing piecewise linearization of the photokinetic factor, is based on. Thus it is straight forward to measure the pseudo quantum yield Q for any pH of the solution. To decompose Q into the partial pseudo quantum yields ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) and
and  , one has to determine the composition of the photostationary state, which can be done by any convenient analytical method (cf. below). According to eqn (15) and (16), each of the partial pseudo quantum yields is a linear combination of the individual quantum yields of the pertinent protolytic open or closed forms.32 Since the coefficients ASoXSo, ASoH+YSoH+ASoH22+ZSoH22+ and AScXSc, AScH+YScH+AScH22+ZScH22+ are known for any pHnon-aq, the individual quantum yields ΦSo, ΦSoH+, ΦSoH22+ and ΦSc, ΦScH+, ΦScH22+ can be obtained by fitting the observed values for
, one has to determine the composition of the photostationary state, which can be done by any convenient analytical method (cf. below). According to eqn (15) and (16), each of the partial pseudo quantum yields is a linear combination of the individual quantum yields of the pertinent protolytic open or closed forms.32 Since the coefficients ASoXSo, ASoH+YSoH+ASoH22+ZSoH22+ and AScXSc, AScH+YScH+AScH22+ZScH22+ are known for any pHnon-aq, the individual quantum yields ΦSo, ΦSoH+, ΦSoH22+ and ΦSc, ΦScH+, ΦScH22+ can be obtained by fitting the observed values for ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) and
and  , as a function of pHnon-aq according to eqn (15) and (16).
, as a function of pHnon-aq according to eqn (15) and (16).
The data entering the fit as non-variable parameters is summarized in Table S1 (ESI†). Specifically, the values of pHnon-aq were calculated according to eqn (9) with various trial values of the equilibrium constants for the open-ring isomer, assuming again Ko,1 = Ko,2 (cf. ESI†). The value of Q was derived from the photokinetics observed under irradiation at 313 nm in 1.25 × 10−5 M solutions of So in the presence of various amounts of TFAH as described in the experimental part. The PSS composition of each sample was derived from its A583,pss value with the help of a reference sample analyzed by 1H-NMR, where A583,pss = 0.273 correlated to 97% conversion to the closed form in the PSS. The variation of the absorbance of the three individual protolytic forms at 583 nm (A1 = 0.266, A2 = 0.256, A3 = 0.255, obtained from the fit shown in Fig. 6b lower panel) was very small, hence a pHnon-aq dependence of the reference value was considered negligible.
As shown in detail in the ESI,† a consistent fit of the partial quantum yield ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) of the ring closing reaction as a function of pHnon-aq fixes the acceptable value of Ko,1 = Ko,2 to a rather narrow range around 0.08, which is in compliance with the conductometric results and places the spectrum of SoH+ right in the middle between those of So and SoH22+. From the fit shown in Fig. 7, the individual quantum yields ΦSo = 0.0037, ΦSoH+ < 0.01 and ΦSoH22+ = 0.11 were obtained. A more precise value of the quantum yield after single protonation cannot be given, because the best fit is obtained if we neglect its contribution altogether, or even taken it slightly negative (cf. Fig. S3, ESI†). In Fig. 7, we also show the contribution of form SoH+, that one would obtain for ΦSoH+ = 0.01. The deviation from the data points is clearly outside the uncertainty of the experimental data, thus fixing an upper bound to ΦSoH+. Probably its real value is close to that of the unprotonated So. In any case, however, from the fit, there is unequivocal evidence that the overall rise of
of the ring closing reaction as a function of pHnon-aq fixes the acceptable value of Ko,1 = Ko,2 to a rather narrow range around 0.08, which is in compliance with the conductometric results and places the spectrum of SoH+ right in the middle between those of So and SoH22+. From the fit shown in Fig. 7, the individual quantum yields ΦSo = 0.0037, ΦSoH+ < 0.01 and ΦSoH22+ = 0.11 were obtained. A more precise value of the quantum yield after single protonation cannot be given, because the best fit is obtained if we neglect its contribution altogether, or even taken it slightly negative (cf. Fig. S3, ESI†). In Fig. 7, we also show the contribution of form SoH+, that one would obtain for ΦSoH+ = 0.01. The deviation from the data points is clearly outside the uncertainty of the experimental data, thus fixing an upper bound to ΦSoH+. Probably its real value is close to that of the unprotonated So. In any case, however, from the fit, there is unequivocal evidence that the overall rise of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) in acidified solutions is dominated by the diprotonated form which exhibits an increase of the ring closing quantum yield by at least a factor of more than 10 relative to the single protonated and almost 30 relative to the unprotonated form. So far, to the best of our knowledge, comparably strong protolytic gating effects have not been reported in the literature.20
in acidified solutions is dominated by the diprotonated form which exhibits an increase of the ring closing quantum yield by at least a factor of more than 10 relative to the single protonated and almost 30 relative to the unprotonated form. So far, to the best of our knowledge, comparably strong protolytic gating effects have not been reported in the literature.20
 |
| | Fig. 7 Partial pseudo quantum yield ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) as a function of pHnon-aq. Experimentally observed: black data points, simulation: black solid line. The individual contributions of the various protolytic forms of So to the simulated value of as a function of pHnon-aq. Experimentally observed: black data points, simulation: black solid line. The individual contributions of the various protolytic forms of So to the simulated value of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) are: ΦSoASoXSo (blue, for better visibility multiplied by a factor of 5), ΦSoH22+ASoH22+ZSoH22+ (red), the latter dominating the overall value of are: ΦSoASoXSo (blue, for better visibility multiplied by a factor of 5), ΦSoH22+ASoH22+ZSoH22+ (red), the latter dominating the overall value of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) . In calculating the solid black curve for the total value of . In calculating the solid black curve for the total value of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) , the contribution of the intermediate form (SoH+) was completely neglected (ΦSoH+ = 0). On the other hand, the dotted orange line represents the contribution of SoH+ assuming ΦSoH+ = 0.01. The black dotted curve, representing the overall , the contribution of the intermediate form (SoH+) was completely neglected (ΦSoH+ = 0). On the other hand, the dotted orange line represents the contribution of SoH+ assuming ΦSoH+ = 0.01. The black dotted curve, representing the overall ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) in that case, is clearly outside the experimental error limits. For details, cf. ESI,† Fig. S3. in that case, is clearly outside the experimental error limits. For details, cf. ESI,† Fig. S3. | |
In a similar procedure, the pHnon-aq dependence of  at 313 nm irradiation wavelength was fitted using eqn (S27) (ESI†). The result of the fitting procedure is shown in Fig. S4 (ESI†). The individual quantum yields for the back irradiation from the closed to the open form under irradiation with 313 nm light were determined to be: ΦSc = 0.007, ΦScH+ = 0.001 and ΦScH22+ = 0.004 with error margins of ±30% due to the large relative scatter of the data (cf. ESI,† Fig. S4). In this case, the protonation does not show a pronounced increase of the quantum yield. Since it had been found that the quantum yield of ring opening induced by irradiation in the visible band at 576 nm did not show a protonation-gated effect either, the finer details of the pH-dependence of partial quantum yields at that wavelength were not further investigated in this work. The fact that photochemical ring closing of the open form of DAEs is much more sensitive to changes of substitution patterns than ring opening of the closed form has been pointed out by Uchida et al.16 It is paralleled by effects on the absorption spectra which are much more pronounced in the open form than in the closed form, a fact also apparent for the compound investigated in this work.
at 313 nm irradiation wavelength was fitted using eqn (S27) (ESI†). The result of the fitting procedure is shown in Fig. S4 (ESI†). The individual quantum yields for the back irradiation from the closed to the open form under irradiation with 313 nm light were determined to be: ΦSc = 0.007, ΦScH+ = 0.001 and ΦScH22+ = 0.004 with error margins of ±30% due to the large relative scatter of the data (cf. ESI,† Fig. S4). In this case, the protonation does not show a pronounced increase of the quantum yield. Since it had been found that the quantum yield of ring opening induced by irradiation in the visible band at 576 nm did not show a protonation-gated effect either, the finer details of the pH-dependence of partial quantum yields at that wavelength were not further investigated in this work. The fact that photochemical ring closing of the open form of DAEs is much more sensitive to changes of substitution patterns than ring opening of the closed form has been pointed out by Uchida et al.16 It is paralleled by effects on the absorption spectra which are much more pronounced in the open form than in the closed form, a fact also apparent for the compound investigated in this work.
Conclusion
In this paper, the method for the photostationary kinetic analysis of a coupled system of equilibrium forms of two photoisomers was rigorously developed in the framework of the Gauglitz method of photostationary kinetics. For protolytic equilibria, it was demonstrated how the individual quantum yields for each protolytic form can be isolated from the pH-dependence of the overall pseudo quantum yield Q. But in general, the method would be also applicable to other equilibria, potentially causing photochemical gating effects, such as e.g. complex formation or thermal isomerization equilibria. In case of the studied switchable molecular wire, it could be proven that it needs protonation on both side arms to achieve the large increase of the quantum yield of ring closure, whereby it is worth of note that the sites of protonation are located at some distance from the switching center.
Acknowledgements
Financial support of this work by the Deutsche Forschungsgemeinschaft through the SFB 767 is gratefully acknowledged. The authors thank MCat Company for a generous gift of palladium based cross coupling catalysts.
References
- J. Wolf, I. Eberspächer, U. Groth and T. Huhn, J. Org. Chem., 2013, 78, 8366–8375 CrossRef CAS PubMed.
- D. Dulić, S. J. van der Molen, T. Kudernac, H. T. Jonkman, J. J. D. de Jong, T. N. Bowden, J. van Esch, B. L. Feringa and B. J. van Wees, Phys. Rev. Lett., 2003, 91, 207402 CrossRef.
- S. J. van der Molen and P. Liljeroth, J. Phys.: Condens. Matter, 2010, 22, 133001 CrossRef PubMed.
- Y. Kim, T. J. Hellmuth, D. Sysoiev, F. Pauly, T. Pietsch, J. Wolf, A. Erbe, T. Huhn, U. Groth, U. E. Steiner and E. Scheer, Nano Lett., 2012, 12, 3736–3742 CrossRef CAS PubMed.
- S. H. Kawai, S. L. Gilat and J.-M. Lehn, Eur. J. Org. Chem., 1999, 2359–2366 CrossRef CAS.
- F. M. Raymo and S. Giordani, J. Am. Chem. Soc., 2002, 124, 2004–2007 CrossRef CAS PubMed.
- S. Sortino, S. Petralia, S. D. Bella, M. Tomasulo and F. M. Raymo, New J. Chem., 2006, 30, 515–517 RSC.
- S. Silvi, E. C. Constable, C. E. Housecroft, J. E. Beves, E. L. Dunphy, M. Tomasulo, F. M. Raymo and A. Credi, Chem. – Eur. J., 2009, 15, 178–185 CrossRef CAS PubMed.
- B. M. Neilson and C. W. Bielawski, ACS Catal., 2013, 3, 1874–1885 CrossRef CAS.
- M. M. Russew and S. Hecht, Adv. Mater., 2010, 22, 3348–3360 CrossRef CAS PubMed.
- C. Sciascia, R. Castagna, M. Dekermenjian, R. Martel, A. R. Srimath Kandada, F. Di Fonzo, A. Bianco, C. Bertarelli, M. Meneghetti and G. Lanzani, J. Phys. Chem. C, 2012, 116, 19483–19489 CAS.
- S. E. Braslavsky, Pure Appl. Chem., 2007, 79, 293–465 CrossRef CAS.
- S. Kobatake and Y. Terakawa, Chem. Commun., 2007, 1698–1700 RSC.
- K. Yumoto, M. Irie and K. Matsuda, Org. Lett., 2008, 10, 2051–2054 CrossRef CAS PubMed.
- M. Irie, K. Sakemura, M. Okinaka and K. Uchida, J. Org. Chem., 1995, 60, 8305–8309 CrossRef CAS.
- K. Uchida, T. Matsuoka, S. Kobatake, T. Yamaguchi and M. Irie, Tetrahedron, 2001, 57, 4559–4565 CrossRef CAS.
- H. H. Liu and Y. Chen, J. Mater. Chem., 2009, 19, 706–709 RSC.
- M. Cipolloni, A. Heynderickx, F. Maurel, A. Perrier, D. Jacquemin, O. Siri, F. Ortica and G. Favaro, J. Phys. Chem. C, 2011, 115, 23096–23106 CAS.
- F. Ortica, M. Cipolloni, A. Heynderickx, O. Siri and G. Favaro, Photochem. Photobiol. Sci., 2012, 11, 785–793 CAS.
- J. Massaad, J.-C. Micheau, C. Coudret, R. Sanchez, G. Guirado and S. Delbaere, Chem. – Eur. J., 2012, 18, 6568–6575 CrossRef CAS PubMed.
- Y. Kutsunugi, C. Coudret, J. C. Micheau and T. Kawai, Dyes Pigm., 2012, 92, 838–846 CrossRef CAS.
- G. Gauglitz, J. Photochem., 1976, 5, 41–47 CrossRef CAS.
- G. Gauglitz and S. Hubig, J. Photochem., 1981, 15, 255–257 CrossRef CAS.
- H. D. Brauer, R. Schmidt, G. Gauglitz and S. Hubig, Photochem. Photobiol., 1983, 37, 595–598 CrossRef CAS.
- D. Sysoiev, A. Fedoseev, Y. Kim, T. E. Exner, J. Boneberg, T. Huhn, P. Leiderer, E. Scheer, U. Groth and U. E. Steiner, Chem. – Eur. J., 2011, 17, 6663–6672 CrossRef CAS PubMed.
- The 95% conversion rate reported in ref. 4 was carefully re-checked for the present experiment and found to be slightly higher (97%) than previously reported.
-
Wolfram Research Inc., Mathematica. Version 9.0 ed., Wolfram Research, Inc., Champaign, Illinois, 2012 Search PubMed.
- In case of the dicarboxylic acid of the photoactive dithienylethene unit, the authors of ref. 20 attempted to evaluate the two deprotonation constants independently. The result of the mono-anion being more acidic than the neutral diacid is not really convincing, the more so, since the spectrum of the monoanion resulting from the analysis exhibits a sharp spectral maximum, where both, neutral form and dianion exhibit only weak shoulders, and although the spectral series on base titration appears to change in a motonic way at all wavelengths. Also, apart from the charge, the intramolecular hydrogen bridge in the monoacid anion would be expected to exhibit a further weakening effect on the acidity of this species.
- J. F. Coetzee and G. P. Cunningham, J. Am. Chem. Soc., 1965, 87, 2529–2534 CrossRef CAS.
- S. Delbaere, G. Vermeersch and J. C. Micheau, J. Photochem. Photobiol., C, 2011, 12, 74–105 CrossRef CAS.
- A detailed introduction to the mathematical description of a reversible photoreaction according to the method described by Gauglitz22,23 can be found in the Supporting Information given for ref. 25.
- The corresponding equation for decomposing the effective quantum yield as a function of pH, as given by Massaad et al.20 (cf. Supporting Information of that paper, page 5, Section 2) applies only for irradiations at isosbestic points, i.e. in situations where the absorption coefficients of the species involved are equal. In the presence of more than two species such wavelengths are rarely found.
Footnotes |
| † Electronic supplementary information (ESI) available: It refers to the topics: (1) system of equations for calculating the equilibrium concentrations of the species B, BH+, BH22+, HA and A−; (2) absorbance/absorbance diagrams for the spectral change on titration of So by TFAH; (3) simulated spectra of the three protolytic forms; (4) defining a pHnon-aq in a non-aqueous aprotic solvent; (5) calculation of the fractions of the protolytic forms during forward and back titration; (6) derivations of the pH dependent quantum yields of individual protolytic forms. See DOI: 10.1039/c4cp05258g |
| ‡ Present address: Solar & Photovoltaics Engineering Research Center, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia. |
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
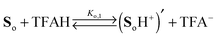






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the specific conductance κ of the solution should be described by eqn (8)
2, the specific conductance κ of the solution should be described by eqn (8)



![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) the optical path length, A the total absorbance at the wavelength of irradiation and the various ε parameters are the molar absorption coefficients of the respective open and closed species. As shown in Section 6 of the ESI† (eqn (S20)–(S28)), eqn (11) can be reduced to the form
the optical path length, A the total absorbance at the wavelength of irradiation and the various ε parameters are the molar absorption coefficients of the respective open and closed species. As shown in Section 6 of the ESI† (eqn (S20)–(S28)), eqn (11) can be reduced to the form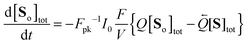


![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) = ΦSoASoXSo + ΦSoH+ASoH+YSoH+ + ΦSoH22+ASoH22+ZSoH22+
= ΦSoASoXSo + ΦSoH+ASoH+YSoH+ + ΦSoH22+ASoH22+ZSoH22+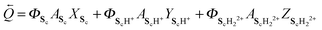
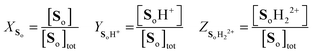

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [So]tot ASoH+ = εSoH+
[So]tot ASoH+ = εSoH+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [So]tot ASoH22+ = εSoH22+
[So]tot ASoH22+ = εSoH22+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [So]tot
[So]tot![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [Sc]tot AScH+ = εScH+
[Sc]tot AScH+ = εScH+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [Sc]tot AScH22+ = εScH22+
[Sc]tot AScH22+ = εScH22+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) [Sc]tot
[Sc]tot
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) [S]tot = Q[Sc]tot,pss
[S]tot = Q[Sc]tot,pss

![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) and
and  , one has to determine the composition of the photostationary state, which can be done by any convenient analytical method (cf. below). According to eqn (15) and (16), each of the partial pseudo quantum yields is a linear combination of the individual quantum yields of the pertinent protolytic open or closed forms.32 Since the coefficients ASoXSo, ASoH+YSoH+ASoH22+ZSoH22+ and AScXSc, AScH+YScH+AScH22+ZScH22+ are known for any pHnon-aq, the individual quantum yields ΦSo, ΦSoH+, ΦSoH22+ and ΦSc, ΦScH+, ΦScH22+ can be obtained by fitting the observed values for
, one has to determine the composition of the photostationary state, which can be done by any convenient analytical method (cf. below). According to eqn (15) and (16), each of the partial pseudo quantum yields is a linear combination of the individual quantum yields of the pertinent protolytic open or closed forms.32 Since the coefficients ASoXSo, ASoH+YSoH+ASoH22+ZSoH22+ and AScXSc, AScH+YScH+AScH22+ZScH22+ are known for any pHnon-aq, the individual quantum yields ΦSo, ΦSoH+, ΦSoH22+ and ΦSc, ΦScH+, ΦScH22+ can be obtained by fitting the observed values for ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) and
and  , as a function of pHnon-aq according to eqn (15) and (16).
, as a function of pHnon-aq according to eqn (15) and (16).![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) of the ring closing reaction as a function of pHnon-aq fixes the acceptable value of Ko,1 = Ko,2 to a rather narrow range around 0.08, which is in compliance with the conductometric results and places the spectrum of SoH+ right in the middle between those of So and SoH22+. From the fit shown in Fig. 7, the individual quantum yields ΦSo = 0.0037, ΦSoH+ < 0.01 and ΦSoH22+ = 0.11 were obtained. A more precise value of the quantum yield after single protonation cannot be given, because the best fit is obtained if we neglect its contribution altogether, or even taken it slightly negative (cf. Fig. S3, ESI†). In Fig. 7, we also show the contribution of form SoH+, that one would obtain for ΦSoH+ = 0.01. The deviation from the data points is clearly outside the uncertainty of the experimental data, thus fixing an upper bound to ΦSoH+. Probably its real value is close to that of the unprotonated So. In any case, however, from the fit, there is unequivocal evidence that the overall rise of
of the ring closing reaction as a function of pHnon-aq fixes the acceptable value of Ko,1 = Ko,2 to a rather narrow range around 0.08, which is in compliance with the conductometric results and places the spectrum of SoH+ right in the middle between those of So and SoH22+. From the fit shown in Fig. 7, the individual quantum yields ΦSo = 0.0037, ΦSoH+ < 0.01 and ΦSoH22+ = 0.11 were obtained. A more precise value of the quantum yield after single protonation cannot be given, because the best fit is obtained if we neglect its contribution altogether, or even taken it slightly negative (cf. Fig. S3, ESI†). In Fig. 7, we also show the contribution of form SoH+, that one would obtain for ΦSoH+ = 0.01. The deviation from the data points is clearly outside the uncertainty of the experimental data, thus fixing an upper bound to ΦSoH+. Probably its real value is close to that of the unprotonated So. In any case, however, from the fit, there is unequivocal evidence that the overall rise of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) in acidified solutions is dominated by the diprotonated form which exhibits an increase of the ring closing quantum yield by at least a factor of more than 10 relative to the single protonated and almost 30 relative to the unprotonated form. So far, to the best of our knowledge, comparably strong protolytic gating effects have not been reported in the literature.20
in acidified solutions is dominated by the diprotonated form which exhibits an increase of the ring closing quantum yield by at least a factor of more than 10 relative to the single protonated and almost 30 relative to the unprotonated form. So far, to the best of our knowledge, comparably strong protolytic gating effects have not been reported in the literature.20
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) as a function of pHnon-aq. Experimentally observed: black data points, simulation: black solid line. The individual contributions of the various protolytic forms of So to the simulated value of
as a function of pHnon-aq. Experimentally observed: black data points, simulation: black solid line. The individual contributions of the various protolytic forms of So to the simulated value of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) are: ΦSoASoXSo (blue, for better visibility multiplied by a factor of 5), ΦSoH22+ASoH22+ZSoH22+ (red), the latter dominating the overall value of
are: ΦSoASoXSo (blue, for better visibility multiplied by a factor of 5), ΦSoH22+ASoH22+ZSoH22+ (red), the latter dominating the overall value of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) . In calculating the solid black curve for the total value of
. In calculating the solid black curve for the total value of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) , the contribution of the intermediate form (SoH+) was completely neglected (ΦSoH+ = 0). On the other hand, the dotted orange line represents the contribution of SoH+ assuming ΦSoH+ = 0.01. The black dotted curve, representing the overall
, the contribution of the intermediate form (SoH+) was completely neglected (ΦSoH+ = 0). On the other hand, the dotted orange line represents the contribution of SoH+ assuming ΦSoH+ = 0.01. The black dotted curve, representing the overall ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) in that case, is clearly outside the experimental error limits. For details, cf. ESI,† Fig. S3.
in that case, is clearly outside the experimental error limits. For details, cf. ESI,† Fig. S3. at 313 nm irradiation wavelength was fitted using eqn (S27) (ESI†). The result of the fitting procedure is shown in Fig. S4 (ESI†). The individual quantum yields for the back irradiation from the closed to the open form under irradiation with 313 nm light were determined to be: ΦSc = 0.007, ΦScH+ = 0.001 and ΦScH22+ = 0.004 with error margins of ±30% due to the large relative scatter of the data (cf. ESI,† Fig. S4). In this case, the protonation does not show a pronounced increase of the quantum yield. Since it had been found that the quantum yield of ring opening induced by irradiation in the visible band at 576 nm did not show a protonation-gated effect either, the finer details of the pH-dependence of partial quantum yields at that wavelength were not further investigated in this work. The fact that photochemical ring closing of the open form of DAEs is much more sensitive to changes of substitution patterns than ring opening of the closed form has been pointed out by Uchida et al.16 It is paralleled by effects on the absorption spectra which are much more pronounced in the open form than in the closed form, a fact also apparent for the compound investigated in this work.
at 313 nm irradiation wavelength was fitted using eqn (S27) (ESI†). The result of the fitting procedure is shown in Fig. S4 (ESI†). The individual quantum yields for the back irradiation from the closed to the open form under irradiation with 313 nm light were determined to be: ΦSc = 0.007, ΦScH+ = 0.001 and ΦScH22+ = 0.004 with error margins of ±30% due to the large relative scatter of the data (cf. ESI,† Fig. S4). In this case, the protonation does not show a pronounced increase of the quantum yield. Since it had been found that the quantum yield of ring opening induced by irradiation in the visible band at 576 nm did not show a protonation-gated effect either, the finer details of the pH-dependence of partial quantum yields at that wavelength were not further investigated in this work. The fact that photochemical ring closing of the open form of DAEs is much more sensitive to changes of substitution patterns than ring opening of the closed form has been pointed out by Uchida et al.16 It is paralleled by effects on the absorption spectra which are much more pronounced in the open form than in the closed form, a fact also apparent for the compound investigated in this work.





