 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solid state concentration quenching of organic fluorophores in PMMA†
Adam P.
Green
and
Alastair R.
Buckley
*
The Electronic and Photonic Molecular Materials Group (EPMM), The Physics and Astronomy Department, The University of Sheffield, Sheffield, S3 7RH, England. E-mail: alastair.buckley@sheffield.ac.uk
First published on 21st November 2014
Abstract
In this study the concentration quenching phenomenon is explored for seven organic singlet emitters (Rhodamine 6G, Pyridine 2, Lumogen F Red 305, Perylene, Coumarin 102, DCM and DCJTB) in an inert host of poly(methyl methacrylate) (PMMA). Combining fluorescence lifetime and quantum yield measurements on samples of different molecular separation allows a deep decay rate analysis to be performed yielding, for each fluorophore, a monomial power law that indicates the strength and type of interaction. The fluorophores studied exhibit interactions in between that of FRET-like dipole–dipole (R−6) and surface–surface (R−2) with many lying close to that expected for surface–dipole (R−3) interactions. With no observed dependence on molecular structure it is concluded that the concentration quenching rate in singlet emitters follows a power law as kCQ = aR−3.1±0.7 with aggregation expected to increase the magnitude of the observed power.
Introduction
The photophysical properties of emissive materials in the solid state are of fundamental importance in the development of optoelectronic devices such as organic light emitting diodes1–4 and luminescent solar concentrators.5–8 In such devices a major source of loss occurs through concentration quenching (CQ) mechanisms where decreased separation, R, between chromophores results in enhanced non-radiative de-excitation pathways. These mechanisms are distinct from those involving quenching agents9 (e.g. molecular oxygen) or due to bleaching/molecular degradation.10 The ramifications of CQ are far reaching for optoelectronic devices, resulting in lowering of the quantum yield of emission, ηQY, and thus limitations on device design and performance.Experimental studies of CQ mechanisms have shown a number of different possible interactions depending on the host environment and materials involved. Förster theory (FRET) predicts an R−6 dependence for point-like dipole–dipole energy transfer interactions, as in eqn (1).
 | (1) |
A study looking at energy transfer between the Nile Red fluorophore in a polymer host, poly(9,9-dioctylfluorene) (F8), shows a R−3 dependence on Nile Red concentration.12 This is qualitatively explained through comparison to the theoretical formulation of the rate of a point–surface interaction, as given in eqn (2).
 | (2) |
In another study looking at energy transfer between F8 and poly(9,9-dioctylfluorene-co-benzothiadiazole) (F8BT) in Langmuir–Blodgett (LB) nanostructures an R−2 dependence was observed.13 This is indicative of surface–surface interaction between polymer layers in the LB nanostructures and would not be expected to be observed in spin cast films due to the irregularity of chromophore separations.
Clearly there is diversity in the interactions between materials in different types of systems. Small molecules might be expected to self-interact as point-like dipoles, as with the Iridium complexes doped into organic hosts, but as was seen in the F8:Nile Red system this is not always the case. The differing fabrication methods could explain this difference with spin coating producing more disordered and aggregated films, compared with the thermal co-deposition method.
In the present work the CQ interactions for a number of small molecular organic singlet emitters, or fluorophores (shown in Fig. 1), are studied in an electronically inert polymer host, poly(methyl methacrylate) (PMMA). This inert host ensures the interaction is between same species dye molecules rather than the surrounding host material. The choice of both host and processing methods will affect the dye distribution in the films, in this case spin coating is used, and therefore some level of aggregation will likely present itself as fluorophore concentration increases.
To determine the dependence of CQ on molecular separation it is necessary in the first instance to assume a homogenous distribution of dye molecules with a mean separation, R. By measurement of fluorescence lifetime, τ, by single photon counting and absolute fluorescence quantum yield, ηQY, as a function of concentration the radiative decay rate, kfl, can be determined from the ratio of the latter to the former. By definition the quantum yield is given as the ratio of the radiative decay rate to the sum of all decay rates, as in eqn (3).
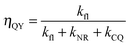 | (3) |
 | (4) |
From the ratio of eqn (3) and (4) we find kfl and hence by rearranging (3) the sum of non-radiative and CQ decay rates is found, as in eqn (5).
 | (5) |
At this point another assumption is necessary which is that the intrinsic non-radiative decay rate is a constant so that at some low concentration, when kCQ = 0, kNR can be determined. Then as fluorophore concentration increases CQ switches on and can be determined by subtraction of kNR from eqn (5). This assumption means that the non-radiative rate is independent of molecular separation, which needs careful consideration. The non-radiative rate is equal to the sum of various non-radiative decay modes such as internal conversion, intersystem crossing and conformational change. The assumption of kNR = constant therefore assumes that all these processes are constant, or zero, and hence intrinsic to the fluorophore in the sense that as a function of separation, R, between the fluorophores they remain unchanged. By modelling the concentration quenching rate, kCQ, as a monomial power law, as in eqn (1) or (2), one can elucidate this; it would be expected that the addition of CQ and changes to non-radiative mechanisms would cause deviation from a monomial power law interaction.
Experimental
Materials
Organic small molecular fluorophores were used as received from various sources. Perylene and 4-(dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM) are from Sigma Aldrich, 4-(dicyanomethylene)-2-tert-butyl-6-(1,1,7,7-tetramethyljulolidin-4-yl-vinyl)-4H-pyran (DCJTB) is from Jilin Optical and Electronic Materials Co. Ltd, 4-[4-[4-(dimethylamino)phenyl]-1,3-butadienyl]-1-ethyl-pyridinium perchlorate (Pyridine 2) and Lumogen F Red 305 are from Exciton, 2-[6-(ethylamino)-3-(ethylimino)-2,7-dimethyl-3H-xanthene-9-yl]benzoic acid ethyl esther (Rhodamine 6G) is from Acros Organics and 2,3,6,7-tetrahydro-9-methyl-1H,5H-quinolizino(9,1-gh)coumarin (Coumarin 102) was from Lambda Physik. The host polymer poly(methyl methacrylate) (PMMA) was sourced via Sigma Aldrich with molecular weight, Mw = 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 by GPC. The solvents used for this study are chlorobenzene (CB) and dimethylsulfoxide (DMSO), depending on the organic fluorophore to be dissolved, and were all used as received from Sigma Aldrich.
000 by GPC. The solvents used for this study are chlorobenzene (CB) and dimethylsulfoxide (DMSO), depending on the organic fluorophore to be dissolved, and were all used as received from Sigma Aldrich.
Sample fabrication
Samples were fabricated by spin coating at 1000 rpm from solution. Stock solutions of organic fluorophores and PMMA are first filtered through PTFE membranes of pore size 0.45 μm and then blended in different ratios to achieve a range of fluorophore concentrations in the resultant thin films. The laser dye salts, Pyridine 2 and Rhodamine 6G, were dissolved in DMSO due to low solubility in other organic solvents mutual with PMMA. For these compounds a separate stock of PMMA in DMSO was prepared for the blends. Due to the high boiling point of DMSO it is necessary to perform spin coating followed by drying on a hotplate at 150 °C to form a thin film. Resultant film thicknesses across all samples vary between approximately 200 nm and 4 μm depending on the total solute concentration in the blended solutions. For the different samples the mean molecular separation R was determined by assuming a homogenous distribution of chromophores in the solid host. The molar concentration of the chromophore in the host was converted into a number density, the inverse cube root of which gives the chromophore separation R. For example, for DCM, solutions of fluorophore concentration ranging from 2 wt% to 0.005 wt% were spun onto glass substrates. The final molar concentrations of DCM in the thin film ranges between 7.89 × 10−2 M to 1.92 × 10−4 M, leading to number densities of 4.75 × 1019 cm−3 to 1.15 × 1017 cm−3 and final intermolecular separations of 2.76 nm to 20.5 nm.Measurement
Absorption and emission spectrums are recorded using a Horiba Jobin Yvon Fluoromax-4 using the optimum slit width for the measurement, typically 1 nm or 2 nm. Fluorescence quantum yield is measured by the absolute method14,15 using a Labsphere integration sphere and, as a light source, either a Fianium supercontinuum white laser with a 10 nm bandpass filter centred at 500 nm or a 405 nm GaN diode laser or a mode-locked Ti:sapphire laser tuned and frequency doubled to 385 nm. The excitation source used depends on the absorption and emission regions of the fluorophore. The integration sphere is coupled via a fibre optic to a ORIEL Instaspec spectrometer using a 50 μm slit, a diffraction grating blazed at 500 nm and a wavelength range of 300 nm to 720 nm. Fluorescence lifetime is determined by single photon counting (SPC) using the Verdi V10 pumped Mira900 Ti:sapphire mode-locked laser system from Coherent, which is subsequently frequency doubled using an APE second harmonic generator. Excitation using this system is performed between 385 and 420 nm and the excitation beam is intensity modulated by a reflective neutral density filter wheel. Bandpass filters are used to isolate the emission wavelengths of the sample before this emission is collected by an avalanche photodiode. BNC connections from the laser and photodiode are made to the timing electronics of a SPC-830 PCI card from Becker & Hickl GmbH for signal analysis.Results
Spectroscopy
Before measurement of fluorescence lifetime and quantum yield the absorption and emission spectrums for all fluorophores are measured to ascertain the excitation wavelengths to use. Fig. 2 exhibits these spectra which, referring to the experimental section on measurement, shows the necessary excitation source. For quantum yield measurement it is seen that Coumarin 102 requires the 385 nm excitation provided by the frequency doubled mode-locked Ti:sapphire laser, Perylene and DCM benefit from the more stable 405 nm GaN laser and the others worked well with the filtered supercontinuum laser, which is also very stable. For fluorescence lifetime using the Coherent mode-locked laser system best results were found by tuning the laser to below 400 nm after frequency doubling, though for Rhodamine 6G 420 nm was used. | ||
| Fig. 2 Shown here are the absorption (dashed lines) and emission (coloured lines) spectrums of the fluorophores shown in Fig. 1, in the same letter order; (a) Rhodamine 6G, (b) Pyridine 2, (c) Lumogen F Red 305, (d) Perylene, (e) Coumarin 102, (f) DCM and (g) DCJTB. | ||
Now ηQY(R) and τ(R) are measured as described in the experimental section giving the results shown in Fig. 3. Rhodamine 6G, Lumogen F Red 305 and Perylene all show unity or near unity quantum yield at large molecular separation thus exhibiting how intrinsically efficient the emission from these fluorophores is. Also note that the exponential best fits make excellent models for the regimes of fluorophore concentration explored here.
 | ||
| Fig. 3 Shown here are the fluorescence quantum yields (black squares and lines) and fluorescence lifetimes (blue squares and lines) as a function of molecular separation for the fluorophores shown in Fig. 1, in the same letter order; (a) Rhodamine 6G, (b) Pyridine 2, (c) Lumogen F Red 305, (d) Perylene, (e) Coumarin 102, (f) DCM and (g) DCJTB. The lines are exponential best fits. | ||
By the exponential fits both ηQY(R) and τ(R) appear to reach definitive plateaus at high molecular separation which indicates an onset of concentration quenching and also that determination of the non-radiative decay constant, kNR, should be possible. In all cases, except perhaps for Pyridine 2, the form of ηQY(R) and τ(R) is similar but it is not possible at this stage to draw conclusions on the interactions taking place. However, the CQ onset point in terms of molecular separation does, with an experienced eye, have relevance to this as will be seen. The onset point is very similar for all fluorophores, lying between separations of 6 nm and 12 nm, which suggests similar CQ power laws will be seen and that similar interactions are involved. The maximum fluorescence lifetime and quantum yield are given from these fits in Table 1, including standard errors.
| Fluorophore | Max. ηQY | Max. τ (ns) |
|---|---|---|
| Rhodamine 6G | 0.98 ± 0.07 | 5.8 ± 0.2 |
| Pyridine 2 | 0.32 ± 0.01 | 2.21 ± 0.04 |
| Lum. F Red 305 | 0.91 ± 0.02 | 7.91 ± 0.05 |
| Perylene | 0.94 ± 0.01 | 4.71 ± 0.07 |
| Coumarin 102 | 0.46 ± 0.01 | 3.94 ± 0.05 |
| DCM | 0.33 ± 0.01 | 2.32 ± 0.01 |
| DCJTB | 0.68 ± 0.01 | 2.88 ± 0.02 |
The maximum QY shown in Table 1 are limited by both the minimum concentration of chromophore in the sample set, but also by interactions between the chromophore and the PMMA host polymer. While PMMA has been chosen because of its excellent film forming properties, optical transparency and ease of solution processing, as described in ref. 16 the polarity of the solvent can have a strong influence on the QY for particular chromophores. These sensitivities are highlighted in particular when comparing the QY of DCM in PMMA in ref. 16; measured to be 76%. However in ref. 16 there is no information about the final concentration, and importantly the method of PMMA synthesis was “in situ”, with DCM already present in a solution of methacrylate monomer (the structure of which is not fully disclosed) before polymerization. When comparing the QY of particular chromophores between different literature studies it is important to note the sensitivity to local host environment as well dependence on intermolecular spacing. Further work would be required to fully understand whether the discrepancy between16 and our current work is due to a difference in sample concentration or due to differences in PMMA polarity.
Decay rate analysis
From the data in Fig. 3 an analysis of decay rates can be performed. The fluorescence rate, kfl, is found by eqn (3) divided by eqn (4) and then the sum of non-radiative and CQ decay rates is found through eqn (5). The results of these calculations are shown in Fig. 4. | ||
| Fig. 4 Shown here are the fluorescence decay rate (black squares and lines) and the sum of non-radiative and concentration quenching rates (red squares and lines) as a function of molecular separation for the fluorophores shown in Fig. 1, in the same letter order; (a) Rhodamine 6G, (b) Pyridine 2, (c) Lumogen F Red 305, (d) Perylene, (e) Coumarin 102, (f) DCM and (g) DCJTB. The lines are exponential best fits. | ||
Lumogen F Red 305, Perylene and Coumarin 102 all show fluorescence decay rates that are almost constant with molecular separation. This is concurrent with the constant phosphorescent decay rate seen for Iridium phosphors in OLED host materials11 though is not reflected in the other fluorophores explored here.
This presents a puzzle; what might cause the fluorescence decay rate for some materials to decrease faster with molecular separation than others? From these data it is not possible to identify an exact mechanism though preferential non-radiative de-excitation of longer lived excited states may play an important role. That being said the three fluorophores exhibiting the least decrease in kfl all have relatively long measured fluorescence lifetimes. For this to be consistent these fluorophores must either experience stronger CQ or else have a non-constant kNR, according to eqn (3). Such effects may be due to a differing propensity to form aggregates or differing levels of interaction strength due to shielding of excited state distributions within the fluorophore. Other effects not considered here may also be present.
Looking now at the sum of non-radiative and CQ rates, kNR + kCQ, a low plateau is seen at high molecular separation corresponding to the onset of CQ. From this plateau a value for the assumed constant kNR is determined allowing the CQ rate to be extracted. Note that for the near unity quantum yield emitters this non-radiative constant approaches zero and because of this there is a larger error associated with its value. Subtracting kNR from the red data of Fig. 4 provides kCQ(R) which, when plotted on a log–log graph, follows a straight line as expected of a monomial power law of the form kCQ = aRb. This is shown in Fig. 5 with monomial best fits and two power law models for comparison. Decay rate and power law parameters are summarised in Table 2.
| Fluorophore | k fl [×108 s−1] | k NR [×108 s−1] | b (kCQ = aRb) | a (kCQ = aRb) [×109] |
|---|---|---|---|---|
| Rhodamine 6G | 1.66 ± 0.07 | 0.12 ± 0.08 | −2.4 ± 0.2 | 7 ± 2 |
| Pyridine 2 | 1.48 ± 0.03 | 3.14 ± 0.07 | −2.6 ± 0.2 | 6 ± 2 |
| Lum. F Red 305 | 1.17 ± 0.02 | 0.18 ± 0.04 | −3.92 ± 0.03 | 7.3 ± 0.2 |
| Perylene | 2.5 ± 0.3 | 0.11 ± 0.04 | −4.16 ± 0.07 | 20 ± 2 |
| Coumarin 102 | 1.23 ± 0.04 | 1.46 ± 0.08 | −3.2 ± 0.2 | 1.9 ± 0.3 |
| DCM | 1.40 ± 0.04 | 2.96 ± 0.04 | −2.9 ± 0.2 | 6 ± 1 |
| DCJTB | 2.36 ± 0.03 | 1.12 ± 0.03 | −2.6 ± 0.2 | 3.0 ± 0.5 |
From Fig. 5 it is seen that all the fluorophores exhibit CQ interactions lying between that of FRET (R−6 law) and surface–surface interactions (R−2 law). This is further shown in Table 2 with associated standard error from the best fits to the data. In most cases the CQ mechanism lies somewhere between surface–surface and surface–point interactions, except for Perylene and Lumogen F Red 305 which have monomial powers around −4; significantly higher than for the other dyes.
Notice that in many cases the data points at higher separation tend to drop below the best fit line. This would seem to indicate an onset regime where kCQ tends towards zero in an asymptotic manner. However, the log–log space accentuates this onset effect as well as enhancing the size of error bars at longer R. Although the error bars are not shown in Fig. 5 for clarity, at short R they are generally negligible whereas at long R they become so large that the accuracy of data itself becomes negligible. This highlights the difficulty in identifying the true onset of CQ. Individual kCQ plots for each fluorophore are provided in the ESI† to exhibit the error bars.
Comparing and contrasting the different fluorophores there appears to be few obvious trends in the decay and CQ parameters as a result of fluorophore size or structure. Looking at Fig. 1 and the summary tables in this context the fluorescence decay rate appears quite random though of a similar order in each case. A strong correlation is seen between kNR and ηQY as would be expected but note that the ratio kfl/(kfl + kNR) is equal to the maximum quantum yield (where kCQ = 0); hence it is the relative proportion of these quantities that is significant for fluorescence efficiency. ηQY values calculated from the decay rates will differ from Table 1 due to kfl and kNR being derived from the exponential fits of Fig. 4. For parameters a and b both size and structure appear to play no role in their magnitudes, which is surprising as these fluorophore properties were expected to influence self-interaction and aggregation.
To explain the observed interactions consider the influence expected from aggregation of fluorophores. In a homogenous distribution the interaction strength between fluorophores would be constant between nearest neighbours. With aggregation present one imagines a proportion of fluorophores in aggregate clusters whereas the rest are still distributed with a mean separation, R. Within the aggregates the true separation will be smaller than the calculated mean and thus the CQ interaction strength will locally be stronger than the bulk of the thin film. It is expected that this would give the appearance of enhanced CQ and thus would act to increase the observed power, b, of the monomial interaction. It is not, however, possible to measure the extent of aggregation in these films to confirm any inhomogeneities. Through this line of reasoning the true power of a homogeneous interaction should be lower than that which is observed. One might suggest also that Lumogen F Red 305 and Perylene are exhibiting signs of stronger aggregation with powers so much higher.
The conclusion that follows is that singlet excited states experience CQ by a power law somewhere between b = −2.4 and −4.2 or rather that b = −3.1 ± 0.7 with the error calculated through the standard deviation of values in Table 2. This is consistent with that observed previously for the Nile Red fluorophore in F8,12 also fabricated by spin coating.
Conclusion
From these observations there is clear evidence that FRET-like dipole–dipole interactions are not dominant in singlet CQ and therefore other interactions must be taking place, particularly surface–dipole interactions. No obvious relationship with molecular structure is seen but with no way measure of aggregation, which should increase the observed R dependence, it is impossible to say that there is no relationship, masked as it may be by an aggregation bias. In general for singlet CQ a power law of kCQ = aR−3.1±0.7 is observed.It would be interesting to perform the same analysis on these fluorophores in host environments cast by different methods such as by thermal evaporation, co-deposited with OLED host materials such as AlQ3. One would expect much greater control of fluorophore distribution in such an environment, which should remove some aggregation effects.
References
- Z. Liu, Z. Chen and Q. Gong, Chin. Phys. Lett., 2005, 22, 1536 CrossRef CAS.
- V. Bulović, R. Deshpande, M. E. Thompson and S. R. Forrest, Chem. Phys. Lett., 1999, 308, 317 CrossRef.
- G. Cerullo, S. Stagira, M. Zavelani-Rossi, S. De Silvestri, T. Virgili, D. G. Lidzey and D. D. C. Bradley, Chem. Phys. Lett., 2001, 335, 27 CrossRef CAS.
- R. N. Bera, Y. Sakakibara and M. Tokumoto, J. Mater. Sci.: Mater. Electron., 2005, 16, 549 CrossRef CAS PubMed.
- A. A. Earp, J. B. Franklin and G. B. Smith, Sol. Energy Mater. Sol. Cells, 2011, 95, 1157 CrossRef CAS PubMed.
- W. G. J. H. M. van Sark, Renewable Energy, 2013, 49, 207 CrossRef CAS PubMed.
- M. G. Debije and P. P. C. Verbunt, Adv. Energy Mater., 2012, 2, 12 CrossRef CAS.
- B. C. Rowan, L. R. Wilson and B. S. Richards, IEEE J. Sel. Top. Quantum Electron., 2008, 14, 1312 CrossRef CAS.
- S. A. Bagnich and V. N. Knyukshto, J. Appl. Spectrosc., 2006, 73, 846 CrossRef CAS PubMed.
- W.G. J. H. M. van Sark, et al. , Opt. Express, 2008, 16, 21773 CrossRef CAS.
- Y. Kawamura, J. Brooks, J. J. Brown, H. Sasabe and C. Adachi, Phys. Rev. Lett., 2006, 96, 017404 CrossRef.
- J. Cabanillas-Gonzalez, A. M. Fox, J. Hill and D. D. C. Bradley, Chem. Mater., 2004, 16, 4705 CrossRef CAS.
- J. Hill, S. Y. Heriot, O. Worsfold, T. H. Richardson, A. M. Fox and D. D. C. Bradley, Synth. Met., 2003, 139, 787 CrossRef CAS.
- A. R. Johnson, S. Lee, J. Klein and J. Kanicki, Rev. Sci. Instrum., 2007, 78, 086105 CrossRef PubMed.
- A. P. Green and A. R. Buckley, Rev. Sci. Instrum., 2012, 83, 073108 CrossRef CAS PubMed.
- A. L. Bondarev, V. N. Knyukshto, V. I. Stepuro, A. P. Stupak and A. A. Turban, J. Appl. Spectrosc., 2004, 71, 194 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: In the supporting information are plots for each fluorophore showing the concentration quenching rate, kCQ, as a function of molecular separation, R, with error bars. See DOI: 10.1039/c4cp05244g |
| This journal is © the Owner Societies 2015 |


