Native like helices in a specially designed β peptide in the gas phase

Abstract

In the natural peptides, helices are stabilized by hydrogen bonds that point backward along the sequence direction. Until now, there is only little evidence for the existence of analogous structures in oligomers of conformationally unrestricted β amino acids. We specifically designed the β peptide Ac-(β²hAla)₆-LysH⁺ to form native like helical structures in the gas phase. The design follows the known properties of the peptide Ac-Ala₆-LysH⁺ that forms a α helix in isolation. We perform ion-mobility mass-spectrometry and vibrational spectroscopy in the gas phase, combined with state-of-the-art density-functional theory simulations of these molecular systems in order to characterize their structure. We can show that the straightforward exchange of alanine residues for the homologous β amino acids generates a system that is generally capable of adopting native like helices with backward oriented H-bonds. By pushing the limits of theory and experiments, we show that one cannot assign a single preferred structure type due to the densely populated energy landscape and present an interpretation of the data that suggests an equilibrium of three helical structures.

---

1 Introduction

Proteins – the polymers of α amino acids – play an essential role in virtually all biochemical processes. Their often highly specific function is directly correlated to their distinctive ability to fold into a well-defined, three-dimensional structure, in which functional groups are spatially arranged to form reaction centers, binding sites, etc. Utilizing the toolbox of organic synthesis, chemists have long sought to mimic these folding characteristics using polymers that contain non-natural amino acids – so-called “peptide foldamers”.¹ The advantage here is that peptide bonds involving non-natural building blocks are less prone to proteolytic cleavage and, as such, of enormous interest for drug development.^2–4

The first step toward successful foldamer design is the identification of polymeric backbones which fold into a well-defined structure that is ideally native-like. In this context, much effort has been spent to design peptide foldamers that imitate the characteristics of the most prominent secondary structure element – the α helix.^5–15 A promising route to achieve this goal is backbone homologation, i.e. the extension of the amino acid's backbone by methylene units.⁵ The first homologs of natural α amino acids are β amino acids (Fig. 1a), followed by γ amino acids, δ amino acids, etc. In particular, β peptides were found to form secondary structures, which are similar in shape to α helices, and some of them have been used to design modulators for native protein–protein interactions.^3,16–18 Surprisingly, none of these structures directly resembles the periodically repeating backbone H-bonding pattern of α helices. The characteristic α helical i ← (i + 4) H-bonding pattern¹⁹ is depicted in Fig. 1b: H-bonds form between the NH of residue (i + 4) and the backbone carbonyl group of residue i. As a result pseudocycles of 13 atoms are formed. The alternative H-bonding patterns in Fig. 1b are either tighter wound (i ← (i + 3)) and characterize the 3₁₀ helix with 10-membered pseudocycles or feature the wider 16-membered H-bonded pseudocycles (i ← (i + 5)) of the π helix. The interconversion between these helices is possible by tightening or widening the helix, that is by changing the H-bonding pattern from i ← (i + 3) to i ← (i + 4) to i ← (i + 5) and back. By this mechanism, transitions will always happen from or to (via) the α helix.^20,21 In experimental and theoretical structural studies, mainly the α helix is found. This is not only due to enthalpy, e.g. H-bond cooperativity, but also due to a significant vibrational entropic stabilization that sets helices apart from competing compact conformers at room temperature.²²

Fig. 1 Structure of α and β amino acids and their oligomers. (a) α Amino acids and β amino acids are homologs that differ by a single backbone CH₂ group. (b) In α peptides, –(CH₂)₁–, and β peptides, –(CH₂)₂–, different backbone H-bonding patterns may lead to helical structures with H-bonds pointing in backward direction along the sequence, for example, the α helix and the H16 helix (see c).

It is well established that polyalanine sequences form α helices in the gas-phase, especially in the presence of a protonated lysine residue at the C terminus.^22–29 These prototypical peptides follow the sequence Ac-Ala_n-LysH⁺; members of this series have been extensively studied by ion mobility-mass spectrometry (IM-MS),^23–25 gas-phase vibrational spectroscopy,^26,28 and density-functional theory (DFT).^22,26–29 The placement of a positive charge at the C-terminus stabilizes the helix via coordination of dangling backbone carbonyls and favorable interaction with the helix macro-dipole. As an example for these polyalanine systems, we study here the peptide Ac-Ala₆-LysH⁺, for which the formation of an α helical structure at room temperature has been predicted.²²

β Peptides have been demonstrated to form various helices with H bonds pointing in forward (from N to C terminus), in backward (from C to N terminus), or in alternating direction (“mixed” helices) along the sequence.^{5–10,30–32} We are here however specifically interested in helix types that resemble the α helix, i.e. with H bonds that point backward relative to the sequences direction (from C to N terminus), as indicated in the H bonding scheme in Fig. 1b. The resulting helices are characterized by H bonds that form pseudo cycles with 12, 16, or 20 atoms and are therefore consistently named H12, H16, and H20, respectively. An illustrative example for the helix H16 is shown in Fig. 1b along with its α peptide equivalent, the α helix. Both feature H bonds with the same i ←(i + 4) pattern as depicted in Fig. 1b. According to the H-bonding patterns, H12, H16, and H20 are related to the 3₁₀, α, and π helix motifs of the α peptides.^10,33 The H12 helix was first described by Gellman and co-workers. Its formation, however, required cyclic β amino acids that are sterically restricted.^34–36 The α helix equivalent H16 helix has been proposed theoretically by Hartree–Fock calculations,¹⁰ but to date there has been only limited experimental evidence for its existence, most of it stemming from diffraction patterns of Nylon-3 polymers,^37,38 which have the same backbone structure as their oligomeric β peptide relatives.

In order to study the formation of helices with native like H bonds in backward direction along the sequence (see Fig. 1b and c), we employed the above-described design principle of Ac-Ala₆-LysH⁺.^22–29 To obtain a β peptide, we replaced the alanine residues by (R)-β-aminoisobutyric acid (β²hAla) – an alanine derivative with an extended backbone (Fig. 1a). The resulting foldamer Ac-(β²hAla)₆-LysH⁺ was investigated by gas-phase experiments and simulations.

2 Methods

2.1 Ion mobility-mass spectrometry

IM-MS experiments to determine collision cross sections (CCSs) were performed using an in-house built drift-tube instrument following a design described previously.³⁹ Briefly, ions are formed in a nano-electrospray ionization source (nESI) and transferred into the vacuum. An electrodynamic ion funnel collects and pulses ions into the drift region where they move through a buffer gas (He) under the influence of a weak electric field. At the end of the drift-tube, a second electrodynamic ion funnel guides the ions into a quadrupole mass spectrometer, which separates the ions according to their mass-to-charge ratio (m/z). By measuring the time-dependent ion current of m/z selected ions, characteristic arrival time distributions (ATDs) can be obtained. From these ATDs, absolute CCSs of a particular ion species can be determined.⁴⁰

2.2 Gas-phase vibrational spectroscopy

The experiments were performed at the free-electron laser facility FELIX⁴¹ (Nieuwegein, the Netherlands) using a Fourier-transform ion cyclotron (FT-ICR) mass spectrometer.⁴² For ionization a nESI source (MS Vision, Almere, NL) and capillaries prepared in-house were used. Ions were accumulated in a hexapole ion trap and transferred into a home-built FT-ICR mass spectrometer that is optically accessible via a KRS-5 window at the back end. The ions were irradiated by IR photons of the free electron laser FELIX. Resonance of the IR light with an IR active vibrational mode in the molecule results in the absorption of multiple photons, which causes the dissociation of the ions. Monitoring the depletion of the individual parent ion signals as a function of IR wavelength leads to the IR spectra.

2.3 Simulation details

The conformational search for the peptide Ac-Ala₆-LysH⁺ was described previously by Rossi et al.²² For the β-peptide Ac-(β²hAla)₆-LysH⁺ an extensive sampling of the potential energy surface (PES) of the OPLS-AA force field⁴³ has been performed independently by two approaches. We employed the basin hopping algorithm that is implemented in Tinker.^44,45 Furthermore, we employed replica-exchange molecular dynamics (REMD) simulations with the Gromacs program.⁴⁶ The simulations yielded an overall sampling time of 8 μs distributed over 16 replicas, finally, snapshots in 2 ps intervals were extracted from the 300 K trajectory and clustered.⁴⁷

Altogether, basin hopping and REMD simulations yielded 13 119 structures that were then relaxed by density-functional theory (DFT) calculations employing the PBE functional⁴⁸ that was corrected for long-range dispersion interactions⁴⁹ (PBE + vdW). Electronic structure theory calculations, including geometry optimizations, harmonic vibrational frequencies from finite differences, AIMD simulations, and replica-exchange AIMD simulations, were performed with the FHI-aims program package which employs numeric atom-centered orbitals as basis sets.⁵⁰ In order to reduce the bias of the empirical force field and following our focus on helical structures, we further sampled the local conformational space by means of replica-exchange AIMD simulations starting from representative structures of the H12, H16, and H20 helices that were obtained in the OPLS structure search (schemes for i ← (i + 3), i ← (i + 4), and i ← (i + 5) in Fig. 1b). The total sampling times were 486 ps, 576 ps, and 558 ps, respectively, each of them distributed over 18 replicas in a temperature range between 300 K and 687 K. We used a time step of 1 fs and swaps between replicas were attempted every 100 fs. Structure snapshots of all replicas were taken after each ps and post-relaxed with PBE + vdW. In summary, 14 739 PBE + vdW relaxations of candidate structures of the β-peptide Ac-(β²hAla)₆-LysH⁺ were performed. A free-energy correction that includes vibrational free energies in the harmonic approximation and rotational contributions in the rigid-rotor approximation, both computed with PBE + vdW at T = 300 K, was applied. Additionally, we tested modifications of the theory towards a higher-level functional, PBE0,⁵¹ and with the improved many-body description of the long-range dispersion,⁵² similar to a recent study of the validity of exchange–correlation functionals and dispersion corrections for the prediction of peptide secondary structures.⁵³

The infrared spectra were calculated from the Fourier transform of the dipole time derivative autocorrelation function^27,28 obtained from micro-canonical AIMD simulations of 25 ps length (after at least 5 ps equilibration at 300 K). Some anharmonicity effects will be missing in the spectra, because averages from classical trajectories were used for the dipole–dipole time correlation instead of exact quantum mechanical averages. However, this approach is currently at the limit of what is computationally feasible. To account for experimental broadening, the simulated spectra were convoluted with a Gaussian function with a variable width of 0.5% of the wavenumber. For a quantitative comparison we employed the Pendry reliability factor,⁵⁴ which has been successfully used in the context of IR spectroscopy before.^28,55 Perfect agreement yields R_P = 0 while no correlation between the spectra yields R_P = 1. An optimal fit between two spectra (based on R_P) is achieved by rigid shifts along x and y axes.

3 Results

3.1 Ion mobility-mass spectrometry

In an IM-MS experiment a package of ions is injected into a cell filled with an inert neutral buffer gas (in this work: helium). Aided by a weak electric field, the ions traverse the cell where they undergo many low energy collisions with buffer-gas molecules. Compact ions undergo fewer collisions and therefore traverse the cell faster than ions with a more extended conformation, which allows the separation of species with identical mass and charge but different size and shape. Moreover, the recorded drift or arrival times can be converted into collision cross sections, which are universally comparable values that can be calculated theoretically on the basis of molecular models. The typical arrival time distribution (ATD) depends on the shape of the ions and can be converted into a collision cross section (CCS) via the Mason-Shamp equation.⁴⁰ CCS values are independent of a specific experimental setup (machine, experimental conditions). An ATD of Ac-Ala₆-LysH⁺ is shown in the upper plot of Fig. 2a. The α-peptide ion cloud arrives at a drift time of 12 ms with a full-width half maximum (FWHM_exp.) of 0.38 ms. Fig. 2b shows the ATD for the β peptide Ac-(β²hAla)₆-LysH⁺. The backbone extension from α to β amino acid building blocks results in a longer drift time of about 13 ms and a peak width of FWHM_exp. = 0.38 ms.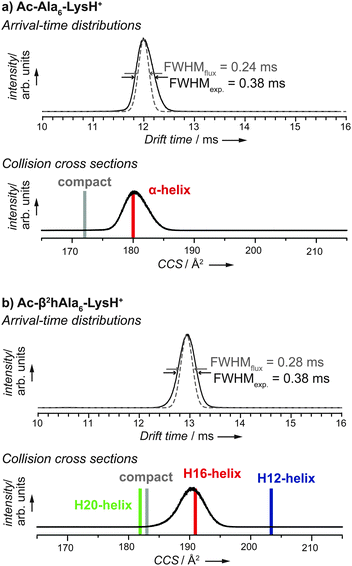

Fig. 2 Ion-mobility mass-spectrometry (IM-MS) of peptides Ac-Ala₆-LysH⁺ (a) and Ac-(β²hAla)₆-LysH⁺ (b). The experimental arrival-time distributions (ATDs, black lines in the two plots on top) were converted into collision cross sections (CCSs, black lines in the two plots at the bottom). In the plots of the ATDs, a flux-based estimate of the peak width is given as dashed line, the full-width at half-maximum (FWHM) peak width for experiment and flux-based model are given. Vertical bars in the CCS plots indicate CCSs calculated for predicted conformers shown in Fig. 3.

For each of the two systems, the α-peptide and the β-peptide, single and narrow peaks are observed in the ATD. If one assumes only a single type of conformation to be present in the drifting ion cloud, the peak width depends entirely on the initial pulse width and the broadening due to diffusion. This flux-based broadening of the ATD can be calculated by:⁴⁰

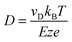where P(t′) is a function describing the shape of the ion cloud as it enters the drift region, for which we assume a rectangle pulse of 100 μs length in this case. C is a constant and D is the diffusion coefficient given by the Einstein relation , where ze is the charge of the ion, E is the applied electric field, and v_D is the average drift velocity. L denotes the length of the drift tube. The resulting theoretical flux-based broadening of the experimental ATD peak is plotted as dashed lines in Fig. 2. The experimentally observed FWHM_exp. are only slightly broader than the theoretical FWHM_flux values (see Fig. 2).

However, a narrow peak is not necessarily linked to a single conformer. The ion cloud traverses the drift tube in a time of 12 ms or 13 ms, respectively; within such a time scale, a molecular system may adopt numerous different conformational states if the barriers that separate them on the free energy surface are not too high. Assuming such a scenario, the width of the peak now provides information whether the interconversion between multiple minima is fast enough to average out over the drift time. In other words, a narrow peak may also indicate that each individual ion in the cloud has reached conformational equilibrium, namely the time average over all accessible conformers. The conformer distribution in the ensemble equals the conformer distribution in the time average of the individual ion due to the relatively long drift time. The relatively narrow peaks we observe by comparing FWHM_exp. and FWHM_flux indicate that all ions drift with the same average velocity and thus: (i) belong to a single conformational family, or (ii) belong to multiple conformational families with the same drift time, or (iii) interconvert between multiple conformers and reach equilibrium within the drift time of 12 or 13 ms, respectively.

3.2 Tackling the conformational problem by simulation

We narrow down the conformational problem for the α-peptide and the β-peptide applying a two-step procedure. First, the conformational space defined by an empirical force field is sampled in order to generate input for the subsequent first-principles relaxations. In a second step, a local refinement is performed that employs density-functional theory at the PBE + vdW level^48,49 Finally, free energies at 300 K (ΔF_300K) were estimated by including harmonic vibrations and rotational contributions in the rigid rotor approximation.

Fig. 3a shows the free energy hierarchy at 300 K (in the harmonic oscillator and rigid rotor approximation) and the two lowest free-energy structures of Ac-Ala₆-LysH⁺ that were identified by a recent first-principles (PBE + vdW) based conformational search by Rossi et al.²² Vibrational free energy contributions particularly stabilize helical structures with respect to more compact structures.²² This can be seen in the qualitative changes from the potential energy hierarchy to the free energy hierarchy as displayed in Fig. 3a for the α peptide. Consistently, the α helix is the preferred conformation for Ac-Ala₆-LysH⁺ confirmed by harmonic free energies at T = 300 K with the PBE + vdW approach. From the Cartesian coordinates of the conformers, theoretical CCSs can be calculated and compared to their experimental counterparts. For this, we employ the projection approximation (PA) method,⁵⁶ which is known to yield reliable values for ions with less than 200 atoms.⁵⁷ The theoretical CCS of the α-helical conformer of Ac-Ala₆-LysH⁺ agrees best with the experimental peak of the distribution of CCSs derived from experiment (Fig. 2a).

Fig. 3 Free energy hierarchy and examples of conformation of peptides Ac-Ala₆-LysH⁺ (a) and Ac-(β²hAla)₆-LysH⁺ (b). (a) A first-principles-based conformational search by Rossi et al.²² yielded a compact (grey) and an α-helical (red) structure as the two most likely conformations of α-peptide Ac-Ala₆-LysH⁺ at room temperature. (b) A compact conformation (grey) as well as the helices H12 (blue), H16 (red), and H20 (green) are displayed along with a plot of the free energy hierarchy. The displayed structures are highlighted in the hierarchy with their assigned color.

The β peptide Ac-(β²hAla)₆-LysH⁺ is expected to be structurally more flexible than the α peptide due to the additional methylene group per residue. In order to sample the larger structure space of the β peptide system, a far more extensive first-principles guided conformational search had to be performed. The multi-step search protocol that is described in the methods section yielded approximately 14 000 optimized geometries at the PBE + vdW level within a relative energy window of 156 kJ mol⁻¹. Re-relaxations of all minima within a relative energy window of 38.6 kJ mol⁻¹ with tight computational settings and harmonic free-energy calculations were performed. Harmonic free-energy contributions favor helical structures over more compact structures in Ac-(β²hAla)₆-LysH⁺ – an effect observed before for the Ac-Ala_n-LysH⁺ systems.²² The high density of structures of Ac-(β²hAla)₆-LysH⁺ with low harmonic free energies is remarkable (see Fig. 3b). However, the comparison to the hierarchy of the α peptide²² might be misleading. The conformational search strategies differ, especially in the local refinement step of the search results for the β peptide by means of replica exchange AIMD simulations. The three lowest free-energy conformers of Ac-(β²hAla)₆-LysH⁺ at 300 K are the helix H12, a compact structure, and the helix H20 (Fig. 3b), all within a free-energy window of about 3 kJ mol⁻¹. The α helix equivalent H16 helix is about 10 kJ mol⁻¹ above the global minimum in free energy, among a total of 16 conformers that are present within this narrow energy window. Helix types with forward oriented H bond patterns along the sequence¹⁰ were not found. This is due to the, by design of the peptides, selective stabilization of backward oriented H bonded structures via favorable charge dipole interactions.

For all these β peptide conformers depicted in Fig. 3b theoretical CCSs based on the PA method were computed.⁵⁶ Simulation and experiment are compared in Fig. 2b. We get a perfect match between the calculated CCS of H16 and the experimental peak position with a negligible deviation of about 1.5%. The computed CCS values for H12 and H20 as well as for the compact conformer clearly deviate from the CCS value of the experimental peak.

3.3 Gas-phase vibrational spectroscopy

The experimental spectra for the α-peptide Ac-Ala₆-LysH⁺ and the β-peptide Ac-(β²hAla)₆-LysH⁺ were measured at room temperature and are shown in the upper plots in Fig. 4a and b. At a first glance, the experimental vibrational spectrum of the β peptide (Fig. 4b) shares many features with that of the helical α-peptide (Fig. 4b), with the amide-I (C=O stretch mode, approximately 1679 cm⁻¹) and amide-II (N–H bending mode, approximately 1510 cm⁻¹) resonances being the most prominent peaks. A comparison of both spectra, however, shows characteristic differences in band position, width, and intensity, especially in the region between 1000 and 1400 cm⁻¹. This region is sensitive to the main chemical difference between both peptides, the additional methylene units in the backbone of the β-amino acid building blocks. At the other end of the spectrum (around 1760 cm⁻¹), both experimental spectra feature a vibrational mode of low intensity that hints to a free terminal C=O group. The experimental spectra were each averaged over four individual recordings and the background level was determined multiple times throughout each wavelength scan; the peak is real and not noise. The un-smoothed spectra are shown, together with error bars, in Fig. S1 of the ESI.†

Fig. 4 Gas-phase vibrational spectroscopy of (a) the α-peptide Ac-Ala₆-LysH⁺ and (b) the β-peptide Ac-(β²hAla)₆-LysH⁺ at room temperature. The plots show the experimental spectra (black lines) and the show simulated spectra (colored lines) from AIMD calculations. Experimental IR spectra were smoothed, see ESI† for the raw data. Vibrational spectra were simulated for the conformers shown in Fig. 3a. A magnification is shown for the wavenumber region from 1000 to 1400 cm⁻¹. Theoretical vibrational spectra were uniformly shifted, not scaled, by Δ_x and Δ_y along the wavenumber and intensity axes to best fit the experiment.²⁸

For the α peptide, constant-energy AIMD simulations (with 〈T〉 = 300 K) were performed for the two lowest-free energy conformers, the α helix and the compact conformer. From this data, theoretical vibrational spectra were derived and compared to the experimental spectrum. A quantitative comparison is crucial here and can be achieved by employing the Pendry reliability factor⁵⁴ that was previously introduced to the field of peptide vibrational spectroscopy.²⁸ Simulated spectra are rigidly shifted in x and y direction in order to yield the optimal R_P with respect to the experiment, values Δ_x and Δ_y are given in Fig. 4. The shift along the x-axis accounts for a mode softening (redshift) in the simulated spectra that probably results from the approximations made. This can for instance be due to the use of the exchange–correlation functional approximation (PBE) to DFT or the classical propagation of the AIMD trajectories that neglects quantum nuclear effects.^27,28 The intensity shift (along the y-axis) accounts for offsets in the experiment. The theoretical spectrum of the α helical conformer fits better to the experimental spectrum (R_P = 0.31) than the compact structure with R_P = 0.46 (Fig. 4a). Theoretical and experimental vibrational spectroscopy strongly support the interpretation of only the α helix being present in the gas phase and at room temperature for the α-peptide Ac-Ala₆-LysH⁺.

For the β peptide Ac-(β²hAla)₆-LysH⁺ we follow the same approach and select the low free energy conformers H12, compact, and H20 (see Fig. 3) as starting points for AIMD simulations. Even though the H16 conformer is higher in free energy, we still consider it here, as it is the direct analog of the α helix. The computational cost of such simulations is substantial and can only be performed for selected conformers. The individual simulated spectra are again compared to the experimental spectrum. The compact structure as well as the H12 helical structure agree only poorly based on the R_P criterion that rationalizes mismatches in the peak positions. The theoretical spectra of H16 and H20 have a slightly better agreement with experiment based on the R_P criterion, but still much worse than the R_P of 0.31 that we saw with the assignment above for the α peptide. Another possible criterion is the diagnostic peak that was found in the high wavenumber region (around 1760 cm⁻¹). This diagnostic feature results from the C-terminal carboxyl group not being involved in H bonds and is consequently only reproduced in the simulated spectra of the H12 and H16 helices. However, it is evident that we do not reach a clear conclusion from gas-phase vibrational spectroscopy of the β peptide Ac-(β²hAla)₆-LysH⁺, but there might be slight hints that point towards the H16 helix as possible dominant conformer for the β peptide in the gas phase.

4 Discussion

The data for the α peptide Ac-Ala₆-LysH⁺ points to one clear and obvious solution: the expected dominance of the α-helix in the gas phase. Contrarily, the data from gas-phase experiments and first-principles simulations for the β-peptide Ac-(β²hAla)₆-LysH⁺ is less clear, even contradictory. The simulation results, specifically the harmonic free energy hierarchy at T = 300 K, point towards the H12 helix as being most stable in the gas phase, next in line are a compact conformer and the helical structure H20, all within a ΔF_300K range of about 3 kJ mol⁻¹. The α-helix like conformer H16 is about 10 kJ mol⁻¹ higher in this free energy scale. However, the IM-MS measurements find a narrow drift peak with a CCS distribution that agrees very well with the shape of this H16 helix. The vibrational spectroscopy experiments reveal no particularly reliable agreement with any of the theoretically predicted spectra, but might weakly hint towards the H16 helix. In the following, we will discuss in detail two possible interpretations that could help explain the situation.

We then also assess the applicability and accuracy of the applied method by comparing two different density functionals in combination with two different corrections for long-range dispersion.

4.1 A step back

In order to critically assess a possible assignment of the H16 helix as most-likely conformer to be present in the gas phase, we take a step back and evaluate the full pool of structures for which we calculated the harmonic free energy. For each of the 163 low free-energy conformers (up to ΔF_300K = 38.5 kJ mol⁻¹) we have a data point that envelopes three values:

• the free energy at 300 K in the harmonic oscillator and rigid rotor approximation,

• the agreement between the experimental and the predicted vibrational spectrum measured by R_P,⁵⁴ and

• the agreement between the calculated (PA) and measured CCS expressed by the difference ΔCCS.

The vibrational spectra derived from AIMD simulations are computationally too costly to be routinely computed for a large number of conformers, consequently we can only use harmonic vibrational spectra for this number of conformers. Fig. 5 shows again the conformational free-energy hierarchy in the harmonic approximation at 300 K. When considering the full conformational pool up to 38.5 kJ mol⁻¹ for plotting R_P and ΔCCS of each conformer (see Fig. 5a), it is hard to draw a conclusion. However, it is obvious that there are conformations for which a good agreement with the experimental observables is predicted (low R_P and ΔCCS close to 0). Fortunately, there is a third dimension to be considered, the computed free energy. Stepwise lowering the cut-off ΔF_300K for plotting (see Fig. 5b and c), the conformer H16 appears more and more isolated in the plots and suggests itself as a likely conformer to be present in the experiment, especially due to the perfect agreement of experimentally observed and calculated CCS. However, further lowering the energy cut-off will remove the H16 structure from the candidate list.

Fig. 5 The conformational free-energy hierarchy of the β peptide Ac-(β²hAla)₆-LysH⁺ (right panel) and the R_P (harmonic spectra) versus ΔCCS plots (left panel). The the filled circles in the three plots represent all predicted structures up to a relative free-energy threshold of (a) 38.5 kJ mol⁻¹, (b) 16.5 kJ mol⁻¹, and (c) 10.2 kJ mol⁻¹, respectively. The compact conformer and the helices H12, H16, H20 are highlighted in gray, blue, red, and green, respectively. In plot (c), also the R_P values for the vibrational spectra of compact, H12, H16, and H20 derived from AIMD simulation are shown as open squares, connected by a straight line to the respective value for the harmonic spectrum.

Another problem with a structure assignment based on R_P is illustrated in Fig. 5c, where also the R_P values for the four spectra (H12, H16, H20, compact) derived from AIMD simulations are plotted as open squares. The MD derived spectra are in better agreement with the experiment than the respective ones calculated in the harmonic approximation as it is indicated by the lower R_P value. However, the improvement is not uniform; while there is, for instance, only minor improvement for H16, the improvement from the harmonic to the MD treatment for H20 is substantial. This limits the applicability of the harmonic vibrational spectra for structure assignment. Overall, a reliable structure assignment seems impossible with the theory-experiment agreement achieved here.

4.2 Equilibrium

In isolation, structural changes that involve the rearrangement of H bonds can be hindered due to the lack of compensation by transient interactions with water molecules. However, the structural interconversion between the helix types shown in Fig. 1b can happen via tightening or loosening the helical twist and the intermediate formation of bifurcated H bonds in some sort of “breathing” motion.^20,21 The path of this interconversion always features the H16 helix as an intermediate as it lies in between its relatives H12 and H20 when considering a meaningful reaction coordinate like helical twist, the diameter vs. length ratio, or the here used CCSs of the structures. Again, structural transitions between these helices would always be H12 ⇌ H16 ⇌ H20 if we exclude the possibility of full unfolding and the refolding to an alternative helix type. The same concept in turn also holds for the possible helices of the α peptide, where transitions 3₁₀ ⇌ α ⇌ π would occur. Combining this view with the relative free energies ΔF₃₀₀ that were calculated yields the two differing pictures shown in Fig. 6. Please note, the free-energy and CCS values for the helical conformers stem from actual calculations, but the gray lines are only an illustrative representation of a possible free-energy surface (FES). In fact we do not have knowledge about barriers (yet). The interpretation of the illustrative α peptide FES is straightforward, the α helix is the most stable structure and the barriers to the neighboring helical structures must be high, as even the respective minima of the 3₁₀ and π are above the energy window used in the representation in Fig. 6. Consequently, the experimental CCS distribution only features one peak that fits best the theoretical CCS of the α helix. Also the experimental CCS distribution of the β peptide fits best to the α helix-like H16 structure. However, here the H16 is least stable of three alternative helical structures. How to bring these seemingly contradictory findings in line? First of all, the drift time of 13 ms has to be considered. All individual ions of the ion cloud should be in structural equilibrium and have visited the possible states on our FES, the H12, H16, and H20 minima, several times. As a consequence, the experimental CCS distribution represents an average of the visited states that matches the CCS value predicted for the H16 structure that is located between the two lower free-energy conformers H12 and H20. This interpretation brings at least the free-energy prediction and the IM-MS measurements in line. The reasons for the disagreement between the experimental IR spectrum and the four simulated spectra from AIMD simulations remain to be investigated. Straightforward mixing of the four individual spectra with the target function of reducing the R_P to the experiment does not yield satisfying agreement. The R_P values for the helical conformers H12, H16, and H20 of the β peptide are 0.64, 0.49, and 0.47, respectively (see also Fig. 4). The best combination of the three spectra, to which H16 and H20 contribute equally and H12 does not contribute at all, has an R_P of 0.42.

Fig. 6 The predicted CCS can be used as a reduced coordinate together with the computed free energies to draw a free-energy profile that relates the helical structures to each other. Please note, the gray lines are illustrative and do not represent results from simulation. For the α peptide Ac-Ala₆-LysH⁺ (a), the α helix is the only helical conformer within the considered free energy range. Consequently, we would assume a deep potential well to flank the α helical minimum. For the β peptide Ac-(β²hAla)₆-LysH⁺ (b), three helices are present in the considered energy range of about 12 kJ mol⁻¹. CCS as a conformational coordinate places H16 right between the two alternative helices H12 and H20 like a barrier that has to be overcome whenever the helices interconvert. The CCS plots from Fig. 2 are shown again to illustrate how two very different (hypothetical) energy landscapes can potentially result in a very similar IM-MS signal.

4.3 Exact exchange and many-body dispersion

The conformational free energy hierarchy shown in Fig. 3 is sensitive to the various approximations that we employ. In one of our recent studies⁵³ we assessed the accuracy of pairwise (vdW)⁴⁹ and many-body dispersion corrections (MBD*)⁵² in combination with the density functionals PBE (generalized-gradient approximation)⁴⁸ and PBE0 (with Hartree–Fock like exchange)⁵¹ for the description of the conformational energy hierarchy of peptides in the gas phase. In the same spirit we have tested how PBE + MBD*, PBE0 + vdW, and PBE0 + MBD*, treat the low energy regime of the β peptide Ac-(β²hAla)₆-LysH⁺ predicted at the PBE + vdW level of theory. The energies of conformers of the β peptide with a relative free energy below 11.2 kJ mol⁻¹ were recalculated. The resulting potential energies were then combined with the harmonic vibrational free energy corrections computed with PBE + vdW. The results are summarized in Fig. 7. The change from PBE + vdW to PBE0 + MBD* stabilizes H16, while H12 is slightly destabilized. Furthermore, two additional compact conformers, highlighted as A and B in Fig. 7, are ranked more stable. At the PBE0 + MBD* level, four conformers, namely A, compact, B, and H12, have to be considered within the narrow free energy window of only 1 kJ mol⁻¹. However, for none of them the match between experimental CCS value and computed value is as good as for the H16 conformer (see ESI,† Table S2).

Fig. 7 The potential energy of selected conformers with a relative free energy (PBE + vdW) of 11.2 kJ mol⁻¹ was recalculated with PBE + MBD*, PBE0 + vdW, and PBE0 + MBD*. The relative free energies contain the potential energy calculated at the given level and the harmonic free energy contribution computed at the PBE + vdW level. The energy levels of selected conformers are highlighted.

We discuss here a free energy range of about 10 kJ mol⁻¹ for the considerably large β-peptide with its 108 atoms. This translates to roughly 0.1 kJ mol⁻¹ per atom, in other units: 0.02 kcal mol⁻¹ or 1 meV. The comparison of relative energy hierarchies of 27 conformers of Ac-Ala₃-NMe reproduced with PBE + vdW and PBE + MBD*⁵³ to a CCSD(T) reference hierarchy⁵⁸ shows mean absolute errors of only the potential energy description of 0.05 kJ mol⁻¹ per atom (in other units: 0.01 kcal mol⁻¹ or 0.5 meV). Consequently, the minuscule energy differences that we are discussing here are within the uncertainties of the applied approximations to potential energy (e.g. PBE + vdW or PBE0 + MBD*) and free energy (harmonic approximation). Despite these uncertainties, we can identify a group of likely conformers with the error between different functionals being at most 10 kJ mol⁻¹. Within that group making a distinction becomes difficult and we need experimental data to compare with. So it is not only the potential energy description that limits us here, but especially also the conformational and entropic contributions that are of course substantial at 300 K.

5 Conclusion

With this study on the conformational properties of the β-peptide Ac-(β²hAla)₆-LysH⁺, we have clearly pushed the current limits of what is possible in gas-phase experiments and simulation. With respect to the experimental results, the IM-MS experiments give us the simplest, if not even over-simplified answer. The rather narrow peak does, according to our interpretation, not represent a single conformer type but more likely a conformational equilibrium. The gas-phase vibrational spectroscopy on the other hand ideally gives far more structural information that is, however, hard to access, e.g., due to the broadness of the bands in the experimental spectrum. Furthermore, we here focus recording of spectra to the 1000 to 1800 cm⁻¹ region. The flanking wavenumber regions apparently also offer a lot of information as it is evident from the simulated spectra of the β peptide shown in Fig. S2 of the ESI.†

Still we can show that a β peptide that consists of open chain building blocks (not sterically constrained) is generally capable of adopting native like helices with backward oriented H bonds (cf.Fig. 1b), similar to the types observed for the natural α peptides. We derive an explanation how these structures can interconvert in isolation that will be investigated in future experiments and simulations.

The density of conformers of the β peptide at low energies is clearly a challenge for the traditional, single-point plus harmonic free energy approach at 300 K, and this is where future work must focus. The interconversion between helices that we discuss here can be described with plausible conformational coordinates and then be studied with techniques like metadynamics⁵⁹ in combination with DFT. Low-temperature experiments on the other hand might yield sharper IR bands or, with a cooled drift tube, allow the separation of different conformers by hindering the interconversion between structures.

Acknowledgements

This work was supported by the Center for Supramolecular Interactions of the Freie Universität Berlin. We gratefully acknowledge the “Stichting voor Fundamenteel Onderzoek der Materie” (FOM) for providing the beam time on FELIX as well as support by members of the FELIX staff: Britta Redlich, Lex van der Meer, Rene van Buuren, Jos Oomens, Giel Berden, and Josipa Grzetic.

References

1. S. H. Gellman, Acc. Chem. Res., 1998, 31, 173.
2. L. K. A. Pilsl and O. Reiser, Amino Acids, 2011, 41, 709.
3. D. Seebach and J. Gardiner, Acc. Chem. Res., 2008, 41, 1366.
4. J. Frackenpohl, P. I. Arvidsson, J. V. Schreiber and D. Seebach, ChemBioChem, 2001, 2, 445.
5. A. Banerjee and P. Balaram, Curr. Sci., 1997, 73, 1067.
6. R. P. Cheng, S. H. Gellman and W. F. DeGrado, Chem. Rev., 2001, 101, 3219.
7. D. Seebach, D. F. Hook and A. Glättli, Biopolymers, 2006, 84, 23.
8. C. M. Goodman, S. Choi, S. Shandler and W. F. DeGrado, Nat. Chem. Biol., 2007, 3, 252.
9. T. Martinek and F. Fülöp, Chem. Soc. Rev., 2012, 41, 687.
10. C. Baldauf and H.-J. Hofmann, Helv. Chim. Acta, 2012, 95, 2348.
11. C. Baldauf, R. Günther and H.-J. Hofmann, J. Org. Chem., 2006, 71, 1200.
12. R. Rezaei Araghi, C. Jäckel, H. Cölfen, M. Salwiczek, A. Völkel, S. C. Wagner, S. Wieczorek, C. Baldauf and B. Koksch, ChemBioChem, 2010, 11, 335–339.
13. R. Rezaei Araghi, C. Baldauf, U. I. M. Gerling, C. D. Cadicamo and B. Koksch, Amino Acids, 2011, 41, 733–742.
14. T. Sawada and S. H. Gellman, J. Am. Chem. Soc., 2011, 133, 7336.
15. K. Basuroy, B. Dinesh, N. Shamala and P. Balaram, Angew. Chem., 2012, 124, 8866.
16. J. A. Kritzer, J. D. Lear, M. E. Hodsdon and A. Schepartz, J. Am. Chem. Soc., 2004, 126, 9468.
17. J. A. Kritzer, N. W. Luedtke, E. A. Harker and A. Schepartz, J. Am. Chem. Soc., 2005, 127, 14584.
18. Y. Imamura, N. Umezawa, S. Osawa, N. Shimada, T. Higo, S. Yokoshima, T. Fukuyama, T. Iwatsubo, N. Kato, T. Tomita and T. Higuchi, J. Med. Chem., 2013, 56, 1443.
19. M. Crisma, F. Formaggio, A. Moretto and C. Toniolo, Pept. Sci., 2006, 84, 3–12.
20. K.-H. Lee, D. R. Benson and K. Kuczera, Biochemistry, 2000, 39, 13737–13747.
21. R. Armen, D. O. Alonso and V. Daggett, Protein Sci., 2003, 12, 1145–1157.
22. M. Rossi, M. Scheffler and V. Blum, J. Phys. Chem. B, 2013, 117, 5574.
23. R. R. Hudgins, M. A. Ratner and M. F. Jarrold, J. Am. Chem. Soc., 1998, 120, 12974.
24. R. R. Hudgins and M. F. Jarrold, J. Am. Chem. Soc., 1999, 121, 3494.
25. M. F. Jarrold, Phys. Chem. Chem. Phys., 2007, 9, 1659.
26. J. A. Stearns, O. V. Boyarkin and T. R. Rizzo, J. Am. Chem. Soc., 2007, 129, 13820.
27. M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2010, 12, 3336.
28. M. Rossi, V. Blum, P. Kupser, G. von Helden, F. Bierau, K. Pagel, G. Meijer and M. Scheffler, J. Phys. Chem. Lett., 2010, 1, 3465.
29. S. Chutia, M. Rossi and V. Blum, J. Phys. Chem. B, 2012, 116, 14788.
30. D. Seebach, K. Gademann, J. V. Schreiber, J. L. Matthews, T. Hintermann, B. Jaun, L. Oberer, U. Hommel and H. Widmer, Helv. Chim. Acta, 1997, 80, 2033.
31. M. Rueping, J. V. Schreiber, G. Lelais, B. Jaun and D. Seebach, Helv. Chim. Acta, 2002, 85, 2577.
32. C. Baldauf, R. Günther and H.-J. Hofmann, Angew. Chem., Int. Ed., 2004, 43, 1594.
33. K. Möhle, R. Günther, M. Thormann, N. Sewald and H.-J. Hofmann, Biopolymers, 1999, 50, 167.
34. D. H. Appella, L. A. Christianson, I. L. Karle, D. R. Powell and S. H. Gellman, J. Am. Chem. Soc., 1996, 118, 13071.
35. D. H. Appella, L. A. Christianson, D. A. Klein, D. R. Powell, X. L. Huang, J. J. Barchi and S. H. Gellman, Nature, 1997, 387, 381.
36. D. H. Appella, L. A. Christianson, I. L. Karle, D. R. Powell and S. H. Gellman, J. Am. Chem. Soc., 1999, 121, 6206.
37. J. M. Fernández-Santín, S. Muñoz-Guerra, A. Rodríguez-Galán, J. Aymami, J. Lloveras, J. A. Subirana, E. Giraltand and M. Ptak, Macromolecules, 1987, 20, 62.
38. F. López-Carrasquero, C. Alemán, A. M. García-Alvarez, M. de Ilarduya and S. Muñoz-Guerra, Macromol. Chem. Phys., 1995, 196, 253–268.
39. P. R. Kemper, N. F. Dupuis and M. T. Bowers, Int. J. Mass Spectrom., 2009, 287, 46–57.
40. E. Mason and W. McDaniel, Transport properties of ions in gases, Wiley, 1988.
41. D. Oepts, A. van der Meer and P. van Amersfoort, Infrared Phys. Technol., 1995, 36, 297–308.
42. J. J. Valle, J. R. Eyler, J. Oomens, D. T. Moore, A. F. G. van der Meer, G. von Helden, G. Meijer, C. L. Hendrickson, A. G. Marshall and G. T. Blakney, Rev. Sci. Instrum., 2005, 76, 023103.
43. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474.
44. J. W. Ponder, Tinker – software tools for molecular design, http://dasher.wustl.edu/ffe/, We used version 5.0 of the program and theversions of the force fields distributed with the package.
45. R. V. Pappu, R. K. Hart and J. W. Ponder, J. Phys. Chem. B, 1998, 102, 9725–9742.
46. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435.
47. X. Daura, K. Gademann, H. Schäfer, B. Jaun, D. Seebach and W. F. van Gunsteren, J. Am. Chem. Soc., 2001, 123, 2393.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
49. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
50. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175.
51. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
52. A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508.
53. M. Rossi, S. Chutia, M. Scheffler and V. Blum, J. Phys. Chem. A, 2014, 118, 7349–7359.
54. J. B. Pendry, J. Phys. C: Solid State Phys., 1980, 13, 937.
55. C. Baldauf, K. Pagel, S. Warnke, G. von Helden, B. Koksch, V. Blum and M. Scheffler, Chem. – Eur. J., 2013, 19, 11224–11234.
56. G. von Helden, M. T. Hsu, N. Gotts and M. T. Bowers, J. Phys. Chem., 1993, 97, 8182–8192.
57. The Bowers Group, Theoretical Collision Cross Sections, 2014, http://bowers.chem.ucsb.edu/theory_analysis/cross-sections/index.shtml.
58. R. A. DiStasio, R. P. Steele, Y. M. Rhee, Y. Shao and M. Head-Gordon, J. Comput. Chem., 2007, 28, 839–856.
59. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.

---

Footnotes

† Electronic supplementary information (ESI) available: Cartesian coordinates for all structures displayed in the manuscript, unprocessed experimental spectra, and simulated spectra ranging from 0 to 3500 cm⁻¹. See DOI: 10.1039/c4cp05216a

‡ Present address: CSIRO Materials Science and Engineering, Bayview Avenue, Clayton, Victoria 3168, Australia.

---