 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tailoring the optical properties of lanthanide phosphors: prediction and characterization of the luminescence of Pr3+-doped LiYF4†
Harry
Ramanantoanina
*a,
Werner
Urland
a,
Benjamin
Herden
a,
Fanica
Cimpoesu
b and
Claude
Daul
a
aDepartment of Chemistry of the University of Fribourg, Chemin du Musée 9, 1700 Fribourg, Switzerland. E-mail: harry.ra@hotmail.com; claude.daul@unifr.ch; Fax: +41 26 300 9738; Tel: +41 26 300 8700
bInstitute of Physical Chemistry, Splaiul Independentei 202, Bucharest 060021, Romania. E-mail: cfanica@yahoo.com
First published on 11th February 2015
Abstract
We present a theoretical work detailing the electronic structure and the optical properties of (PrF8)5− embedded in LiYF4, complementing the insight with data that are not available by experimental line. The local distortions due to the embedding of the lanthanide ion in the sites occupied in the periodic lattice by smaller yttrium centres, not detectable in regular X-ray analyses, are reproduced with the help of geometry optimization. Then, based on the local coordination environment, the relation structure–optical properties is constructed by Density Functional Theory computations in conjunction with the ligand field theory analyses (LFDFT) determining the [Xe]4f2 → [Xe]4f15d1 transitions. In previous instances we analysed rather symmetric systems, here facing the complexity of low symmetry cases, treated in the Wybourne ligand field parameterization and in the Angular Overlap Model (AOM) frame. A very important improvement at the AOM level is the consideration of the f–d mixing that brings coupling term of odd–even nature, essential for the realistic description of the asymmetric coordination centres. Furthermore, we introduce now a principle for modelling the emission intensity. The results are in agreement with available experimental findings. The relevance of the modelling has a practical face in the rational design of optimal luminescent materials needed in domestic lightening and also an academic side, revisiting with modern computational tools areas incompletely explored by the standard ligand field theories.
Introduction
The recent award of a Nobel prize for the invention of blue light-emitting diodes1 has enhanced the interest in the role already played and further engineering related to this class of devices. An important application concerns the less consuming lighting. In this case the blue main component should be complemented with wavelengths obtained from coating materials, tuning the light toward the solar day spectrum, the so-called warm-white light. Typical coating materials involve lanthanide ions, like the popular Y3Al5O12 doped with Ce3+,1 taking advantage of the optical properties of the f–d transitions. Briefly described, the active centers for the luminescent coating (the phosphors) absorb high energy photons from the violet or the ultraviolet range of the basic source, the light-emitting diode (LED), undergoing after that a stepwise de-excitation and releasing radiation with smaller energy that contributes to the desired alleviation of the overall emitted spectrum. Several lanthanide ions are good candidates for phosphors, which apart from improving the emission profile, play the role of improving the energy yield, transmuting light from the invisible range to the domain appropriate for human eye sensitivity.The Pr3+ ion is a potential activator for modern LED phosphors. It provides the red emission important for the quest for warm-white LED lighting,2 and its electronic structure enables intriguing optical manifestation, for instance the photon-cascade emission.3–5 The Pr3+-doped LiYF4 is also a well studied system applied for laser materials.6,7 For the design of modern LED phosphors, it is of crucial importance to predict the electronic structure and the relation with optical properties to help the synthesis in laboratories by useful thumb rules. The theoretical modeling brings a better understanding of the microscopic origin of the optical phenomenon. In Pr3+ phosphors, the problem is settled with respect to the ground [Xe]4f2 and the excited [Xe]4f15d1 electron configurations.8 Several quantum chemical methods may in principle be used to tackle the problem.9–11 The Ligand Field Density Functional Theory (LFDFT) approach8 is convenient because of its relative simplicity and the chemical intuitiveness of its results. A plus of transparency is gained using as ligand field part the angular overlap model (AOM),12,13 whose parameters are understandable as well-categorized ligand contributions. Special attention should be devoted to the different rates of the nephelauxetic effect in f versus d shells,14 such details being well tracked along the LFDFT algorithm. One must also point that the LFDFT relies on specific features offered by the Amsterdam Density Functional (ADF) code,15–17 enabling the control of orbital population and generating non-aufbau occupation schemes.
Ligand field theory is based on a phenomenological Hamiltonian (eqn (1)) considering the perturbation of the metal center limited to the basis of the partially filled f or d atomic orbitals.18,19 A two-open-shell ligand field theory, as in our case considering both the f and d shells, is a rather special variety, necessary to develop treatments of the enounced type, dealing with inter-shell spectroscopy. The whole Hamiltonian is built considering three important interactions, such as the inter-electron repulsion (HEE), the ligand field potential (VLF) and the spin–orbit coupling interaction (HSO). The respective interactions are parameterized in terms of the Slater–Condon integrals, the ligand field one-electron part and the spin–orbit coupling constants. Since the inter-electron and spin–orbit part are mostly confined to the free atom modeling, the key role is carried by the ligand field part. The ligand field theory is nowadays useful in multifarious aspects of inorganic chemical science, both in theoretical investigations8,9,11,20–27 as well as experimental work.28,29
| H = H0 + HEE + VLF + HSO, | (1) |
Herein we present a theoretical prediction of the electronic structure and optical properties of LiYF4:Pr3+via LFDFT calculations of the multiplet energy levels arising from the ground [Xe]4f2 and the excited [Xe]4f15d1 electron configurations of Pr3+ in a certain chemical environment. We validate the theoretical model taking into account aspects from several experimentally available investigations. Furthermore we include an intensity determination based on zero-phonon lines, advancing toward a more realistic description and simulation of the optical features.
Methodology
In this work, the DFT calculations have been carried out by means of the ADF program package (ADF2013.01).15–17 We use the hybrid B3LYP functional, as it is implemented in the ADF program package15–17 for the exchange and correlation energy and potential, to compute the electronic structure and the related optical properties, in line with previous work.8 However we use the pure local density approximation (LDA) functional and the generalized gradient approximation (GGA) functional for the geometry optimization. The molecular orbitals are expanded using triple-zeta plus two polarization Slater-type orbital (STO) functions (TZ2P+) for the Pr atom and triple-zeta plus one polarization STO function (TZP) for the F, Y and Li atoms. The LFDFT designates computation experiments and post-calculation analyses meant to exploit the DFT calculations in the sense of ligand field theory. This is possible in codes allowing the handling of orbital and spin occupations, generating non-aufbau occupation schemes. The artificial configurations can be regarded in a manner similar to Broken-Symmetry (BS) DFT procedures in relation to the estimation of exchange coupling effects: the BS-DFT configurations are not real states but are objects from where parametric information can be extracted.30–32 The LFDFT implies generating different configurations inside a DFT calculation engine, treated non-iteratively on the basis of orbitals obtained in the conditions of the so-called Average-of-Configuration (AOC) type calculation, followed by the fit of the numeric results in accordance with the Ligand Field master formula in the given frame of the assumed parametric scheme.18,19,27 The states are not excited states, but artificial determinants containing the needed information. The AOC consists in imposing fractional occupation numbers on molecular orbitals assigned to d or f parentage, by smearing to n/5 and m/7, respectively, the electron count of dn, fm or dnfm configurations. Considering that fractional occupations are allowed in DFT,33 the AOC produces optimized orbitals closer to the ligand field meaning, where a spherically averaged reference is assumed especially in the account of two-electron terms by the use of Slater–Condon parameters in a formalism resembling the free ion case.The non-doped crystal structure from the X-ray diffraction data of the LiYF4 is obtained from ref. 34. Then, a Pr3+ ion is introduced, replacing one Y3+ ion. The geometry of the doped system is hardly obtained from the experimental studies. In turn it can be simulated by means of the periodical crystal structure approach based on a super-cell model.35,36 A geometry optimization based on the molecular cluster approach can also be considered requiring a specific restricted region of the crystal structure. This molecular cluster approach of the local crystal environment may look modest with respect to geometry optimization goals. However in previous instances35 we found that it reproduces well the full super-cell band structure calculations.35 The molecular cluster procedure is demanded by a special branch of treatment, concerning the geometries of excited state configurations, which so far cannot be addressed by common band structure algorithms. This gives further insight into the investigation of vibronic coupling effects37,38 or Stokes shift.39
From the crystal structure of LiYF4,34 we pick one Y3+ center together with any chemical elements located inside the sphere of constant radius of 4.5 Å around this center. This yields a cluster of thirty-seven atoms, i.e. five Y3+, eight Li+ and twenty-four F−, where the global charge is exactly −1. The small negative charge is a compromise for keeping the cluster at an initial symmetry corresponding to the yttrium-site, since adding a further lithium ion, for instance to bring neutrality, will introduce a bias into the optimization procedure. In the cluster model, the central Y3+, which will be doped with Pr3+, is eight-fold coordinated by fluoride ligands whereas for the remaining four Y3+ ions only six ligands are included because of charge compensation. The eight Li+ ions are on the other hand coordinated by two fluoride ligands. A graphical representation of this cluster is given in Fig. 1. The geometry optimization proceeds separating the cluster (Fig. 1a) in two distinct regions: one moiety (Fig. 1b) where the geometry optimization is performed and another one (Fig. 1c) whose coordinates are kept frozen to the experimental crystal structure. In this way we focus our interest only in the local changes of the structure of (PrF8)5− embedded in LiYF4. We use the structure of (PrF8)5− obtained in this geometry optimization as input for the determination of the electronic structure and properties we are looking for. We use the methodology illustrated in ref. 8 taking as basis 231 Slater-Determinants energies from the ground [Xe]4f2 (91 microstates) and the excited [Xe]4f15d1 (140 microstates) configurations of Pr3+. The ligand field potential (VLF) is fitted from these Slater-Determinants energies and the Δ(fd) parameter is the difference of the barycenters of the energies of the Slater-Determinants of the excited [Xe]4f15d1 and the ground [Xe]4f2 configurations. This Δ(fd) parameter is algebraically evaluated in the following:
| Δ(fd) = hd − hf + F0(fd) − F0(ff) + B00(d) − B00(f), | (2) |
The Slater–Condon Fk(ff), Fk(fd) and Gk(fd) (k ≠ 0) parameters are obtained from the radial functions of the 4f and 5d Kohn–Sham orbitals of Pr3+ according to eqn (3)–(5), respectively, whose procedure is already described in ref. 36.
 | (3) |
 | (4) |
 | (5) |
The spin–orbit coupling constants ζ4f and ζ5d are calculated using the approach of ZORA relativistic available in the ADF program package.15–17
Results and discussion
Before entering into the ligand field problem, the simulated geometry of the (YF8)5− fragment embedded in LiYF4 is discussed. The LiYF4 crystallizes in the I41/a (No. 88) space group, where the Wyckoff position of the yttrium-site has a S4 environment. In this S4 coordination, the eight fluoride ligands surrounding the Y3+ are four by four identical (Fig. 1b). Their symmetry distinct ligand coordinates can be generated by six polar coordinates, d1, θ1, ϕ1, d2, θ2 and ϕ2, whose experimental values are given in Table 1, collected from ref. 40 and 41. A geometry optimization of (YF8)5− embedded in LiYF4 is performed by means of DFT calculations, based on different exchange and correlation functionals, i.e. the LDA: Xα42 and Vosko–Wilk–Nussair (VWN)43 as well as the GGA: Becke–Perdew (BP86)44,45 and PW91.46 We proceed in this way to make explicit which DFT functional is better appropriate for the structural determination. Table 1 reports the values of the experimental and calculated structures using polar coordinates representation. In general, the deviations with the experimental data are rather small considering the four DFT functionals (Table 1). We can discriminate the influence of the DFT setting in reporting a slight elongation of the Y–F bond lengths using the GGA formalism, i.e. BP86 and PW91 (Table 1). However the calculations based on the LDA formalism, i.e. Xα and VWN, offer the best match to the experimental results (Table 1), a fact that has been already recognized before.35,47| (YF8)5− | (PrF8)5− | |||||
|---|---|---|---|---|---|---|
| Exp.a | Xα | VWN | BP86 | PW91 | VWN | |
| a These values are taken from ref. 40 and 41. b dev. (in Å) stands for the calculated mean deviations between the optimized structure (Cartesian coordinates) of (YF8)5− and the experimental data. | ||||||
| d 1 | 2.246 | 2.2479 | 2.2468 | 2.2650 | 2.2565 | 2.3425 |
| θ 1 | 67.05 | 66.58 | 66.57 | 66.31 | 66.44 | 65.62 |
| ϕ 1 | −33.00 | −35.79 | −35.68 | −36.81 | −36.76 | −37.86 |
| d 2 | 2.293 | 2.3031 | 2.3012 | 2.3217 | 2.3234 | 2.3967 |
| θ 2 | 142.03 | 139.34 | 139.39 | 138.54 | 138.63 | 137.39 |
| ϕ 2 | −36.59 | −36.51 | −36.59 | −36.06 | −35.92 | −36.18 |
| dev.b | — | 0.1900 | 0.1831 | 0.2650 | 0.2628 | — |
We consider explicitly here the VWN functional for any structural determination. Therefore the structure of (PrF8)5− embedded in LiYF4 is determined and the coordinates are presented in Table 1. It is worth mentioning that while the (YF8)5− is a closed-shell cluster, the (PrF8)5− has an open-shell electronic structure due to the presence of two valence electrons in the 4f orbitals of Pr3+, leading to a non-trivial issue in the optimization of the geometry. The rational way is to impose the average of configuration (AOC) type calculation,48–50i.e. equal smearing of the two valence electrons into the seven-fold 4f orbitals of Pr3+, amending the tedious issue due to possible divergence in the self-consistent field (SCF) electronic structure. This is in line with the conceptual frame of ligand field theory, relying on an averaged reference which is fully equivalent, in technical respects, to the AOC procedure. Moreover the 4f orbitals being shielded by the outer shells in the lanthanide system, the 4f electrons are not participating in the chemical bonding. Thus a specific population of the two electrons in the 4f orbitals will not affect the geometry of (PrF8)5− like it is explicitly stated in ref. 35 for the case of Ce3+ compounds. We specifically notice an elongation of the Pr–F bond lengths, although the polar and azimuthal angles remain similar to the (YF8)5− (Table 1), in agreement with the Shannon radii51 of Pr3+ and fluoride ligand in such an eight coordination.
The LFDFT treatment is performed on the cluster (PrF8)5− according to the structure given in Table 1, where the positions of the next nearest neighbouring Li+ and Y3+ ions (Fig. 1) are used as point charges to neutralize the high negative charge of the cluster. The ligand field treatment works on the basis of LMLSMS microstates and solves the complete [Xe]4f2 and [Xe]4f15d1 matrix interactions corresponding to the ground and excited electron configurations of Pr3+, respectively. The atomic spectral terms of the ground [Xe]4f2 electron configuration are 1S, 3P, 1D, 3F, 1G, 3H and 1I, whose total number of microstates equals 91. The atomic spectral terms of the excited [Xe]4f15d1 electron configuration are composed by the low spin 1P, 1D, 1F, 1G and 1H as well as the high spin 3P, 3D, 3F, 3G and 3H, whose total number of microstates equals 140. In total, we consider here 231 states. The inter-electron effects are accounted by the Slater–Condon parameters: F2(ff), F4(ff) and F6(ff) for the [Xe]4f2 configuration and F2(fd), F4(fd), G1(fd), G3(fd) and G5(fd) for the [Xe]4f15d1 configuration.52 The corresponding values are calculated from the radial functions of the 4f and 5d Kohn–Sham orbitals of Pr3+ (Fig. 2) using eqn (3)–(5).36
The spin–orbit coupling constants ζ4f and ζ5d are estimated by relativistic calculations, as described in the previous section.
The ligand field interaction is expressed on the basis of the merged 4f and 5d atomic orbitals using a twelve by twelve ligand field matrix elements, which can be represented using either the AOM12,13 formalism or the Wybourne-normalized crystal field parameters.53 The afore-mentioned parameters are theoretically evaluated by means of the LFDFT and compared with available experimental data listed in Table 2.
| # | (PrF8)5− | ||
|---|---|---|---|
| Exp. | Calc. | ||
| a These parameters are taken from ref. 55. b The Δ(fd) represents the difference of the barycentres of the energy between the multiplet levels from the [Xe]4f15d1 and [Xe]4f2 configuration of Pr3+. It is listed for clarity being replaced by the ΔAOM(fd).54 c We refer to the parameters given for the optical measurement reported in ref. 40. d We refer to ref. 40 and use the ratios eσ(f)/eπ(f) = 5.34, eσ,1(f)/eσ,2(f) = (d1/d2)7 and eπ,1(f)/eπ,2(f) = (d1/d2)7 given there. e We consider the Wybourne parameters in ref. 55 and transform them to AOM using the coordinates of (PrF8)5− in Table 1. | |||
| 1 | F 2(ff) | 306.78a | 323.49 |
| 2 | F 4(ff) | 46.45a | 42.24 |
| 3 | F 6(ff) | 4.53a | 4.51 |
| 4 | F 2(fd) | 216.22a | 209.54 |
| 5 | F 4(fd) | 16.33a | 16.35 |
| 6 | G 1(fd) | 276.49a | 294.54 |
| 7 | G 3(fd) | 26.57a | 27.31 |
| 8 | G 5(fd) | 4.28a | 4.36 |
| 9 | ζ 4f | 750.1a | 736.26 |
| 10 | ζ 5d | 1149a | 944.66 |
| 11 | Δ(fd) | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966a,b 966a,b |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943b 943b |
| Δ AOM(fd) | — | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 734 |
|
| 12 | e σ,1(f) | 552c | 533 |
| 13 | e π,1(f) | 103c,d | 226 |
| 14 | e σ,2(f) | 473c,d | 488 |
| 15 | e π,2(f) | 88c,d | 192 |
| 16 | e σ,1(d) | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639e 639e |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 171 |
| 17 | e π,1(d) | 3482e | 2575 |
| 18 | e σ,2(d) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512e 512e |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
| 19 | e π,2(d) | 4875e | 3314 |
| 20 | e σ,1(fd) | — | 1864 |
| 21 | e π,1(fd) | — | 850 |
| 22 | e σ,2(fd) | — | 1534 |
| 23 | e π,2(fd) | — | 244 |
The nephelauxetic effect denominates the reduction of the Slater–Condon parameters from the free ion to the coordinated Pr3+.14 It is characterized by the expansion of the electron cloud toward the ligand atoms shown in Fig. 2. A weak nephelauxetic effect is observed for the 4f electrons (Fig. 2). Sed contra, the change in the 5d radial function from the free ion to (PrF8)5− is much more pronounced, leading to a sensible nephelauxetic reduction of the inter-electron parameters. The ligand field part is presented in Table 2 according to the AOM formalism. In the AOM, the ligand field interaction becomes a summation over individual interactions between the Pr3+ and each ligand entity. This interaction possesses a σ, π, δ and φ bonding nature with the 4f as well as the 5d orbitals (Fig. 3), which is characterized by the AOM eσ, eπ, eδ and eφ parameters. Nevertheless eδ and eφ are by convenience neglected being engulfed in the eσ and eπ parameters.54 In the explicit case of (PrF8)5− embedded in LiYF4, we consider two sets of parameters appropriate to each group of four fluoride ligands being symmetrized in S4. Thus we obtain eσ,1(f), eπ,1(f), eσ,2(f) and eπ,2(f) perturbation of the 4f; eσ,1(d), eπ,1(d), eσ,2(d) and eπ,2(d) perturbation of the 5d; and eσ,1(fd), eπ,1(fd), eσ,2(fd) and eπ,2(fd) perturbation in a second order due to a mixing between the 4f and the 5d orbitals in S4 symmetry. The idea to establish the ligand field with respect to the AOM results is the fact that the AOM are intuitive parameters, which can be transferred to comparable systems. Recently we constructed the extension of the AOM for two-open-shell f and d electrons.54 Because the AOM matrices are not non-traceless, as usual ligand field parameterization, it is convenient to redefine a new energy gap ΔAOM(fd) instead of Δ(fd),54 which for clarity is also listed in Table 2. The ligand field Hamiltonian (eqn (1)) operates in total with twenty-three parameters (Table 2). The computed parameters are compared to experimental measurements, due to the previous work of Urland40 and Reid et al.,55 who have used parameters to fit their experimental spectra of LiYF4:Pr3+. Note however that experimental values for the mixed 4f/5d-type AOM parameters are not provided, since they are not found in the literature. The calculated parameters are in general of the order of magnitude of the experimental values (Table 2), apart from discrepancies originating from the self-consistent error in the DFT setting.
 | ||
| Fig. 3 Graphical representation of the 4f-type (left-hand-side) and 5d-type (right-hand-side) AOM parameters. | ||
More explicitly, the F2(ff) and G1(fd) parameters are overestimated if compared to the experimental values, while the F4(ff) and the F2(fd) are underestimated, aspects that are already visible in earlier investigations.8,39,54 The 4f-type AOM parameters are particularly overestimated in the π-interaction (Table 2), depending on the choice of the exchange and correlation functional in the DFT setting. This does underpin the motivation of using a hybrid functional along the LFDFT8 although the pure functional performed better in the geometry optimization. Table 3 shows the multiplet energy levels corresponding to the 3H ground state of the ground [Xe]4f2 electron configuration of Pr3+ in LiYF4:Pr3+. Under the influence of the spin–orbit coupling, the 3H splits over 3H4, 3H5 and 3H6 terms, whose total number of microstates equals 9, 11 and 13, respectively. These terms are then split into ligand field components according to a, b and e irreducible representations (irreps) of the S4 point group (Table 3). A good qualitative agreement between the experimentally observed energy levels56 and the non-empirical calculated ones is observed (Table 3). The deviation is evaluated, in least mean squares, about 17 cm−1, which is mostly due to the misrepresentation of the eπ,1(f) and eπ,2(f) parameters by the non-empirical calculation. On the other hand, the calculation underestimates the 5d-type AOM parameters in the π-interaction (Table 2). The ligand field splitting of the 5d orbitals, which confers the most important interaction within the [Xe]4f15d1 configuration of Pr3+, deserves a special attention. In LiYF4:Pr3+, the splitting pattern of the five-fold 5d orbitals of Pr3+ follows the representations b, a, e and b of the S4 point group. Following the Wybourne formalism,53 three parameters are taken into consideration such as B20(d), B40(d) and B44(d) since the B4−4(d) is the complex conjugate of the analogue B44(d). The first two parameters are by definition real, whereas the third one is complex. It is possible to retrieve a real value of B44(d) by forcing the cluster to belong to the higher D2d point group, as it is already observed in other studies.9,55,57 Taking the AOM (Table 2), we calculate (in cm−1) 3256, −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 and −23
626 and −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576 + i13
576 + i13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410, respectively for B20(d), B40(d) and B44(d). The diagonalization of the ligand field potential (VLF) yields the eigenvalues and the associated normalized eigenvectors (Table 4). The coefficients which appear in these eigenvectors are complex numbers specific to the basis of the one-electron ligand field matrix |l,ml〉, i.e. the merged 4f (l = 3) and 5d (l = 2) atomic orbitals. In the explicit case of the 5d ligand field, the results are numerically given in Table 4, represented with respect to the Wybourne formalism. We use the indices (ξ and η) to differentiate between the components of the two-fold degenerate eigenvalues of e symmetry and (ε and ζ) between the two distinct eigenvalues belonging to the same b irrep. For these latter ones, the eigenvectors in case of enforcement to D2d coordination of Pr3+ can be determined analytically by symmetry adapted linear combination of the |2,+2〉 and the |2,−2〉 basis functions within a symmetrical (eqn (6)) and anti-symmetrical (eqn (7)) composition. Note however that the expressions in eqn (6) and (7) are no longer retrieved in the actual S4 coordination of Pr3+ (Table 4) and help for a better visibility of the eigenvectors given in Table 4.
410, respectively for B20(d), B40(d) and B44(d). The diagonalization of the ligand field potential (VLF) yields the eigenvalues and the associated normalized eigenvectors (Table 4). The coefficients which appear in these eigenvectors are complex numbers specific to the basis of the one-electron ligand field matrix |l,ml〉, i.e. the merged 4f (l = 3) and 5d (l = 2) atomic orbitals. In the explicit case of the 5d ligand field, the results are numerically given in Table 4, represented with respect to the Wybourne formalism. We use the indices (ξ and η) to differentiate between the components of the two-fold degenerate eigenvalues of e symmetry and (ε and ζ) between the two distinct eigenvalues belonging to the same b irrep. For these latter ones, the eigenvectors in case of enforcement to D2d coordination of Pr3+ can be determined analytically by symmetry adapted linear combination of the |2,+2〉 and the |2,−2〉 basis functions within a symmetrical (eqn (6)) and anti-symmetrical (eqn (7)) composition. Note however that the expressions in eqn (6) and (7) are no longer retrieved in the actual S4 coordination of Pr3+ (Table 4) and help for a better visibility of the eigenvectors given in Table 4.
 | (6) |
 | (7) |
| # | (PrF8)5− | |||
|---|---|---|---|---|
| Terms | Level | Exp.a | Calc. | |
| a Taken from ref. 56. | ||||
| 1 | 3H4 | B | 0 | 0 |
| 2, 3 | E | 79 | 75 | |
| 4 | A | 220 | 392 | |
| 5 | A | — | 420 | |
| 6 | A | — | 467 | |
| 7, 8 | E | 496 | 491 | |
| 9 | B | — | 503 | |
| 10, 11 | 3H5 | E | 2272 | 2255 |
| 12 | A | 2253 | 2264 | |
| 13 | B | 2280 | 2265 | |
| 14 | A | 2297 | 2331 | |
| 15, 16 | E | 2341 | 2490 | |
| 17 | B | 2549 | 2541 | |
| 18 | A | — | 2578 | |
| 19, 20 | E | — | 2579 | |
| 21 | 3H6 | B | 4314 | 4331 |
| 22 | A | — | 4361 | |
| 23, 24 | E | 4394 | 4369 | |
| 25 | B | — | 4441 | |
| 26, 27 | E | 4454 | 4470 | |
| 28 | A | 4486 | 4665 | |
| 29 | B | 4557 | 4678 | |
| 30 | A | — | 4818 | |
| 31, 32 | E | 4907 | 4828 | |
| 33 | B | 4945 | 4853 | |
| (PrF8)5− | ||
|---|---|---|
| Calc. | Eigenvectors | |
| |2,bε〉 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 626 |
(0.6147 − i0.3496)|2,−2〉 + 0.7071|2,+2〉 − (0.0019 + i0.0005)|3,0〉 |
| |2,a〉 | −6072 | 0.9990|2,0〉 + (0.0091 + i0.0306)|3,−2〉 + (0.0091 − i0.0306)|3,+2〉 |
| |2,eη〉 | 4850 | 0.7152|2,−1〉 + (0.4704 − i0.5161)|2,+1〉 − (0.0070 + i0.0115)|3,−3〉 − (0.0135 + i0.0026)|3,+3〉 + (0.0141 − i0.0053)|3,−1〉 + (0.0131 − i0.0067)|3,+1〉 |
| |2,eξ〉 | 4850 | 0.7107|2,−1〉 − (0.4639 − i0.5281)|2,+1〉 + (0.0068 − i0.0117)|3,−3〉 − (0.0134 + i0.026)|3,+3〉 + (0.0140 − i0.0053)|3,−1〉 − (0.0131 − i0.0070)|3,+1〉 |
| |2,bζ〉 | 8997 | 0.7067|2,−2〉 − (0.6142 + i0.3494)|2,+2〉 + (0.0090 − i0.0341)|3,0〉 |
The eigenvectors (Table 4) contain small implications of the 4f orbitals caused by the 4f/5d-type AOM parameters (Table 2), which have to be taken into account in the calculation for a realistic simulation of the electronic structure of (PrF8)5− embedded in LiYF4. The splitting of the energy of the 5d orbitals (Table 4) is in line with what can be deduced from experiment.55
Addressing a trustable simulation of the f–d transitions in lanthanide compounds is a challenging problem in computational chemical science. Ligand field theory operated along the non-empirical DFT offers here a promising approach, since a perfect match between the non-empirical parameters and the experimental results might be experienced. There is another aspect making the theoretical consideration very important, when characterizing experimentally observed excitation and emission spectra. An empirical fit to the experimental spectrum with respect to the ligand field theory requires in low symmetry cases a large number of independent parameters.58 The treatment of the present S4 coordination of the Pr3+ ion is still possible: twenty-three parameters (Table 2). However, in the case of no symmetry, the experimental fit is not affordable, having a total of ninety free parameters. In such a situation the computational counterpart offers valuable guidelines in contouring the relative values of the parametric scheme. We use the calculated data from Table 2 to parameterize the ligand field Hamiltonian (eqn (1)), the eigenvalues of which relate the multiplet energy levels arising from [Xe]4f2 and the [Xe]4f15d1 configurations of Pr3+ in LiYF4:Pr3+. These eigenvalues are graphically represented in Fig. 4 using different colours. The corresponding numerical values are given in the ESI.† The excitation [Xe]4f2 → [Xe]4f15d1 and the emission [Xe]4f15d1 → [Xe]4f2 are allowed electric dipole transitions. The matrix elements of the electric dipole moment operator are determined using the vector coupling basis,52 from which the radiative transition probability based on zero-phonon lines (Fig. 4, in black) is determined as proportional to the 4f–5d mixing. From Fig. 4, the [Xe]4f15d1 configuration is characterized by three dominant bands, in line with the experimental excitation spectrum given by Reid et al.55
 | ||
| Fig. 4 Calculated multiplet energy levels from the [Xe]4f2 (in blue) and [Xe]4f15d1 (in red) configurations of Pr3+ in LiYF4:Pr3+ (see also the ESI†) together with the intensities of the excitation [Xe]4f2 → [Xe]4f15d1 transitions, i.e. zero-phonon lines (in black). The green curve represents a superimposition of a Gaussian band with a width of 1000 cm−1 on the zero-phonon lines. | ||
This does not directly reflect the splitting of the 5d orbitals shown in Table 4, where four bands would be expected, because the fourth band is less resolved due to the small energy difference calculated between the double degenerate |2,e〉 and the |2,bζ 〉 states (Table 4). In a strict numerical simulation, we can tune the influence of all the parameters in Table 2 by setting some values of them to zero and seeing the change in Fig. 4. We find out that the excitation transitions (Fig. 4) are not only due to the ligand field splitting of the 5d orbitals but also to a subtle influence of the spin–orbit coupling in the 4f electrons. On the other hand the spin–orbit coupling of the 5d electrons and the ligand field of the 4f orbitals have a weak effect.
Besides the general lighting applications, the multiplet energy levels of Pr3+a priori favour a quantum cutting process by possible photon cascade emissions from the [Xe]4f15d1 to the [Xe]4f2 levels.3–5 The quantum cutter exhibits a two or more photon luminescence process, where at least two low energy photons are emitted per one high energy photon absorbed.3–5 Therefore, quantum efficiencies larger than 100% are achievable, which was already demonstrated in the literature.3–5,59,60 This optical manifestation is possible because of the energy gap between the [Xe]4f2 and the [Xe]4f15d1 multiplets. Pr3+ doped into fluoride hosts mostly achieves such a phenomenon. A systematic review of the quantum cutting process in general is recently available.61 Unfortunately in the present LiYF4:Pr3+ case, there is no energy gap observed between the [Xe]4f2 (Fig. 4, in blue) and the [Xe]4f15d1 (Fig. 4, in red) manifolds, i.e. the multiplet levels arising from the [Xe]4f15d1 configuration overlap those from the [Xe]4f2 (see Fig. 4). Therefore, the LiYF4:Pr3+ system is not a quantum cutter, in agreement with the earlier experimental observations,62 where the observed emission spectrum is dominated by the inter-configuration [Xe]4f15d1 → [Xe]4f2 transitions in the spectral range of 200 nm and 400 nm. A simulation of the emission spectrum is possible, taking advantage of the dipole allowed f–d transitions. This simulation of the emission [Xe]4f15d1 → [Xe]4f2 is done by taking into account a change of the geometry of (PrF8)5− embedded in LiYF4 in the excited configuration. Although apparently counter-intuitive, in the excited [Xe]4f15d1 state, the coordination bond lengths and implicitly the overall ligand field strength are higher than in the [Xe]4f2 ground configuration. We encountered and discussed such a situation in our precedent work35 analyzing the octahedral cluster (CeCl6)3−. A similar behavior is expected in the actual Pr3+ system. The situation is due to the fact that the bonding regime in lanthanide complexes is mainly ensured by the 5d orbitals,63,64 which behave as acceptors for the lone pairs of the ligands, while the 4f shell is too shielded to play an effective role (outside the pure electrostatics of the whole lanthanide body). The promotion of one electron in the 5d virtuals enhances their bonding capability, by an increment in the nephelauxetic effect, favorable to the overlap with the environment. Consequently, a surge of electron population of the empty 5d orbitals results in shortening of the lanthanide–ligand bond lengths. Considering again the DFT geometry optimization based on the molecular cluster approach (Methodology section), we work with the excited [Xe]4f15d1 configuration of Pr3+ in the system (PrF8)5− embedded in LiYF4. In this respect, the optimized structure of (PrF8)5− in Table 1 is taken, then the electron population of the orbitals is changed inasmuch as one electron is evenly distributed amongst the seven-fold 4f orbitals and the other one is placed in the lowest energy |2,bε〉 component of the 5d orbitals (Table 4). We let the structure to relax following the totally symmetric displacements of (PrF8)5− in its S4 coordination, according to the procedure described in the methodology section within the constrained electronic structure. We obtain by means of the VWN functional the following coordinates using the same representation as Table 1:
| d1 = 2.2881 Å, θ1 = 66.33° and ϕ1 = −37.63°; |
| d2 = 2.3394 Å, θ2 = 138.09° and ϕ2 = −35.05°, |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309, eπ,1(d) = 2219, eσ,2(d) = 10
309, eπ,1(d) = 2219, eσ,2(d) = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 and eπ,2(d) = 3971, leading to an enlargement of the gap between higher and lower values of the 5d-type ligand field eigenvalues. This is seen when comparing excited state values of the ligand field potential (in cm−1): −14
226 and eπ,2(d) = 3971, leading to an enlargement of the gap between higher and lower values of the 5d-type ligand field eigenvalues. This is seen when comparing excited state values of the ligand field potential (in cm−1): −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080, −5960, 4832 and 10
080, −5960, 4832 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 376, respectively for the |2,bε〉, |2,a〉, |2,e〉 and |2,bζ〉 levels with the quantities from Table 4. The 5d-type AOM parameters in the excited-state case are slightly but firmly higher than the ground-state ones, except the case of the eπ,1(d) value which shows a reverse change. Since in this case the used four parameters are uniquely determined from the four energy spacings of the relative 5d-type ligand field scheme, the effect is not a numerical ambiguity, being however difficult to understand. Tentatively, we can assign the slight lapse to a general drawback of the ligand field schemes in surroundings without the inversion center, namely the so-called holohedrization effect.67 In this conjuncture, a certain artificial compensation may appear between eπ,1(d) and eπ,2(d) values. However, we will not advance here to the further discrimination of possible subtle parameterization issues. Since the whole ligand field strength goes towards the noticed intensification in the excited-state, the particular situation of the eπ,1(d) value does not impinge upon the general conclusion about enhanced covalency along with the promotion of one electron in the 5d-type virtuals of the lanthanide coordination spheres. The other parameters (Table 2) are less influenced, as expected and proved by the LFDFT calculation (see also the ESI†). The emission lines originating from the lowest [Xe]4f15d1 state of Pr3+ in LiYF4:Pr3+ are given in Fig. 5. In line with the experimental observation,62 the inter-configuration [Xe]4f15d1 → [Xe]4f2 transitions are mainly in the ultraviolet spectral range, where the most intense is [Xe]4f15d1 → [Xe]4f2 (3H) (Table 3).
376, respectively for the |2,bε〉, |2,a〉, |2,e〉 and |2,bζ〉 levels with the quantities from Table 4. The 5d-type AOM parameters in the excited-state case are slightly but firmly higher than the ground-state ones, except the case of the eπ,1(d) value which shows a reverse change. Since in this case the used four parameters are uniquely determined from the four energy spacings of the relative 5d-type ligand field scheme, the effect is not a numerical ambiguity, being however difficult to understand. Tentatively, we can assign the slight lapse to a general drawback of the ligand field schemes in surroundings without the inversion center, namely the so-called holohedrization effect.67 In this conjuncture, a certain artificial compensation may appear between eπ,1(d) and eπ,2(d) values. However, we will not advance here to the further discrimination of possible subtle parameterization issues. Since the whole ligand field strength goes towards the noticed intensification in the excited-state, the particular situation of the eπ,1(d) value does not impinge upon the general conclusion about enhanced covalency along with the promotion of one electron in the 5d-type virtuals of the lanthanide coordination spheres. The other parameters (Table 2) are less influenced, as expected and proved by the LFDFT calculation (see also the ESI†). The emission lines originating from the lowest [Xe]4f15d1 state of Pr3+ in LiYF4:Pr3+ are given in Fig. 5. In line with the experimental observation,62 the inter-configuration [Xe]4f15d1 → [Xe]4f2 transitions are mainly in the ultraviolet spectral range, where the most intense is [Xe]4f15d1 → [Xe]4f2 (3H) (Table 3).
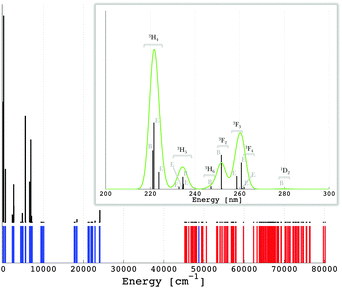 | ||
| Fig. 5 Calculated multiplet energy levels from the [Xe]4f2 (in blue) and [Xe]4f15d1 (in red) configurations of Pr3+ in LiYF4:Pr3+ (see also the ESI†) together with the intensities of the emission [Xe]4f15d1 → [Xe]4f2 transitions, i.e. zero-phonon lines (in black). The energy region showing the maximum emission transitions is magnified and represented in units of wavelength (nm). The green curve represents a superimposition of a Gaussian band with a width of 2 nm on the emission lines. | ||
Conclusions
In the beginning of the twenty first century, many governments inclined towards the phase-out of the incandescent light bulbs, which have lightened the world for over 100 years since their first development by Edison. This corresponds to the effort to diminish nowadays considerable energy demand. Therefore the progress toward modern domestic lighting will focus in the future on how efficiently the energy will be consumed. Light emitting diode (LED) bulbs are amongst the light source alternatives and offer a bunch of advantages, due to the interesting optical properties exhibited by some lanthanide phosphors.In the perspective that the theory can help the experiment in finding the optimal materials by identifying clue parameters on a first principle route, we have drawn some points on this line of the structure–property correlations, potentially serving material engineering. The model relevant for the calculation of the optical properties of lanthanide compounds is based on the phenomenological Hamiltonian adjusted from the ligand field theory. It is demonstrated that using standard quantum chemistry tools, e.g. Density Functional Theory (DFT), the parameterization of the ligand field effective Hamiltonian can be obtained in a very efficient way. The obtained parameters are in principle transferable to other systems of similar nature, further investigation being necessary for the complete charting of all the lanthanide–ligand couples acting as potential candidates for phosphor materials.
In this work, we have determined by means of DFT calculations the multiplet energy levels arising from the ground [Xe]4f2 and excited [Xe]4f15d1 electron configurations of Pr3+ in the two-open-shell problem encountered in the system LiYF4:Pr3+. The treatment of the local distortions due to the presence of the Pr3+ impurity in LiYF4 is addressed by standard geometry optimization, circumventing the use of band structure algorithms and gaining aspects demanded by a pure chemical vision like the geometry in the excited states. The parametric scheme offered by ligand field theory is used to provide a chemical intuitiveness of the non-empirical investigation. The calculated parameters are therefore compared to available experimental results collected also here for the purpose of the work. A qualitative agreement between the non-empirical investigation and the experimental findings is stated, allowing the prediction of the luminescence of LiYF4:Pr3+ in the frame of 4f and 5d electrons. The experimentally observed excitation and emission spectra are theoretically reproduced here, enabling a better understanding of the optical phenomenon and a good connection between spectroscopy studies and theoretical investigations in inorganic chemical science.
Acknowledgements
This work is supported by the Swiss National Science Foundation (SNF) and the Swiss State Secretariat for Innovation and Research. Support from the UEFISCDI Romania research grant PCE 14/2013 is also acknowledged.Notes and references
- S. Nakamura and G. Fasol, The Blue Laser Diode, Springer, Berlin, 1997 Search PubMed.
- T. Jüstel, H. Nikol and C. Ronda, Angew. Chem., Int. Ed., 1998, 37, 3084 CrossRef.
- J. L. Sommerdijk, A. Bril and A. W. de Jager, J. Lumin., 1974, 8, 341 CrossRef CAS.
- W. W. Piper, J. A. DeLuca and F. S. Ham, J. Lumin., 1974, 8, 344 CrossRef CAS.
- R. T. Wegh, H. Donker, K. D. Oskam and A. Meijerink, Science, 1999, 29, 663 CrossRef.
- A. Richter, E. Heumann, E. Osiac, G. Huber, W. Seelert and A. Diening, Opt. Lett., 2004, 29, 2638 CrossRef CAS.
- T. Gün, P. Metz and G. Huber, Appl. Phys. Lett., 2011, 99, 181103 CrossRef PubMed.
- H. Ramanantoanina, W. Urland, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2013, 15, 13902 RSC.
- M. D. Faucher and O. K. Moune, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 4150 CrossRef CAS.
- M. Krosnicki, A. Kedziorski, L. Seijo and Z. Barandiaran, J. Phys. Chem. A, 2014, 118, 358 CrossRef CAS PubMed.
- P. A. Tanner, C. S. K. Mak and M. D. Faucher, J. Chem. Phys., 2001, 114, 10860 CrossRef CAS PubMed.
- C. Schäffer and C. Jørgensen, Mol. Phys., 1965, 9, 401 CrossRef.
- W. Urland, Chem. Phys., 1976, 14, 393 CrossRef CAS.
- P. A. Tanner and Y. Y. Yeung, J. Phys. Chem. A, 2013, 117, 10726 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. F. Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 CAS.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Berces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. F. Guerra, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Koostra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodriguez, P. Ros, P. R. T. Shipper, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Sola, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Vissher, O. Visser, F. Wang, T. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yarkolev, ADF2013.01, available at http://www.scm.com Search PubMed.
- J. S. Griffith, The Theory of Transition Metal Ions, Cambridge University Press, Cambridge, 1961 Search PubMed.
- B. N. Figgis and M. A. Hitchman, Ligand Field Theory and its Applications, Wiley-VCH, New York, 2000 Search PubMed.
- B. R. McGarvey and J. Telser, Inorg. Chem., 2012, 51, 6000 CrossRef CAS PubMed.
- M. Atanasov, P. Surawatanawong, K. Wieghardt and F. Neese, Coord. Chem. Rev., 2013, 257, 27 CrossRef CAS PubMed.
- F. Cimpoesu, N. Dragoe, H. Ramanantoanina, W. Urland and C. Daul, Phys. Chem. Chem. Phys., 2014, 16, 11337 RSC.
- J. Paulovic, F. Cimpoesu, M. Ferbinteanu and K. Hirao, J. Am. Chem. Soc., 2004, 126, 3321 CrossRef CAS PubMed.
- M. Ferbinteanu, T. Kajiwara, K.-Y. Choi, H. Nojiri, A. Nakamoto, N. Kojima, F. Cimpoesu, Y. Fujimura, S. Takaishi and M. Yamashita, J. Am. Chem. Soc., 2006, 128, 9008 CrossRef CAS PubMed.
- S. Tanase, M. Ferbinteanu and F. Cimpoesu, Inorg. Chem., 2011, 50, 9678 CrossRef CAS PubMed.
- F. Cimpoesu, F. Dahan, S. Ladeira, M. Ferbinteanu and J.-P. Costes, Inorg. Chem., 2012, 51, 11279 CrossRef CAS PubMed.
- M. Atanasov, C. A. Daul and C. Rauzy, Struct. Bonding, 2004, 106, 97 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef CAS PubMed.
- M. F. Reid, F. S. Richardson and P. A. Tanner, Mol. Phys., 1987, 60, 881 CrossRef CAS.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131 CrossRef.
- E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297 CrossRef CAS.
- M. Mitani, K. Mori, Y. Takano, D. Yamaki, Y. Yoshioka and K. Yamaguchi, Chem. Phys., 2000, 113, 4035 CAS.
- E. K. U. Gross, L. N. Oliveria and W. Kohn, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 37, 2809 CrossRef CAS.
- E. Garcia and R. R. Ryan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 2053 CrossRef.
- H. Ramanantoanina, W. Urland, A. Garcia-Fuente, F. Cimpoesu and C. Daul, Chem. Phys. Lett., 2013, 588, 260 CrossRef CAS PubMed.
- H. Ramanantoanina, W. Urland, A. Garcia-Fuente, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2014, 16, 14625 RSC.
- I. B. Bersuker, The Jahn-Teller Effect, Cambridge University Press, Cambridge, 2006 Search PubMed.
- I. B. Bersuker and V. Z. Polinger, Vibronic interactions in Molecules and Crystals, Springer-Verlag, Berlin, 1989 Search PubMed.
- W. W. Parson, Modern Optical Spectroscopy, Springer-Verlag, Berlin, 2007 Search PubMed.
- W. Urland, Chem. Phys. Lett., 1981, 77, 58 CrossRef CAS.
- Vishwamittar and S. P. Puri, J. Phys. C: Solid State Phys., 1974, 7, 1337 CrossRef CAS.
- J. C. Slater, Qunatum Theory of Molecules and Solids, McGraw-Hill, NewYork, 1963 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Sing and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- M. T. Yin and M. L. Cohen, Phys. Rev. Lett., 1980, 45, 1004 CrossRef CAS.
- C. Daul, Int. J. Quantum Chem., 1994, 52, 867 CrossRef CAS.
- M. Atanasov, C. Daul and C. Rauzy, Struct. Bonding, 2004, 106, 97 CrossRef CAS.
- I. Ciofini and C. A. Daul, Coord. Chem. Rev., 2003, 238–239, 187 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- R. D. Cowan, The theory of atomic structure and spectra, University of California Press, Berkeley, 1997 Search PubMed.
- S. Hüfner, Optical spectra of transparent rare earth compounds, Academic Press, New York, 1978 Search PubMed.
- H. Ramanantoanina, W. Urland, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2014, 16, 12282 RSC.
- P. S. Peijzel, P. Vergeer, A. Meijerink, M. F. Reid, L. A. Boatner and G. W. Burdick, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 045116 CrossRef.
- L. Esterowitz, F. J. Bartoli, R. E. Allen, D. E. Wortman, C. A. Morrison and R. P. Leavitt, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 6442 CrossRef CAS.
- M. Laroche, J.-L. Doulanm, S. Girard, J. Margerie and R. Moncorgé, J. Opt. Soc. Am. B, 2000, 17, 1291 CrossRef CAS.
- D. J. Newman and B. K. C. Ng, Crystal Field Handbook, Cambridge University Press, Cambridge, 2000 Search PubMed.
- C. Ronda, J. Lumin., 2002, 100, 301 CrossRef CAS.
- B. Herden, A. Meijerink, F. T. Rabouw, M. Haase and T. Jüstel, J. Lumin., 2014, 146, 302 CrossRef CAS PubMed.
- Q. Y. Zhang and X. Y. Huang, Prog. Mater. Sci., 2010, 55, 353 CrossRef CAS PubMed.
- M. Laroche, A. Braud, S. Girard, J.-L. Doualan, R. Moncorgé and M. Thuau, J. Opt. Soc. Am. B, 1999, 16, 2269 CrossRef CAS.
- D. L. Clark, J. C. Gordon, P. J. Hay and R. Poli, Organometallics, 2005, 24, 5747 CrossRef CAS.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394 CrossRef CAS PubMed.
- P. Dorenbos, J. Lumin., 2000, 91, 91 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2000, 91, 155 CrossRef CAS.
- C. F. Schäffer, Proc. R. Soc. London, Ser. A, 1967, 297, 96 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical data for the multiplet energy levels given in Fig. 4 and 5 obtained for the [Xe]4f2 and [Xe]4f15d1 electron configurations of Pr3+ in LiYF4:Pr3+. See DOI: 10.1039/c4cp05148c |
| This journal is © the Owner Societies 2015 |


