 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrochemical oxidation stability of anions for modern battery electrolytes: a CBS and DFT study†
Erlendur
Jónsson
 * and
Patrik
Johansson
* and
Patrik
Johansson
Department of Applied Physics, Chalmers University of Technology, SE-412 96 Göteborg, Sweden. E-mail: erlendur@chalmers.se; Fax: +46-31-7722090
First published on 5th January 2015
Abstract
The electrochemical stability vs. oxidation is a crucial property of anions in order to be suitable as components in lithium-ion batteries. Here the applicability of a number of computational approaches and methods to assess this property, employing a wide selection of DFT functionals, has been studied using the CCSD(T)/CBS method as the reference. In all, the vertical anion oxidation potential, ΔEv, is a fair way to calculate the stability vs. oxidation, however, a functional of at least hybrid quality is recommended. In addition, the chemical hardness, η, is identified as a novel approach to calculate the stability vs. oxidation.
1 Introduction
Electrolytes are a key component of batteries and their electrochemical stability windows (ESWs); the potential range wherein none of its components breaks down due to oxidation or reduction, currently limit the capabilities of Li-ion batteries (LIBs).1 This is due to the high voltages possible for LIBs, often above 4 V. As there is a strong desire to produce even higher voltage cathodes,2 to allow for even higher energy density LIBs – a very high oxidation stability (preferably >5 V vs. Li+/Li) is aimed at for future electrolytes. For the complementary/competing sodium-ion battery technology,3 currently seeing a rapid increase in attention, the overall development is foreseen to take the same direction. In order to reduce trial-and-error efforts, tools to predict electrochemical stability from chemical structure alone are of large interest. Generally, one way is by in silico screening, which allows for rapid evaluation of candidates for future synthesis.Indeed, the ESWs of electrolyte solvents has been tackled computationally previously.4–6 This is in part due to the large importance of the solid electrolyte interphase (SEI) passivation layer on the LIB anode, formed by (controlled) electrolyte degradation.7 As the solvent tends to be reduced, the reduction limit of the ESW has had focus on the solvent, with extensive studies to understand the SEI formation.8–11 While the reduction limit of the anions has been studied in special solvents such as ionic liquids,12–14 the anions are not in general reduced in LIB (or SIB) electrolytes. The creation of a SEI, partially by anion reduction, is a vast subject outside the scope of this paper.
In contrast, it is the (lithium) salt anion that often sets the oxidation limit, e.g. for ClO4− it is 6.1 V vs. Li+/Li, while it is 6.8 V for PF6− in the same solvent.15 In contrast, the solvents used are known to have a fair stability vs. oxidation, e.g. the standard blend of ethylene and dimethyl carbonate (EC/DMC) was found to have a limit of 6.7 V vs. Li+/Li.4 The stability of the anions versus oxidation are therefore often reported whenever novel salts for LIBs or SIBs are reported, either as experimental16 or computed17 values.
The experimentally measured ESWs have some variance due to the large number of factors affecting the final value, such as the sweep rate, solvent(s), and electrode(s) used.4,15,18,19 Thus reference values for the ESWs, e.g. the intrinsic anion redox potentials, properties solely of the anions and independent of the electrode/solvent chemistry and physics, are highly warranted.
For the anion oxidation stability, a common approach is to calculate the HOMO energy,20EHOMO, due to the correlation between EHOMO and the oxidation stability (based on the Koopmans theorem21). This approach can for example utilize Hartree–Fock (HF) methods with a small to medium sized basis set (e.g. 6-31G* or 6-311+G*) and is applicable to a vast number of compounds as it is computationally inexpensive.
To increase the accuracy, electron correlation must be taken in to account, such as with density functional theory (DFT). Unfortunately, the Koopmans theorem is often not valid within the DFT formalism, due to the poor quality of the orbitals,22 despite their physical relevance.23–25 Thus an alternative approach, using the energy difference from a vertical excitation, is often used, either within the Frank–Condon approximation26,27 (ΔEv) or allowing also for geometry relaxation of the excited state28 to obtain the ionization potential (IP). Both approaches are illustrated in Fig. 1. As hybrid (or better) functionals are recommended for anions,22 the computational cost for such calculations is higher than for a pure HF calculation, as this approach at least involves an extra single-point calculation and significantly higher if geometry optimization of the excited state is performed. Allowing for geometry relaxation, however, also allows for a thermodynamic approach.28,29 If double-hybrid functionals are used, the computational cost increases even more.
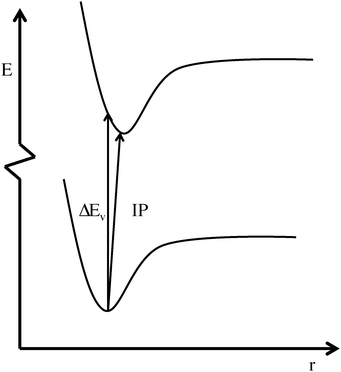 | ||
| Fig. 1 Illustration of the different approaches used to calculate the anion oxidation potential using DFT; the vertical excitation energy (ΔEv) and the ionization potential (IP). | ||
Yet another approach is to study the chemical hardness, η – a concept that arises naturally from conceptual DFT:30
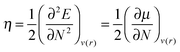 | (1) |
Here the first systematic study involving CCSD(T), MP2, and DFT calculations with a series of basis sets is presented – employed to obtain reference values for the intrinsic anion oxidation potentials at the complete basis set (CBS) limit. This enables a thorough assessment of the applicability and performance of the various methods available to calculate intrinsic oxidation potentials of anions.26–28
2 Computational methodology
A number of anions that all at some point have been considered for LIB electrolytes were selected to be studied in detail (a subset of those previously studied by us32); BF4−, PF6−, ClO4−, TFSI ([(CF3SO2)2N]−), BOB ([B(C2O4)2]−), TDI (C5N4CF3−), Tf (CF3SO3−), N5−, N5C2−, N5C4− (two isomers), N5C6− (two isomers), Im(BF3)2− and N5C10−. A number of small anions were also added, as a control set. Additionally, some anions were found to be too large for the CBS method, and only partial results are therefore listed in the ESI.†Single point energies were calculated with each of the following DFT functionals (with the 6-311+G* basis set): B3LYP,33–35 BMK,36 PBE0,37 TPSS,38 TPSSh,39 the M06 suite (M06, M06-2X, M06-L),40 VSXC,41,42 B2PLYP,43 and mPW2PLYP.44 The B3LYP/6-311+G* equilibrium geometry was used for the anions and for the oxidized and reduced species.
The CCSD(T) calculations with the aug-cc-pVXZ (X = T, Q, 5) basis sets used an extrapolation to the CBS limit:45
| E(n) = ECBS + An−3 | (2) |
Due to the O(N7) scaling of CCSD(T), the rise in computational cost and time is staggering‡ – making the full CCSD(T)/CBS treatment not feasible at present for all of the anions. Therefore, a mixed CBS method was employed, wherein a correction term is added to a MP2/CBS value (also extrapolated using eqn (2)). The correction term, ΔCCSD(T), was calculated with MP2/6-31G* and CCSD(T)/6-31G* (a small but reasonable basis set for our purpose47):
| ΔCCSD(T) = E6-31G*CCSD(T) − E6-31G*MP2 | (3) |
| ECBSCCSD(T) = ECBSMP2 + ΔCCSD(T) | (4) |
A finite difference scheme was used for the calculation of the chemical hardness:
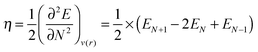 | (5) |
E HOMO values were extracted from the HF/6-311+G* calculations.
The vertical anion oxidation potentials, ΔEv, were calculated using single point energies (ΔEv = EN−1 − EN). As the experimental results in general are given vs. Li+/Li, the computed ΔEv are all shifted by 1.46 V.8 The Gaussian 0948 program was used for all calculations and the Int = ExactBasisTransform keyword was used for the CBS calculations in order to ensure that no basis functions that contribute to the energy were pruned away during basis transformations.
3 Results & discussion
The analysis of the results starts with a comparison between the CBS and the ΔCBS methods for small anions, followed by a further analysis of ΔCBS values of larger anions. Thereafter, we compare the performance of different functionals. Each section treats and discusses the HOMO, ΔEv, and η approaches.3.1 CBS vs. ΔCBS
Only a portion of the anions were small enough to allow CCSD(T) calculations with the aug-cc-pV5Z basis sets. Therefore, most anions had to resort to the ΔCBS measure rather than CBS. As MP2 energies are included in the results of the CCSD(T) calculations, the anions in Table 1 can also function as an internal benchmark for the ΔCBS method. In general, the values obtained from the ΔCBS method are close to the values from the CCSD(T)/CBS method. This holds for both the ΔEv and η approaches, showing the general validity of the ΔCBS method. For BF4−, however, the ΔCBS values are 10% and 6% lower than the CBS values, giving a possible upper bound for possible errors. The BF4− values are close to revised experimental value of 6.2 V vs. Li+/Li.| Anion | ΔEv | ΔEv | η | η | E HOMO | E ox |
|---|---|---|---|---|---|---|
| CCSD(T)/CBS | ΔCBS | CCSD(T)/CBS | ΔCBS | HF/6-311+G* | Experimental | |
| Br− | 2.12 | 2.10 | 4.37 | 4.36 | −3.79 | 4.149 |
| F− | 1.96 | 1.99 | 6.02 | 6.07 | −4.08 | 5.949 |
| Cl− | 2.21 | 2.25 | 4.89 | 4.89 | −4.83 | 4.449 |
| HS− | 0.89 | 0.93 | 2.93 | 2.92 | −2.56 | — |
| HF2− | 4.93 | 4.97 | 5.40 | 5.44 | −7.73 | — |
| NO3− | 2.72 | 2.74 | 4.40 | 4.30 | −6.33 | — |
| OCN− | 2.33 | 2.35 | 4.06 | 4.07 | −4.35 | — |
| SCN− | 2.16 | 2.22 | 3.64 | 3.66 | −3.84 | — |
| BF4− | 7.03 | 6.35 | 6.42 | 6.06 | −10.45 | 6.2;28 6.6, 8.315 |
| BrO3− | 3.44 | 3.54 | 4.48 | 4.55 | −6.04 | — |
| ClO4− | 4.34 | 4.36 | 5.06 | 5.06 | −7.89 | 6.0;28 6.1, 7.015 |
| HCO2− | 2.80 | 2.85 | 3.80 | 3.81 | −5.11 | — |
| BH4− | 3.21 | 3.23 | 3.90 | 3.85 | −5.19 | — |
Surprisingly, neither the CBS nor the ΔCBS ΔEv values for the halides are in the expected order of F− > Cl− > Br−, instead Cl− > Br− > F− is observed. Comparing the Eox values with the ΔEv values for the halides, shows that the ΔEv value is drastically lower. Similarly, the experimental Eox value of ClO4− of 6.0 V vs. Li+/Li is far higher than expected from the CBS calculations, with a ΔEv value of 4.34 V vs. Li+/Li. It seems as if the atomic anions have a problem with a proper radical description affecting this measure.
The hardness, η, has the expected ordering for the halides, furthermore, the hardness values are on average closer to the Eox than the ΔEv values. For example, BF4− has a hardness that is well within the range of the Eox values, despite having the highest difference between η values calculated by CBS and ΔCBS. BF4− is also the only anion with a higher ΔEv than η. ClO4− is the only anion for which all Eox values are larger than the hardness.
The EHOMO values have the same issues for the halides as the ΔEv values, i.e. wrong ordering. Unfortunately, it is not the same ordering, i.e. Cl− > F− > Br−. Looking at the Eox values, the EHOMO value for BF4− is very large, −10.45 eV, far larger than expected. It is not clear what causes BF4− to stand out for all measures.
3.2 ΔCBS
In Table 2 we show the ΔCBS values only for the larger anions for which CBS was not viable. A comparison vs. experimental data show that the ΔEv approach tends to overestimate the oxidation potentials. This includes the BOB (by 1.63 V) and MOB (by 1.09 V) anions – with BOB correctly described to be more stable. Furthermore, some values are very close to the measured Eox with Im(BF3)2− as the stellar example (only 0.07 V difference). For some other anions, a definite comparison is not possible, due to the large variations in Eox values. These include TFSI, where the ΔEv value is close to some of the Eox values. Both AsF6− and PF6− have ΔEv values close to the Eox maximum values.| Anion | ΔEv | η | E HOMO | E ox |
|---|---|---|---|---|
| Experimental | ||||
| N5− | 4.54 | 5.80 | −6.10 | — |
| NCN2− | 2.86 | 4.44 | −4.82 | — |
| AsF6− | 8.38 | 7.02 | −12.13 | 6.5;28 6.8, 8.615 |
| PF6− | 8.57 | 7.21 | −11.67 | 6.3;28 6.8, 8.415 |
| C(CN)3− | 2.78 | 3.81 | −4.60 | — |
| CH3COO− | 1.48 | 2.99 | −5.10 | — |
| N5C2− | 4.27 | 4.62 | −5.70 | — |
| Tf | 5.31 | 5.04 | −7.50 | 5.0, 5.9;28 6.0, 7.015 |
| FSI | 5.34 | 5.24 | −8.66 | >4.550 |
| N5C4a− | 4.32 | 5.51 | −5.78 | >4.051,52 |
| N5C4b− | 4.05 | 5.01 | −5.55 | — |
| N5C6a− | 4.45 | 5.02 | −6.04 | — |
| N5C6b− | 4.08 | 5.37 | −5.49 | — |
| BOB | 6.13 | 5.30 | −8.81 | 4.553 |
| N5C8− | 4.20 | 4.47 | −5.80 | — |
| TDI | 4.02 | 5.21 | −5.54 | 4.8054 |
| TFSI | 6.12 | 5.62 | −8.60 | 5.3, 6.1;28 6.3, 7.1;15 5.4055 |
| Im(BF3)2− | 4.92 | 4.53 | −6.32 | 4.8516 |
| MOB | 5.49 | 5.23 | −8.72 | 4.456 |
| N5C10− | 4.59 | — | −6.24 | — |
| B(CH3)4− | 3.01 | 3.57 | −5.34 | 2.915 |
Overall, the hardness has qualitatively similar predictive power, as the ΔEv values. In general, the η values are close to the Eox values. Starting with the anions with single Eox values, the η values are slightly higher, however, the difference is not as large as for the ΔEv values. BOB and MOB have the largest differences, both 0.8 V, between Eox and η. The η values of TFSI, Tf, PF6− and AsF6− are all within the range of reported Eox values. Looking at the relative stability of BOB and MOB, we note that the difference between the ΔEv values (0.6 V) is far higher than the η values (0.1 eV), the latter being closer to the Eox difference.
The EHOMO values show an unexpected ordering of oxidative stability; the third most stable anion, is the BOB anion (−8.81 eV), more stable than TFSI (−8.60 eV) and TDI (−5.54 eV), despite both having higher Eox values than BOB. It is also notable that EHOMO is the only measure that indicates AsF6− to be more stable than PF6−, as obtained by the maximum Eox values.
3.3 Functional dependency
The analysis of the DFT functional performance is discussed first for ΔEv and subsequently for η and grouped by functional type.The ΔEv values from DFT and HF in Table 3 in general underestimate ΔEv – using ΔCBS as reference – with an average deviation negative for HF and all functionals (except M06-2X, +0.01 V), as seen in Fig. 2.
| Anion | ΔCBS | B2PLYP | B3LYP | HF | M06-L | M06-2X | mPW2PLYP | PBE0 | TPSSh | VSXC |
|---|---|---|---|---|---|---|---|---|---|---|
| Br− | 2.10 | 1.91 | 2.13 | 1.02 | 1.85 | 2.03 | 1.93 | 2.05 | 2.06 | 2.02 |
| Cl− | 1.99 | 2.02 | 2.26 | 1.02 | 2.26 | 2.23 | 2.02 | 2.17 | 2.15 | 2.20 |
| F− | 2.25 | 1.84 | 2.03 | −0.21 | 1.70 | 1.71 | 1.80 | 1.76 | 1.78 | 2.01 |
| HS− | 0.93 | 0.62 | 0.87 | −0.33 | 0.74 | 0.84 | 0.63 | 0.77 | 0.76 | 0.81 |
| HF2− | 4.97 | 4.72 | 4.60 | 4.94 | 4.05 | 5.12 | 4.81 | 4.56 | 4.22 | 4.09 |
| NO3− | 2.74 | 2.30 | 2.64 | 3.31 | 2.19 | 3.22 | 2.45 | 2.63 | 2.31 | 2.11 |
| OCN− | 2.35 | 2.20 | 2.23 | 0.95 | 2.05 | 2.37 | 2.21 | 2.16 | 2.05 | 2.00 |
| SCN− | 2.22 | 1.96 | 2.08 | 0.95 | 1.95 | 2.19 | 1.98 | 2.05 | 1.99 | 1.95 |
| BF4− | 6.35 | 6.43 | 5.98 | 6.05 | 5.36 | 6.85 | 6.58 | 6.03 | 5.52 | 5.31 |
| BrO3− | 3.54 | 3.19 | 3.31 | 2.95 | 2.89 | 3.61 | 3.27 | 3.28 | 3.05 | 2.97 |
| ClO4− | 4.36 | 4.20 | 4.20 | 4.08 | 3.80 | 4.74 | 4.31 | 4.21 | 3.88 | 3.72 |
| HCO2− | 2.85 | 2.14 | 2.31 | 2.13 | 1.91 | 2.57 | 2.23 | 2.24 | 2.03 | 1.94 |
| BH4− | 3.23 | 3.00 | 3.11 | 2.27 | 2.80 | 3.10 | 3.02 | 3.01 | 2.96 | 2.70 |
| N5− | 4.54 | 4.15 | 4.26 | 4.72 | 3.81 | 4.72 | 4.25 | 4.26 | 3.95 | 3.74 |
| N(CN)2− | 2.86 | 2.67 | 2.65 | 1.37 | 2.49 | 2.88 | 2.68 | 2.62 | 2.47 | 2.38 |
| AsF6− | 8.38 | 7.22 | 7.00 | 9.16 | 6.26 | 8.24 | 7.46 | 7.11 | 6.47 | 6.19 |
| PF6− | 8.57 | 6.95 | 6.66 | 8.94 | 5.96 | 7.85 | 7.16 | 6.78 | 6.16 | 5.93 |
| C(CN)3− | 2.78 | 2.53 | 2.60 | 1.27 | 2.45 | 2.80 | 2.55 | 2.58 | 2.44 | 2.34 |
| CH3COO− | 1.48 | 2.06 | 2.20 | 0.72 | 1.83 | 2.28 | 2.14 | 2.16 | 1.91 | 1.82 |
| N5C2− | 4.27 | 4.10 | 4.08 | 2.48 | 3.94 | 4.28 | 4.11 | 4.06 | 3.93 | 3.85 |
| Tf | 5.31 | 4.90 | 3.97 | 5.39 | 3.60 | 5.41 | 5.02 | 4.96 | 3.69 | 3.60 |
| FSI | 5.34 | 5.10 | 5.08 | 4.92 | 4.65 | 5.67 | 5.20 | 5.11 | 4.76 | 4.59 |
| N5C4a− | 4.32 | 4.10 | 4.02 | 2.23 | 3.86 | 4.26 | 4.11 | 4.01 | 3.87 | 3.78 |
| N5C4b− | 4.05 | 3.86 | 3.87 | 2.58 | 3.71 | 4.10 | 3.88 | 3.86 | 3.72 | 3.62 |
| N5C6a− | 4.45 | 4.19 | 4.19 | 2.85 | 4.04 | 4.44 | 4.21 | 4.19 | 4.05 | 3.94 |
| N5C6b− | 4.08 | 3.78 | 3.77 | 2.27 | 3.61 | 4.02 | 3.80 | 3.77 | 3.63 | 3.52 |
| BOB | 6.13 | 4.80 | 4.77 | 5.70 | 4.08 | 5.67 | 4.99 | 4.85 | 4.32 | 4.06 |
| N5C8− | 4.20 | 3.95 | 3.97 | 2.70 | 3.81 | 4.23 | 3.97 | 3.98 | 3.83 | 3.71 |
| TDI | 4.02 | 3.80 | 3.79 | 2.32 | 3.60 | 4.05 | 3.82 | 3.77 | 3.64 | 3.57 |
| TFSI | 6.12 | 5.39 | 5.40 | 4.74 | 4.46 | 5.79 | 5.45 | 5.37 | 4.59 | 4.50 |
| Im(BF3)2− | 4.92 | 4.76 | 4.81 | 3.47 | 4.68 | 4.99 | 4.77 | 4.77 | 4.63 | 4.66 |
| MOB | 5.49 | 5.06 | 4.92 | 5.56 | 4.24 | 5.60 | 5.18 | 4.99 | 4.47 | 4.21 |
| N5C10− | 4.59 | 4.26 | 4.26 | 2.95 | 4.09 | 4.55 | 4.28 | 4.28 | 4.11 | 3.99 |
| B(CH3)4− | 3.01 | 2.65 | 2.55 | 2.08 | 2.36 | 2.84 | 2.69 | 2.52 | 2.39 | 2.21 |
| Avg. dev. | −0.35 | −0.36 | −0.92 | −0.70 | 0.01 | −0.29 | −0.35 | −0.62 | −0.73 | |
| Std. dev. | 0.39 | 0.49 | 0.81 | 0.65 | 0.29 | 0.36 | 0.42 | 0.60 | 0.65 | |
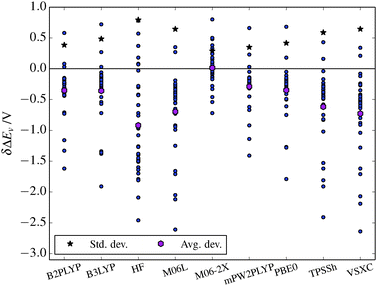 | ||
| Fig. 2 The deviation, δΔEv of the ΔEv value from the ΔCBS reference value for each of the methods. Average and standard deviations are also shown. | ||
Starting with HF, one notable issue is the values for F− and HS−, both negative (vs. Li+/Li). In practice this means that HF predicts that these anions would reduce Li+. HF also has the highest average and standard deviations. Notably, the Hückel anions (N5C2n−, excluding N5−) have far lower values than the ΔCBS reference, with the difference ranging from 1.47 V to 2.09 V. The highly symmetric and quite special anion N5− is, however, slightly higher in energy than the reference, by 0.18 V. Other notable anions are AsF6− and PF6−, higher by 0.78 V and 0.38 V, respectively.
Each of the functionals used have different issues, a few observations, grouped by functional complexity, are here highlighted.
Starting with the non-hybrid functionals, VSXC has the largest average deviation (−0.73 V) of the DFT functionals. It underestimates the ΔEv of a few anions by more than 2 V: PF6− is underestimated by 2.65 V, AsF6− by 2.19 V, and BOB by 2.07 V. A few other anions are underestimated by more than 1 V: Tf, TFSI, MOB and BF4−. Two anions have their ΔEv overestimated compared to the reference; Cl− (by 0.22 V) and CH3COO− (by 0.33 V). M06-L has the second highest average deviation (−0.70 V) of the DFT functionals. The problematic anions are the same as for VSXC with only slightly different values.
The hybrid functionals have better performance characteristics, however, B3LYP has the same problematic cases as VSXC and M06-L. Though, as the average deviation implies, the errors are smaller in magnitude; PF6− is underestimated by 1.91 V and AsF6− by 1.38 V and most others anions are below 1 V in difference. However, the overestimates of CH3COO− and Cl− are somewhat large, 0.72 V and 0.28 V, respectively. PBE0 has similar performance characteristics as B3LYP – including the same problems with PF6−, underestimated by 1.79 V, BOB by 1.28 V, and AsF6− by 1.27 V.
TPSSh performs somewhat worse than B3LYP. It is also the only hybrid functional that has any value that is underestimated by more than 2 V: PF6− by 2.41 V. The deviations for AsF6 and BOB are also large: 1.91 V and 1.81 V, respectively.
M06-2X has the distinction of having the lowest deviation of all of the functionals. However, it has a number of overestimates such as CH3COO− by 0.80 V, BF4 by 0.50 V, and NO3− by 0.48 V. Furthermore, the underestimates are low; PF6− 0.72 V, F− 0.53 V, and BOB 0.46 V. It is also notable that AsF6− is underestimated by only 0.14 V. Interestingly, the BF4− value of 6.85 V is closer to the CBS value (7.03 V), than the ΔCBS value (6.35 V).
The two double hybrid functionals have very small deviations, as mPW2PLYP has the second lowest average deviation (−0.29 V) and only has two values that differ by more than 1 V: PF6− and BOB are underestimated by 1.41 V and 1.14 V, respectively. B2PLYP is similar to mPW2PLYP, however, it has a slightly higher deviation; −0.35 V. It also has three anions that differ by more than 1 V from the reference: PF6− is underestimated by 1.62 V, AsF6− by 1.16 V, and BOB by 1.33 V.
When the results from all the DFT functionals are taken together, a few points become apparent. First, a larger number of electronegative groups present in the anion structure, tends to cause worse results. Thus heavily fluorinated molecules in general have ΔEv values underestimated by 1–2 V. This is readily apparent for the PF6− and AsF6− anions. This is also an issue for BOB, but to a less extent for the MOB variant, which has the less electronegative malonato moiety. This could be an issue for future ab initio work on novel electrolyte anions, as they tend to be themed around strongly electronegative groups.
Second, while DFT on the whole results in too low ΔEv values, the ΔEv value for CH3COO− is in general overestimated from 0.5 V to 0.8 V. The ΔEv for Cl− is also often overestimated.
Third, in general the performance of the DFT functionals follows the Jacob's ladder of DFT.57 The hybrid functionals perform better than the local functionals, VSXC and M06-L, while the double-hybrid functionals, mPW2PLYP and B2PLYP, perform even better. There is one functional that performs far better, M06-2X, though that may be a fortunate cancellation of errors, as this functional is heavily parameterized.
Moving on to the chemical hardness measure, on average the DFT functionals overestimate the hardness (Table 4 and Fig. 3), as all average deviations are positive. Furthermore, with the large standard deviations, there will be outliers for each functional. Each functional must be inspected, following the same analysis layout as above. Starting with VSXC and M06-L, these have the same outliers, albeit differing slightly in magnitude. Both overestimate the F− and HF2− by over 2 eV, and also have issues with CH3COO− and Cl−. The functionals in general underestimate the hardness of the Hückel anions (N5C2n, n = 2…), and BOB, by 0.5 eV or more. Furthermore, both functionals underestimate PF6− and AsF6−, M06-L by 0.89 eV and 0.75 eV and VSXC by 1.11 eV and 1.20 eV, respectively. Interestingly, the average deviations for the two functionals are small, 0.13 eV for VSXC and 0.39 eV for M06-L.
| Anion | ΔCBS | B2PLYP | B3LYP | HF | M06-L | M06-2X | mPW2PLYP | PBE0 | TPSSh | VSXC |
|---|---|---|---|---|---|---|---|---|---|---|
| a N5C10− has no reference value and is thus neglected in the statistics. | ||||||||||
| Br− | 4.36 | 4.92 | 4.93 | 4.69 | 4.86 | 4.88 | 4.94 | 4.90 | 4.94 | 5.06 |
| Cl− | 4.89 | 5.75 | 5.75 | 5.50 | 5.83 | 5.74 | 5.76 | 5.71 | 5.73 | 5.43 |
| F− | 6.07 | 8.47 | 8.42 | 7.83 | 8.33 | 8.30 | 8.46 | 8.30 | 8.31 | 8.58 |
| HS− | 2.92 | 4.17 | 4.16 | 3.87 | 4.14 | 4.12 | 4.18 | 4.10 | 4.10 | 4.14 |
| HF2− | 5.44 | 8.13 | 7.89 | 8.69 | 7.85 | 8.25 | 8.19 | 7.94 | 7.78 | 7.78 |
| NO3− | 4.30 | 5.47 | 5.50 | 5.88 | 5.58 | 5.80 | 5.51 | 5.55 | 5.34 | 5.37 |
| OCN− | 4.07 | 4.73 | 4.66 | 4.26 | 4.80 | 4.73 | 4.73 | 4.63 | 4.59 | 4.44 |
| SCN− | 3.66 | 4.23 | 4.20 | 3.91 | 4.33 | 4.27 | 4.24 | 4.19 | 4.18 | 4.02 |
| BF4− | 6.06 | 6.76 | 6.43 | 6.74 | 6.29 | 6.94 | 6.82 | 6.48 | 6.25 | 6.00 |
| BrO3− | 4.55 | 4.87 | 4.86 | 4.83 | 4.85 | 5.08 | 4.91 | 4.84 | 4.76 | 4.65 |
| ClO4− | 5.06 | 5.81 | 5.72 | 6.07 | 5.97 | 6.08 | 5.86 | 5.78 | 5.65 | 5.43 |
| HCO2− | 3.81 | 5.10 | 4.77 | 4.86 | 4.74 | 4.95 | 5.14 | 4.73 | 4.64 | 4.52 |
| BH4− | 3.85 | 5.10 | 5.07 | 4.88 | 5.04 | 4.96 | 5.11 | 5.01 | 5.01 | 4.75 |
| N5− | 5.80 | 6.61 | 6.49 | 7.09 | 6.48 | 6.86 | 6.64 | 6.57 | 6.39 | 6.39 |
| N(CN)2− | 4.44 | 4.51 | 4.43 | 4.05 | 4.65 | 4.56 | 4.52 | 4.43 | 4.39 | 4.11 |
| AsF6− | 7.02 | 6.54 | 6.29 | 7.86 | 6.27 | 7.16 | 6.64 | 6.42 | 6.11 | 5.83 |
| PF6− | 7.21 | 6.91 | 6.65 | 8.15 | 6.32 | 7.36 | 7.00 | 6.75 | 6.32 | 6.10 |
| C(CN)3− | 3.81 | 4.19 | 4.16 | 3.75 | 4.39 | 4.28 | 4.20 | 4.17 | 4.12 | 3.81 |
| CH3COO− | 2.99 | 4.29 | 4.28 | 3.71 | 4.31 | 4.35 | 4.33 | 4.26 | 4.16 | 4.04 |
| N5C2− | 4.62 | 5.07 | 4.99 | 5.00 | 5.45 | 5.14 | 5.08 | 4.98 | 4.94 | 4.75 |
| Tf | 5.04 | 5.67 | 5.11 | 6.05 | 5.19 | 5.97 | 5.72 | 5.62 | 5.01 | 4.85 |
| FSI | 5.24 | 5.56 | 5.44 | 5.80 | 5.61 | 5.89 | 5.60 | 5.52 | 5.35 | 5.12 |
| N5C4a− | 5.51 | 5.02 | 4.78 | 4.33 | 4.79 | 4.99 | 5.00 | 4.80 | 4.75 | 4.74 |
| N5C4b− | 5.01 | 5.06 | 4.85 | 4.74 | 4.86 | 5.09 | 5.05 | 4.88 | 4.82 | 4.37 |
| N5C6a− | 5.02 | 4.68 | 4.48 | 4.31 | 4.47 | 4.69 | 4.68 | 4.50 | 4.45 | 4.43 |
| N5C6b− | 5.37 | 4.65 | 4.44 | 4.14 | 4.44 | 4.65 | 4.64 | 4.46 | 4.41 | 4.39 |
| BOB | 5.30 | 5.05 | 4.87 | 5.76 | 4.69 | 5.37 | 5.12 | 4.94 | 4.69 | 4.48 |
| N5C8− | 4.47 | 4.32 | 4.11 | 3.95 | 4.09 | 4.33 | 4.31 | 4.13 | 4.08 | 4.05 |
| TDI | 5.21 | 4.74 | 4.54 | 4.26 | 4.54 | 4.74 | 4.73 | 4.55 | 4.51 | 4.49 |
| TFSI | 5.62 | 5.53 | 5.38 | 5.51 | 5.15 | 5.78 | 5.55 | 5.41 | 5.01 | 4.83 |
| Im(BF3)2− | 4.53 | 5.06 | 4.99 | 4.57 | 5.39 | 5.17 | 5.05 | 4.98 | 4.94 | 5.02 |
| MOB | 5.23 | 5.23 | 4.98 | 5.75 | 4.78 | 5.39 | 5.27 | 5.06 | 4.81 | 4.58 |
| N5C10− | —a | 4.30 | 4.08 | 3.87 | 4.05 | 4.30 | 4.29 | 4.10 | 4.04 | 4.01 |
| B(CH3)4− | 3.57 | 4.21 | 4.07 | 4.15 | 4.32 | 4.27 | 4.23 | 4.08 | 4.04 | 3.77 |
| Avg. dev. | 0.49 | 0.35 | 0.45 | 0.39 | 0.61 | 0.52 | 0.38 | 0.26 | 0.13 | |
| Std. dev. | 0.78 | 0.82 | 0.89 | 0.86 | 0.74 | 0.78 | 0.79 | 0.83 | 0.90 | |
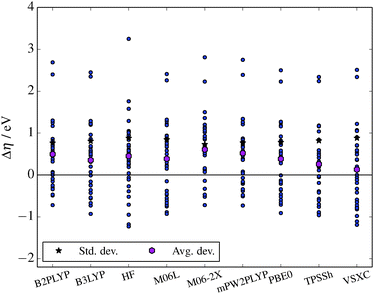 | ||
| Fig. 3 The deviation of the hardness from the ΔCBS reference value for each of the methods. Average and standard deviations are also shown. | ||
Looking at the hybrid functionals; B3LYP, M06-2X, PBE0, and TPSSh, all reveal the same pattern as for the VSXC and M06-L functionals, e.g. an overestimated hardness for F− and HF2−, in each case by ≥2 eV. However, the underestimates of the PF6− and AsF6− anions are much reduced for all the hybrid functionals (except TPSSh). M06-2X has even a slight overestimate of the PF6− and AsF6−, by 0.16 eV and 0.14 eV, respectively.
The double hybrid functionals, B2PLYP and mPW2PLYP, have some of the largest average deviations of all the functional of Table 4, however, they have some of the smallest standard deviations, implying that they tend to overestimate the hardness. They also have many of the same outliers as the other functionals, in particular F− and HF2−, which are overestimated by ≥2.4 eV. Furthermore, Cl− and CH3COO− continue to have some overestimation (≈0.8 eV and 1.3 eV, respectively). The Hückel anions (N5C2n, n = 2…), continue to have some underestimation. However, the magnitude of the underestimate for PF6− and AsF6− is smaller than for most of the hybrid functionals, with 0.30 eV and 0.38 eV for B2PLYP and 0.21 eV and 0.38 eV for mPW2PLYP, respectively.
Comparing the deviations from the reference values for both approaches, ΔEv (Fig. 2) and η (Fig. 3), it must be noted that the magnitude of the deviations of η are far larger (note the figure scales). Furthermore, looking at Fig. 1 and 2 of the ESI,† show that while DFT can tackle ΔEv calculations, the same is not clear for η, due to the low correlation with the ΔCBS values.
4 Conclusions
For the calculation of the stability vs. oxidation for the present set of anions, using the methodology of ΔEv, a hybrid (or better yet, double hybrid) functional is recommended. Their resulting ΔEv values are closer to the benchmark, surpassing the previously recommended VSXC functional of older works.26,27 Out of the DFT functionals tested, M06-2X performs the best.Using the EHOMO measure to predict the stability vs. oxidation is debatable, due to the unexpected ordering of the anions' oxidative stability. Furthermore, neither the EHOMO nor the ΔEv approaches were able to predict the expected ordering of F− > Cl− > Br−.
Hardness is another interesting property to study in connection with oxidation potentials, though the origin of its strong correlation with Eox is not clear. Out of the many DFT functionals tested, no strong general recommendation can be made, however, the double hybrids and M06-2X are candidates for the calculation of hardnesses.
Acknowledgements
We would like to thank the Swedish Energy Agency for funding via a VR/STEM grant and SNIC for the computational resources. Prof. Johan Scheers is thanked for his helpful comments and questions. Support to Patrik Johansson from Chalmers Areas of Advance Transport is gratefully acknowledged.References
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- A. Ponrouch, R. Dedryvère, D. Monti, A. E. Demet, J. M. Ateba Mba, L. Croguennec, C. Masquelier, P. Johansson and M. R. Palacn, Energy Environ. Sci., 2013, 6, 2361–2369 CAS.
- K. Xu, S. P. Ding and T. R. Jow, J. Electrochem. Soc., 1999, 146, 4172–4178 CrossRef CAS.
- X. Zhang, J. K. Pugh and P. N. Ross, J. Electrochem. Soc., 2001, 148, E183–E188 CrossRef CAS.
- L. Xing and O. Borodin, Phys. Chem. Chem. Phys., 2012, 14, 12838–12843 RSC.
- R. Fong, U. von Sacken and J. R. Dahn, J. Electrochem. Soc., 1990, 137, 2009–2013 CrossRef CAS.
- J. M. Vollmer, L. A. Curtiss, D. R. Vissers and K. Amine, J. Electrochem. Soc., 2004, 151, A178–A183 CrossRef CAS.
- G. V. Zhuang, K. Xu, H. Yang, T. R. Jow and P. N. Ross, J. Phys. Chem. B, 2005, 109, 17567–17573 CrossRef CAS PubMed.
- I. A. Shkrob, Y. Zhu, T. W. Marin and D. Abraham, J. Phys. Chem. C, 2013, 19255–19269 CAS.
- I. A. Shkrob, Y. Zhu, T. W. Marin and D. Abraham, J. Phys. Chem. C, 2013, 19270–19279 CAS.
- P. C. Howlett, E. I. Izgorodina, M. Forsyth and D. R. MacFarlane, Z. Phys. Chem., 2006, 220, 1483–1498 CrossRef CAS.
- E. Markevich, R. Sharabi, V. Borgel, H. Gottlieb, G. Salitra, D. Aurbach, G. Semrau and M. A. Schmidt, Electrochim. Acta, 2010, 55, 2687–2696 CrossRef CAS.
- S. P. Ong, O. Andreussi, Y. Wu, N. Marzari and G. Ceder, Chem. Mater., 2011, 23, 2979–2986 CrossRef CAS.
- M. Ue, M. Takeda, M. Takehara and S. Mori, J. Electrochem. Soc., 1997, 133, 2684–2688 CrossRef.
- T. J. Barbarich and P. F. Driscoll, Electrochem. Solid-State Lett., 2003, 6, A113–A116 CrossRef CAS.
- E. Jónsson, M. Armand and P. Johansson, Phys. Chem. Chem. Phys., 2012, 14, 6021–6025 RSC.
- J. M. Tarascon and D. Guyomard, Solid State Ionics, 1994, 69, 293–305 CrossRef CAS.
- K. Xu and C. A. Angell, J. Electrochem. Soc., 1998, 145, L70–L72 CrossRef CAS.
- F. Kita, A. Kawakami, J. Nie, T. Sonoda and H. Kobayashi, J. Power Sources, 1997, 68, 307–310 CrossRef CAS.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
- F. Jensen, J. Chem. Theory Comput., 2010, 6, 2726–2735 CrossRef CAS.
- E. J. Baerends and O. V. Gritsenko, J. Phys. Chem. A, 1997, 101, 5383–5403 CrossRef CAS.
- R. Stowasser and R. Hoffmann, J. Am. Chem. Soc., 1999, 121, 3414–3420 CrossRef CAS.
- E. Baerends, Theor. Chem. Acc., 2000, 103, 265–269 CrossRef CAS.
- P. Johansson, J. Phys. Chem. A, 2006, 110, 12077–12080 CrossRef CAS PubMed.
- P. Johansson, J. Phys. Chem. A, 2007, 111, 1378–1379 CrossRef CAS.
- M. Ue, A. Murakami and S. Nakamura, J. Electrochem. Soc., 2002, 149, A1572–A1577 CrossRef CAS.
- O. Borodin, W. Behl and T. R. Jow, J. Phys. Chem. C, 2013, 117, 8661–8682 CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- P. Johansson, J. Tegenfeldt and J. Lindgren, J. Phys. Chem. A, 2000, 104, 954–961 CrossRef CAS.
- E. Jónsson and P. Johansson, Phys. Chem. Chem. Phys., 2012, 14, 10774–10779 RSC.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. Tao, J. Perdew, V. Staroverov and G. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. Perdew, A. Ruzsinszky, J. Tao, G. Csonka and G. Scuseria, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 042506 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chim. Acta, 2008, 120, 215–241 CrossRef CAS.
- T. Van Voorhis and G. E. Scuseria, J. Chem. Phys., 1998, 109, 400–410 CrossRef CAS.
- T. Van Voorhis and G. E. Scuseria, J. Chem. Phys., 2008, 129, 219901 CrossRef.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 4398 RSC.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- D. Feller, K. A. Peterson and J. Grant Hill, J. Chem. Phys., 2011, 135, 044102 CrossRef PubMed.
- M. Pitoňák, T. Janowski, P. Neogrády, P. Pulay and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1761–1766 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision B.01.
- This is calculated from the standard reduction potentials by assuming that the difference between the value for the anion and lithium is the oxidation potential.
- H.-B. Han, S.-S. Zhou, D.-J. Zhang, S.-W. Feng, L.-F. Li, K. Liu, W.-F. Feng, J. Nie, H. Li, X.-J. Huang, M. Armand and Z.-B. Zhou, J. Power Sources, 2011, 196, 3623–3632 CrossRef CAS.
- M. Egashira, B. Scrosati, M. Armand, S. Béranger and C. Michot, Electrochem. Solid-State Lett., 2003, 6, A71–A73 CrossRef CAS.
- M. Armand, private communication.
- W. Xu and C. A. Angell, Electrochem. Solid-State Lett., 2001, 4, E1–E4 CrossRef CAS.
- L. Niedzicki, S. Grugeon, S. Laruelle, P. Judeinstein, M. Bukowska, J. Prejzner, P. Szczeciński, W. Wieczorek and M. Armand, J. Power Sources, 2011, 196, 8696–8700 CrossRef CAS.
- V. R. Koch, L. A. Dominey, C. Nanjundiah and M. J. Ondrechen, J. Electrochem. Soc., 1996, 143, 798–803 CrossRef CAS.
- W. Xu, A. J. Shusterman, R. Marzke and C. A. Angell, J. Electrochem. Soc., 2004, 151, A632–A638 CrossRef CAS.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: A table showing the extrapolation details of the CBS approach, the ΔEv and η values for a number of additional anions and functionals. See DOI: 10.1039/c4cp04592k |
| ‡ Illustrating this, moving from TZ (230 basis functions) to 5Z (635 basis functions) for BF4−, increases the CPU time needed by a factor 100. |
| This journal is © the Owner Societies 2015 |
