On the mechanism of nanoparticle formation in a flame doped by iron pentacarbonyl
Marina
Poliak
a,
Alexey
Fomin
a,
Vladimir
Tsionsky
a,
Sergey
Cheskis
a,
Irenaeus
Wlokas
b and
Igor
Rahinov
*c
aSchool of Chemistry, Tel Aviv University, Tel Aviv 69978, Israel
bInstitute for Combustion and Gasdynamics - Fluid Dynamics, University of Duisburg-Essen, 47057 Duisburg, Germany
cDepartment of Natural Sciences, The Open University of Israel, Raanana 4353701, Israel. E-mail: igorra@openu.ac.il
First published on 11th November 2014
Abstract
In this work we have investigated the mechanism of nanoparticle synthesis in a low pressure, premixed, laminar flat flame of CH4–O2, doped with iron pentacarbonyl using a combined quartz-crystal-microbalance-particle-mass-spectrometry apparatus. We have unambiguously demonstrated that the formation of nanoparticles in iron pentacarbonyl-doped flames occurs very early, in close proximity to the burner surface, prior to the flame front. This early rise of nanoparticle mass concentration is followed by a sharp drop in nanoparticle concentration at the high temperature flame front. This “prompt” nanoparticle generation is consistent with kinetic models describing iron cluster formation. The observation of this phenomenon in a quasi-one-dimensional premixed flat flame strengthens our previous findings and points out that the “prompt” nanoparticle formation is a general phenomenon, not limited to diffusion flames. It presents a challenge and a trigger for further development of the existing mechanisms for gas phase synthesis of iron oxide particles in flames.
1 Introduction
Iron oxide nanoparticles (NPs) are used in diverse applications, including optical magnetic recording, catalysis, gas sensors, targeted drug delivery, magnetic resonance imaging, and hyperthermic malignant cell therapy (see for instance review of Lu et al.1 and references therein). Flame synthesis of NPs offers several important advantages, including control over particle size and morphology and a route to large-scale production of nanomaterials.2 Iron pentacarbonyl, Fe(CO)5, (IPC) is commonly used as a flame additive for iron oxide NP synthesis due to its relatively high vapor pressure. Iron pentacarbonyl has also been used as precursor for synthesis of iron NPs, which act as catalysts for the growth of single walled carbon nanotubes (SWCNTs).3–5 Reaction conditions, such as pressure, temperature distribution, species concentration and residence time are the parameters which determine the properties of the synthesized nanoparticles.Flame synthesis of iron oxide nanoparticles with tailored functionalities should rely, therefore, on detailed understanding of the mechanism governing their formation and nucleation from the gas phase. Fundamental studies conducted in laminar, premixed laboratory scale burners can deliver information required to validate and challenge, if needed, the existing models of particle growth and precursor chemistry. The kinetics of NP formation in flames doped with IPC gained considerable attention and was studied by molecular beam sampling followed by particle mass spectrometry (PMS) analysis,6–9 as well as with light scattering methods.10–12 PMS allows measuring the mass equivalent diameter of charged NPs, but not their total number and mass concentrations.
The commonly accepted mechanisms of iron oxide NP formation in flames doped with IPC postulate the decomposition of the precursor, followed by oxidation of the nascent Fe atoms and nucleation of the iron oxides, giving rise to NP formation at large distances from the burner surface, far away from the flame front. Simulations based of the existing mechanism of the NP formation6,9,13 predicted monotonic growth of the total mass concentration of iron oxide NPs with the increase of the reaction coordinate, along with growth of the NP diameter. The total NP number concentration can decrease due to the coagulation and coalescence of smaller particles.
Recently, we have introduced the combined Particle Mass Spectrometer-Quartz Crystal Microbalance (PMS-QCM) apparatus14 which allows to measure the total NP mass concentration (both charged and uncharged) along with determination of the probability distribution function of the particle mass. In these experiments NP formation was observed early, prior to the luminous zone of the IPC-doped flame, followed by a sharp drop (to the level below the QCM detection sensitivity) of their total mass concentration. Similar behavior, which cannot be rationalized in the framework of the commonly accepted mechanisms of particle growth6,13 observed by means of light scattering was reported also by Rumminger and Linteris.11,15 In our previous studies14,16 as well as in the experiments conducted by light scattering methods11,15 the flame configuration was not one-dimensional, therefore leaving some ambiguity as the simulations utilizing detailed reaction models were restricted to one-dimensional flows.
In the present work a flat, laminar, premixed, low pressure CH4–O2 flame doped with IPC was studied for the first time using the recently developed PMS-QCM technique, to address the kinetic mechanism of NP formation. The flat synthesis flame stabilized on a sinter plate provides relatively simple, nearly one-dimensional flow geometry, allowing for direct comparison of species concentrations measurements and kinetic models output.
2 Experimental
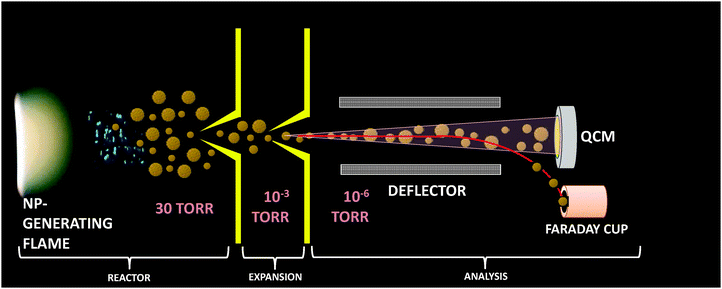
The low pressure (30 Torr) premixed methane (450 standard cubic centimeters, sccm)–oxygen (900 sccm) synthesis flame doped with IPC (20–920 ppm) was stabilized on a McKenna flat flame burner (60 mm diam.) situated in the combustion synthesis reactor of the PMS-QCM apparatus described in detail by Fomin et al.14 (see Fig. 1).Briefly, the distance between the burner surface and the sampling orifice (0.5 mm diameter) on top of a stainless steel conical skimmer (hereinafter referred to as the distance from the burner, DFB) allows to form a free jet by directing NP loaded gas from the flame into the expansion chamber, forming a frozen sample of the flame aerosol. The central part of the free jet is then extracted by a second skimmer and propagates as a particle-loaded molecular beam into the analysis chamber.
The analysis protocol following molecular beam sampling of the flame aerosol incorporates sorting the charged particles according to mass/charge ratio (m/z) via electrostatic deflection and detection of neutral particles by monitoring the oscillation frequency of the quartz crystal exposed to the particle-laden molecular beam. This yields the information regarding total mass concentration, probability density distribution of m/z and particle number density. In addition, samples of flame-generated NPs were collected on carbon mesh copper grids, placed into the particle-laden molecular beam in the analysis camber for 0.5–5 min. The samples were then analyzed by a transmission electron microscope (TEM).
The OH spectra (R-branch of the (0,0) band of the A2Σ+ − X2Πi system centered around 307 nm) were measured by laser induced fluorescence (LIF) and used for the evaluation of temperature profiles of flame gases according to protocol described elsewhere.17
3 Results and discussion
Fig. 2A depicts the slope of the QCM frequency variation versus the distance from the burner (DFB). During the exposure of the quartz crystal to the particle-laden molecular beam the crystal mass is increasing due to particle deposition, leading to a decrease in its resonant frequency. The decrease of the frequency can be related to the mass increase by the Sauerbrey equation:18 | (1) |
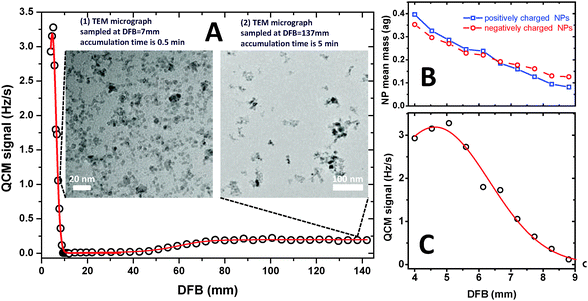
Two features of the NP mass concentration profile are immediately apparent from Fig. 2A: the first, and more trivial one, is the “late” formation of NPs (at DFB > 40 mm), which is consistent with previous PMS measurements of metal oxide NP formation in flames.6–9
The second, more surprising feature is the formation of “prompt” NPs appearing as a sharp and strong peak at DFB = 4.5 mm in close proximity to the luminous zone of the premixed flame. Shortly past the flame front this peak (see the zoom-in in Fig. 2C) decreases steeply and vanishes to the levels below the QCM sensitivity at 10 mm < DFB < 40 mm. The higher mass concentration of NPs within the “prompt” peak compared to “late” NP tail correlates well with TEM micrographs of the NP samples taken at DFB = 7 mm (“prompt peak”) and 137 mm (“late tail”) (see insets in Fig. 2A): note that 10 times longer exposure time was used for the TEM sample taken at DFB = 137 mm.
Small particles within the size range of 3–5 nm are predominantly observed within the prompt NP peak (see inset (1) in Fig. 2A), while mostly large (20–100 nm) aggregates are observed at large distances from the burner (see for example inset (2) in Fig. 2A). The analysis of high resolution TEM images (not shown here) reveals crystallographic parameters characteristic for iron oxides. The measurement of the QCM frequency was conducted at each DFB simultaneously with the measurement of the PMS current dependence on the deflection voltage. In this manner probability density distributions of m/z were obtained for each DFB. Within the assumption of singly charged particles, which is conceivable for size range of 3–5 nm,14,20 variation of NP mean mass across the prompt NP peak was derived – see Fig. 2B. Remarkably, the PMS measurement reveals about 4-fold decrease of the NP mean mass (from 0.4 attogram (ag) to 0.08 ag and from 0.35 to 0.13 ag for positively and negatively charged NPs, respectively) across the narrow 5 mm range of the prompt NP peak.
High NP concentration at short DFBs followed by the sharp decrease towards the flame front along with the particle mass (size) decrease is similar to our previous observation in the bulb-shaped flame.14 However, for the bulb-shaped flame the sharp drop of particle concentration towards the flame front could be attributed to particles traveling along diverging (radial) trajectories originating from the curved flame front as well as to particle oxidation/decomposition in the high temperature flame front rich with free radicals. The present measurements conducted in a flat flame configuration, indicating a sharp concentration drop along with a particle size decrease allow to outrule the strong expansion of the NP-laden gas and unambiguously prove that NP oxidation/decomposition is the predominant reason for the NP concentration drop towards the flame front.
The formation of NPs at very short DFBs can be rationalized by taking into account the fast decomposition of the IPC precursor at moderately elevated temperatures.4,21 The decomposition of Fe(CO)5 results in a fast release of atomic Fe in close proximity to the burner surface. In the vicinity of the burner surface the temperature is high enough for the thermal decomposition of Fe(CO)5 and low enough for iron atoms to condense (600–800 K) by adding to dimers and larger clusters through bimolecular association reactions.4 This process gives rise to formation of the “prompt peak” of the NP mass concentration profile. It is hard to identify ex situ elemental iron NPs within the size range of 3–5 nm that were observed at this work. According to literature22 iron nanoparticles sized above 10 nm can be oxidized at room temperature to the core–shell structure with an iron oxide shell 2–3 nm thick. Particles smaller than 7 nm oxidize entirely to iron oxide at room temperature. Therefore, ex situ analysis pointing to formation of iron oxides is not inconsistent with presence of nascent iron clusters in the vicinity of the burner. As the temperature continues to increase towards the flame front (up to ∼1700 K) the nascent particles undergo a gasification process through evaporation followed by gas phase oxidation and/or direct heterogeneous oxidation, which results in the reduction of particle size (mass) and mass concentration (see Fig. 2B and C). As the temperature decreases at large DFBs, the nucleation occurs again and particles reappear, producing the “late tail” of iron oxide NPs. We attribute the different magnitudes of the QCM signal at the “prompt peak” and the “late tail” to thermophoretic redistribution of particles and gas composition dependence of the nucleation process.
Within this line of thought it is reasonable to assume that the load of the IPC precursor should be high enough to produce sufficient concentration of Fe atoms for the nucleation process to occur in the vicinity of the burner surface. In order to test this hypothesis we carried out experiments examining dependence of particle formation on Fe(CO)5 concentration. The dependence of the QCM-measured NP mass concentration (at DFB = 8 mm) on the IPC concentration in the unburned premixed gases is shown in Fig. 3 along with very simple analytical, kinetic model and results of numerical calculation based on more elaborate assumptions. Indeed, the experiment indicates that for an IPC load below 50 ppm the particle mass concentration in the vicinity of the burner surface is below the QCM sensitivity and virtually indistinguishable from an undopped flame.
 | ||
| Fig. 3 Dependence of NP mass concentration, measured at DFB = 8 mm on the load of the Fe(CO)5 precursor in the unburned, premixed gases. Empty diamonds – QCM measured experimental data (normalized to the value of mass concentration predicted by numerical simulation at the highest precursor load). Red solid line – prediction based on a numerical simulation using a detailed reaction mechanism.23 Blue dashed line – behavior predicted by the simple analytical model based on 2 reactions (see text). | ||
The simplistic model aiming to describe the “prompt” NP generation process assumes very fast decomposition of Fe(CO)5 yielding gas phase Fe atoms with number concentration equal to the initial concentration of IPC (denoted by A0). The nascent Fe atoms participate in two parallel competing processes:
The first one is a second order process, yielding Fe2 dimers, followed by formation of NPs by adding to dimers and larger clusters via bimolecular association reactions:
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 and A0 – is the initial number concentration of Fe-atoms (equal to the initial concentration of Fe(CO)5).
and A0 – is the initial number concentration of Fe-atoms (equal to the initial concentration of Fe(CO)5).
Since the number concentration of the gas phase products (denoted by G) formed in the reaction (3) is governed by the equation:
 | (6) |
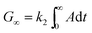 | (7) |
 | (8) |
To further assess the feasibility of “prompt” NP formation under our experimental conditions with more detailed realistic chemistry we carried out a numerical simulation invoking a mechanism of IPC oxidation in a methane–oxygen flame proposed in the work of Feroughi et al.,23 comprising of 85 species and 458 reactions. This mechanism is compiled from three sources. The CH4–O2 system is described by the GRI 3.0 mechanism,24 while the thermal decomposition of Fe(CO)5 and the formation of Fe2<n<8 clusters were simulated using the mechanism proposed by Wen et al.4 The interplay of iron containing species with hydrocarbon flame chemistry and the formation of iron oxide was described using a modified and extended mechanism of Rumminger et al.25 and Wlokas et al.6 The 1-D simulation of the flat laminar synthesis flame was conducted using the reaction kinetics library Cantera.26 The flame temperature profile measured by the OH-LIF technique was used as input for the simulation to effectively account for heat losses in the reactor. The calculated mole fractions of Fe2<n<8 clusters, solid Fe2O3 and Fe(CO)5 are shown in Fig. 4.
 | ||
| Fig. 4 Calculated mole fractions of iron pentacarbonyl, iron clusters and Fe2O3(s) along with the OH-LIF measured temperature profile (right Y-axis), used as an input for 1-D numerical simulation. | ||
The thermal decomposition of Fe(CO)5 starts immediately as the cold gases emerge from the burner surface. The resulting gas phase Fe and Fe(CO)n (mainly Fe(CO)2) react with each other or via self bimolecular, nearly barrierless, reactions which seed the subsequent nucleation.4 Therefore, competition with concurrent Fe + O2 + M = FeO2 + M main oxidation reaction (with activation barrier of ∼16.5 kJ27) becomes feasible despite the excess of molecular oxygen. The model predicts an iron clusters (2 < n < 8) peak at DFB ∼ 0.5 mm, where the Fe(CO)5 mole fraction becomes negligible. The flame temperature reaches its peak value of ∼1700 K at DFB ∼ 4 mm, where the model predicts the cumulative iron cluster mole fraction to vanish due to evaporation processes (reverse reactions to those of bimolecular addition, responsible for cluster formation). The competition between cluster formation and destruction processes gives rise to the sharp “early” cluster peak prior to the flame front, qualitatively consistent with experimental observations. The iron atom oxidation process eventually leads to the formation of iron oxide NPs represented in the model as Fe2O3(s), which extends to large distances from the burner consistent with experimental observations. Similar to the experiment, the calculation with the ref. 23. Mechanism, predicts highly nonlinear, “threshold-like” dependence of cumulative cluster mass concentration dependence on the precursor load (see the red solid line in Fig. 3).
One has to stress out that while the model interpretation strengthens the experimental data, the comparison has to be taken only semi-quantitatively due to obvious shortcomings currently existing both in experiment and the model: The measured mass NP concentration is in relative units, which precludes us from comparison of the absolute mass concentration values; while assuming formation of small iron clusters (2 < n < 8), the model does not include formation of real NPs in the 3–5 nm size range containing thousands of iron atoms. Note that the seeding, dimer formation processes from Fe and Fe(CO)2 are the rate determining steps of the particle formation process. Direct oxidation of iron clusters (other than evaporation and oxidation via the Fe-atom path) is presently not included in the model. Once large particles formation is “allowed” in the model they will grow very rapidly by adsorbing Fe-atoms from the gas phase. This is due to the large heat capacity of the large NPs allowing them to absorb the excess bond energy and serve as an effective “third body”, bringing the rate constants of the Fe adsorption reaction to the high-pressure-limit.4 Therefore, it is conceivable that inclusion of large particles formation into the model will significantly increase the mass concentration of the particles in the “prompt peak”, potentially improving the agreement with the model. Moreover, for direct quantitative comparison of the position of the “prompt peak” and the “late tail” between model and experiment, both temperature measurements and computational fluid dynamics (CFD) simulations of the two- or three-dimensional flame, taking into account the probe effects will be required. These efforts are currently underway.
4 Conclusions
In summary, we have demonstrated that the formation of NPs in IPC-doped flames starts very early, in close proximity to the burner surface, prior to the flame front. Then, the NP mass concentration falls abruptly at high temperature flame front. The early NP formation followed by the sharp decrease of NP mass concentration at the flame front gives rise to the “prompt” NP peak, which is semi-quantitatively consistent with kinetic models including iron cluster formation. The unequivocal observation of “prompt” NP formation in a premixed flat flame is consistent with our observations in a bulb shaped flame14 and suggests that this is a general phenomenon, not limited to diffusion flames.23 This observation highlights the deficiencies of the presently existing mechanisms describing iron oxide particle synthesis in flames and calls for the development of new models enabling predictive synthesis of NPs from the gas phase both for laboratory and industrial scale applications.Acknowledgements
This work was supported in part by the Israel Science Foundation (Grant No. 1149/12), Israel Ministry of Energy and Water Resources (Grant No. 211-11-007/2011-7-10) and the Research Authority of The Open University of Israel (Grant No. 47324).References
- A.-H. Lu, E. L. Salabas and F. Schüth, Angew. Chem., Int. Ed., 2007, 46, 1222–1244 CrossRef CAS PubMed.
- G. Beaucage, H. K. Kammler, R. Mueller, R. Strobel, N. Agashe, S. E. Pratsinis and T. Narayanan, Nat. Mater., 2004, 3, 370–374 CrossRef CAS PubMed.
- M. Height, J. Howard and J. Tester, Proc. Combust. Inst., 2005, 30, 2537–2543 CrossRef PubMed.
- J. Z. Wen, C. F. Goldsmith, R. W. Ashcraft and W. H. Green, J. Phys. Chem. C, 2007, 111, 5677–5688 CAS.
- J. Z. Wen, H. Richter, W. H. Green, J. B. Howard, M. Treska, P. M. Jardim and J. B. Vander Sande, J. Mater. Chem., 2008, 18, 1561 RSC.
- I. Wlokas, A. Faccinetto, B. Tribalet, C. Schulz and A. Kempf, Int. J. Chem. Kinet., 2013, 45, 487–498 CrossRef CAS.
- C. Hecht, H. Kronemayer, T. Dreier, H. Wiggers and C. Schulz, Appl. Phys. B: Lasers Opt., 2008, 94, 119–125 CrossRef PubMed.
- C. Janzen and P. Roth, Combust. Flame, 2001, 125, 1150–1161 CrossRef CAS.
- H.-R. Paur, W. Baumann, H. Mätzing and H. Seifert, Nanotechnology, 2005, 16, S354–S361 CrossRef PubMed.
- B. McMillin, P. Biswas and M. Zachariah, J. Mater. Res., 1996, 11, 1552–1561 CrossRef CAS.
- M. Rumminger and G. Linteris, Combust. Flame, 2002, 128, 145–164 CrossRef CAS.
- M. Rumminger and G. Linteris, Combust. Flame, 2000, 120, 451–464 CrossRef CAS.
- P. Roth and A. Hospital, J. Aerosol Sci., 1994, 25, 61–73 CrossRef CAS.
- A. Fomin, M. Poliak, I. Rahinov, V. Tsionsky and S. Cheskis, Combust. Flame, 2013, 160, 2131–2140 CrossRef CAS PubMed.
- M. Rumminger and G. Linteris, Combust. Flame, 2000, 123, 82–94 CrossRef CAS.
- A. Hevroni, H. Golan, A. Fialkov, I. Rahinov, V. Tsionsky, G. Markovich and S. Cheskis, Meas. Sci. Technol., 2011, 22, 115102 CrossRef.
- I. Rahinov, A. Goldman and S. Cheskis, Combust. Flame, 2006, 145, 105–116 CrossRef CAS PubMed.
- G. Sauerbrey, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- S. L. Howard, R. J. Locke, R. C. Sausa and A. W. Miziolek, Rapid Commun. Mass Spectrom., 1992, 6, 278–283 CrossRef CAS.
- N. Fuchs, Pure Appl. Geophys., 1963, 56, 185–193 CrossRef.
- D. Woiki, A. Giesen and P. Roth, Proceedings of International Symposium on Shock Waves, 2001 Search PubMed.
- J. Antony, Y. Qiang, D. Baer and C. Wang, J. Nanosci. Nanotechnol., 2006, 6, 568–572 CAS.
- O. M. Feroughi, S. Hardt, I. Wlokas, T. Hülser, H. Wiggers, T. Dreier and C. Schulz, Proc. Combust. Inst., 2014 DOI:10.1016/j.proci.2014.05.039.
- C. Bowman, R. Hanson, D. Davidson, W. Gardiner, V. Lissianski, G. Smith, D. Golden, M. Frenklach, H. Wang and M. Goldenberg, GRI mechanism ver 3.0, see http://www.me/berkeley.edu/gri_mech, 1997 Search PubMed.
- M. Rumminger, D. Reinelt, V. Babushok and G. Linteris, Combust. Flame, 1999, 116, 207–219 CrossRef CAS.
- D. Goodwin, N. Malaya, H. Moffat and R. Speth, Cantera, An object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes, available at http://code.google.com/p/cantera/.
- U. S. Akhmadov, I. Zaslonko and V. Smirnov, Kinet. Catal., 1988, 29, 251–257 Search PubMed.
| This journal is © the Owner Societies 2015 |