Oxygen adsorption onto pure and doped Al surfaces – the role of surface dopants

Abstract

Using density functional theory (DFT) with the PBE0 density functional we investigated the role of surface dopants in the molecular and dissociative adsorption of O₂ onto Al clusters of types Al₅₀, Al₅₀Al_ad, Al₅₀X and Al₄₉X, where X represents a dopant atom of the following elements Si, Mg, Cu, Sc, Zr, and Ti. Each dopant atom was placed on the Al(111) surface as an adatom or as a substitutional atom, in the last case replacing a surface Al atom. We found that for the same dopant geometry, the closer is the ionization energy of the dopant element to that of elemental Al, the more exothermic is the dissociative adsorption of O₂ and the stronger are the bonds between the resulting O atoms and the surface. Additionally we show that the Mulliken concept of electronegativity can be applied in the prediction of the dissociative adsorption energy of O₂ on the doped surfaces. The Mulliken modified second-stage electronegativity of the dopant atom is proportional to the exothermicity of the dissociative adsorption of O₂. For the same dopant element in an adatom position the dissociation of O₂ is more exothermic when compared to the case where the dopant occupies a substitutional position. These observations are discussed in view of the overlap population densities of states (OPDOS) computed as the overlap between the electronic states of the adsorbate O atoms and the clusters. It is shown that a more covalent character in the bonding between the Al surface and the dopant atom causes a more exothermic dissociation of O₂ and stronger bonding with the O atoms when compared to a more ionic character in the bonding between the dopant and the Al surface. The extent of the adsorption site reconstruction is dopant atom dependent and is an important parameter for determining the mode of adsorption, adsorption energy and electronic structure of the product of O₂ adsorption. The PBE0 functional could predict the existence of the O₂ molecular adsorption product for many of the cases investigated here.

---

Introduction

Interactions between oxygen and aluminum are of interest for many technological applications that involve this metal, such as catalysis and diverse areas of material technology.¹ Aluminum, the most abundant metal in the earth's crust, is already used in a wide variety of processes but still finds innovative usages in many different applications. Upon exposure to oxygen, aluminum metal surfaces are readily passivated by a layer of oxide which enhances their corrosion resistance.² The high exothermicity of the reaction of aluminum with oxygen leads to the formation of an oxide which is thermodynamically stable under a wide variety of conditions.³ Understanding the interactions between oxygen and aluminum is thus important in order to further improve and better predict the performance of aluminum based materials.

Gaining detailed knowledge of the interactions, adsorption and further reactions of O₂ with metal surfaces is challenging for both experimental and theoretical approaches.⁴ This is mostly due to the fact that these processes are fast and involve changes in the spin state of O₂ as the gas-phase molecule interacts with surfaces of metals.⁵ It is known from experimental^1,6,7 and theoretical^1,7–9 investigations that the reaction of dissociation of O₂ at Al surfaces is very fast: the molecular adsorption product of O₂ has little stability and consequently it is short-lived. Nevertheless, at the Al(111) surface, the molecular adsorption of O₂ occurs leading to a stable product.^8,9 The adsorption of the O atoms resulting from the dissociation of O₂ is generally considered as the initial step of the process of oxidation of Al.^8,10–12 The fact that an energy barrier for O₂ adsorption is not predictable in many computational studies has been attributed to the limitations of single determinant electronic structure calculation methods in describing the triplet–singlet transition that occurs in O₂ when the molecule starts to interact with a metal surface.^4,13 The change in spin multiplicity in O₂—that is subject to the Wigner spin selection rules—has been appointed as one of the main underlying causes for the existence of an energy barrier for the homolytic cleavage of the O–O bond in O₂ at metal surfaces.^5,14 Other phenomena such as non-local exchange effects¹⁵ or short-ranged correlation effects¹³ also contribute for the existence of the energy barrier for O₂ cleavage. All these phenomena are at the origin of the low dissociative sticking probability^7,16 (<0.01) for O₂ at Al(111).¹⁷ Additionally, the presence of other chemical elements at the surface of Al is known to affect the chemistry and dynamics of the interactions of O₂ with these surfaces.¹⁸ These systems present an additional level of complexity in what concerns the electronic structure of the surface–adsorbate complex when compared with the surface of a pure metal.

It has been shown experimentally that the adsorption of O₂ onto Al(111) at low temperatures between 85 and 150 K gives rise to close-spaced dimers of surface bound O atoms which are distributed at the surface at large separations—of several tenths of Å between dimers.¹⁹ The spacing between the O atoms in the dimers lies in the range of one to three Al interatomic distances. In the cited study it was found that even though these O atoms are close-spaced, they are not bound to each other and are in the form of atomic O. The underlying reason for the close spacing of these species might reside on the fact that after homolytic O₂ splitting, due to their strong interactions with the surface, the adsorption of the resulting O atoms is very exothermic—in the order of 5 eV per O atom.¹¹ This fact, together with the interactions between the O atoms, limits the surface mobility of the O atoms at low temperatures. A reason for the apparent randomness of the surface distribution of O dimers has not been specified but based on the existing knowledge of the effect of surface defects in lowering many energy barriers for homolytic bond cleavage in adsorbates, the role of surface defects should not be excluded as an underlying cause for this apparent randomness.²⁰

The adsorption of O₂ onto a metal surface is accompanied by charge transfer from the surface to the O₂ molecule. The lowest unoccupied molecular orbital (LUMO) of O₂ is an anti-bonding 2π* orbital. Populating this orbital leads to the weakening and ultimately to the splitting of the bond in O₂. In spite of the challenges which electronic structure methods face for correctly describing the chemistry of O₂ at metal surfaces,²¹ hybrid DFT functionals could previously successfully grasp the details of the molecular adsorption structure and the energy barrier for splitting the O₂ molecule at the Al(111) surface.²² The pure DFT functionals based only on the generalized gradient approach (GGA) or local density approximation (LDA) fail to account for an energy barrier for dissociative adsorption of O₂ and thus cannot locate the molecular adsorption structure in the adiabatic potential energy surface.^5,8,23,24 The reason for this discrepancy with experiments has been attributed to the fact that the energy of the LUMO of O₂ as predicted by GGA or LDA type of functionals lies below the Fermi level of Al.²² According to the authors, this makes the charge transfer from the Al surface to O₂ a spontaneous and barrierless process when described using such functionals. The hybrid DFT functionals place the LUMO orbital of O₂ at energies above the Fermi level of Al and consequently can account for the existence of an energetic barrier for electron transfer from the surface to the O₂ orbitals. This suggestion that hybrid DFT is always able to predict the existence of a barrier for the cleavage of O₂ in view of the placement of the electronic energy levels of O₂ and of the surface will be discussed in this work.

In this work, we report the results of the investigation of the effect of the presence of dopant atoms on the adsorption of O₂ onto the Al(111) surface using DFT. This study compares the adsorption of O₂ onto a plane Al(111) surface and onto surfaces where one dopant atom of the following elements was added, Zr, Ti, Si, Sc, Mg, and Cu. Two types of geometry for the dopant atom were investigated: one consisting of the dopant as an adatom; the second is the case where the dopant substitutes an Al(111) surface atom—making a plane Al(111) surface with a substitutional impurity. We found that both the type of doping element and its disposition at the Al(111) surface can greatly affect the bonding, the mechanism and the energetics of O₂ adsorption onto the Al(111) surface.

Computational details

The DFT calculations were performed using cluster²⁵ models of Al and the software package Jaguar 7.9.²⁶ The geometry optimizations were done using the hybrid density functional PBE0.^27,28 The PBE0 functional has previously provided a good description of the electronic properties and structures of Al clusters.^29,30 For geometry optimizations, the all-electron 6-31G basis set was employed for non-transition metal atoms. This implies 13 basis functions per Al atom. For the transition-metal atoms, Zr, Cu, Ti, and Sc, the LACVP basis set was used. The basis set LACVP is a combination of the split valence basis set 6-31+G(d) and the Los Alamos effective core potential (ECP) (ref. 31) for transition metals. The single point energy calculations were done using the split valence, all-electron triple-ζ basis set 6-311G++** for non-transition metals, which corresponds to 21 basis functions per Al atom. This basis set supplements all atoms with polarization and diffuse functions. The transition metals were treated with the LACV3P++** basis set which is the triple-ζ implementation of the LACVP basis set and augments the transition metal basis set with polarization and diffuse functions. The effect of the addition of an a posteriori term of D3 type to the energies obtained with PBE0 for accounting for dispersion interactions was also investigated. This is the zero-damping, two-body only correction as previously suggested by Grimme et al.^32,33 Tight convergence criteria and ultrafine integration grids were used for all the calculations (atomic units): rms gradient <3 × 10⁻⁴; maximum gradient <4.5 × 10⁻⁴; rms step <1.2 × 10⁻³; maximum step <1.8 × 10⁻³; maximum change in total energy between two consecutive steps <5 × 10⁻⁵.

The adsorption energies reported herein were calculated as

ΔE_ads = E_{adsorbate/cluster} − (E_adsorbate + E_cluster)

where E_{adsorbate/cluster}, E_adsorbate, and E_cluster represent the 0 K electronic energies in the gas-phase for the adsorbate binding to the cluster, free adsorbate and bare cluster respectively. This definition means that the more negative is the adsorption energy, the stronger is the adsorption. The cluster models implemented here conform to the three principles proposed to model metal oxides using clusters.^34,35 These principles are the neutrality principle, the stoichiometry principle and the coordination principle.

The electronic structure descriptors such as density of states and orbital analysis were calculated using the software package AOMix.³⁶ The methods used to compute the overlap population density of states (OPDOS) as well as the contribution of O atom orbitals to bonding, both as a function of the orbital energies, are the standard methods employed^37,38 and described in AOMix. The fragments considered for computing the OPDOS consist of the clusters (fragment 1) and the O atoms (fragment 2). The OPDOS shown and discussed in this work are the result of the overlap between the electronic states of these two fragments. The OPDOS computation method allows the determination of the contribution of the orbitals of a given fragment—at certain energies—to the one-electron levels of a product where such fragment is part of. OPDOS plots use Mulliken population analysis³⁹ (MPA) as a method for the electron population analysis. When used to study changes in electron populations due to adsorption⁴⁰ or to compare the electron populations of clusters that only differ slightly in chemical composition,⁴¹ the MPA approach has proved to be a reliable method.

Results and discussion

Pure Al clusters

It has been demonstrated previously that adsorption and further reactions on surfaces of pure metals and alloys can be fairly well-modelled using cluster models provided that low coverages of adsorbates are considered.^18,42–44 The clusters of Al used in this work were built following some fundamental criteria recurrently suggested to model surfaces using cluster models.⁴⁵ The clusters were built keeping in mind that these properties should be conserved when the surfaces are sliced from the extended crystal structures. It has been shown additionally that a high level of symmetry is a desirable feature of cluster models of metals in order to avoid instabilities in the corresponding wave-function and to speed up its determination.⁴⁶ The clusters used in this work are of types Al₅₀ (C_3v), Al₅₀Al_ad, Al₅₀X_ad and Al₄₉X_sub,—with X representing the surface dopant, ad in the adatom position and sub in the substitutional position replacing an Al(111) atom. The dopants considered are Si, Mg, Cu, Sc, Zr and Ti. These clusters have the highest symmetry possible for a 50-atom pyramidal-shaped cluster based on the (111) surface cut from a fcc crystal structure. For the geometry optimizations, the coordinates of the (111) surface and the inner atoms were allowed to relax while the coordinates of the atoms comprising the other facets of the clusters were kept fixed.

It has been also previously illustrated the need for using an all-electron basis set for accurately describing the chemistry of higher oxidation states of Al.⁴⁷ For the present work, this fact was taken into account given that the goal is to investigate the molecular adsorption of O₂, its cleavage and the formation of the first Al–O bonds that will further lead to stoichiometric aluminum oxide. Furthermore, a study on the binding of O₂ to transition metals revealed high sensitivity of the overlap populations obtained in what concerns the type of basis set used.⁴⁸ Employing a triple-ζ all-electron basis set avoids orbital overlap artifacts due to the rigidity of the ECP approach for describing the charge-exchange reactions involving a small atom such as Al. Additionally, the limitations of the double-ζ basis sets for describing the perturbed orbitals of Al when these interact with O are avoided.⁴⁹ An all-electron basis set was used for all the calculations involving the clusters of Al₅₀ type. It is known that the cohesive energy of Al clusters with sizes ranging from 36 to 72 Al atoms shows only small fluctuations with cluster size.⁵⁰ For the first ionization energy of closed shell Al clusters, convergence within less than 0.25 eV occurs already for clusters larger than 30 Al atoms.⁵¹ Furthermore, the PBE0 density functional has demonstrated very good accuracy for describing electronic and structural properties of Al₉ type of clusters.²⁹ Additionally, due to bonding with the O atoms of O₂, the loss of electron density from the Al atoms of the Al₅₀ cluster is delocalized over the whole cluster and implies a loss of ≈0.04 e⁻/Al atom. Based on this, we employed the Al₅₀ model for the investigation of O₂ adsorption mechanisms.

Oxygen on pure Al₅₀ and Al₅₀Al_ad clusters

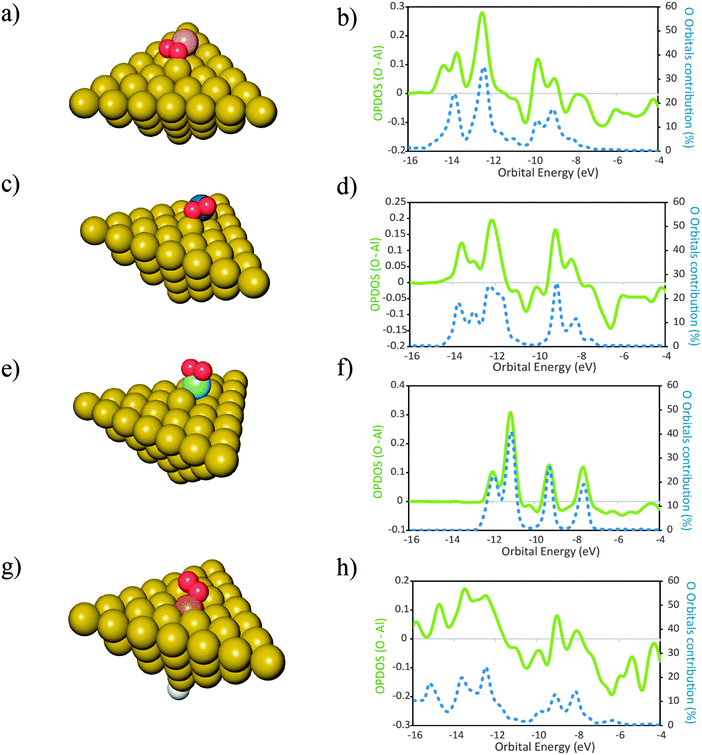
The optimized structures of the clusters Al₅₀Al_ad and Al₅₀ are shown in Fig. 1a and b respectively. All clusters used in this study are in the singlet spin state as this is the favored spin state previously found for Al clusters of this size.⁵² In order to achieve this, when necessary, a H atom was bound to an Al atom situated in the opposite side of the (111) surface of the cluster, as shown in Fig. 1b. The spatial coordinates of the H atom were allowed to relax during geometry optimizations.

Fig. 1 Clusters of 50 (a) (Al₅₀) and 51 (b) (Al₅₀Al_ad) Al atoms used to study the reactions of O₂. A H atom was added to the Al₅₀Al_ad cluster in order to maintain the closed shell singlet spin state. Al (), H ().

The products of the reaction of O₂ with the clusters of Fig. 1 are shown in Fig. 2. For the molecular adsorption, the O₂ molecule shows a preference for geometry almost parallel to the surface plane. This is in agreement with previous literature data.¹⁷ For each product is also shown the plot of the respective overlap population densities of states (OPDOS) between the O atoms and the Al cluster (Fig. 2). Also shown is the contribution of the orbitals of the O atoms to the electronic densities of states of the products. Positive OPDOS values correspond to the bonding overlap while negative values correspond to the anti-bonding overlap between the cluster and the oxygen atoms. It can be seen that the contribution of the O atom orbitals for the newly formed electronic states is smaller than 50% in all the cases. This indicates that the larger contribution for the new bonding states formed upon adsorption of O atoms comes from the cluster populated electronic states. In turn this is an indication of delocalization of the electronic density from the clusters to the O atoms in order to form the resulting bonding states, ultimately leading to the oxidation of the surface site where the O atoms adsorb. This is consistent with previous observations of bonding of radicals to metal surfaces.⁵³ We recall that when the O–O bond in O₂ undergoes splitting—and before any electronic relaxation of the newly formed O atom orbitals occurs—the O atoms are radical species with an open shell electronic structure. The interactions with the surface cause displacement of the electron density from the surface in order to form the bonded states that will lead to a closed-shell electronic structure of the complex: adsorbate–adsorption site.⁵ The extent of the interactions between the adsorbate O radicals and the surface will depend on how close in energy are the populated electronic states of the O radicals and those of the surface—in this case, the cluster Fermi level. If the difference is large, the newly formed states are more diffuse in nature. If the difference is small the newly formed states are less diffuse in terms of their energies. This model is consistent with the OPDOS plots shown in Fig. 2. For the case of the cluster with the surface adatom (Fig. 2e)—which has electronic states that lay closer to the O molecule than the case of the perfect (111) surface (Fig. 2b)—upon molecular adsorption of O₂ the newly formed states are less diffuse in energy than for the case of the perfect surface. Additionally, for the surface with the adatom, also the contribution of the O orbitals to bonding is larger than for the case of the perfect surface. This indicates that the delocalization of the electronic density from the surface to the O₂ molecule in order to form the molecular adsorption product is smaller for the case when the surface adatom is present when compared to the case of the perfect surface. Similarly, for the binding of O atoms, the contribution of these atom orbitals to the resulting bonding states is larger for the case of the surface with an adatom when compared with the perfect surface. This means that for Al(111), when a surface adatom is present, the bonding between O atoms and the surface has more covalent character than for the case when the O atoms bind to the perfect (111) surface. This has implications on the molecular and dissociative adsorption energies of O₂. The molecular adsorption is 0.5 eV more exothermic when a surface adatom is present, ΔE_ads,mo (O₂–Al₅₀Al_ad) = −2.97 eV, when compared to adsorption onto the perfect surface, ΔE_ads,mo (O₂–Al₅₀) = −2.47 eV. For dissociative adsorption of O₂, the difference in energy is smaller with adsorption onto the surface with an adatom slightly less exothermic than the perfect surface: ΔE_ads,dis (O₂–Al₅₀Al_ad) = −8.53 eV; ΔE_ads,dis (O₂–Al₅₀) = −8.64 eV. The reason for this is that even though it is more favorable—from an electronic structure point of view, due to more similarities on their energy levels—to bind the O atoms to the surface containing the adatom, for this case, the surface site where the O atoms bind to also goes through a more extensive reconstruction when compared to the case of the perfect surface. This has an associated energetic cost⁵⁴ and the energy initially gained due to the presence of the adatom is in this case decreased due to the energetic penalty involved in the reconstruction of the surface. This fact is not always verified for other dopants as it will be shown in the next section. The inclusion of the dispersion energy computed with a term of D3 type leads to slightly more exothermic adsorption energies, ≈0.11 eV for molecular adsorption and ≈0.16 eV for dissociative adsorption (Table 1) for both the clean surface and the surface with adatom respectively. An increase in the exothermicity of adsorption due to the inclusion of dispersion effects is expected and is in agreement with literature data.⁴¹

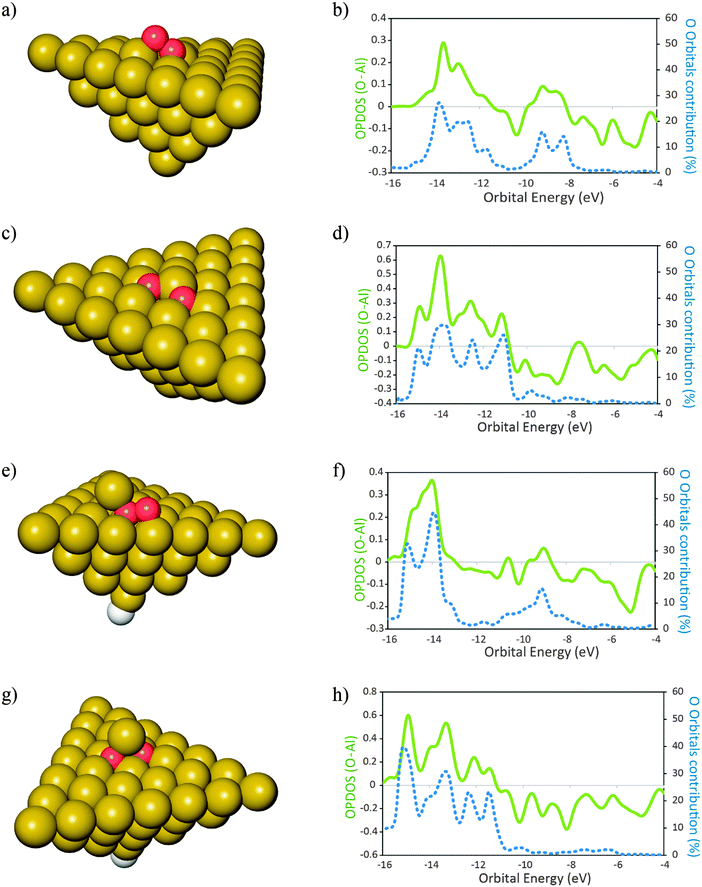Fig. 2 Products of adsorption of O₂ onto Al₅₀ (a and c) and Al₅₀Al_ad (e and g) clusters. In the plots (b), (d), (f) and (h) are represented the overlap population densities of electronic states (OPDOS) ()—resulting from the overlap between the O atom states and the cluster states—and the contribution of the O atom orbitals to the final states () both as a function of orbital energy (eV). Only populated states are shown. (a) and (e) Products of the molecular adsorption of O₂; (c) and (g) products of the dissociative adsorption of O₂. The corresponding adsorption energies are given in Table 1. Al (), O () H (). OPDOS > 0 = bonding interactions; OPDOS < 0 = anti-bonding interactions.

Table 1 Electronic adsorption energies for different modes of adsorption of O₂ onto the (111) surface of Al clusters. Al₅₀ – flat (111) surface (Fig. 1a); Al₅₀Al_ad – (111) surface with an Al adatom (Fig. 1b). ΔE_mo (molecular adsorption); ΔE_dis (dissociative adsorption). To the values labeled with − D3 has been added a D3 type dispersion correction component to the energy. All values in eV

Cluster		O2 adsorption
		ΔEmo	ΔEmo − D3	ΔEdis	ΔEdis − D3
Al50	Fig. 1a	−2.465	−2.580	−8.644	−8.800
Al50Alad	Fig. 1b	−2.966	−3.084	−8.525	−8.689

---

Effect of the presence of Si, Mg, Cu, Sc, Zr and Ti on the molecular and dissociative adsorption of O₂ onto Al(111)

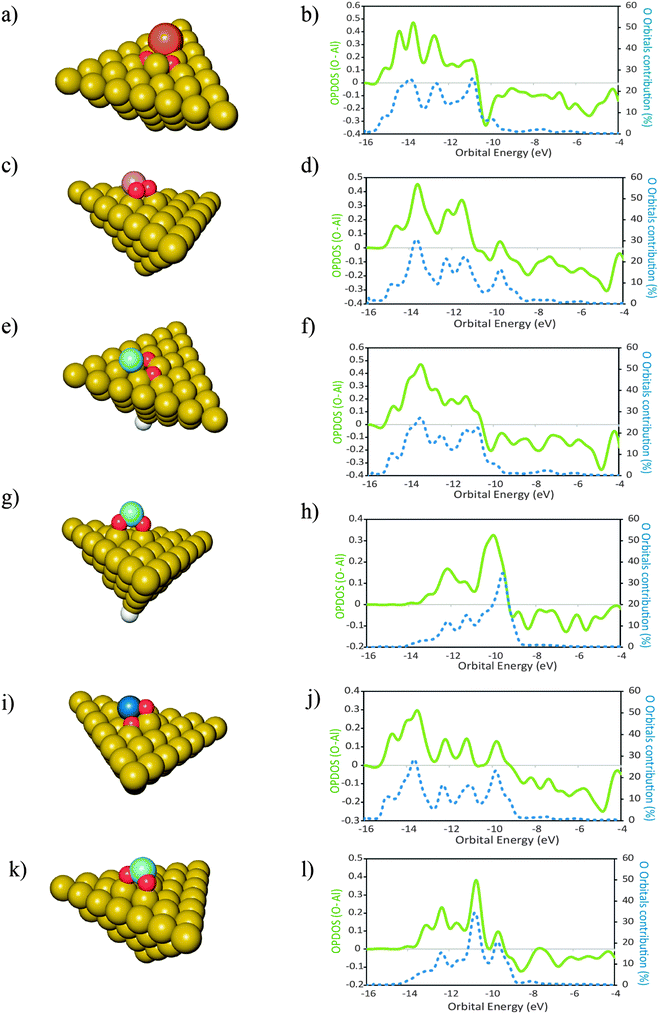
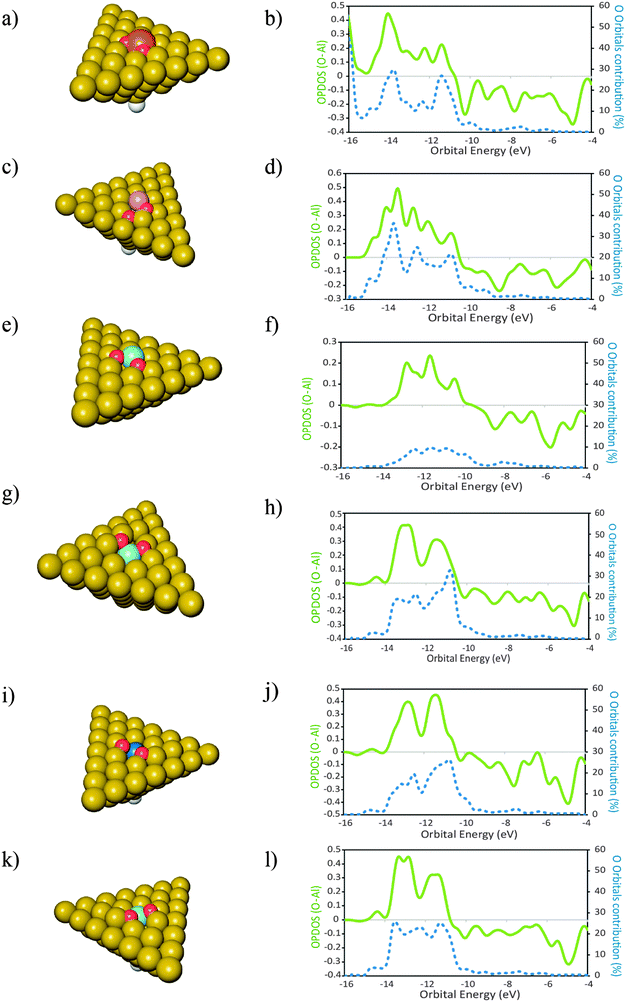
In this section we report investigations on the effect of the presence of different atomic elements on the adsorption of O₂ onto Al(111). We also studied the geometric effects that accompany the placement of dopant atoms at the surface, by placing these atoms in two distinct geometries. The dopant atoms were placed both as an adatom and as a substituent for a surface Al atom, occupying a substitutional site on the Al(111) surface.

The geometries of the products of dissociative adsorption of O₂ and their corresponding OPDOS plots are shown in Fig. 4 (dopants in adatom geometries) and Fig. 5 (dopants in substitutional position geometries). The molecular adsorption products are shown in Fig. 3. The corresponding adsorption energies are given in Table 2.

Fig. 3 Structures of the products of molecular adsorption of O₂ onto clusters of the type Al₅₀X_ad (a, c, e) with X in the adatom position: Mg (a) (); Zr (c) (); Ti (e) () and Al₄₉X_sub (g) with X placed as a surface substitutional atom: Si (g) (), Al (), H (). In the respective plots (b), (d), (f) and (h) are represented the overlap population densities of electronic states (OPDOS) ()—resulting from the overlap between the O atom states and the cluster states—and the contribution of the O atom orbitals to the final states () both as a function of orbital energy (eV). Only populated states are shown. OPDOS > 0 = bonding interactions; OPDOS < 0 = anti-bonding interactions.

Fig. 4 Structures of the products of dissociative adsorption of O₂ onto clusters of Al₅₀X_ad type. With X = Si (a, b) (); Mg (c, d) (); Cu (e, f) (); Sc (g, h) (); Zr (i, j) (); and Ti (k, l) (). X placed as a surface adatom. Al (), H (). In the plots are represented the overlap population densities of electronic states (OPDOS) ()—resulting from the overlap between the O atom states and the cluster states—and the contribution of the O atom orbitals to the final states () both as a function of orbital energy (eV). Only populated states are shown. OPDOS > 0 = bonding interactions; OPDOS<0 = anti-bonding interactions.

Fig. 5 Structures of the products of dissociative adsorption of O₂ onto clusters of Al₄₉X_sub type. With X = Si (a, b) (); Mg (c, d) (); Cu (e, f) (); Sc (g, h) (); Zr (i, j) (); and Ti (k, l) (). X placed as a surface substitutional adatom. Al (), H (). In the plots are represented the overlap population densities of electronic states (OPDOS) ()—resulting from the overlap between the O atom states and the cluster states—and the contribution of the O atom orbitals to the final states () both as a function of orbital energy (eV). Only populated states are shown. OPDOS > 0 = bonding interactions; OPDOS < 0 = anti-bonding interactions.

Table 2 Electronic energies for different modes of adsorption of O₂ onto the (111) surface of Al clusters. Al₄₉X_sub – flat (111) surface with the dopant X in a substitutional surface position; Al₅₀X_ad – (111) surface with a dopant in an adatom position. ΔE_mo (molecular adsorption); ΔE_dis (dissociative adsorption). To the values labeled with – D3 has been added a D3 type dispersion correction component to the energy. All values in eV. References in parentheses are the number of the respective figure showing the product structure; n/a means the level of theory used could not predict the molecular adsorption product of O₂ for the respective cluster

Dopant	Geometry	O2 adsorption
		ΔEmo	ΔEmo − D3	ΔEdis	ΔEdis − D3
Si	Substitutional	−2.335 (3g)	−2.425 (3g)	−8.090 (5a)	−8.272 (5a)
	Adatom	n/a	n/a	−8.299 (4a)	−8.463 (4a)
Mg	Substitutional	n/a	n/a	−8.800 (5c)	−8.955 (5c)
	Adatom	−3.377 (3a)	−3.494 (3a)	−8.006 (4c)	−8.172 (4c)
Cu	Substitutional	n/a	n/a	−6.370 (5e)	−6.551 (5e)
	Adatom	n/a	n/a	−8.163 (4e)	−8.332 (4e)
Sc	Substitutional	n/a	n/a	−8.065 (5g)	−8.191 (5g)
	Adatom	n/a	n/a	−9.206 (4g)	−9.208 (4g)
Zr	Substitutional	n/a	n/a	−7.554 (5i)	−7.713 (5i)
	Adatom	−3.750 (3c)	−3.818 (3c)	−8.416 (4i)	−8.525 (4i)
Ti	Substitutional	n/a	n/a	−2.822 (5k)	−2.918 (5k)
	Adatom	−3.731 (3e)	−3.755 (3e)	−8.403 (4k)	−8.376 (4k)

---

Only for some dopant atoms and geometries the level of theory employed here predicted molecular adsorption products of O₂. For the remaining cases, when placed on the surface, the O₂ molecule splits without an energy barrier. It has been suggested that when O₂ adsorption is computed with DFT, spontaneous splitting of the molecule occurs whenever the computed LUMO of O₂ lies at energies more negative than the computed HOMO (Fermi level) of the surface and in this way a spontaneous, barrierless charge transfer from the surface to the O₂ molecule would also occur leading to a barrierless splitting of O₂.²² This fact was not confirmed with our calculations and no correlation exists between barrierless splitting of O₂ and the relationship between the LUMO of this molecule and the HOMO of the surfaces. Upon charge transfer from the surface to the O₂ molecule, the rearrangement of the orbitals of the newly formed O₂ⁿ⁻ species will also be accompanied by a change in its bond length and such processes implicate an energy barrier.¹³ The fact that DFT could not predict the existence of barriers for O₂ splitting in some cases is probably due to the fact that in those cases the energy barriers are small enough to lie within the error interval of computed energies for reactant structures.⁵⁵ However, a detailed discussion of this topic is outside the scope of this work.

Molecular adsorption of O₂

The importance of the surface geometry effects in determining the mode of adsorption of O₂ is highlighted with the fact that for the adatom structures the elements that lead to a molecular adsorption product are Mg, Zr and Ti while for the substitutional structures only Si leads to a product of molecular adsorption of O₂. For the remaining cases, the O₂ molecule splits spontaneously when placed on the surfaces of the clusters. Even though we are not fully certain that this DFT description is correct—due to the lack of experimental data to support these findings—it is important to remark that the place occupied by the dopant atom at the surface has large implications in the mode of adsorption of O₂ and on the geometries of the products formed (Fig. 5). This happens even for cases where the adsorption energies do not differ considerably (Table 2). Such similarity may lead to misinterpretations when concluding about adsorption modes of O₂ using only the adsorption energies to support those statements. As the surface geometric effects need to be considered we can only make fair comparisons of the electronic structure between the clusters where the dopant atom occupies the same geometry. For the case of the adatom geometries, the OPDOS plots reveal that for Mg, the contribution of the O atom orbitals of O₂ for the states formed is less significant than for the cases of Zr and Ti. This observation is in agreement with the fact that both Zr and Ti have higher Pauling electronegativities of 1.33 and 1.54, respectively, when compared with that of Mg which is 1.31.⁵⁶ Because the molecular adsorption of O₂ occurs both via the interactions of its non-bonding electron pairs with the metal atoms and also due to the hybridization of the O₂ orbitals with the orbitals of the cluster,⁵⁷ a higher Pauling electronegativity of the metal atom means that these electrons involved in the bonding with O₂ are being more pulled away from the O₂ orbitals, become more delocalized and will occupy orbitals with less O₂ character than for the case where the electronegativity of the metal atom is smaller and does not exert a delocalization effect on the electrons of O₂ to such an extent. The value of ΔE_ads,mo (O₂–Al₅₀X) is less exothermic by approximately 0.38 eV for the case of Mg than for the cases of Ti and Zr. These facts, together with the data from the OPDOS plots, indicate that the molecular adsorption of O₂ is stronger for the cases where the newly formed states have more contribution from the orbitals of O₂ than for the cases where this contribution is smaller.

When the dopant atom occupies a substitutional position at the surface, the only case for which DFT predicted the existence of a molecular adsorption product was that of Si. Additionally, also for the non-doped Al surface, the adsorption of O₂ leads to a molecular adsorption geometry. This is a consequence of the similarities between the electronic structures of the two elements—Al and Si—as they occupy neighboring places in the same block in the periodic table. Because the orbitals of the other elements investigated here differ more extensively from those of Al than the orbitals of Si, the energy barriers for splitting molecular adsorbed O₂ are possibly lower for surfaces doped with such elements.⁵⁸ It is plausible that the energy barriers are low enough to lie within the errors associated with the DFT calculations as described above.

Dissociative adsorption of O₂

For the cases where the dopant atoms occupy substitutional positions, the type of dopant has a very large effect on the dissociative adsorption energies of O₂. It can be seen in Table 2 that the least exothermic value is found for the case of Ti doping while the dopant that leads to a more exothermic dissociation of O₂ is Mg. Even though the OPDOS plots of the Mg and Ti doped surfaces (Fig. 4d and l respectively) differ only moderately, the difference in exothermicity between these two extreme cases is 6 eV. This is because the dissociative adsorption of O₂ onto Al₄₉Ti causes a more extensive adsorption site reconstruction than the equivalent process on Al₄₉Mg. The energy cost for displacing the surface atoms at the adsorption site is a factor that contributes to the decrease in the exothermicity of the adsorption process.⁵⁹ In the case of Al₄₉Ti, the bonding between the reconstructed adsorption site and the O atoms is not exothermic enough to compensate for such energetic cost, causing the whole process of adsorption to be less exothermic. It can also be seen in Table 2 that the dissociative adsorption of O₂ onto the surfaces where the dopant is an adatom is more exothermic than the corresponding process occurring on a surface where the dopant occupies a substitutional position. The only exception to this is for Si with a difference of 0.21 eV between both geometries. It can be seen in the OPDOS plots of both Si geometries that more anti-bonding states are populated for the case where Si occupies a substitutional position when compared to the adatom case. Overall, there are less differences in the OPDOS plots of different dopants for the cases where the dopant atom is in a substitutional position.

For the adatom geometries, Sc and Ti are the cases that show larger differences in their OPDOS plots when compared with the remaining dopants (Fig. 3). It can be seen on the product geometries (Fig. 3) that for the cases of Sc and Ti, upon dissociative adsorption of O₂ these elements are displaced away from the surface, along the perpendicular direction, causing the dopant atoms to minimize their contact with the surface Al atoms. This makes the states of the resulting adsorption product that originates from these atom states to have more “free-atom-like” character and hence less spread in energies in the OPDOS for these two cases when compared with the remaining dopants. For elements belonging to the third row of the periodic table, there are large differences in the resulting adsorption geometries and OPDOS—Cu different from the other two third row elements Sc and Ti. This can be attributed to the involvement of either d or s orbitals in the interactions with O atoms. Cu with the valence shell as 3d¹⁰4s¹ involves the more diffuse s orbitals in the bonding with O leading to an OPDOS which is more spread in energies—also the bonding with Al is stronger for this case because of the more symmetry favorable interactions between the Cu s and Al p orbitals. On the other hand, Sc with a 3d¹4s² valence shell and Ti with 3d²4s² involve the more localized d orbitals in the bonding with O causing less spread in the OPDOS and weaker interactions with Al, making the bonding between these elements and the Al surface easier to break due to the adsorption of O atoms. This effect can also be seen on the OPDOS plots of the substitutional dopant geometries. In this case, the transition metals that are located to the left of the periodic table—Sc, Ti and Zr—also lead to less spread in the energies of the bonding OPDOS than Cu when interacting with O atoms. For these dopants, it can be seen (Fig. 4) that the bonding part of their OPDOS has two broad peaks close spaced and localized at around the same energies for the three cases, while the bonding OPDOS of Cu shows a more delocalized character.

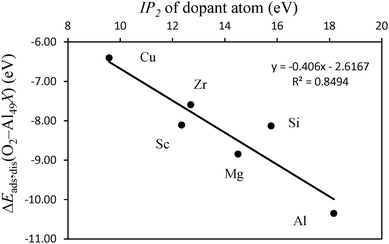
The differences in adsorption energies between the adatom and substitutional atom geometries can be further analyzed in terms of the charge of the dopant atom. It has been previously observed that for neutral clusters of Al₁₂X, with X = Mg, Al, Si, the dopant atom has a negative partial charge.⁶⁰ The authors further found that the magnitude of the dopant atom charge increases with the electronegativity and ionization potential (IP) of the dopant atom. In the cited work it was also found that for the same dopant atom, the charge is more negative for substitutionally placed dopants when compared to the case where the same dopant is an adatom. Translated into the results of this work, this implies that upon adsorption of O atoms, the more negatively charged the dopant atom is, the stronger it will bound to the O atoms because more charge is available to be displaced to the O atoms to form bonding states. Also, the polarization of the Al(111) surface will be less when the ionization energy of the dopant atom is closer to that of Al. This means that the higher the ionization energy of the dopant atom, the more the negative charge is located at this atom after forming bonded states with Al, and the more covalent character the bonding between the dopant and Al has. Based on these observations, the data in Table 2 and what is stated above for the pure Al clusters, we found that for the same surface geometry, the higher is the ionization energy of the dopant atom, the more exothermic is the adsorption of O atoms and the stronger are the bonds between the surface and the O atoms. This effect is visible in the plot of Fig. 6. The plot shows the variation in the dissociative adsorption energy of O₂ as a function of the second ionization potential (IP₂) of the dopant atoms. The second ionization potential was chosen for the reasons that will be discussed in the next section. The O₂ adsorption data are for the dopants in the substitutional position. The higher the IP₂ of the dopant atom, the more negatively charged is this atom and the stronger is the bonding with the O atoms. It can be seen that the dopant atoms that have a higher IP₂ lead to more exothermic dissociative adsorption of O₂. The correlation between both quantities supports the statement that the more covalent character the bonding between the dopant atom and the Al surface has, the stronger will be the bonds between the O atoms and the doped surface site.

Fig. 6 Plot of the dissociative adsorption energy of O₂ on an Al₄₉X_sub cluster where X represents a surface dopant atom in a substitutional position (ΔE_ads,dis (O₂–Al₄₉, X)) (eV), as a function of the second ionization potential (IP₂) of the dopant atom (eV). X = Al, Si, Mg, Cu, Sc, Zr.

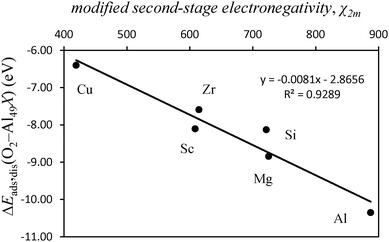
Mulliken electronegativity of the dopant atom and dissociative adsorption energy of O₂

The charge transfer between the dopant atom, X, and the Al(111) surface and further between the O atoms and the adsorption site (XAl(111)) can be analyzed based on Mulliken^61,62 concepts of electronegativity (χ), ionization potential (IP), electron affinity (EA) and the significance of these quantities for describing charge transfer to and from atoms. For the present case the charge transfer and the surface polarizability at and near the dopant site can be schematized as follows:

X + Al(111) → Xⁿ⁺Al(111)ⁿ⁻ (R1)

Xⁿ⁺Al(111)ⁿ⁻ + O₂ → (OO)^m−X^{[(m/x)+]+(n+)}Al(111)^{[(m/y)+]+(n−)} ∴ (1/x + 1/y) = 1 (R2)

where n and m can be either a fractional or an integer, and represent a partial or complete charge transfer, respectively; (R1) represents the reaction that leads to the placement of the initially charged neutral X atom at the surface; and (R2) represents the dissociative adsorption of O₂ that leads to the formation of the two surface adsorbed O atoms (OO). According to the Mulliken definition of electronegativity, χ = [(IP + EA)/2].⁶¹ For different dopants, X, keeping the same substrate, Al(111), according to the original paper by Mulliken,⁶¹ the amount of charge transferred from X to Al(111) in reaction (R1) depends on the first-stage electronegativity (χ₁) of X. Consequently, in (R2), for the series of different dopants, the difference in the amount of charge that is removed from the X (m/x) or from the Al surface (m/y) is dependent on the capability of the dopant to maintain the electrons on its orbitals when subject to a positive external potential such as that created by the O atoms. This property of the dopant atom now oxidized to the oxidation state n+ will depend on the second-stage electronegativity (χ₂) of the dopant. The property χ₂ has been defined by Mulliken as χ₂ = [(IP₂ + EA₂)/4], where IP₂ is the second ionization potential of X (for forming the species X²⁺) and EA₂ is the double electron affinity. In the present case we used Mulliken formulation but employing the first electron affinity because reaction (R1) also depends on this property of the dopant atom. We call this property the modified second-stage electronegativity (χ_2m). A plot of the dissociative adsorption energy of O₂ (ΔE_ads,dis (O₂–Al₄₉X)) as a function of the modified second-stage electronegativity (χ_2m) of the dopant atom in the substitutional position is shown in Fig. 7. The good correlation seen between ΔE_ads,dis for O₂ and χ_2m demonstrates that the Mulliken concept is applicable to both the bonding between a dopant and a surface and also to the adsorption of O₂ onto the doped surface site. It is important to note that this correlation is valid for the substitutional geometries of the adatoms. The geometric effects present when the dopant is in an adatom position cause a deviation from linearity when plotting the equivalent data. Also worth noticing is that the data for Al was included (doping with Al corresponds to the perfect Al surface) and is the ideal case where the surface, where O₂ adsorbs onto, is non-polarized. This is the case that leads to more exothermic adsorption of O₂.

Fig. 7 Plot of the dissociative adsorption energy of O₂ on an Al₄₉X_sub cluster where X represents a surface dopant atom in a substitutional position (ΔE_ads,dis (O₂–Al₄₉, X)) (eV), as a function of the Mulliken modified second-stage electronegativity, χ_2m of the dopant atom. X = Al, Si, Mg, Cu, Sc, and Zr.

The variation in adsorption energies for the geometries where the different dopants occupy an adatom position differs considerably from the variation found when the dopants occupy a substitutional position. For the different dopants in adatom geometries, the dissociative adsorption energies of O₂ vary only by 0.19 eV. The variation in the substitutional geometries is much larger, 6.0 eV. This can be interpreted as a geometric effect that has implications on the mode of interaction between the orbitals of oxygen and those of the adsorption site. The adatom geometries lead to stronger bonding between the O atoms and the XAl(111) site because of the more adsorbate readily available spatial disposition of the orbitals of the dopant when this is an adatom. This is in contrast to the case when the dopant is substitutional at the surface. In the case of the adatom geometries, the interactions between O atoms and the adsorption site occur without extensive rearrangements of the surface—even though some displacement occurs for the dopant atom in some cases, the energetic cost of this process is fairly low. In contrast, for the substitutional geometries, for the interactions between O atoms and the adsorption site to be maximized, some rearrangement of the adsorption site has to occur and this rearrangement decreases the exothermicity of the whole process of adsorption. Most importantly, for the substitutional geometries there are geometrical constraints for the orbitals of the O atoms to achieve the optimal interactions with the orbitals of the adsorption site when compared with the adatom geometries where these interactions are closer to the optimal case i.e. more free-atom-like character.

Conclusions

We investigated the effects of the presence of dopants on the Al(111) surface in the bonding with O₂ and O atoms and the modes of adsorption of these species. For the dissociative adsorption of O₂—adsorption of O atoms—different dopants at the surface lead to different types of bonding with the O atoms. This effect is dependent on both the type of the dopant atom and the geometric placement of this atom at the surface. For dopants occupying a substitutional position at the Al(111) surface—i.e. replacing a surface Al atom—dopants with a higher ionization potential lead to a more covalent type of bonding with the Al surface. This situation causes a more exothermic adsorption of O₂ compared to when the bonding between the dopant and the Al surface is more ionic in nature. It is also demonstrated that the concepts of electronegativity as developed by Mulliken can be applied with success to predict the dissociative adsorption energy of O₂ onto Al(111) when the surface is doped with atoms that occupy substitutional positions. The larger the Mulliken electronegativity of the dopant atom, the stronger is the dissociative adsorption of O₂. This is because the more covalent is the bonding between the dopant and the Al surface the more negative charge is localized at the dopant atom. In turn, the more negative charge is available at the dopant atom the easier it is to delocalize this charge from the surface to the O atoms. For the same underlying reasons, when the dopant atoms occupy an adatom geometry, the adsorption of O₂ is more exothermic when compared with the situation where the dopant is at the Al(111) surface in an substitutional position. For the same dopant atom, the adatom position allows for a better overlap of electronic states between the surface adsorption site and the orbitals of O₂ leading to a stronger bonding when compared with the adsorption onto the surface with an adatom in the substitutional position. Even though surface reconstruction leads to a better overlap between the electronic states of the O atoms and those of the surface, the energetic cost associated with this process is not always compensated by the formation of the new electronic states and in some cases, such as those involving the dopant Sc, reconstruction led to less exothermic adsorption. Additionally, the PBE0 functional could not predict an energy barrier for O₂ dissociation for all the cases investigated here.

Acknowledgements

Financial support from the Swedish Foundation for Strategic Research (SSF, project ALUX) is gratefully acknowledged. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC), Linköping.

References

1. I. P. Batra and L. Kleinman, J. Electron Spectrosc. Relat. Phenom., 1984, 33, 175–241.
2. P. J. Eng, T. P. Trainor, G. E. Brown Jr., G. A. Waychunas, M. Newville, S. R. Sutton and M. L. Rivers, Science, 2000, 288, 1029–1033.
3. G. E. Totten and D. S. MacKenzie, Handbook of Aluminum volume 2 Alloy Production and Materials Manufacturing, Marcel Dekker, 2003.
4. C. Carbogno, A. Groß, J. Meyer and K. Reuter, in Dynamics of Gas-Surface Interactions, ed. R. Díez Muiño and H. F. Busnengo, Springer, Berlin Heidelberg, 2013, ch. 16, vol. 50, pp. 389–419.
5. J. Behler, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421.
6. J. Trost, H. Brune, J. Wintterlin, R. J. Behm and G. Ertl, J. Chem. Phys., 1998, 108, 1740–1747.
7. H. Brune, J. Wintterlin, R. J. Behm and G. Ertl, Phys. Rev. Lett., 1992, 68, 624–626.
8. Y. Yourdshahyan, B. Razaznejad and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 075416.
9. Y. F. Zhukovskii, P. W. M. Jacobs and M. Causá, J. Phys. Chem. Solids, 2003, 64, 1317–1331.
10. A. Kiejna and B. I. Lundqvist, Surf. Sci., 2002, 504, 1–10.
11. J. Jacobsen, B. Hammer, K. W. Jacobsen and J. K. No/rskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14954–14962.
12. A. Kiejna and B. I. Lundqvist, Surf. Sci., 2002, 504, 1–10.
13. F. Libisch, C. Huang, P. Liao, M. Pavone and E. A. Carter, Phys. Rev. Lett., 2012, 109, 198303.
14. J. Behler, B. Delley, S. Lorenz, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2005, 94, 036104.
15. H.-R. Liu, H. Xiang and X. G. Gong, J. Chem. Phys., 2011, 135, 214702.
16. L. Österlund, I. Zoric-acute and B. Kasemo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15452–15455.
17. M. Kurahashi and Y. Yamauchi, Phys. Rev. Lett., 2013, 110, 246102.
18. C. Lacaze-Dufaure, C. Blanc, G. Mankowski and C. Mijoule, Surf. Sci., 2007, 601, 1544–1553.
19. M. Schmid, G. Leonardelli, R. Tscheließnig, A. Biedermann and P. Varga, Surf. Sci., 2001, 478, L355–L362.
20. F. Sebastian, E.-K. Lydia, V. E. Sergey, E. T. Oleg, S. Christoph, L. Peter, A. K. Konstantin, V. C. Evgueni, V. K. Tatyana, I. G. Vladimir, B. Hendrik, B. Matthias and R. Friedrich, New J. Phys., 2014, 16, 075013.
21. G. Itziar, B. Juan, M. Jörg, J. I. Juaristi, A. Maite and R. Karsten, New J. Phys., 2012, 14, 013050.
22. H.-R. Liu, H. Xiang and X. G. Gong, J. Chem. Phys., 2011, 135, 214702.
23. K. Honkala and K. Laasonen, Phys. Rev. Lett., 2000, 84, 705–708.
24. L. C. Ciacchi and M. C. Payne, Phys. Rev. Lett., 2004, 92, 176104.
25. P. Deák, Phys. Status Solidi B, 2000, 217(1), 9–21.
26. Jaguar, version 7.9, Schrödinger, LLC, New York, NY, 2012.
27. K. Burke, M. Ernzerhof and J. P. Perdew, Chem. Phys. Lett., 1997, 265, 115–120.
28. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
29. V. O. Kiohara, E. F. V. Carvalho, C. W. A. Paschoal, F. B. C. Machado and O. Roberto-Neto, Chem. Phys. Lett., 2013, 568–569, 42–48.
30. S. R. Miller, N. E. Schultz, D. G. Truhlar and D. G. Leopold, J. Chem. Phys., 2009, 130, 024304.
31. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
34. X. Xu, H. Nakatsuji, M. Ehara, X. Lu, N. Q. Wang and Q. E. Zhang, Chem. Phys. Lett., 1998, 292, 282–288.
35. X. Lü, X. Xu, N. Wang, Q. Zhang, M. Ehara and H. Nakatsuji, Chem. Phys. Lett., 1998, 291, 445–452.
36. S. I. Gorelsky, Revision 6.82 edn, Ottawa, ON, 2013.
37. R. Hoffmann, Solids and surfaces: a chemist's view of bonding in extended structures, VCH Publishers, New York, NY, 1988.
38. T. Hughbanks and R. Hoffmann, J. Am. Chem. Soc., 1983, 105, 3528–3537.
39. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
40. M. N. D. S. Cordeiro, A. S. S. Pinto and J. A. N. F. Gomes, Surf. Sci., 2007, 601, 2473–2485.
41. C. M. Lousada, A. J. Johansson, T. Brinck and M. Jonsson, Phys. Chem. Chem. Phys., 2013, 15, 5539–5552.
42. F. Illas, N. López, J. M. Ricart, A. Clotet, J. C. Conesa and M. Fernández-García, J. Phys. Chem. B, 1998, 102, 8017–8023.
43. M. Fernández-García, J. C. Conesa, A. Clotet, J. M. Ricart, N. López and F. Illas, J. Phys. Chem. B, 1998, 102, 141–147.
44. S. González, C. Sousa and F. Illas, Surf. Sci., 2004, 548, 209–219.
45. R. A. Evarestov, T. Bredow and K. Jug, Phys. Solid State, 2001, 43, 1774–1782.
46. F. Weigend and R. Ahlrichs, Philos. Trans. R. Soc., A, 2010, 368, 1245–1263.
47. J. E. Fowler and J. M. Ugalde, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 383–388.
48. M. Chen, S. P. Bates, R. A. van Santen and C. M. Friend, J. Phys. Chem. B, 1997, 101, 10051–10057.
49. M. Sierka, J. Döbler, J. Sauer, G. Santambrogio, M. Brümmer, L. Wöste, E. Janssens, G. Meijer and K. R. Asmis, Angew. Chem., Int. Ed., 2007, 46, 3372–3375.
50. A. K. Starace, C. M. Neal, B. Cao, M. F. Jarrold, A. Aguado and J. M. López, J. Chem. Phys., 2008, 129, 144702.
51. A. Aguado and J. M. López, J. Chem. Phys., 2009, 130, 064704.
52. R. Ahlrichs and S. D. Elliott, Phys. Chem. Chem. Phys., 1999, 1, 13–21.
53. A. M. Pessoa, J. L. C. Fajín, J. R. B. Gomes and M. N. D. S. Cordeiro, Surf. Sci., 2012, 606, 69–77.
54. D. P. Woodruff, in Chemical Bonding at Surfaces and Interfaces, ed. A. N. G. M. P. K. Nørskov, Elsevier, Amsterdam, 2008, pp. 1–56.
55. C. A. Farberow, J. A. Dumesic and M. Mavrikakis, ACS Catal., 2014, 3307–3319.
56. W. M. L. D. R. Haynes, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, CRC Press, Boca Raton, Fla, 2011.
57. B. Yoon, H. Häkkinen and U. Landman, J. Phys. Chem. A, 2003, 107, 4066–4071.
58. W. V. Glassey and R. Hoffmann, Surf. Sci., 2001, 475, 47–60.
59. S. Maier, P. Cabrera-Sanfelix, I. Stass, D. Sánchez-Portal, A. Arnau and M. Salmeron, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075421.
60. A. Varano, D. J. Henry and I. Yarovsky, J. Phys. Chem. A, 2010, 114, 3602–3608.
61. R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793.
62. R. S. Mulliken, J. Chem. Phys., 1935, 3, 573–585.

---