Kinetic dielectric decrement revisited: phenomenology of finite ion concentrations
Marcello
Sega
 *a,
Sofia
Kantorovich
bc and
Axel
Arnold
d
*a,
Sofia
Kantorovich
bc and
Axel
Arnold
d
aDepartment of Computational Biological Chemistry, University of Vienna, Währinger Strasse 17, 1090 Vienna, Austria. E-mail: marcello.sega@univie.ac.at
bFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria
cUral Federal University, Lenin av. 51, 620083 Ekaterinburg, Russia
dInstitute for Computational Physics, Universität Stuttgart, Allmandring 3, 70569 Stuttgart, Germany
First published on 5th November 2014
Abstract
With the help of a recently developed non-equilibrium approach, we investigate the ionic strength dependence of the Hubbard–Onsager dielectric decrement. We compute the depolarization of water molecules caused by the motion of ions in sodium chloride solutions from the dilute regime (0.035 M) up close to the saturation concentration (4.24 M), and find that the kinetic decrement displays a strong non-monotonic behavior, in contrast to the prediction of available models. We introduce a phenomenological modification of the Hubbard–Onsager continuum theory, which takes into account the screening due to the ionic cloud at the mean-field level and, which is able to describe the kinetic decrement at high concentrations including the presence of a pronounced minimum.
More than thirty years ago, in what was one of the last articles written by Onsager, he and Hubbard made a captivating prediction that has eluded direct observation until now. They stated that in a saline solution, due to the motion of ions, polar solvent molecules should show a tendency to orient against any external, static electric field, in apparent contradiction with electrostatics.1–3 According to the continuum model presented by Hubbard and Onsager, the rotational current induced in the solvent by ionic currents should generate a net solvent depolarization that survives in the zero frequency limit. As a consequence, a decrement of the static permittivity of the solution should be observed, even though the effect is purely dynamic, and as such cannot be explained in terms of molecular configurations only. Systems containing free charges can be thought as being infinitely polarizable, since the positive and negative ions in a pair can be brought at an infinite distance by a static electric field. Strictly speaking, the static dielectric permittivity of an electrolyte solution cannot be measured; instead, the real part of the dielectric spectrum at low (but finite) frequencies is used as a measure of the permittivity. To date, however, no direct experimental proof of the kinetic decrement exists, because its detection is complicated by the presence of dielectric saturation, from which it cannot be easily separated.4–8
A quantitative picture of the kinetic contribution to the dielectric decrement is therefore key to the investigations of ion solvation properties, which rely on a correct estimate of the static contribution of the decrement.9–11
The continuum theory of the kinetic decrement predicts that the static permittivity ε0 of a solvent should change upon addition of salt by an amount (in CGS units) due to a subtle interplay between motion of ions and rotational orientation of the solvent molecules,
| ΔεHO = −4πpστ(ε0 − ε∞)/ε0, | (1) |
Here, σ denotes the conductivity of the solution and τ is the time constant of the Debye relaxation process that characterizes the dielectric susceptibility of the solvent, and ε∞ is the infinite frequency dielectric constant.1,2 The factor p can take values between 2/3 and 1, depending on the type of boundary condition at the surface of the ion (full slip and no slip, respectively). Strictly speaking, the continuum theory is valid only in the infinite dilution limit, and for large ionic radii.3
Despite these limitations, the formula for the decrement bears an enthralling elegance, and explains qualitatively the dependence of the dielectric permittivity of electrolyte solutions on their conductivity, even well within the concentrated solution regime.12 However, the kinetic decrement is not the only effect that is expected to lower the dielectric permittivity of electrolyte solutions. The strong local electric field in the vicinity of the ions tends to polarize solvent molecules more than any external electric field in the linear regime. Such a high field saturates the dielectric response of solvent molecules next to ions, effectively reducing the dielectric permittivity of the solution. This effect depends on the salt concentration c and, implicitly, on the conductivity σ. For this reason it becomes hard, if not impossible, to separate the kinetic contribution from dielectric saturation experimentally.4,5,7,8 This situation prevents not only a direct observation of the kinetic decrement, but also a precise evaluation of the effect of saturation6 and, consequently, a correct estimate of the number of solvent molecules coordinated by the ions.
Here, we use a non-equilibrium molecular dynamics approach to compute the kinetic decrement over an unprecedented wide range of concentrations, which is not accessible with conventional, equilibrium approaches.13 Moreover, we present a simple phenomenological theory that gives a quantitative account of the features of the kinetic decrement at higher concentrations.
The kinetic decrement can be seen as the sum of two complementary contributions: the first is the depolarization due to the moving ions, which exerts a torque on the solvent molecules; the second, more subtle effect, is a change in the imaginary part of the ion conductivity, a lag in the response of ions induced by the rotation of solvent molecules which are oriented along the external electric field. The two contributions must have exactly the same value, as a consequence of Onsager reciprocal relations. A straightforward way to see this is through the Green–Kubo expression for the kinetic decrement. The change in solvent polarization current Jp due to the ionic one Ji leads to a contribution to the conductivity spectrum 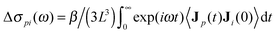 , where β is the inverse thermal energy, L3 the simulation box volume, and 〈·〉 is a suitable ensemble average. This change in conductivity reflects a change in permittivity, since ε(ω) − 1 = i4πσ(ω)/ω,14 and results in the first contribution to the kinetic decrement Δεpi = limω→04πiΔσpi(ω)/ω. Owing to the symmetry of the current cross-correlation function, the second contribution, which originates from the action of the rotating solvent molecules on the ions, is Δεip = Δεpi. The total kinetic decrement is therefore twice the first contribution, Δε = 2Δεpi.
, where β is the inverse thermal energy, L3 the simulation box volume, and 〈·〉 is a suitable ensemble average. This change in conductivity reflects a change in permittivity, since ε(ω) − 1 = i4πσ(ω)/ω,14 and results in the first contribution to the kinetic decrement Δεpi = limω→04πiΔσpi(ω)/ω. Owing to the symmetry of the current cross-correlation function, the second contribution, which originates from the action of the rotating solvent molecules on the ions, is Δεip = Δεpi. The total kinetic decrement is therefore twice the first contribution, Δε = 2Δεpi.
However elegant, the Green–Kubo expression is not very much suited for the computation of the kinetic decrement, because the signal-to-noise ratio at extreme dilutions would be too small for any practical purposes. A much more efficient way to compute Δεpi consists instead in applying an external fictitious field Ef, that couples to the ions only, and in calculating the resulting polarization of the solvent P, so that Δεpi = 4πP/(L3Ef).15 This is evidently the out-of-equilibrium counterpart of the Green–Kubo formula for Δεpi, because Ji is the current that couples to the external field Ef, and Jp the one generating the polarization P.
We applied this non-equilibrium calculation to an aqueous solution of sodium chloride at 11 different salt concentrations. In our simulations we model water molecules using the three-sites SPC/E potential16 and sodium and chloride ions using the thermodynamics consistent Kirkwood–Buff potential.17 The salt concentration c varies from 0.035 to 4.24 M, keeping the water content fixed at 1621 molecules per simulation box and changing the number of salt pairs from 1 to 140. We kept constant temperature (300 K) and pressure (1 atm) using the Nosé–Hoover18,19 and Parrinello–Rahman20 algorithms with relaxation times of 5 ps. Electrostatic interactions were computed using the smooth particle mesh Ewald method21 with tin–foil boundary conditions, a 4th order spline interpolation on a grid with spacing not larger than 0.12 nm and a relative interaction strength of 10−5 at 0.9 nm. We switched the short range part of the electrostatic interaction and of the Lennard-Jones potential smoothly to zero between 0.9 and 1.2 nm using a fourth-degree polynomial. Simulations were performed using an in-house modified version of Gromacs22 for the online calculation of the currents associated to the different species, and an integration time step of 1 fs was used.
To check that we are performing calculations in the linear regime, we applied our non-equilibrium approach for the system of 100 ion pairs using applied external fictitious fields of magnitude varying from 0.1 to 2 V nm−1, sampling the resulting depolarization of water −4πPx/L3 during 500 ps long simulation runs (Fig. 1) as a function of the applied field. The linear behavior holds even for rather high fields, and this allows us to collect meaningful statistics also for very dilute solutions with relatively short simulation runs, making this non-equilibrium approach the key to calculating the kinetic decrement over an unprecedented broad range of concentrations.
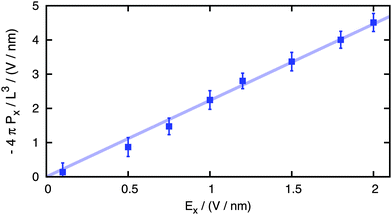 | ||
| Fig. 1 Calculated water depolarization as a function of the applied fictitious field (points) and the linear fit (line). | ||
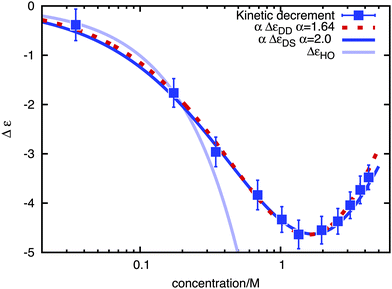
Using an external fictitious field of 0.5 V nm−1 we proceeded to calculate the kinetic decrement for different salt concentrations in 1 ns long runs, obtaining the values of dielectric decrement presented in Fig. 2. The kinetic decrement shows a marked non-monotonic dependence on the concentration, with a clear minimum right before c = 2 M. To test the Hubbard–Onsager formula, eqn (1), we also calculated the molar conductivity Λ of the solution at the different concentrations, as reported in Fig. 3. A best fit to the Kohlrausch law, 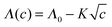 , allows us to extrapolate the molar conductivity to infinite dilution, and estimate the limiting molar conductivity Λ0 separately for the sodium and chloride ions. Therefore, we can write the Hubbard–Onsager decrement for the mixture of sodium and chloride in the form ΔεHO = −4πpτ(ΛNa0 + ΛCl0)c(ε0 − ε∞)/ε0. The Hubbard–Onsager decrement so calculated (Fig. 2, light line) is not compatible with the simulation data above a concentration of 0.2 M. The presence of a pronounced minimum and the subsequent increase of Δε cannot be explained even qualitatively with the continuum Hubbard–Onsager theory.
, allows us to extrapolate the molar conductivity to infinite dilution, and estimate the limiting molar conductivity Λ0 separately for the sodium and chloride ions. Therefore, we can write the Hubbard–Onsager decrement for the mixture of sodium and chloride in the form ΔεHO = −4πpτ(ΛNa0 + ΛCl0)c(ε0 − ε∞)/ε0. The Hubbard–Onsager decrement so calculated (Fig. 2, light line) is not compatible with the simulation data above a concentration of 0.2 M. The presence of a pronounced minimum and the subsequent increase of Δε cannot be explained even qualitatively with the continuum Hubbard–Onsager theory.
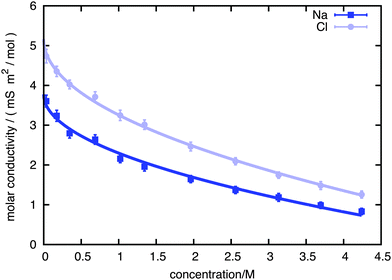 | ||
| Fig. 3 Molar conductivity of sodium and chloride ions, as a function of the concentration. Squares: sodium; circles: chloride; solid lines: best fit to Kohlrausch law. | ||
Physical intuition suggests that the local field of the ions, which determines the torque on water molecules, should be screened by the presence of oppositely charged ions in its vicinity. To formalize this, we introduce a mean-field correction to the Hubbard–Onsager theory, along the lines of the Debye–Hückel theory. The crucial step in the Hubbard–Onsager theory is the calculation of the rotational current JR induced in the polar medium by an ion travelling with speed u. The coupling between electrostatics and Navier–Stokes equations allows us to express the rotational current as a functional of the local field generated by the ion, E0, as JR = ∫(χ/2ε0)E0 × (∇ × v)dr, where v is the velocity field of the solvent surrounding the ion and χ its dielectric susceptibility.1 For large ionic radii R, the velocity field can be approximated (in the low salt concentration limit) by Stokes' solution, v(r) = (3R/4r3)[r2u + (r·u)r]. If, instead of using the Coulomb field, we use the Debye–Hückel one, E0 = (q/ε0r3)exp(−κr)(1 + κr)r, the rotational current can be evaluated analytically as JR = (2π/ε0)uχq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−κR). Here
exp(−κR). Here 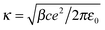 is the inverse Debye screening length.
is the inverse Debye screening length.
Since the ratio between the ion speed u and the driving electric field Ex is u/Ex = σ/q, it is possible to express the dielectric decrement (which we denote here as ΔεDS, and where the suffix hints at the use of the Debye–Hückel field and of the Stokes' flow solution) in terms of the rotational current
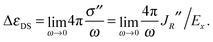 | (2) |
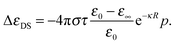 | (3) |
The solution resembles the classical Hubbard–Onsager one, but features an additional factor exp(−κR) which depends on the (effective) ion size. This difference is an important one, because it shows that even at the mean-field level there is an additional length scale, the screening length κ−1, that governs the non-monotonic behaviour of the kinetic decrement. The screening, however, affects not only the electric field generated by the ion, but also the velocity of the fluid around it, so that at finite concentrations the Debye–Hückel-corrected velocity field is expressed by23v(r) = (3R/4r3)exp(−κr)(4/3)r2u + 2κ−2[1 + κr + κ2r2/3 − exp(κr)][u − 3(r·u)r/r2]. This flow can be integrated in a similar way to the Stokes' one, yielding the decrement
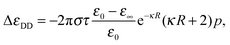 | (4) |
In Fig. 2 we compare the simulation results with the mean-field results eqn (3) and (4), summed over the contributions of the two ionic species, and multiplied by a phenomenological scaling factor α, that takes into account the effect of ionic correlations arising at high salt concentration. The relaxation time τ has been computed from a fit of the Debye process χ(ω) to the spectrum of the pure solvent, and the solution conductivity has been calculated from the limiting molar ones as for the Hubbard–Onsager case. The relaxation of water is not described by a single Debye process, and often a Cole–Cole relaxation or two Debye processes24 are used to fit experimental data. However, the dominant water contribution at lower frequencies comes from the main Debye relaxation, which is the one we are using here to calculate the decrement.
A very good qualitative agreement is already achieved by using the Stokes' flow based solution, eqn (3), and α = 2 (dark curve in Fig. 2), taking as a value for the effective ionic radius R the size of the first hydration shell of the ion. R is defined as the sum of the position of the first minimum in the ion–water radial distribution function and of the Lennard-Jones diameter of a water molecule. Also taking into account the screening of the flow due to the counterion clouds introduces a qualitative difference in the formula for the decrement, eqn (4), which is characterized by the presence of an additional term proportional to κ. In fact the smaller scaling factor α = 1.64 is sufficient to obtain an equivalently good fit, if at the same time the value of both effective ionic radii is increased by 1.5 Å. Both models are thus able to give a qualitatively correct picture of the concentration dependence of the kinetic dielectric decrement at finite concentrations, underlining the importance of the screening induced by the counterion clouds in determining the effective water–ion interaction in the hydrodynamic regime.
As a final remark, we note that due to the presence of the scaling factor α, both curves do not converge, for κR ≪ 1, to the solution of Hubbard and Onsager, the latter being a better approximation at low concentrations. Nevertheless, the simulation data show that the applicability range of the Hubbard–Onsager theory is limited to concentrations smaller than approximately 0.2 M, a condition which has been often not fulfilled when searching for experimental evidence of the kinetic decrement.12 Our simulation results thus resolve the doubts which were cast on the attribution of the measured dielectric decrement5 in favor of the hypothesis of a static effect arising from dielectric saturation,7 which is definitely the largest contribution to the dielectric decrement.
M. S. acknowledges support from the European Community's the Seventh Framework Programme (FP7-PEOPLE-2012-IEF) funded under grant No. 331932 SIDIS. S. S. K. acknowledges support from RFBR grant mol-a-ved 12-02-33106, the Ministry of Science and Education of RF 2.609.2011, the URFU Stimulating Program, and, the Austrian Science Fund (FWF): START-Projekt Y 627-N27. The authors thank Christian Schröder and Othmar Steinhauser for useful discussions. A. A. would like to thank the German Research Foundation (DFG) for financial support through the Cluster of Excellence in Simulation Technology (EXC 310/1) at the University of Stuttgart.
References
- J. B. Hubbard and L. J. Onsager, J. Chem. Phys., 1977, 67, 4850 CrossRef CAS PubMed.
- J. B. Hubbard, J. Chem. Phys., 1978, 68, 1649 CrossRef CAS PubMed.
- J. B. Hubbard, P. Colonomos and P. G. Wolynes, J. Chem. Phys., 1979, 71, 2652–2661 CrossRef CAS PubMed.
- P. Winsor IV and R. H. Cole, J. Chem. Phys., 1982, 86, 2491–2494 CrossRef.
- Y.-Z. Wei, P. Chiang and S. Sridhar, J. Chem. Phys., 1992, 96, 4569 CrossRef CAS PubMed.
- K. Nörtemann, J. Hilland and U. Kaatze, J. Phys. Chem. A, 1997, 101, 6864–6869 CrossRef.
- U. Kaatze, J. Solution Chem., 1997, 26, 1049–1112 CrossRef CAS.
- U. Kaatze, J. Mol. Liq., 2011, 162, 105–112 CrossRef CAS PubMed.
- K. Tielrooij, N. Garcia-Araez, M. Bonn and H. Bakker, Science, 2010, 328, 1006–1009 CrossRef CAS PubMed.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CrossRef CAS.
- N. Nandi, K. Bhattacharyya and B. Bagchi, Chem. Rev., 2000, 100, 2013–2046 CrossRef CAS PubMed.
- J. Hubbard, L. Onsager, W. Van Beek and M. Mandel, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 401–404 CrossRef CAS.
- A. Chandra, J. Chem. Phys., 2000, 113, 903 CrossRef CAS PubMed.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London, 1986 Search PubMed.
- M. Sega, S. Kantorovich, C. Holm and A. Arnold, J. Chem. Phys., 2014, 140, 211101 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. Weerasinghe and P. E. Smith, J. Chem. Phys., 2003, 119, 11342–11349 CrossRef CAS PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- D. Long and A. Ajdari, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 29–32 CrossRef CAS.
- J. Barthel, K. Bachhuber, R. Buchner and H. Hetzenauer, Chem. Phys. Lett., 1990, 165, 369–373 CrossRef CAS.
| This journal is © the Owner Societies 2015 |