Transient anions of cis- and trans-cyclooctene studied by electron-impact spectroscopy

Abstract

The effect which deformation of the double bond in trans-cyclooctene (TCO), compared to cis-cyclooctene (CCO), has on its negative ion – and indirectly on the π* virtual orbital – was studied by electron-impact spectroscopy. Differential elastic and vibrational excitation cross sections were measured at a scattering angle of θ = 135°. The vertical attachment energy (VAE) derived from the vibrational excitation spectra is 1.87 eV in TCO, only 0.09 eV lower than in the unstrained CCO, 1.96 eV. The substantial deformation of the C=C bond in TCO thus stabilizes its transient negative ion by a surprisingly small amount and this effect is ascribed in part to the Pauli (steric) destabilization of the TCO π* orbital by the alkyl chain facing the π* lobes. An interesting effect is observed in the elastic cross section which is about 45% larger for TCO at low energies (∼0.4 eV), despite the similar geometrical size of the two molecules. Ramsauer–Townsend minima are observed in the elastic cross section at 0.13 and 0.12 eV for CCO and TCO, respectively. Implications of the findings on enhancement of the dienophile capacity of TCO are discussed.

---

1 Introduction

Geometrical distortion is an interesting means of activating chemical bonds, an important example being the deformation of the C=C bond in trans-cyclooctene (TCO) as compared to cis-cyclooctene (CCO). The distortion has dramatic consequences on bonding in metal–olefin complexes,¹ leads to an increasing number of applications of TCO as a “voracious dienophile” for bioorthogonal labeling,^2–4 assists ring-opening metathesis polymerization⁵ and has biological implications – TCO counteracts ethylene at the receptor level in plants.⁶ In this paper we investigate what are the changes in the frontier orbitals, in particular the normally unoccupied orbital, between CCO and TCO, and whether they could contribute to the enhanced reactivity of TCO.

Electron spectroscopies are a powerful means of studying electronic structure of molecules, providing insight into the causes of the increased reactivity. UV-photoelectron spectroscopy removes electrons from the molecules and measures the ionization energies, related to energies of the occupied orbitals by the Koopmans' theorem.⁷ Photoelectron spectra revealed that the π* highest occupied molecular orbital (HOMO) is destabilized by 0.29 eV in TCO relative to CCO.⁸ Electron impact spectroscopy inserts electrons into normally empty orbitals, generating transient negative ions (synonymously called ‘resonances’), and measures the corresponding electron attachment energies. The attachment energies are related to energies of virtual orbitals, becoming temporarily occupied in the electron collision, although the relation is less direct than in the case of the positive ions, and requires empirical scaling.⁹ TCO and CCO were already studied in our laboratory by the simplest version of electron impact spectroscopy, the Electron Transmission Spectroscopy (ETS).¹⁰

In the present work we make advantage of the much more sophisticated experimental techniques constructed in our laboratory in the mean time. Resonance energies, energies where the incoming electrons are temporarily captured to form a transient anion, can now be determined as enhancements of vibrational excitation, caused by geometry relaxation, a consequence of the different equilibrium geometry of the anion as compared to the neutral molecule. This avoids the problem of the large background of direct scattering encountered when resonances are deduced from elastic scattering in the ETS technique. Furthermore, the mode selectivity of the vibrational excitation yields information on the type of geometrical distortion caused by the occupation of the π* orbital. Finally, the present experiment may shed light onto the puzzling observation of the early study¹⁰ that the ETS signal, approximately given by the total scattering, decreased below the π* resonance in CCO, as expected, but increased in TCO. The present work is related to the electron impact spectroscopy study of the effect of pyramidalization on the C=C bond.¹¹

2 Methods

2.1 Electron impact spectrometer

The measurements were performed using an electron-impact spectrometer described earlier.^12,13 It employs hemispherical analyzers to improve resolution, which was 16 meV (in the energy-loss mode), at an electron beam current of 300 pA. The energy scales are accurate to within ±10 meV. The sensitivity of the instrument is not constant when the electron energies are varied, but this effect, expressed as the “instrumental response function”, was quantized on elastic scattering in helium and all spectra were corrected as described earlier.¹³ Moreover, the probabilities for the various processes, expressed as cross sections, were determined quantitatively (i.e., we report absolute cross sections) by the relative flow technique as described earlier.^12,13 The confidence limit of the magnitudes of the measured cross sections is ±15% for the elastic cross sections and ±25% for the vibrational excitation cross sections (two standard deviations). All spectra were recorded at the large scattering angle of 135° to emphasize resonant processes and reduce the extent of direct excitation in the spectrum (which is prevalent in forward scattering).

2.2 Preparation of trans-cyclooctene

N,N-Dimethylcyclooctylamine was synthesized from cyclooctylamine via a procedure similar to that reported by Icke et al.¹⁴ Methylation with methyl iodide gave N,N,N-trimethylcyclooctylammonium iodide.¹⁵cis–trans mixture of cyclooctene was prepared by the reaction of the salt with 2 equivalents of potassium tert-butoxide in anhydrous DMSO. trans-Cyclooctene was separated from the mixture making use of the higher stability of its complex with Ag⁺ as reported,¹⁵ and distilled over a vigreux column.

3 Results and discussion

3.1 Vibrational electron energy-loss spectra

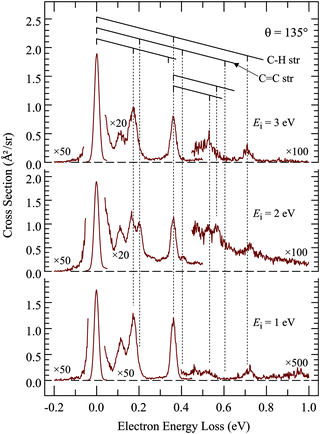
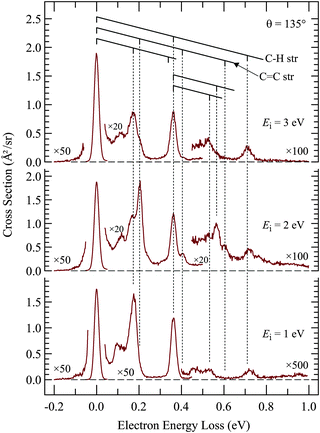
Of interest in this paper are primarily resonances – transient negative ions formed by temporary electron capture at well defined energies of the incident electrons – which are related to virtual (normally unoccupied) orbitals.¹⁶ Measuring vibrational excitation by electron impact is the preferable method of determining resonances because the force field in the molecule is modified during the temporary capture of the incident electron, primarily as a function of the bonding/antibonding character of the temporarily occupied virtual orbital, leading to relaxation, setting the nuclei in motion, and to a vibrationally excited molecule after the departure (autodetachment) of the electron. The residence time of the electron in the resonance is generally in the ps range, comparable to the classical vibrational period, but this short time is sufficient to dramatically increase the vibrational excitation cross section, permitting detection of resonances without the problem of an overwhelming background of direct scattering encountered with the elastic cross section. As an additional benefit, the vibrational modes excited are indicative of the direction in which the relaxation occurred, i.e., about what change of molecular geometry the resonantly captured electron caused. There is a second mechanism of vibrational excitation, not interesting in the present context: IR active vibrations can be excited directly by the dipole mechanism, operative primarily at low electron energies (i.e., peaking at the excitation threshold), and at forward scattering angles. All measurements in this study were therefore performed at the large scattering angle of 135° to reduce the signal due to direct scattering and to enhance resonant processes.

The first step of studying resonances by this method is to determine which vibrations are relevant in the sense of being significantly excited by electron impact. This is achieved by recording electron energy-loss spectra (EELS) in the energy range corresponding to vibrational excitation, as shown in Fig. 1 and 2. TCO and CCO have too many vibrational modes to be resolved by EELS, but groups of vibrations of a similar type can be recognized. Comparison with published and DFT calculated frequencies reveals that the peak at ΔE = 365 meV is due to C–H stretch vibrations and the band at ΔE = 170 meV to C–H bend vibrations. Most importantly, the C=C stretch vibration is isolated and can be discerned individually at ΔE = 202 meV, with only a partial overlap with the ΔE = 170 meV peak. It is the most relevant vibrational mode for this study because it is expected to be excited by a temporary occupation of the π* orbital, which temporarily weakens the C=C bond, causing a relaxation consisting of C=C bond lengthening and vibrational excitation after the electron departure. Fig. 1 and 2 show that C=C stretch is appreciably excited only in the spectra recorded at 2 eV energy, confirming a π* electron attachment around this energy as already reported in the early work.¹⁰ Excitation of two quanta, in the cis-compound even three quanta, may be discerned with the incident energy of 2 eV, indicating substantial relaxation of the nuclei during the resonance lifetime, and thus characteristic of a resonant mechanism, as opposed to direct excitation by dipole mechanism which favors, like IR excitation, excitation of single quanta.

Fig. 1 Electron energy-loss spectra of trans-cyclooctene.

Fig. 2 Electron energy-loss spectra of cis-cyclooctene.

3.2 Transient anion

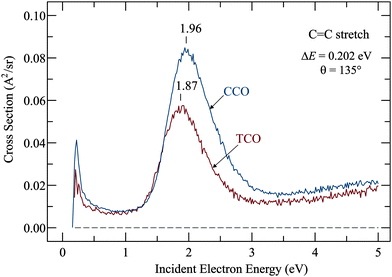
Resonances were determined by recording the cross sections for exciting the various vibrations identified in the preceding section as a function of incident electron energy, and the most relevant example, excitation of the C=C stretch vibration, is shown in Fig. 3. The signal starts at the ‘threshold’ of 0.202 eV, the minimum electron energy required to excite the C=C stretch vibration. Both spectra have a ‘threshold peak’, a phenomenon which has been much studied in electron collisions (ref. 17 and references therein) but is not particularly relevant in the present context. It could be caused by direct, dipole mediated excitation of an IR-active vibration or it could be a manifestation of a more exotic phenomenon, the virtual resonance (see also ref. 17 and references therein for more details). The slow rise of cross section above about 3 eV is doubtlessly caused by a very broad resonance with a temporary occupation of various σ* orbitals which has been identified already in the prototype case of ethene^18,19 and is found in all hydrocarbons.²⁰

Fig. 3 Cross sections for exciting the C=C stretch vibration as a function of electron energy.

The relevant features here are the intense bands which peak at 1.87 eV for TCO and at 1.96 eV for CCO and reveal the temporary electron capture into the π* orbitals. The vertical attachment energies (VAEs) given in our earlier publication¹⁰ were 1.79 eV and 1.93 eV, and are, in view of the large widths of the bands, in good agreement with the present numbers. (A small upward shift when comparing vibrational excitation data with ETS data is actually expected because of slightly different Franck–Condon factors involved in the elastic (v = 0 → 0) as compared to inelastic (v = 0 → 1) scattering.²¹) These VAEs may be compared to the value of 1.78 eV in the parent molecule ethene,^18,19,22 and to 2.25 eV in the highly alkylated bicyclohexylidene,²³ – revealing the well-known destabilization of π* orbitals by alkyl substitution.

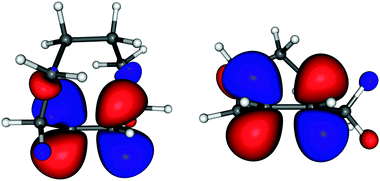
The stabilization of the anion (and indirectly of the π* orbital) in TCO respective to CCO is only 0.09 eV. This is surprisingly small in view of the simple expectation that the change is given primarily by the decrease of the interaction parameter β (given by the overlap of the p_z orbitals of which the π* MO is composed) due to the twisting of the double bond. One would thus expect a π* stabilization comparable to the destabilization of the π orbital, which is, revealed by UV-photoelectron spectroscopy, either 0.20 eV or 0.29 eV depending whether vertical or v = 0 IEs are taken. (The IEs are 8.55 and 8.84 eV (v = 0 values) and 8.80 and 9.00 eV (vertical values) for TCO and CCO, respectively.⁸) In search of a qualitative explanation of this asymmetry between HOMO destabilization and LUMO stabilization we point out that the alkyl chain is largely confined to the nodal plane of the π* orbital in CCO, whereas it faces the π* lobes in TCO (see Fig. 4), thus destabilizing the π* by Pauli (steric) repulsion. This effect is larger for the π* MO than for the π MO because of the more diffuse nature of the former. The effect is comparable to the destabilization of Rydberg orbitals by Pauli repulsion in highly alkylated alkenes.²³

Fig. 4 The π* orbitals of TCO (left) and CCO (right).

The widths (full width at half maximum) of the bands in Fig. 3 are 0.75 eV for TCO and 0.78 eV for CCO, that is, they are identical within the confidence limit. The widths of the band are given by two factors: (i) the electronic width, given via Heisenberg's uncertainty relation by the short lifetime of the transient negative ion, and (ii) by the Franck–Condon width, given by the fact that vertical electron attachment transfers the initial nuclear wavepacket to a sloped section of the potential surface of the anion. The Franck–Condon width is thus indicative of how strongly the electron attachment changes the geometry of the molecule. The electronic width of the present π* resonances, by analogy with molecules with similar π* resonances at similar energies, is judged to be about 0.1 eV so that the total widths given above are given nearly exclusively by the Franck–Condon width, thus estimated as 0.75 eV for both TCO and CCO. This width indicates a substantial change of geometry upon electron attachment, and the strong excitation of the C=C stretch indicates that an important part of this change is C=C bond lengthening. Somewhat surprisingly, the Franck–Condon width is nearly the same for TCO and CCO, although one may naively expect that TCO is already ‘pre-distorted’, in particular in terms of C=C bond twist and pyramidalization, implying less geometry change upon electron attachment, yielding a narrower Franck–Condon width.

The spectra are given in absolute vertical units, permitting the observation that the C=C stretch excitation is weaker in the trans-compound, indicating a weaker coupling of the electronic and nuclear motion. This is likely to be a consequence of a shorter interaction time, i.e., the electron departs faster in the trans-compound. This may be because the π* orbital on the twisted bond deviates more from the d_π symmetry, causing a less pure d-wave, stronger s- and p-wave contributions, providing a lesser centrifugal barrier and a path for the extra electron to ‘leak out’.¹⁶

Useful qualitative insight into the nature of the singly occupied orbitals of the transient anions is gained by considering the virtual orbitals of TCO and CCO in Fig. 4.† They are drawn at geometries of the neutral molecules to be representative of vertical attachment. It is seen that both π* orbitals extend onto the alkyl skeleton, with a appreciable contribution of the carbon atoms of the alkyl bridge extending over the C=C bond in the case of TCO.

3.3 Elastic scattering

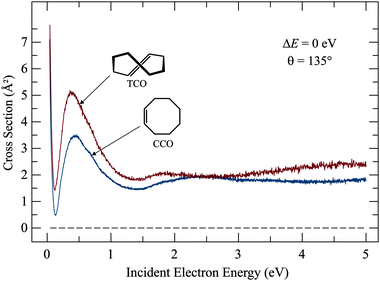
The elastic cross sections shown in Fig. 5 express the probability of an electron to scatter from the molecule without exciting it (i.e., the electron changes its direction of flight but does not lose energy). Elastic cross sections are not of primary interest in this work, but we present them for completeness and because an interesting dependence on structure was observed. They are interesting in view of the theory of electron collisions and of potential applications in plasmas. Elastic cross sections are generally dominated by direct scattering, where the electron ‘bounces off’ without being captured, even temporarily, and resonant scattering, with temporary electron capture, affects them only weakly. Elastic cross section is thus not a very effective method of determining resonances. Our earlier study using the electron transmission spectroscopy, which relies essentially on elastic scattering, revealed the π* resonances, but a large background of direct scattering had to be subtracted, thus reducing the reliability of the findings. Fig. 5 makes this point clear, the weak humps around 2 eV are barely discernible on the background of direct scattering.

Fig. 5 Elastic cross sections of CCO and TCO.

The cross sections in Fig. 5 are essentially flat above 1 eV, and there are only small differences between CCO and TCO, but below about 1 eV the cross sections increase with decreasing electron energy and the magnitude of the cross section at the peak near 0.5 eV is 45% higher for TCO than for CCO. This is surprising because the elastic scattering cross section would be expected to be given primarily by the physical size of the molecule, which is not very different for CCO and TCO. The elastic cross section at low energies is generally larger for molecules with a dipole moment and TCO does have a larger dipole moment (μ = 0.82 D) than CCO (μ = 0.43 D),²⁷ but the dipole moments of both molecules are small and the large difference of the magnitudes of the elastic cross sections remains surprising. The difference between the elastic cross sections below the π* resonance in Fig. 5 explains the difference between the early transmission spectra,¹⁰ where the transmission signal decreased smoothly with decreasing energy below the π* resonance for CCO, but started to rise for TCO – an intriguing observation which could not be studied in further detail with the instrumentation available at the time. Deep Ramsauer–Townsend minima are seen in the elastic cross sections for both compounds, at 0.13 and 0.12 eV for CCO and TCO, respectively. Ramsauer–Townsend minima are a consequence of an anomalous transparency of an atom or a nearly-spherical molecule for very slow electrons. They were observed originally for the heavier noble gases²⁸ and are considered to be the earliest experimental evidence for the wave nature of the electron. The elastic cross sections then rise very steeply at very low energies for both compounds. The detailed behavior of the elastic cross section can not be explained by qualitative means – it would be interesting whether a high level scattering calculation could reproduce and explain the difference between the CCO and TCO.

4 Conclusions

Cross sections for vibrational excitation revealed vertical electron attachment energies of 1.87 and 1.96 eV for TCO and CCO, respectively. The difference is surprisingly small in view of the dramatically different chemical properties, both in the reactivity towards dienes and in the stability of metal–olefin complexes. This finding is in line with the conclusions of Liu, Liang and Houk³ that the greatly enhanced reactivity is primarily a consequence of TCO being pre-distorted in the correct way to engage in the transition state – and not by the HOMO and LUMO energies. Moreover, the reaction with tetrazines is an inverse electron-demand Diels–Alder reaction, that is, the alkene LUMO is not the primary factor in determining the binding in the transition state. The partial occupation of the π* (olefin) orbital does not appear significant for the action of cyclooctene as a dienophile towards tetrazines, which are dominated by the π (olefin)–π* (tetrazine) interaction.

Our finding is also in line with the conclusion that the increased stability of the metal–olefin complex in TCO is a consequence of the C=C bond being pre-relaxed in the strained olefin for the d_π (metal)–π* (olefin) bond, and not a consequence of a stabilized π* orbital.¹

The large values of the C=C stretch vibrational cross sections are indicative of a substantial C=C bond lengthening brought by electron attachment. The nearly symmetrical shape and large width of the attachment band provide a second indication of a substantial geometry change as a consequence of the electron attachment, that is, a large difference between the adiabatic and vertical attachment energies.

The present finding that C=C bond distortion has the consequences of (i) stabilizing the transient anion only to a negligible degree and (ii) destabilizing the positive ion more than stabilizing the negative ion, is not a general phenomenon. The situation is reverse for the pyramidalized alkene tricyclo[3.3.3.03,7]undec-3(7)-ene, where the positive ion is destabilized by 0.31 eV with respect to the reference compound bicyclooctene, whereas the negative ion is stabilized by 0.7 eV by pyramidalization of the C=C bond.¹¹

A final finding, not related to chemical reactivity but interesting from the point of view of electron scattering, is the large dependence of the magnitude of the elastic cross sections around 0.5 eV on structure, the cross section of TCO being about 45% larger.

Acknowledgements

This work has been supported by the Swiss National Science Foundation and by the COST Action CM1301 CELINA.

References

1. D. L. Cedeño and R. Sniatynsky, Organometallics, 2005, 24, 3882–3890.
2. R. Selvaraj and J. M. Fox, Curr. Opin. Chem. Biol., 2013, 17, 753.
3. F. Liu, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 11483–11493.
4. A. Darko, S. Wallace, O. Dmitrenko, M. M. Machovina, R. A. Mehl, J. W. Chin and J. M. Fox, Chem. Sci., 2014, 5, 3770–3776.
5. R. Walker, R. M. Conrad and R. H. Grubbs, Macromolecules, 2009, 42, 599–605.
6. E. C. Sisler, Biotechnol. Adv., 2006, 24, 357–367.
7. T. Koopmans, Physica, 1934, 1, 104–113.
8. M. B. Robin, G. N. Taylor, N. A. Kuebler and R. D. Bach, J. Org. Chem., 1973, 38, 1049.
9. D. Chen and G. A. Gallup, J. Chem. Phys., 1990, 93, 8893.
10. M. Allan, E. Haselbach, M. von Büren and H.-J. Hansen, Helv. Chim. Acta, 1982, 65, 2133.
11. J. M. Smith, D. A. Hrovat, W. T. Borden, M. Allan, K. Asmis, C. Bulliard, E. Haselbach and U. Meier, J. Am. Chem. Soc., 1993, 115, 3816.
12. M. Allan, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 3531–3544.
13. M. Allan, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 042706.
14. R. N. Icke, B. B. Wisegarver and G. A. Alles, Org. Synth., 1945, 25, 89.
15. A. C. Cope and R. D. Bach, Org. Synth., 1969, 49, 39.
16. G. J. Schulz, Rev. Mod. Phys., 1973, 45, 423.
17. H. Hotop, M.-W. Ruf, M. Allan and I. I. Fabrikant, Adv. At., Mol., Opt. Phys., 2003, 49, 85.
18. I. C. Walker, A. Stamatovic and S. F. Wong, J. Chem. Phys., 1978, 69, 5532.
19. M. Allan, C. Winstead and V. McKoy, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 042715.
20. M. Allan and L. Andrić, J. Chem. Phys., 1996, 105, 3559–3568.
21. M. Allan, J. Electron Spectrosc. Relat. Phenom., 1989, 48, 219.
22. K. D. Jordan and P. D. Burrow, J. Am. Chem. Soc., 1980, 102, 6882.
23. M. Allan, P. A. Schnyder and M. B. Robin, J. Phys. Chem., 1985, 89, 4900–4903.
24. A. A. Granovsky, Firefly version 8.0.0, http://classic.chem.msu.su/gran/firefly/index.html.
25. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
26. U. Varetto, MOLEKEL 5.4, Swiss National Supercomputing Centre:Manno, Switzerland.
27. N. L. Allinger, J. Am. Chem. Soc., 1958, 80, 1953.
28. C. Ramsauer, Ann. Phys., 1921, 369, 513.

---

Footnote

† Shown are SCF 6-31G(d) orbitals calculated at the DFT B3LYP/6-31G(d) optimized geometries of the neutral molecules, using the Firefly code,²⁴ based partly on GAMESS,²⁵ and drawn by the program Molekel.²⁶

---