Spectroscopic and ab initio investigation of 2,6-difluorophenylacetylene–amine complexes: coexistence of C–H⋯N and lone-pair⋯π complexes and intermolecular coulombic decay†
Sohidul Islam
Mondal
a,
Arghya
Dey
a,
Saumik
Sen
a,
G. Naresh
Patwari
*a and
Debashree
Ghosh
*b
aDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400 076, India. E-mail: naresh@chem.iitb.ac.in
bPhysical and Materials Chemistry Division, CSIR-National Chemical Laboratory, Dr. Homi Bhabha Road, Pune 411 008, India. E-mail: debashree.ghosh@gmail.com
First published on 31st October 2014
Abstract
Binary complexes of 2,6-difluorophenylacetylene with methylamine, dimethylamine, trimethylamine and triethylamine were investigated using one colour resonant two photon ionization and infrared-optical double resonance spectroscopic techniques combined with high level ab initio calculations. All four amines form CAc–H⋯N hydrogen-bonded complexes. Additionally trimethylamine and triethylamine form complexes characterized by Lp⋯π interactions, due to the electron deficient nature of the phenyl ring of 2,6-difluorophenylacetylene. The Lp⋯π interacting structure of the 2,6-difluorophenylacetylene–trimethylamine complex is about 1.5 kJ mol−1 higher in energy than the CAc–H⋯N hydrogen-bonded structure, which is the global minimum. Energy decomposition analysis indicates that the electrostatics and dispersion interactions favour the formation of CAc–H⋯N and Lp⋯π complexes, respectively. Interestingly the CAc–H⋯N hydrogen-bonded complex of 2,6-difluorophenylacetylene–triethylamine showed a smaller shift in the acetylenic C–H stretching frequency than the 2,6-difluorophenylacetylene–trimethylamine complex. The observed fragmentation of the binary complexes of 2,6-difluorophenylacetylene with the four amines following resonant two-photon ionization can be explained on the basis of the intermolecular coulombic decay process.
1. Introduction
One of the major challenges in hydrogen bonding is to predict, a priori, how the individual functional groups in a multifunctional molecule behave when they are made to interact with suitable hydrogen bonding partners. In the case of phenylacetylene (PHA) it has been shown that the intermolecular structures are highly dependent on the nature of the interacting molecule and even subtle changes, such as the addition of a methyl group, can change the intermolecular structure drastically.1 Therefore PHA has been termed as a hydrogen bonding chameleon.2 Interaction of ammonia and amines with PHA led to a plethora of structures. Two isomers of PHA–ammonia and PHA–methylamine complexes were observed and include a CAc–H⋯N hydrogen-bonded complex in each case.3,4 On the other hand CAc–H⋯N hydrogen-bonded complexes were not observed for the binary complexes of PHA with several tertiary amines, and they largely interact via dispersion dominated CMe–H⋯π interactions.5 Substitution of fluorine on the benzene ring of PHA can lead to the following changes: (a) increase in the acidity of both the acetylenic and aromatic C–H groups (especially in the ortho position), (b) lowering of the π electron density of the benzene ring, and (c) participation of fluorine in hydrogen bonding interactions.An interesting question that arises is whether the CMe–H⋯π complexes between PHA and tertiary amines persist with the substitution of fluorine on the benzene ring of PHA? Or does it lead to the formation of lone-pair⋯π (Lp⋯π) complexes? Several examples of Lp⋯π interaction have been reported in the literature, both in chemistry and biology.6 This interaction mostly pertains to the aromatic rings with reduced π electron density, such as in fluorine substituted aromatic rings.7 In an effort to understand the Lp⋯π interaction vis-à-vis the conventional hydrogen bonding, investigations on binary complexes of 2,6-difluorophenylacetylene (DFPHA) with four alkyl amines viz. methylamine (MA), dimethylamine (DMA), trimethylamine (TMA) and triethylamine (TEA) were carried out. The present investigation uses a double-barrel approach with the infrared-optical double-resonance spectroscopic technique along with ab initio calculations to understand the nature of the interaction of the amines with DFPHA.
Intermolecular coulombic decay (ICD) is an efficient and fast charge migration process following the ionization of the inner valence electrons.8 The ICD process can be described with respect to a hetero-dimer A⋯B interacting via intermolecular forces (such as hydrogen bonding) as the following. If the adiabatic ionization energy (AIE) of A is greater than that of B, and if the ionization of A is achieved, the electron ejection occurs from B instead of the initially excited (ionized) molecule A. The excess energy, which is the difference between the AIEs of A and B, can lead to doubly ionizing B or fragmentation of B and other reactive pathways. The ICD process, as described above, is much more efficient than the excitation energy transfer process as the acceptor state lies in the continuum. It has been recently reported that the ICD processes can be relevant in a number of chemical and biological systems interacting with a variety of radiation sources.9 In this work, DFPHA with the AIE of about 9.11 eV can be considered as fragment A, while the four amines, having AIEs in the order MA (9.04 eV) > DMA (8.32 eV) > TMA (7.82 eV) > TEA (7.5 eV), can be considered as fragment B.10–12 The DFPHA⋯amine complexes offer an opportunity to investigate ICD processes systematically in non-covalently bonded systems as the energy gap between the two states involved in the ICD process can be tuned. This article also deals with the consequences of the ICD process following resonant two photon ionization of the DFPHA⋯amine complexes.
2. Methods
The details of the experimental setup have been described elsewhere.13 Spectra were acquired using a time-of-flight (TOF) mass spectrometer coupled with the supersonic jet expansion technique. Molecular complexes were created by passing helium buffer gas at 2 atm over 2,6-difluorophenylacetylene (Aldrich) and MA, DMA, TMA (50% aqueous solutions; Aldrich) and TEA (Aldrich) kept at room temperature and expanding through a 0.5 mm diameter pulsed nozzle (Series 9, Iota One; General Valve Corporation) operating at 10 Hz into a vacuum chamber at 10−6 Torr. The expanded molecular beam was crossed with the frequency doubled output of a dye laser (Narrow Scan GR; Radiant Dyes) operating with the Rhodamine-19 dye, pumped with second harmonic of a Nd:YAG laser (Surelite I-10; Continuum). LIF excitation spectra were recorded by monitoring the total fluorescence using a photo-multiplier tube (PMT – 9780SB + 1252-5F; Electron Tubes Limited) and a filter (WG-320) combination, while scanning the UV laser frequency. On the other hand, one-color resonant two-photon ionization (1C-R2PI) spectra were recorded by monitoring the appropriate mass ion signal using a two stage Wiley-McLaren TOF spectrometer and a channel electron multiplier (CEM-KBL-25RS; Sjuts Optotechnik) and a preamplifier (SR445A; Stanford Research Systems). The signal from the PMT/CEM was digitized by a digital storage oscilloscope (TDS-1012; Tektronix), which is interfaced to a personal computer using a data acquisition program written in LabView. The integrated signal intensity is plotted against the wavelength to get the LIF/1C-R2PI spectrum. The infrared spectra in the acetylenic C–H stretching region were obtained using the fluorescence-dip infrared (FDIR)/ion-dip infrared (IDIR) spectroscopic technique.14 The identification and assignment of a particular band in the 1C-R2PI spectrum among several other bands were carried out using IR-UV hole-burning spectroscopy. In our experiments the source of tunable IR light is an idler component of LiNbO3 OPO (Custom IR OPO; Euroscan Instruments) pumped with an injection-seeded Nd:YAG laser (Brilliant-B; Quantel). The typical bandwidth of both UV and IR lasers is about 1 cm−1 and the absolute frequency calibration is within ±2 cm−1.A detailed conformational search was followed by geometry optimization by the MP2 method using cc-pVDZ and cc-pVTZ basis sets (unless specified). In order to check the accuracy of the structures of the DFPHA–TMA complexes, they were also optimized by ωB97X-D,15 B2PLYP-D16 and B2PLYP-D317 methods using the cc-pVTZ basis set. The vibrational frequency calculations were carried out using the MP2/cc-pVDZ optimized structures at the same level of theory. A scaling factor of 0.954 was chosen to match the experimental vibrational frequencies of the monomers and the same scaling factor was used for the complexes.
The stabilization energy was determined as the difference between the dimer energy and the sum of monomer energies. The CCSD(T)/CBS stabilization energies were determined as the sum of MP2/CBS energies and the CCSD(T) correction term according to eqn (1).
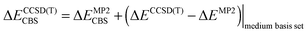 | (1) |
The equation of motion ionization potential coupled cluster with single and double excitation (EOM-IP-CCSD) method is very accurate and reliable for describing the closely spaced electronic states and ionization levels of the molecules,24 and has already been successfully applied to calculate the ionization energies of various neutral and ionized species.25 This was, therefore, used as our method of choice for the calculation of ionization energies. For the adiabatic ionization energy (AIE) calculations, geometries of all monomers and the binary complexes in their ground state were optimized at the MP2/cc-pVDZ level of theory. For the cationic state the MP2 calculations are unreliable due to spin contamination, and therefore the geometries were optimized using a long range corrected ωB97X functional with empirical dispersion correction (ωB97X-D) using the cc-pVDZ basis set.15 Furthermore, the frequency calculations for both the ground and cationic states at ωB97X-D/cc-pVDZ level of theory were used to account for the zero-point energy (ZPE) corrections. The optimized geometries of the cations were then subjected to EOM-IP-CCSD calculations to estimate the AIEs. The lowest AIEs were calculated as the difference between the EOM-IP-CCSD energy of the first ionized state at the cation geometries and the CCSD energy at the neutral ground state geometries. For the CCSD and EOM-IP-CCSD calculations cc-pVTZ and 6-311++G(d,p) basis sets were used. EOM-IP-CCSD/cc-pVTZ calculations use the resolution of identity (RI) approximation with the auxiliary RIMP2-cc-pVTZ basis set at the CCSD level.26 The frozen natural orbital (FNO) approach was used in the calculation for the complexes (dimers) to largely reduce the computational cost using a natural orbital population threshold of 99.5%.27 Geometry optimization and frequency calculations were carried out using the GAUSSIAN 09 suite of programs,28 and all the calculations required for the IP calculations were carried out using Q-Chem-4.0.1 ab initio package.29 All the structures and the vibrations were visualized using GaussView-5 and ChemCraft.30,31
3. Results and discussion
A. Spectra and intermolecular structures
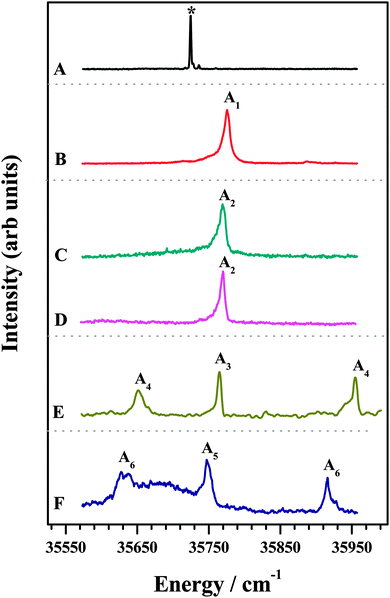
The 1C-R2PI spectra of various amine complexes of DFPHA are shown in Fig. 1 and Table 1 lists the observed S1 ← S0 band-origin excitation energies along with the shifts relative to the DFPHA monomer. Also shown in Fig. 1 (trace A) is the LIF spectrum of DFPHA and the strong band at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725 cm−1 is assigned to the S1 ← S0 band-origin. The 1C-R2PI spectrum of DFPHA could not be recorded as its ionization potential is greater than double of the S1 ← S0 band-origin excitation energy of 71
725 cm−1 is assigned to the S1 ← S0 band-origin. The 1C-R2PI spectrum of DFPHA could not be recorded as its ionization potential is greater than double of the S1 ← S0 band-origin excitation energy of 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 cm−1 (8.859 eV). Fig. 1B depicts the 1C-R2PI spectra of the DFPHA–MA complex recorded by monitoring the parent mass signal at 169 Da. This spectrum shows a single band which corresponds to the band-origin of S1 ← S0 excitation of the DFPHA–MA complex at 35
450 cm−1 (8.859 eV). Fig. 1B depicts the 1C-R2PI spectra of the DFPHA–MA complex recorded by monitoring the parent mass signal at 169 Da. This spectrum shows a single band which corresponds to the band-origin of S1 ← S0 excitation of the DFPHA–MA complex at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 cm−1 (A1). In the case of the DFPHA–DMA complex, 1C-R2PI spectra could be recorded either by monitoring the parent (183 Da) or fragment (45 Da) mass signals. The two spectra (traces C and D of Fig. 1) are identical with band-origin of S1 ← S0 excitation at 35
776 cm−1 (A1). In the case of the DFPHA–DMA complex, 1C-R2PI spectra could be recorded either by monitoring the parent (183 Da) or fragment (45 Da) mass signals. The two spectra (traces C and D of Fig. 1) are identical with band-origin of S1 ← S0 excitation at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769 cm−1 (A2). For the TMA and TEA complexes of DFPHA the parent mass signal could not be detected following the 1C-R2PI process and only fragment mass signals corresponding to TMA (59 Da) and TEA (101 Da) were observed, respectively. The 1C-R2PI spectra of DFPHA complexes with TMA and TEA were recorded by monitoring the fragment mass signals which are also shown in Fig. 1 (traces E and F, respectively). The 1C-R2PI spectra of the DFPHA–TMA and DFPHA–TEA complexes show several bands, which have been assigned to two isomers in each case, A3 and A4 for the TMA complex and A5 and A6 for the TEA complex, using IDIR and hole-burning spectroscopic methods, vide infra.
769 cm−1 (A2). For the TMA and TEA complexes of DFPHA the parent mass signal could not be detected following the 1C-R2PI process and only fragment mass signals corresponding to TMA (59 Da) and TEA (101 Da) were observed, respectively. The 1C-R2PI spectra of DFPHA complexes with TMA and TEA were recorded by monitoring the fragment mass signals which are also shown in Fig. 1 (traces E and F, respectively). The 1C-R2PI spectra of the DFPHA–TMA and DFPHA–TEA complexes show several bands, which have been assigned to two isomers in each case, A3 and A4 for the TMA complex and A5 and A6 for the TEA complex, using IDIR and hole-burning spectroscopic methods, vide infra.
| E(S1 ← S0) | ΔE(S1 ← S0) | ν(C–H) | Δν(C–H) | |
|---|---|---|---|---|
| DFPHA | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725 725 |
— | 3335 | — |
| DFPHA–MA (A1) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776 |
51 | 3183 | −152 |
| DFPHA–DMA (A2) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769 769 |
44 | 3150 | −185 |
| DFPHA–TMA1 (A3) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765 765 |
40 | 3116 | −219 |
| DFPHA–TMA2 (A4) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 652 652 |
−73 | 3331 | −4 |
| DFPHA–TEA1 (A5) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
20 | 3136 | −199 |
| DFPHA–TEA2 (A6) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 627 627 |
−98 | 3333 | −2 |
In an attempt to identify the mode of interaction between the various amines and DFPHA infrared spectra in the acetylenic C–H stretching region were recorded and the results are presented in Fig. 2. Table 1 also lists the observed bands of the acetylenic C–H stretching frequency of the DFPHA moiety in various amine complexes and they shift relative to the DFPHA monomer. The FDIR spectrum of DFPHA (Fig. 2A) shows two strong bands at 3332 and 3340 cm−1, accompanied by two weaker bands at 3347 and 3351 cm−1. The appearance of multiple peaks in the acetylenic C–H stretching region of PHA and its substituted analogues has been attributed to Fermi resonance and other higher order anharmonic coupling terms.1,32 With the assumption that the two intense bands are entirely due to Fermi resonance coupling, a simple two-state de-perturbation model places the unperturbed acetylenic C–H stretching vibration of DFPHA at 3335 cm−1 with a coupling constant of 4 cm−1.13 The IDIR spectra of DFPHA–MA (A1; Fig. 2B) and DFPHA–DMA (A2; Fig. 2C) complexes, recorded by monitoring the parent mass signals, show single bands at 3183 and 3150 cm−1, respectively. The IDIR spectrum of the DFPHA–DMA complex was also recorded by monitoring the DMA fragment (45 Da) and was identical to the one shown in Fig. 2C (not shown). The interaction of MA and DMA with DFPHA leads to the lowering of the acetylenic C–H stretching vibration by 152 and 185 cm−1, respectively. Therefore the A1 and A2 complexes can be unambiguously assigned to CAc–H⋯N hydrogen-bonded complexes.
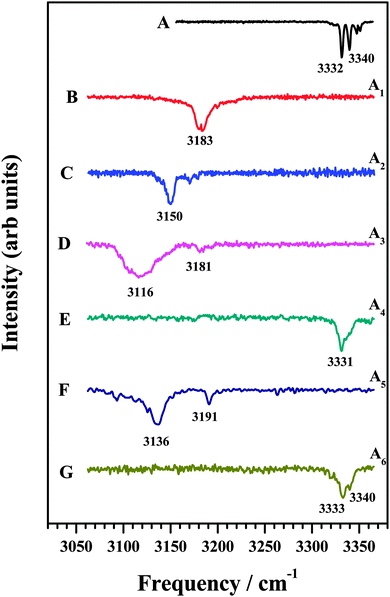 | ||
| Fig. 2 (A) FDIR spectrum of DFPHA. IDIR spectra of (B) DFPHA–MA, (C) DFPHA–DMA (D) DFPHA–TMA1, (E) DFPHA–TMA2, (F) DFPHA–TEA1 and (G) DFPHA–TEA2 complexes. Traces (B)–(G) correspond to IDIR spectra of complexes A1–A6 marked in Fig. 1. | ||
The 1C-R2PI spectra of TMA and TEA complexes of DFPHA show multiple bands, which are assigned to two isomers in each case (see Fig. 1). The IDIR spectrum of the A3 band, depicted in Fig. 2D, has a broad band centred at 3116 cm−1 accompanied by a weak band at 3181 cm−1. Similarly, the IDIR spectrum of the A5 band (Fig. 2F) shows a strong band at 3136 cm−1, along with a weak band at 3191 cm−1. In these two spectra the bands at 3116 cm−1 (Fig. 2D) and 3136 cm−1 (Fig. 2F) can be assigned to the acetylenic C–H stretching vibration of the DFPHA–TMA and DFPHA–TEA complexes, which will correspond to low frequency shifts of 219 and 199 cm−1, respectively. Once again, the A3 and A5 complexes can be assigned to CAc–H⋯N hydrogen-bonded structures straightforwardly. Furthermore, in these two spectra weak bands at 3181 cm−1 (Fig. 2D) and 3191 cm−1 (Fig. 2F) can probably be assigned to a combination band over the hydrogen-bonded C–H stretching vibration in both the complexes.
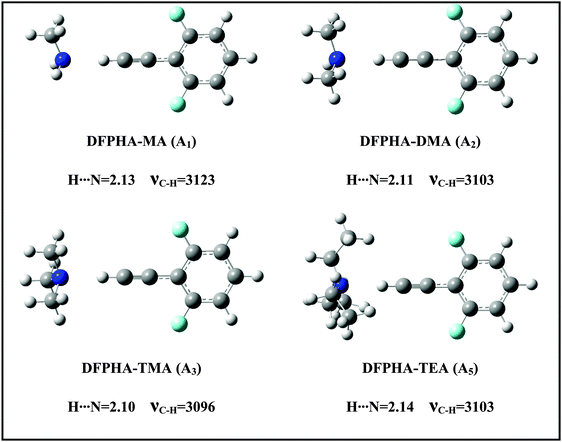
The IDIR spectra presented in Fig. 2 clearly indicate the formation of CAc–H⋯N hydrogen-bonded complexes of DFPHA with MA (A1), DMA (A2), TMA (A3) and TEA (A5), (calculated optimized structures shown in Fig. 3). One of the interesting observations that can be made from the IDIR spectra is the lowering of the acetylenic C–H stretching frequency for the complexes of MA, DMA, TMA and TEA, which is 152, 185, 219 and 199 cm−1, respectively. Clearly, the lowering of the acetylenic C–H stretching frequency for the TMA complex (219 cm−1) is greater than that of TEA complex (199 cm−1). This observation is very surprising given the fact that TEA is a stronger base than TMA and is expected to form stronger hydrogen bonds, which in turn is expected to show a larger shift in the acetylenic C–H stretching frequency. In the case of hydrogen-bonded complexes of phenol the lowering of the O–H stretching frequency for the TMA and TEA complexes is 590 and 670 cm−1, respectively.33 MP2/aug-cc-pVDZ calculated structures reveal that the H⋯N hydrogen-bonding distances are in the order MA > DMA > TMA < TEA, which is in accordance with the observed lowering of the acetylenic C–H stretching frequency (see Fig. 3).
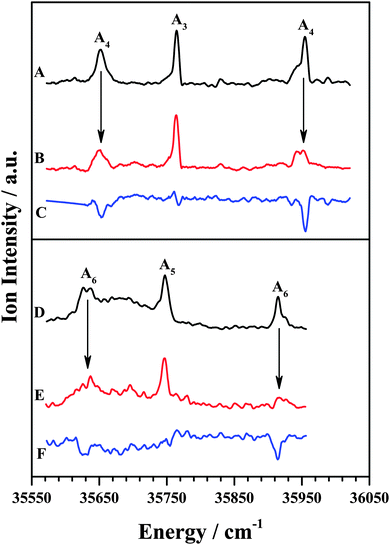
The IDIR spectra of the other DFPHA–TMA (A4 band; Fig. 2E) and DFPHA–TEA (A6 band; Fig. 2G) complexes are very similar with a slightly broad band at around 3332 cm−1 along with a shoulder at 3340 cm−1. These two spectra are similar to that of the DFPHA monomer (Fig. 2A), albeit broadened by a few cm−1, and indicate that the mode of interaction of TMA and TEA with DFPHA might be very similar. Furthermore the 1C-R2PI spectra of DFPHA complexes of TMA and TEA are very similar in appearance, which also suggests that the mode of interaction of TMA and TEA with DFPHA is very similar. The assignment of the different bands appearing in the 1C-R2PI spectra of the DFPHA complexes with TMA (Fig. 1E) and TEA (Fig. 1F) to various structural isomers was carried out by IR-UV hole-burning spectroscopy and the results are presented in Fig. 4. Fig. 4A shows the 1C-R2PI spectrum of the DFPHA–TMA complex, which was recorded by monitoring the fragment mass signal at 59 Da. The hole-burnt spectrum was recorded by pumping the acetylenic C–H stretching vibration of the A4 complex at 3331 cm−1 and scanning the UV laser energy and is shown in Fig. 4B. All the bands corresponding to complex A4 show diminished intensities in the hole-burnt spectrum in comparison with the 1C-R2PI spectrum (indicated by arrows). The intensity of the band corresponding to complex A3 remains unaltered. Fig. 4C is the difference spectrum generated by subtracting the 1C-R2PI spectrum from the hole-burnt spectrum. The bands corresponding to complex A4 appear as dips in the difference spectrum. Traces D, E, and F of Fig. 4 depict the 1C-R2PI spectrum of the DFPHA–TEA complex, the IR-UV hole-burnt spectrum recorded by pumping the acetylenic C–H stretching vibration of complex A6 at 3333−1, and the difference spectrum, respectively. The presence of two distinct isomers for the DFPHA–TMA complex (A3 and A4) and the DFPHA–TEA complex (A5 and A6) can be inferred from the hole-burnt spectra.
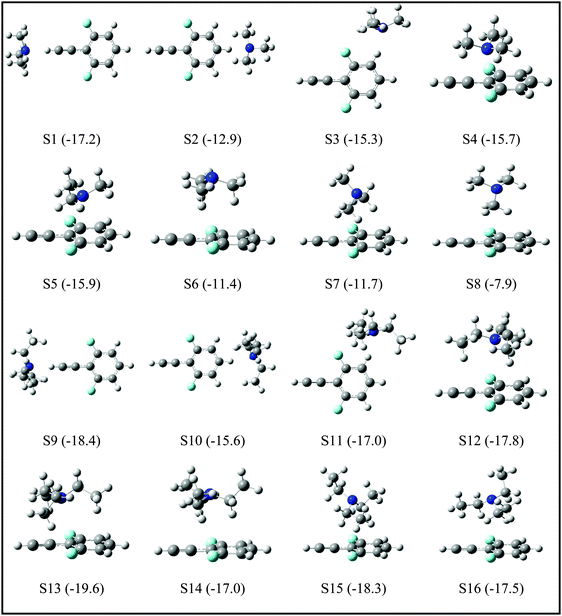
Since the assignment of the DFPHA complexes of MA (A1) and DMA (A2) to CAc–H⋯N hydrogen-bonded structures is straightforward, calculations of these two complexes are not presented here. Furthermore, the A3 and A5 complexes of TMA and TEA, respectively, have also been assigned to the CAc–H⋯N hydrogen-bonded structures. The structures of the DFPHA–TMA complex optimized at the MP2/cc-pVTZ level are shown in Fig. 5. The intermolecular structures optimized at the MP2/cc-pVDZ and MP2/cc-pVTZ levels are almost identical with the exception of S8 structure, in which the orientation of the methyl group is slightly different. Furthermore, the coordinates of various structures of the DFPHA–TMA complex optimized at various levels of theory (MP2/cc-pVDZ, MP2/cc-pVTZ, ωB97X-D/cc-pVTZ, B2PLYP-D/cc-pVTZ and B2PLYP-D3/cc-pVTZ) are listed in Table S1 (ESI†). The effect of various theoretical methods on the intermolecular structures was found to be minimal. The atoms-in-molecules (AIM) analysis was used to characterize the interactions present in various structures of the DFPHA–TMA complex. Molecular graphs derived from the AIM analysis are shown in Fig. S1 (ESI†).
For the DFPHA–TMA complex, the first structure S1 is a CAc–H⋯N hydrogen-bonded structure. In S2 the aromatic C–H group in the para position to the acetylenic group interacts with TMA leading to the formation of a CAr–H⋯N hydrogen bond. Similarly, S3 is characterized by the CAr–H⋯N hydrogen bond with the aromatic C–H group in the meta position interacting with the nitrogen atom of TMA, along with two CMe–H⋯F hydrogen bonds formed by two hydrogen atoms of two methyl groups interacting with the fluorine atom in the ortho position. Structures S4 and S5 can be considered as Lp⋯π complexes, wherein the primary interaction is between the nitrogen atom of the TMA and the electron deficient phenyl ring of DFPHA. Furthermore, the S4 structure also incorporates CMe–H⋯π interaction. The structures S6 and S7 contain primarily CMe–H⋯π contacts with the extended π electron density of DFPHA along with CMe–H⋯F interaction in the S7 structure. Finally, it is very interesting to note that the S8 structure incorporates interaction between the carbon atom and the π electron density of DFPHA. Table 2 lists ZPE and BSSE corrected MP2/CBS and CCSD(T)/CBS stabilization energies extrapolated using aug-cc-pVNZ and cc-pVNZ (N = D,T) basis sets.
| Structure | MP2/CBSa | MP2/CBSb | CCSD(T)/CBSa,c | CCSD(T)/CBSb | ν(C–H) | Δν(C–H) |
|---|---|---|---|---|---|---|
| a aug-cc-pVNZ (N = D, T) basis with MP2/cc-pVDZ optimized geometries. b cc-pVNZ (N = D, T) basis with MP2/cc-pVDZ optimized geometries. c Best estimate. | ||||||
| S1 | −19.1 | −16.9 | −17.2 | −14.8 | 3096 | −239 |
| S2 | −13.7 | −13.9 | −12.9 | −12.3 | 3335 | +1 |
| S3 | −16.8 | −15.2 | −15.3 | −13.5 | 3332 | −2 |
| S4 | −22.1 | −20.5 | −15.7 | −15.1 | 3332 | −2 |
| S5 | −22.9 | −21.7 | −15.9 | −16.3 | 3333 | −1 |
| S6 | −15.1 | −14.0 | −11.4 | −10.4 | 3332 | −2 |
| S7 | −15.2 | −14.3 | −11.7 | −10.9 | 3332 | −2 |
| S8 | −10.2 | −11.8 | −7.9 | −9.2 | 3334 | −1 |
The IR spectrum of the DFPHA monomer (Fig. 2A) shows the presence of Fermi resonance coupling. In the case of PHA and its substituted analogues, the Fermi resonance coupling involves the acetylenic C–H stretching vibration and a combination of one quantum of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretch and two quanta of the acetylenic C–H out-of-plane bend and is localized on the acetylenic moiety, which implies that the Fermi resonance coupling is localized on the acetylenic moiety. As stated earlier the DFPHA–TMA A3 complex was assigned to the CAc–H⋯N hydrogen-bonded structure, rather straightforwardly. The IR spectrum of the DFPHA–TMA A4 complex (Fig. 2E) also shows Fermi resonance coupling, albeit broadening by a few cm−1, which indicates that the interaction of TMA does not perturb the acetylenic moiety in DFPHA thereby retaining the Fermi resonance coupling to a large extent. From Fig. 5 it can be inferred that any of the seven S2–S8 structures fit this description. However, unlike the assignment of S1 structure to the A3 complex, the experimental observations in the present case cannot unambiguously distinguish between any of the structures. The CCSD(T)/CBS extrapolation with aug-cc-pVNZ (N = D,T) is widely used,34 therefore it is the best estimate for the stabilization energies of various structures of the DFPHA–TMA complex. This is further confirmed by the fact that the cc-pVTZ//cc-pVDZ and cc-pVTZ//cc-pVTZ energies are comparable (see Table S1, ESI†). Therefore based on the calculated stabilization energy considerations the observed DFPHA–TMA A4 complex is assigned to S5 structure with Lp⋯π interaction. The energy decomposition analysis using the SAPT0 method was also carried out for various structures of the DFPHA–TMA complex and the results are listed in Table 3. The stabilization of the CAc–H⋯N complex (S1 structure assigned to the A3 complex) is dominated by the electrostatic component, while the Lp⋯π complex (S5 structure assigned to the A4 complex) is dominated by the dispersion component. Furthermore, it can also be noted from Table 3 that the electrostatics and dispersion components are overwhelming for the S1 and S5 structures among all the structures considered.
C stretch and two quanta of the acetylenic C–H out-of-plane bend and is localized on the acetylenic moiety, which implies that the Fermi resonance coupling is localized on the acetylenic moiety. As stated earlier the DFPHA–TMA A3 complex was assigned to the CAc–H⋯N hydrogen-bonded structure, rather straightforwardly. The IR spectrum of the DFPHA–TMA A4 complex (Fig. 2E) also shows Fermi resonance coupling, albeit broadening by a few cm−1, which indicates that the interaction of TMA does not perturb the acetylenic moiety in DFPHA thereby retaining the Fermi resonance coupling to a large extent. From Fig. 5 it can be inferred that any of the seven S2–S8 structures fit this description. However, unlike the assignment of S1 structure to the A3 complex, the experimental observations in the present case cannot unambiguously distinguish between any of the structures. The CCSD(T)/CBS extrapolation with aug-cc-pVNZ (N = D,T) is widely used,34 therefore it is the best estimate for the stabilization energies of various structures of the DFPHA–TMA complex. This is further confirmed by the fact that the cc-pVTZ//cc-pVDZ and cc-pVTZ//cc-pVTZ energies are comparable (see Table S1, ESI†). Therefore based on the calculated stabilization energy considerations the observed DFPHA–TMA A4 complex is assigned to S5 structure with Lp⋯π interaction. The energy decomposition analysis using the SAPT0 method was also carried out for various structures of the DFPHA–TMA complex and the results are listed in Table 3. The stabilization of the CAc–H⋯N complex (S1 structure assigned to the A3 complex) is dominated by the electrostatic component, while the Lp⋯π complex (S5 structure assigned to the A4 complex) is dominated by the dispersion component. Furthermore, it can also be noted from Table 3 that the electrostatics and dispersion components are overwhelming for the S1 and S5 structures among all the structures considered.
| Structure | E elec | E ind | E disp | E exch | E ch.tr. | E SAPT0 |
|---|---|---|---|---|---|---|
| S1 | −32.8 | −8.2 | −13.3 | 29.8 | −1.5 | −24.5 |
| S2 | −18.2 | −5.0 | −16.4 | 21.1 | −0.8 | −18.5 |
| S3 | −23.1 | −6.4 | −17.0 | 24.9 | −1.1 | −21.6 |
| S4 | −18.5 | −6.2 | −37.6 | 39.9 | −0.6 | −22.4 |
| S5 | −14.9 | −4.8 | −39.6 | 36.0 | −0.5 | −23.3 |
| S6 | −11.2 | −4.6 | −28.3 | 29.7 | −0.6 | −14.4 |
| S7 | −10.7 | −3.6 | −27.5 | 27.6 | −0.5 | −14.1 |
| S8 | −7.8 | −3.6 | −20.6 | 21.1 | −0.2 | −10.9 |
The TEA monomer can manifest in 6 different conformations, and the structures and relative energies of these conformations are shown in Fig. S2 (ESI†). Since the experiments were carried out under jet-cooled conditions only the lowest energy conformation was used in all subsequent calculations. The structures of the DFPHA–TEA complex were optimized at MP2/cc-pVDZ level of theory and are also shown in Fig. 5. Due to limitation in computational resources the stabilization energies of the DFPHA–TEA complex were calculated at the MP2/aug-cc-pVDZ level and were corrected for ZPE and BSSE. The stabilization energies of various structures of the DFPHA–TEA complex are shown in Fig. 5 along with the structures. In the case of the DFPHA–TEA complex, once again, the A5 complex is assigned to CAc–H⋯N hydrogen-bonded structure (S9) based on the appearance of the IR spectrum (Fig. 2F). Among the calculated structures of the DFPHA–TEA complex S13 is the global minimum, which incorporates Lp⋯π and CMe–H⋯F/CMe–H⋯π interactions. In the S13 structure the acetylenic moiety is minimally perturbed, and therefore, it is a possible structure for the A6 complex. It can be seen from Fig. 1 and 2 that the appearance of the 1C-R2PI and the IDIR spectra of the DFPHA–TEA are almost identical to that of the DFPHA–TMA A4 complex. Therefore the structure of the DFPHA–TEA A6 complex is assigned to the S13 structure, which is similar to the DFPHA–TMA A4 complex, wherein the nitrogen atom of TEA interacts with the electron deficient phenyl ring.
All four amines (MA, DMA, TMA and TEA) form CAc–H⋯N hydrogen-bonded complexes with DFPHA. Furthermore, TMA and TEA also form complexes by Lp⋯π interaction. The formation of Lp⋯π complexes can be attributed to the reduced π electron density due to fluorine substitution on the phenyl ring and enhanced Lewis basicity of TMA and TEA relative to MA and DMA. The observation of both CAc–H⋯N and Lp⋯π complexes and ab initio calculations suggest that the stabilization energies are comparable and can coexist.
B. Intermolecular coulombic decay
The AIEs were calculated for DFPHA and the four amines MA, DMA, TMA and TEA using the EOM-IP-CCSD method and cc-pVTZ and 6-311++G(d,p) basis sets and the values are listed in Table 4. The basis set dependence is weak predicting the AIEs to be within 0.1 eV of the computed values. In order to set the confidence limit the AIEs of PHA and three singly fluorine substituted fluorophenylacetylenes viz. 2-fluorophenylacetylene (2FPHA), 3-fluorophenylacetylene (3FPHA) and 4-fluorophenylacetylene (4FPHA) were also calculated as the experimental AIEs of these four molecules are known with very high accuracy (also listed in Table 4).35 Both basis sets underestimate the AIEs by about 0.1–0.2 eV. In the case of MA the experimental AIE measured by the mass analysed threshold ionization method is 9.04 eV,10 while the two set of calculations underestimate the AIE by about 0.2–0.3 eV.| cc-pVTZ | 6-311++G(d,p) | Expt | |
|---|---|---|---|
| a Ref. 35. b Ref. 10. c Ref. 11. d Ref. 12. | |||
| DFPHA | 9.11 | 9.14 | >8.86 |
| PHA | 8.68 | 8.63 | 8.82a |
| 2FPHA | 8.77 | 8.76 | 8.92a |
| 3FPHA | 8.87 | 8.85 | 9.00a |
| 4FPHA | 8.60 | 8.60 | 8.80a |
| MA | 8.81 | 8.70 | 9.04b |
| DMA | 8.10 | 7.99 | 8.32c |
| TMA | 7.64 | 7.53 | 7.82c |
| TEA | 7.43 | 7.33 | 7.50d |
| DFPHA–MA (D1) | 8.93 | 8.95 | — |
| DFPHA–MA (D2) | 8.65 | 8.68 | — |
| DFPHA–MA (D3) | 8.19 | 8.18 | — |
| DFPHA–MA (D4) | 8.15 | 8.10 | — |
| DFPHA–DMA (CAc–H⋯N) | 8.39 | 8.36 | — |
| DFPHA–TMA (CAc–H⋯N) | 8.25 | 8.22 | — |
| DFPHA–TEA (CAc–H⋯N) | — | 8.11 | — |
Fig. 6 shows the energy level schematic for the AIEs of DFPHA and all the four amines. The calculated AIE for DFPHA is 9.11 eV, which is higher than the energy available in the 1C-R2PI process (2 × 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725 cm−1 = 8.86 eV), therefore the 1C-R2PI spectrum of the DFPHA monomer could not be recorded. It is well known that the AIEs of the hydrogen-bonded complexes of substituted benzenes are usually lower than the corresponding monomers (substituted benzene). For example, the AIE of the phenol–water complex (7.94 eV) is lower than phenol (8.51 eV) which has been attributed to the difference in the hydrogen bond energies in the neutral and cationic ground states.36 Extending this argument to the present case, it can be inferred that the AIEs of hydrogen-bonded complexes of DFPHA with MA, DMA, TMA and TEA would be lower than the DFPHA monomer and therefore could be ionized using the 1C-R2PI process. Fig. 7 shows four distinct structures optimized for the DFPHA–MA complex in the cationic state and Table 4 lists their AIEs. The AIE depends strongly on the intermolecular structure with CAc–H⋯N hydrogen-bonded structure (D1) having the highest AIE while the Lp⋯π structure (D4) having the lowest AIE. Table 4 also lists the AIEs of CAc–H⋯N hydrogen-bonded structures of DFPHA complexes with DMA, TMA and TEA. In the case of the DFPHA–MA complex the 1C-R2PI process can access any of the structures with AIE less than 8.86 eV leading to the formation of the DFPHA–MA complex cation. It must be pointed out here that the 1C-R2PI ensures that initially excitation is localized on the DFPHA moiety in all the amine complexes. As noted earlier no fragmentation was observed for the DFPHA–MA complex following the 1C-R2PI process since the appearance energy of the MA cation would be at least 9.04 eV (AIE), which is higher than the experimentally available energy of 8.86 eV. However in the case of DFPHA complexes with DMA, TMA and TEA complexes the experimentally available energy of 8.86 eV is higher than the AIE of respective amines.
725 cm−1 = 8.86 eV), therefore the 1C-R2PI spectrum of the DFPHA monomer could not be recorded. It is well known that the AIEs of the hydrogen-bonded complexes of substituted benzenes are usually lower than the corresponding monomers (substituted benzene). For example, the AIE of the phenol–water complex (7.94 eV) is lower than phenol (8.51 eV) which has been attributed to the difference in the hydrogen bond energies in the neutral and cationic ground states.36 Extending this argument to the present case, it can be inferred that the AIEs of hydrogen-bonded complexes of DFPHA with MA, DMA, TMA and TEA would be lower than the DFPHA monomer and therefore could be ionized using the 1C-R2PI process. Fig. 7 shows four distinct structures optimized for the DFPHA–MA complex in the cationic state and Table 4 lists their AIEs. The AIE depends strongly on the intermolecular structure with CAc–H⋯N hydrogen-bonded structure (D1) having the highest AIE while the Lp⋯π structure (D4) having the lowest AIE. Table 4 also lists the AIEs of CAc–H⋯N hydrogen-bonded structures of DFPHA complexes with DMA, TMA and TEA. In the case of the DFPHA–MA complex the 1C-R2PI process can access any of the structures with AIE less than 8.86 eV leading to the formation of the DFPHA–MA complex cation. It must be pointed out here that the 1C-R2PI ensures that initially excitation is localized on the DFPHA moiety in all the amine complexes. As noted earlier no fragmentation was observed for the DFPHA–MA complex following the 1C-R2PI process since the appearance energy of the MA cation would be at least 9.04 eV (AIE), which is higher than the experimentally available energy of 8.86 eV. However in the case of DFPHA complexes with DMA, TMA and TEA complexes the experimentally available energy of 8.86 eV is higher than the AIE of respective amines.
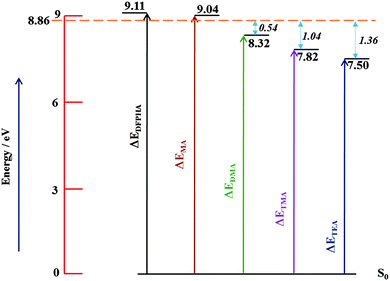 | ||
| Fig. 6 Schematic energy level diagram depicting AIEs of DFPHA, MA, DMA, TMA and TEA. The horizontal line at 8.86 eV represents experimentally available energy. | ||
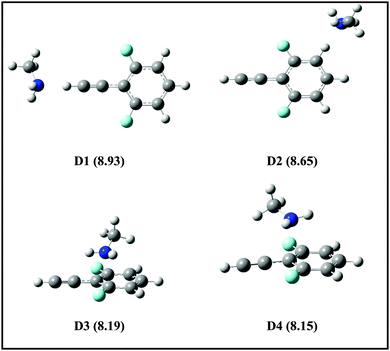 | ||
| Fig. 7 Structures of DFPHA–MA complexes in the cationic state optimized at ωB97X-D/cc-pVDZ level of theory. The calculated AIEs (in eV) are shown in parentheses. | ||
In the case of the DFPHA–DMA complex both the parent ion mass signal (183 Da) and the fragment ion mass signal were (45 Da) observed. Since the AIE of DMA is 8.33 eV, the appearance energy of the DMA cation from the DFPHA–DMA complex would be at least 8.33 eV, which is about 0.54 eV lower than available energy. On the other hand for the DFPHA complexes of TMA and TEA only the fragment ions of TMA (59 Da) and TEA (101 Da) were observed. The excess energy available over the appearance energy of TMA and TEA cations is 1.04 and 1.36 eV, respectively (see Fig. 6). For the DMA, TMA and TEA complexes the available excess energy increases and concurrently the density of states is also expected to increase both on account of energy and also the size of the molecule, which leads to extensive fragmentation in the case of TMA complexes following ICD. Therefore it can be inferred that the efficacy of the ICD process depends on the density of acceptor states.
4. Conclusions
In summary, we have investigated amine complexes of DFPHA using 1C-R2PI and IR-UV double resonance spectroscopic techniques. All the four amines form CAc–H⋯N hydrogen-bonded complexes, while TMA and TEA also form complexes which incorporate Lp⋯π interaction. One of the most interesting observations is that the shift in the CAc–H stretching frequency of the DFPHA moiety in the TEA complex is lower than the TMA complex. In the case of the DFPHA–TMA complex the Lp⋯π structure is about 1.5 kJ mol−1 higher in energy than the CAc–H⋯N hydrogen-bonded structure, while the trend is reversed in the case of the DFPHA–TEA complex. These results point out that the Lp⋯π interactions can be competitive with normal hydrogen bonds. The SAPT0 energy decomposition analysis indicates that the CAc–H⋯N hydrogen bonding is electrostatics driven, while the Lp⋯π interaction is favored by dispersion interaction. Finally, the efficiency of fragmentation following an intermolecular coulombic decay process depends on the density of the acceptor states.Author contributions
The problem was formulated by GNP. SIM and AD carried out experiments and some initial calculations in consultation with GNP. Most of the calculations were carried out by SS in consultation with DG. The results were interpreted jointly by GNP and DG along with SIM, AD and SS.Acknowledgements
SIM thanks UGC and SS thanks IITB for their research fellowship. This material is based upon the work supported by Department of Science and Technology (Grant No. SR/S1/PC/23/2008) and Board of Research in Nuclear Science (Grant No. 2012/34/14) to GNP. High performance computing facility of IIT Bombay is gratefully acknowledged. DG would like to thank CSIR-National Chemical Laboratory for Startup grant and CSIR for funding from XIIth five year plan on Multiscale modelling (CSC0129).References
- (a) P. C. Singh and G. N. Patwari, J. Phys. Chem. A, 2008, 112, 4426–4431 CrossRef CAS PubMed; (b) P. C. Singh and G. N. Patwari, J. Phys. Chem. A, 2008, 112, 5121–5125 CrossRef CAS PubMed; (c) R. Sedlak, P. Hobza and G. N. Patwari, J. Phys. Chem. A, 2009, 113, 6620–6625 CrossRef CAS PubMed.
- S. Maity, M. Guin, P. C. Singh and G. N. Patwari, ChemPhysChem, 2011, 12, 26–46 CrossRef CAS PubMed.
- A. Dey, S. I. Mondal and G. N. Patwari, ChemPhysChem, 2013, 14, 746–753 CrossRef CAS PubMed.
- S. Maity, A. Dey, G. N. Patwari, S. Karthikeyan and K. S. Kim, J. Phys. Chem. A, 2010, 114, 11347–11352 CrossRef CAS PubMed.
- S. Maity, G. N. Patwari, S. Karthikeyan and K. S. Kim, Phys. Chem. Chem. Phys., 2010, 12, 6150–6156 RSC.
- (a) Q. Gou, G. Feng, L. Evangelisti and W. Caminati, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef PubMed; (b) M. Egli and S. Sarkhel, Acc. Chem. Res., 2007, 40, 197–205 CrossRef CAS PubMed; (c) G. J. Bartlett, R. W. Newberry, B. VanVeller, R. T. Raines and D. N. Woolfson, J. Am. Chem. Soc., 2013, 135, 18682–18688 CrossRef CAS PubMed.
- (a) J. P. Gallivan and D. A. Dougherty, Org. Lett., 1999, 1, 103–105 CrossRef CAS; (b) Y. Danten, T. Tassaing and M. Besnard, J. Phys. Chem. A, 1999, 103, 3530–3534 CrossRef CAS; (c) N. Mohan, C. H. Suresh, A. Kumar and S. R. Gadre, Phys. Chem. Chem. Phys., 2013, 15, 18401–18409 RSC; (d) S. K. Singh, S. Kumar and A. Das, Phys. Chem. Chem. Phys., 2014, 16, 8819–8827 RSC.
- (a) L. S. Cederbaum, J. Zobeley and F. Tarantelli, Phys. Rev. Lett., 1997, 79, 4778–4781 CrossRef CAS; (b) J. Zobeley, L. S. Cederbaum and F. Tarantelli, J. Chem. Phys., 1998, 108, 9737–9751 CrossRef CAS PubMed.
- (a) B. Boudaiffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660 CrossRef CAS; (b) P. H. P. Harbach, M. Schneider, S. Faraji and A. Dreuw, J. Phys. Chem. Lett., 2013, 4, 943–949 CrossRef CAS.
- S. J. Baek, K.-W. Choi, Y. S. Choi and S. K. Kim, J. Chem. Phys., 2003, 118, 11040–11047 CrossRef CAS PubMed.
- A. Bodi, B. Sztaray and T. Baer, Phys. Chem. Chem. Phys., 2006, 8, 613–623 RSC.
- J. E. Mathis and R. N. Compton, J. Chem. Phys., 1996, 104, 8341–8347 CrossRef CAS PubMed.
- P. C. Singh and G. N. Patwari, Curr. Sci., 2008, 95, 469 CAS.
- (a) R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 5362–5376 CrossRef CAS PubMed; (b) S. Tanabe, T. Ebata, M. Fujii and N. Mikami, Chem. Phys. Lett., 1993, 215, 347–352 CrossRef CAS; (c) A. Fujii, G. N. Patwari, T. Ebata and N. Mikami, Int. J. Mass Spectrom., 2002, 220, 289–312 CrossRef CAS.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS.
- P. Jurecka and P. Hobza, Chem. Phys. Lett., 2002, 365, 89–94 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- S. K. Min, E. C. Lee, H. M. Lee, D. Y. Kim, S. Kim and K. S. Kim, J. Comput. Chem., 2008, 29, 1208–1221 CrossRef CAS PubMed.
- S. Scheiner, Comput. Theor. Chem., 2012, 998, 9–13 CrossRef CAS PubMed.
- R. F. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- (a) J. F. Stanton and J. Gauss, J. Chem. Phys., 1994, 101, 8938–8944 CrossRef CAS PubMed; (b) P. A. Pieniazek, S. A. Arnstein, S. E. Bradforth, A. I. Krylov and C. D. Sherrill, J. Chem. Phys., 2007, 127, 164110 CrossRef PubMed; (c) A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- (a) T. Das and D. Ghosh, J. Phys. Chem. A, 2014, 118, 5323–5332 CrossRef CAS PubMed; (b) D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280 CrossRef CAS PubMed.
- F. Weigend and M. Haser, Theor. Chem. Acc., 1997, 97, 331–340 CrossRef CAS.
- A. Landau, K. Khistyaev, S. Dolgikh and A. I. Krylov, J. Chem. Phys., 2010, 132, 014109 CrossRef PubMed.
- M. J. Frisch, et al., Gaussian-09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- (a) Y. Shao, et al. , Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC; (b) A. I. Krylov and P. M. W. Gill, WIREs Comput. Mol. Sci., 2013, 3, 317–326 CrossRef CAS; (c) Y. Shao, et al. , Mol. Phys., 2014, 9, 1–32 CrossRef.
- T. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- http://www.chemcraftprog.com .
- (a) G. W. King and S. P. So, J. Mol. Spectrosc., 1971, 37, 543–570 CrossRef CAS; (b) J. A. Stearns and T. S. Zwier, J. Phys. Chem. A, 2003, 107, 10717 CrossRef CAS.
- (a) A. Iwasaki, A. Fujii, T. Ebata and N. Mikami, J. Phys. Chem., 1996, 100, 16053–16057 CrossRef CAS; (b) A. Fujii, T. Ebata and N. Mikami, J. Phys. Chem. A, 2002, 106, 8554–8560 CrossRef CAS.
- (a) S. J. Grabowski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. A, 2005, 109, 4331–4341 CrossRef CAS PubMed; (b) K. Berka, R. Laskowski, K. E. Riley, P. Hobza and J. Vondrasek, J. Chem. Theory Comput., 2009, 5, 982–992 CrossRef CAS; (c) A. Bhattacherjee, Y. Matsuda, A. Fujii and S. Wategaonkar, ChemPhysChem, 2013, 14, 905–914 CrossRef CAS PubMed.
- V. S. Shivatare, A. Kundu, G. N. Patwari and W.-B. Tzeng, J. Phys. Chem. A, 2014, 118, 8277–8286 CrossRef CAS PubMed.
- O. Dopfer, G. Reiser, K. Muller-Dethlefs, E. W. Schlag and S. D. Colson, J. Chem. Phys., 1994, 101, 974–989 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp03445g |
| This journal is © the Owner Societies 2015 |